Quantum Computation and Measurements from an Exotic Space-Time R4
Abstract
1. Introduction
2. Excerpts on the Theory of 4-Manifolds and Exotic s
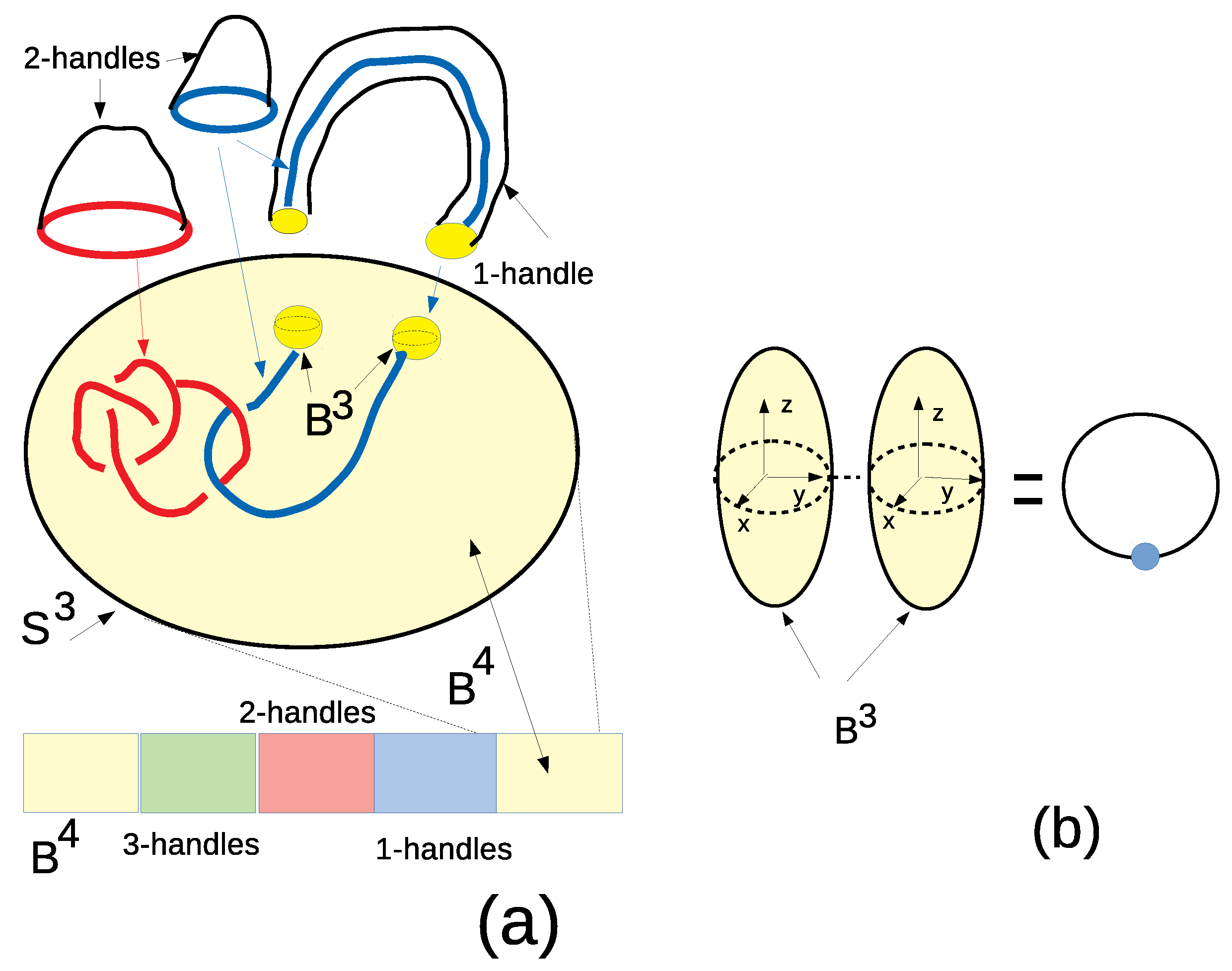
2.1. Handlebody of a 4-Manifold
2.2. Akbulut Cork
2.3. Exotic Manifold
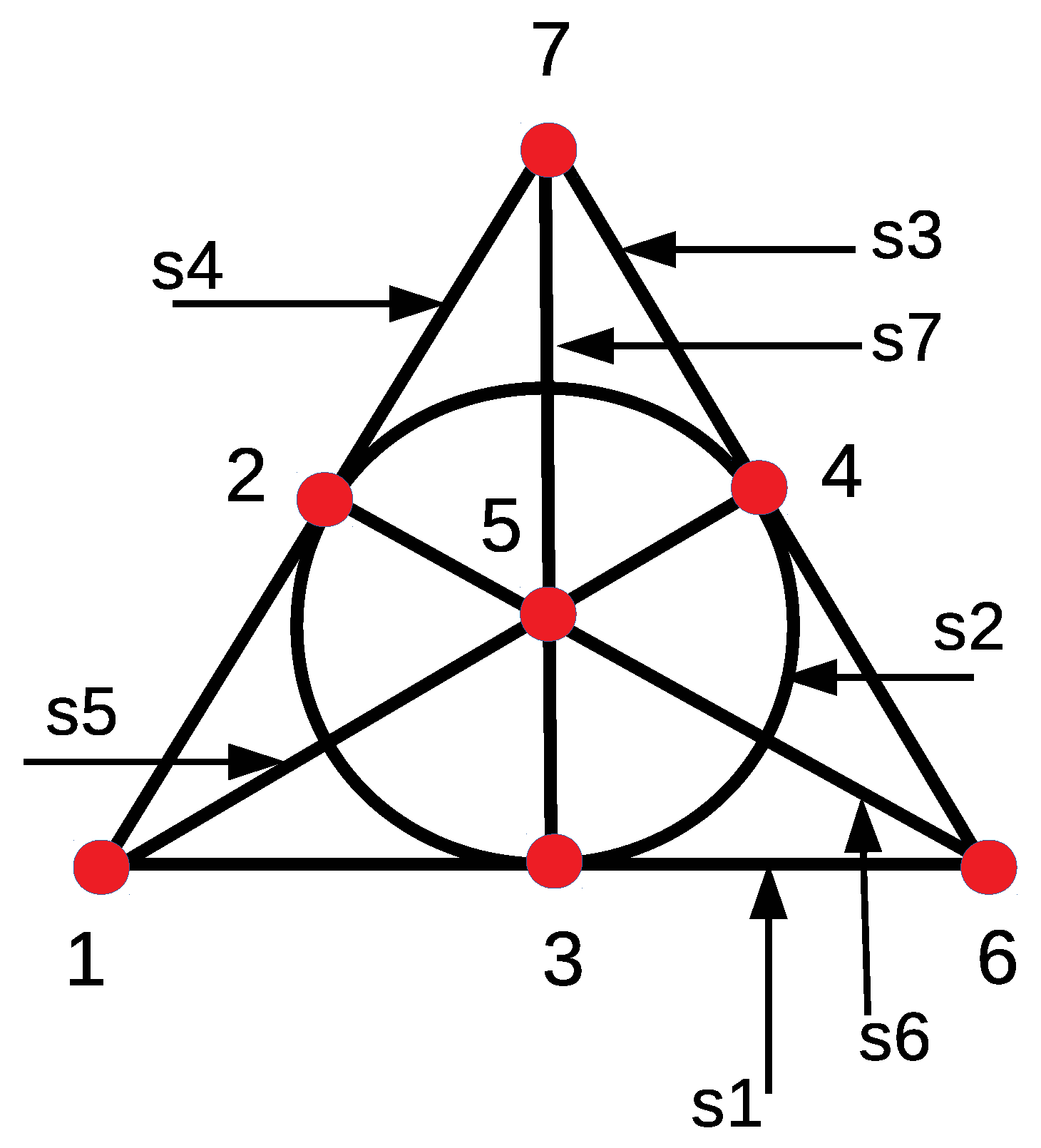
3. Finite Geometry of Small Exotic R4s and Quantum Computing
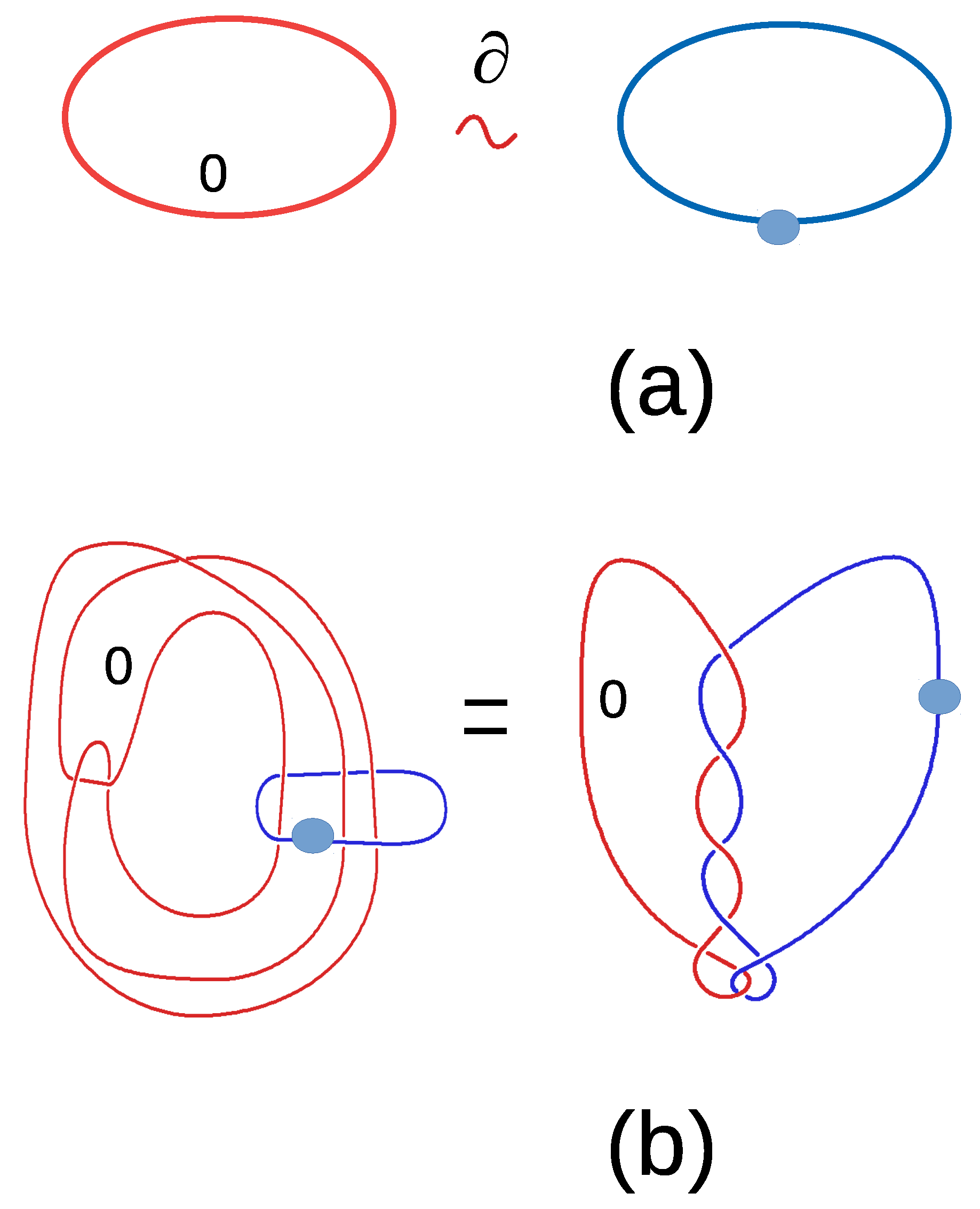
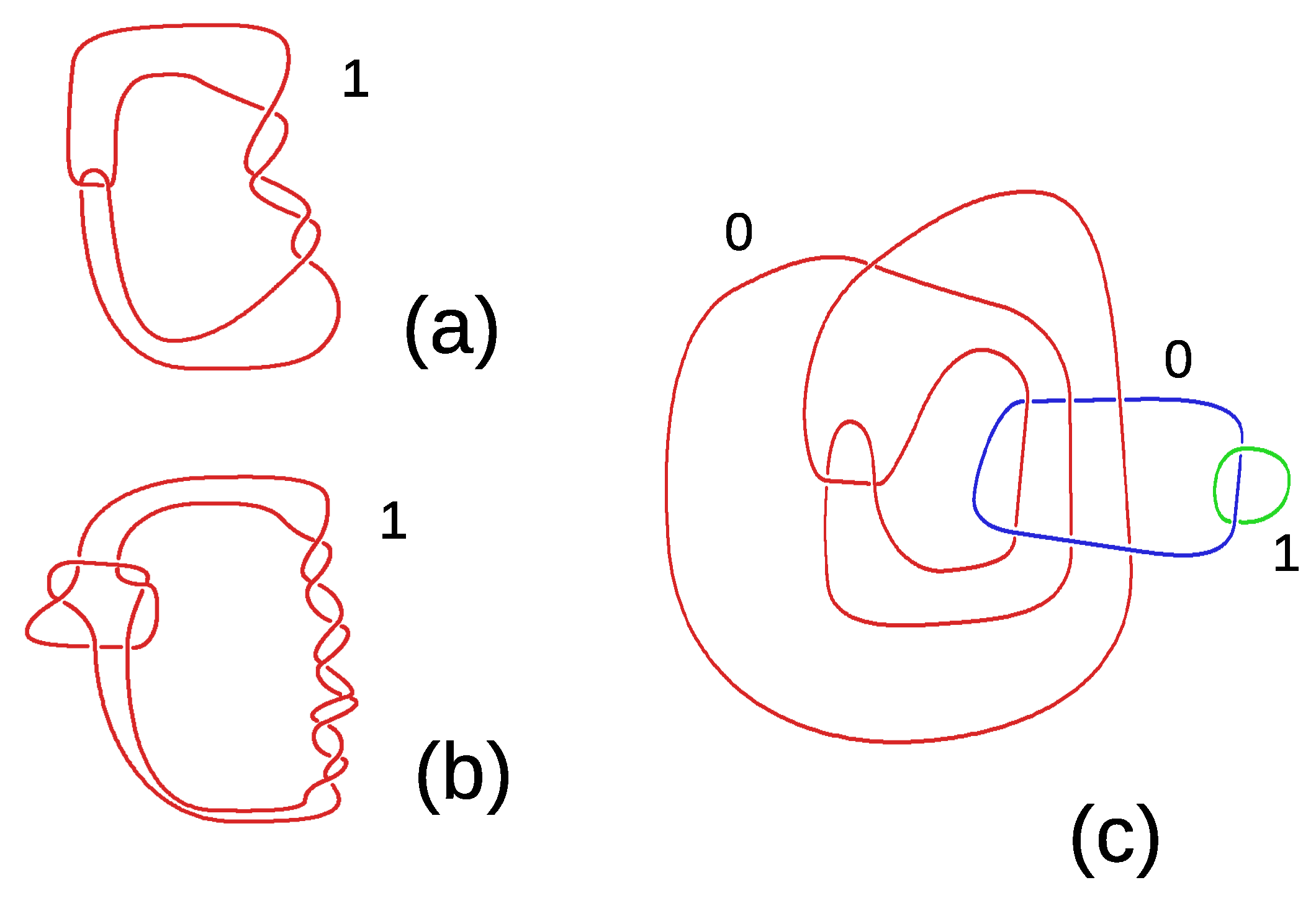
3.1. The Boundary of Akbulut Cork
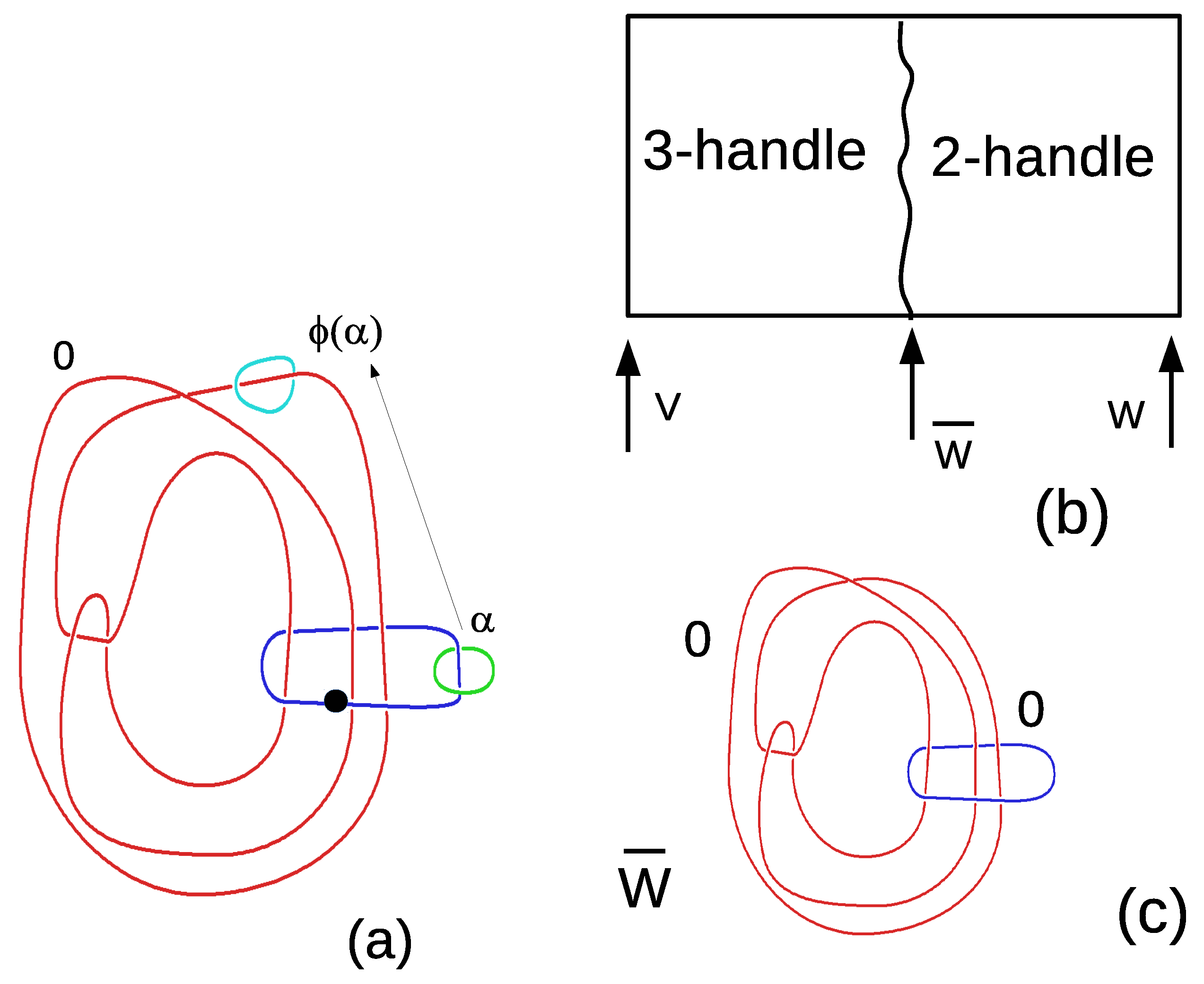
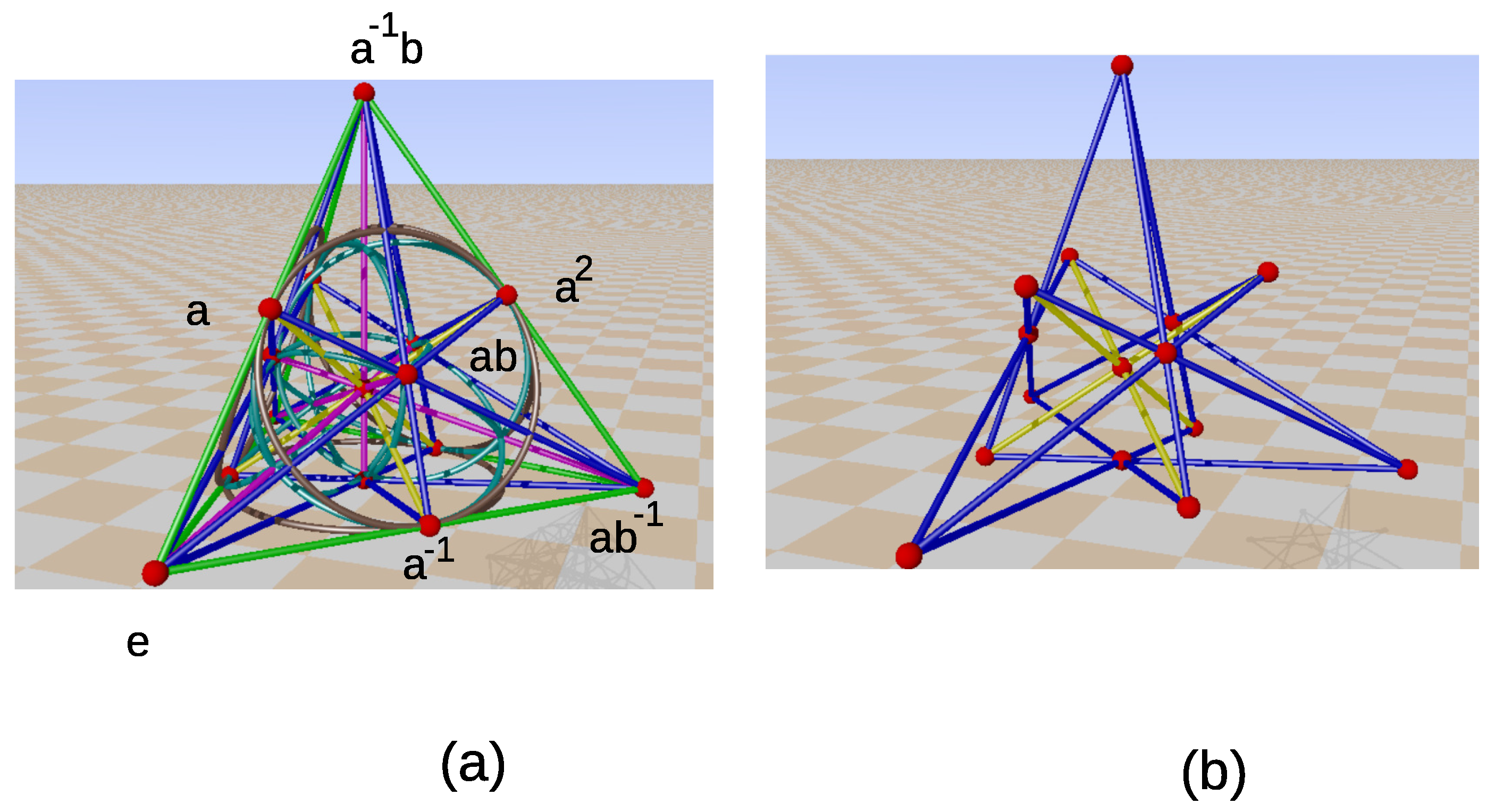
3.2. The Manifold Mediating the Akbulut Cobordism between Exotic Manifolds V and W
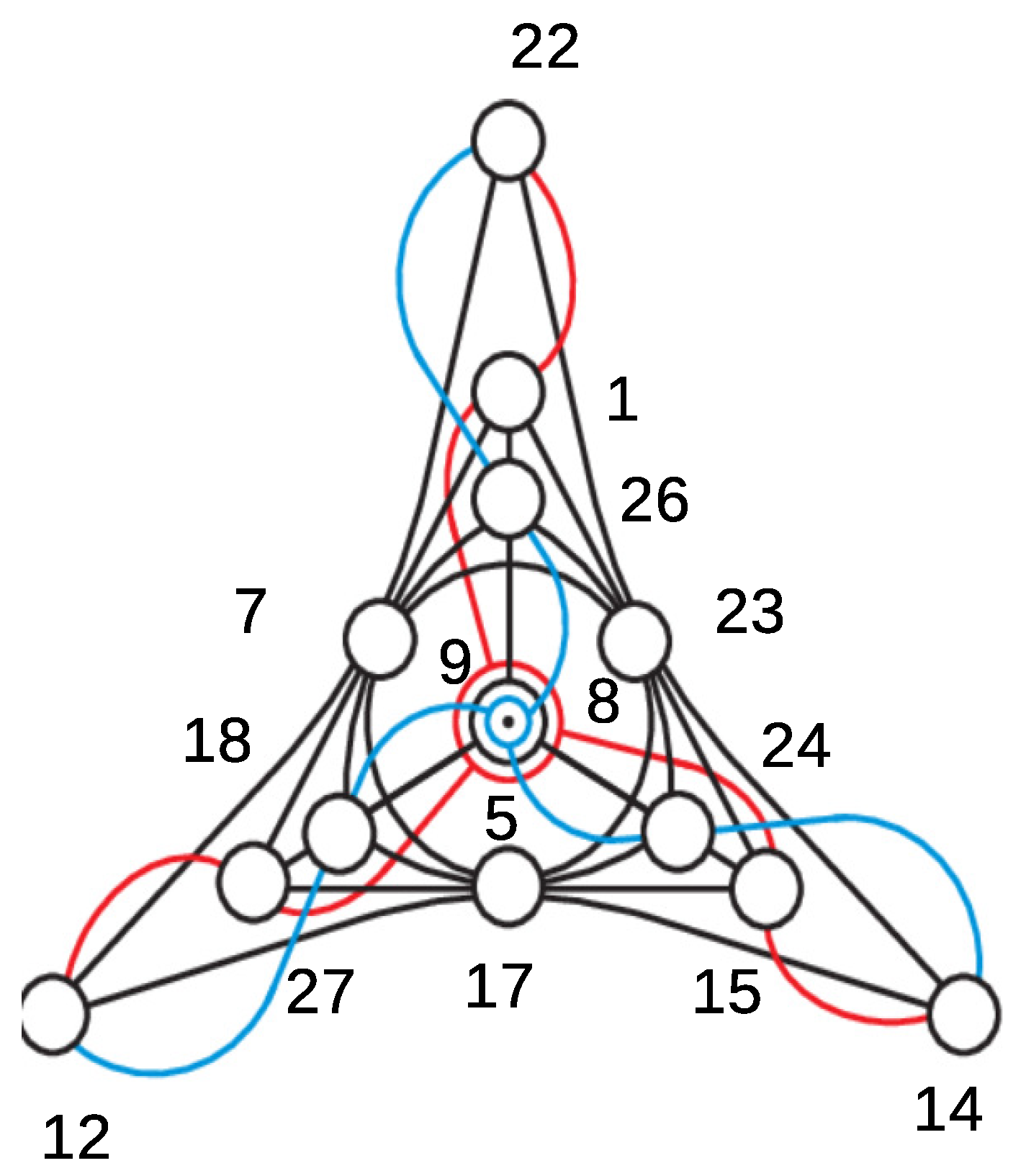
3.3. The Middle Level Q between the Diffeomorphic Connected Sums
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
References
- Planat, M.; Gedik, Z. Magic informationally complete POVMs with permutations. R. Soc. Open Sci. 2017, 4, 170387. [Google Scholar] [CrossRef] [PubMed]
- Planat, M.; Aschheim, R.M.; Amaral, M.; Irwin, K. Universal quantum computing and three-manifolds, Universal quantum computing and three-manifolds. Symmetry 2018, 10, 773. [Google Scholar] [CrossRef]
- Planat, M.; Aschheim, R.; Amaral, M.M.; Irwin, K. Quantum computing, Seifert surfaces and singular fibers. Quantum Rep. 2019, 1, 12–22. [Google Scholar] [CrossRef]
- Planat, M.; Aschheim, R.; Amaral, M.M.; Irwin, K. Group geometrical axioms for magic states of quantum computing. Mathematics 2019, 7, 948. [Google Scholar] [CrossRef]
- Akbulut, S. 4-Manifolds, Oxford Graduate Texts in Mathematics; Oxford University Press: Oxford, UK, 2016; Volume 25. [Google Scholar]
- Gompf, R.E.; Stipsicz, A.I. 4-Manifolds and Kirby Calculus; Graduate Studies in Mathematics; American Mathematical Society: Providence, RI, USA, 1999; Volume 20. [Google Scholar]
- Scorpian, A. The Wild World of 4-Manifolds; American Mathematical Society: Providence, RI, USA, 2011. [Google Scholar]
- Akbulut, S. A fake compact contractible 4-manifold. J. Diff. Geom. 1991, 33, 335–356. [Google Scholar] [CrossRef]
- DeWitt, B.S. Quantum mechanics and reality. Phys. Today 1970, 23, 30. [Google Scholar] [CrossRef]
- Bravyi, S.; Kitaev, A. Universal quantum computation with ideal Clifford gates and noisy ancillas. Phys. Rev. 2005, A71, 22316. [Google Scholar] [CrossRef]
- Planat, M. Geometry of contextuality from Grothendieck’s coset space. Quantum Inf. Process. 2015, 14, 2563–2575. [Google Scholar] [CrossRef]
- Bosma, W.; Cannon, J.J.; Fieker, C.; Steel, A. (Eds.) Handbook of Magma Functions, 2.23 ed.; University of Sidney: Sydney, Australia, 2017; 5914p. [Google Scholar]
- Culler, M.; Dunfield, N.M.; Goerner, M.; Weeks, J.R. SnapPy, a Computer Program for Studying the Geometry and Topology of 3-Manifolds. Available online: http://snappy.computop.org (accessed on 1 January 2019).
- Akbulut, S. An exotic 4-manifold. J. Diff. Geom. 1991, 33, 357–361. [Google Scholar] [CrossRef]
- Akbulut, S.; Durusoy, S. An involution acting nontrivially on Heegard-Floer homology. In Geometry and Topology of Manifolds; Fields Inst. Commun. Amer. Math. Soc.: Providence, RI, USA, 2005; Volume 47, pp. 1–9. [Google Scholar]
- Gompf, R.E. An exotic menagerie. J. Differ. Geom. 1993, 37, 199–223. [Google Scholar] [CrossRef]
- Marceaux, J.P.; Rau, A.R. Mapping qubit algebras to combinatorial designs. Quantum Inf. Proc. 2020, 19, 49. [Google Scholar] [CrossRef]
- Marcelis, F. Available online: https://fgmarcelis.wordpress.com (accessed on 1 January 2019).
- Saniga, M. The complement of binary Klein quadric as a combinatoriam Grassmannian. Mathematics 2015, 3, 481–486. [Google Scholar] [CrossRef]
- Saniga, M.; Holweck, F.; Pracna, P. Pracna, From Cayley-Dickson algebras to combinatorial Grassmannians. Mathematics 2015, 3, 1192–1221. [Google Scholar] [CrossRef]
- Baez, J.C. The Octonions. Bull. Am. Math. Soc. 2002, 39, 145–205. [Google Scholar] [CrossRef]
- Koeplinger, J. Nonassociative quantum theory on octooctonionalgebra. J. Phys. Math. 2009, 1, S090501. [Google Scholar]
- Aschheim, R.; Irwin, K. Constructing numbers in quantum gravity: Infinions. J. Phys. Conf. Ser. 2019, 1194, 012008. [Google Scholar] [CrossRef]
- Etesi, G. The von Neumann algebra of smooth four-manifolds and a quantum theory of space-time and gravity. arXiv 2018, arXiv:1712.01828. [Google Scholar]
- Asselmeyer-Maluga, T.; Król, J.; Bielas, K.; Klimasara, P. From quantum to cosmological regime. The role of forcing and exotic 4-Smoothness. Universe 2017, 3, 31. [Google Scholar]
- Tozzi, A.; Ahmad, M.Z.; Peters, J.F. Quantum computing in four spatial dimensions. Available online: https://www.preprints.org/manuscript/201905.0021/v1 (accessed on 1 March 2020).
- Antoniou, S.; Kauffman, L.H.; Lambropoulou, S. Topological surgery in cosmic phenomena. arXiv 2018, arXiv:1812.00837. [Google Scholar] [CrossRef]
- Luminet, J.P.; Weeks, J.; Riazuelo, A.; Lehoucq, R.; Uzan, J.-P. Uzan, Dodecahedral space topology as an explanation for weak wide-angle temperature correlations in the cosmic microwave background. Nature 2003, 425, 593–595. [Google Scholar] [CrossRef]
- Asselmeyer-Maluga, T.; Krol, J. How to obtain a cosmological constant from small exotic R4. Phys. Dark Univers. 2018, 19, 66–77. [Google Scholar] [CrossRef]
- Asselmeyer-Maluga, T. Braids, 3-manifolds, elementary particles, number theory and symmetry in particle physics. Symmetry 2019, 10, 1297. [Google Scholar] [CrossRef]
- Fuchs, C.A. On the quantumness of a Hilbert space. Quantum Inf. Comp. 2004, 4, 467–478. [Google Scholar]
Sample Availability: The codes were written on softwares Snappy and Magma. Part of the calculation is detailed in Section 3.1 and Appendix B. |

| d | P | Geometry | MIC Fiducial | pp |
|---|---|---|---|---|
| 5 | 1 | |||
| 6 | 2 | |||
| 7 | ||||
| 10 | Mermin pentagram | no | ||
| 12 | ||||
| K(2,2,2,2,2,2) | no | |||
| 13 | ||||
| 14 | , | |||
| K(2,2,2,2,2,2,2) | ||||
| 15 | ||||
| K(3,3,3,3,3) | yes | 3 | ||
| PG(3,2) | ||||
| 16 |
| d | P | Geometry | MIC Fiducial | pp |
|---|---|---|---|---|
| 6 | 2 | |||
| 7 | Fano plane | 2 | ||
| 8 | no | |||
| 10 | yes | 5 | ||
| 14 | K(2,2,2,2,2,2,2) | no | ||
| 15 | PG(3,2), GQ(2,2) | yes | 4 | |
| 16 | no | |||
| K(2,2,2,2,2,2,2,2) | no |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Planat, M.; Aschheim, R.; Amaral, M.M.; Irwin, K. Quantum Computation and Measurements from an Exotic Space-Time R4. Symmetry 2020, 12, 736. https://doi.org/10.3390/sym12050736
Planat M, Aschheim R, Amaral MM, Irwin K. Quantum Computation and Measurements from an Exotic Space-Time R4. Symmetry. 2020; 12(5):736. https://doi.org/10.3390/sym12050736
Chicago/Turabian StylePlanat, Michel, Raymond Aschheim, Marcelo M. Amaral, and Klee Irwin. 2020. "Quantum Computation and Measurements from an Exotic Space-Time R4" Symmetry 12, no. 5: 736. https://doi.org/10.3390/sym12050736
APA StylePlanat, M., Aschheim, R., Amaral, M. M., & Irwin, K. (2020). Quantum Computation and Measurements from an Exotic Space-Time R4. Symmetry, 12(5), 736. https://doi.org/10.3390/sym12050736






