A Filter and Nonmonotone Adaptive Trust Region Line Search Method for Unconstrained Optimization

Abstract

In this paper, a new nonmonotone adaptive trust region algorithm is proposed for unconstrained optimization by combining a multidimensional filter and the Goldstein-type line search technique. A modified trust region ratio is presented which results in more reasonable consistency between the accurate model and the approximate model. When a trial step is rejected, we use a multidimensional filter to increase the likelihood that the trial step is accepted. If the trial step is still not successful with the filter, a nonmonotone Goldstein-type line search is used in the direction of the rejected trial step. The approximation of the Hessian matrix is updated by the modified Quasi-Newton formula (CBFGS). Under appropriate conditions, the proposed algorithm is globally convergent and superlinearly convergent. The new algorithm shows better performance in terms of the Dolan–Moré performance profile. Numerical results demonstrate the efficiency and robustness of the proposed algorithm for solving unconstrained optimization problems.

1. Introduction

Consider the following unconstrained optimization problem:

$$\underset{x\in R^n}{\min }f(x),$$

(1)

where $f$: $R^n\to R$ is a twice continuously differentiable function. The problem has widely used in many applications based on medical science, optimal control, and functional approximation, etc. As we all know, there are many methods for solving unconstrained optimization problems, such as the conjugate gradient method [1,2,3], the Newton method [4,5], and the trust region method [6,7,8]. Constrained optimization problems can also be solved by processing constraint conditions and transforming them into unconstrained optimization problems. Motivated by this, it is quite necessary to propose a new modified trust region method for solving unconstrained optimization problems.

As is commonly known, the trust region method and the line search method are two frequently used iterative methods. Line search methods involve the process of calculating the step length ${\alpha }_k$ in the specific direction $d_k$ and driving a new point as $x_{k+1}=x_k+{\alpha }_k{d}_k$. The primary idea of the trust region method is as follows: at current iteration point $x_k$, the trial step $d_k$ is obtained by solving the following subproblem:

$$\underset{d\in R^n}{\min }{m}_k(d)=g_k^{T}d+\frac{1}{2}{d}^T{B}_{k}d,$$

(2)

$$\Vert d\Vert \le {\Delta }_k,$$

(3)

where $\Vert .\Vert$ is the Euclidean norm, $f_k=f(x_k)$, $g_k=\nabla f(x_k)$, $B_k$ is a symmetric approximation matrix of $G_k={\nabla }^{2}f(x_k)$, and ${\Delta }_k$ is a trust region radius.

Traditional trust region methods have some disadvantages, such as the fact that the subproblem needs to be solved many times to obtain an acceptable trial step within one iteration, which leads to high computational costs for the iterative process. One way to overcome this disadvantage is to use a line search strategy in the direction of the rejected trial step. Based on this situation, Nocedal and Yuan [9] proposed an algorithm in 1998, combining the trust region method and the line search method for the first time. Inspired by this, Michael et al., Li et al., and Zhang et al. proposed a trust region method with the line search strategy ([10,11,12], respectively).

As can be seen in other works [4,7,8] monotone techniques are distinguished from nonmonotone techniques in that the value of the function needs to be reduced at each iteration; at the same time, the use of nonmonotone techniques can not only guarantee finding the global optimal solution effectively, but also improve the convergence rate of the algorithm. The watchdog technique was presented by Chamberlain et al. [13] in 1982 to overcome the Maratos effect of constrained optimization problems. Motivated by this idea, a nonmonotone line search technique was proposed by Grippo et al. [14] in 1986. The step length ${\alpha }_k$ satisfies the following inequality:

$$f(x_k+{\alpha }_k{d}_k)\le f_{l(k)}+\sigma {\alpha }_k{g}_k^T{d}_k,$$

(4)

where $\sigma \in (0,1)$,$f_{l(k)}=\underset{0\le j\le m(k)}{\max }\left\{f_{k-j}\right\}$, $m(0)=0$, $0\le m(k)\le \min \{m(k-1)+1,N\}$, and $N\ge 0$ is an integer constant.

However, the common nonmonotone term $f_{l(k)}$ suffers from various drawbacks. For example, the valid value of the produced function $f$ in any iteration is essentially discarded, and the numerical results highly depend on the choice of $N$. To overcome these drawbacks, Cui et al. [15] proposed another nonmonotone line search method as follows:

$$f(x_k+{\alpha }_k{d}_k)\le C_k+\sigma {\alpha }_k{g}_k^T{d}_k,$$

(5)

where the nonmonotone term $C_k$ is defined by

$$C_k=\{\begin{array}{ll}f(x_k),& k=0\\ \frac{{\eta }_{k-1}{Q}_{k-1}{C}_{k-1}+f(x_k)}{Q_k},& k\ge 1\end{array},$$

(6)

and

$$Q_k=\{\begin{array}{ll}1,& k=0\\ {\eta }_{k-1}{Q}_{k-1}+1,& k\ge 1\end{array},$$

(7)

where $\sigma \in (0,1)$, ${\eta }_k\in [{\eta }_{\min },{\eta }_{\max }]$, ${\eta }_{\min }\in [0,1]$, and ${\eta }_{\max }\in [{\eta }_{\min },1]$.

Based on this idea, in order to include the minimum value of ${\alpha }_k$ in an acceptable interval and keep the consistency of the nonmonotone term, we proposed a trust region method with the Goldstein-type line search technique. The step length ${\alpha }_k$ satisfies the following inequalities:

$$f(x_k+{\alpha }_k{d}_k)\le R_k+c_1{\alpha }_k{g}_k^T{d}_k,$$

(8)

$$f(x_k+{\alpha }_k{d}_k)\ge R_k+c_2{\alpha }_k{g}_k^T{d}_k,$$

(9)

where

$$R_k={\eta }_k{f}_{l(k)}+(1-{\eta }_k)f_k,$$

(10)

$c_1\in (0,\frac{1}{2})$, $c_2\in (c_1,1)$, ${\eta }_k\in [{\eta }_{\min },{\eta }_{\max }]$, ${\eta }_{\min }\in [0,1]$, and ${\eta }_{\max }\in [{\eta }_{\min },1]$.

To evaluate the consistency between the quadratic model and the objective function, the ratio is defined by Ahookhosh et al. [16] as follows:

$${\widehat{\rho }}_k=\frac{R_k-f(x_k+d_k)}{m_k(0)-m_k(d_k)},$$

(11)

It is well-known that the adaptive radius plays a valuable role in performance. In 1997, an adaptive strategy for automatically determining the initial trust region radius was proposed by Sartenear [17]. However, it can be seen that the gradient or Hessian information is not explicitly used to update the radius. Motivated by the first-order information and second-order information of the objective function, Zhang et al. [18] proposed a new scheme to determine trust region radius in 2002 as follows: ${\Delta }_k=c^p\Vert g_k\Vert \Vert {\widehat{B}}_k^{-1}\Vert$, where ${\widehat{B}}_k=B_k+iI$,$i\in N$. In order to avoid computing the inverse of the matrix and the Euclidean norm of ${\widehat{B}}_k^{-1}$ at each iteration point $x_k$, Zhou et al. [19] proposed an adaptive trust region radius as follows: ${\Delta }_k=c^p\frac{\Vert d_{k-1}\Vert }{\Vert y_{k-1}\Vert }\Vert g_k\Vert$, where $y_{k-1}=g_k-g_{k-1}$, and $c$ and $p$ are parameters. Prompted by the adaptive technique, Wang et al. [8] proposed a new adaptive trust region radius as follows: ${\Delta }_k=c_k{\Vert g_k\Vert }^{\gamma }$, which reduces the related workload and calculation time. Based on this fact, other authors also proposed modified adaptive trust region methods [20,21,22].

In order to overcome the difficulty of selecting penalty factors when using penalty functions, Fletcher et al. first recommended the filter techniques for constrained nonlinear optimization (see [23] for details). More recently, Gould et al. [24] explored a new nonmonotone trust region method with multidimensional filter techniques for solving unconstrained optimization problems. This idea incorporates the concept of nonmonotone to build a filter that can reject poor iteration points, and enforce convergence from random starting points. At the same time, the prototype of the multidimensional filter techniques relax the requirements of monotonicity in the classic trust region framework. This idea has been popularized by some authors [25,26,27].

In the following, we refer to $\nabla f(x_k)$ by $g_k=(g_k^1,g_k^2,\dots ,g_k^n)$; when the $i-\mathrm{th}$ component of $g_k=g(x_k)$ is needed, it is denoted with $g_k^i$, where $i\in \left\{1,2,3,\dots ,n\right\}$. We say that an iteration point $x_1$ dominates $x_2$ whenever

$$\left|g_1^i\right|\le \left|g_2^i\right|-{\gamma }_g\Vert g_2\Vert ,$$

(12)

where ${\gamma }_g\in (0,\frac{1}{\sqrt{n}})$ is a small positive constant.

Based on [8], we know that a multidimensional filter $\mathcal{F}$ is a list of $n$-tuples of the form $(g_k^1,g_k^2,\dots ,g_k^n)$, such that

$$\left|g_k^j\right|\le \left|g_l^j\right|j\in \left\{1,2,3,\dots ,n\right\},$$

(13)

where $g_k$ and $g_l$ belong to $\mathcal{F}$.

For all $g_l\in \mathcal{F}$, a new trial point $x_k$ is acceptable if there exists $j\in \left\{1,2,3,\dots ,n\right\}$, such that

$${\left|g_k^j\right|}^{{\gamma }_2}+{\lambda }_2{\Vert g_k^j\Vert }^{{\gamma }_1}\le {\left|g_l^j\right|}^{{\gamma }_2}+{\lambda }_1{\Vert g_l\Vert }^{{\gamma }_1},$$

(14)

where ${\gamma }_1$ and ${\gamma }_2$ are positive constants, and ${\lambda }_1$ and ${\lambda }_2$ satisfy the inequality $0\le {\lambda }_1<{\lambda }_2<\frac{1}{\sqrt{n}}$.

When an iteration point $x_k$ is accepted by the filter, we add $g\left(x_k\right)$ to the filter, and $g\left(x_l\right)\in \mathcal{F}$ with the following property

$${\left|g_k^j\right|}^{{\gamma }_2}+{\lambda }_2{\Vert g_k^j\Vert }^{{\gamma }_1}\le {\left|g_l^j\right|}^{{\gamma }_2}+{\lambda }_1{\Vert g_l\Vert }^{{\gamma }_1}$$

(15)

is removed from the filter.

The rest of this article is organized as follows. In Section 2, we describe a new nonmonotone adaptive trust region algorithm. We establish the global convergence and superlinear convergence of the algorithm in Section 3. In Section 4, numerical results are given, which show that the new method is effective. Finally, some concluding comments are provided in Section 5.

2. The new algorithm

In this section, a new filter and nonmonotone adaptive trust region Goldstein-type line search method is proposed. The trust region ratio is used to determine whether the trial step $d_k$ is accepted. Following the trust region ratio of Ahookhosh et al. in [16], we define a modified form as follows:

$${\widehat{\rho }}_k=\frac{R_k-f(x_k+d_k)}{f_{l(}{}_{k)}-f_k-m_k(d_k)},$$

(16)

We can see that the effect of nonmonotonicity can be controlled the numerator and denominator, respectively. Thus, the new trust region ratio may find the global optimal solution effectively. Compared with the general filter trust region algorithm in [24], we propose a new criteria, that is, whether the trial point $x_k^{+}$ satisfies $0<{\widehat{\rho }}_k<{\mu }_1$, and verify whether it is accepted by the filter $\mathcal{F}$.

At the same time, a new adaptive trust region radius is presented as follows:

$${\Delta }_k=c^p{\Vert g_k\Vert }^{\gamma },$$

(17)

where $0<\gamma <1$, $0<c<1$, and $p$ is a nonnegative integer. Compared with the adaptive trust region method in [8], the new method has the following effective properties: the parameter $p$ plays a vital role in adjusting the radius, and it can also reduce the workload and computational time. However, the new trust region radius only uses gradient function information, not function information.

On the other hand, in each iteration, $d_k$ is the trial step to be calculated by

$$\underset{d\in R^n}{\min }{m}_k(d)=g_k^{T}d+\frac{1}{2}{d}^T{B}_{k}d,$$

(18)

$$\Vert d\Vert \le {\Delta }_k:=c^p{\Vert g_k\Vert }^{\gamma },$$

(19)

More formally, a filter and nonmonotone adaptive trust region line search method, which we call the FNATR, is described as follows.

Algorithm 1. A new filter and nonmonotone adaptive trust region line search method.

Step 0. (Initialization) Start with $x_0\in R^n$ and the symmetric matrix $B_0\in R^n\times R^n$. The constants $\epsilon >0$, $N>0$, $0<{\mu }_1<1$, $p=0$, $0<{\beta }_1<1<{\beta }_2$, $0<c_1<\frac{1}{2}<c_2<1$ and ${\Delta }_0=\left|\right|g_0\left|\right|$ are also given. Set $\mathcal{F}=\varnothing$, $k=0$.

Step 1. If $\left|\right|g_k\left|\right|\le \epsilon$, then stop.

Step 2. Solve the subproblems of Equations (18) and (19) to find the trial step $d_k$, set $x_k^{+}=x_k+d_k$.

Step 3. Compute $R_k$ and ${\widehat{\rho }}_k$, respectively.

Step 4. Test the trial step.

If ${\widehat{\rho }}_k\ge {\mu }_1$, then set $x_{k+1}=x_k^{+}$, ${\mathcal{F}}_{k+1}={\mathcal{F}}_k$, and go to Step 5.

Otherwise, compute $g_k^{+}=\nabla f\left(x_k^{+}\right)$.

if $x_k^{+}$ is accepted by the filter $\mathcal{F}$, then $x_{k+1}=x_k^{+}$; add $g_k^{+}=\nabla f\left(x_k^{+}\right)$ into the filter $\mathcal{F}$, and go to Step 5.

Otherwise, find the step length ${\alpha }_k$, satisfying Equations (8) and (9), and set $x_{k+1}=x_k+{\alpha }_k{d}_k$. Then, set

$p=p+1$, and go to Step 5.

Step 5. Update the symmetric matrix $B_k$ by using a modified Quasi-Newton formula. Set $k=k+1$, $p=0$, and go to Step 1.

In particular, we consider the following assumptions to analyze the convergence properties of Algorithm 1.

Assumption 1. 

The level set$L(x_0)=\{x\in R^n|f(x)\le f(x_0)\}$satisfies$L(x_0)\subseteq \mathsf{\Omega }$;$f(x)$is continuously differentiable and has a lower bound.

Assumption 2. 

The matrix$B_k$is uniformly bounded, i.e., there exists a constant$M_1>0$such that$\Vert B_k\Vert \le M_1$.

Remark 1.

There is a constant$\tau \in (0,1)$;$B_k$is a positive definite symmetric matrix, and$d_k$satisfies the following inequalities:

$$m_k(0)-m_k(d_k)\ge \tau \Vert g_k\Vert \min \left\{{\Delta }_k,\frac{\Vert g_k\Vert }{\Vert B_k\Vert }\right\},$$

(20)

$$g_k^T{d}_k\le -\tau \Vert g_k\Vert \min \left\{{\Delta }_k,\frac{\Vert g_k\Vert }{\Vert B_k\Vert }\right\}.$$

(21)

Remark 2.

If$f$is continuously differentiable and$\nabla f(x)$is Lipschitz continuous, there is a positive constant$L$so that

$$\Vert \nabla f(x)-\nabla f(y)\Vert \le L\Vert x-y\Vert \forall x,y\in \mathsf{\Omega }.$$

(22)

3. Convergence Analysis

In order to easily derive convergence results, we define the following indexes: $D=\left\{k|{\widehat{\rho }}_k\ge {\mu }_1\right\}$, $A=\left\{k|0<{\widehat{\rho }}_k<{\mu }_1\mathrm{and}{x}_k^{+}\mathrm{is}\mathrm{accepted}\mathrm{by}\mathrm{the}\mathrm{filter}\mathcal{F}\right\}$, and $S=\left\{k|x_{k+1}=x_k+d_k\right\}$. Then, $S=\left\{k|{\widehat{\rho }}_k\ge {\mu }_1\mathrm{or}{x}_k^{+}\mathrm{is}\mathrm{accepted}\mathrm{by}\mathrm{the}\mathrm{filter}\mathcal{F}\right\}$. At the time of $k\notin S$, we obtain $x_{k+1}=x_k+{\alpha }_k{d}_k$.

Lemma 1.

Suppose that Assumptions 1 and 2 holds, and$d_k$is the solution of Equation (18); then,

$$f_{l(}{}_{k)}-f_k-m_k(d_k)\ge \tau \Vert g_k\Vert \min \left\{{\Delta }_k,\frac{\Vert g_k\Vert }{\Vert B_k\Vert }\right\}.$$

(23)

Proof. 

According to $f_{l(k)}=\underset{0\le j\le m(k)}{\max }\{f_{k-j}\}$, we have $f_{l(}{}_{k)}\ge f_k$. Thus, we obtain

$$f_{l(}{}_{k)}-f_k-m_k(d_k)\ge m_k(0)-m_k(d_k).$$

(24)

Taking into account Equation (24) and Remark 1, we can conclude that Equation (23) holds. □

Lemma 2.

For all$k$, we can find that

$$\left|f_k-f\left(x_k+d_k\right)-\left(m_k\left(0\right)-m_k\left(d_k\right)\right)\right|\le O\left({\Vert d_k\Vert }^2\right).$$

(25)

Proof. 

The proof can be obtained by Taylor’s expansion and H3. □

Lemma 3.

Suppose that the infinite sequence $\left\{x_k\right\}$ is generated by Algorithm 1. The number of successful iterations is infinite, that is,$\left|S\right|=+\infty$. Then, we have$\left\{x_k\right\}\subset L(x_0)$.

Proof. 

We can proceed by induction. When $k=0$, apparently we obtain $x_0\in L(x_0)$.

Assuming that $x_k\in L(x_0)$$(k\ge 0)$ holds, we get $f_k\le f_0$. Then, we prove $x_{k+1}\in L(x_0)$. Consider the following two cases:

Case 1: When $k\in D$, according to Equation (16) we have,

$$R_k-f_{k+1}\ge {\mu }_1(f_{l(k)}-f_k-m_k(d_k)),$$

(26)

Thus,

$$R_k\ge f_{k+1}+{\mu }_1(f_{l(k)}-f_k-m_k(d_k)),$$

(27)

According to Equations (23) and (27), we can obtain $R_k\ge f_{k+1}$. Using the definition of $R_k$ and $f_{l(k)}$, we get

$$R_k={\eta }_k{f}_{l(k)}+(1-{\eta }_k)f_k\le {\eta }_k{f}_{l(k)}+(1-{\eta }_k)f_{l(k)}=f_{l(k)},$$

(28)

The above two inequalities show that

$$f_{k+1}\le R_k\le f_{l(k)}\le f_0,$$

(29)

Case 2: When $k\in A$, according to $0<{\widehat{\rho }}_k<{\mu }_1$, we have $R_k-f(x_k+d_k)>0$. Thus, we obtain $f_{k+1}\le R_k\le f_{l(k)}\le f_0$. This shows the sequence $\left\{x_k\right\}\subset L\left(x_0\right)$. □

Lemma 4.

Suppose that Assumptions 1 and 2 holds, and the sequence$\left\{x_k\right\}$is generated by Algorithm 1. Then, the sequence$\left\{f_{l\left(k\right)}\right\}$is not monotonically increasing and convergent.

Proof. 

The proof is similar to the proof of Lemma 5 in [8] and is here omitted. □

Lemma 5.

Suppose that Assumptions 1 and 2 holds, and the sequence$\left\{x_k\right\}$is generated by Algorithm 1. Moreover, assume that there exists a constant$0<\epsilon <1$, so that$\Vert g_k\Vert >\epsilon$, for all$k$. Then, Algorithm 1 is well defined; that is, the algorithm terminates in a limited number of steps.

Proof. 

In contradiction, suppose that Algorithm 1 cycles infinitely at iteration $k$. Then, we have

$${\widehat{\rho }}_k^p<{\mu }_{1}p\to \infty ,$$

(30)

Following Equation (17), we have $c^p\to 0$ as $p\to \infty$. Thus, we get,

$$\Vert d_k^p\Vert \le {\Delta }_k^p\to 0,$$

(31)

where $d_k^p$ is a solution of the subproblem of Equation (18) corresponding to $p$ in the $k-\mathrm{th}$ iteration. Combining Lemma 1, Lemma 2, and Equation (28), we obtain

$$\begin{array}{ll}\left|{\widehat{\rho }}_k^p-1\right|=\left|\frac{R_k-f(x_k+d_k^p)}{f_{l(k)}-f_k-m_k(d_k^p)}-1\right|& =\left|\frac{R_k-f(x_k+d_k^p)-f_{l(k)}+f_k+m_k(d_k^p)}{f_{l(k)}-f_k-m_k(d_k^p)}\right|\\ & \le \left|\frac{f_k-f(x_k+d_k^p)+m_k(d_k^p)}{f_{l(k)}-f_k-m_k(d_k^p)}\right|\\ & \le \frac{O\left({\Vert d_k^p\Vert }^2\right)}{\tau \Vert g_k\Vert \min \left\{{\Delta }_k,\frac{\Vert g_k\Vert }{\Vert B_k\Vert }\right\}}\\ & \le \frac{O\left({\Vert d_k^p\Vert }^2\right)}{\tau \epsilon \min \left\{{\Delta }_k,\frac{\epsilon }{M_1}\right\}}\\ & \le \frac{O\left({\Vert {\Delta }_k\Vert }^2\right)}{O\left({\Delta }_k\right)}\to 0\left(p\to \infty \right)\end{array}$$

(32)

which implies that there exists a sufficiently large $p$ such that ${\widehat{\rho }}_k^p\ge {\mu }_1$ as $p\to \infty$. This contradicts Equation (30), and shows that Algorithm 1 is well defined. □

Lemma 6.

Suppose that Assumptions 1 and 2 holds, and there exists a constant$\epsilon$such that$\Vert g_k\Vert \ge \epsilon$for all$k$. Therefore, there is a constant$\upsilon$such that

$${\Delta }_k>\upsilon ,k=0,1,2,\dots ,,$$

(33)

Proof. 

The proof is similar to that of Theorem 6.4.3 in [28], and is therefore omitted here. □

In what follows, we establish global convergence of Algorithm 1 based on the above and the lemmas.

Theorem 1.

(Global Convergence) Suppose that Assumptions 1 and 2 holds, and the sequence$\left\{x_k\right\}$is generated by Algorithm 1, such that,

$$\underset{k\to \infty }{\lim }\inf \Vert g_k\Vert =0$$

(34)

Proof. 

Divide the proof into the following two cases:

Case 1: The number of successful iterations and many filter iterations are infinite, i.e., $\left|S\right|=+\infty$, $\left|A\right|=+\infty$.

Suppose, on the contrary, that Equation (34) does not hold. Thus, there exists a constant $\epsilon$ such that $\Vert g_k\Vert >\epsilon$, as $k$ is sufficiently large. Introduce the index of set $S=\left\{k_i\right\}$. Following Assumption 1, we can find that $\left\{\Vert g_k\Vert \right\}$ is bounded. Therefore, there is a subsequence $\left\{k_t\right\}\subseteq \left\{k_i\right\}$ such that

$$\underset{t\to \infty }{\lim }\Vert g_{k_t}\Vert =\overline{\epsilon },$$

(35)

where $\overline{\epsilon }$ is a constant. The iteration point $x_{k_t}$ is accepted by the filter ${\mathcal{F}}_k{}_{{}_t}$; then there exists $j\in \left\{1,2,\dots ,n\right\}$, for every $t>1$, that is

$$\left|g_{k_t}^j\right|-\left|g_{{}_{k_{t-1}}}^j\right|\le -{\gamma }_g\Vert g_{k_{t-1}}\Vert$$

(36)

As $t$ is sufficiently large, we have

$$\underset{t\to \infty }{\lim }\left(\left|g_{k_t}^j\right|-\left|g_{{}_{k_{t-1}}}^j\right|\right)=0.$$

(37)

However, we obtain $-{\gamma }_g\Vert g_{k_{t-1}}\Vert \le -{\gamma }_g\epsilon <0$, which means that Equation (37) does not hold. The proof is completed.

Case 2: The number of successful iterations is infinite, and the number of filter iterations is finite, i.e., $\left|S\right|=+\infty$, $\left|A\right|<+\infty$.

We proceed from the following proof with a contradiction. Suppose that there exists a constant $\epsilon >0$, such that $\Vert g_k\Vert \ge \epsilon$, for sufficiently large $k$. Based on $\left|A\right|<+\infty$, for sufficiently large $k\in S$, we have ${\widehat{\rho }}_k\ge {\mu }_1$. Thus, set

$${\xi }_k=\left|\left\{p,p+1,\dots ,k\right\}\cap S\right|.$$

(38)

Based on Assumption 2, Equation (28), Lemma 1, and Lemma 6, we write

$${\displaystyle \sum _{k\in T}\left(f_{l(k)}-f_{k+1}\right)}\ge {\displaystyle \sum _{k\in T}\left(R_k-f_{k+1}\right)}\ge {\xi }_k{\mu }_1\tau \epsilon \min \left\{\upsilon ,\frac{\epsilon }{M_1}\right\}.$$

(39)

As $p$ and $k$ are sufficiently large, according to $\left|S\right|=+\infty$ and $\left|A\right|<+\infty$, we know that ${\xi }_k$ is sufficiently large. Thus, we can find that ${\xi }_k{\mu }_1\tau \epsilon \min \left\{\upsilon ,\frac{\epsilon }{M_1}\right\}\to +\infty$, and the left end of Equation (39) has no lower bound. We can deduce that

$$\begin{array}{ll}{\displaystyle \sum _{k\in T}\left(f_{l(k)}-f_{k+1}\right)}& \ge {\displaystyle \sum _{j=p}^k\left(f_{l(j)}-f_{l(j+1)}\right)}\\ & =f_{l(p)}-f_{l(k+1).}\end{array}$$

(40)

Using Lemma 4, as $p$ and $k$ are sufficiently large, the left end of Equation (40) has a lower bound, which contradicts Equation (39). This completes the proof of Theorem 1. □

Now, based on the appropriate conditions, the following superlinear convergence is presented for Algorithm 1.

Theorem 2.

(Superlinear Convergence) Suppose that Assumptions 1 and 2 holds, and the sequence$\left\{x_k\right\}$generated by Algorithm 1 converges to$x^{*}$. Moreover, it is reasonable to assume that the Hessian matrix${\nabla }^{2}f(x^{*})$is positive definite. If$\Vert d_k\Vert \le {\Delta }_k$, where$d_k=-B_k^{-1}{g}_k$, and

$$\underset{k\to \infty }{\lim }\frac{\Vert (B_k-{\nabla }^{2}f(x^{*})d_k\Vert }{\Vert d_k\Vert }=0,$$

(41)

then the sequence$\left\{x_k\right\}$converges to$x^{*}$in a superlinear manner.

Proof. 

Found using the same method as in the proof of Theorem 4.1 in [29]. □

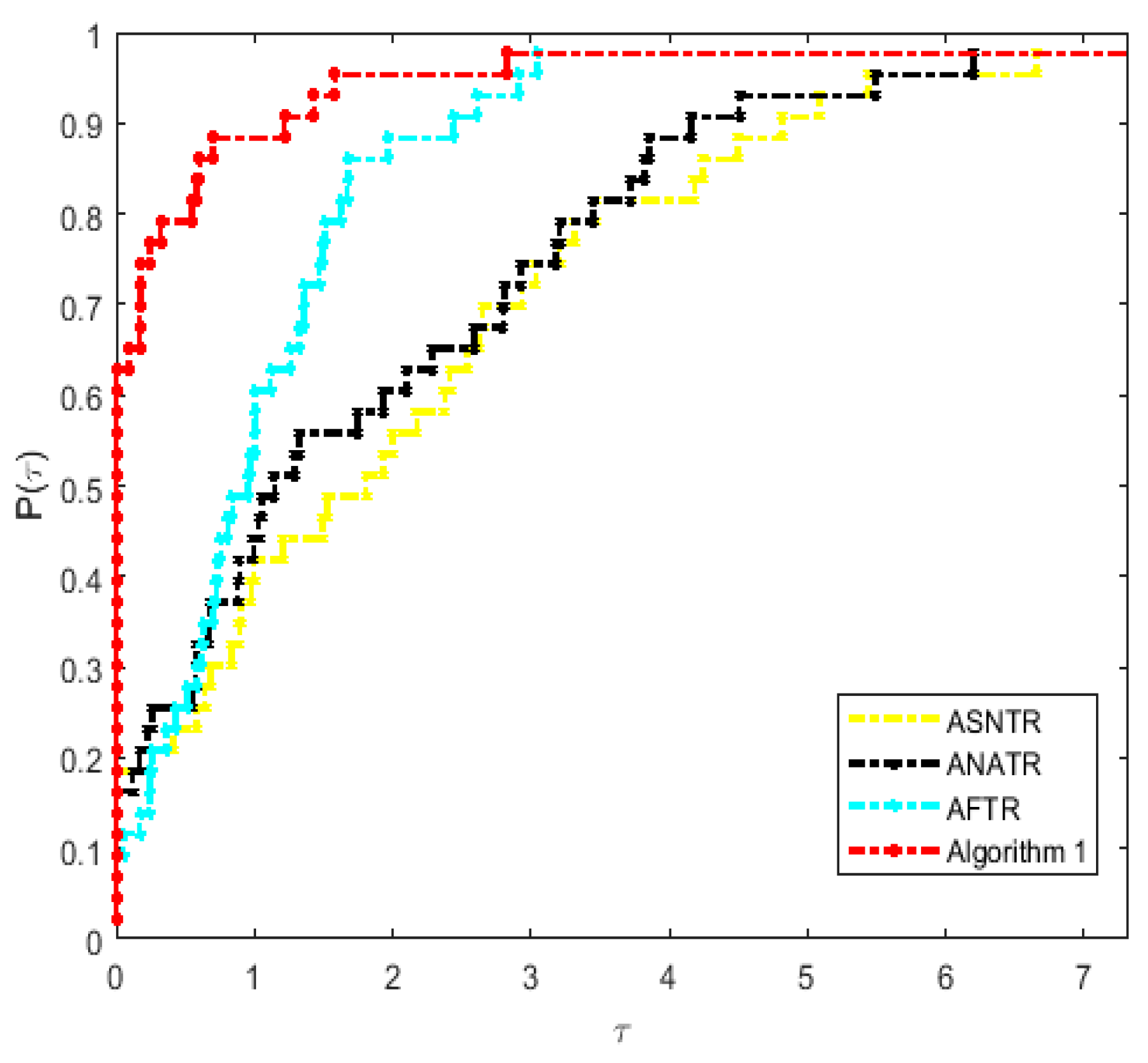
4. Preliminary Numerical Experiments

In this section, we present numerical results to illustrate the performance of Algorithm 1 in comparison with the standard nonmonotone trust region algorithm of Pang et al. in [30] (ASNTR), the nonmonotone adaptive trust region algorithm of Ahookhoosh et al. in [16] (ANATR), and the multidimensional filter trust region algorithm of Wang et al. in [8] (AFTR). We performed our codes in double precision format of algorithm in MATLAB 9.4 programming, and the codes are given in the Appendix A. A set of unconstrained optimization test problems are selected from Andrei [31] with the some medium-scale and large-scale problems. The stopping criteria are that the number of iterations exceeds 10,000 or $\Vert g_k\Vert \le {10}^{-6}(1+\left|f(x_k)\right|)$. $n_f$,$n_i$, and CPU represent the total number of function evaluations, the total number of gradient evaluations, and running time in seconds, respectively. Following Step 0, we exploit the following values:${\mu }_1=0.25$, ${\beta }_1=0.25$, ${\beta }_2=1.5$, ${\eta }_0=0.25$, $N=5$, $\epsilon =0.5$, $c_1=0.25$, $c_2=0.75$, and $B_0=I\in R^n\times R^n$. In addition, ${\eta }_k$ is updated by the following recursive formula:

$${\eta }_k=\{\begin{array}{ll}{\eta }_0/2,& \mathrm{if}k=1\\ ({\eta }_{k-1}+{\eta }_{k-2})/2,& \mathrm{if}k\ge 2\end{array},$$

(42)

The matrix $B_k$ is updated using a CBFGS formula [32]:

$$B_{k+1}=\{\begin{array}{ll}{B}_k+\frac{y_k{y}_k^T}{d_k^T{y}_k}-\frac{B_k{d}_k{d}_k^T{B}_k}{d_k^T{B}_k{d}_k},& \frac{y_k^T{d}_k}{{\Vert d_k\Vert }^2}\ge \epsilon {\Vert g_k\Vert }^{\alpha }\\ B_k,& \frac{y_k^T{d}_k}{{\Vert d_k\Vert }^2}<\epsilon \Vert g_k\Vert ,\end{array}$$

(43)

where $d_k=x_{k+1}-x_k$, and $y_k=g_{k+1}-g_k$.

In

Table 1. Numerical comparisons on a subset of test problems. ASNTR: The standard nonmonotone trust region algorithm of Pang et al.; ANATR: The nonmonotone adaptive trust region algorithm of Ahookhoosh et al.; AFTR: The multidimensional filter trust region algorithm of Wang et al.

Problem	$\mathit{n}$	${\mathit{n}}_{\mathit{f}}/{\mathit{n}}_{\mathit{i}}$
		ASNTR	CPU	ANATR	CPU	AFTR	CPU	Algorithm 1	CPU
Extended Rosenbrock	500	2649/1326	1867.254	1071/840	1545.386	547/387	642.091	86/47	70.369
Extended White and Holst function	500	13/7	26.788	5/3	6.524	5/3	2.125	3/2	0.218
Extended Beale	500	29/15	4.386	43/22	15.351	40/36	8.532	22/17	2.953
Penalty i	500	13/8	32.186	5/3	6.593	7/4	2.176	3/2	0.171
Pert.Quad	36	153/80	0.5523	128/67	0.4704	101/73	0.8631	86/45	0.167
Raydan 1	100	26/14	0.862	130/98	2.263	208/105	3.5009	82/42	0.923
Raydan 2	500	13/8	0.9660	13/8	0.9966	11/6	0.9549	9/5	0.780
Diadonal 1	500	82/42	40.591	1459/812	1957.794	59/43	21.091	21/11	9.107
Diadonal 2	500	4765/3529	1532.176	251/198	106.641	390/201	43.252	2116/1062	430.600
Diagonal 3	500	1634/933	1822.091	1389/766	1536.226	349/288	327.056	201/101	88.049
Hager	500	42/23	30.258	1418/760	270.837	87/46	45.342	51/26	14.278
Generalized Tridiagonal 1	500	63/32	5.6490	53/28	8.349	46/24	13.419	70/36	11.163
Extended Tridiagonal 1	500	25/13	0.9857	25/13	3.448	14/10	3.2337	8/7	0.823
Extended TET	500	15/8	4.2638	15/9	1.632	17/9	2.5044	17/9	1.452
Diadonal 4	500	7/4	0.3293	7/4	0.857	9/8	4.0362	5/4	0.419
Diadonal 5	500	106/54	43.3048	134/112	57.032	127/106	41.096	155/79	19.024
Diadonal 7	1000	96/78	29.197	88/73	22.309	34/15	10.265	19/15	2.561
Diadonal 8	1000	159/122	18.542	133/126	43.067	76/36	6.781	27/21	1.550
Extended Him	1000	35/18	7.150	30/16	17.975	108/87	514.843	28/18	22.572
Full Hessian FH3	1000	11/6	1.755	11/6	5.555	17/13	5.1472	11/6	3.912
Extended BD1	1000	43/25	61.358	30/16	17.9073	35/19	23.4119	30/19	26.971
Quadratic QF1	1000	287/195	157.332	293/219	0.259	400/274	87.043	197/99	43.280
FLETCHCR34	1000	847/505	67.511	345/225	100.676	24/16	73.265	8/5	33.145
ARWHEAD	1000	47/24	38.4334	29/16	24.338	64/41	38.552	24/17	18.299
NONDIA	1000	197/104	96.176	92/47	56.432	33/23	34.726	51/35	22.318
DQDRTIC	1000	23/12	52.102	36/19	40.949	46/37	86.265	22/15	16.526
EG2	1000	55/30	79.991	28/16	16.042	19/19	14.169	51/26	32.424
Broyden Tridiagonal	1000	1978/1488	1545.221	1553/1288	1266.076	1226/987	782.560	754/646	456.105
Almost Perturbed Quadratic	1600	2548/2267	1960.433	2118/1829	1543.253	1078/718	1067.206	657/425	279.316
Perturbed Tridiagonal Quadratic	3000	1342/1025	1672.434	1132/876	1033.255	745/552	835.265	453/357	572.371
DIXMAANA	3000	576/463	132.240	223/198	88.211	378/320	108.452	209/165	78.542
DIXMAANB	3000	248/201	64.215	165/122	40.233	67/56	25.109	48/32	37.120
DIXMAANC	3000	279/197	177.221	246/167	134.272	95/43	30.140	58/24	19.011
Extended DENSCH	3000	673/418	476.214	533/388	309.605	254/105	199.421	87/42	219.167
SINCOS	3000	2067/1554	1045.301	1653/1274	836.022	337/233	472.032	275/141	165.665
HIMMELH	3000	967/721	526.211	506/349	255.629	197/196	109.276	45/32	40.127
BIGGSB1	3000	3760/2045	2321.509	2254/1886	1308.227	1836/1025	904.234	4051/2381	1987.456
ENGVAL1	3000	1784/1087	1643.092	587/423	960.421	63/43	243.840	58/32	167.991
BDEXP	3000	2259/1876	978.432	1342/978	832.013	172/137	385.439	67/43	59.276
INDEF	3000	325/209	2430.215	178/156	1023.211	34/31	721.343	19/11	479.263
NONSCOMP	3000	264/107	1742.856	96/47	1389.123	34/18	921.324	22/14	679.120
QUARTC	3000	167/123	643.254	332/289	921.313	22/20	425.995	67/54	356.762

, it is easily can be seen that Algorithm 1 outperforms the ASNTR, ANATR, and AFTR algorithms with respect to $n_f$, $n_i$, and CPU, especially for some problems. The Dolan–Moré [33] performance profile was used to compare the efficiency using the number of functional evaluations, the number of gradient evaluations, and running time. A performance index can be selected as measure of comparison among the mentioned algorithms, and the results can be illustrated by a performance profile. For every $\tau \ge 1$, the performance profile gives the proportion $\rho (\tau )$ of the test problems. The performance of each considered algorithmic variant was the best within a range of $\tau$ of the best.

It can be easily seen from Figure 1, Figure 2 and Figure 3 that the new algorithm shows a better performance than the other algorithms from the perspective of the number of function evaluations, the number of gradient evaluations, and running time, especially in contrast to ASNTR. As a general result, we can infer that the new algorithm is more efficient and robust than the other mentioned algorithms in terms of the total number of iterations and running time.

5. Conclusions

In this paper, we combine the nonmonotone adaptive line search strategy with multidimensional filter techniques, and propose a nonmonotone trust region method with a new adaptive radius. Our method possesses the following attractive properties:

(1) The new algorithm is quite different from the standard trust region method; in order to avoid resolving the subproblem, a new nonmonotone Goldstein-type line search is performed in the direction of the rejected trial step.

(2) A new adaptive trust region radius is presented, which decreases the amount of work and computational time. However, full use of the function information for the new trust region radius is not made. A modified trust region ratio is computed which provides more information about evaluating the consistency between the quadratic model and the objective function.

(3) The approximation of the Hessian matrix is updated by the modified BFGS method.

Convergence analysis has shown that the proposed algorithm preserves global convergence as well as superlinear convergence. Numerical experiments were performed on a set of unconstrained optimization test problems in [31]. The numerical results showed that the proposed method is more competitive than the ASNTR, ANATR, and AFTR algorithms for medium-scale problems and large-scale problems with respect to the performance profile explained by Dolan–Moré in [33]. Thus, we can draw the conclusion that the new algorithm works quite well for solving unconstrained optimization problems. In the future, it will be interesting to see the new nonmonotone trust region method used to solve constrained optimization problems and nonlinear equations with constrained conditions. On the other hand, it also will be interesting to combine an improved conjugate gradient algorithm with an improved nonmonotone trust region method to solve many optimization problems.