Abstract
This paper introduces a new three-step algorithm to solve the split feasibility problem. The main advantage is that one of the projective operators interferes only in the final step, resulting in less computations at each iteration. An example is provided to support the theoretical approach. The numerical simulation reveals that the newly introduced procedure has increased performance compared to other existing methods, including the classic CQ algorithm. An interesting outcome of the numerical modeling is an approximate visual image of the solution set.
MSC:
47H10; 54H25; 37C25
1. Introduction
The split feasibility problem (abbreviated SFP) was first introduced by Censor and Elfving [1] for solving a class of inverse problems. In their paper, Censor and Elfving produced also consistent algorithms to solve the newly introduced type of problem. However, their procedure did not benefit from much popularity, as it was requiring matrix inverses at each step, thus making it less efficient.
Soon enough, Byrne [2] (see also [3]) proposed a new iterative method called CQ-method that involves only the orthogonal projections onto C and Q (subsets of the Euclidean arithmetic spaces and , respectively) and it is not requiring the matrix inverse. His study generated important developments on different directions, based on the fact that the procedure itself has multiple possible interpretations. For instance, it is well known that the SFP can be naturally rephrased as a constrained minimization problem. From this perspective, the CQ algorithm is exactly the gradient projection algorithm applied to the optimization problem. Several studies provided alternative gradient (projection) algorithms, using selection techniques (see [4,5] for the multiple-sets split equality or feasibility problems, [6] for split equality and split feasibility problems, or [7] for a self-adaptive method).
In addition, the SPF could be rephrased as a fixed point searching issue, the involved operator being nonexpansive. This opens to the perspective of using alternative iteration procedures for reckoning a solution. For instance, in [8], Xu introduced a Krasnosel’skii–Mann algorithm; in [9], Dang and Gao introduced a three-step KM-CQ-like algorithm, inspired by Noor’s three-step iteration procedure; similarly, Feng et al. introduced a three-step SFP algorithm inspired by the TTP iterative procedure defined by Thakur et al. in [10].
Moreover, in [11], the possibility of seeing the CQ algorithm as a special case of Krasnosel’skii-Mann type algorithm was pointed out. Basically, this ensures the weak convergence of the procedure. In fact, assuming the solution set of the SFP is consistent, Byrne proved that his algorithm (running for Euclidean (arithmetic) spaces) is strongly convergent to a solution. In [11], Wang and Xu pointed out that the strong convergence is kept also for arbitrary finite dimensional Hilbert spaces, but it is most likely lost when dealing with infinite dimension. Starting from the CQ algorithm, improved procedures where searched in order to ensure the strong convergence toward a solution. For instance, Wang and Xu proposed in [11] a modified CQ algorithm based on the idea of using contractions to approximate nonexpansive mappings. The three-step procedures defined by Dang and Gao in [9], and Feng et al. in [12] turned out to be strongly convergent under additional assumptions.
Inspired by Feng et al.’s three-step procedure (hereinafter referred to as SFP-TTP algorithm), we define a new algorithm, using one of the projection mappings only partially. Making fewer projections at each step, the running time of the algorithm is expected to be lower. A numerical simulation will prove the new algorithm to be more efficient than both SFP-TTP and CQ algorithms. Moreover, an approximate visual image of the set of solutions will be obtained during numerical modeling. Last, but not least, we consider that this study opens new research perspectives. Extensions to SFP constrained by variational inequalities [13], fixed point problems [14,15,16], and zeros of nonlinear operators or equilibrium problems [17,18] could be challenging research topics.
2. Preliminaries
Let and be two real Hilbert spaces, C and Q be closed, convex, and nonempty subsets of and , respectively, and let be a bounded and linear operator. The split feasibility problem can be mathematically described by finding a point x in such that
In this paper, we assume that the split feasibility problem is consistent, meaning that the solution set
of the SFP (1) is nonempty. If so, it is not difficult to note that is closed and convex.
The CQ algorithm (see [2,3]) relies on an iteration procedure defined as follows.
Algorithm 1.
For an arbitrarily chosen initial point , the sequence is generated by
where and denote the projections onto sets C and Q, respectively, , with being the transpose of A, while is the spectral radius or the largest eigenvalue of the selfadjoint operator .
Let us note that we may assume . Otherwise, after performing the first iteration step, we reach a point belonging to C. The CQ algorithm converges to a solution of the SFP, for any initial approximation , whenever the SFP has solutions. When the SFP has no solutions, the CQ algorithm converges to a minimizer of the function
over the set C, provided such constrained minimizers exist. Therefore, the CQ algorithm is an iterative constrained optimization method. This algorithm could be easily extended to arbitrary (even infinite) real Hilbert spaces (naturally, must be substituted by , the adjoint operator); a significant difference is the fact, in this case, that the algorithm is only weakly convergent.
To make the presentation self-contained, we review some concepts and basic results that will be used later.
Definition 1
([3] and the references herein). Let H be a a Hilbert space and be a (possibly nonlinear) selfmapping of H. Then,
- T is said to be nonexpansive, if
- T is said to be an averaged operator if , where , I is the identity map and is a nonexpansive mapping.
- T is called monotone if
- Assume . Then, T is called ν-inverse strongly monotone (ν-ism) if
- Any 1-ism T is also known as being firmly nonexpansive; that is,
Several properties are worth to be mentioned next.
Lemma 1
([3] and the references herein). The following statements hold true on Hilbert spaces.
- (i)
- Each firmly nonexpansive mapping is averaged and each averaged operator is nonexpansive.
- (ii)
- T is a firmly nonexpansive mapping if and only if its complement is firmly nonexpansive.
- (iii)
- The composition of a finite number of averaged operators is averaged.
- (iv)
- An operator N is nonexpansive if and only if its complement is a -ism.
- (v)
- An operator T is averaged if and only if its complement is a ν-ism, for some . Moreover, if , then is a -ism.
- (vi)
- If T is a ν-ism and , then is -ism.
Let be a nonempty, closed and convex subset of a Hilbert space. Then, for each , there exists a unique such that
The function assigning to each x the unique proximal point is usually denoted by , and it is known as the metric projection, or the nearest point projection, proximity mapping, or the best approximation operator. Hence, one could define
The following Lemma lists some important properties of the metric projection.
Lemma 2.
Let be a nonempty closed convex subset of a Hilbert space and let denote the metric projection on C. Then,
- (i)
- .
- (ii)
- is a firmly nonexpansive operator, hence also averaged and nonexpansive.
Lemma 3
([19]). If in a Hilbert space H, the sequence is weakly convergent to a point x then, for any , the following inequality holds true
Lemma 4
([19]). In a Hilbert space H, for every nonexpansive mapping defined on a closed convex subset , the mapping is demiclosed at 0 (if and , then ).
Lemma 5
([20], Lemma 1.3). Suppose that X is a uniformly convex Banach space and for all (i.e., is bounded away from 0 and 1). Let and be two sequences of X such that , and hold true for some . Then, .
3. Main Results
Feng et al. initiated in [12] a three-step algorithm to solve the split feasibility problem. Their starting point was the TTP three-step iterative procedure introduced in [10], adapted for a properly chosen projective type nonexpansive mapping.
Algorithm 2
([12]). For an arbitrarily chosen initial point , the sequence is generated by the procedure
where , and are three real sequences in (0,1).
Note that Feng et al.’s approach relies on the following two key elements:
- (1)
- A point solves the SFP (1) if and only if it solves the fixed point equation (see [8])where denotes a positive constant. Hence, .
- (2)
- the iteration function inside Algorithm 2, namely is nonexpansive, for properly chosen (see Lemma 3.1 in [12]).
Turning back to the CQ Algorithm 1, we may rewrite it as follows:
where
By introducing the mapping
one finds
We notice that the resulting procedure has the pattern of a Krasnosel’skii iterative process. This inspires us a study involving the TTP procedure. Our algorithm is defined as follows.
Algorithm 3.
For an arbitrarily chosen initial point , the sequence is generated by
where are three real sequences in (0,1). We shall refer to this algorithm as partially projective TTP iteration procedure, since it runs as a classical TTP iterative scheme, except the last step, where a projection is included.
Lemma 6.
.
Proof.
According to conditions , we have for each mapping with . Looking more closely to , we note that
which proves the first equality. Let us prove next the inclusion . Indeed, if , it follows that and . Then, , and the proof of this statement is complete.
Finally, let us also check that . We start with an arbitrary point . Then, and , resulting in
Hence, and the proof is complete. □
Lemma 7.
The mapping S introduced in (3) is nonexpansive.
Proof.
We start by pointing out that the mapping is -ism, where (see Lemma 3.1 in [12]). On the other hand,
hence U is in fact -ism. According to Lemma 1 (iv), is nonexpansive. □
Lemma 8.
Let be the sequence generated by Algorithm 3. Then, exists for any .
Proof.
Let (according to Lemma 6). Since S is nonexpansive, it follows that S is also quasi-nonexpansive, i.e., for each . Thus, the procedure in Algorithm 3 leads to
therefore
The same reasoning applies to , and one obtains
Now, using inequality (5), one finds
In addition, using the property of the projection mapping being nonexpansive and the fact that , p being thus a fixed point of , we find that
therefore
We conclude from (8) that is bounded and decreasing for all . Hence, exists. □
Lemma 9.
Let be the sequence generated by Algorithm 3. Then,
Proof.
Let . By Lemma 8, it follows that exists. Let us denote
From (5), it is known that . Taking lim sup on both sides of the inequality, one obtains
Again, since S is quasi-nonexpansive, one has
Dividing the above relation by results in
and it follows that
that is,
Relation (13) can be rewritten as
Theorem 4.
Let be the sequence generated by Algorithm 3. Then, is weakly convergent to a point of Ω.
Proof.
Let
denote the weakly subsequential limit set of the sequence . One immediate consequence of Lemma 8 is that is bounded. In conclusion, there exists at least one weakly convergent subsequence, hence is a nonempty subset. We prove next that it contains exactly one weak limit point. To start, let us assume the contrary: let , and let and . By Lemma 9, we have , where S is a nonexpansive mapping (see Lemma 7). Applying Lemma 4, we find that , hence . On the other hand, since C is closed and convex, it follows that it is also weakly closed, hence it contains the weak limits of all its weakly convergent sequences. Therefore, and ultimately . Similar arguments provide . In general, .
From Lemma 8, the sequences and are convergent. These properties, together with Lemma 3, generate the following inequalities:
This provides the expected contradiction. Hence, is a singleton. Let . We just need to prove that . Assume the contrary. Then, for a certain point , there exists such that, for all , one could find satisfying . The resulting subsequence is itself bounded (since is bounded), hence it contains a weakly convergent subsequence . However, this new subsequence is also a weakly convergent subsequence of , hence its weak limit must be p. Taking in the inequality
one finds , contradicting consequence. Hence, . □
The next two theorems provide sufficient conditions for strong convergence. In order to phrase these conditions, let us consider the mapping . Then, T is a nonexpansive mapping and . Moreover,
hence
The arguments to prove the following statements are not different at all from those used in the proof of Theorems 3.2 and 3.3 in [12].
Theorem 5.
Let be the sequence defined by Algorithm 3. Then, is strongly convergent to a point in Ω if and only if , where .
In [21], the so-called Condition was defined in connection with nonexpansive mappings. A mapping is said to satisfy Condition , if there exists a nondecreasing function with , , for all , such that , for all , where C is a nonempty subset of a normed space X.
Theorem 6.
Let be the sequence generated by Algorithm 3. If satisfies Condition , then is strongly convergent to a point in Ω.
4. Numerical Simulation
In the following, we shall provide an example to analyze the efficiency of the partially projective TTP algorithm compared to the SFP-TTP and the CQ algorithms.
Example 1.
Let , , and . The projection mappings and are defined as follows:
Consider
The associated matrix of this linear operator is and its spectral norm is , hence .
The purpose of our numerical experiment is to apply the newly introduced algorithm in order to determine the number of iterations required to remain below an acceptable error, say . Moreover, we look to apply the analysis to all the points of the domain . An immediate consequence of this approach is obtaining an approximative visual image of the solution set (as being the set of the points needing just one iterative step). Since we already established that it is sufficient to choose initial points inside the set C (the unit disc), we can limit our analysis to the square. One possible problem could be the existence of initial points with very long orbits, which would slow down the performance of the algorithm considerably. However, these points are not particularly interesting to us (they do not belong to ). Hence, in order to increase the performance of the numerical algorithm, we add an additional exit criterion: if a solution is not found with error less than , we set the algorithm to break after iterative steps.
Let us start by assigning some values to the parameters involved in the experimental procedure. Consider, for instance, . For each point in the selected squared area, we apply the algorithm until one of the two previous mentioned exit criteria are satisfied ( or ). Meanwhile, we count the number of iterations performed. Depending on the number of iterative steps taken, we associate the starting point with a certain color. For instance, we assign olive color to the points needing just one iteration step (the set ), a darker yellow-green to the points needing two iterations and so on (all the color assignments are gathered into the right-sided colorbar of every image; running the color band from bottom to top, we find the number of iterations corresponding to each color.)
The final result is the image included in Figure 1. Similar numerical simulation, involving the SFP-TTP procedure in Algorithm 2, or the -algorithm 1, provide the images in Figure 2 and Figure 3, respectively. For these two procedures, we have set the parameter to the value .
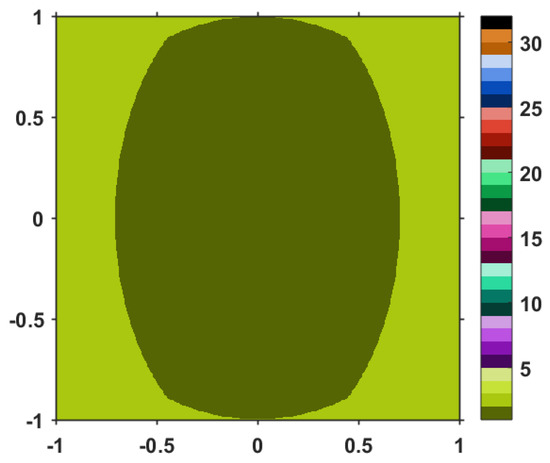
Figure 1.
The partially projective TTP algorithm.
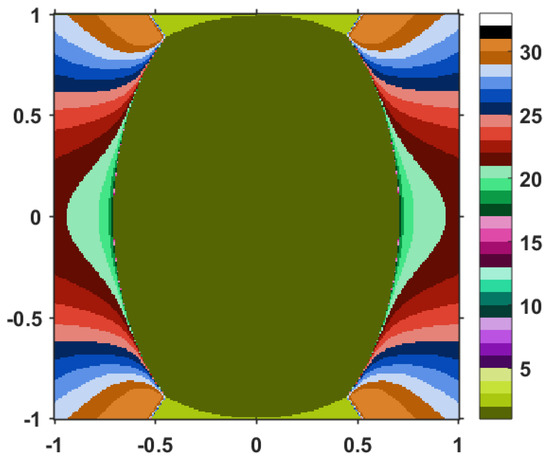
Figure 2.
The SFP-TTP algorithm.
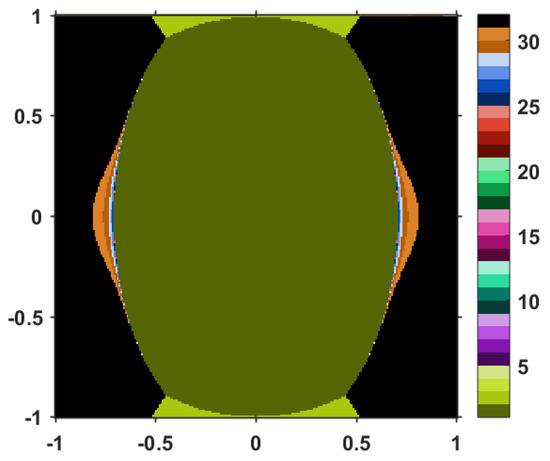
Figure 3.
The CQ algorithm.
Let us analyze the first image i.e., the one corresponding to the partially projective TTP iterative process. The central elliptic disc is olive colored, meaning that its points require just one iteration to reach the requested error. This is an approximate visual representation of the solution set . Identical visual images for are obtained when using the other two algorithms. Nevertheless, when comparing the three figures, except this central part, they are completely distinct. In Figure 1, corresponding to the partially projective TTP procedure, all the points outside the central elliptic disc are colored with yellow-green. Checking with the color bar display, this means that they require two iteration steps to reach the exit criterion. This changes dramatically in Figure 2. We can see that these outer points take on all kinds of colors and shades, going up to light orange, which corresponds to 30 iterative steps. This proves that the partially projective TTP procedure is in general convergent faster than the SFP-TTP and the CQ procedures. Going further and analyzing Figure 3, we notice that many points are black, meaning that they require more that 30 iteration steps. Hence, the CQ algorithm has the slowest convergence of all.
We point out again that the SFP-TTP algorithm, as well as the algorithm, require an additional parameter, namely . For the example under consideration, this parameter range must be the interval . Figure 2 and Figure 3 resulted for . We wondered if changing this parameter would cause major changes in the convergence behavior of the algorithms. We perform this analysis for a fixed initial approximation . By assigning various values to between and , and counting the number of iteration steps to be performed using the three algorithms, it results in the graph in Figure 4. As expected, the partially projective TTP procedure does not depend on . The interesting fact is that the CQ algorithm also reveals a uniform distribution of the number of iteration steps, despite the change of . Again, Algorithm 3 appears to be the most efficient, while Algorithm 1 is the slowest. Moreover, the SFP-TTP algorithm seems to improve its efficiency as approaches 1.
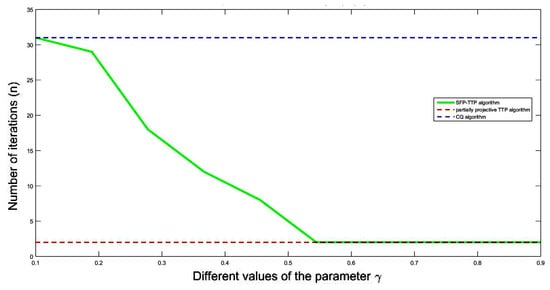
Figure 4.
Number of iteration steps for variable parameter.
5. Conclusions
Our paper finds its motivation in recently developed approaches on split feasibility concerning the search for new algorithms, as well as strong convergence results. The reasoning behind our study was to avoid the excessive interference of the projection mappings in each iteration step. Consequently, we provided a partially projective three-step procedure, as a less computational resource-consuming alternative to other existing algorithms (including the classical CQ). In this regard, several weak and strong convergence results were stated and proved. In addition, a numerical simulation involving the new algorithm and other existing procedures revealed its advantages concerning the convergence speed. Perhaps the most important novelty comes from generating an approximate visual representation of the solution set.
Author Contributions
The conceptualization: A.B. and M.P., formal analysis: A.B. and M.P., and validation A.B. and M.P. Both authors have read and agreed to the published version of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Censor, Y.; Elfving, T. A multiprojection algorithm using Bregman projections in a product space. Numer. Algorithms 1994, 8, 221–239. [Google Scholar] [CrossRef]
- Byrne, C. Iterative oblique projection onto convex sets and the split feasibility problem. Inverse Probl. 2002, 18, 441–453. [Google Scholar] [CrossRef]
- Byrne, C. An unified treatment of some iterative algorithms in signal processing and image reconstruction. Inverse Probl. 2004, 20, 103–120. [Google Scholar] [CrossRef]
- Tian, D.; Jiang, L.; Shi, L. Gradient methods with selection technique for the multiple-sets split equality problem. Mathematics 2019, 7, 928. [Google Scholar] [CrossRef]
- Yao, Y.; Postolache, M.; Zhug, Z. Gradient methods with selection technique for the multiple-sets split feasibility problem. Optimization 2020, 69, 269–281. [Google Scholar] [CrossRef]
- Vuong, P.T.; Strodiot, J.J.; Nguyen, V.H. A gradient projection method for solving split equality and split feasibility problems in Hilbert spaces. Optimization 2014, 64, 2321–2341. [Google Scholar] [CrossRef]
- Yao, Y.; Postolache, M.; Liou, Y.C. Strong convergence of a self-adaptive method for the split feasibility problem. Fixed Point Theory Appl. 2013, 2013, 201. [Google Scholar] [CrossRef]
- Xu, H.K. A variable Krasnosel’skii-Mann algorithm and the multiple-set split feasibility problem. Inverse Probl. 2006, 22, 2021–2034. [Google Scholar] [CrossRef]
- Dang, Y.Z.; Gao, Y. The strong convergence of a three-step algorithm for the split feasibility problem. Optim. Lett. 2013, 7, 1325–1339. [Google Scholar] [CrossRef]
- Thakur, B.S.; Thakur, D.; Postolache, M. A new iteration scheme for approximating fixed points of nonexpensive mapping. Filomat 2016, 30, 2711–2720. [Google Scholar] [CrossRef]
- Wang, F.; Xu, H.K. Approximating curve and strong convergence of the CQ algorithm for the split feasibility problem. J. Inequal. Appl. 2010, 102085. [Google Scholar] [CrossRef]
- Feng, M.; Shi, L.; Chen, R. A new three-step iterative algorithm for solving the split feasibility problem. U. Politeh. Buch. Ser. A 2019, 81, 93–102. [Google Scholar]
- Yao, Y.; Postolache, M.; Yao, J.C. Iterative algorithms for generalized variational inequalities. U. Politeh. Buch. Ser. A 2019, 81, 3–16. [Google Scholar]
- Yao, Y.; Agarwal, R.P.; Postolache, M.; Liu, Y.C. Algorithms with strong convergence for the split common solution of the feasibility problem and fixed point problem. FixedPoint Theory Appl. 2014, 2014, 183. [Google Scholar] [CrossRef]
- Yao, Y.; Leng, L.; Postolache, M.; Zheng, X. Mann-type iteration method for solving the split common fixed point problem. J. Nonlinear Convex Anal. 2017, 18, 875–882. [Google Scholar]
- Yao, Y.; Postolache, M.; Yao, J.C. Strong convergence of an extragradient algorithm for variational inequality and fixed point problems. U. Politeh. Buch. Ser. A 2020, 82, 3–12. [Google Scholar]
- Dadashi, V.; Postolache, M. Forward-backward splitting algorithm for fixed point problems and zeros of the sum of monotone operators. Arab. J. Math. 2020, 9, 89–99. [Google Scholar] [CrossRef]
- Dadashi, V.; Postolache, M. Hybrid proximal point algorithm and applications to equilibrium problems and convex programming. J. Optim. Theory Appl. 2017, 174, 518–529. [Google Scholar] [CrossRef]
- Opial, Z. Weak convergence of the sequence of successive approximations for nonexpensive mappings. Bull. Am. Math. Soc. 1967, 73, 591–597. [Google Scholar] [CrossRef]
- Schu, J. Weak and strong convergence of fixed points of asymptotically nonexpansive mappings. Bull. Austral. Math. Soc. 1991, 43, 153–159. [Google Scholar] [CrossRef]
- Senter, H.F.; Dotson, W.G. Approximating fixed points of nonexpansive mappings. Proc. Am. Math. Soc. 1974, 44, 375–380. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).