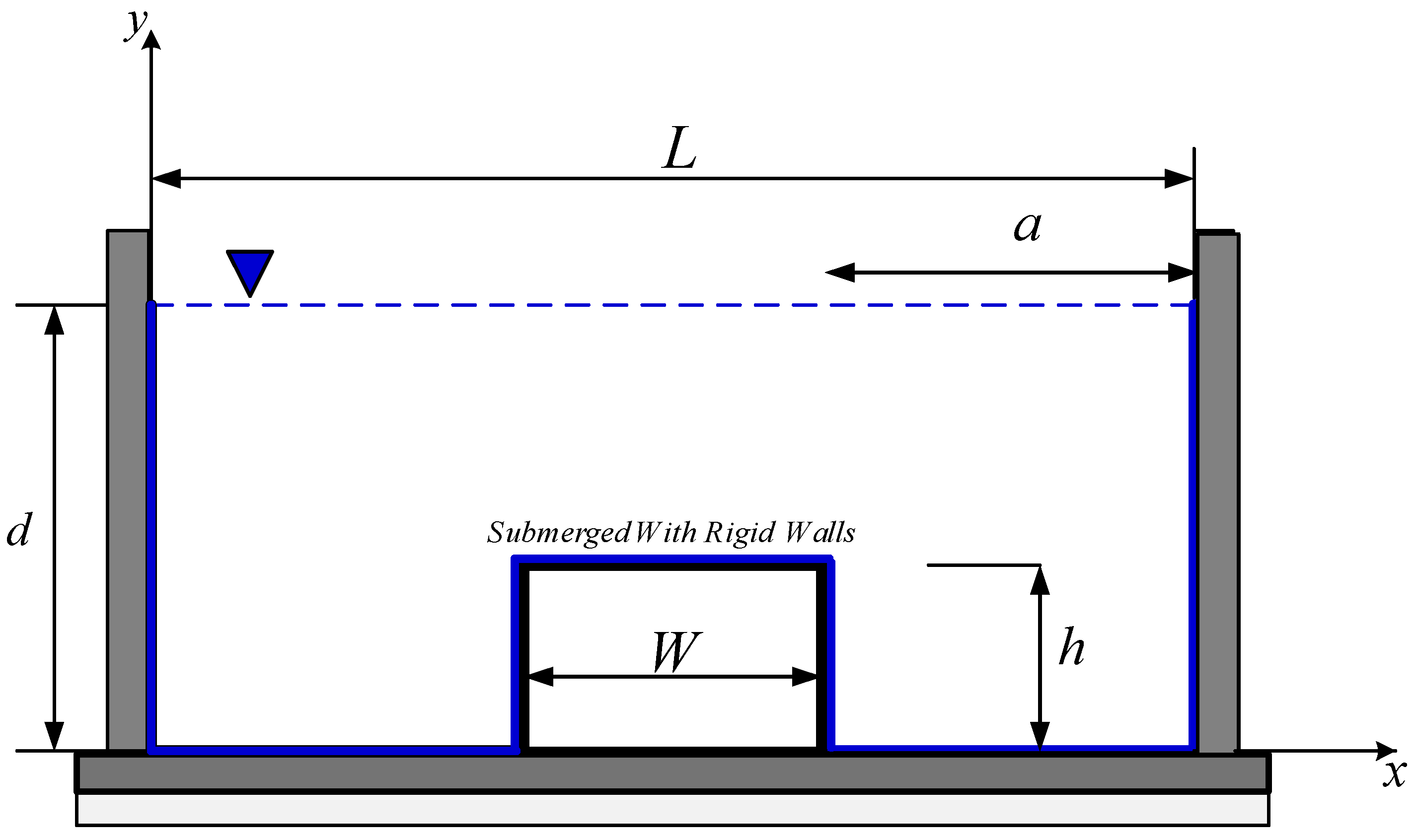
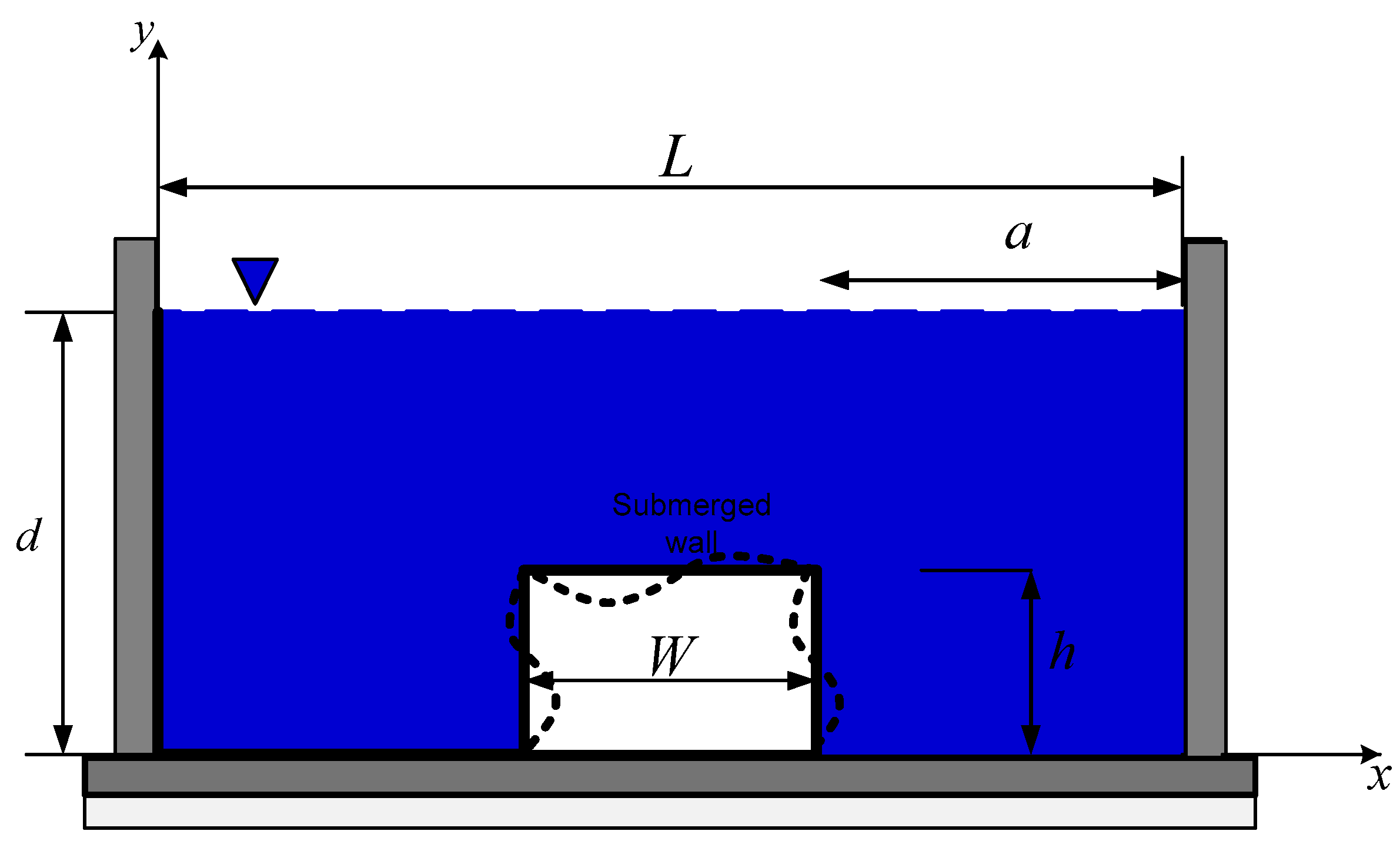
Numerical Modeling of Sloshing Frequencies in Tanks with Structure Using New Presented DQM-BEM Technique
Abstract
1. Introduction
2. Governing Equations
2.1. Flow-Field Governing Equations
2.2. Developing the Boundary Element Model
2.3. Fluid–Solid Interaction Modeling
3. Numerical Results
3.1. Test Case 1
3.2. Test Case 2
3.3. Test Case 3
3.4. Test Case 4
4. Conclusions
- 1-
- According to the model outputs, the existence of fluid in the investigated system leads to the reduction in the frequencies.
- 2-
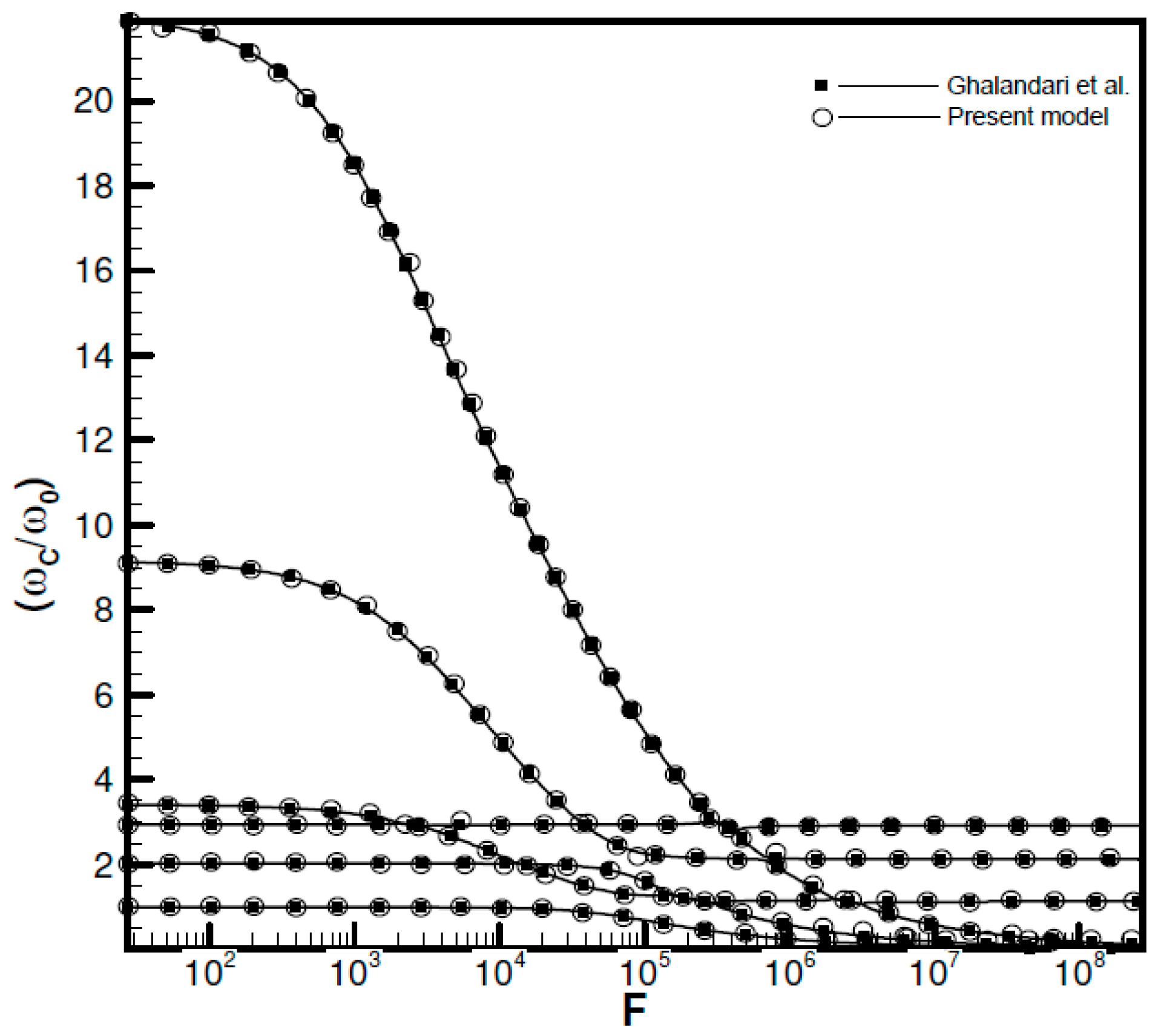
- Comparing the results of the model to the data of previous studies shows a maximum relative error of 1.5% between the DQM-BEM model and literature, indicating the reliability of the results obtained by the developed model.
- 3-
- The effect of the immersed structures on the dynamic response of the sloshing is more tangible than the submerged structure.
- 4-
- The sloshing effect on the structural frequencies is revealed itself in a high-flexibility parameter for both submerged and immersed structures.
Author Contributions
Funding
Conflicts of Interest
References
- Shadloo, M.S.; Weiss, R.; Yildiz, M.; Dalrymple, R.A. Numerical simulation of long wave runup for breaking and nonbreaking waves. Int. J. Offshore Polar Eng. 2015, 25, 1–7. [Google Scholar]
- Hopp-Hirschler, M.; Shadloo, M.S.; Nieken, U. A smoothed particle hydrodynamics approach for thermo-capillary flows. Comput. Fluids 2018, 176, 1–19. [Google Scholar] [CrossRef]
- Almasi, F.; Shadloo, M.S.; Hadjadj, A.; Ozbulut, M.; Tofighi, N.; Yildiz, M. Numerical simulations of multi-phase electro-hydrodynamics flows using a simple incompressible smoothed particle hydrodynamics method. Comput. Math. Appl. 2019. [Google Scholar] [CrossRef]
- Jiang, Y.; Dahi-Taleghani, A. Modified extended finite element methods for gas flow in fractured reservoirs: A pseudo-pressure approach. J. Energy Resour. Technol. 2018, 140, 073101. [Google Scholar] [CrossRef]
- Tarfaoui, M.; Shah, O.R.; Nachtane, M. Design and optimization of composite offshore wind turbine blades. J. Energy Resour. Technol. 2019, 141, 051204. [Google Scholar] [CrossRef]
- Wang, N.; Maleki, A.; Alhuyi Nazari, M.; Tlili, I.; Safdari Shadloo, M. Thermal conductivity modeling of nanofluids contain MgO particles by employing different approaches. Symmetry 2020, 12, 206. [Google Scholar] [CrossRef]
- Abdelmalek, Z.; Alamian, R.; Shadloo, M.S.; Maleki, A.; Karimipour, A. Numerical study on the performance of a homogeneous charge compression ignition engine fueled with different blends of biodiesel. J. Therm. Anal. Calorim. 2020, 1–11. [Google Scholar] [CrossRef]
- Abramson, H.N. The dynamic behavior of liquids in moving containers. NASA SP-106. NASA Spec. Publ. 1966, 106, 1–21. [Google Scholar]
- Ibrahim, R.A. Liquid Sloshing Dynamics: Theory and Applications; Cambridge University Press: Cambridge, UK, 2005; ISBN 1139444131. [Google Scholar]
- Jamalabadi, M.Y.A.; Ho-Huu, V.; Nguyen, T.K. Optimal design of circular baffles on sloshing in a rectangular tank horizontally coupled by structure. Water 2018, 10, 1504. [Google Scholar] [CrossRef]
- Gedikli, A.; Ergüven, M.E. Evaluation of sloshing problem by variational boundary element method. Eng. Anal. Bound. Elem. 2003, 27, 935–943. [Google Scholar] [CrossRef]
- Biswal, K.C.; Bhattacharyya, S.K. Dynamic response of structure coupled with liquid sloshing in a laminated composite cylindrical tank with baffle. Finite Elem. Anal. Des. 2010, 46, 966–981. [Google Scholar] [CrossRef]
- Scholl, H.F.; Stephens, D.G. Effectiveness of Flexible and Rigid Ring Baffles for Damping Liquid Oscillations in Large-Scale Cylindrical Tanks; National Aeronautics and Space Administration: Washington, DC, USA, 1967.
- Watson, E.B.B.; Evans, D.V. Resonant frequencies of a fluid in containers with internal bodies. J. Eng. Math. 1991, 25, 115–135. [Google Scholar] [CrossRef]
- Choun, Y.-S.; Yun, C.-B. Sloshing characteristics in rectangular tanks with a submerged block. Comput. Struct. 1996, 61, 401–413. [Google Scholar] [CrossRef]
- Choun, Y.; Yun, C. Sloshing analysis of rectangular tanks with a submerged structure by using small-amplitude water wave theory. Earthq. Eng. Struct. Dyn. 1999, 28, 763–783. [Google Scholar] [CrossRef]
- Mitra, S.; Sinhamahapatra, K.P. Slosh dynamics of liquid-filled containers with submerged components using pressure-based finite element method. J. Sound Vib. 2007, 304, 361–381. [Google Scholar] [CrossRef]
- Bellman, R.; Casti, J. Differential quadrature and long-term integration. J. Math. Anal. Appl. 1971, 34, 235–238. [Google Scholar] [CrossRef]
- Li, Z.; Hu, T.; Tao, Y.; Zhang, T.; Li, Z. Fast calculation method for transient response of transmission line based on chebyshev pseudospectral–two-step three-order boundary value coupled method. Symmetry 2019, 11, 721. [Google Scholar] [CrossRef]
- Malik, M.; Bert, C.W. Three-dimensional elasticity solutions for free vibrations of rectangular plates by the differential quadrature method. Int. J. Solids Struct. 1998, 35, 299–318. [Google Scholar] [CrossRef]
- Striz, A.G.; Jang, S.K.; Bert, C.W. Nonlinear bending analysis of thin circular plates by differential quadrature. Thin-Walled Struct. 1988, 6, 51–62. [Google Scholar] [CrossRef]
- Jang, S.K.; Bert, C.W.; Striz, A.G. Application of differential quadrature to static analysis of structural components. Int. J. Numer. Methods Eng. 1989, 28, 561–577. [Google Scholar] [CrossRef]
- Kang, K.-J.; Kim, B.-S. In-Plane Extensional Vibration Analysis of Curved Beams Using DQM. J. Korean Soc. Saf. 2002, 17, 99–104. [Google Scholar]
- Hassan, M.T.; Nassar, M. Analysis of stressed Timoshenko beams on two parameter foundations. Ksce J. Civ. Eng. 2015, 19, 173–179. [Google Scholar] [CrossRef]
- Ghalandari, M.; Shamshirband, S.; Mosavi, A.; Chau, K. Flutter speed estimation using presented differential quadrature method formulation. Eng. Appl. Comput. Fluid Mech. 2019, 13, 804–810. [Google Scholar] [CrossRef]
- Ghalandari, M.; Mirzadeh Koohshahi, E.; Mohamadian, F.; Shamshirband, S.; Chau, K.W. Numerical simulation of nanofluid flow inside a root canal. Eng. Appl. Comput. Fluid Mech. 2019, 13, 254–264. [Google Scholar] [CrossRef]
- Ghalandari, M.; Ziamolki, A.; Mosavi, A. Mechanics Aeromechanical optimization of first row compressor test stand blades using a hybrid machine learning model of genetic algorithm, artificial neural networks and design of experiments. Eng. Appl. Comput. Fluid Mech. 2019, 13, 892–904. [Google Scholar]
- Alizadeh, H.; Ghasempour, R.; Shafii, M.B.; Ahmadi, M.H.; Yan, W.-M.; Nazari, M.A. Numerical simulation of PV cooling by using single turn pulsating heat pipe. Int. J. Heat Mass Transf. 2018, 127, 203–208. [Google Scholar] [CrossRef]
- Zarandi, S.; Lai, H.-W.; Wang, Y.-C.; Aizikovich, S. Residual stress analysis of an orthotropic composite cylinder under thermal loading and unloading. Symmetry 2019, 11, 320. [Google Scholar] [CrossRef]
- Zhang, M.; Ayala, L.F. A general boundary integral solution for fluid flow analysis in reservoirs with complex fracture geometries. J. Energy Resour. Technol. 2018, 140, 052907. [Google Scholar] [CrossRef]
- Christensen, E.; Brunty, J.; Christensen, E.; Brunty, J. Launch vehicle slosh and hydroelastic loads analysis using the boundary element method. In Proceedings of the 38th Structures, Structural Dynamics, and Materials Conference, Kissimmee, FL, USA, 7–10 April 1997; p. 1036. [Google Scholar]
- Dutta, S.; Laha, M.K. Analysis of the small amplitude sloshing of a liquid in a rigid container of arbitrary shape using a low-order boundary element method. Int. J. Numer. Methods Eng. 2000, 47, 1633–1648. [Google Scholar] [CrossRef]
- Nakayama, T.; Washizu, K. The boundary element method applied to the analysis of two-dimensional nonlinear sloshing problems. Int. J. Numer. Methods Eng. 1981, 17, 1631–1646. [Google Scholar] [CrossRef]
- Zhu, R.; Saito, K. Multiple domain boundary element method applied to fluid motions in a tank with internal structure. J. Soc. Nav. Archit. Jpn. 2000, 2000, 135–141. [Google Scholar] [CrossRef]
- Ghalandari, M.; Bornassi, S.; Ahmadi, M.H. Investigation frequencies of elastic submerged structure on sloshing. Eng. Appl. Comput. Fluid Mech. 2019, 13, 519–528. [Google Scholar]
- Jamalabadi, M.Y.A.; Alamian, R.; Yan, W.M.; Li, L.K.B.; Leveneur, S.; Shadloo, M.S. Effects of nanoparticle enhanced lubricant films in thermal design of plain journal bearings at high reynolds numbers. Symmetry 2019, 11, 1–18. [Google Scholar]
- Ghalandari, M.; Bornassi, S.; Shamshirband, S.; Mosavi, A.; Chau, K.W. Investigation of submerged structures flexibility on sloshing frequency using a boundary element method and finite element analysis. Eng. Appl. Comput. Fluid Mech. 2019, 13, 519–528. [Google Scholar] [CrossRef]


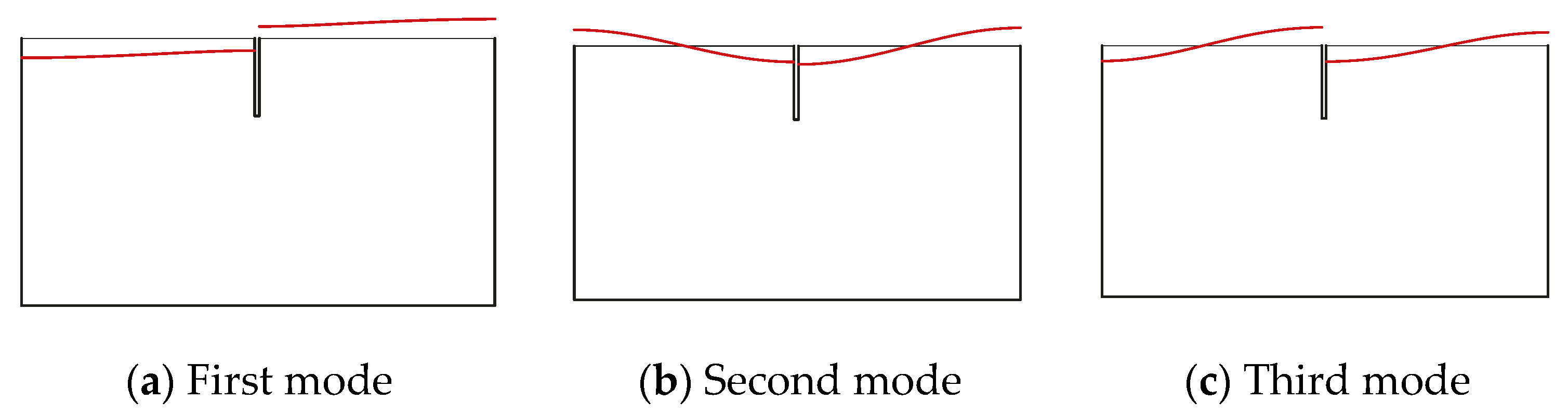
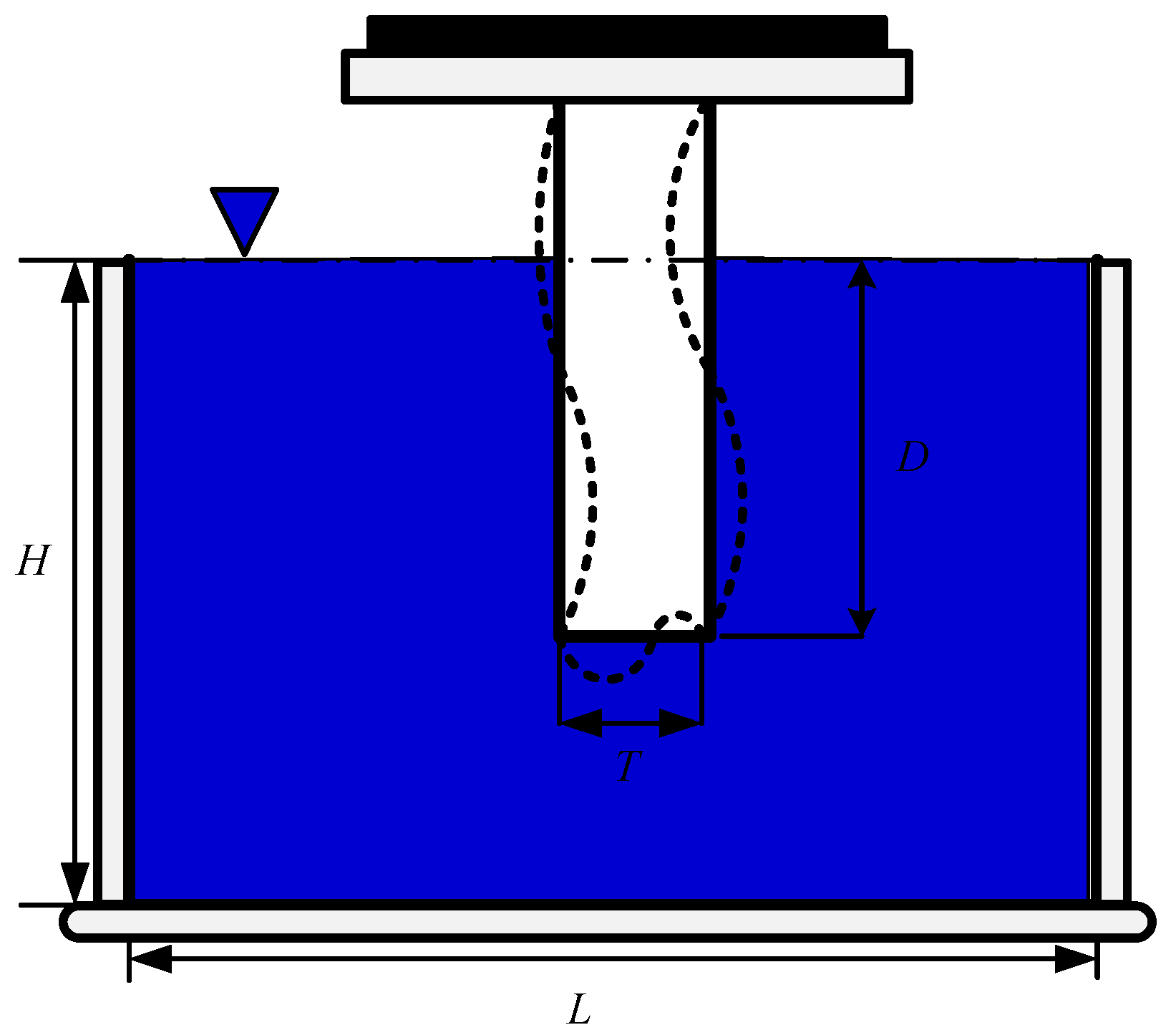
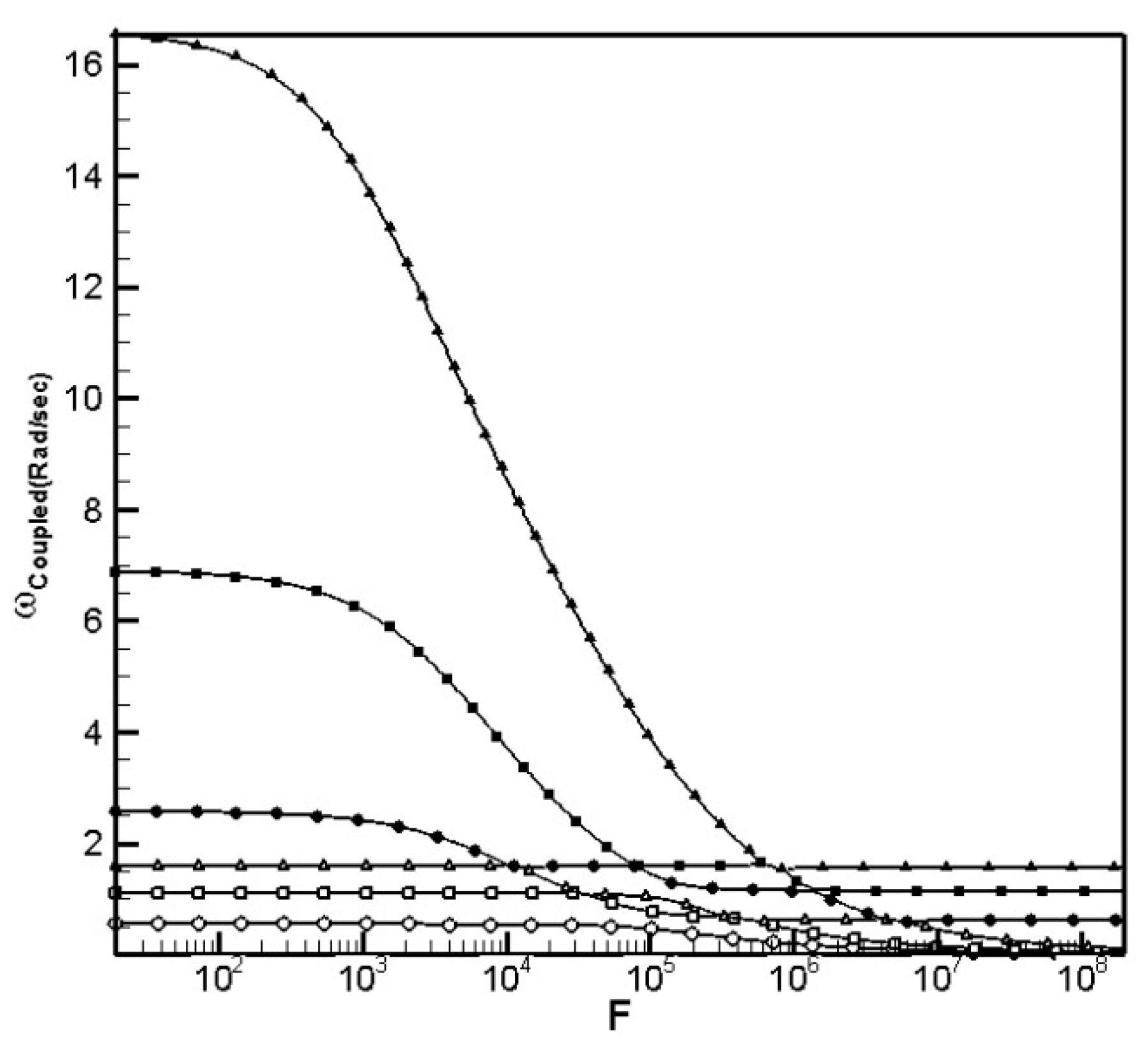
| UINT (rad/s) | h/d | |||||
|---|---|---|---|---|---|---|
| Present | Ghalandari et al. | Choun and Yun | S. Mitra, K.P. Sinhamahapatra | ANSYS | ||
| 0.2 | ||||||
| MODE1 | 0.9091 | 0.9127 | 0.897 | 0.898 | 0.9094 | |
| MODE2 | 1.4312 | 1.428 | 1.415 | 1.415 | 1.4612 | |
| MODE3 | 1.7645 | 1.7647 | 1.744 | 1.746 | 1.7644 | |
| 0.4 | ||||||
| MODE1 | 0.8391 | 0.8396 | 0.849 | 0.842 | 0.8392 | |
| MODE2 | 1.4042 | 1.3964 | 1.404 | 1.406 | 1.4306 | |
| MODE3 | 1.7577 | 1.7564 | 1.742 | 1.74 | 1.7588 | |
| 0.6 | ||||||
| MODE1 | 0.725 | 0.7251 | 0.731 | 0.731 | 0.7252 | |
| MODE2 | 1.3222 | 1.3109 | 1.343 | 1.347 | 1.3437 | |
| MODE3 | 1.7225 | 1.7215 | 1.733 | 1.734 | 1.73 | |
| 0.8 | ||||||
| MODE1 | 0.5355 | 0.5333 | 0.55 | 0.552 | 0.5383 | |
| MODE2 | 1.1011 | 1.0691 | 1.19 | 1.192 | 1.1044 | |
| MODE3 | 1.5661 | 1.5522 | 1.73 | 1.732 | 1.5809 |
| Tank Walls | Rigid |
|---|---|
| Submerged Walls | Elastic |
| Modes | Ghalandari et al. [32] | Represented Model |
|---|---|---|
| 1 | 1.8358 | 1.82844 |
| 2 | 4.9269 | 4.7921 |
| 3 | 11.8579 | 11.853 |
| Sloshing Mode | ANSYS (rad/s) | Present Method (rad/s) | Error Difference (%) |
|---|---|---|---|
| 1 | 1.911 | 1.9299 | 0.9375 |
| 2 | 3.2518 | 3.2021 | 1.5786 |
| 3 | 3.3296 | 3.3100 | 0.6387 |
| Tank Walls | Rigid |
|---|---|
| Immersed Walls | Elastic |
| Structure modes | 1 | 4.8287 |
| 2 | 14.0805 | |
| 3 | 32.5552 |
| Slosh dominant modes | 1 | 1.42815 |
| 2 | 1.8763 | |
| 3 | 1.9789 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Z.; Feng, J.; Ghalandari, M.; Maleki, A.; Abdelmalek, Z. Numerical Modeling of Sloshing Frequencies in Tanks with Structure Using New Presented DQM-BEM Technique. Symmetry 2020, 12, 655. https://doi.org/10.3390/sym12040655
Wei Z, Feng J, Ghalandari M, Maleki A, Abdelmalek Z. Numerical Modeling of Sloshing Frequencies in Tanks with Structure Using New Presented DQM-BEM Technique. Symmetry. 2020; 12(4):655. https://doi.org/10.3390/sym12040655
Chicago/Turabian StyleWei, Zhenda, Junwen Feng, Mohammad Ghalandari, Akbar Maleki, and Zahra Abdelmalek. 2020. "Numerical Modeling of Sloshing Frequencies in Tanks with Structure Using New Presented DQM-BEM Technique" Symmetry 12, no. 4: 655. https://doi.org/10.3390/sym12040655
APA StyleWei, Z., Feng, J., Ghalandari, M., Maleki, A., & Abdelmalek, Z. (2020). Numerical Modeling of Sloshing Frequencies in Tanks with Structure Using New Presented DQM-BEM Technique. Symmetry, 12(4), 655. https://doi.org/10.3390/sym12040655