Triangular Single Valued Neutrosophic Data Envelopment Analysis: Application to Hospital Performance Measurement

Abstract

The foremost broadly utilized strategy for the valuation of the overall performance of a set of identical decision-making units (DMUs) that use analogous sources to yield related outputs is data envelopment analysis (DEA). However, the witnessed values of the symmetry or asymmetry of different types of information in real-world applications are sometimes inaccurate, ambiguous, inadequate, and inconsistent, so overlooking these conditions may lead to erroneous decision-making. Neutrosophic set theory can handle these occasions of data and makes an imitation of the decision-making procedure with the aid of thinking about all perspectives of the decision. In this paper, we introduce a model of DEA in the context of neutrosophic sets and sketch an innovative process to solve it. Furthermore, we deal with the problem of healthcare system evaluation with inconsistent, indeterminate, and incomplete information using the new model. The triangular single-valued neutrosophic numbers are also employed to deal with the mentioned data, and the proposed method is utilized in the assessment of 13 hospitals of Tehran University of Medical Sciences of Iran. The results exhibit the usefulness of the suggested approach and point out that the model has practical outcomes for decision-makers.

1. Introduction

As a strong analytical tool for benchmarking and efficiency evaluation, DEA (data envelopment analysis) is a technique for evaluating the relation efficiency of decision-making units (DMUs), developed initially by Charens et al. [1] on a printed paper named the Charnes, Cooper, and Rhodes (CCR) model. They extended the nonparametric method introduced by Farrell [2] to gauge DMUs with multiple inputs and outputs. The Banker, Charnes, and Cooper (BCC) model is an extension of the previous model under the assumption of variable returns-to-scale (VRS) [3]. With this technique, managers can obtain the relative efficiency of a set of DMUs. In time, many theoretical and empirical studies have applied DEA to several fields of science and engineering, such as healthcare, agriculture, banking supply chains, and financial services, among others. For more details, the reader is referred to the studies of [4,5,6,7,8,9,10,11,12,13,14].

Conventional DEA models require crisp information that may not be permanently accessible in real-world applications. Nevertheless, in numerous cases, data are unstable, uncertain, and complicated; therefore, they cannot be accurately measured. Zadeh [15] first proposed the theory of fuzzy sets (FSs) against certain logic. After this work, many researchers studied this topic; details of some approaches can be observed in [16,17,18,19,20]. Several researchers also proposed some models of DEA under a fuzzy environment [21,22,23,24,25].

However, Zadeh’s fuzzy sets consider only the membership function and cannot deal with other parameters of vagueness. To overcome this lack of information, Atanassov [26] introduced an extension of FSs called intuitionistic fuzzy sets (IFSs). There are also several models of DEA with intuitionistic fuzzy data: see [27,28,29,30].

Although the theory of IFSs can handle incomplete information for various real-world issues, it cannot address all types of uncertainty such as inconsistent and indeterminate evidence. Therefore, Smarandache [31,32] established the neutrosophic set (NS) as a robust overall framework that generalizes classical and all kinds of fuzzy sets (FSs and IFSs).

NSs can accommodate indeterminate, ambiguous, and conflicting information where the indeterminacy is clearly quantified, and define three kinds of membership function independently.

In the past years, some versions of NSs such as interval neutrosophic sets [33,34], bipolar neutrosophic sets [35,36], single-valued neutrosophic sets [37,38,39], and neutrosophic linguistic sets [40] have been presented. In addition, in the field of neutrosophic sets, logic, measure, probability, statistics, pre-calculus and calculus, and their applications in multiple areas have been extended: see [41,42,43,44].

In real circumstances, some data in DEA may be uncertain, indeterminate, and inconsistent, and considering truth, falsity, and indeterminacy membership functions for each input/output of DMUs in the neutrosophic sets help decision-makers to obtain a better interpretation of information. In addition, by using the NS in DEA, analysts can better set their acceptance, indeterminacy, and rejection degrees regarding each datum. Moreover, with NSs, we can obtain a better depiction of reality through seeing all features of the decision-making procedure. Therefore, the NS can embrace imprecise, vague, incomplete, and inconsistent evidence powerfully and efficiently. Although there are several approaches to solve various problems under neutrosophic environments, there are not many studies that have dealt with DEA under NSs.

The utilization of neutrosophic logic in DEA can be traced to Edalatpanah [45]. Kahraman et al. [46] proposed a hybrid algorithm based on a neutrosophic analytic hierarchy process (AHP) and DEA for bringing a solution to the efficiency of private universities. Edalatpanah and Smarandache [47], based on some operators and natural logarithms, proposed an input-oriented DEA model with simplified neutrosophic numbers. Abdelfattah [48], by converting a neutrosophic DEA into an interval DEA, developed a new DEA model under neutrosophic numbers. Although these approaches are interesting, some restrictions exist. One of them is that these methods have high running times, mainly when we have many inputs and outputs. Furthermore, the main flaw of [48] is the existence of several production frontiers in the steps of efficiency measure, and this leads to the lack of comparability between efficiencies.

Therefore, in this paper, we design an innovative simple model of DEA in which all inputs and outputs are triangular single-valued neutrosophic numbers (TSVNNs), and establish a new efficient strategy to solve it. Furthermore, we use the suggested technique for the performance assessment of 13 hospitals of Tehran University of Medical Sciences (TUMS) of Iran.

The paper unfolds as follows: some basic knowledge, concepts, and arithmetic operations on NSs and TSVNNs are discussed in Section 2. In Section 3, some concepts of DEA and the CCR model are reviewed. In Section 4, we establish the mentioned model of DEA under the neutrosophic environment and propose a method to solve it. In Section 5, the suggested model is utilized for a case study of TUMS. Lastly, conclusions and future directions are presented in Section 6.

2. Preliminaries

In this section, we discuss some basic definitions related to neutrosophic sets and single-valued neutrosophic numbers, respectively.

Smarandache put forward an indeterminacy degree of membership as an independent component in his papers [31,32], and since the principle of excluded middle cannot be applied to new logic, he combines non-standard analysis with three-valued logic, set theory, probability theory, and philosophy. As a result, neutrosophic means “neutral thinking knowledge.” Given this meaning and the use of the term neutral, along with the components of truth (membership) and falsity (non-membership), its distinction is marked by fuzzy sets and intuitionistic fuzzy sets. Here, it is appropriate to give a brief explanation of the non-standard analysis.

In the early 1960s, Robinson developed non-standard analysis as a form of analysis and a branch of logic in which infinitesimals are precisely defined [49]. Formally, $x$is called an infinitesimal number if and only if for any non-null positive integer n we have $\left|x\right|\le \frac{1}{n}.$ Let $\epsilon >0$ be an infinitesimal number; then, the extended real number set is an extension of the set of real numbers that contains the classes of infinite numbers and the infinitesimal numbers. If we consider non-standard finite numbers $1^{+}=1+\epsilon$ and $-0=0-\epsilon ,$ where $0$ and $1$ are the standard parts and $\epsilon$ is the non-standard part, then ${]}^{-}0,1^{+}[$ is a non-standard unit interval. It is clear that $0, 1$, as well as the non-standard infinitesimal numbers that are less than zero and infinitesimal numbers that are more than one belong to this non-standard unit interval. Now, let us define a neutrosophic set:

Definition 1

([31,32,41]) (neutrosophic set). A neutrosophic set in universal U is defined by three membership functions for the truth, indeterminacy, and falsity of x in the real non-standard ${]}^{-}0,1^{+}[$, where the summation of them belongs to [0, 3].

Definition 2

([34]). If the three membership functions of a NS are singleton in the real standard [0, 1], then a single-valued neutrosophic set (SVNS) $\psi$ is denoted by:

$$\psi =\left\{\left(x,{\tau }_{\psi }\left(x\right),{\iota }_{\psi }\left(x\right),{\nu }_{\psi }\left(x\right)\right)\right|x\in U\},$$

which satisfies the following condition:

$$0\le {\tau }_{\psi }\left(x\right)+{\iota }_{\psi }\left(x\right)+{\nu }_{\psi }\left(x\right)\le 3.$$

Definition 3

([38]). A TSVNN $A^{\aleph }=\langle \left(a^l,a^m,a^u\right),\left(b^l,b^m,b^u\right),\left(c^l,c^m,c^u\right)\rangle$ is a particular single-valued neutrosophic number (SVNN) whose ${\tau }_{A^{\aleph }}$ (x), ${\iota }_{A^{\aleph }}$ (x), and ${\nu }_{A^{\aleph }}$ (x) are presented as follows:

$$\begin{gathered} {\tau }_{{}_{A^{\aleph }}}(x)=\{\begin{array}{l}\frac{\left(x-a^l\right)}{\left(a^m-a^l\right)} a^l\le x<a^m,\\ 1 x=a^m,\\ \frac{\left(a^u-x\right)}{\left(a^u-a^m\right)} a^m<x\le a^u,\\ 0 otherwise.\end{array}, \\ {\iota }_{{}_{A^{\aleph }}}(x)=\{\begin{array}{l}\frac{\left(b^m-x\right)}{\left(b^m-b^l\right)} b^l\le x<b^m,\\ 0 x=b^m,\\ \frac{\left(x-b^m\right)}{\left(b^u-b^m\right)} b^m<x\le b^u,\\ 1 otherwise.\end{array}, \\ {\nu }_{{}_{A^{\aleph }}}(x)=\{\begin{array}{l}\frac{\left(c^m-x\right)}{\left(c^m-c^l\right)} c^l\le x<c^m,\\ 0 c=c^m,\\ \frac{\left(x-c^m\right)}{\left(c^u-c^m\right)} c^m<x\le c^u,\\ 1 otherwise.\end{array}, \end{gathered}$$

Definition 4

([38]). Let $A^{\aleph }=\langle \left(a^l,a^m,a^u\right),\left(b^l,b^m,b^u\right),\left(c^l,c^m,c^u\right)\rangle$ and $B^{\aleph }=\langle \left(d^l,d^m,d^u\right),$ $\left(e^l,e^m,e^u\right),\left(f^l,f^m,f^u\right)\rangle$ be two TSVNNs, where their elements are in $\left[L_1,U_1\right].$ Then, Equations (1) to (3) are true:

$$\begin{array}{lll}\left(i\right)A^{\aleph }\oplus B^{\aleph }& =& \langle \left(min(a^l+d^l,U_1\right),min(a^m+d^m,U_1),min(a^u+d^u,U_1);\\ & & \left(min(b^l+e^l,U_1\right),min(b^m+e^m,U_1),min(b^u+e^u,U_1);\\ & & \left(min(c^l+f^l,U_1\right),min(c^m+f^m,U_1),min(c^u+f^u,U_1)\rangle ,\end{array}$$

(1)

$$\left(ii\right)-A^{\aleph }=\langle \left(-a^u,-a^m,-a^l\right),\left(-b^u,-b^m,-b^l\right),\left(-c^u,-c^m,-c^l\right)\rangle ,$$

(2)

$$\left(iii\right)\lambda A^{\aleph }=\langle \left(\lambda a^l,\lambda a^m,\lambda a^u\right),\left(\lambda b^l,\lambda b^m,\lambda b^u\right),\left(\lambda c^l,\lambda c^m,\lambda c^u\right)\rangle ,\begin{array}{c}\end{array}\lambda >0.$$

(3)

Definition 5

([38]). Consider $A^{\aleph }=\langle \left(a^l,a^m,a^u\right),\left(b^l,b^m,b^u\right),\left(c^l,c^m,c^u\right)\rangle$ as a TSVNN. Then, the ranking function of $A^{\aleph }$ can be defined with Equation (4):

$$\xi \left(A^{\aleph }\right)=\frac{\left(a^l+b^l+c^l\right)+2\left(a^m+b^m+c^m\right)+\left(a^u+b^u+c^u\right)}{12}$$

(4)

Definition 6

([20]). Suppose $P^{\aleph }$ and $Q^{\aleph }$ are two TSVNNs, then:

(i) 

$P^{\aleph }\le Q^{\aleph }$if and only if$\xi \left(P^{\aleph }\right)\le \xi \left(Q^{\aleph }\right)$,

(ii) 

$P^{\aleph }<Q^{\aleph }$if and only if$\xi \left(P^{\aleph }\right)<\xi \left(Q^{\aleph }\right)$.

3. Data Envelopment Analysis

Let a set of $n$ DMUs, with each DMUj $\left(j=1,2,\dots ,n\right)$ using $m$inputs $p_{ij}$ $\left(i=1,2,\dots ,m\right)$ produce $s$ outputs $q_{rj}\left(r=1,2,\dots ,s\right)$. If DMU_o is under consideration, then the input-oriented CCR multiplier model for the relative efficiency is computed on the basis of Equation (5) [1]:

$${\theta }_o{}^{*}=max\frac{{{\displaystyle \sum }}_{r=1}^s{v}_r{q}_{ro}}{{{\displaystyle \sum }}_{i=1}^m{u}_i{p}_{io}}$$

(5)

s.t:

$$\begin{gathered} \frac{{{\displaystyle \sum }}_{r=1}^s{v}_r{q}_{rj}}{{{\displaystyle \sum }}_{i=1}^m{u}_i{p}_{ij}}\le 1,\begin{array}{cc}& \end{array}j=1,2,\dots ,n \\ {v}_r,u_i\ge 0r=1,\dots ,s,i=1,\dots ,m. \end{gathered}$$

where $v_r$ and $u_i$ are the related weights. The above nonlinear programming may be converted as Equation (6) to simplify the computation:

$${\theta }_o{}^{*}=max{\displaystyle \sum }_{r=1}^s{v}_r{q}_{ro}$$

(6)

s.t:

$$\begin{gathered} {\displaystyle \sum }_{i=1}^m{u}_i{p}_{io}=1 \\ {\displaystyle \sum }_{r=1}^s{v}_r{q}_{rj}-{\displaystyle \sum }_{i=1}^m{u}_i{p}_{ij}\le 0,\begin{array}{cc}& \end{array}j=1,2,\dots ,n \\ {v}_r,u_i\ge 0r=1,\dots ,s,i=1,\dots ,m. \end{gathered}$$

The DMU_o is efficient if ${\theta }_o{}^{*}=1$; otherwise, it is inefficient.

4. Neutrosophic Data Envelopment Analysis

Like every other model, DEA has been the subject of evolution. One of the critical improvements in this field is related to circumstances where the information of DMUs is characterized and measured beneath conditions of uncertainty and indeterminacy. Indeed, one of the traditional DEA models’ assumptions is their crispness of inputs and outputs.

However, it seems questionable to assume the data and observations are crisp in situations where uncertainty and indeterminacy are inevitable features of a real environment. In addition, most management decisions are not made based on known calculations, and there is a lot of uncertainty, indeterminacy, and ambiguity in decision-making problems. The DEA under a neutrosophic environment is more advantageous than a crisp DEA because a decision-maker, in the preparation of the problem, is not obliged to make a subtle formulation. Furthermore, because of a lack of comprehensive knowledge and evidence, precise mathematics are not sufficient to model a complex system. Therefore, the approach based on neutrosophic logic seems fit for such problems [31,32]. In this section, we establish DEA under a neutrosophic environment.

Consider the input and output for the $j$th DMU as follows:

$${\stackrel{⃛}{p}}_{ij}=\langle {\stackrel{a_i}{p}}_{ij},{\stackrel{b_i}{p}}_{ij},{\stackrel{c_i}{p}}_{ij}\rangle =\langle [{\stackrel{a_1}{p}}_{ij},{\stackrel{a_2}{p}}_{ij},{\stackrel{a_3}{p}}_{ij}],[{\stackrel{b_1}{p}}_{ij},{\stackrel{b_2}{p}}_{ij},{\stackrel{b_3}{p}}_{ij}],[{\stackrel{c_1}{p}}_{ij},{\stackrel{c_2}{p}}_{ij},{\stackrel{c_3}{p}}_{ij}]\rangle ,$$

$${\stackrel{⃛}{q}}_{rj}=\langle {\stackrel{a_i}{q}}_{rj},{\stackrel{b_i}{q}}_{rj},{\stackrel{c_i}{q}}_{rj}\rangle =\langle [{\stackrel{a_1}{q}}_{rj},{\stackrel{a_2}{q}}_{rj},{\stackrel{a_3}{q}}_{rj}],[{\stackrel{b_1}{q}}_{rj},{\stackrel{b_2}{q}}_{rj},{\stackrel{b_3}{q}}_{rj}],[{\stackrel{c_1}{q}}_{rj},{\stackrel{c_2}{q}}_{rj},{\stackrel{c_3}{q}}_{rj}]\rangle ,$$

which are TSVNNs. Then, the triangular single-valued neutrosophic CCR model called TSVNN-CCR is defined as follows:

$${\theta }_o^{{\aleph }^{*}}=max{\displaystyle \sum }_{r=1}^s{v}_r{\stackrel{⃛}{q}}_{ro}$$

(7)

s.t:

$$\begin{gathered} {\displaystyle \sum }_{i=1}^m{u}_i{\stackrel{⃛}{p}}_{io}=1 \\ {\displaystyle \sum }_{r=1}^s{v}_r{\stackrel{⃛}{q}}_{rj}-{\displaystyle \sum }_{i=1}^m{u}_i{\stackrel{⃛}{p}}_{ij}\le 0,\begin{array}{cc}& \end{array}j=1,2,\dots ,n \\ {v}_r,u_i\ge 0r=1,\dots ,s,i=1,\dots ,m. \end{gathered}$$

Next, to solve Model (7), we propose the following algorithm:

Algorithm 1. The solution of TSVNN-CCR Model
Step 1. Construct the problem based on Model (8).
Step 2. Using Definition 3 (ii, iii), transform the TSVNN-CCR model of Step 1 into Model (8):
${\theta }_o^{{\aleph }^{*}}=max{\displaystyle {\displaystyle \sum }_{r=1}^s}\langle [v_r{\stackrel{a_1}{q}}_{ro},v_r{\stackrel{a_2}{q}}_{ro},v_r{\stackrel{a_3}{q}}_{ro}],[v_r{\stackrel{b_1}{q}}_{ro},v_r{\stackrel{b_2}{q}}_{ro},v_r{\stackrel{b_3}{q}}_{ro}],[v_r{\stackrel{c_1}{q}}_{ro},v_r{\stackrel{c_2}{q}}_{ro},v_r{\stackrel{c_3}{q}}_{ro}]\rangle$	(8)
s.t:
${\displaystyle {\displaystyle \sum }_{i=1}^m}\langle [u_i{\stackrel{a_1}{p}}_{io},u_i{\stackrel{a_2}{p}}_{io},u_i{\stackrel{a_3}{p}}_{io}],[u_i{\stackrel{b_1}{p}}_{io},u_i{\stackrel{b_2}{p}}_{io},u_i{\stackrel{b_3}{p}}_{io}],[u_i{\stackrel{c_1}{p}}_{io},u_i{\stackrel{c_2}{p}}_{io},u_i{\stackrel{c_3}{p}}_{io}]\rangle =1$
${\displaystyle {\displaystyle \sum }_{r=1}^s}\langle [v_r{\stackrel{a_1}{q}}_{rj},v_r{\stackrel{a_2}{q}}_{rj},v_r{\stackrel{a_3}{q}}_{rj}],[v_r{\stackrel{b_1}{q}}_{rj},v_r{\stackrel{b_2}{q}}_{rj},v_r{\stackrel{b_3}{q}}_{rj}],[v_r{\stackrel{c_1}{q}}_{rj},v_r{\stackrel{c_2}{q}}_{rj},v_r{\stackrel{c_3}{q}}_{rj}]\rangle \oplus$ ${\displaystyle {\displaystyle \sum }_{i=1}^m}\langle [-u_i{\stackrel{a_3}{p}}_{ij},-u_i{\stackrel{a_2}{p}}_{ij},-u_i{\stackrel{a_1}{p}}_{ij}],[-u_i{\stackrel{b_3}{p}}_{ij},-u_i{\stackrel{b_2}{p}}_{ij},-u_i{\stackrel{b_1}{p}}_{ij}],-[u_i{\stackrel{c_3}{p}}_{ij},-u_i{\stackrel{c_2}{p}}_{ij},-u_i{\stackrel{c_1}{p}}_{ij}]\rangle \le 0,$ $v_r,u_i\ge 0r=1,\dots ,s,i=1,\dots ,m.$
Step 3. Transform Model (8) into the following model:
${\theta }_o^{{\aleph }^{*}}=max\langle \left({\displaystyle {\displaystyle \sum }_{r=1}^s}{v}_r{\stackrel{a_1}{q}}_{ro},{\displaystyle {\displaystyle \sum }_{r=1}^s}{v}_r{\stackrel{a_2}{q}}_{ro},{\displaystyle {\displaystyle \sum }_{r=1}^s}{v}_r{\stackrel{a_3}{q}}_{ro}\right),\left({\displaystyle {\displaystyle \sum }_{r=1}^s}{v}_r{\stackrel{b_1}{q}}_{ro},{\displaystyle {\displaystyle \sum }_{r=1}^s}{v}_r{\stackrel{b_2}{q}}_{ro},{\displaystyle {\displaystyle \sum }_{r=1}^s}{v}_r{\stackrel{b_3}{q}}_{ro}\right),\left({\displaystyle {\displaystyle \sum }_{r=1}^s}{v}_r{\stackrel{c_1}{q}}_{ro},{\displaystyle {\displaystyle \sum }_{r=1}^s}{v}_r{\stackrel{c_2}{q}}_{ro},{\displaystyle {\displaystyle \sum }_{r=1}^s}{v}_r{\stackrel{c_3}{q}}_{ro}\right)\rangle$	(9)
s.t:
$\langle \left({\displaystyle {\displaystyle \sum }_{i=1}^m}{u}_i{\stackrel{a_1}{p}}_{io},{\displaystyle {\displaystyle \sum }_{i=1}^m}{u}_i{\stackrel{a_2}{p}}_{io},{\displaystyle {\displaystyle \sum }_{i=1}^m}{u}_i{\stackrel{a_3}{p}}_{io}\right),\left({\displaystyle {\displaystyle \sum }_{i=1}^m}{u}_i{\stackrel{b_1}{p}}_{io},{\displaystyle {\displaystyle \sum }_{i=1}^m}{u}_i{\stackrel{b_2}{p}}_{io},{\displaystyle {\displaystyle \sum }_{i=1}^m}{u}_i{\stackrel{b_3}{p}}_{io}\right),\left({\displaystyle {\displaystyle \sum }_{i=1}^m}{u}_i{\stackrel{c_1}{p}}_{io},{\displaystyle {\displaystyle \sum }_{i=1}^m}{u}_i{\stackrel{c_2}{p}}_{io},{\displaystyle {\displaystyle \sum }_{i=1}^m}{u}_i{\stackrel{c_3}{p}}_{io}\right)\rangle =1$
$\langle \left({\displaystyle {\displaystyle \sum }_{r=1}^s}{v}_r{\stackrel{a_1}{q}}_{rj}\oplus {\displaystyle {\displaystyle \sum }_{i=1}^m}-u_i{\stackrel{a_3}{p}}_{ij},{\displaystyle {\displaystyle \sum }_{r=1}^s}{v}_r{\stackrel{a_2}{q}}_{rj}\oplus {\displaystyle {\displaystyle \sum }_{i=1}^m}-u_i{\stackrel{a_2}{p}}_{ij},{\displaystyle {\displaystyle \sum }_{r=1}^s}{v}_r{\stackrel{a_3}{q}}_{rj}\oplus {\displaystyle {\displaystyle \sum }_{i=1}^m}-u_i{\stackrel{a_1}{p}}_{ij}\right),$ $\begin{array}{c}\end{array}\left({\displaystyle {\displaystyle \sum }_{r=1}^s}{v}_r{\stackrel{b_1}{q}}_{rj}\oplus {\displaystyle {\displaystyle \sum }_{i=1}^m}-u_i{\stackrel{b_3}{p}}_{ij},{\displaystyle {\displaystyle \sum }_{r=1}^s}{v}_r{\stackrel{b_2}{q}}_{rj}\oplus {\displaystyle {\displaystyle \sum }_{i=1}^m}-u_i{\stackrel{b_2}{p}}_{ij},{\displaystyle {\displaystyle \sum }_{r=1}^s}{v}_r{\stackrel{b_3}{q}}_{rj}\oplus {\displaystyle {\displaystyle \sum }_{i=1}^m}-u_i{\stackrel{b_1}{p}}_{ij}\right),$ $\begin{array}{c}\end{array}\left({\displaystyle {\displaystyle \sum }_{r=1}^s}{v}_r{\stackrel{c_1}{q}}_{rj}\oplus {\displaystyle {\displaystyle \sum }_{i=1}^m}-u_i{\stackrel{c_3}{p}}_{ij},{\displaystyle {\displaystyle \sum }_{r=1}^s}{v}_r{\stackrel{c_2}{q}}_{rj}\oplus {\displaystyle {\displaystyle \sum }_{i=1}^m}-u_i{\stackrel{c_2}{p}}_{ij},{\displaystyle {\displaystyle \sum }_{r=1}^s}{v}_r{\stackrel{c_3}{q}}_{rj}\oplus {\displaystyle {\displaystyle \sum }_{i=1}^m}-u_i{\stackrel{c_1}{p}}_{ij}\right)\rangle \le 0,$ $v_r,u_i\ge 0r=1,\dots ,s,i=1,\dots ,m.$
Step 4. Based on Definitions 4–5, convert TSVNN-CCR Model (9) into crisp Model (10):
${\theta }_o{}^{*}\approx \xi \left({\theta }_o^{{\aleph }^{*}}\right)=max{\displaystyle {\displaystyle \sum }_{r=1}^s}\xi \left(\langle [v_r{\stackrel{a_1}{q}}_{ro},v_r{\stackrel{a_2}{q}}_{ro},v_r{\stackrel{a_3}{q}}_{ro}],[v_r{\stackrel{b_1}{q}}_{ro},v_r{\stackrel{b_2}{q}}_{ro},v_r{\stackrel{b_3}{q}}_{ro}],[v_r{\stackrel{c_1}{q}}_{ro},v_r{\stackrel{c_2}{q}}_{ro},v_r{\stackrel{c_3}{q}}_{ro}]\rangle \right)$	(10)
s.t:
${\displaystyle {\displaystyle \sum }_{i=1}^m}\xi \left(\langle [u_i{\stackrel{a_1}{p}}_{io},u_i{\stackrel{a_2}{p}}_{io},u_i{\stackrel{a_3}{p}}_{io}],[u_i{\stackrel{b_1}{p}}_{io},u_i{\stackrel{b_2}{p}}_{io},u_i{\stackrel{b_3}{p}}_{io}],[u_i{\stackrel{c_1}{p}}_{io},u_i{\stackrel{c_2}{p}}_{io},u_i{\stackrel{c_3}{p}}_{io}]\rangle \right)=1$ ${\displaystyle {\displaystyle \sum }_{r=1}^s}\xi (\langle [v_r{\stackrel{a_1}{q}}_{rj},v_r{\stackrel{a_2}{q}}_{rj},v_r{\stackrel{a_3}{q}}_{rj}],[v_r{\stackrel{b_1}{q}}_{rj},v_r{\stackrel{b_2}{q}}_{rj},v_r{\stackrel{b_3}{q}}_{rj}],[v_r{\stackrel{c_1}{q}}_{rj},v_r{\stackrel{c_2}{q}}_{rj},v_r{\stackrel{c_3}{q}}_{rj}]\rangle )\oplus$ ${\displaystyle {\displaystyle \sum }_{i=1}^m}\xi \left(\langle \left[-u_i{\stackrel{a_3}{p}}_{ii},-u_i{\stackrel{a_2}{p}}_{ij},-u_i{\stackrel{a_1}{p}}_{ij}\right],\left[-u_i{\stackrel{b_3}{p}}_{ij},-u_i{\stackrel{b_2}{p}}_{ij},-u_i{\stackrel{b_1}{p}}_{ij}\right],\left[-u_i{\stackrel{c_3}{p}}_{ij},-u_i{\stackrel{c_2}{p}}_{ij},-u_i{\stackrel{c_1}{p}}_{ij}\right]\rangle \right)\le 0,$ $v_r,u_i\ge 0r=1,\dots ,s,i=1,\dots ,m.$
Step 5. Run Model (10) and get the optimal efficiency of each DMU.

5. Numerical Experiment

In this section, a case study of a DEA problem under a neutrosophic environment is used to reveal the validity and usefulness of the proposed model.

Case Study: The Efficiency of the Hospitals of TUMS

Performance assessments in healthcare frameworks are a noteworthy worry of policymakers so that reforms to improve performance in the health sector are on the policy agenda of numerous national governments and worldwide agencies. In the related literature, various methods such as least squares and simple ratio analysis have been applied to assess the performance of healthcare systems (see for instance: [50,51,52]). Nonetheless, due to the applicability of DEA in the solution of problems with multiple inputs and outputs, it is most commonly used in healthcare systems [53]. The utilizations of DEA in the healthcare sector can be found in several works of literature, including for crisp data [54,55,56], fuzzy data [57,58], and intuitionistic fuzzy data [59]. To the best of our knowledge, none of these current works assessed the efficiency of healthcare organizations with neutrosophic sets. Therefore, to assess the efficiency of the mentioned systems under a neutrosophic environment, we used the proposed model to evaluate 13 hospitals of TUMS. It is worth emphasizing that due to privacy policies, the names of these hospitals are not shared. Furthermore, for the selection of the most suitable and acceptable items of the healthcare system, which are commonly used for measuring efficiency in the literature, we considered two inputs, namely the number of doctors and number of beds, and three outputs, namely the total yearly days of hospitalization of all patients, number of outpatient department visits, and overall patient satisfaction.

For each hospital, we gathered the related data from the medical records unit of the hospitals, Center of Statistics of the University of Medical Sciences, the reliable library, online resources, and the judgments of some experts. After collecting data, we found that the information was sometimes inconsistent, indeterminate, and incomplete. The investigation revealed that several reforms by the mentioned hospitals and other issues have led to considerable uncertainty and indeterminacy about the data. As a result, we identified them as triangular single-valued neutrosophic numbers (TSVNNs). For example, for “Patient Satisfaction,” we collected data in terms of “satisfaction,” “dissatisfaction,” and “abstention,” and for each term, the related data was expressed by a triangular fuzzy number. In addition, each triangular fuzzy number was constructed based on min, average, and max. All data were expressed by using TSVNNs, and can be found in

Table 1. Input information of the nominee hospitals.

DMU	Inputs 1 Number of Doctors	Inputs 2 Number of Beds
1	$\langle \left[404,540,674\right],\left[350,440,560\right],\left[420,645,700\right]\rangle$	$\langle \left[520,530,535\right],\left[520,525,530\right],\left[532,534,540\right]\rangle$
2	$\langle \left[119,136,182\right],\left[122,125,137\right],\left[125,178,200\right]\rangle$	$\langle \left[177,180,188\right],\left[173,175,179\right],\left[185,189,195\right]\rangle$
3	$\langle \left[139,145,158\right],\left[139,140,147\right],\left[146,155,167\right]\rangle$	$\langle \left[208,214,218\right],\left[195,209,215\right],\left[210,217,230\right]\rangle$
4	$\langle \left[86,93,151\right],\left[83,85,87\right],\left[89,138,160\right]\rangle$	$\langle \left[114,116,118\right],\left[114,115,117\right],\left[116,118,125\right]\rangle$
5	$\langle \left[84,93,143\right],\left[84,89,120\right],\left[90,140,155\right]\rangle$	$\langle \left[110,117,121\right],\left[105,112,120\right],\left[113,119,128\right]\rangle$
6	$\langle \left[101,113,170\right],\left[110,112,115\right],\left[112,120,177\right]\rangle$	$\langle \left[101,107,111\right],\left[95,100,104\right],\left[108,112,115\right]\rangle$
7	$\langle \left[561,694,864\right],\left[510,640,750\right],\left[582,857,930\right]\rangle$	$\langle \left[492,495,508\right],\left[492,494,500\right],\left[493,506,520\right]\rangle$
8	$\langle \left[123,179,199\right],\left[122,125,130\right],\left[195,200,205\right]\rangle$	$\langle \left[66,68,73\right],\left[63,67,69\right],\left[68,70,78\right]\rangle$
9	$\langle \left[101,153,155\right],\left[140,145,150\right],\left[145,149,167\right]\rangle$	$\langle \left[192,195,198\right],\left[185,193,197\right],\left[194,196,205\right]\rangle$
10	$\langle \left[147,164,170\right],\left[147,160,167\right],\left[165,169,180\right]\rangle$	$\langle \left[333,340,357\right],\left[335,338,350\right],\left[338,347,364\right]\rangle$
11	$\langle \left[130,158,192\right],\left[110,144,173\right],\left[146,177,205\right]\rangle$	$\langle \left[96,100,114\right],\left[97,99,103\right],\left[99,110,129\right]\rangle$
12	$\langle \left[128,137,187\right],\left[128,133,164\right],\left[134,184,199\right]\rangle$	$\langle \left[213,220,224\right],\left[208,215,223\right],\left[216,222,231\right]\rangle$
13	$\langle \left[151,160,210\right],\left[151,156,187\right],\left[157,207,222\right]\rangle$	$\langle \left[320,327,331\right],\left[315,322,330\right],\left[323,329,338\right]\rangle$

and

Table 2. Output information of the nominee hospitals.

DMU	Outputs 1 Days of Hospitalization (in Thousands)	Outputs 2 Patient Satisfaction (%)	Outputs 3 Number of Outpatients (in Thousands)
1	$\langle \left[121.13,139.24,140.04\right],$ $\left[138.64,139.14,139.81\right],$ $\left[139.14,140.02,141.17\right]\rangle$	$\langle \left[38,41,45\right],$ $\left[38,40,43\right],$ $\left[41,44,49\right]\rangle$	$\langle \left[104.23,114.04,278.51\right],$ $\left[102.37,109.15,235.72\right],$ $\left[104.81,275.25,279.88\right]\rangle$
2	$\langle \left[31.54,34.93,38.89\right],$ $\langle \left[31.54,34.15,38.27\right],$ $\langle \left[34.86,38.15,39.83\right]\rangle$	$\langle \left[40,44,47\right],$ $\left[35,42,45\right],$ $\left[41,46,50\right]\rangle$	$\langle \left[34.54,36.98,54.82\right],$ $\left[36.45,36.80,41.57\right],$ $\left[47.61,54.25,55.35\right]\rangle$
3	$\langle \left[81.62,82.07,85.51\right],$ $\left[81.41,81.94,83.35\right],$ $\left[81.78,85.49,88.16\right]\rangle$	$\langle \left[18,20,29\right],$ $\left[19,21,23\right],$ $\left[28,30,35\right]\rangle$	$\langle \left[157.75,177.57,264.52\right],$ $\left[157.75,176.68,250.75\right],$ $\left[180.29,263.98,272.16\right]\rangle$
4	$\langle \left[19.54,20.41,20.59\right],$ $\left[20.15,20.25,20.32\right],$ $\left[20.54,20.58,20.70\right]\rangle$	$\langle \left[18,21,25\right],$ $\left[15,19,23\right],$ $\left[20,24,30\right]\rangle$	$\langle \left[32.89,35.56,87.74\right],$ $\left[35.25,35.50,35.61\right],$ $\left[87.50,87.94,88.30\right]\rangle$
5	$\langle \left[23.89,24.60,26.09\right],$ $\left[23.56,23.60,23.68\right],$ $\left[25.97,26.35,26.72\right]\rangle$	$\langle \left[30,36,41\right],$ $\left[34,35,37\right],$ $\left[35,40,57\right]\rangle$	$\langle \left[63.23,69.58,120.73\right],$ $\left[63,65.17,94.93\right],$ $\left[64.47,118.75,124.75\right]\rangle$
6	$\langle \left[21.33,21.49,23.31\right],$ $\left[20.94,24.25,22.68\right],$ $\left[21.38,23.14,23.94\right]\rangle$	$\langle \left[50,55,60\right],$ $\left[50,53,57\right],$ $\left[56,59,70\right]\rangle$	$\langle \left[72.84,82.84,94.18\right],$ $\left[82.15,82.68,84.89\right],$ $\left[85.75,93.50,97.18\right]\rangle$
7	$\langle \left[145.77,148.28,169.01\right],$ $\left[145.77,147.16,168.31\right],$ $\left[150.69,168.95,175.18\right]\rangle$	$\langle \left[40,44,46\right],$ $\left[42,43,45\right],$ $\left[43,44,55\right]\rangle$	$\langle \left[147.59,150.37,227.12\right],$ $\left[147.30,147.45,148.25\right],$ $\left[218.24,224.61,229.63\right]\rangle$
8	$\langle \left[11.56,11.74,12.96\right],$ $\left[11.42,11.61,11.98\right],$ $\left[11.58,12.64,13.16\right]\rangle$	$\langle \left[60,75,80\right],$ $\left[55,60,62\right],$ $\left[78,83,85\right]\rangle$	$\langle \left[189.37,202.08,284.99\right],$ $\left[189.37,200.52,281.63\right],$ $\left[270.16,284.55,289.12\right]\rangle$
9	$\langle \left[57.55,62.67,63.03\right],$ $\left[62.15,62.50,62.93\right],$ $\left[62.50,62.97,63.61\right]\rangle$	$\langle \left[32,35,38\right],$ $\left[32,33,35\right],$ $\left[34,36,45\right]\rangle$	$\langle \left[14.63,14.85,29.40\right],$ $\left[14.70,14.75,15.25\right],$ $\left[24.75,28.36,32.64\right]\rangle$
10	$\langle \left[73.21,76.03,81.90\right],$ $\left[75.76,76.05,76.25\right],$ $\left[81.67,82.27,82.64\right]\rangle$	$\langle \left[22,25,40\right],$ $\left[20,24,27\right],$ $\left[23,25,29\right]\rangle$	$\langle \left[96.77,97.27,110.39\right],$ $\left[96.77,96.89,105.14\right],$ $\left[99.76,108.62,115.27\right]\rangle$
11	$\langle \left[22.90,27.71,35.56\right],$ $\left[22.90,26.45,31.28\right],$ $\left[27.92,34.62,39.41\right]\rangle$	$\langle \left[20,23,26\right],$ $\left[21,22,24\right],$ $\left[22,25,30\right]\rangle$	$\langle \left[171.53,182.46,384.99\right],$ $\left[171.12,178.65,210.34\right],$ $\left[175.59,270.65,400.12\right]\rangle$
12	$\langle \left[58.41,59.12,60.61\right],$ $\left[58.08,58.12,58.20\right],$ $\left[60.49,60.87,61.24\right]\rangle$	$\langle \left[25,31,37\right],$ $\left[29,30,32\right],$ $\left[30,35,52\right]\rangle$	$\langle \left[59.87,66.22,117.37\right],$ $\left[59.64,61.81,91.57\right],$ $\left[61.11,115.39,121.39\right]\rangle$
13	$\langle \left[66.97,67.68,69.17\right],$ $\left[66.64,66.68,66.76\right],$ $\left[69.05,69.43,69.80\right]\rangle$	$\langle \left[20,27,31\right],$ $\left[23,26,28\right],$ $\left[24,30,46\right]\rangle$	$\left[96.97,103.32,154.47\right],$ $\left[96.74,98.91,128.67\right],$ $\langle \left[98.21,152.49,158.50\right]\rangle$

.

Next, we used Algorithm 1 to solve the performance valuation problem. For example, Algorithm 1 for DMU₁ can be used as follows:

First, we construct a DEA model with the mentioned TSVNNs:

$$\begin{gathered} max {\tilde{\theta }}_1\approx \langle \left[121.13, 139.24, 140.04\right],\left[138.64, 139.14, 139.81\right],\left[139.14, 140.02, 141.17\right]\rangle v_1\oplus \\ \begin{array}{ccc}\begin{array}{cc}& \end{array}& & \end{array}\langle \left[38,41, 45\right],\left[38, 40, 43\right],\left[41, 44, 49\right]\rangle v_2\oplus \\ \begin{array}{ccc}\begin{array}{cc}& \end{array}& & \end{array}\langle \left[104.23, 114.04, 278.51\right],\left[102.37, 109.15, 235.72\right],\left[104.81, 275.25, 279.88\right]\rangle v_3 \end{gathered}$$

s.t:

$$\begin{gathered} \langle \left[404, 540, 674\right],\left[350, 440, 560\right],\left[420, 645,700\right]\rangle u_1 \\ \oplus \langle \left[520, 530, 535\right],\left[520, 525, 530\right],\left[532, 534, 540\right]\rangle u_2=1, \end{gathered}$$

$$\begin{gathered} (\langle \left[121.13, 139.24, 140.04\right],\left[138.64, 139.14, 139.81\right],\left[139.14, 140.02, 141.17\right]\rangle v_1\oplus \langle \left[38,41, 45\right],\left[38, 40, 43\right], \\ \left[41, 44, 49\right]\rangle v_2\oplus \langle \left[104.23, 114.04, 278.51\right],\left[102.37,109.15, 235.72\right],\left[104.81,275.25, 279.88\right]\rangle v_3)- \\ (\langle \left[404, 540, 674\right],\left[350, 440, 560\right],\left[420, 645,700\right]\rangle u_1\oplus \langle \left[520, 530, 535\right],\left[520, 525, 530\right],\left[532, 534, 540\right]\rangle u_2)\le 0, \end{gathered}$$

$$\begin{gathered} (\langle \left[31.54, 34.93, 38.89\right],\left[31.54, 34.15, 38.27\right],\left[34.86, 38.15, 39.83\right]\rangle v_1\oplus \langle \left[40, 44, 47\right],\left[35, 52,45\right], \\ \left[41, 46, 50\right]\rangle v_2\oplus \langle \left[34.54, 36.98, 54.82 \right],\left[36.45, 36.80, 41.57\right],\left[47.61, 54.25, 55.35\right]>v_3\rangle )- \\ (\langle <\left[109, 126, 172\right], \left[112, 115, 127\right], \left[115, 168,190\right]\rangle u_1\oplus \left[\langle 177,180, 188\right],\left[173,175,179\right], \left[185,189,195\right]\rangle u_2)\le 0, \end{gathered}$$

$$\begin{gathered} (\langle \left[81.62,82.07,85.51\right],\left[81.41,81.94,83.35\right],\left[81.78, 85.49,88.16\right]\rangle v_1\oplus \langle \left[18,20, 29\right],\left[19,21,23\right], \\ \left[28,30,35\right]\rangle v_2\oplus \left[\langle 157.75, 177.57, 264.52 \right],\left[157.75,176.68, 250.75\right],\left[180.29, 263.98, 272.16\right]\rangle v_3)- \\ (\langle \left[139,145,158\right], \left[139,140,147\right], \left[146,155,167\right]\rangle u_1\oplus \langle \left[208,214,218\right], \left[195,209,215\right], \left[210,217,230\right]\rangle u_2)\le 0, \end{gathered}$$

$$\begin{gathered} (\langle \left[19.54, 20.41, 20.59\right],\left[20.15, 20.25, 20.32\right],\left[20.54, 20.58, 20.70\right]\rangle v_1\oplus \langle \left[18, 21, 25\right],\left[15, 19, 23\right], \\ \left[20, 24, 30\right]\rangle v_2\oplus \langle \left[32.89, 35.56, 87.74 \right],\left[35.25, 35.50, 35.61\right],\left[87.50, 87.94, 88.30\right]\rangle v_3)- \\ (\langle \left[86, 93,151\right], \left[83, 85, 87\right], \left[89, 138, 160\right]\rangle u_1\oplus \langle \left[114, 116, 118\right], \left[114, 115, 117\right], \left[116, 118, 125\right]\rangle u_2)\le 0, \end{gathered}$$

$$\begin{gathered} (\langle \left[23.89,24.60,26.09\right],\left[23.56,23.60,23.68\right],\left[25.97,26.35,26.72\right]\rangle v_1\oplus \langle \left[30,36,41\right],\left[34,35,37\right], \\ \left[35,40,57\right]\rangle v_2\oplus \langle \left[63.23, 69.58, 120.73 \right],\left[63, 65.17, 94.93\right],\left[64.47, 118.75, 124.75 \right]\rangle v_3)- \\ \left(\langle \left[84, 93, 143\right], \left[84, 89, 120\right], \left[90, 140, 155\right]\rangle u_1\oplus \langle \left[110, 117,121\right], \left[105, 112,120\right], \left[113, 119, 128\right]\rangle u_2\right)\le 0, \end{gathered}$$

$$\begin{gathered} (\langle \left[21.33, 21.49, 23.31\right],\left[20.94, 24.25, 22.68 \right],\left[21.38, 23.14, 23.94\right]\rangle v_1\oplus \langle \left[50, 55, 60\right],\left[50, 53, 57\right], \\ \left[56, 59, 70\right]\rangle v_2\oplus \langle \left[72.84, 82.84, 94.18 \right],\left[82.15, 82.68, 84.89 \right],\left[85.75, 93.50, 97.18 \right]\rangle v_3)- \\ (\langle \left[101, 113, 170\right],\left[110, 112, 115\right], \left[112, 120, 177\right]\rangle u_1\oplus \langle \left[101,107, 111\right], \left[95, 100, 104\right],\left[108, 112, 115\right]\rangle u_2)\le 0, \end{gathered}$$

$$\begin{gathered} \begin{array}{l}(\langle \left[145.77,148.28,169.01\right],\left[145.77,147.16,168.31\right],\left[150.69,168.95,175.18\right]\rangle v_1\oplus \langle \left[40,44,46\right], \left[42,43,45\right],\\ \left[43,44,55\right]\rangle v_2\oplus \langle \left[147.59,150.37,227.12\right],\left[147.30,147.45,148.25\right],\left[218.24,224.61,229.63\right]\rangle v_3)-\\ (\langle \left[561,694,864\right],\left[510,640,750\right],\left[582,857,930\right]\rangle u_1\oplus \langle \left[492,495,508\right],\left[492,494,500\right],\left[493,506,520\right]\rangle u_2)\le 0,\end{array} \\ (\langle \left[11.56, 11.74, 12.96\right],\left[11.42, 11.61, 11.98\right],\left[11.58, 12.64, 13.16\right]\rangle v_1\oplus \langle \left[60, 75,80\right],\left[55,60,62\right],\left[78,83,85\right]\rangle v_2\oplus \langle \left[189.37, 202.08, 284.99 \right],\left[189.37, 200.52, 281.63\right],\left[270.16, 284.55, 289.12\right]\rangle v_3)-(\langle \left[123, 179, 199\right],\left[122, 125, 130\right], \left[195, 200, 205\right]\rangle u_1\oplus \langle \left[66, 68, 73\right],\left[63, 67, 69\right],\left[68,70, 78\right]\rangle u_2)\le 0, \end{gathered}$$

$$(\langle \left[57.55,62.67,63.03\right],\left[62.15, 62.50, 62.93\right],\left[62.50,62.97,63.61\right]\rangle v_1\oplus \langle \left[32,35,38\right],\left[32,33,35\right],\left[34,36,45\right]\rangle v_2\oplus \langle \left[14.63,14.85, 29.40\right],\left[14.70,14.75,15.25\right],\left[24.75,28.36,32.64\right]\rangle v_3)-(\langle \left[101,153,155\right], \left[140,145,150\right], \left[145,149,167\right]\rangle u_1\oplus \langle \left[192,195,198\right],\left[185,193,197\right],\left[194,196,205\right]\rangle u_2)\le 0,$$

$$(\langle \left[73.21, 76.03, 81.90 \right],\left[75.76,76.05,76.25\right],\left[81.67,82.27,82.64\right]\rangle v_1\oplus \langle \left[22,25,40\right],\left[20,24,27\right],\left[23,25,29\right]\rangle v_2\oplus \langle \left[96.77,97.27,110.39\right],\left[96.77,96.89,105.14\right],\left[99.76,108.62,115.27\right]\rangle v_3)-(\langle \left[147,164,170\right], \left[147,160,167\right], \left[165,169,180\right]\rangle u_1\oplus \langle \left[333, 340,357\right],\left[335,338,350\right],\left[338,347,364\right]\rangle u_2)\le 0,$$

$$(\langle \left[22.90,27.71,35.56\right],\left[22.90, 26.45, 31.28\right],\left[27.92,34.62,39.41\right]\rangle v_1\oplus \langle \left[20, 23,26\right],\left[21,22,24\right],\left[22, 25,30\right]\rangle v_2\oplus \langle \left[171.53,182.46,384.99 \right],\left[171.12,178.65,210.34\right],\left[175.59,270.65,400.12\right]\rangle v_3)-(\langle \left[130,158,192\right], \left[110,144,173\right], \left[146,177,205\right]\rangle u_1\oplus \langle \left[96,100,114\right],\left[97,99,103\right],\left[99,110,129\right]\rangle u_2)\le 0,$$

$$\begin{array}{l}(\langle \left[58.41,59.12,60.61\right],\left[58.08,58.12,58.20\right],\langle \left[60.49,60.87,61.24\right]\rangle v_1\oplus \langle \left[25,31,37\right], \left[29,30,32\right],\\ \langle \left[30,35,52\right]\rangle v_2\oplus \langle \begin{array}{l}\left[59.87,66.22,117.37\right],\hfill \end{array}\left[59.64,61.81,91.57\right],\left[61.11,115.39,121.39\right]\rangle v_3)-\\ (\langle \left[128,137,187\right],\left[128,133,164\right],\left[134,184,199\right]\rangle u_1\oplus \langle \left[213,220,224\right],\left[208,215,223\right],\left[216,222,231\right]\rangle u_2)\le 0,\end{array}$$

$$(\langle \left[66.97, 67.68, 69.17\right],\left[66.64, 66.68, 66.76\right],\left[69.05, 69.43, 69.80\right]\rangle v_1\oplus \langle \left[20,27,31\right],\left[23,26,28\right],\left[24,30,46\right]\rangle v_2\oplus \begin{array}{c}\langle \left[96.97, 103.32, 154.47 \right],\end{array}\left[96.74, 98.91, 128.67\right],\left[98.21, 152.49, 158.50 \right]\rangle v_3)-(\langle \left[151,160,210\right], \left[151,156,187\right], \left[157,207, 222\right]\rangle u_1\oplus \langle \left[320,327,331\right],\left[315,322,330\right],\left[323,329,338\right]\rangle u_2)\le 0,$$

$$v_r,u_i\ge 0,r=1,2,3,i=1,2.$$

Finally, based on Definition 4, we convert the above model to the following model:

$$max {\tilde{\theta }}_1\approx {138.0608v}_1{+42v}_2+{175.2v}_3$$

s.t:

$$\begin{gathered} {529.8333u}_1+{529.5833u}_2=1, \\ {138.0608v}_1{+42v}_2+{175.2v}_3-{529.8333u}_1-{529.5833u}_2\le 0, \\ {35.7792v}_1+{43.5v}_2+{43.8667v}_3-{146.9167u}_1-{182.0833u}_2\le 0, \\ {83.4025v}_1+{24.5v}_2+{209.9733v}_3{-148u}_1{-213u}_2\le 0, \\ {20.36v}_1+{21.5833v}_2+{57.1075v}_3-{104.3333u}_1-{116.8333u}_2\le 0, \\ {24.9175v}_1{+38v}_2+{86.5092v}_3{-110u}_1-116{.0833u}_2\le 0, \\ {22.6117v}_1+{56.4167v}_2+{86.2525v}_3-{122.9167u}_1{-106u}_2\le 0, \\ {156.9592v}_1+{44.4167v}_2+{180.2492v}_3-{714.9167u}_1-{499.5833u}_2\le 0, \\ {12.0533v}_1+{71.3333v}_2+{239.9117v}_3-{165.1667u}_1-{68.9167u}_2\le 0, \\ {62.3375v}_1+{35.3333v}_2+{20.6075v}_3{-146u}_1-{194.9167u}_2\le 0, \\ {78.3442v}_1+{25.75v}_2+{102.4717v}_3-{163.5u}_1-{343.9167u}_2\le 0, \\ {29.7942v}_1+{23.5833v}_2+{231.4342v}_3-{159.5u}_1-{104.6667u}_2\le 0, \\ {59.4375v}_1+{33.0833v}_2+{83.1492v}_3{-154u}_1-{219.0833u}_2\le 0, \\ {67.9975v}_1+{28.1667v}_2+{120.25v}_3{-177u}_1-{326.0833u}_2\le 0, \\ {v}_r,u_i\ge 0,r=1,2,3,i=1,2. \end{gathered}$$

After computations with Lingo, we obtained ${\theta }_1^{*}=0.6673$ for DMU₁. Similarly, for the other DMUs, we reported the results in

Table 3. The efficiencies of the decision-making units (DMUs) by the triangular single-valued neutrosophic number-Charnes, Cooper, and Rhodes (TSVNN-CCR) model.

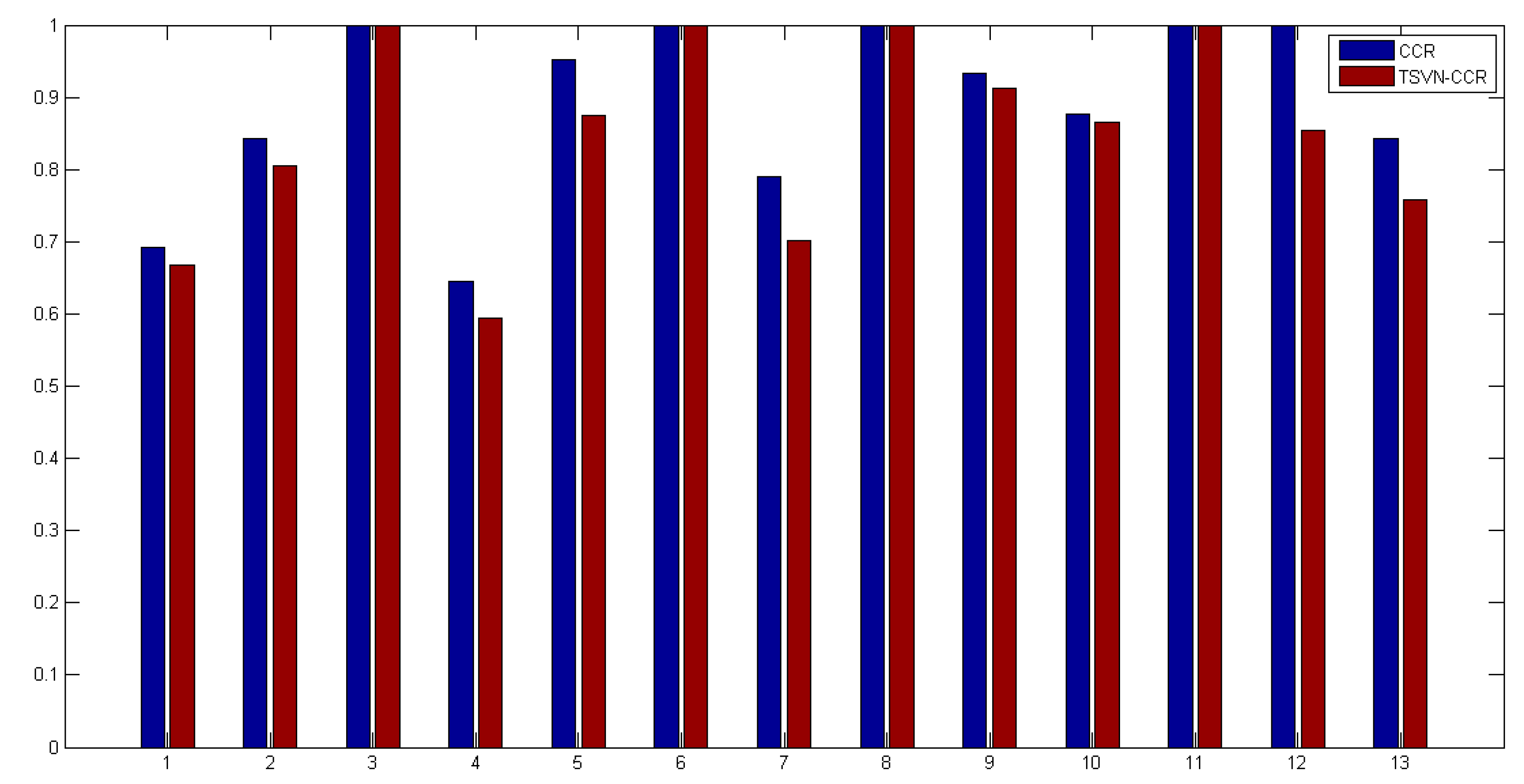
DMUs	Efficiency	Ranking
1	0.6673	9
2	0.8057	6
3	1.00	1
4	0.5950	10
5	0.8754	4
6	1.00	1
7	0.7024	7
8	1.00	1
9	0.9116	2
10	0.8751	3
11	1.00	1
12	0.8536	5
13	0.7587	8

. From these results, we can see that DMUs 3, 6, 8, and 11 are efficient and others are inefficient.

To authenticate the suggested efficiencies, these efficiencies were compared with the efficiencies obtained by the crisp CCR (Model (6)), and are given in Figure 1. In this figure, the efficiencies of DMUs are found to be smaller for TSVNN-CCR compared to crisp CCR.

It is interesting that DMU 12 is efficient in crisp DEA, but it is inefficient with an efficiency score of 0.8536 using TSVNN-CCR. Therefore, TSVNN-CCR is more realistic than crisp CCR. In addition, crisp CCR and TSVNN-CCR may give the same efficiencies for certain data. However, the crisp CCR model does not deal with the uncertain, indeterminate, and incongruous information. Therefore, TSVNN-CCR is more realistic than crisp CCR.

6. Conclusions and Future Work

In this paper, a new approach for data envelopment analysis was proposed in that indeterminacy, uncertainty, vagueness, inconsistent, and incompleteness of data were shown by neutrosophic sets. Furthermore, the sorting of DMUs in DEA has been presented, and using a de-neutrosophication technique, a ranking order has been extracted. The efficiency scores of the proposed model have a similar meaning and interpretation with the conventional CCR model. Finally, the application of the proposed model was examined in a real-world case study of 13 hospitals of TUMS. The new model is appropriate in situations where some inputs or outputs do not have an exact quantitative value, and the proposed approach has produced promising results from computing efficiency and performance aspects.

The proposed study had some barriers: first, the indeterminacy, uncertainty, and ambiguity in the present report was limited to triangular single-valued neutrosophic numbers, but the other forms of NSs such as bipolar NSs and interval-valued neutrosophic numbers can also be used to indicate variables characterizing the neutrosophic core in global problems. Second, the presented model was investigated under a constant returns-to-scale (CRS), but the suggested method can also be extended under a VRS assumption, so we plan to extend this model to the VRS. Moreover, although the arithmetic operations, model, and results presented here demonstrate the effectiveness of our methodology, it could also be considered in other types of DEA models such as network DEA and its applications to banks, supplier selection, tax offices, police stations, schools, and universities. While developing data envelopment analysis, models based on bipolar and interval-valued neutrosophic data is another area for further studies. As for future research, we intend to study these problems.