Utilization of Second Order Slip, Activation Energy and Viscous Dissipation Consequences in Thermally Developed Flow of Third Grade Nanofluid with Gyrotactic Microorganisms
Abstract
1. Introduction
2. Mathematical Modelling
3. Numerical Scheme
4. Results Validation
5. Discussion
6. Conclusions
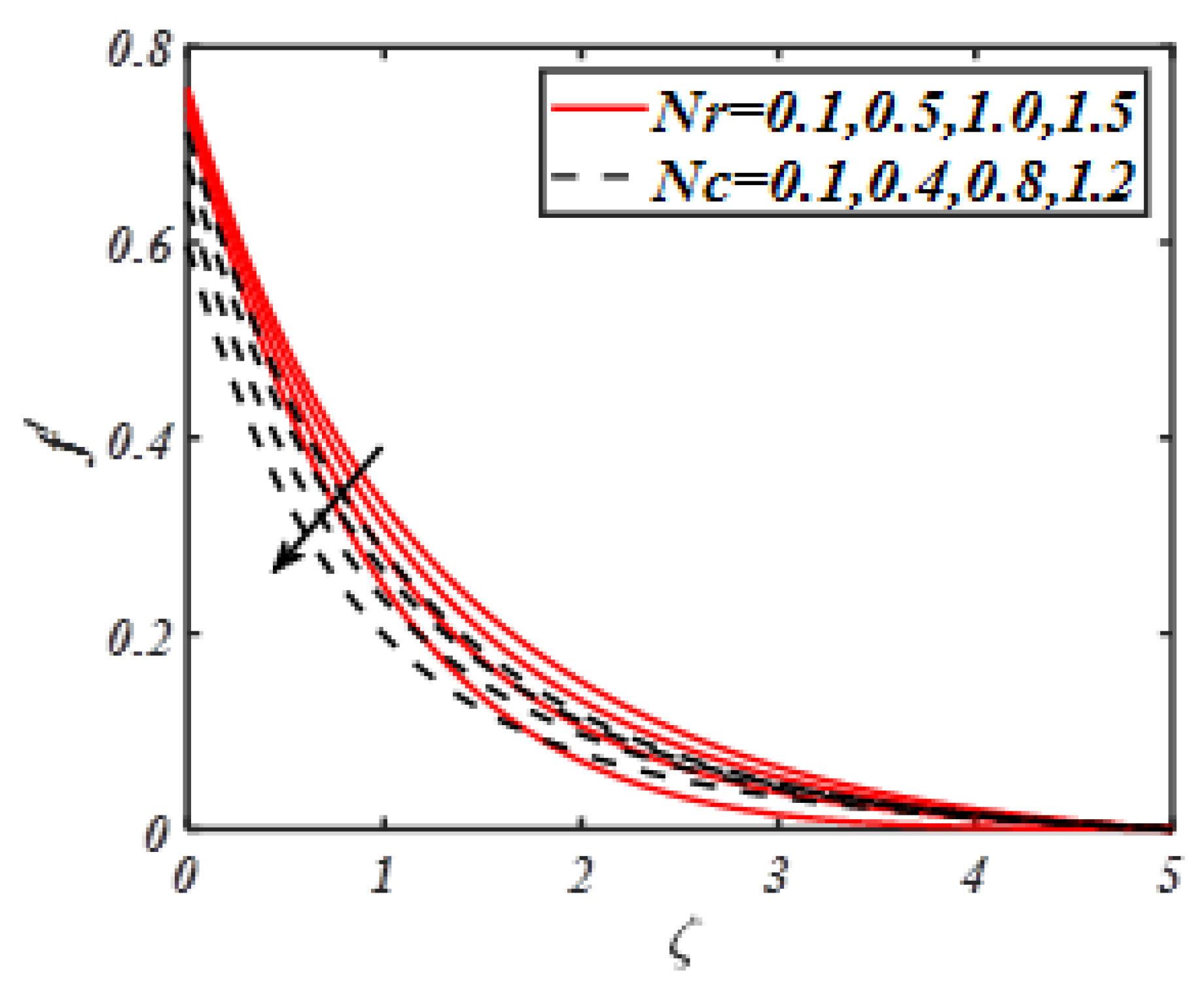
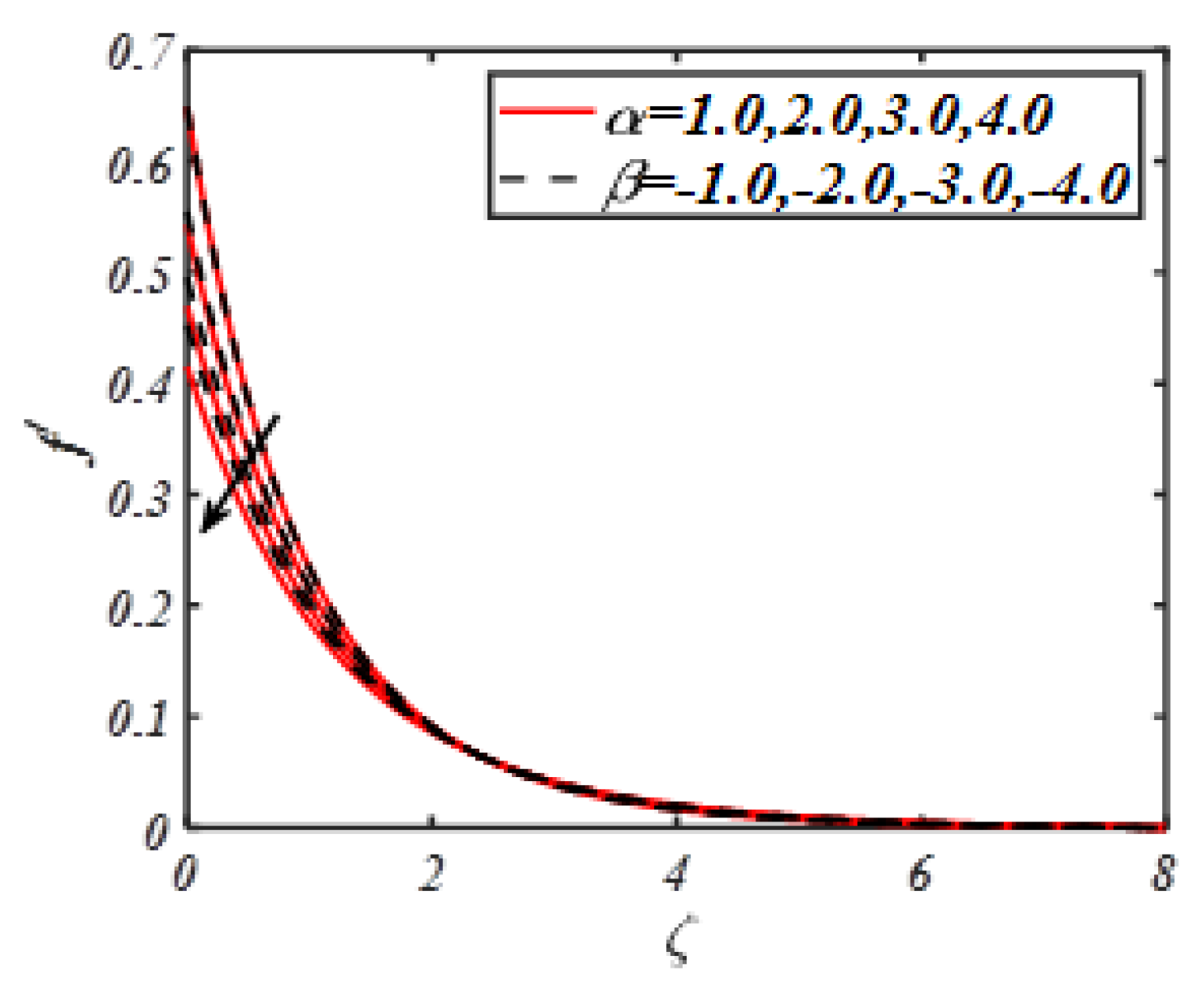
- A lower velocity profile is observed with interaction of buoyancy ratio constant and slip parameters.
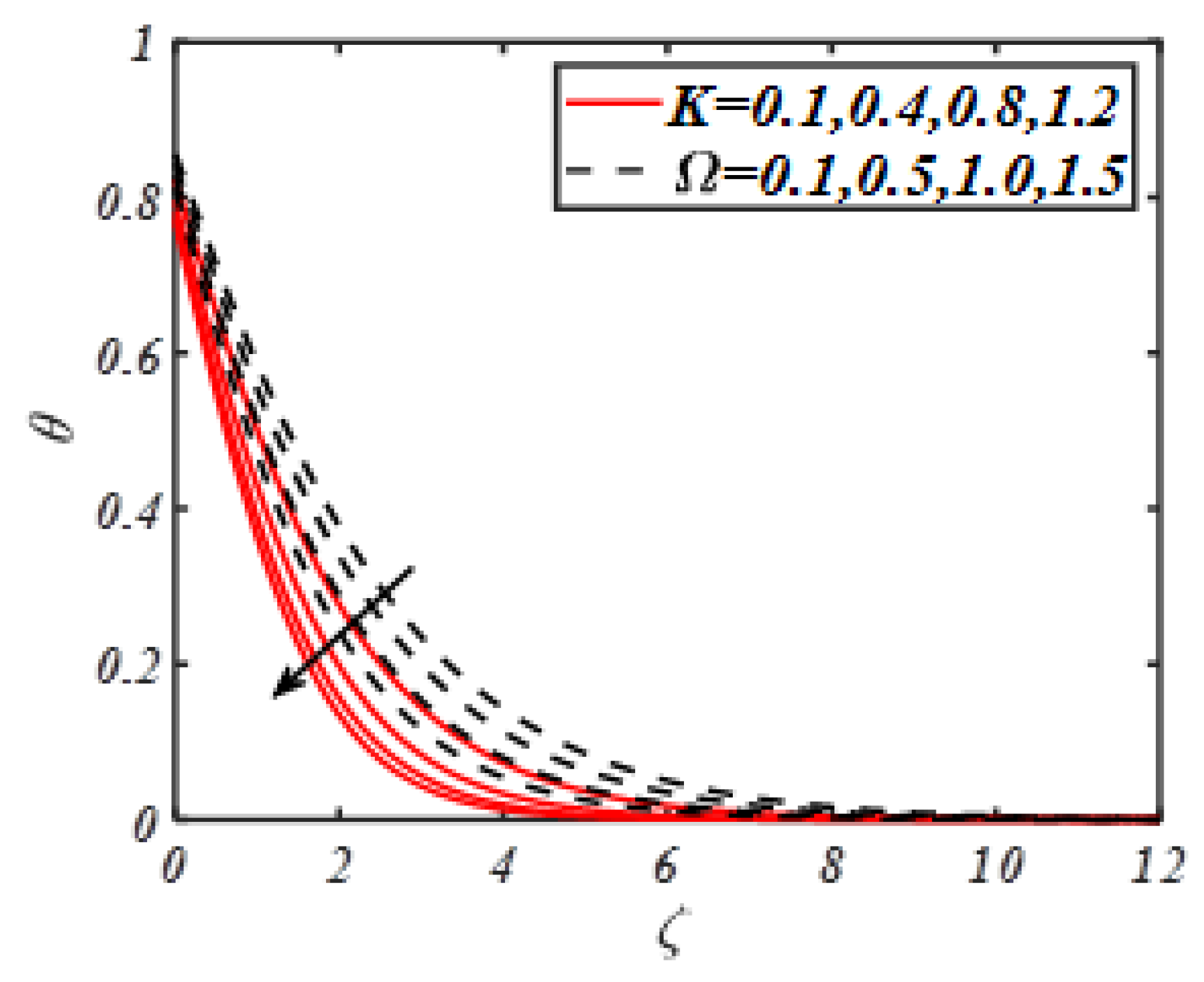
- The change in material parameters depressed the nanoparticles’ temperature effectively.
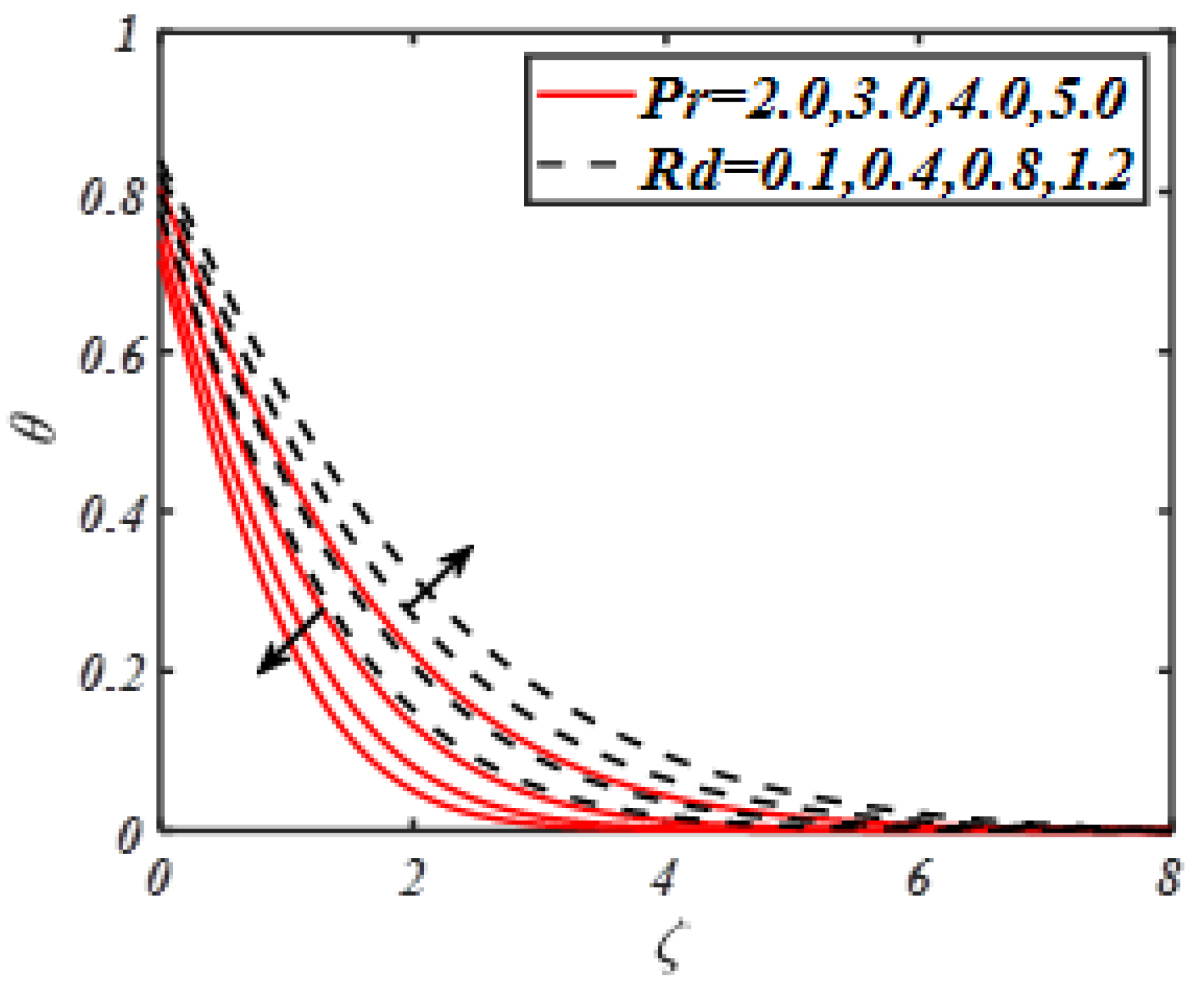
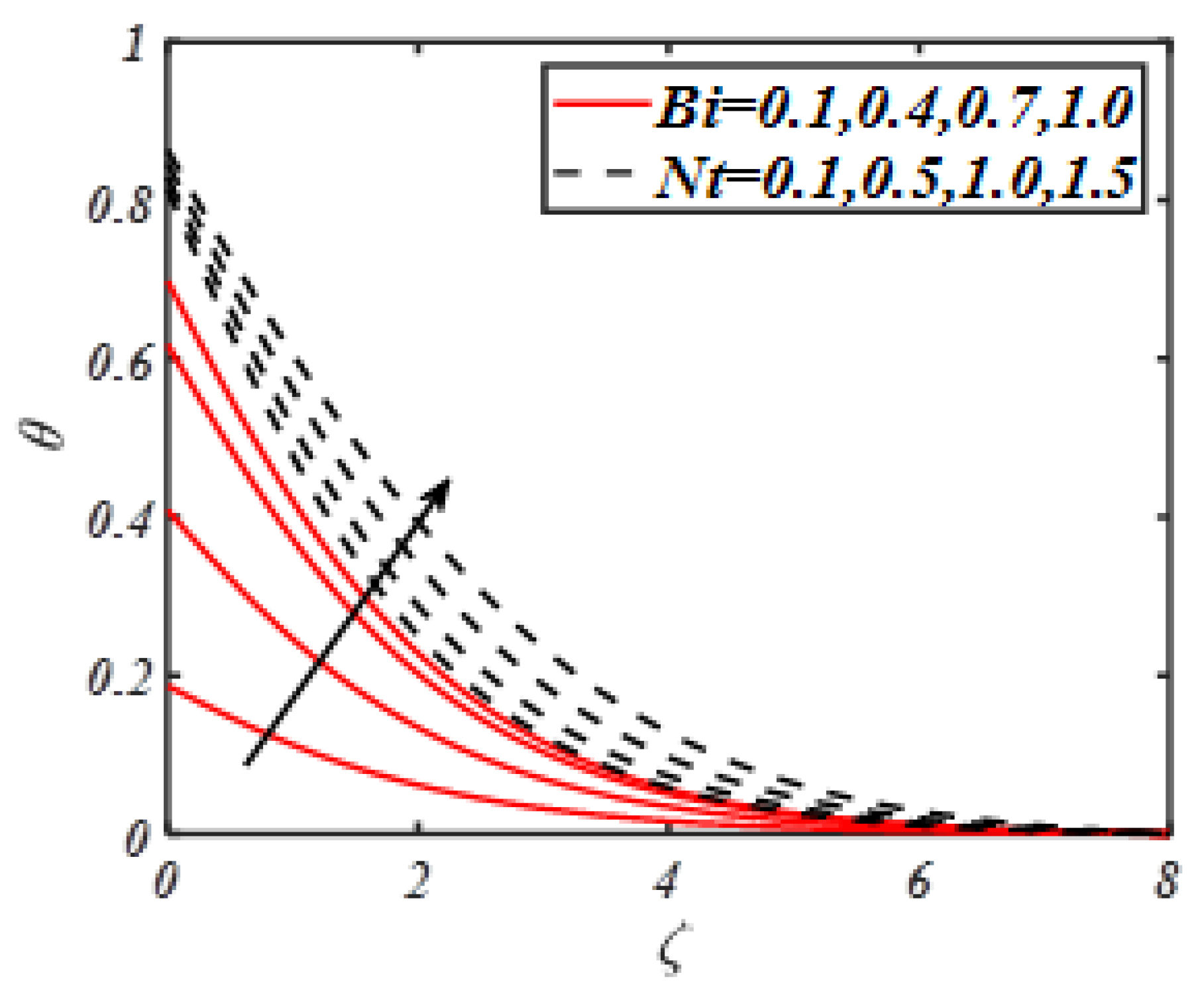
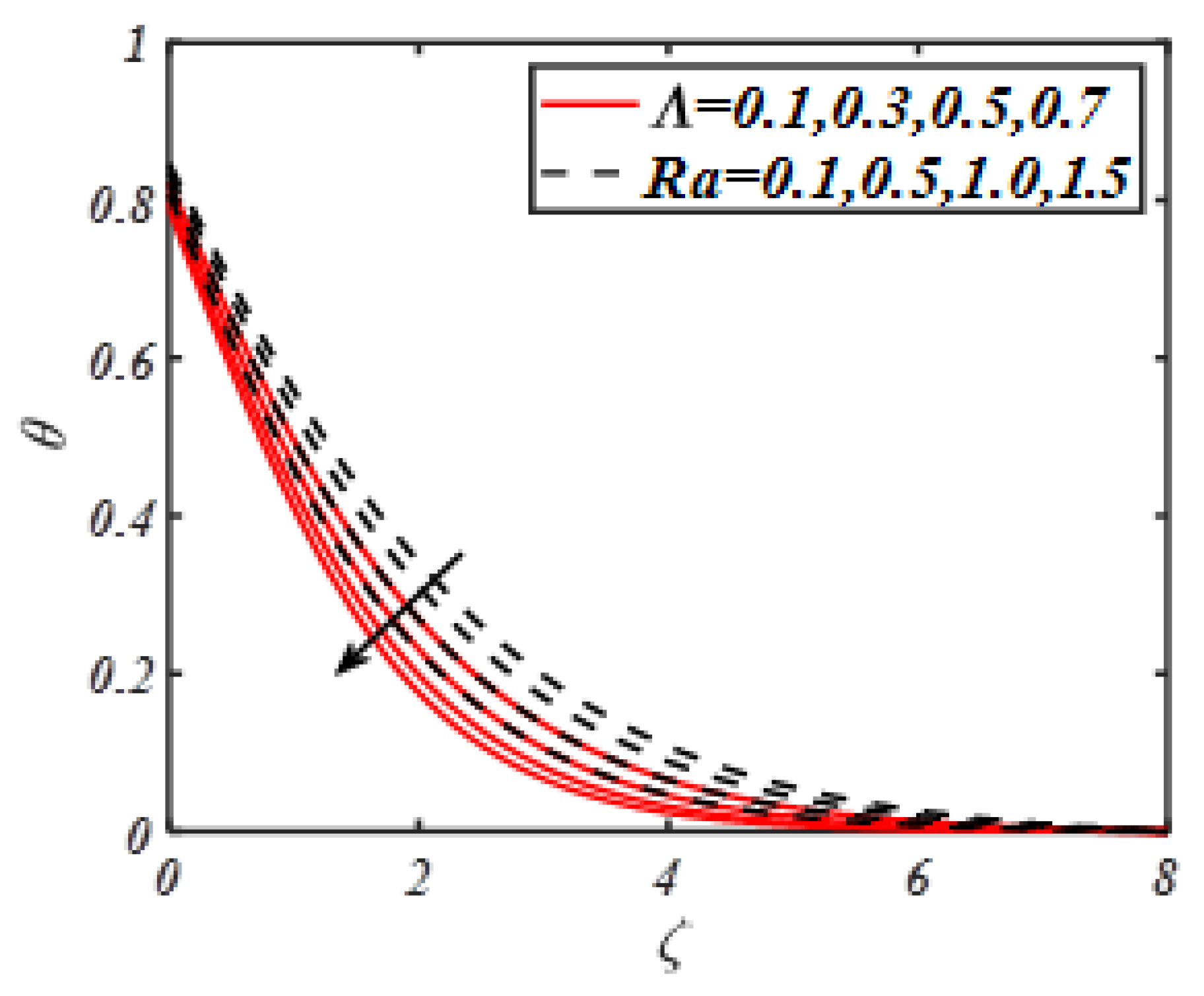
- The temperature profile gets maximum variation with thermophoresis parameter, Biot number and radiation constant.
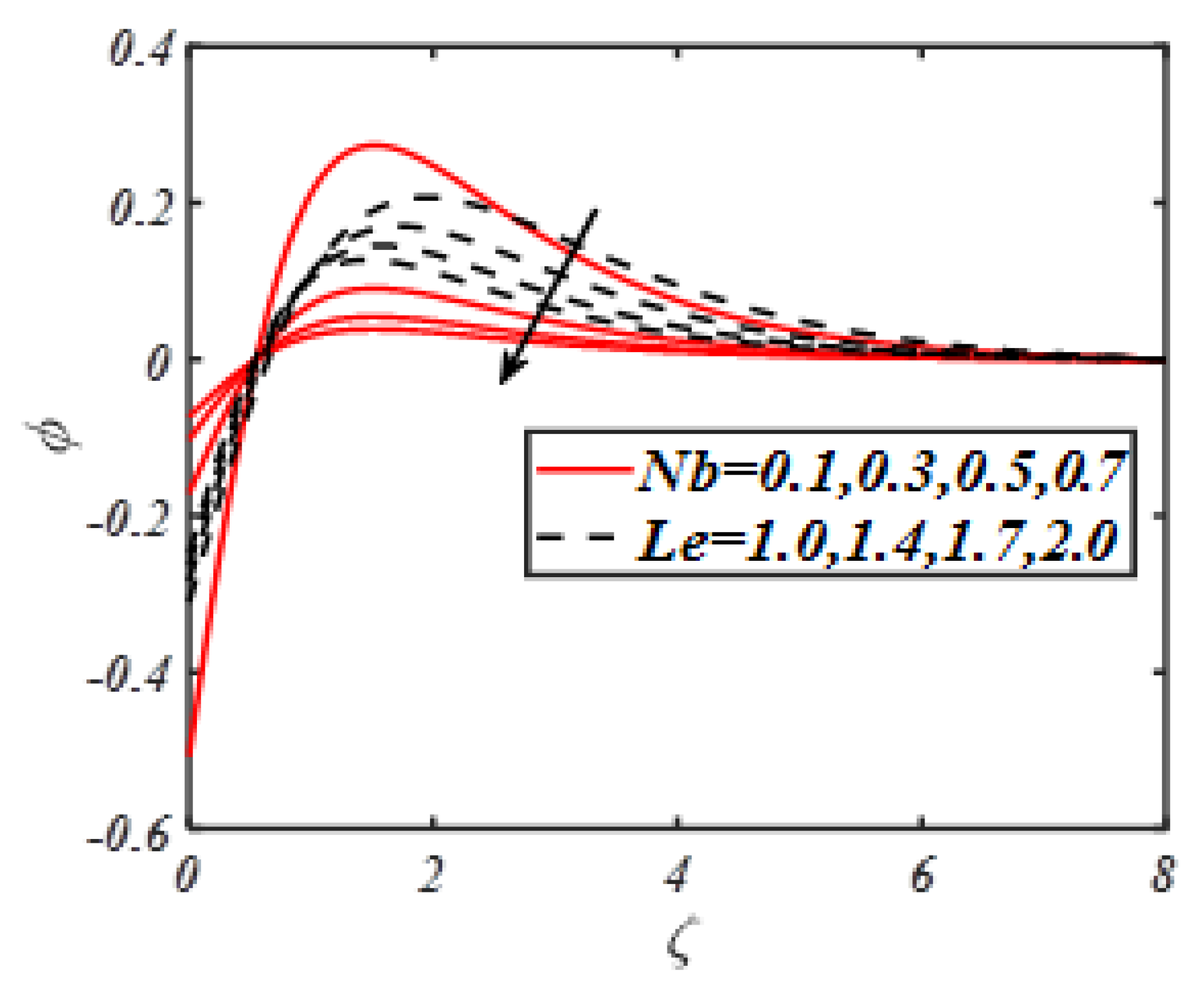
- It further emphasizes that rate of mass transportation can be controlled by increasing Schmidt number and Brownian motion parameter.
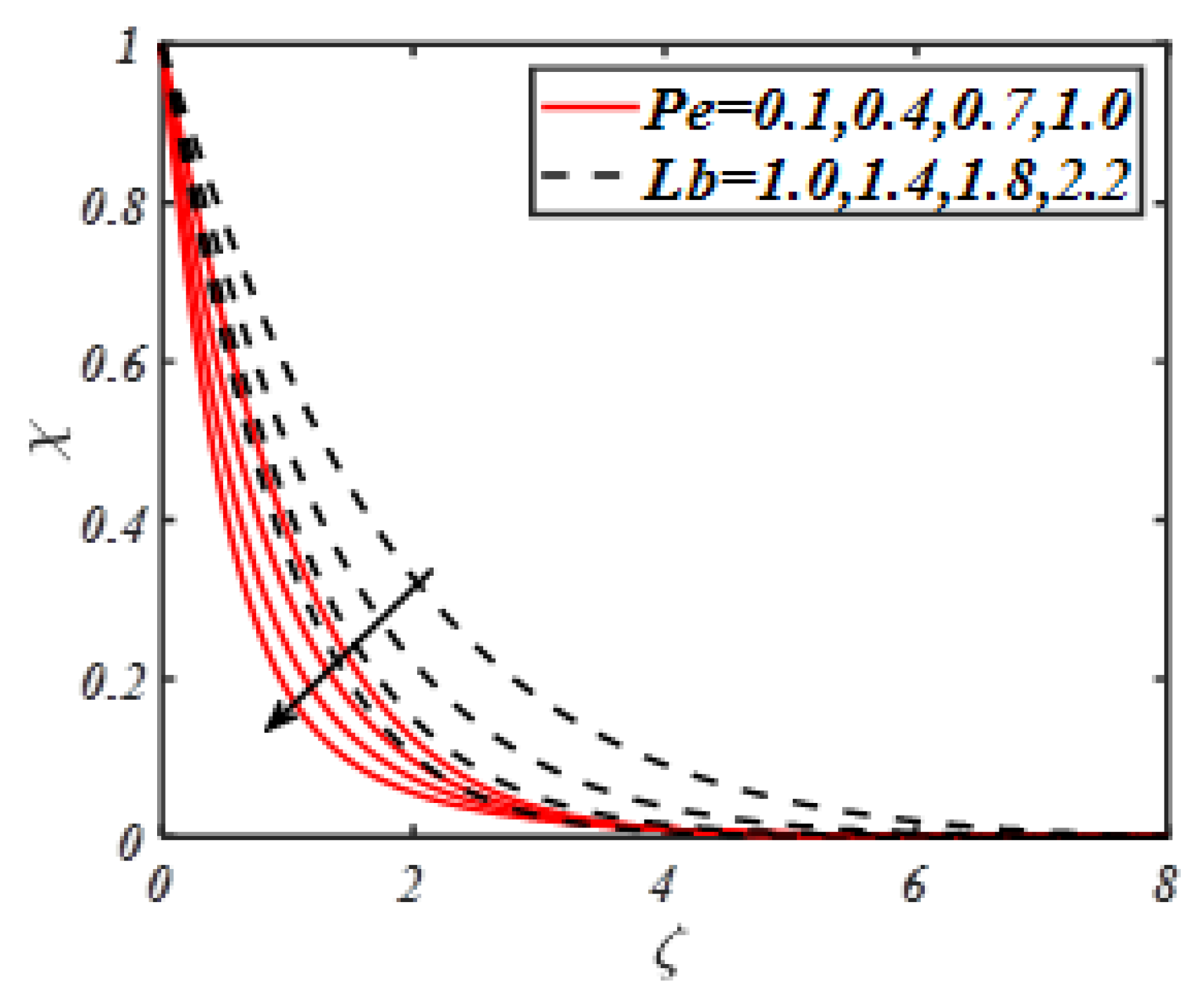
- It is claimed that the presence of slip factors is more useful to improve the combined heat and mass transportation and motile microorganisms’ density profiles.
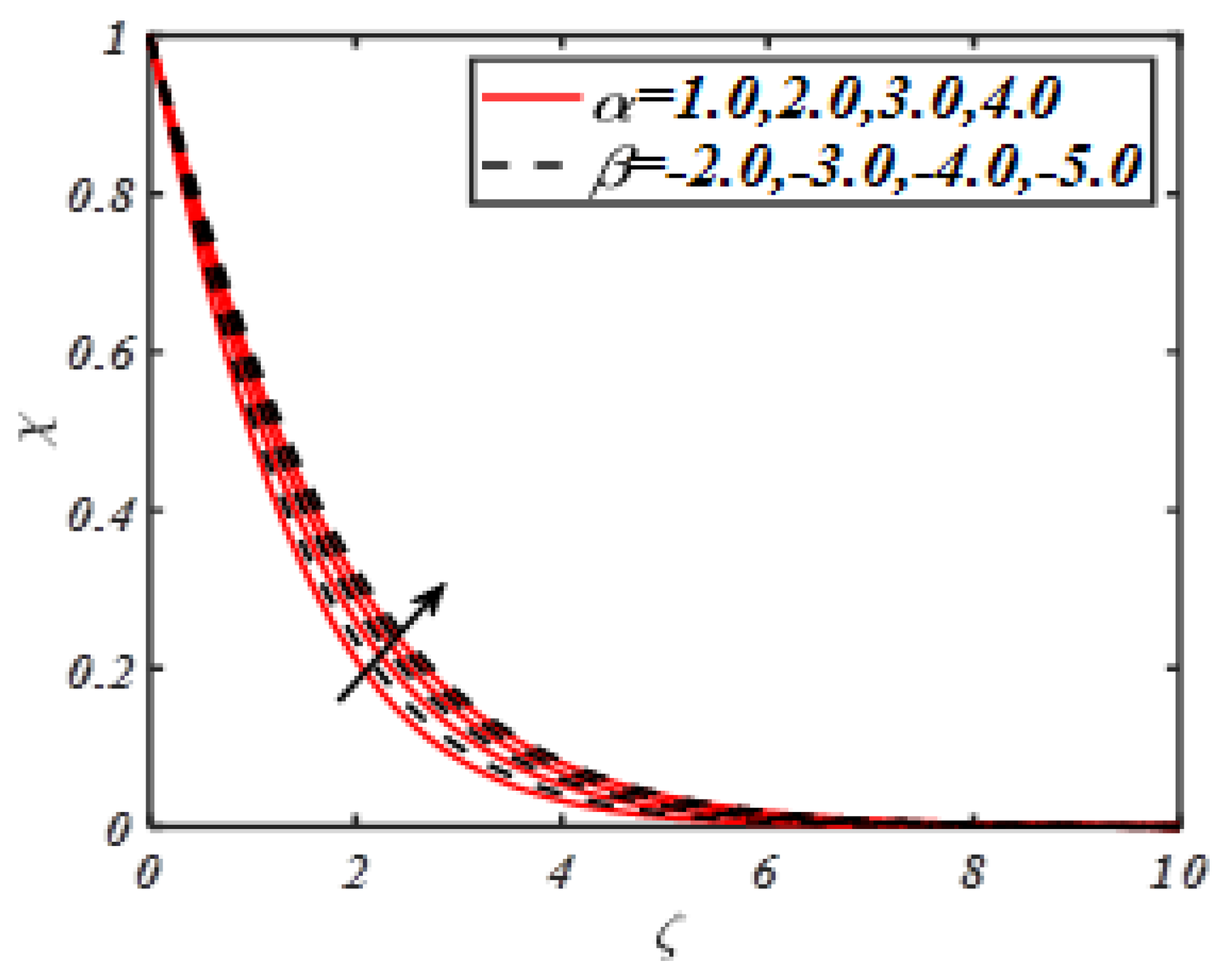
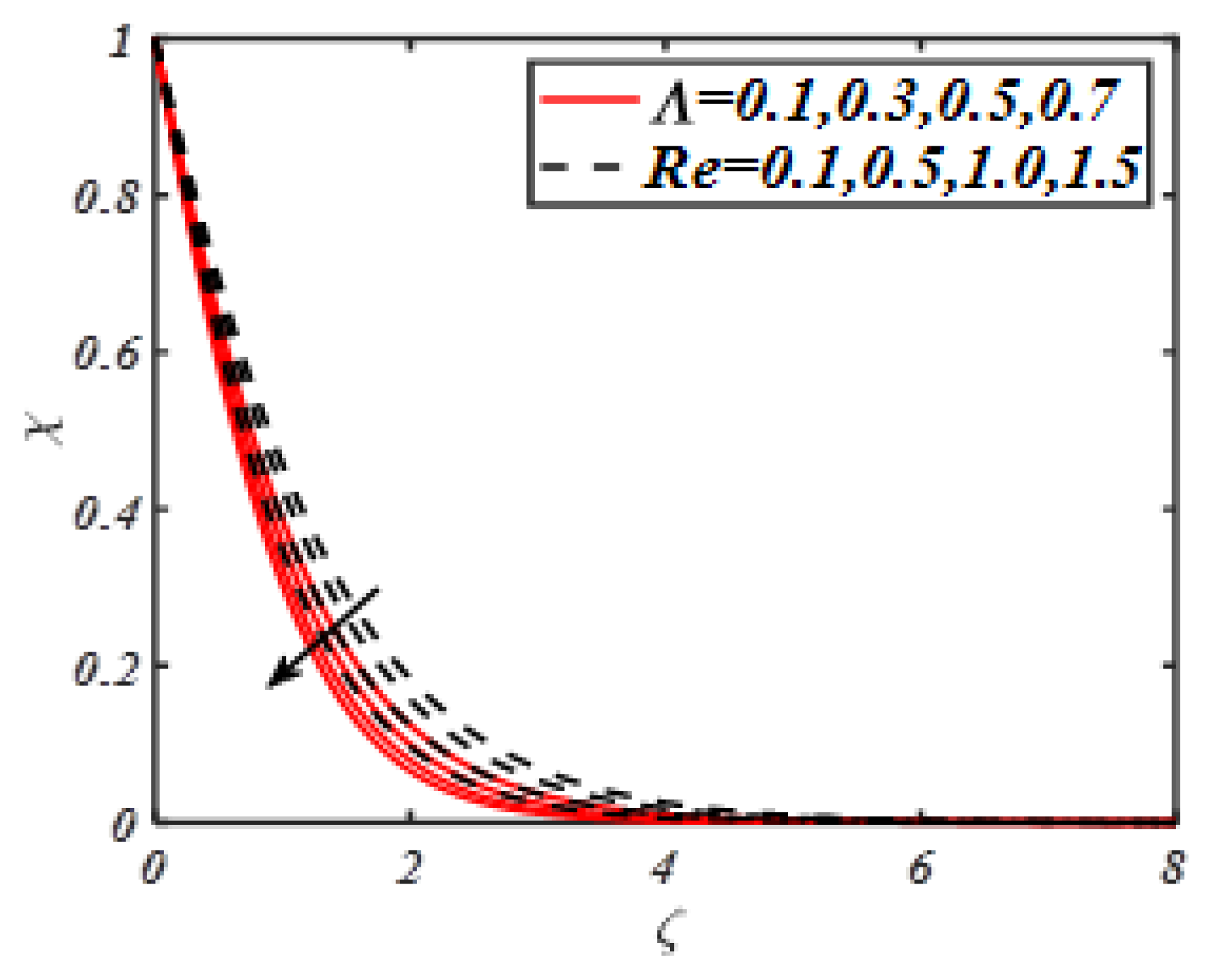
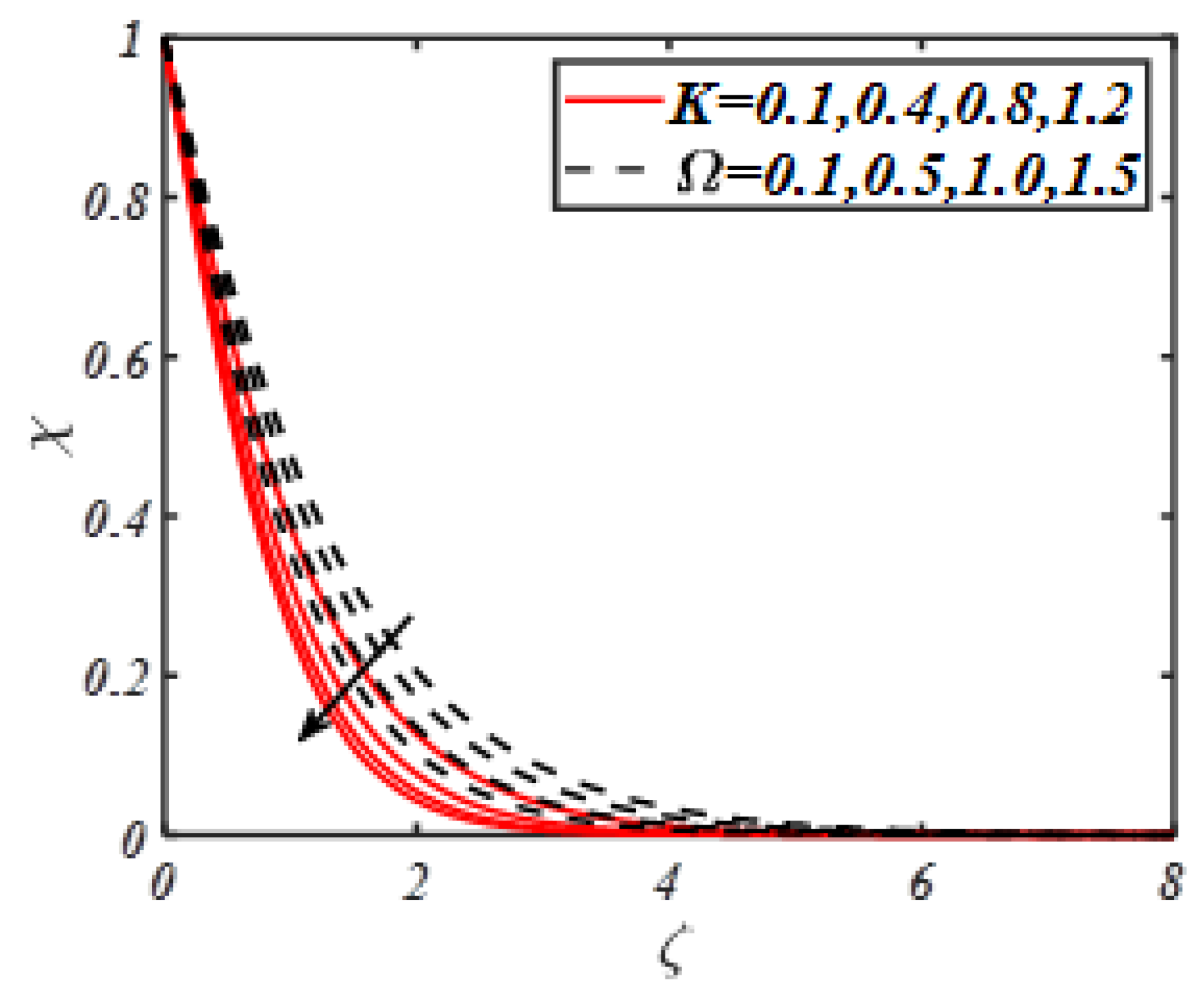
- It is further examined that presence of material parameters reduces the motile microorganisms’ density profiles.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| (u,ν) velocity components | α1 material parameter, |
| ν is kinematic viscosity, | ρf is the fluid density, |
| β3 being third-grade fluid parameter, | β* volume expansion coefficient |
| g* gravity, | ρp is the nanoparticles density, |
| ρm is the microorganisms’ particles’ density, | T is the temperature, |
| C represents the concentration, | N microorganisms’ density, |
| αe thermal diffusivity, | k* mean absorption coefficients, |
| σ* Stephan-Boltzmann, | (ρc)f is effective heat capacity of base fluid, |
| (ρc)p effective heat capacity of nanoparticles, | DB reports the diffusion constant, |
| DT thermodiffusion constant, | K1r reaction rate, κ |
| Boltzmann constant, | Ea activation energy, |
| We is speed of cells | b1 denotes the chemotaxis constant. |
| hf represents the heat transfer coefficient | Tf convective fluid temperature |
| kn, Knudsen number | Λ momentum coefficient |
| ε molecular mean free path | M is Hartmann number |
| K is material parameter, | Λ mixed convection parameter, |
| Nr buoyancy ratio parameter, | Nc bioconvection Rayleigh number |
| Re is Reynolds number, | Ω is third-grade fluid parameter |
| Pr Prandtl number, | Rd radiation parameter |
| Nb Brownian motion parameter, | Nt thermophoresis parameter |
| Ec Eckert number, | Le Lewis number |
| σ** is reaction constant | δ temperature difference parameter |
| E activation energy parameter | δ1 specify microorganism concentration difference constant |
| Pe Peclet number | Lb determine the bioconvection Lewis number |
| Bi thermal Biot number | α first-order slip and |
| β second-order slip constants |
References
- Choi, S.U.S. Enhancing thermal conductivity of fluids with nanoparticles. ASME Pub. Fed. 1995, 231, 99–106. [Google Scholar]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Sandeep, N.; Sulochana, C. Momentum and heat transfer behaviour of Jeffrey, Maxwell and Oldroyd-B nanofluids past a stretching surface with non-uniform heat source/sink. Ain Shams Eng. J. 2018, 9, 517–524. [Google Scholar] [CrossRef]
- Pal, D.; Mandal, G. Thermal radiation and MHD effects on boundary layer flow of micropolar nanofluid past a stretching sheet with non-uniform heat source/sink. Int. J. Mech. Sci. 2016, 126, 308–318. [Google Scholar] [CrossRef]
- Khan, M.; Irfan, M.; Khan, W.A. Impact of heat source/sink on radiative heat transfer to Maxwell nanofluid subject to revised mass flux condition. Results Phys. 2018, 9, 851–857. [Google Scholar] [CrossRef]
- Hayat, T.; Rashid, M.; Khan, M.I.; Alsaedi, A. Melting heat transfer and induced magnetic field effects on flow of water based nanofluid over a rotating disk with variable thickness. Results Phys. 2018, 9, 1618–1630. [Google Scholar] [CrossRef]
- Tlili, I.; Khan, W.A.; Khan, I. Multiple slips effects on MHD SA-Al2O3 and SA-Cu non-Newtonian nanofluids flow over a stretching cylinder in porous medium with radiation and chemical reaction. Results Phys. 2018, 8, 213–222. [Google Scholar] [CrossRef]
- Khan, S.U.; Shehzad, S.A. Brownian movement and thermophoretic aspects in third grade nanofluid over oscillatory moving sheet. Phys. Scr. 2019, 94, 095202. [Google Scholar] [CrossRef]
- Waqas, H.; Imran, M.; Khan, S.U.; Shehzad, S.A.; Meraj, M.A. Slip flow of Maxwell viscoelasticity-based micropolar nano particles with porous medium: A numerical study. Appl. Math. Mech. 2019, 40, 1255–1268. [Google Scholar] [CrossRef]
- Hsiao, K. Micropolar nanofluid flow with MHD and viscous dissipation effects towards a stretching sheet with multimedia feature. Int. J. Heat Mass Transf. 2017, 112, 983–990. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Bhatti, M.M. Forced convection of nanofluid in presence of constant magnetic field considering shape effects of nanoparticles. Int. J. Heat Mass Transf. 2017, 111, 1039–1049. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Fully developed slip flow in a concentric annuli via single and dual phase nanofluids models. Comput. Methods Programs Biomed. 2019, 179, 104997. [Google Scholar] [CrossRef] [PubMed]
- Kuznetsov, A.V. The onset of nanofluid bioconvection in a suspension containing both nanoparticles and gyrotactic microorganisms. Int. Commun. Heat Mass Transf. 2010, 37, 1421–1425. [Google Scholar] [CrossRef]
- Kuznetsov, A.V. Nanofluid bioconvection in water-based suspensions containing nanoparticles and oxytactic microorganisms: Oscillatory instability. Nanoscale Res. Lett. 2011, 6, 100. [Google Scholar] [CrossRef] [PubMed]
- Uddin, M.J.; Alginahi, Y.; Bég, O.A.; Kabir, M.N. Numerical solutions for gyrotactic bioconvection in nanofluid-saturated porous media with Stefan blowing and multiple slip effects. Comput. Math. Appl. 2016, 72, 2562–2581. [Google Scholar] [CrossRef]
- Xun, S.; Zhao, J.; Zheng, L.; Zhang, X. Bioconvection in rotating system immersed in nanofluid with temperature dependent viscosity and thermal conductivity. Int. J. Heat Mass Transf. 2017, 111, 1001–1006. [Google Scholar] [CrossRef]
- Raju, C.S.K.; Hoque, M.M.; Sivasankar, T. Radiative flow of Casson fluid over a moving wedge filled with gyrotactic microorganisms. Adv. Powder Technol. 2017, 28, 575–583. [Google Scholar] [CrossRef]
- Alsaedi, A.; Khan, M.I.; Farooq, M.; Gull, N.; Hayat, T. Magnetohydrodynamic (MHD) stratified bioconvective flow of nanofluid due to gyrotactic microorganisms. Adv. Powder Technol. 2017, 28, 288–298. [Google Scholar] [CrossRef]
- Khan, W.A.; Rashad, A.M.; Abdou, M.M.M.; Tlili, I. Natural bioconvection flow of a nanofluid containing gyrotactic microorganisms about a truncated cone. Eur. J. Mech. B Fluids 2019, 75, 133–142. [Google Scholar] [CrossRef]
- Alwatban, A.M.; Khan, S.U.; Waqas, H.; Tlili, I. Interaction of Wu’s slip features in bioconvection of Eyring Powell nanoparticles with activation energy. Processes 2019, 7, 859. [Google Scholar] [CrossRef]
- Tlili, I.; Waqas, H.; Almaneea, A.; Khan, S.U.; Imran, M. Activation energy and second order slip in bioconvection of Oldroyd-B nanofluid over a stretching cylinder: A proposed mathematical model. Processes 2019, 7, 914. [Google Scholar] [CrossRef]
- Xu, H.; Pop, I. Fully developed mixed convection flow in a horizontal channel filled by a nanofluid containing both nanoparticles and gyrotactic microorganisms. Eur. J. Mech. B Fluids 2014, 46, 37–45. [Google Scholar] [CrossRef]
- Pop, M.A.S.I. Thermo-Bioconvection in a Square Porous Cavity Filled by Oxytactic Microorganisms. Transp. Porous Med. 2014, 103, 191. [Google Scholar] [CrossRef]
- Dunn, J.E.; Rajagopal, K.R. Fluids of differential type: Critical review and thermodynamic analysis. Int. Jr. Eng. Sci. 1995, 33, 689–729. [Google Scholar] [CrossRef]
- Ali, N.; Khan, S.U.; Abbas, Z. Unsteady Flow of Third Grade Fluid over an Oscillatory Stretching Sheet with Thermal Radiation and Heat Source/Sink. Nonlinear Eng. 2015, 4, 223–236. [Google Scholar] [CrossRef]
- Ali, N.; Ullah, M.; Sajid, M.; Khan, S.U. Application of Legendre wavelets method to parallel plate flow of a third grade fluid and forced convection in a porous duct. Eur. Phys. J. Plus 2017, 132, 133. [Google Scholar] [CrossRef]
- Abbas, Z.; Javed, T.; Ali, N.; Sajid, M. Diffusion of Chemically Reactive Species in Stagnation-Point Flow of a Third Grade Fluid: A Hybrid Numerical Method. J. Appl. Fluid Mech. 2016, 9, 195–203. [Google Scholar] [CrossRef]
- Wu, L. A slip model for rarefied gas flows at arbitrary Knudsen number. Appl. Phys. Lett. 2008, 93, 253103. [Google Scholar] [CrossRef]
- Waqas, H.; Khan, S.U.; Hassan, M.; Bhatti, M.M.; Imran, M. Analysis for bioconvection flow of modified second grade fluid containing gyrotactic microorganisms and nanoparticles. J. Mol. Liq. 2019, 291, 111231. [Google Scholar] [CrossRef]
- Khan, S.U.; Waqas, H.; Shehzad, S.A.; Imran, M. Theoretical analysis for tangent hyperbolic nanoparticles with combined electrical MHD, activation energy and Wu’s slip features: A mathematical model. Phys. Scr. 2019, 94, 125211. [Google Scholar] [CrossRef]
- Ibrahim, W. Magnetohydrodynamics (MHD) flow of a tangent hyperbolic fluid with nanoparticles past a stretching sheet with second order slip and convective boundary condition. Results Phys. 2017, 7, 3723–3731. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. The analytical solution of mixed convection heat transfer and fluid flow of a MHD viscoelastic fluid over a permeable stretching surface. Int. J. Mech. Sci. 2013, 77, 263–268. [Google Scholar] [CrossRef]
| M | Turkyilmazoglu | Present Results |
|---|---|---|
| 0 | −1.000000 | −1.000000 |
| 0.5 | −1.224744 | −1.224748 |
| 1 | −1.414213 | −1.414218 |
| 1.5 | −1.581138 | −1.581147 |
| 2.0 | −1.732050 | −1.732057 |
| 0.2 | 0.5 | 0.5 | 0.5 | 0.5 | 1.0 | −1.0 | 0.6678 |
| 0.8 | 0.6795 | ||||||
| 1.4 | 0.6829 | ||||||
| 0.1 | 0.6801 | ||||||
| 0.2 | 0.6772 | ||||||
| 0.3 | 0.6735 | ||||||
| 0.1 | 0.6647 | ||||||
| 0.6 | 0.6643 | ||||||
| 1.2 | 0.6641 | ||||||
| 1.0 | 0.6685 | ||||||
| 2.0 | 0.6755 | ||||||
| 3.0 | 0.6877 | ||||||
| 0.4 | 0.6691 | ||||||
| 0.8 | 0.6485 | ||||||
| 1.2 | 0.6274 | ||||||
| 0.1 | 0.6643 | ||||||
| 0.2 | 0.4950 | ||||||
| 0.3 | 0.3923 | ||||||
| –2.0 | 0.5224 | ||||||
| –3.0 | 0.4416 | ||||||
| –4.0 | 0.3874 |
| 0.4 | 0.2826 | ||||||
| 0.8 | 0.2821 | ||||||
| 1.0 | 0.2812 | ||||||
| 0.4 | 0.2780 | ||||||
| 0.7 | 0.2676 | ||||||
| 1.0 | 0.2573 | ||||||
| 3.0 | 0.2958 | ||||||
| 4.0 | 0.3035 | ||||||
| 5.0 | 0.3084 | ||||||
| 0.7 | 0.2386 | ||||||
| 0.9 | 0.2677 | ||||||
| 1.1 | 0.2947 | ||||||
| 0.2 | 0.2931 | ||||||
| 0.5 | 0.3182 | ||||||
| 0.8 | 0.3361 | ||||||
| 0.4 | 0.2858 | ||||||
| 0.8 | 0.2702 | ||||||
| 1.2 | 0.2585 | ||||||
| 0.1 | 0.3001 | ||||||
| 0.2 | 0.2952 | ||||||
| 0.3 | 0.2904 |
| 0.4 | 0.2120 | ||||||
| 0.8 | 0.1263 | ||||||
| 1.0 | 0.0850 | ||||||
| 0.4 | 0.5560 | ||||||
| 0.7 | 0.9367 | ||||||
| 1.0 | 1.2865 | ||||||
| 3.0 | 0.4215 | ||||||
| 4.0 | 0.4209 | ||||||
| 5.0 | 0.4204 | ||||||
| 0.2 | 0.4397 | ||||||
| 0.5 | 0.4773 | ||||||
| 0.8 | 0.5041 | ||||||
| 0.4 | 0.4287 | ||||||
| 0.8 | 0.4052 | ||||||
| 1.2 | 0.3877 | ||||||
| 0.1 | 0.4502 | ||||||
| 0.2 | 0.4427 | ||||||
| 0.3 | 0.4355 | ||||||
| 0.7 | 0.3578 | ||||||
| 0.9 | 0.4016 | ||||||
| 1.1 | 0.4420 |
| 0.3 | 2 | 0.1 | 0.1 | 0.5 | 0.5 | 0.5 | 0.5 | 0.9872 |
| 0.5 | 1.1321 | |||||||
| 0.7 | 1.2802 | |||||||
| 0.1 | 3.0 | 1.0953 | ||||||
| 4.0 | 1.3104 | |||||||
| 5.0 | 1.5035 | |||||||
| 0.2 | 0.8233 | |||||||
| 0.8 | 0.7173 | |||||||
| 1.4 | 0.6446 | |||||||
| 0.2 | 0.8749 | |||||||
| 0.5 | 0.9416 | |||||||
| 0.8 | 0.9922 | |||||||
| 1.0 | 0.8413 | |||||||
| 2.0 | 0.8310 | |||||||
| 3.0 | 0.8173 | |||||||
| 0.1 | 0.8544 | |||||||
| 0.6 | 0.8434 | |||||||
| 1.2 | 0.8294 | |||||||
| 0.4 | 0.861 | |||||||
| 0.8 | 0.8044 | |||||||
| 1.2 | 0.7606 | |||||||
| 0.1 | 0.9105 | |||||||
| 0.2 | 0.8936 | |||||||
| 0.3 | 0.8771 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdelmalek, Z.; Ullah Khan, S.; Waqas, H.; A. Nabwey, H.; Tlili, I. Utilization of Second Order Slip, Activation Energy and Viscous Dissipation Consequences in Thermally Developed Flow of Third Grade Nanofluid with Gyrotactic Microorganisms. Symmetry 2020, 12, 309. https://doi.org/10.3390/sym12020309
Abdelmalek Z, Ullah Khan S, Waqas H, A. Nabwey H, Tlili I. Utilization of Second Order Slip, Activation Energy and Viscous Dissipation Consequences in Thermally Developed Flow of Third Grade Nanofluid with Gyrotactic Microorganisms. Symmetry. 2020; 12(2):309. https://doi.org/10.3390/sym12020309
Chicago/Turabian StyleAbdelmalek, Zahra, Sami Ullah Khan, Hassan Waqas, Hossam A. Nabwey, and Iskander Tlili. 2020. "Utilization of Second Order Slip, Activation Energy and Viscous Dissipation Consequences in Thermally Developed Flow of Third Grade Nanofluid with Gyrotactic Microorganisms" Symmetry 12, no. 2: 309. https://doi.org/10.3390/sym12020309
APA StyleAbdelmalek, Z., Ullah Khan, S., Waqas, H., A. Nabwey, H., & Tlili, I. (2020). Utilization of Second Order Slip, Activation Energy and Viscous Dissipation Consequences in Thermally Developed Flow of Third Grade Nanofluid with Gyrotactic Microorganisms. Symmetry, 12(2), 309. https://doi.org/10.3390/sym12020309








