1. Introduction
In manufacturing and services, several factors, such as competition, customer expectations and changes and technological developments, encourage producers to increase their commitment to fixing product defects and eliminating performance deficiencies. Otherwise, market share will be lost due to reduced customer satisfaction [
1,
2,
3,
4]. To maintain market share, companies use different procedures to deliver unflawed products to the market. They use risk evaluation techniques to identify potential risks and determine their causes and effects. Various methods for risk assessment have been developed in recent years [
5]. One of these methods is failure mode and effect analysis (FMEA). This method was first used to systematically analyze failure modes and their subsequent effects on military products, especially in the aviation industry [
6]. One of the best features of FMEA is adopting proactive measures instead of reactive ones. If an accident occurs, large sums of money will be spent on solving problems and eliminating failures and if a failure occurs during the design process, the damage will be maximized [
7]. Design modifications result in changes in production tools, templates and fixtures and additional costs in process and product redesign. FMEA is implemented before the design and process failure factor enters production to maximize work efficiency. Spending time and money on a complete and accurate implementation of FMEA allows for easy modifications during process or product design at a minimal cost. FMEA minimizes the problems associated with implementing such changes [
8]. It is a systematic approach that identifies evident and hidden errors, deficiencies and failures in systems, products and processes then applies proper measures to eliminate these problems. Thus, FMEA can be utilized as a tool for the continuous improvement of the quality of products and services in companies.
The main purposes of applying the FMEA technique are to identify potential failure modes in system components, determine their causes, evaluate their effects on system performance, identify ways to reduce the possibility of their occurrence and alleviate consequences and increase the capability to detect failure modes [
9]. Risk priority number (RPN) is used in the conventional FMEA technique to calculate the risk of various system failure modes. RPN is the product of three factors, namely, occurrence (O), severity (S) and detection (D) [
10]. The higher RPN is, the higher the risk associated with the failure mode is. The purpose of RPN calculation is to prioritize failure modes. Despite the widespread use of FMEA, the technique has major drawbacks that limit its application, especially when used for critical analysis in the calculation of RPNs.
This paper presents a new score to improve the deficiencies of conventional RPNs. This score is obtained by developing an FMEA approach based on gray relational analysis (GRA) and stepwise weight assessment ratio analysis (SWARA) methods. The first section identifies the failure modes. In the second section, the SWARA method is used to determine the weights of RPN factors via the proposed approach to keep symmetrical property of their weights. In the third section, the GRA method is applied to consider the uncertainty in RPN factors and the unreliability in these values by using Z-number theory. Time (T) and cost (C) are considered in addition to S, O and D. In this approach, the identified failures are considered the decision-making alternatives and the SODCT factors weighted by SWARA are considered the criteria for evaluating these failures. The advantages of this theory over conventional fuzzy methods are as follows—it considers the uncertainty in experts’ opinions and allocates the credit in their opinions for estimating fuzzy parameters [
11]. The following shows the contributions of this study:
Consideration of crucial management indices, such as cost and time, in the process of prioritizing risks with SOD factors
Assignation of different weights to risk factors according to the uncertainty of decision-makers’ preferences and the symmetric form of the weights with the aim of overcoming the deficiencies of traditional RPN score and making results more interpretable
Simultaneous consideration of the concepts of uncertainty (U) and reliability (R) in the processes of weighting risk factors and prioritizing failures by using Z-number theory
Complete prioritization of failures and distinction between failure ranks by using the SWARA–GRA integrated method based on -number theory.
3. Methodology
3.1. Fuzzy Sets Theory
The fuzzy theory introduces the concept of membership function to discuss various linguistic variables [
71]. There is a certain degree of uncertainty in terms of people’s thoughts, deduction and perception. Fuzzy set (fuzzy logic) works with the sources of uncertainty and imprecision which are vague and non-statistical, in nature. Basic definitions for the fuzzy numbers are provided below.
Definition 1. A fuzzy set, defined in reference, is as Equation (1). In Equation (1), is the membership function of set . Membership value shows the dependence degree at . The degree of membership of each element like to the fuzzy set , in the form of the degree of our acceptance or belief in accepting x, is defined as a member of the fuzzy set or the degree of conformity of member x with the considered concept of set .
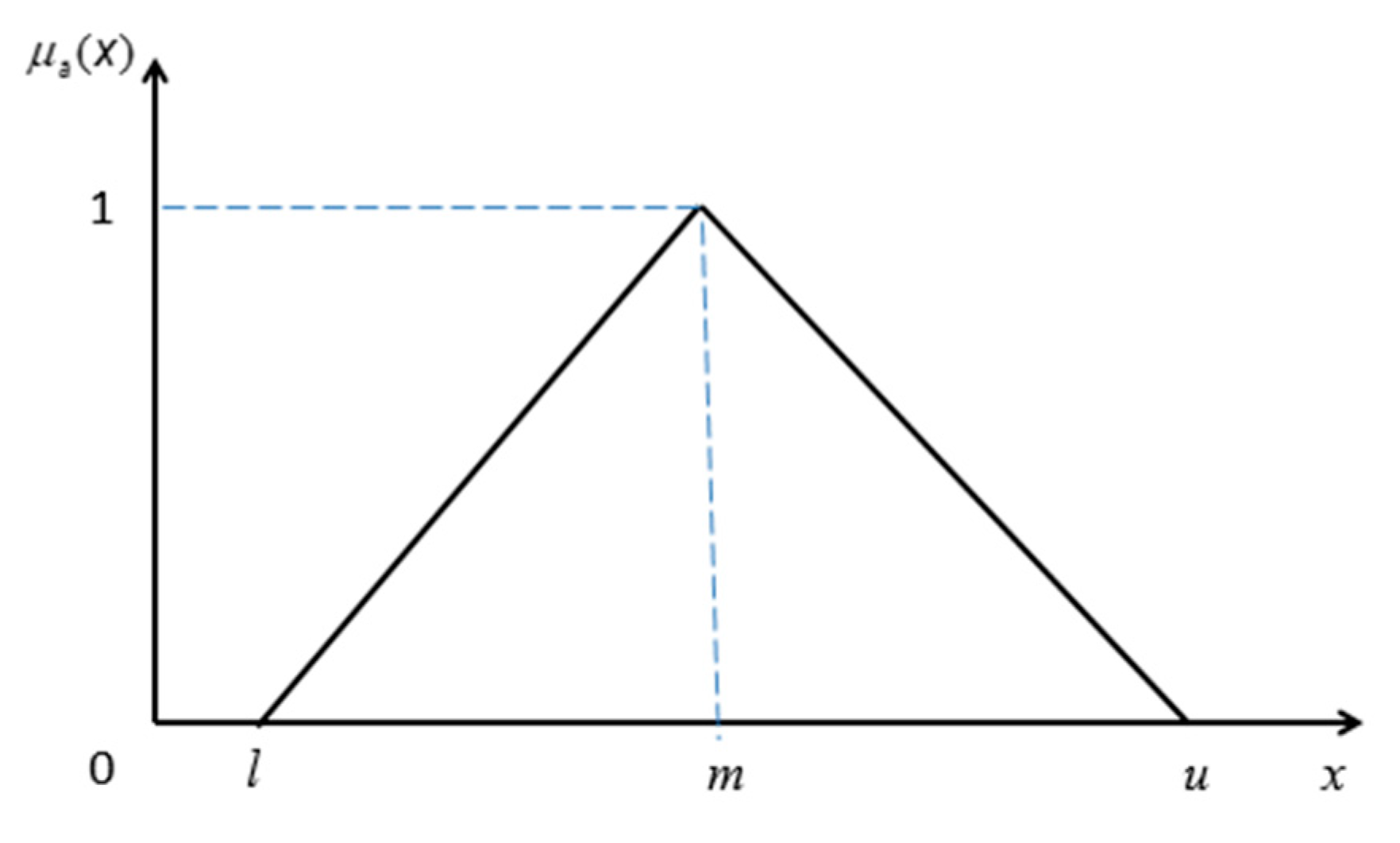
Definition 2. A symmetric triangular fuzzy numberis represented as a triplex ofand the membership function is according to Equation (2) and the diagram is as in Figure 1. Definition 3. Assume that,are symmetric triangular fuzzy numbers. Math operations are done as follow: Definition 4. Assume that,are two positive triangular fuzzy numbers. The distance betweenis defined as in Equation (8). Definition 5. Assume that the triangular fuzzy numberis represented a triplex of. Equation (9) is used to convert it into a crisp number according to the Best Non fuzzy Performance (BNP): 3.2. Z-Number Theory
Zadeh [
11] defined a Z-number associated with an uncertain variable as an ordered pair of fuzzy numbers denoted as
.
is a fuzzy constraint on values of
and
is defined as a partial reliability of a probability criterion of
. According to Kang, et al. [
72], Z-number is to solve problems in controlling, decision making, modeling and other problems. This method is based on the conversion of a Z-number to a fuzzy number on the basis of the expectation of a fuzzy set. However, converting the Z-number to fuzzy numbers will lead to the loss of the original information. Aliev, et al. [
73], Aliev, et al. [
74], Aliev, et al. [
75] presented an effective general and computational approach to calculate the Z-number.
Triple (X, A, B), known as Z-VALUATION, which is equivalent to an assignment statement and is defined as a general constraint on X as in Equation (10).
This constraint is referred to as a probability restriction that shows a probability distribution function. In particular, it can be explained in Equation (11).
where,
is the membership function of A and u is a generic value of X.
may be viewed as a constraint which is associated with
. It means that how much the constraint that covers
, can satisfy
u. when, X is a random variable, the probability distribution of the X acts as the probabilistic restriction on X. Possible restriction and a probability density function are described in Equations (12) and (13):
In Equation (13), shows the components of U derivations.
3.3. Z-SWARA
Keršuliene, Zavadskas and Turskis [
58] proposed the step-wise weight assessment ratio analysis (SWARA) method for the first time.
Different factors, such as non-assessable information, incomplete information and non-accessible information cause uncertainty in decision-making. Since conventional MADM methods cannot solve problems with such ambiguous information, fuzzy multi-criteria decision-making methods have been developed because of ambiguity in evaluating the relative importance of criteria and ranking the alternatives according to the criteria. The process of determining the relative weight of criteria using Z-SWARA, like SWARA method, is as following steps:
Step 1. Sort the evaluation factors in descending order of expected importance.
Step 2. Switch Z-numbers linguistic variables to symmetric triangular fuzzy variables.
In this step, the verbal variables for factors, in the form of Z-Numbers, are transformed into triangular fuzzy verbal variables. The process of this transformation is as follows:
Assume that
, which
is the verbal variable presented in
Table 2 and
is the verbal variable presented in
Table 3 and assume that,
and
are triangular membership functions. According to Equations (14) and (15), reliability of Z-Number is transferred to crisp number
In these Equations,
expresses the weight of reliability,
indicates the degree of dependence
in B and
indicates the degree of dependence
in
. Then, by combining the Linguistics variable for evaluating the factors (see
Table 2) and the Transformation rules of linguistics variables of reliability (see
Table 3), the roles of transforming verbal variables of decision makers, used for maintaining the symmetry of the response, are obtained for the Z-SWARA method.
For instance, assume that
, which is
and
, so it is described as
. Firstly, reliability component of Z-Number converts to a crisp number by using Equations (14) and (15). According to Equation (15), the value of
is 0.5, then, this value is used in Equation (14)
. Now, the Z-number weight is converted to the triangular fuzzy number using Equation (15)
. Other conversions are presented in
Table 4 according to
Table 2 and
Table 3.
Step 3. According to
Table 4, state the relative importance of the factor
j in relation to the previous factor
according by z-number, which has higher importance and follow to the last factor. After determining all relative importance scores by all experts, the geometric mean of the corresponding scores is obtained, to aggregate their judgments.
Step 4. Obtain the coefficient
as (16):
Step 5. Calculate the fuzzy weight
as (17):
Step 6. Calculate the relative weights of the evaluation criteria as (18):
where
is the relative fuzzy weight of
, the criterion and
shows the number of evaluation criteria.
3.4. Z-GRA
Z-GRA approach, is described as follow steps:
Step 1: Decision-making matrix with Z-Number elements is indicated as a matrix, where
and
, respectively, show the number of alternatives and criteria. Also,
and
, respectively, indicate the value of the
th criterion for the
th alternative and the
th reliability for the
jth alternative.
Step 2: Switch Z-numbers linguistic variables to symmetric triangular fuzzy variables.
The elements of above matrix are converted into symmetric triangular fuzzy numbers and a decision-making matrix is obtained with elements of symmetric triangular fuzzy numbers.
Assume that
where
and
are triangular membership functions. Equations (20) and (21) show their transformation to the crisp numbers.
In the Equations above, represents the reliability weight, indicates the dependence degree of in and indicates the dependence degree of in .
Then, by combining linguistic variables presented in
Table 5 and the rules of converting linguistic variables, the components of conversion of linguistic variables by decision makers’ for Z-GRA method are obtained. For example, assume that
where
and the
, then it is converted to
. According to Equations (20) and (21),
. According to the
Table 5 and
Table 6, other conversions are brought in
Table 7.
Step 3: in this step, the decision-making matrix with symmetric triangular fuzzy numbers is formed and it is normalized. In this matrix,
demonstrates the value that the alternative takes in n criteria and m alternative (performance measurement).
Step 4: In this step, fuzzy GRA works as follows:
Decision matrix (22) is converted into the normalized decision matrix ̃. Given ̃ (23), the normalized performance rating can be calculated as (Gumus et al., 2013; Zhang and Liu, 2011):
3.5. Proposed Approach
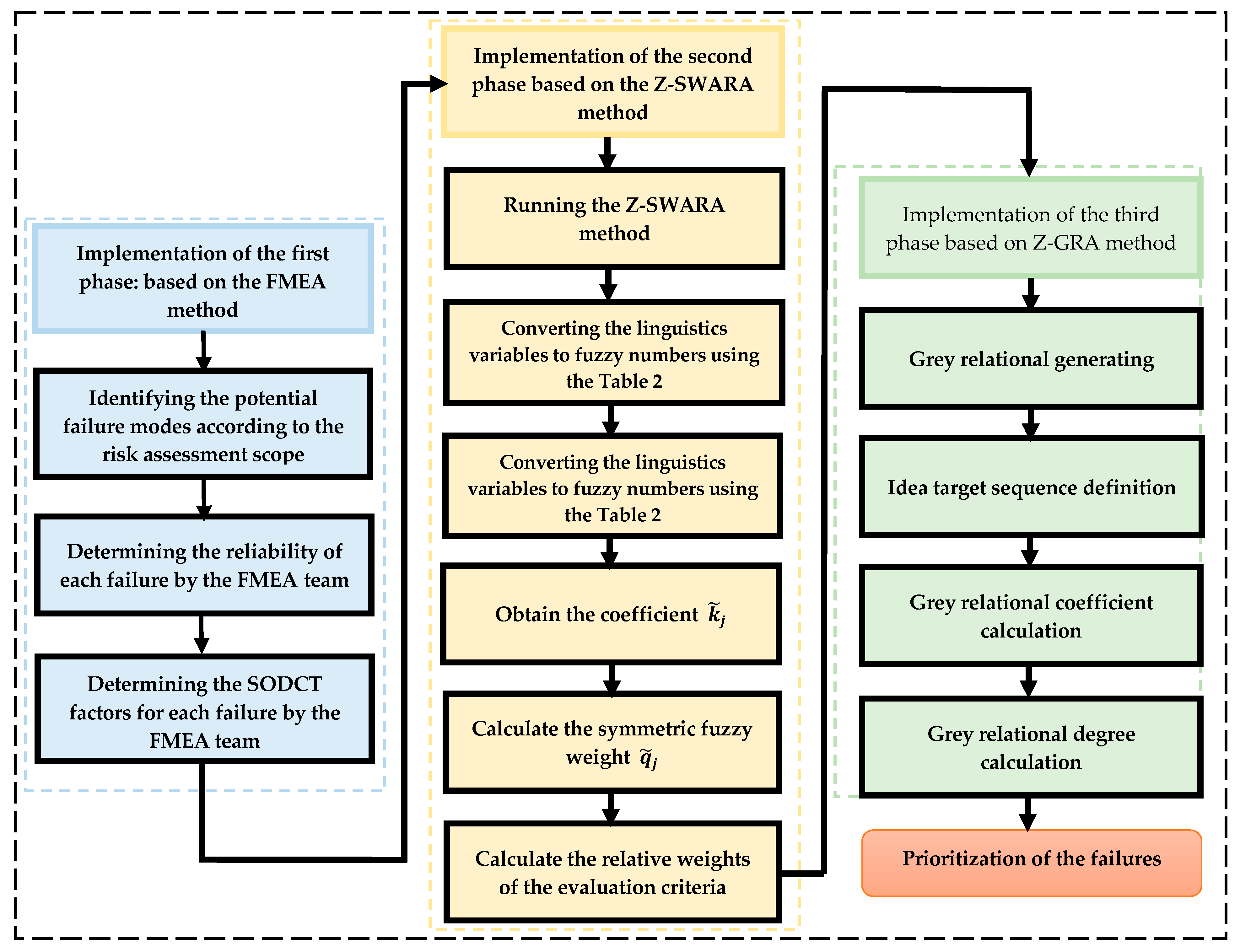
A combination of FMEA, Z-SWARA and Z-GRA is used to evaluate and prioritize failure modes in this study. In the first phase of the research method, the failure modes and reliability of each of mode are determined by the FMEA team. In the second phase, the failure modes are weighted in the symmetric form and the criteria are ranked by decision makers (DMs) via the Z-SWARA method. In the third phase, the primary matrix Z-GRA is formed in consideration of the failure modes identified in the first phase and the final symmetric weights assigned in the second phase of the study.
Figure 2 shows the steps in prioritizing the FMs of solar panels.
4. Analysis of the Results
In accordance with the methodology of this study, 19 failures of solar panels are detected using FMEA and the factor values for each failure are determined by the team. Z-number theory is used to convert uncertain data into fuzzy numbers because of the uncertainty in the factors. The uncertainty in the factors and their reliability values are considered. The Z-number values obtained from the conversion of linguistic numbers based on the team’s opinion are indicated in
Table 8.
Then, in the second phase of the research method and also according to the SWARA method expressed, the values of coefficient k and the weight of
q and
w are calculated on the basis of Equations (16) to (18) for each decision-maker in examining the failures of solar panels as in table (10). In this step, the linguistic variables are converted into triangular fuzzy numbers, based on the Equations shown in
Table 2 and
Table 3. For example, the fuzzy numbers corresponding to the linguistic variable MOL-M are
, respectively. After the conversion of linguistic variables into fuzzy numbers, the coefficient
from Equation (16), the fuzzy weight
from Equation (17) and the final weight of the factors in the form of fuzzy numbers
from Equation (18) are obtained. Final symmetric fuzzy weight of main criteria by each decision maker shown in
Table 9.
Table 10 shows the average of the final symmetric weight, obtained from all the opinions of decision-makers for evaluating and prioritizing the risk of failures in FMEA method. This table consists of the average weight W for each factor of FMEA in all decision-makers’ opinions.
According to
Table 10, the final symmetric weight, obtained in the form of triangular fuzzy numbers, is for each failure factor in FMEA method. The final factor weight for factors are calculated as
,
,
,
and
, respectively. Then the failure modes are prioritized, using the developed Z-GRA method.
Table 11 shows the decision-making matrix Z-GRA in the form of Z-number elements for failure factors of FMEA. The lines in
Table 12 show the failure modes identified in the first phase of the research method by the team.
After the normalization of the primary matrix presented in
Table 11, the normalized weighted matrix, considering the weights of the factor used in FMEA method, is obtained for all the failure modes as in
Table 12.
Now, after normalizing the final symmetric weights, the identified failures are prioritized based on the Z-GRA approach and also a comparison between the outputs of this approach and conventional methods such as Fuzzy GRA and traditional RPN has been presented in
Table 13.
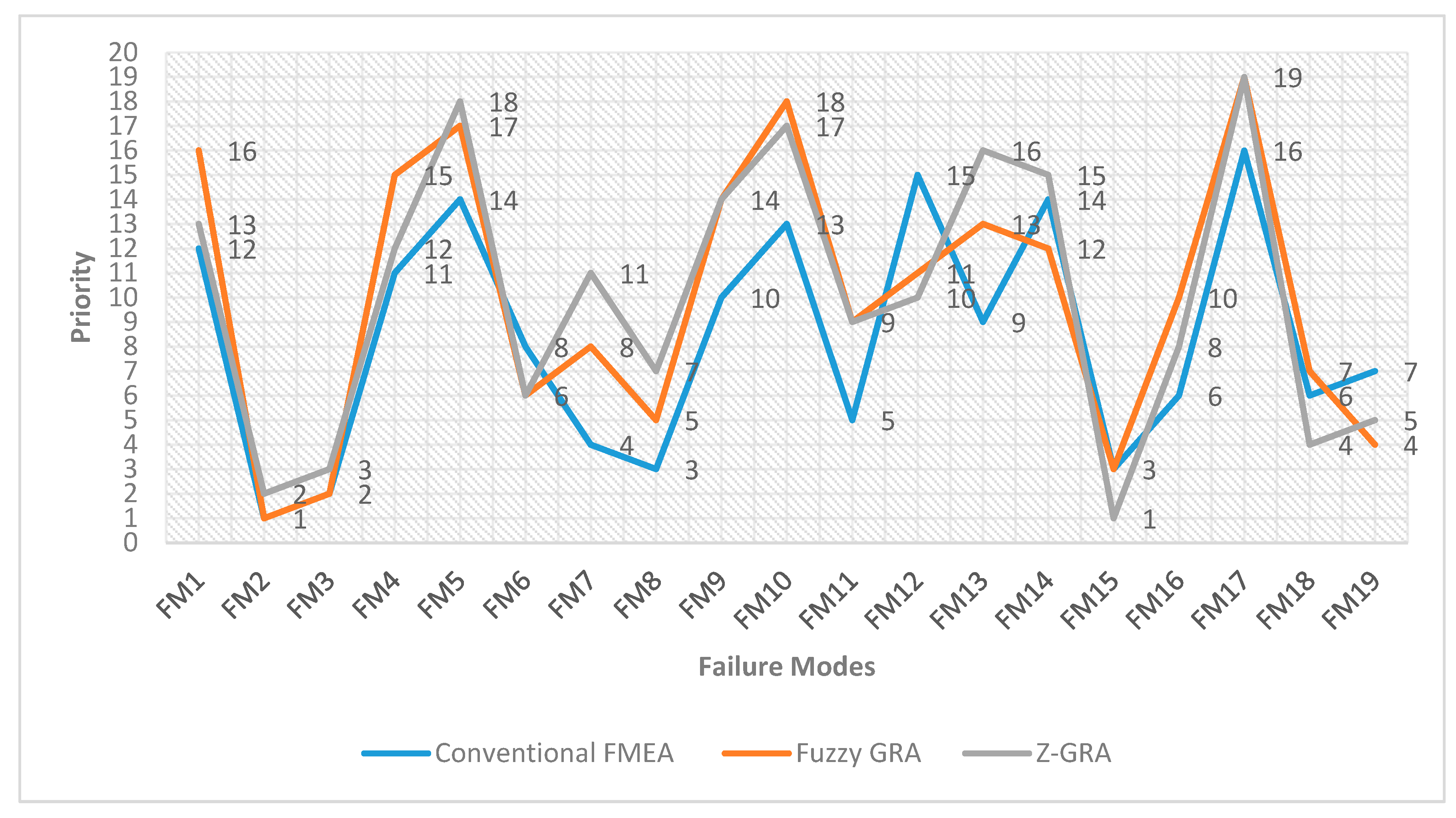
Table 13 implies that failures FM2 with a score of 18,144, FM3 with a score of 11,200 and FM8 and FM15 with a score of 7840 are ranked from 1 to 3, respectively. Consideration of the different weights of risk factors (SODET) demonstrates that although failure FM8 with the FGRA approach ranks fifth, it ranks third based on traditional RPN indices. This change indicates the application of the weights of risk factors in the process of prioritizing failures.
FM2 with a score of 0.815, FM3 with a score of 0.799 and FM15 with a score of 0.797 are ranked from 1 to 3 based on fuzzy GRA, respectively. The fuzzy GRA index has a more substantial impact on distinguishing priorities (complete prioritization of failures) compared with the RPN indices.
On the basis of the Z-GRA approach, FM15 with a score of 0.781, FM2 with a score of 0.773 and FM3 with a score of 0.753 are ranked from 1 to 3, respectively. Further investigation of this index shows that the recommended approach not only considers uncertainty and reliability simultaneously in the processes of prioritizing failures and assigning different weights to risk factors but can also prioritize the failures completely and assign distinct ranks to each risk properly.
A simultaneous comparison of critical failures in the two approaches of Z-GRA and traditional RPN shows that although failures FM8 and FM15 share the third rank based on the RPN indices, they have distinct ranks of seventh and first, respectively, based on the suggested approach. The reason for the lower rank of FM8 compared with that of FM15 is the difference in the values of symmetric weights assigned to the risk factors. For example, FM15, which is ranked first based on the Z-GRA approach, assigns large values to crucial risk factors, such as cost and detection (
Table 11).
Figure 3 shows the resolution of ranks assigned to failures based on traditional FMEA, fuzzy GRA and Z-GRA methods. The conventional FMEA performs an incomplete prioritization of failures by placing 19 risks in 15 categories. By contrast, fuzzy GRA and Z-GRA conduct a complete prioritization by assigning distinct ranks to identified failures. The advantage of this ranking over incomplete prioritization is that it can increase the ability of DMs to discern critical failures and plan corrective actions in accordance with the limitations of sources. Although, the fuzzy GRA method provides DMs with a complete ranking, reliability is disregarded in this ranking. Consequently, the results of the Z-GRA method are more coincident with the FMEA team’s opinion compared with those of the fuzzy GRA method.
5. Sensitivity Analysis
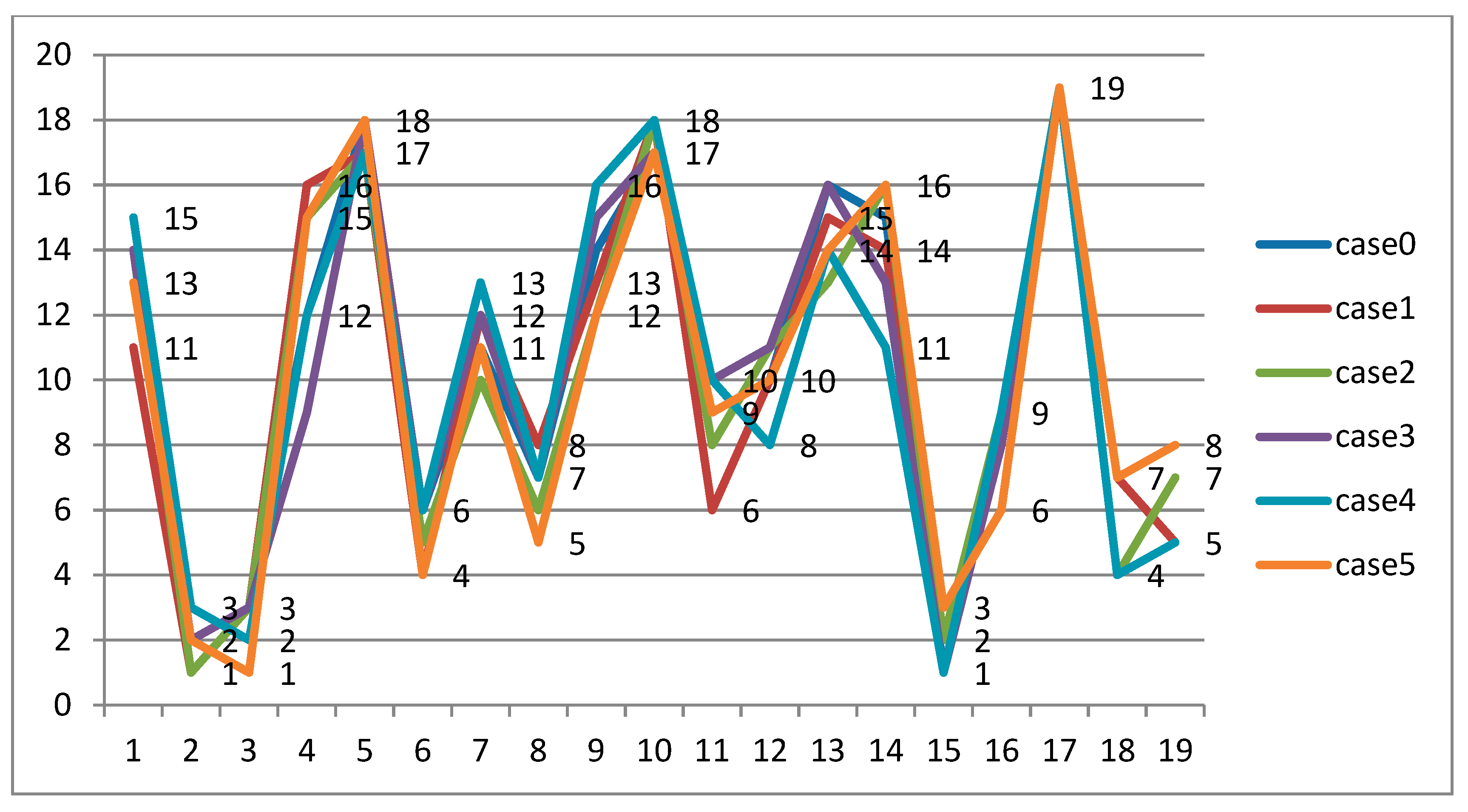
Sensitivity is calculated with the risk factor weights in accordance with the information in
Table 14. For example, the original weight values of the risk factors are shown in Case 0. In Case 1, 0.1 is added to the weight of S and 0.025 is deducted from the weight of O, D, C and T. Similarly, 0.1 is added to the weight of O in Case 2, to the weight of D in Case 3, to the weight of C in case 4 and to the weight of T in Case 5; meanwhile, 0.025 is deducted from the initial weight of the others. The results of the rating sensitivity analysis of solar panels are shown in
Table 15 and
Figure 4. In Case 1, by increasing the weight of S, FM2 (Dust) is upgraded from the second position to the first position, whereas FM15 (Wiring) is downgraded from the first position to the second position. In Case 2, by increasing the weight of O, FM2 (Dust) is upgraded from the second position to the first position, whereas FM15 (Wiring) is downgraded from the first position to the second position. In Case 4, by increasing the weight of C, FM2 (Dust) is downgraded from the second position to the third position. In Case 5, by increasing the weight of T, FM15 (Wiring) is downgraded from the first position to the third position. FM3 (Orientation) is upgraded from the third position to the first one. In all cases, FM17 (Labeling and warning signs) is selected as the last failure mode.