Abstract
Al2O3/water nanofluid conjugate heat transfer inside a microchannel is studied numerically. The fluid flow is laminar and a constant heat flux is applied to the axisymmetric microchannel’s outer wall, and the two ends of the microchannel’s wall are considered adiabatic. The problem is inherently three-dimensional, however, in order to reduce the computational cost of the solution, it is rational to consider only a half portion of the axisymmetric microchannel and the domain is revolved through its axis. Hence. the problem is reduced to a two-dimensional domain, leading to less computational grid. At the centerline (r = 0), as the flow is axisymmetric, there is no radial gradient (∂u/∂r = 0, v = 0, ∂T/∂r = 0). The effects of four Reynolds numbers of 500, 1000, 1500, and 2000; particle volume fractions of 0% (pure water), 2%, 4%, and 6%; and nanoparticles diameters in the range of 10 nm, 30 nm, 50 nm, and 70 nm on forced convective heat transfer as well as performance evaluation criterion are studied. The parameter of performance evaluation criterion provides valuable information related to heat transfer augmentation together with pressure losses and pumping power needed in a system. One goal of the study is to address the expense of increased pressure loss for the increment of the heat transfer coefficient. Furthermore, it is shown that, despite the macro-scale problem, in microchannels, the viscous dissipation effect cannot be ignored and is like an energy source in the fluid, affecting temperature distribution as well as the heat transfer coefficient. In fact, it is explained that, in the micro-scale, an increase in inlet velocity leads to more viscous dissipation rates and, as the friction between the wall and fluid is considerable, the temperature of the wall grows more intensely compared with the bulk temperature of the fluid. Consequently, in microchannels, the thermal behavior of the fluid would be totally different from that of the macro-scale.
1. Introduction
Convective heat transfer plays a vital role in micro thermal systems owing to its widespread utilization in different areas of engineering and in particular energy fields. Inappropriate thermal conductivity of conventional fluids is a restriction for convective heat transfer improvements. In order to solve this problem, nanofluids, composed of suspended particles with nanometer dimensions and a base fluid, are suggested [1,2]. Nanofluids have modified thermal features compared with the base liquid owing to the existence of solid nano-sized particles [3,4,5,6,7,8] Thus, in order to increase the heat transfer coefficient, nanofluids’ utilization in micro and macro channels has been popular. On the other hand, some effects, like viscous dissipation, that can be neglected in macro-scale problems are of particular importance in smaller scales [9].
Numerous studies have focused on the thermal specifications of heat transfer devices with nanofluid and microchannnels. Li et al. [10] stated that, in order to accurately investigate fluid flow and heat transfer in microchannels, many parameters such as axial heat conduction, viscous effect, surface geometry, and so on should be considered. Many researchers [11,12,13,14,15,16,17] showed that utilization of nanoparticles can increase the coefficient of convective heat transfer and, as a result, the rate of heat transfer. The need to increase the efficiency of systems has become widespread in different areas like power systems [18,19,20] while taking into consideration economic issues [21,22]. Celata et al. [23] conducted an experimental research on heat transfer in a microtube with an inner diameter between 50 μm and 528 μm and a uniformly heated wall. By comparison with the conventional value of Nusselt number in a channel with circular cross section, constant heat flux, and fluid properties (Nu = 4.36 [24]), the rate of heat transfer decreased. Mital [25] analytically analyzed the heat transfer of laminar nanofluid developing flow in microchannels. They showed that the ratio of the coefficient of heat transfer in nanofluids to base fluid was noticeably dependent on the size of solid particles and their concentration, while there was weak dependency on the Reynolds number. Faghri and Sparrow [26] studied fluid and wall axial conduction heat transfer in a laminar flow and the importance of the axial heat conduction was determined by their proposed criterion. In another study [27], conjugate heat transfer was theoretically investigated for a microtube. Various lengths, thicknesses, and material for walls of the microtube were considered in the study. It was concluded that the local Nusselt number decreases with a decrease in the channel length and increment in the thickness of wall and its thermal conductivity. Maiga et al. [28] investigated the thermal behavior of a turbulent flow of Al2O3/water nanofluid flowing inside a tube that is put in a uniform wall heat flux. They showed that using nanoparticles enhances the coefficient of heat transfer, and it increases with an augmentation in the fraction of particles. Akbari and Behzadmehr [29] investigated the influence of using nanofluid on heat transfer in a tube installed horizontally with uniform heat flux. They used three different Al2O3 particle concentrations of 0, 2, and 4 percent. They concluded that, for a given Grashof number, the coefficient of convective heat transfer enhances with an augmentation in the particle’s concentration. Thermophysical specifications of a nanofluid such as thermal conductivity and viscosity can influence convective heat transfer [30,31]. Different models, based on various approaches such as correlations, artificial neural network, and support vector machines, are represented for modeling of nanofluids’ properties [32,33,34,35,36,37]. Koo et al. [38] and Chon et al. [39] modeled nanofluid effective thermal conductivity including effects due to both temperature and particle size. Ben Mansour et al. [40] studied nanofluid forced convective heat transfer. They showed that different modeling of nanofluids’ thermophysical features leads to contradictory results. Li et al. [41] investigated the impact of thermophysical properties of the fluid on thermal features. They showed that the thermophysical properties can considerably affect the heat transfer rate. Lelea [42] numerically studied a microchannel and investigated heat transfer and laminar flow of fluid inside it. He used three different fluids with temperature dependency. The results indicated that thermal conductivity has remarkable impact on local Nusselt number behavior in the cases of low Re numbers. As the Re increases, the thermal conductivity has a weaker effect on the local Nusselt number. Another important parameter in microtubes is viscous dissipation, which is like an energy source in the fluid flow and changes the distribution of the temperature. This energy source is actually induced by shear stresses. Many works have been done so far studying this effect. Tso and Mahulikar [43,44,45] investigated the impact of the Brinkman number on the thermal behavior of the fluid flowing in microchannels. Morini [46] studied conjugate heat transfer and the heating due to viscosity in microtubes. The results revealed that the dependency of the average Nusselt number on Re number can be described by including the viscous dissipation and the conjugate effects. In a study by Safaei et al. [47], erosion rate of a two phase fluid flow inside a 90 degree elbow was analyzed. Parameters of fluid velocity, particle diameters, and its volume fraction were investigated, and the results showed that particles’ size and volume fraction, as well as the velocity of the fluid, have a considerable effect on the erosion rate.
From the above review, a great number of studies has been conducted on the topics including viscous dissipation, conjugate heat transfer, nanofluids, and so on. One goal of the study is to investigate the expense of increased pressure loss for increment of the heat transfer coefficient in microchannels. Additionally, this study aims at showing that, despite the macro-scale problems, in microchannels, the viscous dissipation effect cannot be neglected, and affects temperature distribution as well as the heat transfer coefficient. To this end, the influence of different parameters including Reynolds number, diameter of nanofluids, and concentration on heat transfer coefficient, together with the performance evaluation criterion for Al2O3/water laminar flow in an axisymmetric microchannel, are investigated.
2. Numerical Model
Numerical models are applicable for modeling the flow of fluid and heat transfer of complex geometries and operating conditions [48,49,50,51]. In the first step of the present modeling procedure, it is required to define the geometry of the microchannel. The geometry of the investigated problem in the current research is shown in Figure 1. An axisymmetric microchannel with inner diameter of Di = 0.1 mm and outer diameter of Do = 0.3 mm with L = 100 mm length and a constant heat flux applied on the outer wall qo = 5305.3 W m−2 is studied. The wall thermal conductivity is equal to that of the steel, k = 16.3 W m−1 K−1. It is considered that, at the microchannel inlet, the temperature and velocity are uniform. Heat flux in uniform condition is applied on the outer wall and the condition adopted at the outlet is fully developed. At the interface of solid and liquid, conjugate heat transfer procedure is considered and the continuity of heat flux and temperature are defined at the interface.
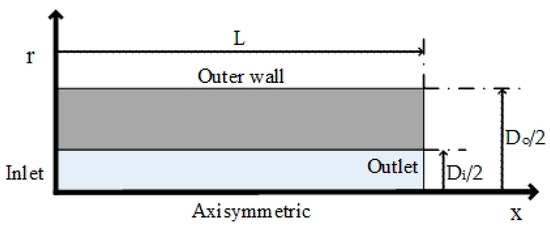
Figure 1.
Schematic of the problem.
The set of equations used to describe the problem is as follows:
Conservation of mass:
Moreover, conservation of momentum is applied as follows:
Equations of conservation of energy that are solved for both the solid and liquid domains, respectively, are as follows:
where Sv is the viscous dissipation term.
Equations of momentum, continuity, and energy along with the reasonable conditions at the boundaries are solved using the finite volume method described in the work of [52,53]. Energy and momentum equations were discretized using first-order upwind approach and SIMPLE scheme was employed for pressure–velocity coupling. Gambit 2.4.6 was used for mesh generation and ANSYS Fluent 6.3.26 was utilized for simulation of the CFD problem.
At the entrance of the microchannel, uniform temperature and velocity profiles are considered:
z = 0; u = u0, T = T0.
At the outlet, the flow is thermally fully developed:
At the centerline of the microchannel (r = 0), the flow is axisymmetric, which implies that there is no radial gradient in the flow. Therefore, the boundary conditions are as follows:
At the fluid–solid interface, the no-slip condition is considered:
Continuity of temperature and heat flux at the fluid–solid interface is applied:
The constant heat flux on the outer surface of the microchannel is defined as follows:
The properties of Al2O3 nanoparticles are represented in the work of [54] as follows:
The nanofluids’ effective thermal conductivity is given as follows [41]:
The nanofluids’ effective dynamic viscosity is determined as follows [55]:
The specific heat and density of the nanofluids are defined, respectively, as follows:
Brinkman number in cases of constant heat flux is expressed as follows:
The pumping power is defined as follows:
Reynolds number is defined as follows:
Local heat transfer coefficient is calculated as follows:
In order to evaluate the thermal performance of the microchannel, the performance evaluation criterion (PEC) is used [56]. It is defined as the ratio of transferred heat to needed power of pumping as follows:
3. Results and Discussion
In order to investigate mesh independency, three different grids of 45,000, 70,000, and 87,500 are used. As the flow is axisymmetric, only the flow in a single plane from the centerline to the microchannel’s wall is required to be solved. In fact, only a half portion of the axisymmetric microchannel is considered and the domain is revolved through its axis. Therefore, the 3D problem is reduced to a 2D problem, leading to less computational grid and consequently less computational cost. Structured mesh with fine mesh adjacent to the walls was used. The convective heat transfer coefficient is obtained for these grids. The maximum deviation for convective heat transfer in grid 2 and grid 3 is less than 0.01%. Therefore, the second grid was used for further investigations. To validate the numerical code, the results of the work of [57] are compared with those of the present study. Figure 2 shows the comparison for different Brinkman numbers. Acceptable agreement is observed between the results of this study with the work of [57]. A maximum error of 6.1% can be seen at the entrance region for Br = 1.0. As can be seen from Figure 2, increasing the Br number—and consequently the inlet mean velocity of the nanofluid—leads to a reduction of convective heat transfer coefficient which is in contrast with the behavior of the fluid in macro-scale channels.
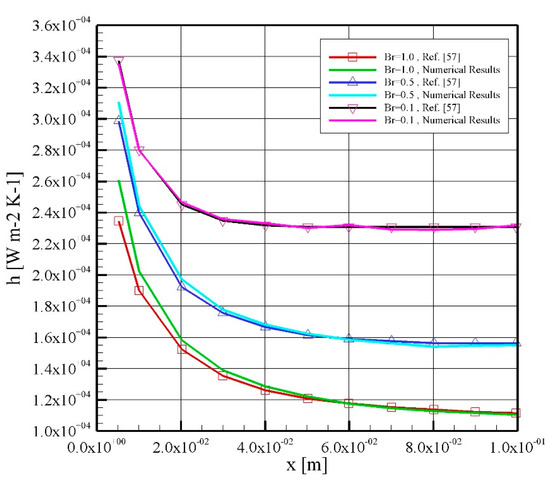
Figure 2.
Heat transfer coefficient of the numerical results with the work of [57] for different Brinkman numbers.
Suspension of Al2O3 nanoparticles in water is considered as the single phase nanofluid. The nanofluid flows inside the microchannel with an inlet temperature of 293.15 K, and its temperature increases as a result of the imposed heat flux on the outer wall. This paper aims to evaluate the impact of different parameters including Reynolds number, nanoparticles diameter, and particle volume fraction on heat transfer characteristics.
In Figure 3 and Figure 4, heat transfer coefficient as well as PEC is depicted for a constant nanoparticle concentration of 2% and an average diameter of 10 nm, respectively. It can be observed that, as the Reynolds number increases, the coefficient of convective heat transfer decreases. This is in contrast with the macro-scale heat transfer problem. In microchannels, an increase in inlet velocity leads to more viscous dissipation rates. As the friction between the wall and fluid is high in microchannels, the temperature of the wall grows more intensely compared with the bulk temperature of the fluid. Therefore, the temperature difference between the bulk of fluid and the wall increases, which leads to decrement of convective heat transfer coefficients for higher Reynolds numbers. The same pattern is observed in the investigation by Lelea and Nisulescu [57], where a higher Br number leads to a lower convective heat transfer coefficient. From Figure 4, it is obvious that an increment in Reynolds number leads to a decrement in performance of the system. PEC is 8.01 for Re = 500 and reduces to 0.50 for Re = 2000. This is attributed to high pumping powers required for higher pressure losses in cases with great values of Reynolds numbers. Increased heat transfer has always been at the expense of increased pressure losses. Therefore, a compromise between these two parameters is needed.
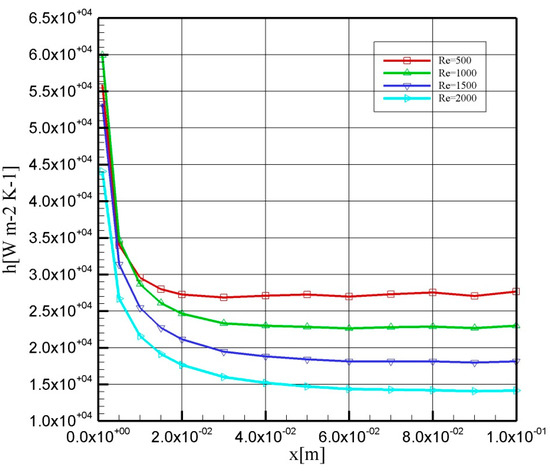
Figure 3.
Coefficient of heat transfer for nanoparticle volume fraction of 2% with an average diameter of 10 nm.
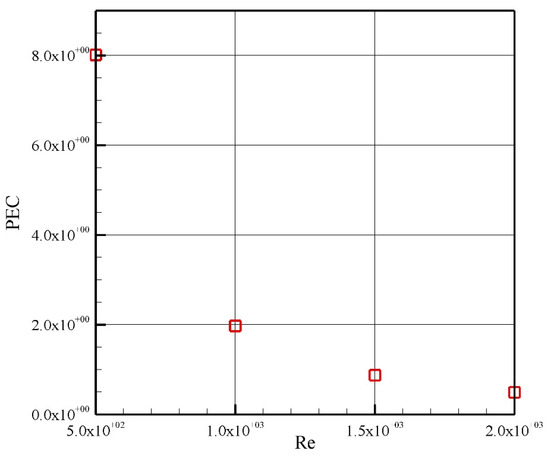
Figure 4.
Performance evaluation criterion (PEC) for nanoparticle volume fraction of 2% with 10 nm average diameter.
In Figure 5 and Figure 6, the heat transfer coefficient as well as PEC is shown for a constant nanoparticle diameter of 10 nm and constant Reynolds number of 1000. It can be seen that, as the volume fraction of the nanoparticle increases, the convective heat transfer coefficient increases as well [29,57,58]. Along the tube, for pure water, h oscillates around a constant amount of 21,000 W/m2 K, while in nanofluid with 6% of Al2O3, this is about 25,000 W/m2 K, which is an increase of 19%. The augmentation in the coefficient of heat transfer is the result of increased thermal conductivity of the nanofluid. In Figure 6, it can be concluded that PEC decreases with an augmentation in the solid phase volume fraction. This is the result of greater pressure losses, which is related to the nanoparticles. However, this decrement is not severe. More specifically, PEC is 2.05 for pure water and reduces to 1.77 for a volume fraction of 6%.
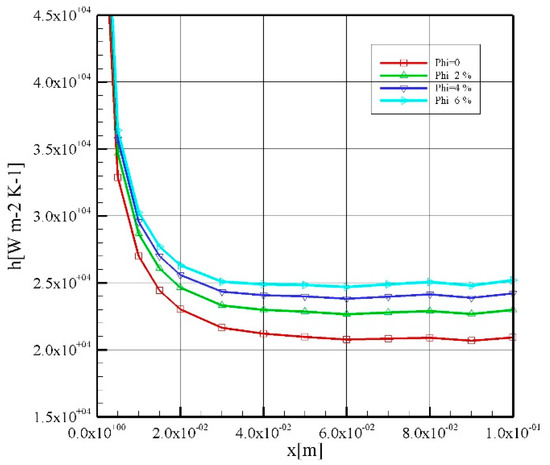
Figure 5.
Heat transfer coefficient for the particles with an average diameter of 10 nm and Re of 1000.
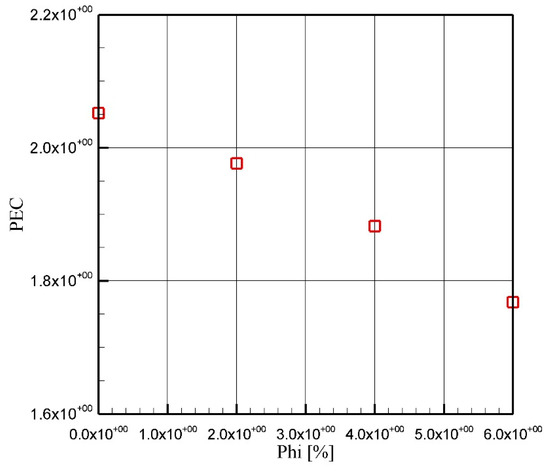
Figure 6.
PEC for the particles with an average diameter of 10 nm and Re of 1000.
In Figure 7 and Figure 8, the heat transfer coefficient as well as PEC is depicted for a constant Re of 1000 and nanoparticle volumetric concentration of 2%. In Figure 7, it is seen that, although the variation is not severe, higher nanoparticle sizes offer lower a convective heat transfer coefficient. In all four nanoparticle diameters of 10, 30, 50, and 70 nm, the convective heat transfer coefficient reaches rather constant values of 22,700, 22,100, 21,800, and 21,700, respectively. Looking at Figure 3 and Figure 5, it can be concluded that the effect of variation of the nanoparticle volume fraction and Reynolds number on convective heat transfer coefficient is considerable. However, the variation of convective heat transfer coefficient owing to the change in diameter of the nanoparticles from 10 nm to 70 nm is less than 5 percent. It is worth noting that this variation for nanoparticles of 30 nm to 70 nm is less that 2 percent. Therefore, it can be concluded that the change in the diameter of the nanoparticles has a negligible effect on the heat transfer coefficient of the system. Figure 8 shows the performance evaluation criterion for four different nanoparticle diameters. The figure is rather constant and is equal to 1.98, which means that it has no effect on pressure loss of the fluid flow. Similarly, it can be concluded that the diameter of the nanoparticle has almost no effect on the PEC of the system.
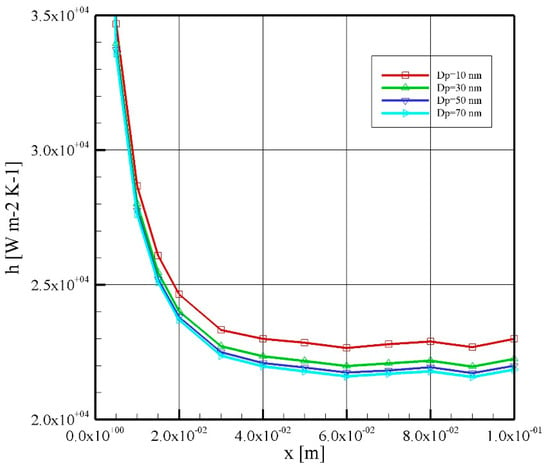
Figure 7.
Heat transfer coefficient for a constant Re of 1000 and 2% volume fraction.
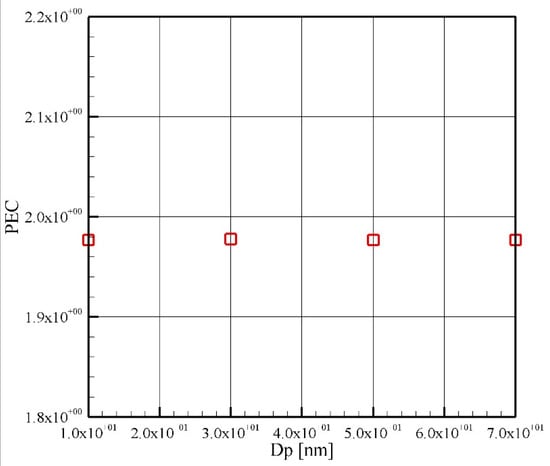
Figure 8.
Performance evaluation criterion (PEC) for a constant Re of 1000 and 2% volume fraction.
4. Conclusions
The thermal and fluid flow behavior of Al2O3/water nanofluid inside a microchannel with an inner diameter of 0.1 mm was investigated numerically. The fluid flow was considered as laminar. A constant heat flux was applied on the microchannel’s outer wall. Four different Re numbers of 500, 1000, 1500, and 2000 and different nanoparticle diameters in the range of 10 nm to 70 nm with four various nanoparticle volume fractions of 0% (pure water), 2%, 4%, and 6% were used in the study. The effects of these parameters were studied on the coefficient of convective heat transfer as well as the performance evaluation criterion.
The main results of the current study can be outlined as follows:
- Owing to the severe impact of viscous dissipation on the temperature of the wall and fluid, in contrast with the macro-scale problem, as the Reynolds number increases, the convective heat transfer coefficient reduces. Therefore, the viscous dissipation effect that is induced by shear stresses cannot be ignored in microchannels. Furthermore, PEC reduces as the Reynolds number increases, which is the result of higher pressure losses in high values of Reynolds numbers.
- Augmentation in the volume fraction of a nanoparticle can increase the heat transfer coefficient, which is in expense of a lower PEC, although the variation of the PEC is not great. The PEC reduces from 2.05 for pure water to 1.77 for a volume fraction of 6%.
- Increasing the diameter of the nanoparticle can decrease heat transfer coefficient. Furthermore, it was observed that variations of the diameter of the nanoparticle have no effect on PEC for four different studied nanoparticle diameters and PEC equal to 1.98.
Author Contributions
All authors participated in conceptualization, methodology, software simulation, validation, formal analysis, investigation, original draft preparation, reviewing, and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Br | Brinkman number |
| cp | Specific heat at constant pressure, J/kg K |
| D | Diameter, m |
| h | Heat transfer coefficient, W/m2 K |
| k | Thermal conductivity, W/m K |
| kb | Boltzmann constant, J/K |
| L | Length, m |
| lb | Mean free path, m |
| Mass flow rate, kg/s | |
| Pr | Prandtl number |
| q | Heat flux, W/m2 |
| Re | Reynolds number |
| r | Spatial coordinates in radial direction, m |
| T | Temperature, K |
| um | Mean entrance velocity of nanofluid, m/s |
| v | Velocity, m/s |
| Volumetric flow rate, m3/s | |
| x | Axial Direction, m |
| PEC | Performance Evaluation Criterion |
| Greek symbols | |
| Φ | Particle volume fraction,% |
| μ | Viscosity, Pa.s |
| ρ | Density, kg/m3 |
| Pumping power, W | |
| ΔP | Pressure drop, Pa |
| Subscripts | |
| b | Bulk |
| bf | Base fluid |
| eff | Effective |
| f | Fluid |
| i | Inner |
| o | Outer |
| p | Particle |
| s | Solid |
| w | Wall |
References
- Ramezanizadeh, M.; Alhuyi Nazari, M.; Ahmadi, M.H.; Lorenzini, G.; Pop, I. A review on the applications of intelligence methods in predicting thermal conductivity of nanofluids. J. Therm. Anal. Calorim. 2019, 138, 827–843. [Google Scholar] [CrossRef]
- Ramezanizadeh, M.; Ahmadi, M.H.; Nazari, M.A.; Sadeghzadeh, M.; Chen, L. A review on the utilized machine learning approaches for modeling the dynamic viscosity of nanofluids. Renew. Sustain. Energy Rev. 2019, 114, 109345. [Google Scholar] [CrossRef]
- Ramezanizadeh, M.; Alhuyi Nazari, M.; Hossein Ahmadi, M.; Chen, L. A review on the approaches applied for cooling fuel cells. Int. J. Heat Mass Transf. 2019, 139, 517–525. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Ramezanizadeh, M.; Nazari, M.A.; Lorenzini, G.; Kumar, R.; Jilte, R. Applications of nanofluids in geothermal: A review. Math. Model. Eng. Probl. 2018, 5, 281–285. [Google Scholar] [CrossRef]
- Abdollahzadeh Jamalabadi, M.; Ghasemi, M.; Alamian, R.; Wongwises, S.; Afrand, M.; Shadloo, M. Modeling of Subcooled Flow Boiling with Nanoparticles under the Influence of a Magnetic Field. Symmetry 2019, 11, 1275. [Google Scholar] [CrossRef]
- Abdollahzadeh Jamalabadi, M.Y.; Alamian, R.; Yan, W.-M.; Li, L.K.B.; Leveneur, S.; Safdari Shadloo, M. Effects of Nanoparticle Enhanced Lubricant Films in Thermal Design of Plain Journal Bearings at High Reynolds Numbers. Symmetry 2019, 11, 1353. [Google Scholar] [CrossRef]
- Karimipour, A.; D’Orazio, A.; Shadloo, M.S. The effects of different nano particles of Al2O3 and Ag on the MHD nano fluid flow and heat transfer in a microchannel including slip velocity and temperature jump. Phys. E Low-Dimens. Syst. Nanostruct. 2017, 86, 146–153. [Google Scholar] [CrossRef]
- Safaei, M.R.; Safdari Shadloo, M.; Goodarzi, M.S.; Hadjadj, A.; Goshayeshi, H.R.; Afrand, M.; Kazi, S.N. A survey on experimental and numerical studies of convection heat transfer of nanofluids inside closed conduits. Adv. Mech. Eng. 2016, 8, 168781401667356. [Google Scholar] [CrossRef]
- Tso, C.P.; Hor, C.H.; Chen, G.M.; Kok, C.K. Heat induction by viscous dissipation subjected to symmetric and asymmetric boundary conditions on a small oscillating flow in a microchannel. Symmetry 2018, 10, 499. [Google Scholar] [CrossRef]
- Li, Z.; He, Y.-L.; Tang, G.-H.; Tao, W.-Q. Experimental and numerical studies of liquid flow and heat transfer in microtubes. Int. J. Heat Mass Transf. 2007, 50, 3447–3460. [Google Scholar] [CrossRef]
- Lee, S.; Choi, S.U.-S.; Li, S.; Eastman, J.A. Measuring Thermal Conductivity of Fluids Containing Oxide Nanoparticles. J. Heat Transf. 1999, 121, 280. [Google Scholar] [CrossRef]
- Eastman, J.A.; Choi, S.U.S.; Li, S.; Yu, W.; Thompson, L.J. Anomalously increased effective thermal conductivities of ethylene glycol-based nanofluids containing copper nanoparticles. Appl. Phys. Lett. 2001, 78, 718–720. [Google Scholar] [CrossRef]
- Halelfadl, S.; Adham, A.M.; Mohd-Ghazali, N.; Maré, T.; Estellé, P.; Ahmad, R. Optimization of thermal performances and pressure drop of rectangular microchannel heat sink using aqueous carbon nanotubes based nanofluid. Appl. Therm. Eng. 2014, 62, 492–499. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Mirlohi, A.; Alhuyi Nazari, M.; Ghasempour, R. A review of thermal conductivity of various nanofluids. J. Mol. Liq. 2018, 265, 181–188. [Google Scholar] [CrossRef]
- Jalali, E.; Akbari, O.A.; Sarafraz, M.M.; Abbas, T.; Safaei, M.R. Heat transfer of oil/MWCNT nanofluid jet injection inside a rectangular microchannel. Symmetry 2019, 11, 757. [Google Scholar] [CrossRef]
- Safaei, M.R.; Togun, H.; Vafai, K.; Kazi, S.N.; Badarudin, A. Investigation of Heat Transfer Enhancement in a Forward-Facing Contracting Channel Using FMWCNT Nanofluids. Numer. Heat Transf. Part A Appl. 2014, 66, 1321–1340. [Google Scholar] [CrossRef]
- Behnampour, A.; Akbari, O.A.; Safaei, M.R.; Ghavami, M.; Marzban, A.; Sheikh Shabani, G.A.; Zarringhalam, M.; Mashayekhi, R. Analysis of heat transfer and nanofluid fluid flow in microchannels with trapezoidal, rectangular and triangular shaped ribs. Phys. E Low-Dimens. Syst. Nanostruct. 2017, 91, 15–31. [Google Scholar] [CrossRef]
- Tian, C.; Maleki, A.; Motie, S.; Yavarinasab, A.; Afrand, M. Generation expansion planning by considering wind resource in a competitive environment. J. Therm. Anal. Calorim. 2019. [Google Scholar] [CrossRef]
- Zhang, W.; Maleki, A.; Rosen, M.A. A heuristic-based approach for optimizing a small independent solar and wind hybrid power scheme incorporating load forecasting. J. Clean. Prod. 2019, 241, 117920. [Google Scholar] [CrossRef]
- Motie, S.; Keynia, F.; Ranjbar, M.R.; Maleki, A. Generation expansion planning by considering energy-efficiency programs in a competitive environment. Int. J. Electr. Power Energy Syst. 2016, 80, 109–118. [Google Scholar] [CrossRef]
- Li, J.; Mohammadi, A.; Maleki, A. Techno-economic analysis of new integrated system of humid air turbine, organic Rankine cycle, and parabolic trough collector. J. Therm. Anal. Calorim. 2019. [Google Scholar] [CrossRef]
- Maleki, A.; Rosen, M.A. Design of a cost-effective on-grid hybrid wind–hydrogen based CHP system using a modified heuristic approach. Int. J. Hydrogen Energy 2017, 42, 15973–15989. [Google Scholar] [CrossRef]
- Celata, G.; Cumo, M.; Marconi, V.; McPhail, S.J.; Zummo, G. Microtube liquid single-phase heat transfer in laminar flow. Int. J. Heat Mass Transf. 2006, 49, 3538–3546. [Google Scholar] [CrossRef]
- Bergman, T.L.; Incropera, F.P. Fundamentals of Heat and Mass Transfer; Wiley: Hoboken, NJ, USA, 2011; ISBN 9780470501979. [Google Scholar]
- Mital, M. Analytical analysis of heat transfer and pumping power of laminar nanofluid developing flow in microchannels. Appl. Therm. Eng. 2013, 50, 429–436. [Google Scholar] [CrossRef]
- Faghri, M.; Sparrow, E.M. Simultaneous Wall and Fluid Axial Conduction in Laminar Pipe-Flow Heat Transfer. J. Heat Transf. 1980, 102, 58–63. [Google Scholar] [CrossRef]
- Nonino, C.; Savino, S.; Del Giudice, S.; Mansutti, L. Conjugate forced convection and heat conduction in circular microchannels. Int. J. Heat Fluid Flow 2009, 30, 823–830. [Google Scholar] [CrossRef]
- El Bécaye Maïga, S.; Tam Nguyen, C.; Galanis, N.; Roy, G.; Maré, T.; Coqueux, M. Heat transfer enhancement in turbulent tube flow using Al2O3 nanoparticle suspension. Int. J. Numer. Methods Heat Fluid Flow 2006, 16, 275–292. [Google Scholar] [CrossRef]
- Akbari, M.; Behzadmehr, A. Developing mixed convection of a nanofluid in a horizontal tube with uniform heat flux. Int. J. Numer. Methods Heat Fluid Flow 2007, 17, 566–586. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Alhuyi Nazari, M.; Ghasempour, R.; Madah, H.; Shafii, M.B.; Ahmadi, M.A. Thermal conductivity ratio prediction of Al2O3/water nanofluid by applying connectionist methods. Colloids Surf. A Physicochem. Eng. Asp. 2018, 541, 154–164. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Ahmadi, M.A.; Nazari, M.A.; Mahian, O.; Ghasempour, R. A proposed model to predict thermal conductivity ratio of Al2O3/EG nanofluid by applying least squares support vector machine (LSSVM) and genetic algorithm as a connectionist approach. J. Therm. Anal. Calorim. 2018. [Google Scholar] [CrossRef]
- Ramezanizadeh, M.; Ahmadi, M.A.; Ahmadi, M.H.; Alhuyi Nazari, M. Rigorous smart model for predicting dynamic viscosity of Al2O3/water nanofluid. J. Therm. Anal. Calorim. 2019, 137, 307–316. [Google Scholar] [CrossRef]
- Ramezanizadeh, M.; Alhuyi Nazari, M. Modeling thermal conductivity of Ag/water nanofluid by applying a mathematical correlation and artificial neural network. Int. J. Low-Carbon Technol. 2019, 14, 468–474. [Google Scholar] [CrossRef]
- Hemmat Esfe, M.; Naderi, A.; Akbari, M.; Afrand, M.; Karimipour, A. Evaluation of thermal conductivity of COOH-functionalized MWCNTs/water via temperature and solid volume fraction by using experimental data and ANN methods. J. Therm. Anal. Calorim. 2015, 121, 1273–1278. [Google Scholar] [CrossRef]
- Komeilibirjandi, A.; Raffiee, A.H.; Maleki, A.; Alhuyi Nazari, M.; Safdari Shadloo, M. Thermal conductivity prediction of nanofluids containing CuO nanoparticles by using correlation and artificial neural network. J. Therm. Anal. Calorim. 2019. [Google Scholar] [CrossRef]
- Bagherzadeh, S.A.; Sulgani, M.T.; Nikkhah, V.; Bahrami, M.; Karimipour, A.; Jiang, Y. Minimize pressure drop and maximize heat transfer coefficient by the new proposed multi-objective optimization/statistical model composed of “ANN + Genetic Algorithm” based on empirical data of CuO/paraffin nanofluid in a pipe. Phys. A Stat. Mech. Its Appl. 2019, 527, 121056. [Google Scholar] [CrossRef]
- Hemmat Esfe, M.; Wongwises, S.; Naderi, A.; Asadi, A.; Safaei, M.R.; Rostamian, H.; Dahari, M.; Karimipour, A. Thermal conductivity of Cu/TiO2–water/EG hybrid nanofluid: Experimental data and modeling using artificial neural network and correlation. Int. Commun. Heat Mass Transf. 2015, 66, 100–104. [Google Scholar] [CrossRef]
- Koo, J.; Kleinstreuer, C. A new thermal conductivity model for nanofluids. J. Nanopart. Res. 2004, 6, 577–588. [Google Scholar] [CrossRef]
- Chon, C.H.; Kihm, K.D.; Lee, S.P.; Choi, S.U.S. Empirical correlation finding the role of temperature and particle size for nanofluid (Al2O3) thermal conductivity enhancement. Appl. Phys. Lett. 2005, 87, 153107. [Google Scholar] [CrossRef]
- Ben Mansour, R.; Galanis, N.; Nguyen, C.T. Effect of uncertainties in physical properties on forced convection heat transfer with nanofluids. Appl. Therm. Eng. 2007, 27, 240–249. [Google Scholar] [CrossRef]
- Li, J.; Peterson, G.; Cheng, P. Three-dimensional analysis of heat transfer in a micro-heat sink with single phase flow. Int. J. Heat Mass Transf. 2004, 47, 4215–4231. [Google Scholar] [CrossRef]
- Lelea, D. Effects of temperature dependent thermal conductivity on Nu number behavior in micro-tubes. Int. Commun. Heat Mass Transf. 2010, 37, 245–249. [Google Scholar] [CrossRef]
- Tso, C.P.; Mahulikar, S.P. Experimental verification of the role of Brinkman number in microchannels using local parameters. Int. J. Heat Mass Transf. 2000, 43, 1837–1849. [Google Scholar] [CrossRef]
- Tso, C.P.; Mahulikar, S.P. The role of the Brinkman number in analysing flow transitions in microchannels. Int. J. Heat Mass Transf. 1999, 42, 1813–1833. [Google Scholar] [CrossRef]
- Tso, C.P.; Mahulikar, S.P. The use of the Brinkman number for single phase forced convective heat transfer in microchannels. Int. J. Heat Mass Transf. 1998, 41, 1759–1769. [Google Scholar] [CrossRef]
- Morini, G.L. Scaling Effects for Liquid Flows in Microchannels. Heat Transf. Eng. 2006, 27, 64–73. [Google Scholar] [CrossRef]
- Safaei, M.R.; Mahian, O.; Garoosi, F.; Hooman, K.; Karimipour, A.; Kazi, S.N.; Gharehkhani, S. Investigation of micro- and nanosized particle erosion in a 90° pipe bend using a two-phase discrete phase model. Sci. World J. 2014, 2014, 740578. [Google Scholar] [CrossRef]
- Lin, C. Application of the Symmetric Model to the Design Optimization of Fan Outlet Grills. Symmetry 2019, 11, 959. [Google Scholar] [CrossRef]
- Chen, C.-W.; Lu, Y.-F. Computational Fluid Dynamics Study of Water Entry Impact Forces of an Airborne-Launched, Axisymmetric, Disk-Type Autonomous Underwater Hovering Vehicle. Symmetry 2019, 11, 1100. [Google Scholar] [CrossRef]
- Qin, Y. Pavement surface maximum temperature increases linearly with solar absorption and reciprocal thermal inertial. Int. J. Heat Mass Transf. 2016, 97, 391–399. [Google Scholar] [CrossRef]
- Qin, Y.; Tan, K.; Meng, D.; Li, F. Theory and procedure for measuring the solar reflectance of urban prototypes. Energy Build. 2016, 126, 44–50. [Google Scholar] [CrossRef]
- Versteeg, H.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method; Prentice Hall: Upper Saddle River, NJ, USA, 2007. [Google Scholar]
- Patankar, S. Numerical Heat Transfer and Fluid Flow; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Perry, R.H.; Green, D.W. Perry’s Chemical Engineers’ Handbook; McGraw-Hill: New York, NY, USA, 2008; ISBN 9780071422949. [Google Scholar]
- Batchelor, G.K. The effect of Brownian motion on the bulk stress in a suspension of spherical particles. J. Fluid Mech. 1977, 83, 97–117. [Google Scholar] [CrossRef]
- Roy, G.; Gherasim, I.; Nadeau, F.; Poitras, G.; Nguyen, C.T. Heat transfer performance and hydrodynamic behavior of turbulent nanofluid radial flows. Int. J. Therm. Sci. 2012, 58, 120–129. [Google Scholar] [CrossRef]
- Lelea, D.; Nisulescu, C. The micro-tube heat transfer and fluid flow of water based Al2O3 nanofluid with viscous dissipation. Int. Commun. Heat Mass Transf. 2011, 38, 704–710. [Google Scholar] [CrossRef]
- Jung, J.Y.; Oh, H.S.; Kwak, H.Y. Forced convective heat transfer of nanofluids in microchannels. Int. J. Heat Mass Transf. 2009, 52, 466–472. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).