1. Introduction
In connection with the new problems arising in geophysics, oceanology, physics of atmosphere, usage of the cryogenic fluids in the engineering sphere, as well as the ecological problems, the operation of complex hydraulic engineering facilities, including the marine oil producing complexes, and a number of other actual problems facing the science and engineering fields, we can observe the growth of interest to the research on the wave dynamics of the different inhomogeneous fluids and, in particular, the stratified fluids [
1,
2,
3,
4,
5,
6,
7]. The solution to the problems of the mechanics of continua and hydrodynamics have always served as the stimulus of new directions in mathematics and mathematical physics [
1,
8,
9]. For the detailed description of the substantial amount of natural phenomena connected with the dynamics of stratified media, it is necessary to use the sufficiently developed mathematical models, which as a rule are the rather complex nonlinear multi-parametric mathematical models and only numerical methods are effective for their research [
10,
11,
12,
13,
14,
15,
16,
17].
The stratification, or the layered structure of the natural media (oceans and the air atmosphere) causing formation of the internal gravity waves (IGW) plays an appreciable role in different oceanic and atmospheric processes and influences on the horizontal and vertical dynamic exchanges. The periods of the internal gravity waves can be from several minutes up to several hours, the lengths of the waves can achieve up to dozens of kilometers, and their amplitudes can exceed dozens of meters [
5,
6]. The interest in the internal gravity waves is caused by their wide presence in nature. Both the air atmosphere, and the oceans are stratified. Reduction in the air pressure and its density at the increase in the elevation are well-known. However, the sea water is also stratified. Here, the rise in the water density with the increase in its depth is determined, mainly, not by the rather small compressibility of the water, but by the fact that with the increase in the depth, as a rule, the temperature of the water is decreasing, and its saltiness grows [
7,
18,
19]. Stratification of the natural mediums (the ocean, the atmosphere) can be caused by different physical reasons, but the most common cause is gravity. In the stratified medium, this force creates such a distribution of the particles dissolved in salts and suspensions, at which point it forms the heterogeneity of the medium along the direction of the gravity field in the stratified medium [
1,
2,
3,
4].
The density stratification, as the experimental and natural observations show, renders the most essential influence, as compared with other kinds of stratification, on the dynamic properties of the medium and on the processes of distribution in the medium of the wave movements. Consequently, a consideration of the wave generations in the stratified mediums usually neglect all other kinds of wave stratification, except for the density stratification, and in the capacity of the stratified medium they consider the medium with density stratification caused by gravity. In the real oceanic conditions, the density changes are small, the periods of oscillations of the internal waves range from several minutes (in the layers with rather fast change of the temperatures and the depth) up to several hours [
5,
6,
7]. Such great periods of fluctuations mean that even at the big amplitude of the internal waves, they can achieve dozens of meters along the vertical direction, and the speeds of the particles in the internal wave are low—for the vertical components the speeds of the particles have the order of mm/s, and for the horizontal—cm/s. Therefore the dissipative losses—the losses caused by the fluid viscosity in the internal gravity waves are very small, and the waves propagation can propagate practically without fading within the big distances [
5,
6,
7,
16,
17]. The speed of internal gravity waves propagation in the ocean is low—the order of dozens of cm/s. These properties of the internal gravity waves mean that they can keep the information about the sources of their generations for a long time [
2,
10,
19,
20,
21,
22]. Unfortunately, it is very difficult to orientate this information because the internal waves pass dozens and hundreds of kilometers from the source of the generations up to the place of supervision; moreover, practically everywhere where the stratification of the ocean takes place, we can observe the internal gravity waves, but simultaneously we can “hear” the “voices” of the most different sources. The qualitative (and the quantitative) properties of the internal gravity waves, caused by that or other concrete sources, depend not only on its physical nature, and its spatial and time distribution, but also depends on the properties of the medium located between the source of the waves and the place of the observation. The internal gravity waves represent the big interest, not only from the point of view of their applications. They are of interest to the theorists occupied with the problem of waves propagation, as the internal gravity waves properties differ, in many respects, from the properties of the acoustic or electromagnetic waves that researchers have become accustomed to. For example, for short harmonious internal waves of the following kind:
, where
)—the rays are not directed perpendicularly to the wave fronts or to the surfaces of the equal phase
, but rather are directed along these surfaces [
1,
2,
19,
20,
21,
22,
23,
24].
The reasons for the excitation of internal gravity waves in the ocean and the atmosphere are very different: the fluctuations of the atmospheric pressure, the flow past of the bottom asperities, movement of the surface or the underwater ship, deformation in the density field, the turbulent spots formed by various reasons, the bottom shift or the underwater earthquake, the surface or underwater explosions, etc. [
4,
12,
13,
20,
21]. One of the mechanisms for the generation of internal gravity waves may be wave fields excitation caused by, for example, a movement of the solid bodies, the turbulent spots, the water lenses and the other non-wave formations with abnormal characteristics [
5,
6,
7]. Of the solutions to the problem of the generation of internal gravity waves—for example, the stream of the stratified fluid, which is flowing past some non-local obstacle—the most widespread are the following two methods [
20,
21,
25,
26,
27]. The first method considers the numerical solution of the linearized system of the hydrodynamics equations of describing the internal waves, a shortcoming of which may be the limitation of the field of integration of the space, in which there is a possibility to have the numerical solution to the problem. The second method provides for substitution of the function describing the form of the non-local source either with the rather simple function, or with the system of the point sources [
8,
9,
11,
12,
13,
14,
15,
16,
18,
19,
20,
21].
2. Formulation of the Problem and Integral Forms of Solutions
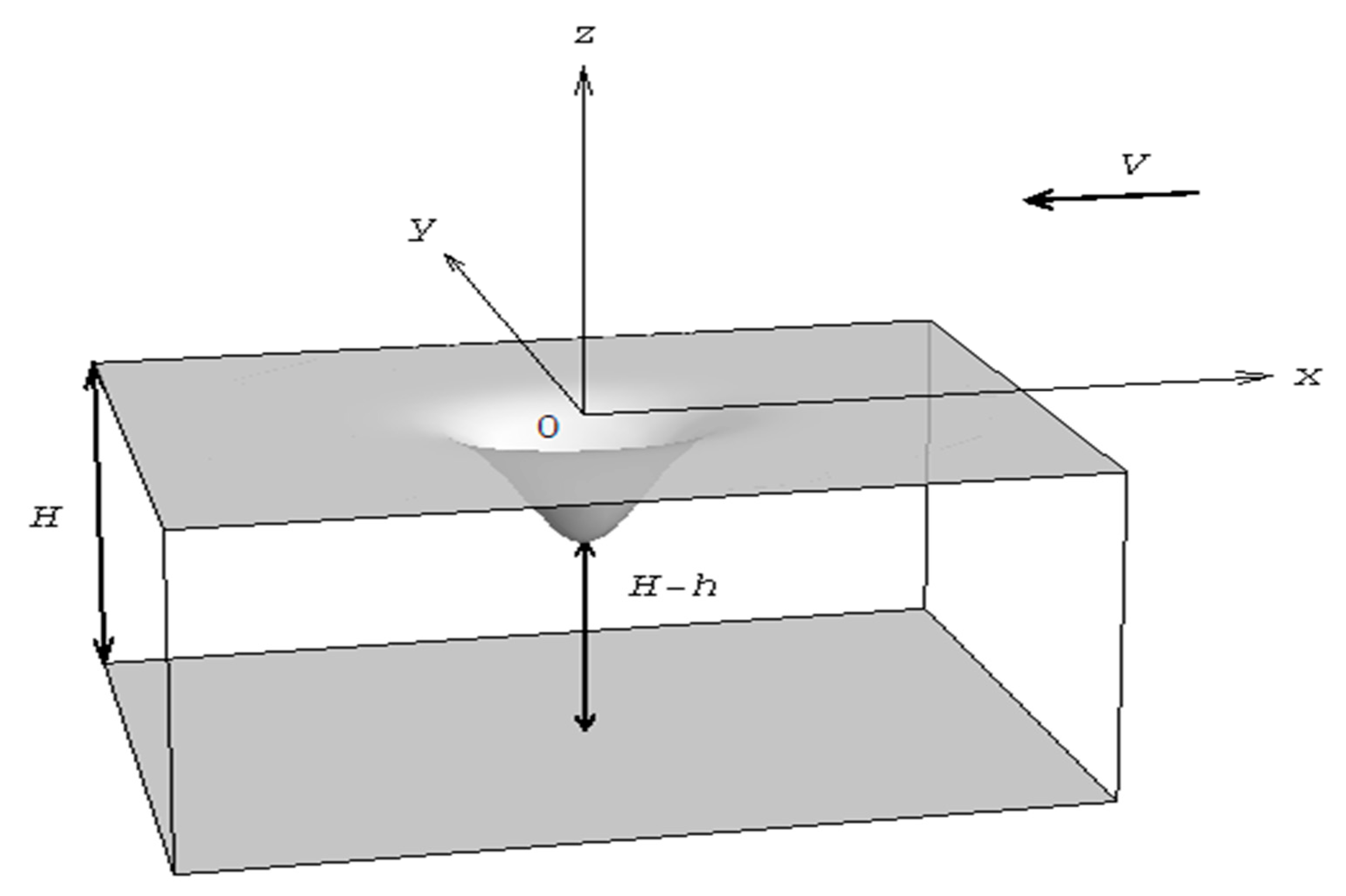
We consider the problem of generating the internal gravity waves by the motion of a source of non-local perturbations in a layer of non-viscous incompressible vertically stratified media of thickness
. We suppose that the body moves on the medium surface with velocity
along the
x-axis, the
z-axis is directed upwards, the shape of non-local source is described by function
, and the maximum height of the perturbation source is equal to
.
Figure 1 illustrates the geometry of the problem under study. The steady-state regime of wave oscillations is considered. In the moving coordinate system under the Boussinesq approximation, we use the following equation for small perturbations of the vertical velocity component
[
1,
2,
25]:
where
is the squared Brunt–Väisälä frequency (buoyancy frequency) which is further assumed constant,
,
is the unperturbed density of the medium, and
is the acceleration due to gravity. We assume that internal Froude number is
. This supposition means that the pattern of trajectories near the streamline body should have the same pattern (qualitatively), as in the case of non-stratified medium [
13,
16,
25]. The linearized boundary condition on the surface is written as [
8,
9,
13,
25]:
The impermeability condition is specified at the bottom:
If we apply dimensionless coordinates and variables
,
, then, Equation (1) and boundary conditions (2) and (3) take the following form (index “*” is further omitted):
The following assumptions are related to function
: this function is radially symmetric
and
. This presentation gives an accurate description of many natural sources of the generation of IGW in the ocean, in particular, the waves generated by moving typhoons and hurricanes [
10]. In what follows, the problem will be solved by the Fourier method. To describe the shape of the non-local source analytically, it is required to choose function
so that the double Fourier transform (which coincides with the Fourier–Bessel transform up to the multiplier
) of this function has singular points only in the form of simples poles [
28,
29]. In this case, it is possible to construct and apply the analytic representations of the solutions for function
. A more complicated structure of singular points of the Fourier transform of function
, for example, the presence of branching points, does not permit solving the problem analytically [
8,
9,
28,
29].
We seek solutions (4)–(6) in the form of the Fourier integral:
Then, to determine function
, it is necessary to solve the boundary-value problem:
where
,
is the Fourier–Bessel transform of function
:
, where
J0 is the Bessel function of order zero [
28,
29]. Solutions (8)–(10) have the form:
3. Analytic Representations of Solutions
We substitute (11) into (7) and integrate with respect to variable
. We move the integration contour on the complex plane of variable
upwards by
. It is necessary to move the contour of integration to satisfy the radiation condition, i.e., to satisfy the condition that there are no waves propagating forward from the source of perturbations. We consider expression (7), i.e., function
in the far region for large values of
. First, we consider the case
. As
, integral (7) is exponentially small, because
. To study the behavior of this integral at
, we displace the contour of integration into the lower half-plane where the integral is exponentially small, and the main contribution is determined by the residues at the real poles:
The real poles
increase with mode number
and are bounded:
. Then, solution (7) can be represented as a sum of wave modes:
The action of IGW generated by moving surface perturbations can result in a noticeable sediment transport and bottom erosion. Internal waves contribute to the sediment diffusion and transport on the sea floor. Therefore, the particle transfer processes associated with the impact of internal gravity waves are actively studied in various applied problems of ecology and engineering oceanology [
5,
6,
30,
31]. At large depths near the bottom, the main contribution to the complete wave field is made by the horizontal components of velocity. The horizontal components of velocity
(
-component) and
(
-component) are related to the vertical component of velocity
as [
2,
8,
9]:
If we take expression (12) into account, we obtain the following expressions for the horizontal components of velocity:
4. Numerical Results and Discussion
The following parameters were used in numerical calculations:
,
,
, and
, for which, in dimensional units, the typical depth of the ocean is equal to
. The vertical scale
of non-local source is equal to tens of meters, the horizontal scale is equal to several hundred meters, and the velocity of the source motion is equal to tens of centimeters per second. Therefore, the values of parameters
used in numerical calculations completely correspond to the spatiotemporal characteristics observed in the ocean in the regions of sea surface perturbations due to moving typhoons which generate intense IGW [
5,
6,
7].
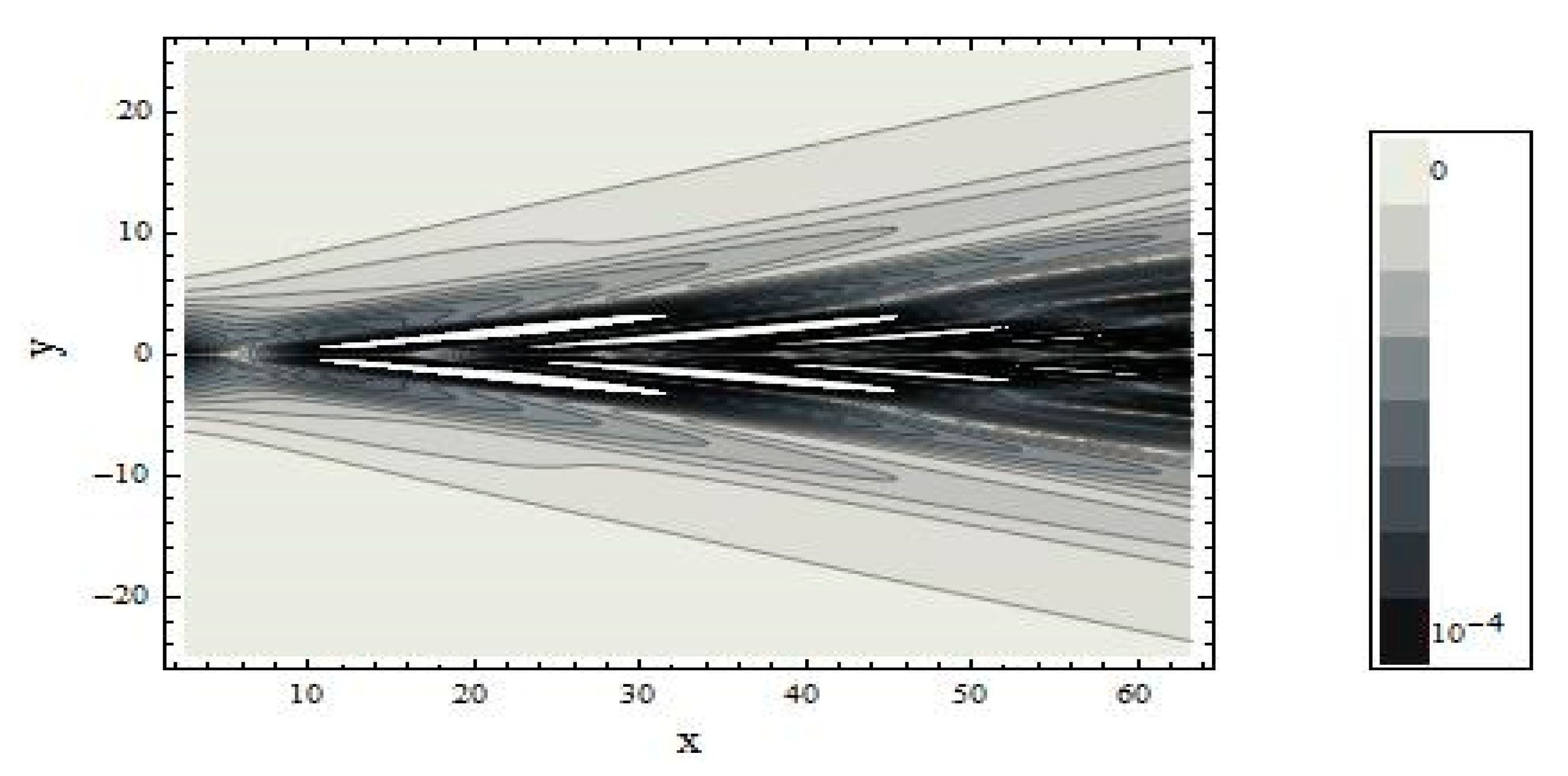
Figure 2 shows the isolines of the absolute values of velocity
of the sum the first three modes at the bottom at
.
Figure 3 presents the isolines of the absolute values of velocity as the sum of the first three modes at
.
Numerical calculations show that, as the depth decreases, the contribution of the vertical component of velocity
to the total field becomes more noticeable, which leads to a significant complication of the amplitude–phase structure of wave fields.
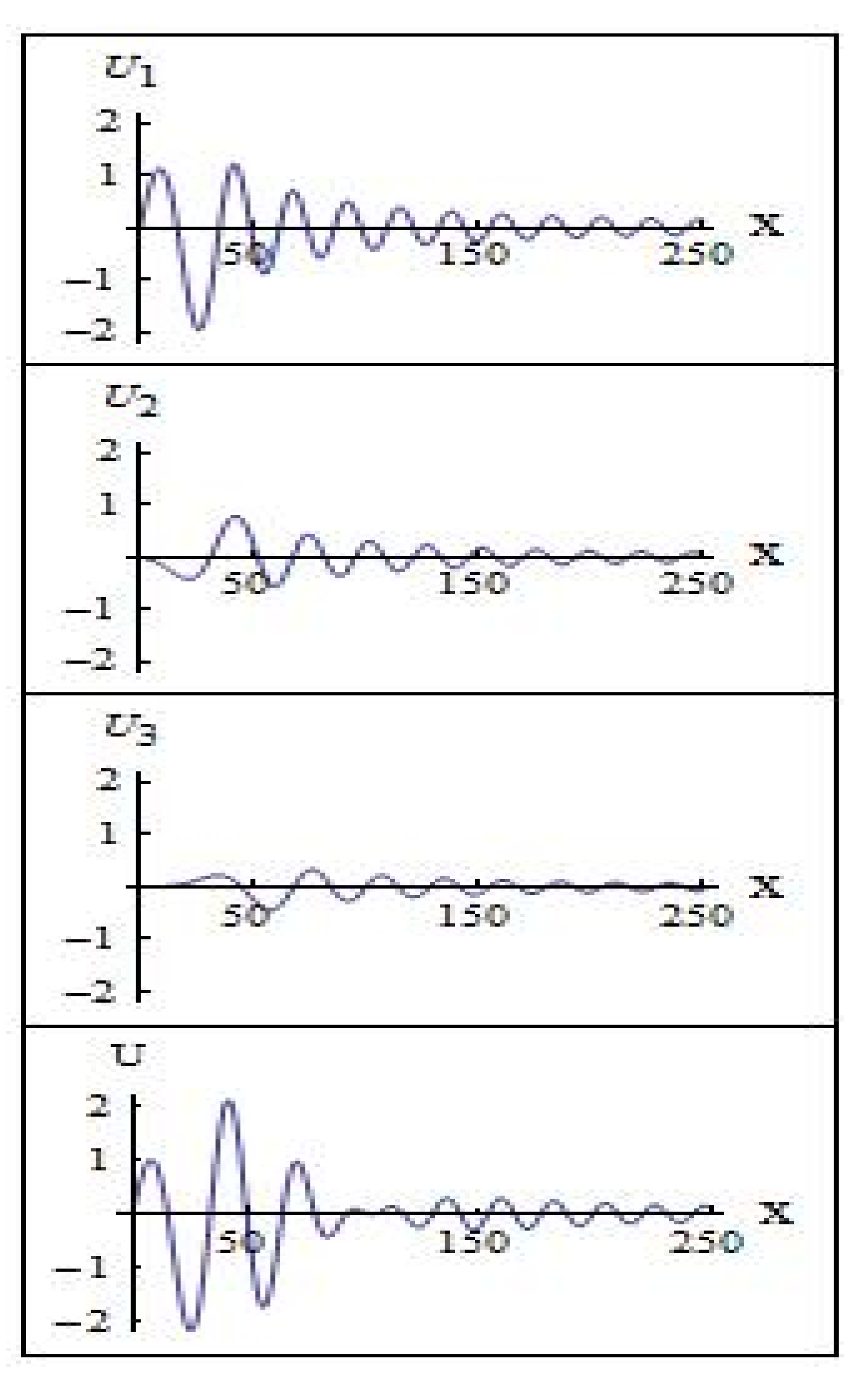
Figure 4 shows the first three wave modes of the horizontal
-component of velocity
and the sum
at the bottom,
at
.
Function
describes the pressure perturbation induced by propagation of IGW from moving surface perturbations [
2,
5,
6] with an accuracy up to multiplier
. This allows one to calculate the pressure variations at the bottom, which is important because bottom pressure transducers are widely used for recording IGW in the ocean [
5,
6,
7]. Obviously, the pressure transducers must also record IGW, and they can be used in the systems of early detection of IGW of large amplitude. Since the amplitudes of IGW can be as large as tens of meters, the relative variations in the bottom pressure can be quite significant. At the same time, the absolute variations in the bottom pressure, which are related to IGW, are proportional to multiplier
; in the real ocean conditions, the latter is two orders of magnitude smaller than a similar multiplier for the surface waves, which is equal to
. This is precisely the cause of problems with recording IGW by bottom pressure transducers, and these problems can be solved by using the frequency filtration, because the frequency of IGW is significantly lower than the frequency of surface waves [
1,
2]. Therefore, the study of far fields of IGW in the ocean which leads to variations in the bottom pressure on the sea floor makes possible to develop methods for recording IGW generated by moving surface sources of perturbations [
5,
6,
7].
5. Summary and Conclusions
In this paper, we examined the linear IGW generated by non-local sources moving with a constant speed in a layer of stratified media of a finite depth. We solved the problem of constructing analytic solutions that describe IGW generation at far distances from a non-local source of perturbations. We used a model distribution of the source shape of radial symmetry, which correctly describes (qualitatively) the main spatiotemporal characteristics of the natural sources responsible for the generation of internal waves in the ocean. The obtained solution is a sum of wave modes. The solution has the form of a series of eigenfunctions of the basic spectral problem for the internal wave equation. The results of numerical calculations of horizontal velocity components of far fields of IGW are given. The far fields of IGW at large distances from a moving non-local source (much larger than the source size) are determined by the dispersion law and the source velocity. The results of our research make it possible to estimate the variations in the bottom pressure at the sea floor, which is important in the development of methods for recording internal waves in the ocean. Since the generation and propagation of IGW under real conditions are essentially non-linear phenomena, using some rational assumptions can allow us to linearize the internal wave generation and propagation equations. This paper investigates the linear approximations of IGW at long distances from the sources of generation in the cases when the source is substituted with a model. Thus, we find it interesting, for example, to consider the combination of model representations and semi-empirical and possibly even experimental results. Since the solutions to the equation of IGW with respect to a point disturbing source have been comprehensively studied [
1,
2,
8,
9,
11,
12,
22,
26], and by knowing such a solution we can write out a solution for the source distributed vertically and horizontally, that is, the source with a finite length; thus, we again apply the model arguments. The following approach can be applicable as well. We assume that there is a disturbing source which leaves behind a turbulence wake (the region of rotational formations, generation zone) that somehow generates internal waves. We locate an imaginary plane that is parallel, for example, to the motion trajectory of the disturbing source and measure all required characteristics on this plane. Then, we can solve the propagation problem of internal waves in linear approximation using the data on the plane as the initial data. This seems to be a reasonable approach because we have to expect some good results from the linear theory far from turbulent areas, generation zones, etc. This “initial” (or “initially-boundary”) data on the plane can be defined either by experimental or by numerical calculations. Similarly, the initial conditions may contain a substantial amount of realistic information upon which the linear theory of IGW, far from nonlinearity regions, must produce satisfactory results. The popularity of the used approaches for the analysis of the dynamics of internal gravity waves can be promoted by the existence of the lot of interesting physical problems that are quite adequately described by these approaches; such approaches can promote the interest in the multiplicity of problems bound to a diversification of the non-uniform stratified mediums.