Abstract
The problem of internal gravity waves fields in a stratified medium of finite depth is considered for model distributions of background shear currents. For the analytical solution of the problem, a constant distribution of the buoyancy frequency and various linear dependences of the background shear current on depth were used. The dispersion dependences are obtained, which are expressed in terms of the modified Bessel function of the imaginary index. Under the Miles–Howard stability condition and large Richardson numbers, the Debye asymptotics of the modified Bessel function of the imaginary index were used to construct analytical solutions. The dispersion equation is solved using the proposed analytical approximation. The properties of the dispersion equation are studied and the main analytical characteristics of the dispersion curves are investigated depending on the parameters of background shear flows.
1. Introduction
Among the large variety of observed wave processes of different physical nature in the ocean and the Earth’s atmosphere, the interaction between generated waves and hydrodynamic flows is of particular interest [1,2,3,4,5,6]. The motion in a stratified medium is one of the main factors that influence the dynamics of internal gravity waves (IGW) both under natural conditions and in technical devices. An important characteristic of natural stratified media (ocean, atmosphere) is the presence of background flows with vertical displacement of velocity which rather weakly depend on time and horizontal coordinates [7]. In the ocean, such currents can manifest in the area of seasonal thermocline and have a noticeable effect on the IGW dynamics. If the scale of variations in background shear flows is horizontally much greater than the IGW length and the scale of time variability is much greater than the IGW periods, then such flows can be considered as stationary and horizontally uniform [7,8,9]. The IGW excited in a stratified medium with background shear currents play an important role in various transfer mechanisms in the depth of the world ocean. Under real ocean conditions, it is necessary to consider IGW propagating against the background of currents with a shift of the vertical velocity, and the vertical velocity variation is of the same order as the IGW maximum velocities [10,11,12,13,14,15]. The presence of such currents should have a significant impact on the IGW dynamics in the ocean and atmosphere. If the scale of horizontal variations in currents is much greater than the IGW length and the scale of time variability is much greater than the periods of these waves, then the case of stationary and horizontally uniform background shear flows is a natural mathematical model [1,7]. In the current scientific research, asymptotic methods for studying analytic models of wave generation are used to analyze the dynamics of IGW in natural stratified media with the presence of currents. In the linear approximation, the existing approaches to describing the wave pattern of the generated IGW fields are based on the representation of wave fields by Fourier integrals and their asymptotic analysis [1,5,16,17,18,19].
One of the main mechanisms for IGW generation in the world ocean with shear flows is moving atmospheric cyclones [4,5,20]. Typhoons have a significant impact on ocean circulation and wave generation. The IGW fields excited by this generation mechanism play a significant role in the energy transfer in the world ocean. The tangential wind stress created by a moving hurricane forms a wake or wake structure in the ocean. The experimental detection of these wave structures was one of the impressive achievements of modern oceanology [4,5,6]. The propagation of IGW in a stratified ocean with shear flows has specific features associated with the analytical properties of dispersion relations. If a source of disturbance moves in a medium with flows, then it creates a wave pattern around itself, the main features of which are lines of constant phase. On the basis of integral representations of solutions and kinematic theory, it is possible to formulate analytical representations for the phase surfaces of waves far from a moving source [8,9,19]. Therefore, the analysis of integral representations of solutions requires the development of asymptotic and analytical methods for studying dispersion relations. Using the analytical properties of the dispersion relations, one can construct the asymptotics of the far IGW fields in a stratified ocean with shear flows. The results obtained can be used for qualitative analysis and calculations of the IGW fields. Analytical expressions for dispersion curves are used, in particular, for the operational analysis of IGW field observations in the ocean. In addition, the obtained analytical results can be used to develop methods for IGW detecting using radar methods [5,6].
At large distances from perturbation sources, the source shape does not practically influence the IGW characteristics which are determined only by the parameters of stratified medium and the corresponding dispersion laws [8,9,19]. The goal in this paper is to study the dispersion relations for constructing the solutions which describe the far fields of IGW in a stratified medium of finite depth for model distributions of shear flows.
2. Statement of the Problem
We consider an ideal incompressible vertically stratified medium of finite depth . Let be the vector of background shear flow at the horizon . In the Boussinesq approximation, the equation for small perturbations of the vertical component of velocity becomes [1,5,7]:
where is the squared Brunt–Väisälä frequency (buoyancy frequency), is the free fall frequency, and is the unperturbed density of the stratified medium.
The boundary conditions are taken in the form (the vertical axis is directed upwards):
Since the problem under study is linear, the vertical component of the velocity and the vector of horizontal velocities are related as [8,9]. Further, we use the following assumptions. The Brunt–Väisälä frequency is assumed to be constant, , and the background shear current is assumed to be one-dimensional, . The function is a linear function of depth: . This hydrology model (constant distribution of buoyancy frequency, multidirectional shear flows) is widely used in real oceanological calculations and allows one to take into account the main features of wave dynamics with regard to the real variations in the density of the marine environment observed in full-scale measurements of IGW in the ocean, as well as to investigate the problem analytically [4,5,12,13,14,15]. The results of numerous studies of natural measurements of internal waves, flows, and their interaction in various regions of the world ocean were analyzed in [4,5], in particular, by using this model. The generation of IGW by a shear current in the Kara Gates Strait was considered in [13]; in this case, the flow fluctuates with the tidal frequency, and the IGW packets appear at intervals determined by the shear instability of flows. Similar results were obtained in [4,5] using the example of the Strait of Gibraltar, where the measurements of flows and IGW whose amplitude can be tens of meters are considered. Numerous measurements of bottom flows in deep waters of the North Atlantic show that, at high depths, the gradients of shear velocities and the buoyancy frequency values are small and the main variations in these hydrophysical parameters are observed in the upper layers of the ocean at depths of about 100–200 m, which allows one to use the proposed hydrology model and the linear dependence of shear flows on the depth [4,5,14,15]. In the presence of background shear currents, the IGW flows can interact with these currents and exchange energy with them, i.e., the natural wave oscillations can increase exponentially [7]. Therefore, it is necessary that the vertical gradient of background shear currents be small as compared to the buoyancy frequency [1,2,3]. Further, we assume that the Miles–Howard stability condition is satisfied for the Richardson number: [21,22,23,24,25,26]. If the Miles–Howard condition is satisfied, then the following spectral problem has no complex eigenvalues [23,25]. In the absence of dynamic instability of shear currents in the world ocean waters, typical values of the Richardson numbers can be in the range from 2 to 20 [4,5,12,13,14,15]. In the dimensionless coordinates and variables , Equations (1) and (2) can be represented as (in what follows, the asterisk “*” is omitted):
The parameter is the inverse of the squared root of the Richardson number: , and the parameter is the ratio of the amplitude of near-surface flow to the maximal group velocity of IGW propagation in the ocean which is equal to [1,8,9]. The solution of problem (3) is sought in the form of free harmonic waves: . Then, to determine the function , we have:
The solutions of problem (4) are:
where is the modified Bessel function of imaginary index , [27,28]. The solution satisfying the boundary condition for has the form: . The functions are complex conjugate, and hence the solution is real. Since we assume that the Miles–Howard stability condition is satisfied for the Richardson number, we have . In particular, this implies that , and hence is real. The requirement to satisfy the boundary condition for determines the dispersion relation:
The asymptotic solutions of dispersion Equation (5) can be obtained under the assumption that the parameter is large, and then can be replaced by . We use the Debye asymptotics of the modified Bessel function of imaginary index , which, in contrast to the classical asymptotics as , determines the behavior of the function for large values of both the index and the argument . The Debye asymptotics of the modified Bessel function of imaginary index (for large values of both the index and the argument ) has the form [16,17,27,28]:
The value is a branch point, the value is a turning point at which the asymptotics (6) do not work. If , then we have , [27,28].
3. Basic Properties of Dispersion Curves
In [23], for a similar model hydrology (constant buoyancy frequency, linear profile of shear flow, finite thickness of stratified layer), a dispersion relation was obtained in a form similar to (5), and it was noted that to solve this equation is a great mathematical difficulty. A more complicated problem is to study the asymptotic properties of the obtained dispersion equation, because this permits efficiently calculating the IGW fields for various modes of wave generation [7,16,17,23]. Further, the basic specific features of solutions of dispersion Equation (5) will be studied and asymptotic representations of solutions of this equation will be constructed. The solutions of dispersion Equation (5) can be represented as , or . In what follows, we study the dispersion dependences and for ( is a fixed parameter). In the models of shear currents used below, ; this means that the amplitudes of background shear currents do not exceed the maximal group velocity of IGW propagation, and precisely this is observed in the world ocean [5,6]. The parameter determines the ratio of the frequency of the free wave to the maximal value of the buoyancy frequency and describes the IGW propagation with a frequency almost two times less than the buoyancy frequency, which is also observed under real ocean conditions [1,6,7]. Starting from numerous results of oceanological observations of shear currents in the world ocean, one can propose three model distributions of one-dimensional background shear current across depth [4,5,17]. The first model is a unidirectional flow such that its amplitude decreases with depth and the amplitude of the bottom flow is different from zero at the bottom (line 1 in Figure 1). The second model is a unidirectional flow such that the amplitude of the bottom flow is small at the bottom as compared to the amplitude of the near-surface bottom (line 2 in Figure 1). The third model presents multidirectional flows, and the amplitude of the bottom flow is comparable in order of magnitude to the amplitude of the near-surface flow (line 3 in Figure 1).
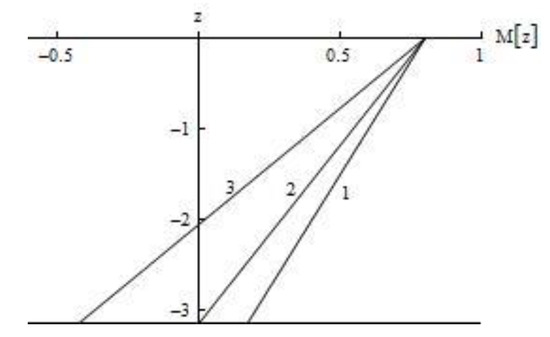
Figure 1.
Three models of shear flows.
Using Debye asymptotics of the modified Bessel function of imaginary index to solve Equation (5), one can investigate qualitative pictures of the behavior of dispersion curves for different models of distribution of the background shear velocity [16,17]. The dispersion curves in the first model are two families of open curves, and each dispersion curve is bounded. The dispersion curves for the second model form a single family, and each of the curves is contained in the corresponding semi-infinite interval. The dispersion curves corresponding to the third model form a single family of closed curves.
A qualitative picture of the behavior of dispersion curves shaped as closed lines is obtained in studying the IGW generation by an oscillating source of perturbations moving with a constant velocity. However, it should be noted that, in this case (constant depth-independent background current), the wave pattern of excited IGW fields is determined by the oscillation frequency , and, for example, the annular waves can exist only at small frequencies [16,17]. For linear background shear currents, a qualitative wave pattern of IGW is determined only by the character of the flow (dimensionless amplitude of the near-surface flow and the vertical gradient ) and is independent of the harmonic wave frequency . In particular, the unidirectional flow generates both wedge (longitudinal) and annular (transverse) waves, and the multidirectional flow generates only annular (transverse) waves. For the first model, since there are two distinct families of dispersion curves, there exists a wave system of wedge (longitudinal) waves. For the second model, the annular (transverse) waves occupy the whole spatial domain inside the wave wedge with half-opening angle , and the length of transverse wave of the -th mode is equal to for . The wedge (longitudinal) waves are bounded for each mode by both the wave front with half-opening angle (, where is a root of the equation ) and the wave front with half-opening angle less than whose position is determined by the asymptotics of for large values of . The phase structure of excited fields of IGW significantly depends on the relationship between the amplitudes of the bottom and near-surface shear currents. In particular, for the third model, if the amplitudes of the bottom and near-surface shear currents are equal to each other, then the corresponding phase pattern of the wave field is symmetric. If the amplitudes of the bottom and near-surface currents are distinct, then the phase pattern of excited IGW fields becomes asymmetric. Therefore, the asymmetry of phase patterns of wave fields of IGW can be a criterion for noticeable reconstruction of the depth distribution of background shear ocean flows [4,5,6,16,17]. The phase pattern of the IGW fields corresponding to the first model is shown in Figure 2. The phase pattern of the IGW fields corresponding to the second model is shown in Figure 3. The phase pattern of the IGW fields corresponding to the third model is a family of annular waves and is shown in Figure 4. We calculate the constant phase lines using the stationary phase method [8,9,29,30]. A parametric family of constant phase lines (with a parameter ) for each wave mode can be represented as: , , . With fixed values , we can calculate a line of constant phase. All calculations for Figure 2, Figure 3 and Figure 4 are given for the first wave mode for the values , where for Figure 2, for Figure 3, for Figure 4. It can be noted that the wave pattern of Figure 2 is basically the classic Kelvin ship pattern of surface water wave [29,30].
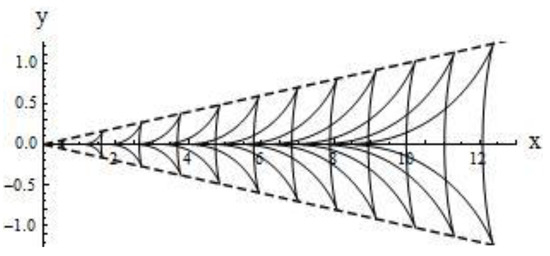
Figure 2.
Phase structure for the first model of shear flows. The phase structure consists of curved triangles embedded in the wave wedges with their vertex lying nearer to the origin.
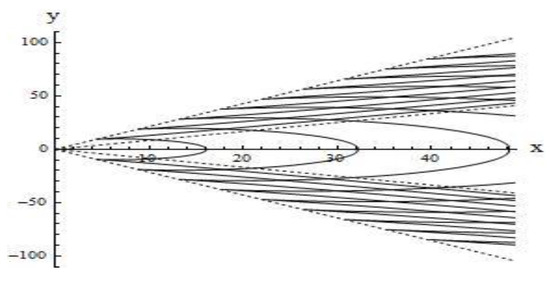
Figure 3.
Phase structure for the second model of shear flows. The wave pattern looks like a system of longitudinal and transverse waves.
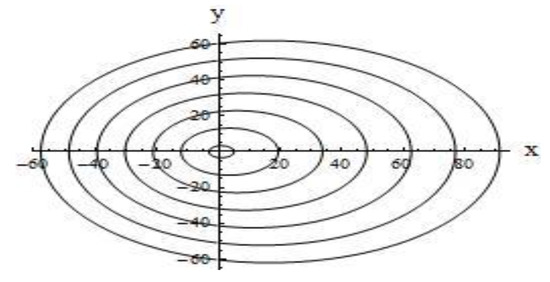
Figure 4.
Phase structure for the third model of shear flows. The wave pattern looks like closed (symmetric or asymmetric) ellipsoids.
4. Analytical Approximation of Dispersion Relations
In the general case, the solution of problem (1)–(2) that describes the IGW far fields, is a sum of vertical wave modes, , and each of modes is a superposition of plane waves of the form: , , where the amplitude is a slowly varying function of the variable and depends on the eigenfunctions of spectral problem (4) [1,8,9]. The integrals of this type can be calculated at large distance (for large values of ) by using the stationary phase method [8,9]. The stationary points of the phase function are determined by solving the equations , or . The phase function can have stationary points, and the complete field of a separate wave mode is the sum over all stationary points [8,9]. The results of numerical calculations of such integrals for real oceanological data show that the main contribution is made by stationary points of the phase function for small values of the wave number , because, for large values of wave numbers, the amplitude is small and decreases not slower than as [8,9]. Therefore, when studying the IGW far fields, it is most interesting to consider the long-wave approximations of dispersion Equation (5), which allows one efficiently to calculate the wave fields at far distances from the perturbation sources. These approximations can be studied by the following two methods. First, one can apply the long-wave approximation directly to Equation (4). Second, one can investigate the corresponding asymptotics of the modified Bessel function of imaginary index, i.e., to consider dispersion relations (5). In what follows, we will illustrate the possibility of using these two approaches.
First method. We assume that and ; then Equation (4) can be written as:
The obtained Equation (7) is the Euler equation whose solution has the form . Taking the boundary conditions into account, one obtains the relation , which can be represented as , which allows one to obtain the dispersion relation in the long-wave approximation:
Then the explicit relation for the dispersion relation becomes:
Second method. We use the expansion of the modified Bessel function at zero (for small values of the argument ) which has the form [27,28]:
where is the Euler gamma function [20,21]. Substituting (9) into (5), one can obtain the dispersion relation in the form:
Using the expansion of the function for small , i.e., , one can obtain from (10), which implies the dispersion relation in explicit form (8). We note that, using the Debye asymptotics of the modified Bessel function for and in the form (6), one can also obtain an asymptotic representation of dispersion Equation (5) in the form (8).
Figure 5, Figure 6 and Figure 7 illustrate the results of calculations of dispersion curves defined parametrically with parameter , which were obtained by solving Equation (5) numerically (solid line) and by using the long-wave approximation (8) (dashed line). The following values of the parameter and Richardson number characterizing the gradient of the corresponding models of background shear currents were used: , (first model); , (second model); , (third model). These results demonstrate that the obtained long-wave approximation (8) agrees well with the description of basic properties of exact dispersion relations for small values of wave numbers. In this case, it is necessary to stress that as the mode number increases, the long-wave approximates the exact solution more and more accurate.
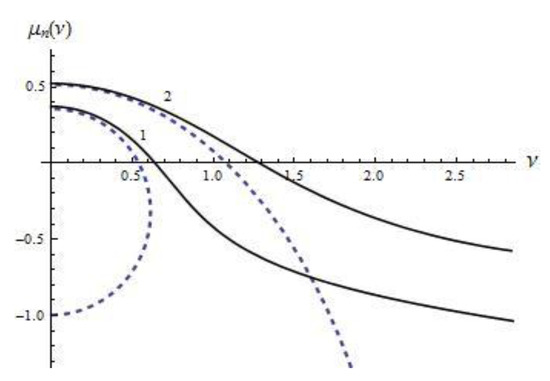
Figure 5.
Dispersion curves and its approximations for the first model, lines 1—first mode, lines 2—second mode.
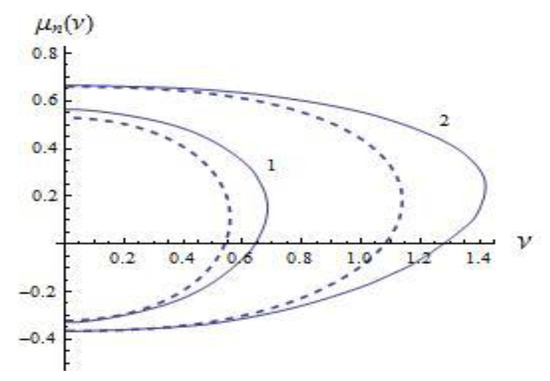
Figure 6.
Dispersion curves and its approximations for the second model, lines 1—first mode, lines 2—second mode.
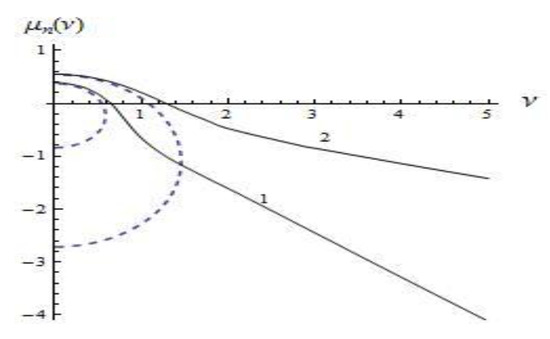
Figure 7.
Dispersion curves and its approximations for the third model, lines 1—first mode, lines 2—second mode.
5. Conclusions
The problem of IGW field in a stratified medium of finite depth was solved for model distributions of background shear currents. The problem was solved analytically by using a constant distribution of the buoyancy frequency and different linear depth-dependences of the background shear current. The obtained dispersion dependences were expressed in terms of the modified Bessel function of imaginary index. The Debye asymptotics of the modified Bessel function of imaginary index were used to construct analytic solutions under satisfied Miles–Howard conditions and for large Richardson numbers. The qualitative properties of the dispersion equation were studied, and the basic analytic properties of dispersion curves were investigated depending on the characteristics of model background shear currents. The far IGW fields are determined by the properties of dispersion relation for small wave numbers, which permits using the corresponding analytical approximations. These approximations allowed us to obtain explicit analytic expressions for the dispersion curves. The qualitative picture of dispersion curves and the corresponding IGW phase patterns are determined by the properties of background shear currents. For relatively small vertical gradients of background shear currents (the flows on the surface and at the bottom differ in the amplitude but are unidirectional), the IGW wave pattern is a system of both wedge (longitudinal) and annular (transverse) waves. For large vertical gradients of background shear currents (shear currents on the surface and at the bottom are multidirectional), the wave pattern consists only of annular (transverse) waves, and the relation between the amplitudes of bottom and near-surface flows determines the degree of asymmetry of the generated wave patterns. The obtained results show that there is a significant dependence of the phase structure of the generated IGW fields on the relation between the bottom and near-surface amplitudes for different models of shear flows.
Analytical representations of dispersion relations make it possible to study the IGW dynamics in a stratified medium with flows and slowly varying parameters [1,31,32]. Horizontal heterogeneity and non-stationarity have a significant impact on the IGW propagation in the world ocean [4,5,12,13,14,15]. If the ocean depth, its density, shear flows are changing slowly as compared to the characteristic length (period) of IGW, which is well done in the real ocean, then for solving the mathematical modeling of IGW dynamics, we may use the WKBJ method (geometrical optics method) and its generalizations. Then, the asymptotic solution can be represented as a sum of wave packets [31]. The phase structure of each wave packet is determined by the analytical properties of the dispersion curves. The phase functions (model integrals) of asymptotic solutions are expressed in terms of various special functions: Fresnel integrals, Airy functions, Pearcey integrals, and others. The specific choice of the phase function (model integrals) is completely determined by the analytical properties of the dispersion relations [8,9,31,32]. The obtained analytical solutions of dispersion relations allow one to efficiently calculate the main phase characteristics of the excited IGW fields and, in addition, to qualitatively analyze the obtained solutions, which is important for the correct statement of more complicated mathematical models of wave dynamics in real natural stratified media (world ocean, Earth’s atmosphere).
Author Contributions
Conceptualization, V.B.; Investigation, V.B. and Y.V.; Methodology, Y.V.; Writing—original draft, V.B.; Writing—review & editing, V.B. All authors have read and agreed to the published version of the manuscript.
Funding
The work was funded by RFBR grant No. 20-01-00111A.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Miropolsky, Y.Z. Dynamics of Internal Gravity Waves in the Ocea; Shishkina, O., Ed.; Springer: Berlin/Heidelberg, Germany, 2001; p. 406. [Google Scholar]
- Pedlosky, J. Waves in the Ocean and Atmosphere: Introduction to Wave Dynamics; Springer: Berlin/Heidelberg, Germany, 2010; p. 260. [Google Scholar]
- Sutherland, B.R. Internal Gravity Waves; Cambridge University Press: Cambridge, UK, 2010; p. 394. [Google Scholar]
- Morozov, E.G. Oceanic Internal Tides: Observations, Analysis and Modeling; Springer: Berlin/Heidelberg, Germany, 2018; p. 317. [Google Scholar]
- Tarakanov, R.Y.; Marchenko, A.V.; Velarde, M.G. (Eds.) Ocean in Motion; Springer: Berlin/Heidelberg, Germany, 2018; p. 625. [Google Scholar]
- Mei, C.C.; Stiassnie, M.; Yue, D.K.-P. Theory and Applications of Ocean Surface Waves: Advanced Series of Ocean Engineering. V.42; World Scientific Publishing: London, UK, 2017; p. 1500. [Google Scholar]
- Fabrikant, A.L.; Stepanyants, Y.A. Propagation of Waves in Shear Flows; World Scientific Publishing: London, UK, 1998; p. 304. [Google Scholar]
- Bulatov, V.V.; Vladimirov, Y.V. Wave Dynamics of Stratified Mediums; Nauka Publishers: Moscow, Russia, 2012; p. 584. [Google Scholar]
- Bulatov, V.V.; Vladimirov, Y.V. A General Approach to Ocean Wave Dynamics Research: Modeling, Asymptotics, Measurements; OntoPrint Publishers: Moscow, Russia, 2012; p. 587. [Google Scholar]
- Fraternale, F.; Domenicale, L.; Staffilan, G.; Tordella, D. Internal waves in sheared flows: Lower bound of the vorticity growth and propagation discontinuities in the parameter space. Phys. Rev. 2018, 97, 063102. [Google Scholar] [CrossRef] [PubMed]
- Bouruet-Aubertot, P.I.; Thorpe, S.A. Numerical experiments of internal gravity waves an accelerating shear flow. Dyn. Atmos. Oceans 1999, 29, 41–63. [Google Scholar] [CrossRef]
- Frey, D.I.; Novigatsky, A.N.; Kravchishina, M.D.; Morozov, E.G. Water structure and currents in the Bear Island Trough in July–August 2017. Russ. J. Earth Sci. 2017, 17, ES3003. [Google Scholar] [CrossRef][Green Version]
- Morozov, E.G.; Paka, V.T.; Bakhanov, V.V. Strong internal tides in the Kara Gates Strait. Geophys. Res. Lett. 2008, 35, L16603. [Google Scholar] [CrossRef]
- Tarakanov, R.Y.; Morozov, E.G.; Frey, D.I. Hydraulic continuation of the abyssal flow from the Vema Channel in the Southwestern part of the Brazil Basin. J. Geophys. Res. Oceans 2020, 125, e2020JC016232. [Google Scholar] [CrossRef]
- Khimchenko, E.E.; Frey, D.I.; Morozov, E.G. Tidal internal waves in the Bransfield Strait, Antarctica. Russ. J. Earth Sci. 2020, 20, ES2006. [Google Scholar] [CrossRef]
- Bulatov, V.V.; Vladimirov, Y.V. Dynamics of internal gravity waves in the ocean with shear flows. Russ. J. Earth Sci. 2020, 20, ES4004. [Google Scholar] [CrossRef]
- Bulatov, V.V.; Vladimirov, Y.V. Internal gravity waves in the ocean with multidirectional shear flows. Atmos. Ocean. Phys. 2020, 56, 85–91. [Google Scholar] [CrossRef]
- Broutman, D.; Rottman, J. A simplied Fourier method for computing the internal wave field generated by an oscillating source in a horizontally moving, depth-dependent background. Phys. Fluids 2004, 16, 3682. [Google Scholar] [CrossRef]
- Svirkunov, P.N.; Kalashnik, M.V. Phase patterns of dispersive waves from moving localized sources. Phys. Uspekhi 2014, 57, 80–91. [Google Scholar] [CrossRef]
- Voelker, G.S.; Myers, P.G.; Walter, M.; Sutherland, B.R. Generation of oceanic internal gravity waves by a cyclonic surface stress disturbance. Dyn. Atmos. Oceans 2019, 86, 116–133. [Google Scholar] [CrossRef]
- Miles, J.W. On the stability of heterogeneous shear flow. J. Fluid Mech. 1961, 10, 495–509. [Google Scholar] [CrossRef]
- Howard, L.N. Note of the paper of John W. Miles. J. Fluid Mech. 1961, 10, 509–512. [Google Scholar] [CrossRef]
- Gavrileva, A.A.; Gubarev, Y.G.; Lebedev, M.P. The Miles theorem and the first boundary value problem for the Taylor–Goldstein equation. J. Appl. Ind. Math. 2019, 13, 460–471. [Google Scholar] [CrossRef]
- Hirota, M.; Morrison, P.J. Stability boundaries and sufficient stability conditions for stably stratified, monotonic shear flows. Phys. Lett. A 2016, 380, 1856–1860. [Google Scholar] [CrossRef]
- Churilov, S. On the stability analysis of sharply stratified shear flows. Ocean Dyn. 2018, 68, 867–884. [Google Scholar] [CrossRef]
- Carpenter, J.R.; Balmforth, N.J.; Lawrence, G.A. Identifying unstable modes in stratified shear layers. Phys. Fluids 2010, 22, 054104. [Google Scholar] [CrossRef]
- Watson, G.N. A Treatise on the Theory of Bessel Functions (Reprint of the 2nd ed.); Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions (Reprint of the 1972 ed.); Dover Publications: New York, NY, USA, 1992. [Google Scholar]
- Stoker, J.J. Water Waves: The Mathematical Theory with Applications; Interscience Publishers: New York, NY, USA, 1957. [Google Scholar]
- Whitham, G.B. Linear and Nonlinear Waves; J. Wiley and Sons: New York, NY, USA, 1974. [Google Scholar]
- Kravtsov, Y.; Orlov, Y. Caustics, Catastrophes and Wave Fields; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Bulatov, V.V.; Vladimirov, Y.V. Asymptotical analysis of internal gravity wave dynamics in stratified medium. Appl. Math. Sci. 2014, 8, 217–240. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).