Influence of Methods Approximating Fractional-Order Differentiation on the Output Signal Illustrated by Three Variants of Oustaloup Filter

Abstract

Fractional-order (FO) differential equations are more and more frequently applied to describe real-world applications or models of phenomena. Despite such models exhibiting high flexibility and good fits to experimental data, they introduce their inherent inaccuracy related to the order of approximation. This article shows that the chosen model influences the dynamic properties of signals. First, we calculated symbolically the steady-state values of an FO inertia using three variants of the Oustaloup filter approximation. Then, we showed how the models influence the Nyquist plots in the frequency domain. The unit step responses calculated using different models also have different plots. An example of FO control system evidenced different trajectories dependent on applied models. We concluded that publicized parameters of FO models should also consist of the name of the model used in calculations in order to correctly reproduce described phenomena. For this reason, the inappropriate use of FO models may lead to drawing incorrect conclusions about the described system.

1. Introduction

Fractional-order (FO) differential calculus, or more simply: fractional calculus, is a field of mathematics. It is an expansion of classical calculus and is suitable for modeling a variety of systems [1]. Science began to deal with this in 1695 with correspondence between two mathematicians: Leibniz and L’Hospital [2]. Due to inherent complexity and the lack of a convincing geometric or physical interpretation, the FO calculus for a long time remained unexplored or its applications in engineering were delayed [3]. Some scientists deem that the book of Mandelbrot [4] was the first contemporary work dealing with fractional integrodifferentiation which resulted in the search for phenomena acting as FO systems [5]. Earlier, at the turn of the 1950s and 1960s, the work of Tustin [6] and next of Manabe (or Manage) [7] began the application of FO in control systems [8]. The monograph by Podlubny [9], which presents the issues of FO differentiation in a very orderly way, echoed with a great deal of interest. New articles related with controls keep appearing, even in metrological journals, which examine the properties of the proportional–integral–derivative (PID) FO controllers [8,10,11,12,13,14,15,16,17]. The popularity results from the property that an additional independent fractional parameter gives the designer an additional degree of freedom when building a model [18]. Other implementations include chemistry, electromagnetic, material science, mechanics [19], viscoelastic damping, robotics and control, signal processing, electric circuits [3], concrete engineering [20], protein folding [21], and others.

In our previous work [22], we noticed that the determined time response trajectory of FO system is influenced by parameters used during the approximation of FO differentiation. This is due to the fact that it is necessary to approximate the FO differential equations with integer-order (IO) equations. According to our best knowledge, the literature lacks a metrological approach to the issue of approximation accuracy. Usually, the authors of published papers determine the parameters for a specific approximation method—the reader may find some examples in the following sources [20,23,24,25]. This results in a close relationship between the determined parameters and the chosen method, as well as other additional factors such as the order of the polynomial. In this work, we decided to explore the problem of peculiar interoperability of parameters of FO differential equations describing selected dynamic models.

2. Background

Today, the main audience for FO analysis is researchers related to control theory. Top 10 journals found by Scopus database for the “fractional-order” term concern automatics. We can, however, observe increasing interests for the application of FO modelings in other fields of science. Below, we list some of them which are, in our opinion, the most valuable or have the most impact on the field of science. We are conscious that the list is very short and some implementations are omitted.

Electrochemistry is the area where we often meet FO differential equations. Differential equations with a fractional time derivative model describe well properties of supercapacitors, batteries (lithium-ion, lead-acid), and fuel cells [26,27]. Characteristics obtained by impedance spectroscopy allow building a generalization for the Poisson–Nernst–Planck equation. The published characteristics fitted better to the experimental data, especially in the low-frequency range [28]. Effective modeling is needed, among other things, in the automotive industry to determine the state-of-charge indication of batteries. It turns out that a more useful model is obtained based on the black-box approach. The obtained fractional description shows a simple structure and a clear physical explanation [29]. Construction of the state observer allowed for another solution to the same issue. A system of four differential equations was obtained, two of which are of FO. The authors report a very good match to experimental results [30]. Another research on the aging process of lithium-ion batteries allowed to build an FO model. The authors noted that as the battery wears out, the order $\alpha$ increases monotonically. This allows determining the degradation level and set the failure threshold to indicate when the battery is worn out [31].

Supercapacitors are another area of application of the FO differential calculus. The resulting model features low complexity and high accuracy. It describes the characteristics much better than typical RC models. Compared to equally accurate models with constant phase elements, the FO model is much simpler [32]. Changing the operating conditions of the supercapacitor makes it necessary to identify their parameters on-line. For the FO model, this is possible using the Grünwald–Letnikov method with short memory principles and Jumarie type derivatives [33]. To make modeling effective, apart from choosing the model structure, it is necessary to determine the parameters of this model. It may be helpful to use more advanced methods such as chaos theory in the particle swarm optimization algorithm [34]. Parameter identification is, in general, a complicated task. Scientists devote many efforts to build an effective algorithm. An important issue during the calculation of derivative equations are initial conditions, often motivelessly assumed zero. For the reason, such an algorithm should account for them [5].

Another electrochemical example includes a voltammetric e-tongue. A set of electrodes immersed in different tea samples allowed for the acquisition of impedance spectroscopy data. Either a simple IO model or a more complicated FO model served for data fitting. Authors showed only a slight improvement in several factors when a more complicated FO model is used [25]. The same authors published a comparison of several FO models describing voltammetric electrodes. Results showed the best fitting to a system with resistance, fractional capacitor, and two fractional coils [35].

A very interesting approach shows an electronic circuit acting as an Ni-Cd cell. In this way, the inherently FO element is emulated by a combination on active and passive filters [36].

Not only capacitors but also inductors are modeled using FO differential equations. An example is a reluctance inductive displacement transducer—the FO approach allowed to increase the linearity of the transducer [37].

Soil hyperspectral reflectance allows for the determination of saline content. A differential transformation used in the data pretreatment increases the strength of the recorded signal. The greatest correlation between the content and the reflectance is obtained when the differentiation order is fractional [38]. In physics, FO modeling finds its application in diffusion. As an example, the classical Richards equation models the infiltration process into porous media. The work [39] compares the classical approach with the proposed generalized FO model.

The use of FO differential equations gives significant benefits when building band-pass filters. The obtained filter can feature almost linear phase characteristics. This is desirable in such applications as coherent signal processing and demodulation, radar signal processing, and audio signal processing [40]. Thanks to the operational transconductance amplifiers, it is possible to build an analogue realization of constant phase elements. These elements allow for the construction of fractional-order capacitors and fractional-order inductors [41].

Medicine professionals try to use FO filters in diagnostics through analysis of electroencephalograms [42]. We find also FO implementation in bio-impedance measurements of skin tissue models [43]. Other denoising medical implementation embraces surface electromyography signals [44].

In one-dimensional vibration analysis, this filtering allows for easy detection of the shaft misalignment [45]. Another work describes the application of vibration analysis to the diagnosis of bearing fault. The FO system resonance makes the techniques very sensitive and suitable for weak signals [46].

FO systems find their implementations also in quite different areas. One of them is a chaotic system. The proposed solution consists of an FPGA circuit realizing fractional-order chaotic differential equations [47].

Although FO models fit well with real data, other methods of describing empirical properties find their supporters. Alternative methods include models derived from physical description, neural networks, fuzzy sets, or fractals [34,48,49]. Therefore, before implementing a given method to describe sensors, which will have a practical implementation, one should be critical of the selected method. This article aims to help in the critical evaluation of FO modeling.

3. Materials and Methods

The MATLAB Simulink environment (version R2016b) with the FOMCON [50] and FOTF  [51] toolboxes served the FO numerical simulations. The symbolic transformations and calculation scripts arose thank to GNU Octave (an open source alternative to MATLAB [52]) environment (version 4.2.2) with the Symbolic package.

4. Theory/Calculation

Many articles dealing with FO calculus start with the definition of the integrodifferentiation operator $\mathcal{D}$ [50,53]:

$${}_{l_1}{\mathcal{D}}_{l_2}^{\alpha }f\left(t\right)=\left\{\begin{array}{cc}\frac{d^{\alpha }}{d{t}^{\alpha }}f\left(t\right)\hfill & \Re \left(\alpha \right)>0\hfill \\ f\left(t\right),\hfill & \Re \left(\alpha \right)=0\hfill \\ {\int }_{l_1}^{l_2}f\left(\tau \right){\left(d\tau \right)}^{-\alpha }\hfill & \Re \left(\alpha \right)<0\hfill \end{array}\right.,$$

(1)

where $l_1$ and $l_2$ are limits of the operations, $\alpha$ is the order that may be non-integer. In the literature, we see many definitions realizing the operation $\mathcal{D}$. These include Riemann–Liouville, Riesz, Weyl, Grünwald–Letnikov, Caputo [54,55,56]. The Laplace transform $\mathcal{L}$ of the integrodifferentiation is [57]

$$\mathcal{L}{\{}_{l_1}{\mathcal{D}}_t^{\alpha }f\left(t\right)\}=s^{\alpha }F\left(s\right);$$

(2)

where s is a complex variable and

$$F\left(s\right)=\mathcal{L}\left\{f\right(t\left)\right\}.$$

(3)

4.1. Variants of Oustaloup Filter Approximations

A transfer function containing operator s raised to a fractional power complicates calculations of time response of such a system (comparing with an integer power). Exact (analytical) calculations of step response are possible only for $F\left(s\right)=1/s^{0.5}$ [57,58]. A popular solution solving the issue is the application of the Oustaloup filter approximation. It approximates the term $s^{\alpha }$ in the frequency band $[{\omega }_{\mathrm{b}},{\omega }_{\mathrm{h}}]$ by [59,60]:

$$s^{\alpha }\approx K\prod _{k=1}^N\frac{s+p_{\mathrm{O}}}{s+z_{\mathrm{O}}}\mathrm{for}0<\alpha <1,$$

(4)

where: $p_{\mathrm{O}}={\omega }_{\mathrm{b}}{\omega }_{\mathrm{ur}}^{(2k-1-\alpha )/N}$ are poles; $z_{\mathrm{O}}={\omega }_{\mathrm{b}}{\omega }_{\mathrm{ur}}^{(2k-1+\alpha )/N}$ are zeros; $K={\omega }_{\mathrm{h}}^{\alpha }$ is a gain; ${\omega }_{\mathrm{ur}}=\sqrt{{\omega }_{\mathrm{h}}/{\omega }_{\mathrm{b}}}$; N is the number of pole-zero pairs. The Matlab FOMCON implementation applies the following relationship (according to the code of the oustafod.m function):

$$s^{\alpha }\approx K\prod _{k=-N_{\mathrm{F}}}^{N_{\mathrm{F}}}\frac{s+p_{\mathrm{F}}}{s+z_{\mathrm{F}}}\mathrm{for}0<\alpha <1,$$

(5)

where: $p_{\mathrm{F}}={\omega }_{\mathrm{b}}{\omega }_{\mathrm{u}}^{(k+N_{\mathrm{F}}+\frac{1}{2}-\frac{1}{2}\alpha )/(2N_{\mathrm{F}}+1)}$; $z_{\mathrm{F}}={\omega }_{\mathrm{b}}{\omega }_{\mathrm{u}}^{(k+N_{\mathrm{F}}+\frac{1}{2}+\frac{1}{2}\alpha )/(2N_{\mathrm{F}}+1)}$; $N_{\mathrm{F}}$ is the order of the filter. ${\omega }_{\mathrm{u}}={\omega }_{\mathrm{h}}/{\omega }_{\mathrm{b}}$; The two notations of the filters are identical if $N=2N_{\mathrm{F}}+1$. The Matlab FOMCON toolbox defines also the refined Oustaloup approximations (according to the code of the new_fod.m function):

$$s^{\alpha }\approx {\left(\frac{d}{b}{\omega }_{\mathrm{h}}\right)}^{\alpha }\frac{d{s}^2+b{\omega }_{\mathrm{h}}s}{d(1-\alpha )s^2+b{\omega }_{\mathrm{h}}s+d\alpha }\prod _{k=-N_{\mathrm{F}}}^{N_{\mathrm{F}}}\frac{s+p_{\mathrm{F}}}{s+z_{\mathrm{F}}}.$$

(6)

with $b=10$ and $d=9$. Xue et al. [61] propose another approximation, also known as the refined Oustaloup filter approximation. It has the form of:

$$s^{\alpha }\approx {\left(\frac{d}{b}{\omega }_{\mathrm{b}}\right)}^{\alpha }\left(\prod _{k=-N_{\mathrm{F}}}^{N_{\mathrm{F}}}\frac{z_{\mathrm{X}}}{p_{\mathrm{X}}}\right)\frac{d{s}^2+b{\omega }_{\mathrm{h}}s}{d(1-\alpha )s^2+b{\omega }_{\mathrm{h}}s+d\alpha }\prod _{k=-N_{\mathrm{F}}}^{N_{\mathrm{F}}}\frac{s+p_{\mathrm{X}}}{s+z_{\mathrm{X}}},$$

(7)

where: $p_{\mathrm{X}}={\left(\frac{d}{b}{\omega }_{\mathrm{b}}\right)}^{(\alpha -2k)/(2N_{\mathrm{F}}+1)}$; $z_{\mathrm{X}}={\left(\frac{b}{d}{\omega }_{\mathrm{h}}\right)}^{(\alpha +2k)/(2N_{\mathrm{F}}+1)}$; and the parameters are chosen “through confirmation by experimentation and theoretical analysis” [62] as $b=10$ and $d=9$. Xue is also an author of the FOTF toolbox which also defines the new_fod.m function [51]. It uses the product over indices starting from 1, as in the original Oustaloup notations. Nevertheless, both functions (from FOMCOM and FOTF toolboxes) are equivalent to each other and realize Equation (6), not Equation (7); the last index has, however, another meaning.

The order of the filters, $N_{\mathrm{F}}$, should be chosen reasonably. Although the accuracy increases with the increase in $N_{\mathrm{F}}$, the state dimension increases significantly [63].

4.2. Steady-State Value

The Final Value Theorem (FVT) allows for the determination of the steady-state value in time domain basing on the transfer function in the s domain. For the unit step excitation and the system described by $G\left(s\right)$, the following is valid [64]:

$$y(\infty )=\underset{s\to 0}{lim}\frac{1}{s}sG\left(s\right)=G\left(0\right).$$

(8)

In the z domain, the unit step sequence corresponds to $\frac{1}{1-z^{-1}}$. The steady-state value of a system after the unit stimulation acts following the discrete version of the FVT [64]:

$$y(\infty )=\underset{z\to 1^{+}}{lim}(z-1)\frac{1}{1-z^{-1}}{G\left(z\right)=G\left(z\right)|}_{z\to 1^{+}}.$$

(9)

4.3. Nyquist Plot and Time Response

The following substitution:

$$s\leftarrow j\omega ,$$

(10)

where $j=\sqrt{-1}$ and $\omega$ is the angular frequency, allowing investigating the frequency properties of the continuous system described by $G\left(s\right)$. The Nyquist plot arose by drawing points on the Cartesian plane where the x and y coordinates are the real and imaginary part of the $G\left(j\omega \right)$.

To calculate the time response of a system numerically, we need to build a digital filter basing on analogue one. It requires that the transfer function changes from continuous domain to a discrete one, in other words: from operator s to z. Among available methods, we apply the Tustin one with the following conversion [1,2]:

$$s\leftarrow \frac{2}{T_s}\frac{1-z^{-1}}{1+z^{-1}}$$

(11)

where $T_s$ is the sampling time. The digital filter obtained in this way allows for the calculation of the output signal for every sampled excitation. The coefficients related to $z^{-1}$ in the discrete transfer function is the weight of the previous sample. The reader may find more information in textbooks related to digital filter or review articles, such as [65].

4.4. Approximation Errors

We define the (relative) magnitude error as

$$\delta \left|G\right|=\frac{|G_{\mathrm{approx}.}|-|G_{\mathrm{reference}}|}{|G_{\mathrm{reference}}|},$$

(12)

where $|G_{\mathrm{approx}.}|$ and $|G_{\mathrm{reference}}|$ are the moduli of the transfer function $G\left(j\omega \right)$ calculated for a given frequency using the Oustaloup approximation and the reference method, respectively. Similarly, we define the phase error as

$$\Delta \phi ={\phi }_{\mathrm{approx}.}-{\phi }_{\mathrm{reference}},$$

(13)

where ${\phi }_{\mathrm{approx}.}$ and ${\phi }_{\mathrm{reference}}$ are arguments of the same transfer functions. The modulus $\left|G\right|$ and argument $\phi$ are properties of a complex number G notated in the polar form:

$$G=\Re \left(G\right)+j\Im \left(G\right)=\left|G\right|·e^{j\phi }$$

(14)

where $\Re \left(\right)$ and $\Im \left(\right)$ mean real and imaginary part of the complex number, respectively. For more about complex number foundations, see textbooks such as [66].

5. Results and Discussion

5.1. Steady-State Value

As the object of interest, we take the FO inertia (without delay) in the form of its transfer function [23]:

$$G\left(s\right)=\frac{k}{s^{\alpha }T+1}$$

(15)

with the gain k and fractional time constant T. Note that the unit of T is second only for $\alpha =1$. The alternative form of $G\left(s\right)=\frac{k}{{\left(s{T}^{\prime }\right)}^{\alpha }+1}$; $T^{\prime }$ has the unit of second; $T=T^{\prime \alpha }$. The following transfer function

$$G\left(s\right)=\frac{k}{{(sT+1)}^{\alpha }}$$

(16)

is also known as the inertial fractional order element [67], which is not equivalent to Equation (15) and is not an object of interest in this work.

Table 1. Parameters used during simulations.

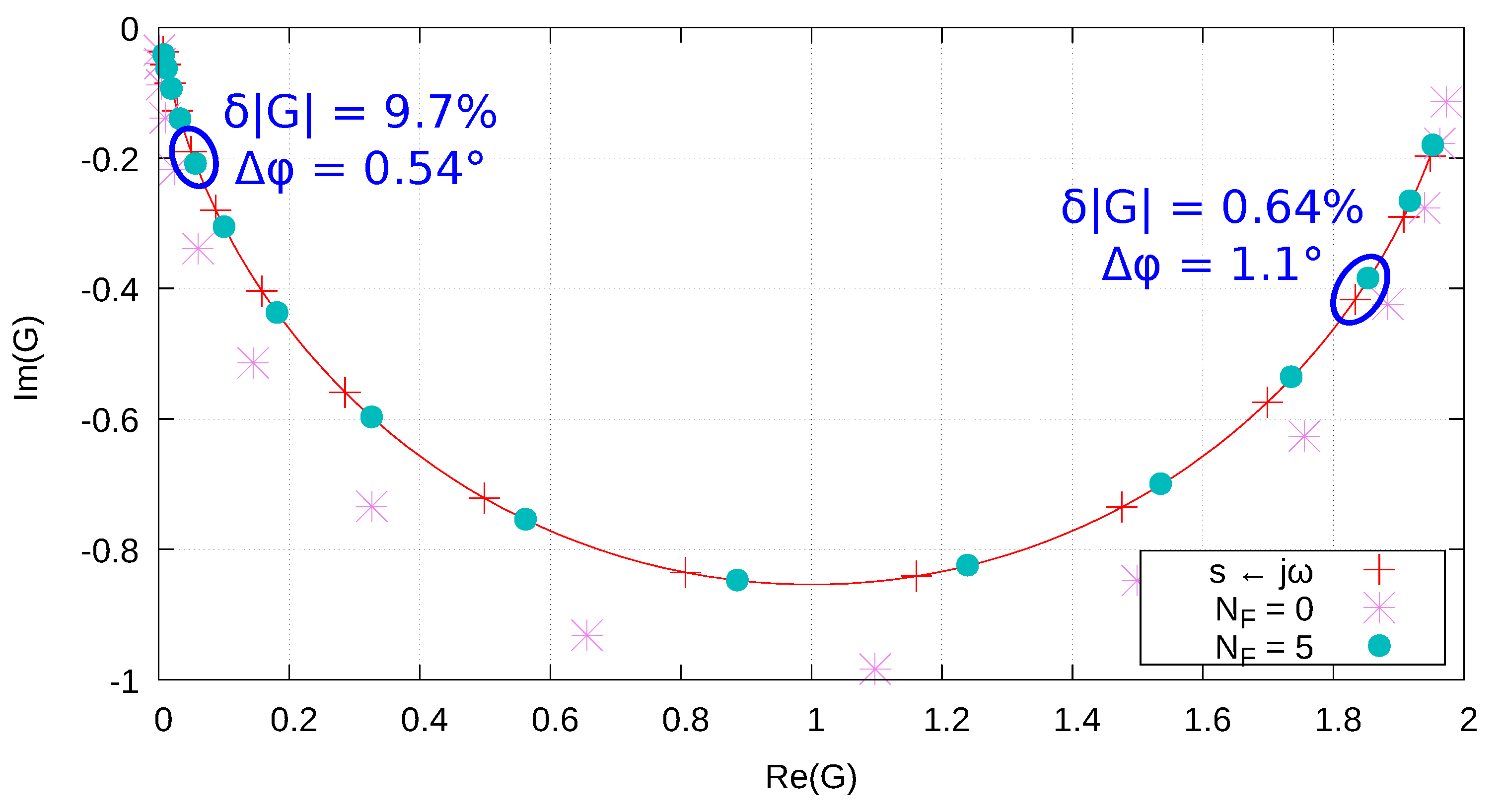
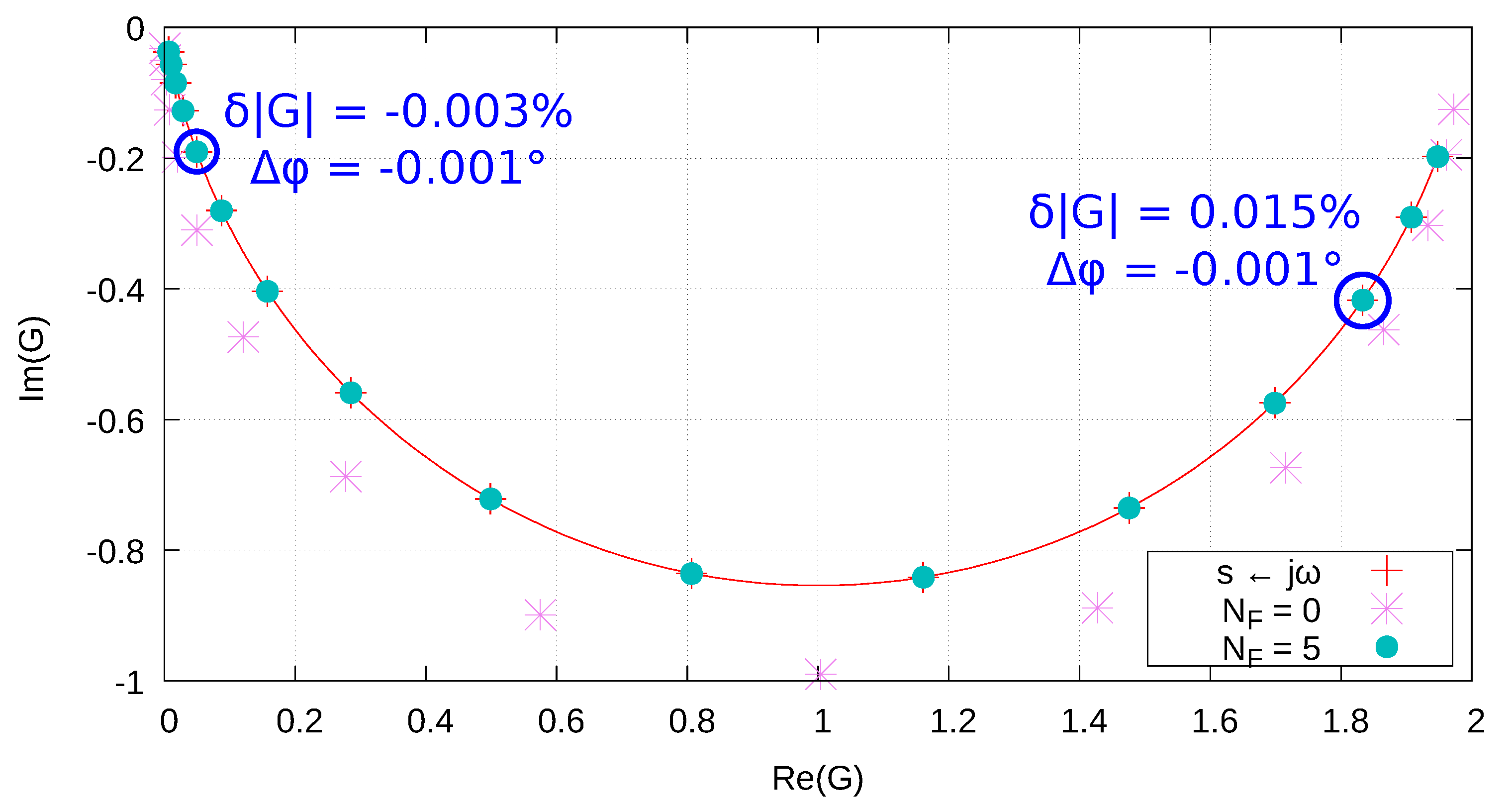
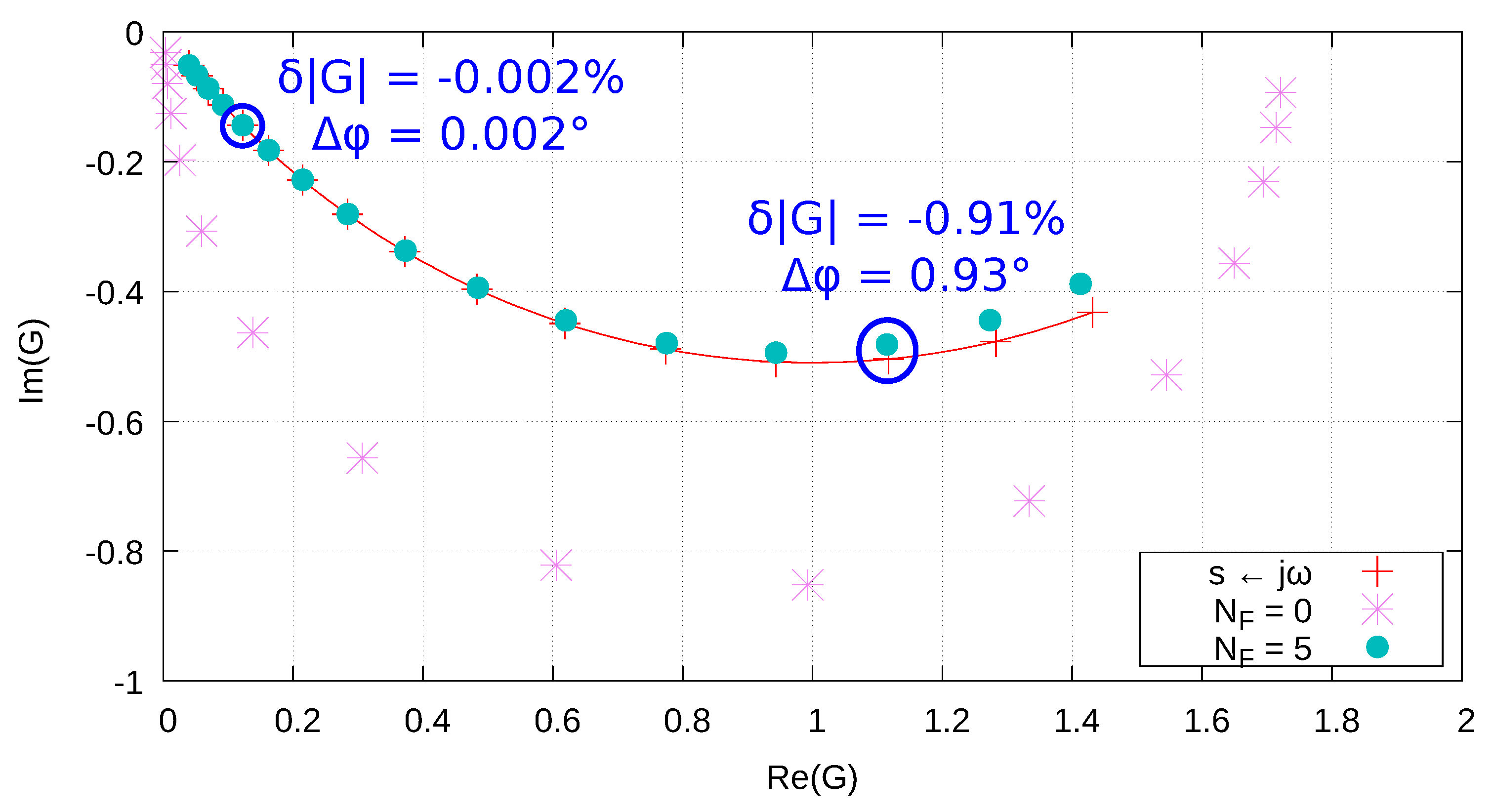
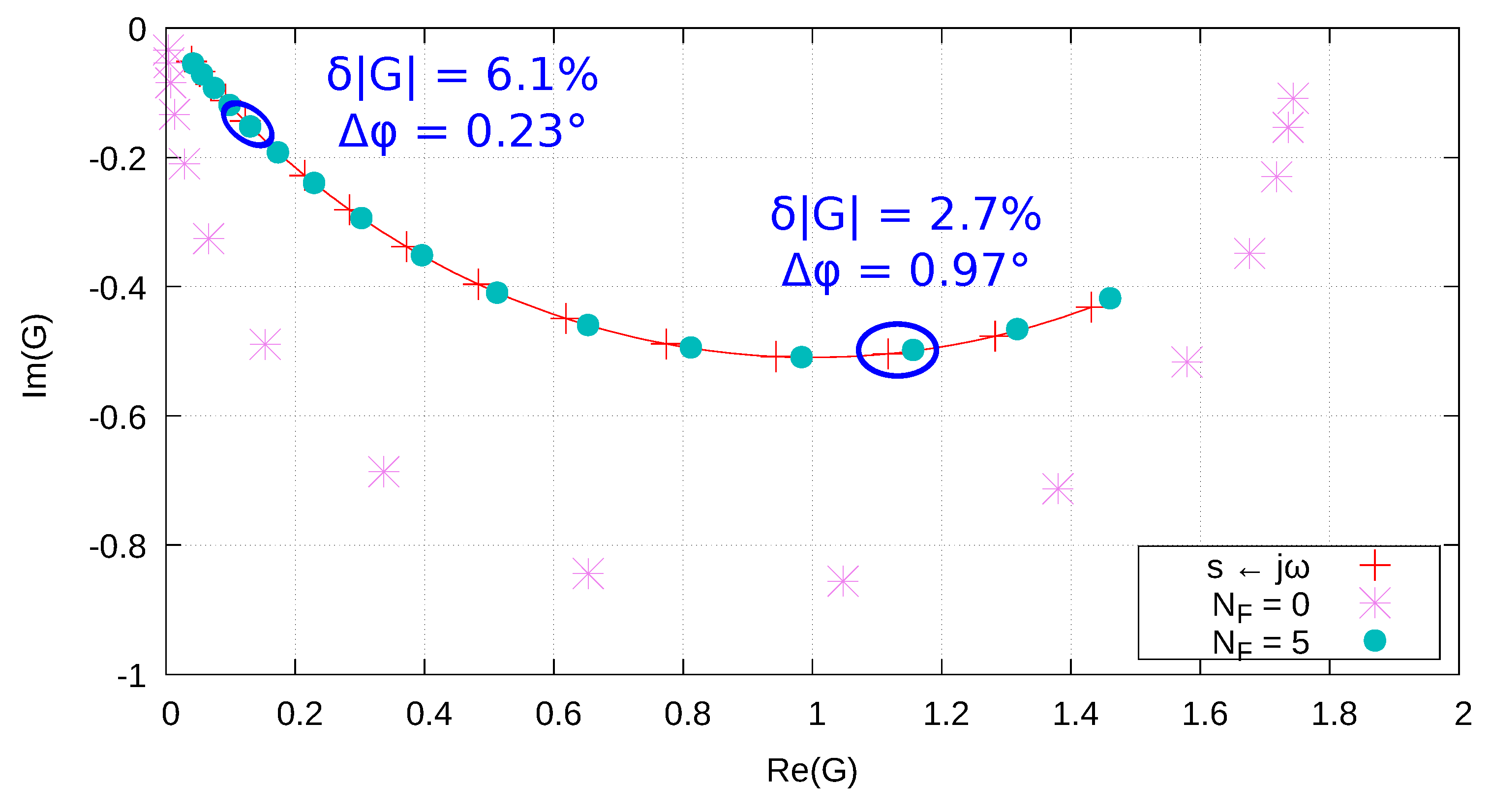
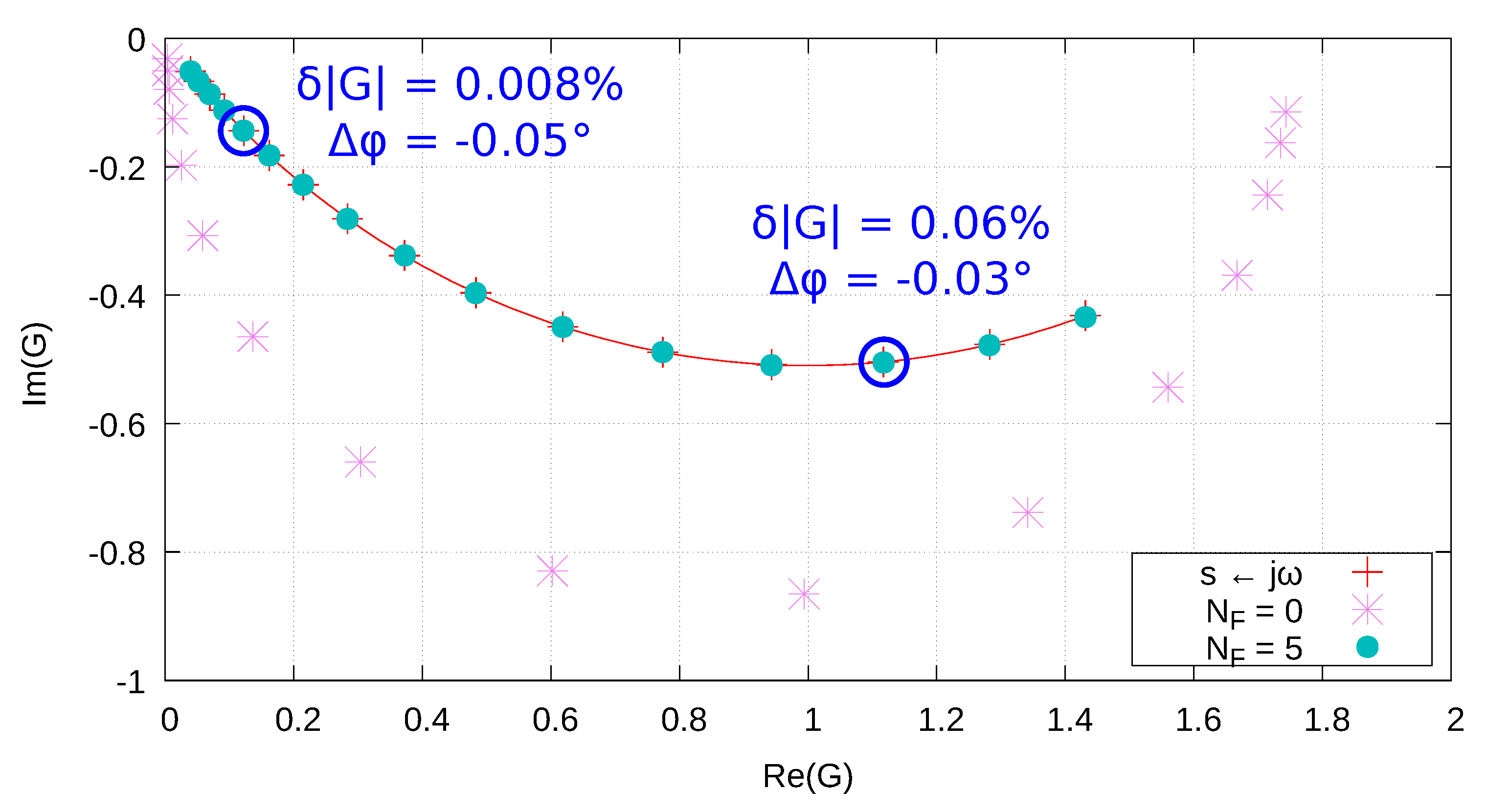
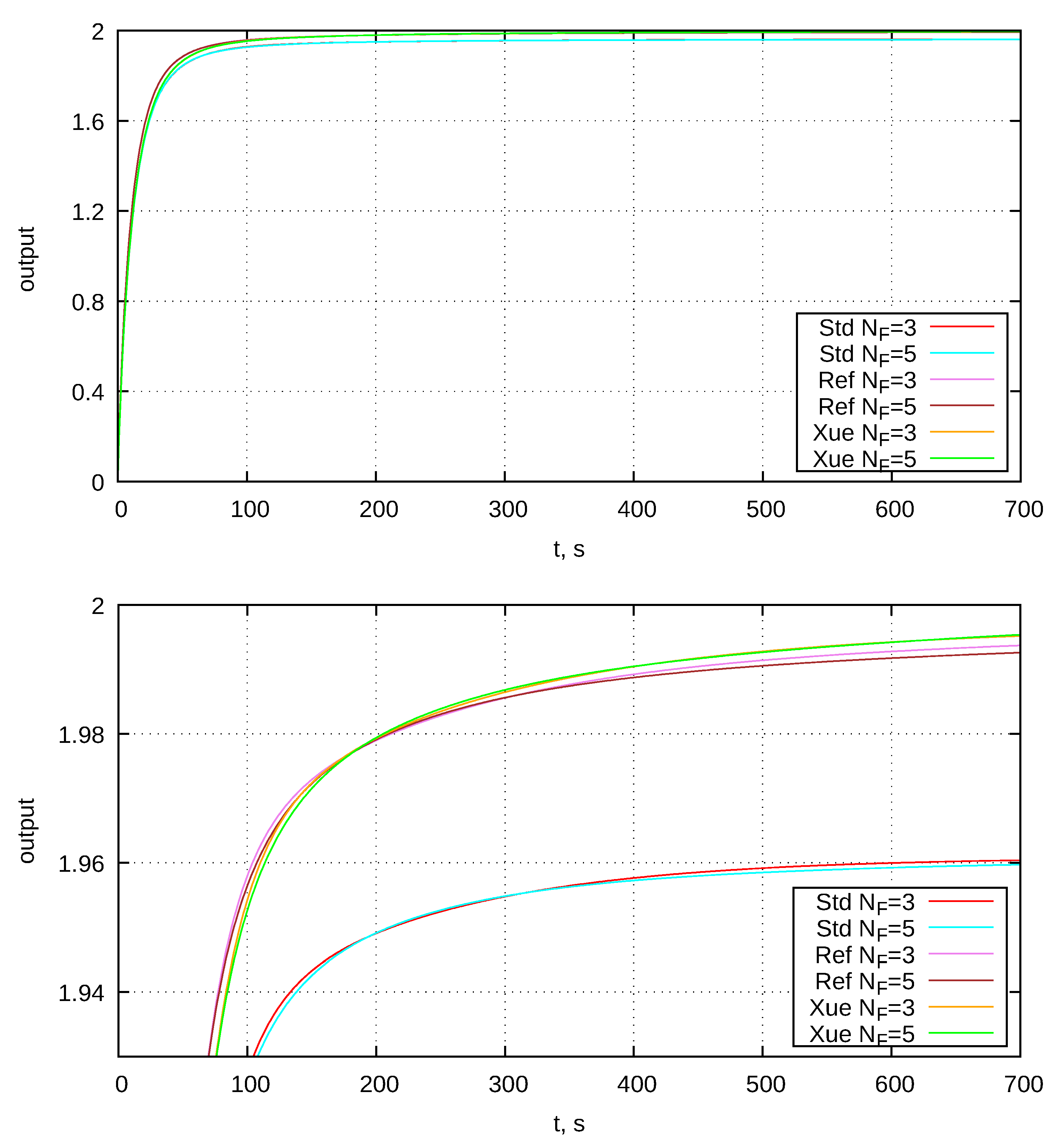
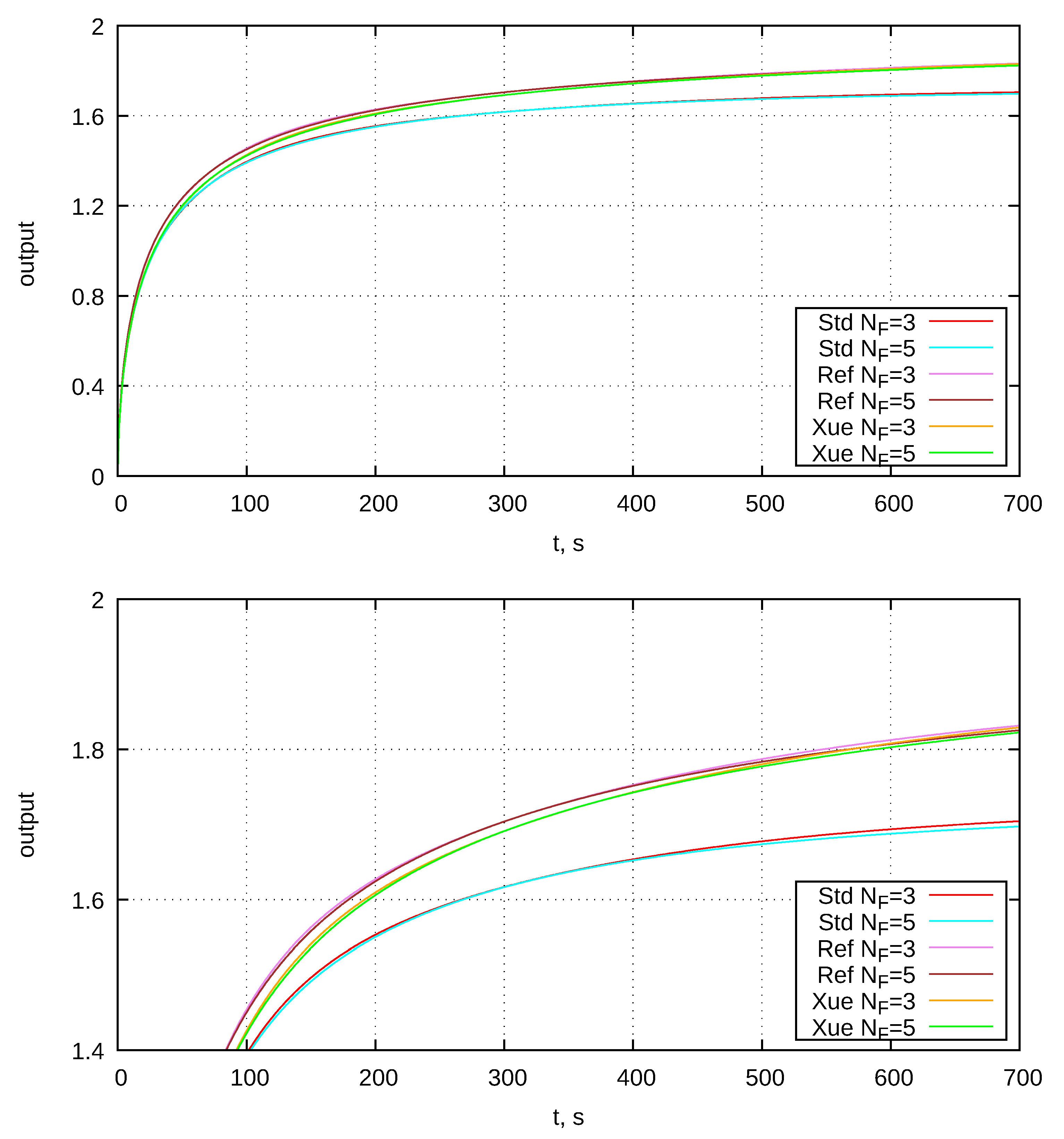
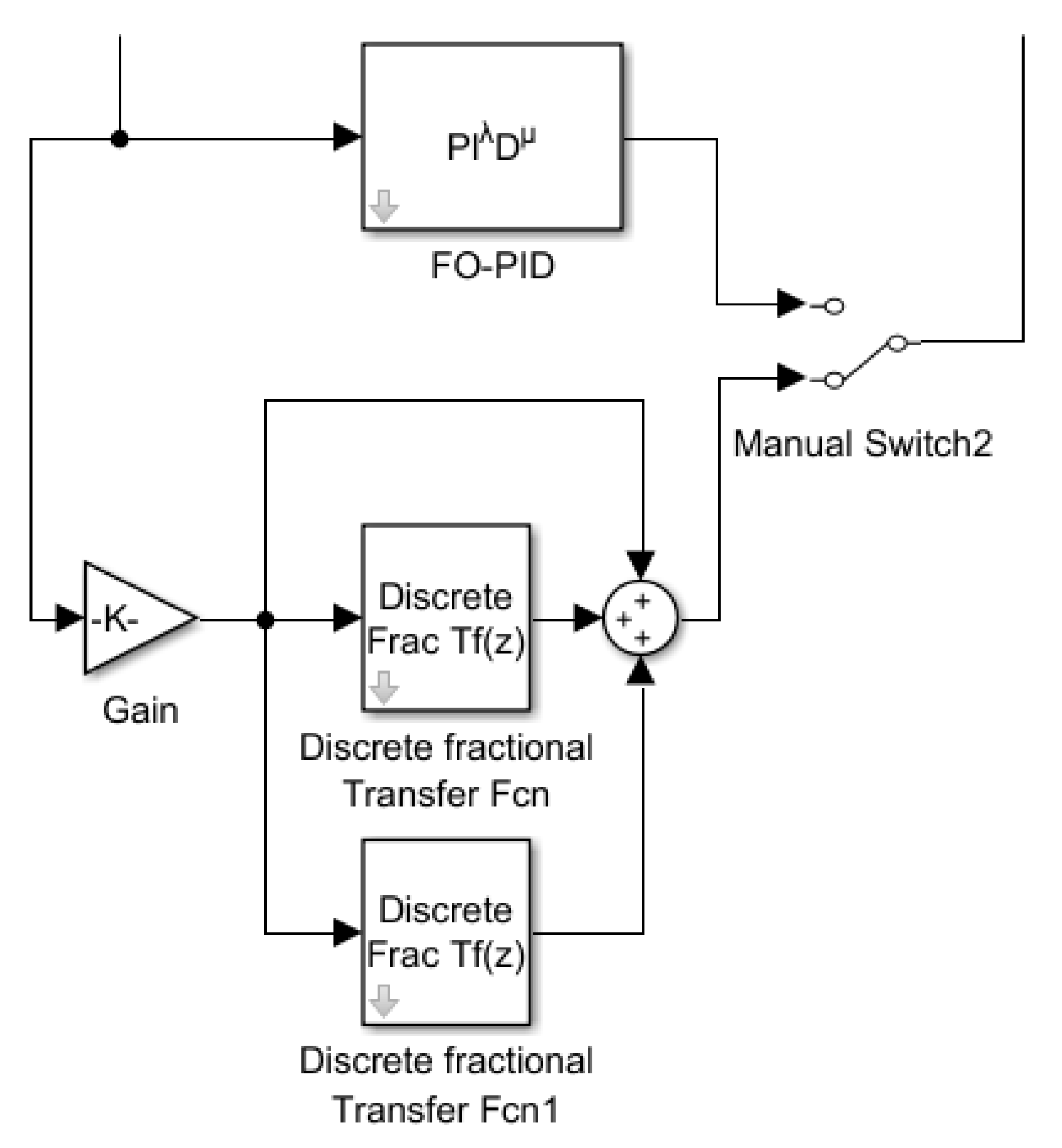
Parameter	Value	Parameter	Value
Inertia		Oustaloup Approximation
k	2	$N_{\mathrm{F}}$	0 or 5
T	10 s${}^{\alpha }$	${\omega }_{\mathrm{b}}$	0.001 rad/s
$\alpha$	0.9 or 0.6	${\omega }_{\mathrm{h}}$	1000 rad/s
f	$(0.001;1)$ Hz	b	10
$\omega$	$2\pi f$	d	9

gathers parameters used during this work, including the parameters of the inertia.

We can calculate precisely the steady-state value of the unit step response applying Equation (8), which is:

$$y(\infty )=G\left(0\right)=\frac{k}{0^{\alpha }T+1}=k.$$

(17)

The steady-state value is such a feature which governs the accuracy of a system. In the case of no external excitations, the output of the modeled inertia should tend to the constant value. Imprecise approximation changes directly the gain k being the parameter of the inertia.

Thanks to the Symbolic package in GNU Octave, we replace the fractional term in the transfer function of the fractional inertia, Equation (15), with the Oustaloup approximation, Equation (5). First, the order $N_{\mathrm{F}}=0$. The obtained approximation is:

$$G\left(s\right)\approx \frac{k}{\frac{T{\omega }_{\mathrm{h}}^{\alpha }\left({\omega }_{\mathrm{b}}{\left(\frac{{\omega }_{\mathrm{h}}}{{\omega }_{\mathrm{b}}}\right)}^{\frac{1}{2}-\frac{\alpha }{2}}+s\right)}{{\omega }_{\mathrm{b}}{\left(\frac{{\omega }_{\mathrm{h}}}{{\omega }_{\mathrm{b}}}\right)}^{\frac{\alpha }{2}+\frac{1}{2}}+s}+1}.$$

(18)

The steady-state value calculated according to FVT is inconsistent with the expected one:

$$y(\infty )=\frac{k}{T{\omega }_{\mathrm{h}}^{\alpha }{\left(\frac{{\omega }_{\mathrm{h}}}{{\omega }_{\mathrm{b}}}\right)}^{-\alpha }+1}=\frac{k}{T{\omega }_{\mathrm{b}}^{\alpha }+1}\ne k\mathrm{if}{\omega }_{\mathrm{b}}>0.$$

(19)

Substituting the numerical values of the parameters, we obtain the steady states of 1.961 and 1.726 for $\alpha =0.9$ and $0.6$, respectively, causing the relative errors of $-1.9$% and $-14$%, respectively.

The similar calculations performed for the order $N_{\mathrm{F}}=1$ give:

$$G\left(s\right)\approx \frac{k}{T{\omega }_{\mathrm{h}}^{\alpha }\frac{\left({\omega }_{\mathrm{b}}{\left(\frac{{\omega }_{\mathrm{h}}}{{\omega }_{\mathrm{b}}}\right)}^{\frac{1}{6}-\frac{\alpha }{6}}+s\right)\left({\omega }_{\mathrm{b}}{\left(\frac{{\omega }_{\mathrm{h}}}{{\omega }_{\mathrm{b}}}\right)}^{\frac{1}{2}-\frac{\alpha }{6}}+s\right)\left({\omega }_{\mathrm{b}}{\left(\frac{{\omega }_{\mathrm{h}}}{{\omega }_{\mathrm{b}}}\right)}^{\frac{5}{6}-\frac{\alpha }{6}}+s\right)}{\left({\omega }_{\mathrm{b}}{\left(\frac{{\omega }_{\mathrm{h}}}{{\omega }_{\mathrm{b}}}\right)}^{\frac{\alpha }{6}+\frac{1}{6}}+s\right)\left({\omega }_{\mathrm{b}}{\left(\frac{{\omega }_{\mathrm{h}}}{{\omega }_{\mathrm{b}}}\right)}^{\frac{\alpha }{6}+\frac{1}{2}}+s\right)\left({\omega }_{\mathrm{b}}{\left(\frac{{\omega }_{\mathrm{h}}}{{\omega }_{\mathrm{b}}}\right)}^{\frac{\alpha }{6}+\frac{5}{6}}+s\right)}+1}.$$

(20)

The steady-state has then the same value:

$$y(\infty )=\frac{k}{T{\omega }_{\mathrm{h}}^{\alpha }{\left(\frac{{\omega }_{\mathrm{h}}}{{\omega }_{\mathrm{b}}}\right)}^{-\alpha }+1}=\frac{k}{T{\omega }_{\mathrm{b}}^{\alpha }+1}\ne k\mathrm{if}{\omega }_{\mathrm{b}}>0.$$

(21)

Simulations performed for $N_{\mathrm{F}}=2$ give a much more complicated formula describing $G\left(s\right)$ but still the same formula of the steady-state. Basing on the above, we conclude that (1) the steady-state is independent of approximation order $N_{\mathrm{F}}$ and (2) the higher the ${\omega }_{\mathrm{b}}$ is, the greater the steady-state error is.

Very similar investigations for the refined Oustaloup approximation, Equation (6), starting from $N_{\mathrm{F}}=0$, give:

$$G\left(s\right)\approx \frac{k}{T{\left(\frac{d{\omega }_{\mathrm{h}}}{\mathrm{b}}\right)}^{\alpha }·\frac{{\omega }_{\mathrm{b}}{\left(\frac{{\omega }_{\mathrm{h}}}{{\omega }_{\mathrm{b}}}\right)}^{\frac{1}{2}-\frac{\alpha }{2}}+s}{{\omega }_{\mathrm{b}}{\left(\frac{{\omega }_{\mathrm{h}}}{{\omega }_{\mathrm{b}}}\right)}^{\frac{1}{2}+\frac{\alpha }{2}}+s}·\frac{b{\omega }_{\mathrm{h}}s+d{s}^2}{\alpha d+b{\omega }_{\mathrm{h}}s+d{s}^2\left(1-\alpha \right)}+1}.$$

(22)

Here, we obtain the appropriate value of the steady-state $y(\infty )=G\left(0\right)=k$. Similar symbolic manipulations performed for Xue’s variant of the refined Oustaloup filter approximation, Equation (7), and $N_{\mathrm{F}}=0$ leads to:

$$G\left(s\right)=\frac{k}{T{\left(\frac{b{\omega }_{\mathrm{h}}}{d}\right)}^{\alpha }·\frac{{\left(\frac{d{\omega }_{\mathrm{b}}}{\mathrm{b}}\right)}^{\alpha }+s}{{\left(\frac{b{\omega }_{\mathrm{h}}}{d}\right)}^{\alpha }+s}·\frac{b{\omega }_{\mathrm{h}}s+d{s}^2}{\alpha d+b{\omega }_{\mathrm{h}}s+d{s}^2\left(1-\alpha \right)}+1}.$$

(23)

Additionally, the steady-state is correct. The symbolic calculations performed up to $N_{\mathrm{F}}=5$ give still $y(\infty )=k$. The simulations prove that the refined Oustaloup approximations, in both variants, provide the correct steady-state value.

5.2. Nyquist Plot

The determination of the Nyquist plots for FO systems can be done in the way introducing no additional errors. For it, we simply use Equation (10):

$$s\leftarrow j\omega .$$

We treat results calculated in this way as the reference. Now, we can assess the quality of the approximations for different frequencies. For better illustration, we assume constant values of the parameters of FO inertia, as in the left-hand side of Table 1. The parameters of the Oustaloup approximation used during calculations were as in the right-hand side of the same table.

Figure 1 presents the Nyquist plot for $\alpha =0.9$. The approximations performed with a very low order of $N_{\mathrm{F}}=0$ make the plot different than the reference one. We observe a significant phase shift for the lowest frequencies while the magnitude is near the correct one. In the middle frequency range, the magnitude error becomes huge. These properties result from very rough approximation when the order is low. The plot fits much better if the order is higher, it means $N_{\mathrm{F}}=5$. The approximated points lay quite close to the reference ones. For a better image of the approximation errors, we placed the magnitude and phase errors for two cases in the figure. We gather all calculated errors in

Table 2. Errors of fractional-order (FO) approximation models calculated for FO inertia with $\alpha =0.9$ and $N_{\mathrm{F}}=5$.

Frequency		$\mathit{\delta }\left|\mathit{G}\right|$	$\mathbf{\Delta }\mathit{\phi }$		$\mathit{\delta }\left|\mathit{G}\right|$	$\mathbf{\Delta }\mathit{\phi }$		$\mathit{\delta }\left|\mathit{G}\right|$	$\mathbf{\Delta }\mathit{\phi }$
Hz		%	${}^{\circ }$		%	${}^{\circ }$		%	${}^{\circ }$
Model		Oustaloup			Ref. Oust.			Xue’s Oust.
0.00100		−1.38	0.203		0.118	0.516		0.0180	−0.00590
0.00158		−1.28	0.229		0.300	0.765		0.0104	−0.00532
0.00251		−1.16	0.268		0.643	1.11		0.0149	−0.000791
0.00398		−1.01	0.300		1.26	1.53		0.0147	−0.00860
0.00631		−0.831	0.335		2.28	1.98		−0.00200	−0.00126
0.0100		−0.584	0.343		3.82	2.30		0.0219	−0.00143
0.0158		−0.384	0.298		5.58	2.30		−0.00670	−0.0129
0.0251		−0.214	0.259		7.19	2.04		−0.000391	0.00989
0.0398		−0.0883	0.178		8.37	1.58		0.0195	−0.0112
0.0631		−0.0749	0.135		9.04	1.15		−0.0247	−0.00247
0.100		−0.0134	0.118		9.47	0.815		0.0171	0.0101
0.158		−0.0141	0.0860		9.67	0.537		0.00328	−0.0161
0.251		−0.0313	0.119		9.76	0.382		−0.0216	0.00749
0.398		0.0126	0.149		9.88	0.258		0.0260	0.00192
0.631		−0.0229	0.202		9.87	0.169		−0.0122	−0.0161
1.00		−0.0149	0.340		9.90	0.149		−0.0102	0.0105

$\delta \left|G\right|$—relative magnitude error; $\Delta \phi$—phase error; models calculated according to: Oustaloup—Equation (5), Ref. Oust.—Equation (6), Xue’s Oust.—Equation (7).

—the left collection.

With the increase in frequency, the absolute values of relative magnitude errors become lower, it means that the approximations are better. The phase error oscillates between ca. 0.1${}^{\circ }$ and 0.3${}^{\circ }$ in the whole frequency range.

The application of the refined variant of the Oustaloup filter approximation leads to the Nyquist plot as in Figure 1. The results for $N_{\mathrm{F}}=0$ are still poor. For higher order of the filter, we observe a change of locations of the points. They lay now very close to the reference circle. Unfortunately, the magnitude and phase errors are, in general, worse. It is clearly visible in the middle collection of Table 2. The magnitude error increases with frequency up to nearly 10% at 1 Hz. The phase error is the greatest for the most negative value of imagine component of the transfer function.

The FO inertia approximated with Xue’s variant of the Oustaloup filter gives much better results than with the earlier models—cf. Figure 2 and the third collection gathered in Table 2. The magnitude error is approximately two orders lower than earlier and does not exceed 0.025% (as the absolute value). The phase error is also extremely small and lower than 0.017${}^{\circ }$ (as the absolute value).

The presented data show the influence of the approximation model on the placement of the points. The influence of the order of the approximation filter on errors was investigated in our previous work [22]. Here, we gather selected data for FO inertia in

Table 3. Magnitude errors dependent on filter order for refined Oustaloup filter with $\alpha =0.9$. The errors are relative and expressed in %.

Frequency	0	1	2	3	4	5	6	7
0.00100	16.8	9.8	1.2	1.3	1.7	1.6	1.5	1.5
0.0100	103.2	−8.5	5.8	4.7	4.2	4.4	4.4	4.4
0.100	36.2	21.2	10.8	7.2	6.2	6.0	6.0	6.0
1.00	−47.8	−7.7	11.3	7.0	6.1	6.4	6.4	6.4

. If the order is very small, the relative magnitude error is significant and changes dramatically with $N_{\mathrm{F}}$. However, the errors remain nearly constant and are specific for the model if the order is greater than four.

Calculations performed for the FO inertia with the order $\alpha =0.6$ allow for plotting similar Nyquist plots: Figure 3 for the standard variant of the Oustaloup method, Figure 4 for the refined method, and Figure 5 for Xue’s method.

Table 4. Errors of FO approximation models calculated for FO inertia with $\alpha =0.6$ and $N_{\mathrm{F}}=5$.

Frequency		$\mathit{\delta }\left|\mathit{G}\right|$	$\mathbf{\Delta }\mathit{\phi }$		$\mathit{\delta }\left|\mathit{G}\right|$	$\mathbf{\Delta }\mathit{\phi }$		$\mathit{\delta }\left|\mathit{G}\right|$	$\mathbf{\Delta }\mathit{\phi }$
Hz		%	${}^{\circ }$		%	${}^{\circ }$		%	${}^{\circ }$
Model		Oustaloup			Ref. Oust.			Xue’s Oust.
0.00100		−2.01	1.42		1.59	0.811		0.0530	−0.0954
0.00158		−1.44	1.16		2.08	0.907		−0.00114	−0.0506
0.00251		−0.914	0.925		2.71	0.973		0.0616	−0.0275
0.00398		−0.595	0.666		3.29	0.937		0.00696	−0.0559
0.00631		−0.397	0.527		3.83	0.939		−0.0182	0.0057
0.0100		−0.157	0.364		4.45	0.846		0.0661	−0.0208
0.0158		−0.157	0.230		4.81	0.721		−0.0484	−0.0318
0.0251		−0.0649	0.209		5.23	0.670		0.0106	0.0323
0.0398		0.0117	0.0950		5.59	0.503		0.0480	−0.0360
0.0631		−0.0854	0.0843		5.71	0.427		−0.0737	−0.00225
0.100		0.0330	0.0966		6.01	0.372		0.0527	0.0293
0.158		−0.00155	0.0225		6.11	0.232		0.00784	−0.0468
0.251		−0.0629	0.0941		6.15	0.238		−0.0642	0.0236
0.398		0.0629	0.0993		6.36	0.175		0.0779	0.00726
0.631		−0.0466	0.101		6.30	0.099		−0.0364	−0.0465
1.00		−0.0269	0.248		6.37	0.149		−0.0314	0.0348

$\delta \left|G\right|$—relative magnitude error; $\Delta \phi$—phase error; models calculated according to: Oustaloup—Equation (5), Ref. Oust.—Equation (6), Xue’s Oust.—Equation (7).

consists of numerical results. The observations, in general, are here very similar to those performed for the order of $\alpha =0.9$. The curve, however, becomes flatter—the imaginary part reaches a maximum of approximately $-0.5$ while for $\alpha =0.9$ it was nearly $-0.9$.

For the standard variant of the Oustaloup filter approximation, the character of the phase error slightly changed (Figure 3 and Table 4—left collection). Nearly 1.5% error is for the lowest calculated frequency, decreasing with the increase of frequency and is the lowest for 0.158 Hz, and finally increases for the highest frequency.

Figure 4 and the middle collection of Table 4 illustrate the case of the refined filter approximation. While the magnitude error was quite small for the lowest frequency in the earlier case of the refined variant, here it is 10 times greater. Simultaneously, it does not reach a high value and is approximately 6.4% at 1 Hz. The variation of the phase error is also much lower and the error does not exceed 1%.

Figure 5 and the right-hand collection of Table 4 relate to Xue’s variant. For $\alpha =0.6$, the greatest absolute value of the errors are 0.08% and 0.095${}^{\circ }$, respectively. This means a deterioration of the results, although this model is still much more accurate than the others.

5.3. Unit Step Response

From the metrological point of view, the analysis of the step responses is difficult due to the lack of a reference plot. Therefore, we compare only the responses between each other. We start with $\alpha =0.9$. Figure 6 compares responses calculated using the three variants of the Oustaloup approximation. The filter order is both $N_{\mathrm{F}}=3$ and $N_{\mathrm{F}}=5$. The figure consist of two panels, each has the same time horizon but the output range is changed. The upper panel illustrates the variability of the response. The bottom panel is a magnification to illustrate differences.

The standard Oustaloup method, as we evidenced in Section 5.1, suffers the steady-state value, which should tend to 1. Here, we see that it tends to the value calculated in Section 5.1, meaning 1.961. The remaining plots overcome the drawback. There is no relevant difference between plots calculated for $N_{\mathrm{F}}=3$ and $N_{\mathrm{F}}=5$. Xue’s model provides a bit slower response than the refined model in the first stage—the green curve is on the right hand side from the brown one. However, after approximately 170 s, the green curve crosses the brown one and reaches the steady-state faster.

Figure 7 illustrates a similar analysis but performed for $\alpha =0.6$. The bottom panel has lower magnification than earlier due to the slower response of the inertia. The properties of the models keep the same as for $\alpha =0.9$. We observe that the refined models go up to obtain the proper steady-state, while the standard Oustaloup ones keep the biased steady-state causing the $-13$% error. The curves calculated for the same models and different orders $N_{\mathrm{F}}$ are very close to each other.

5.4. Closed-Loop Control System

To validate the influence of the selected model on the answer of FO control system, we take the same example as in our previous works [22,68]. It is a real case described elsewhere [24]. The plant is a motor-generator system approximated by second-order inertia with a small delay, described by:

$$G_p\left(s\right)=\frac{0.63606}{(42.77s+1)(7.45s+1)}{e}^{-0.61s}.$$

(24)

The controller is PI${}^{\lambda }$D${}^{\mu }$ type with the transfer function of

$$G_c\left(s\right)=k\left(1+\frac{1}{T_{\mathrm{i}}{s}^{\lambda }}+T_{\mathrm{d}}{s}^{\mu }\right).$$

(25)

Parameters of the controller are cited after [24] and gathered in

Table 5. Tuning parameters of the PI${}^{\lambda }$D${}^{\mu }$ controllers used in simulations—taken from [24].

k	${\mathit{T}}_{\mathbf{i}}$	${\mathit{T}}_{\mathbf{d}}$	$\mathit{\lambda }$	$\mathit{\mu }$
$0.133$	$2.5$	$0.76$	$0.89$	$0.44$

.

The MATLAB Simulink diagram consists of the FO-PID block realizing the PI${}^{\lambda }$D${}^{\mu }$ function. We compare the response of the system containing this block with the system with PI${}^{\lambda }$D${}^{\mu }$ controller built from Discrete Fractional Transducer Functions (DFTFs)—see Figure 8. The DFTF allows switching between the refined and standard variant of the Oustaloup filter approximation—see Figure 9. Additionally, we calculate the response of the system using our own procedure run in Octave which implements the three variants of the filter.

Figure 10 presents the responses of the control system. We observe very similar trajectory calculated using FO-PID, DFTF with unselected refined variant, and our procedure with the standard variant of the Oustaloup filter approximation. It proves that our procedure does not consist of defects and that the FO-PID block uses the standard filter. The slight difference shown at about 150 s comes probably from different sampling period which is unselectable in the FO-PID block. The responses calculated using Simulink and Octave are practically the same. Xue’s variant of the filter has the trajectory similar to that of refined filter but differs slightly. The fundamental conclusion led from the observation is that the shape of the response is dependent on the chosen model. The previous work [22] proves that also parameters used in the approximation influence the shape. It means that the parameters of the FO model obtained by best-fitting to experimental results are biased by choosing the approximation model and its parameters. In the same way, models of sensors, chemical, or physical systems, described by FO differential equations, will have parameters whose values are dependent on the chosen model approximating FO differentiation.

6. Conclusions

The article emphasizes the very often diminished problem, that numerical values calculated by fractional-order differential equations are not accurate. The beginning example shows that the steady-state value of an FO dynamic system may differ from expected value making a bias. The bias is dependent on the selected approximation method and its parameters. It is possible in the frequency domain to calculate the Nyquist plots accurately. It allows for a calculation of the amplitude and phase errors which arose by applying the approximations. Comparison of three variants of the Oustaloup filter approximation evidenced that Xue’s approach, Equation (7), is the most accurate. The impact of the order of the approximation filter (if it is high enough, greater than four for the studied example) on the Nyquist plot is lower than of the approximation model. It is impossible to calculate a reference (accurate) time response of an FO system, so errors cannot be provided in. Plotted unit step responses show different trajectories dependent mostly on models approximating the FO derivative, less on the order of the approximation. Similarly, a control system with a PI${}^{\lambda }$D${}^{\mu }$ controller gives time responses dependent on the applied model. For models of systems, including sensors, providing parameters related to FO differential equation are poor without explicitly specified the approximation method. The more flexible trajectory of the time response of the FO system is paid for by an increase in computational complexity, additional errors (biases) arisen from the selected approximation method and the influence of the method used on parameters of the model.

This work studied only three variants of the Oustaloup filter approximating the fractional derivative. Other known approaches dealing with fractional calculus may introduce similar inaccuracies which should be taken into consideration especially in implementations requiring high precision.