Influence of Methods Approximating Fractional-Order Differentiation on the Output Signal Illustrated by Three Variants of Oustaloup Filter
Abstract
1. Introduction
2. Background
3. Materials and Methods
4. Theory/Calculation
4.1. Variants of Oustaloup Filter Approximations
4.2. Steady-State Value
4.3. Nyquist Plot and Time Response
4.4. Approximation Errors
5. Results and Discussion
5.1. Steady-State Value
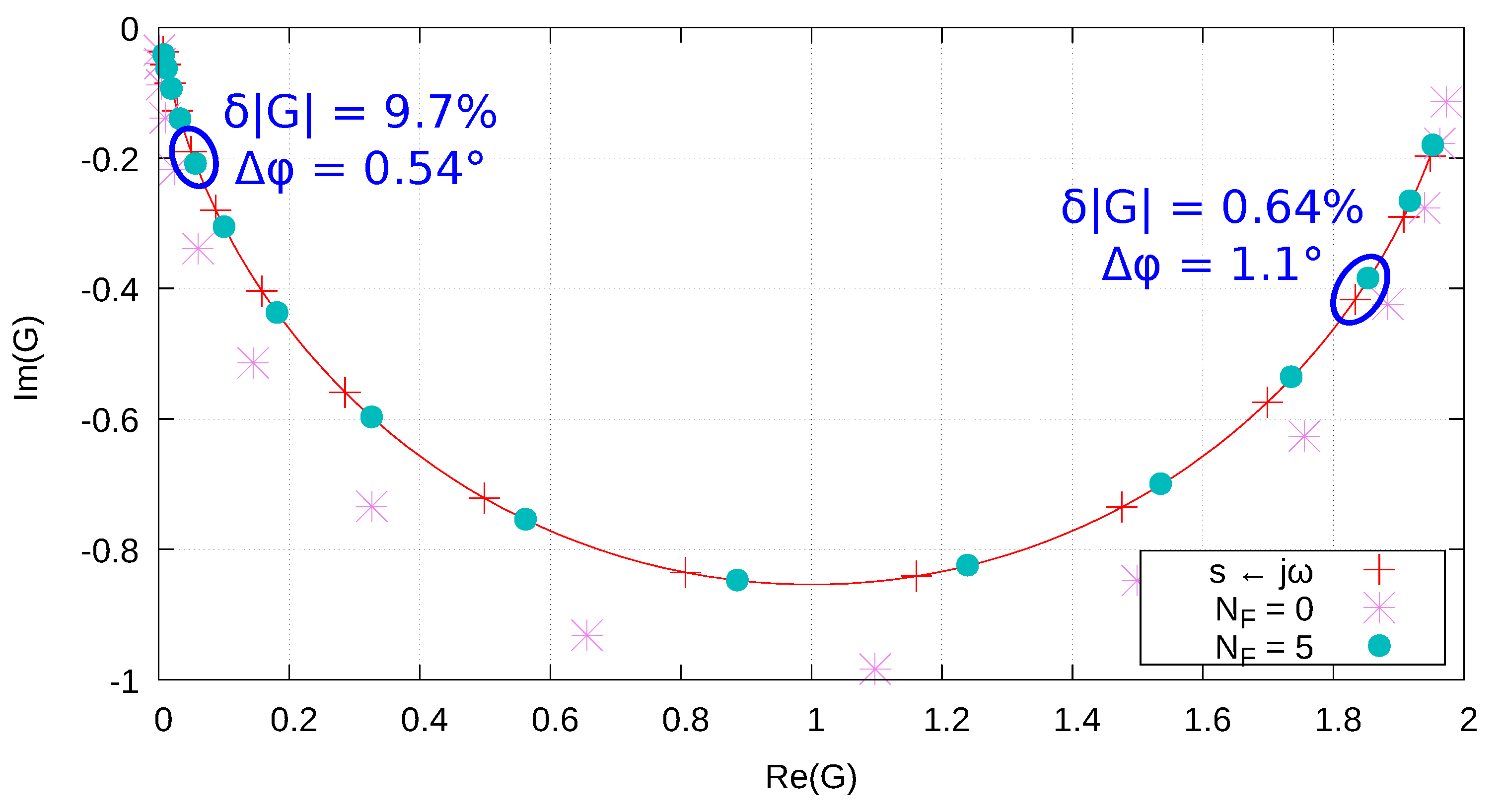
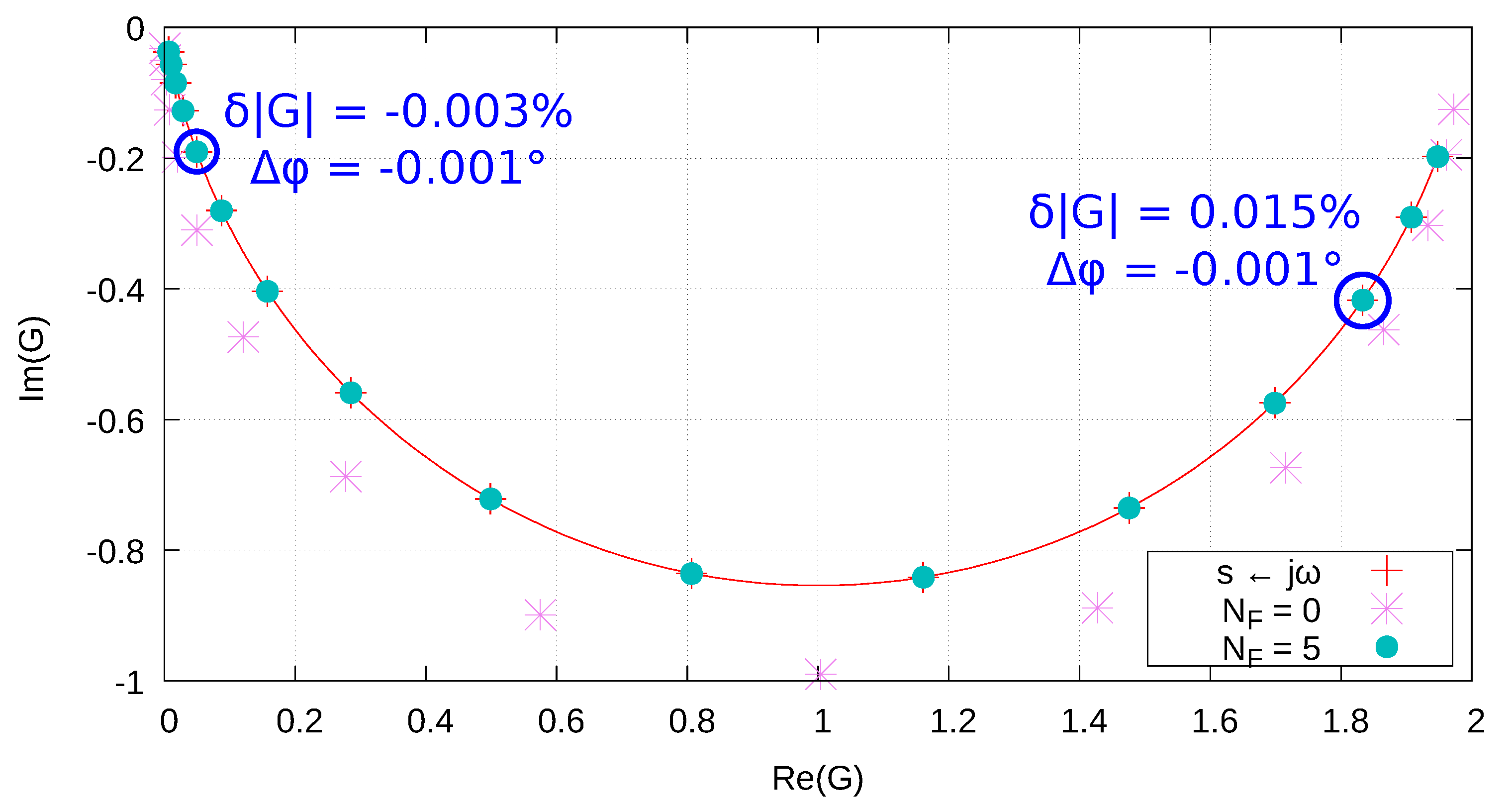
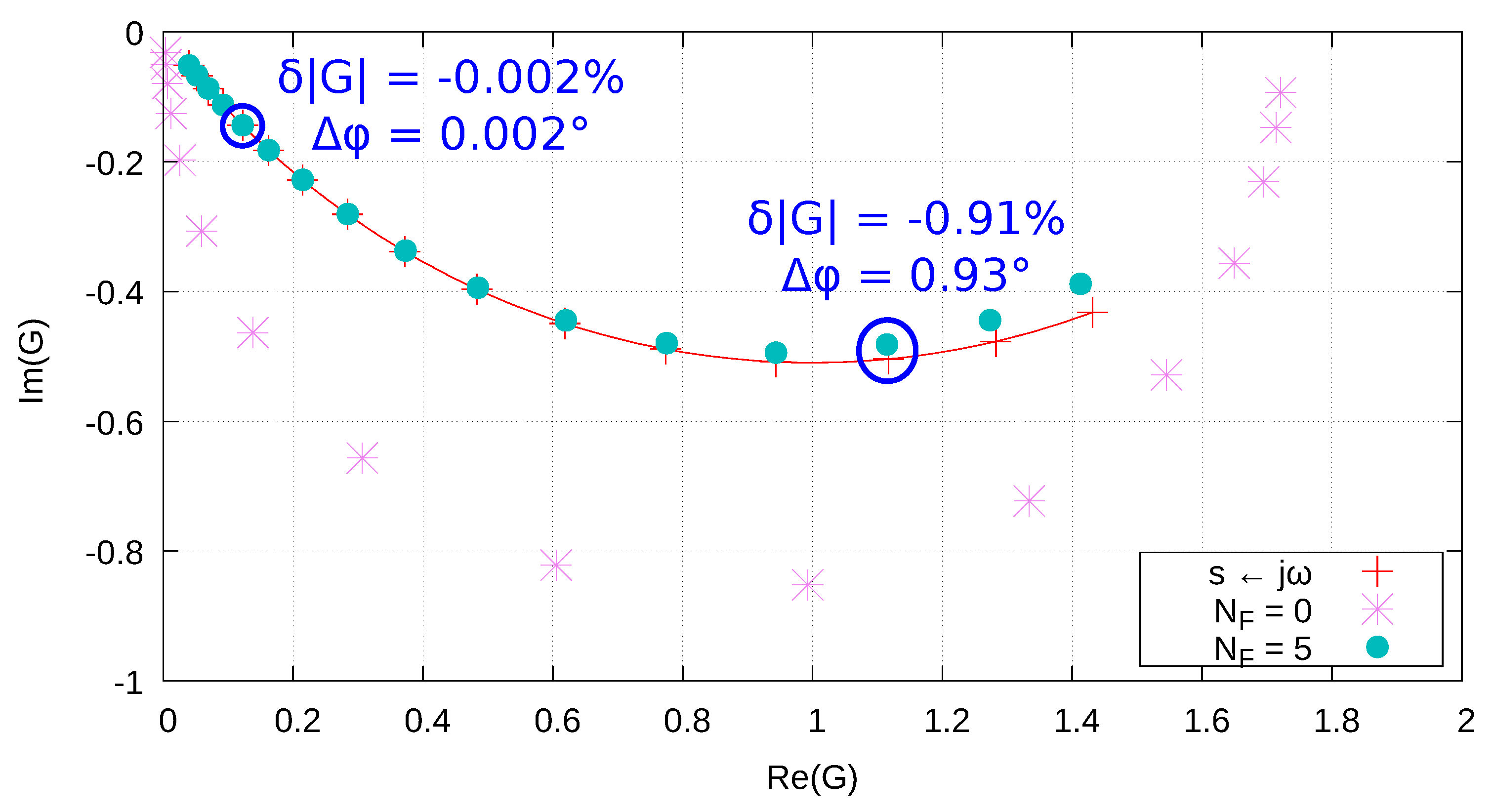
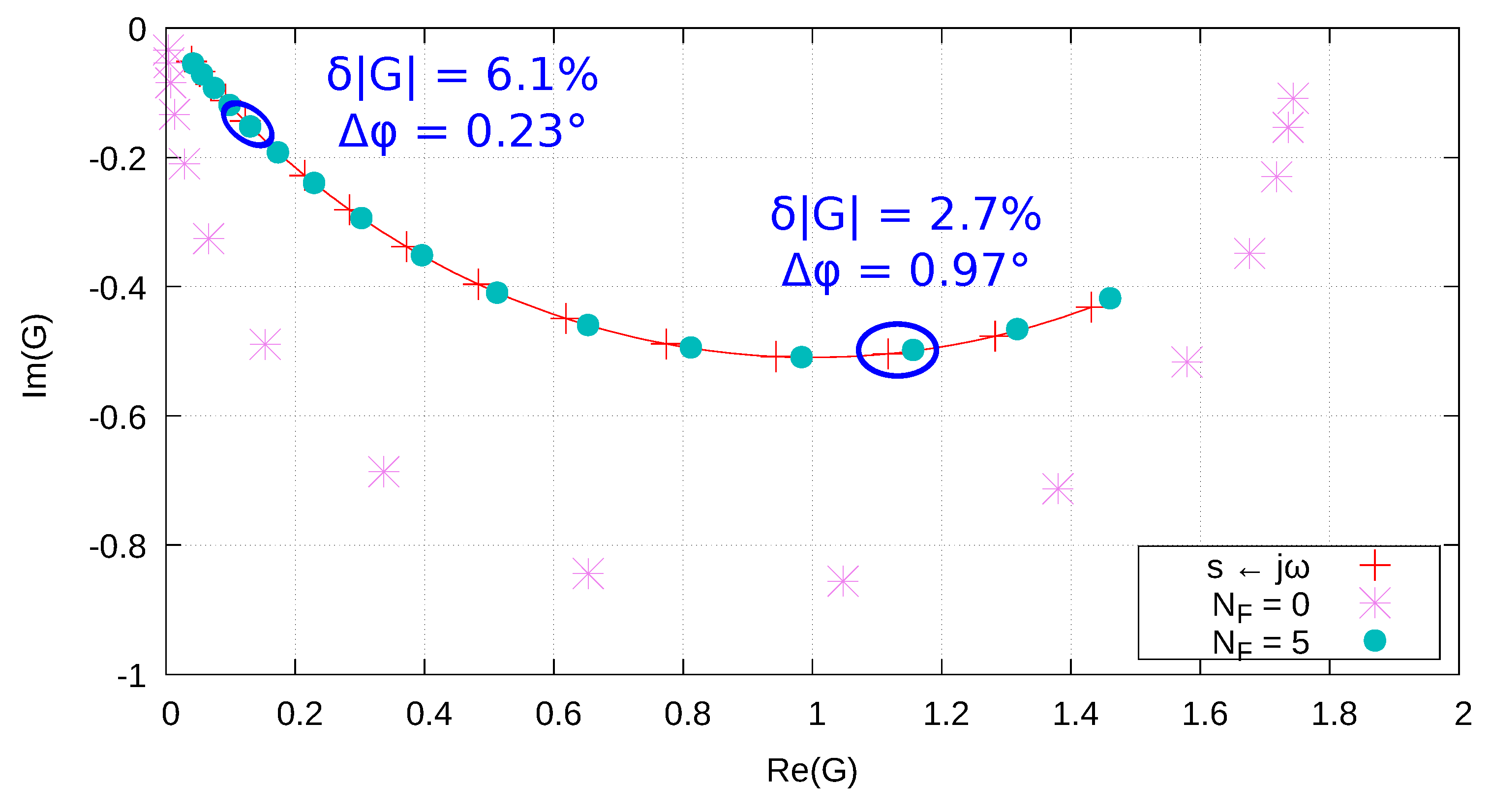
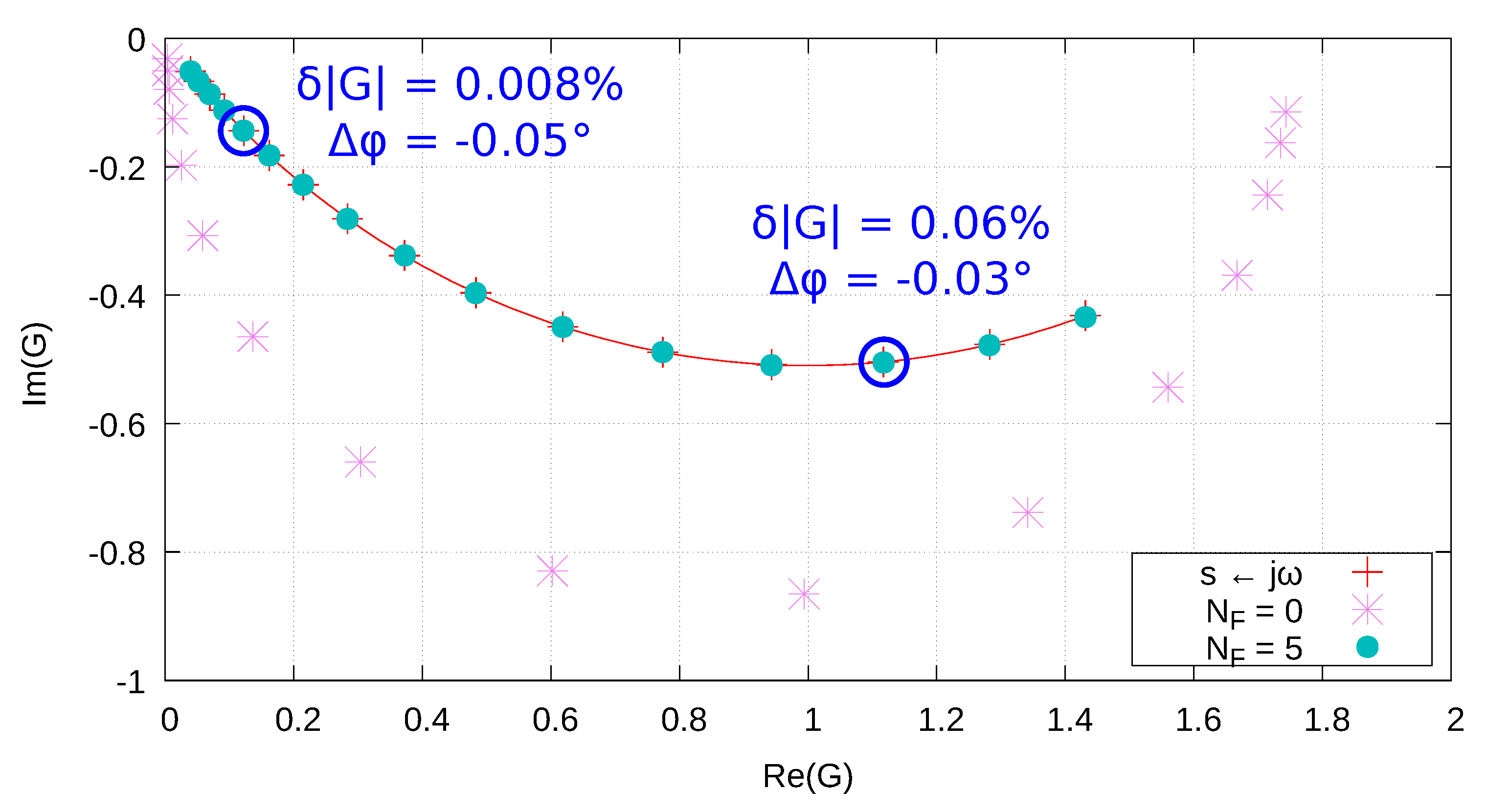
5.2. Nyquist Plot
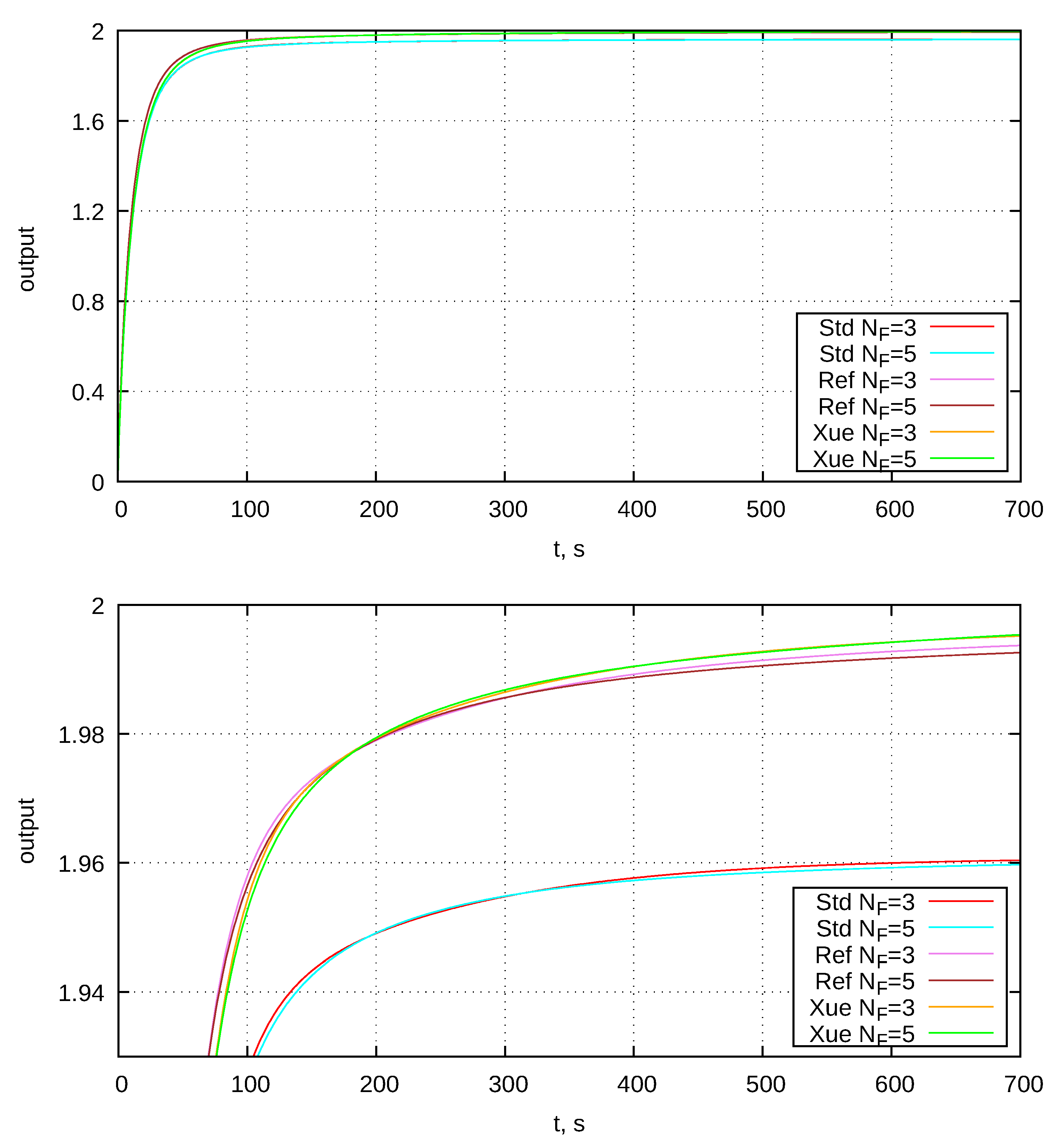
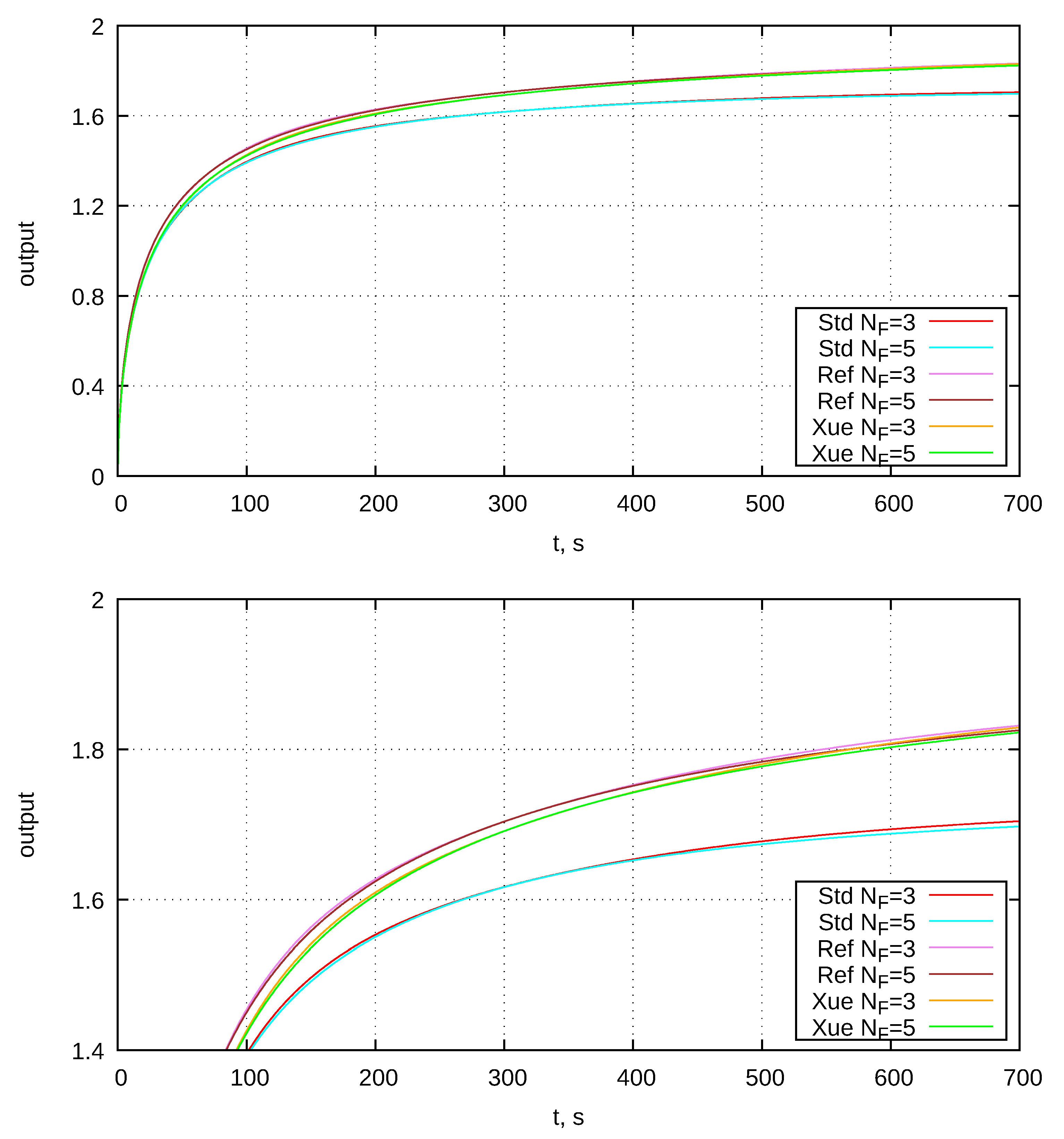
5.3. Unit Step Response
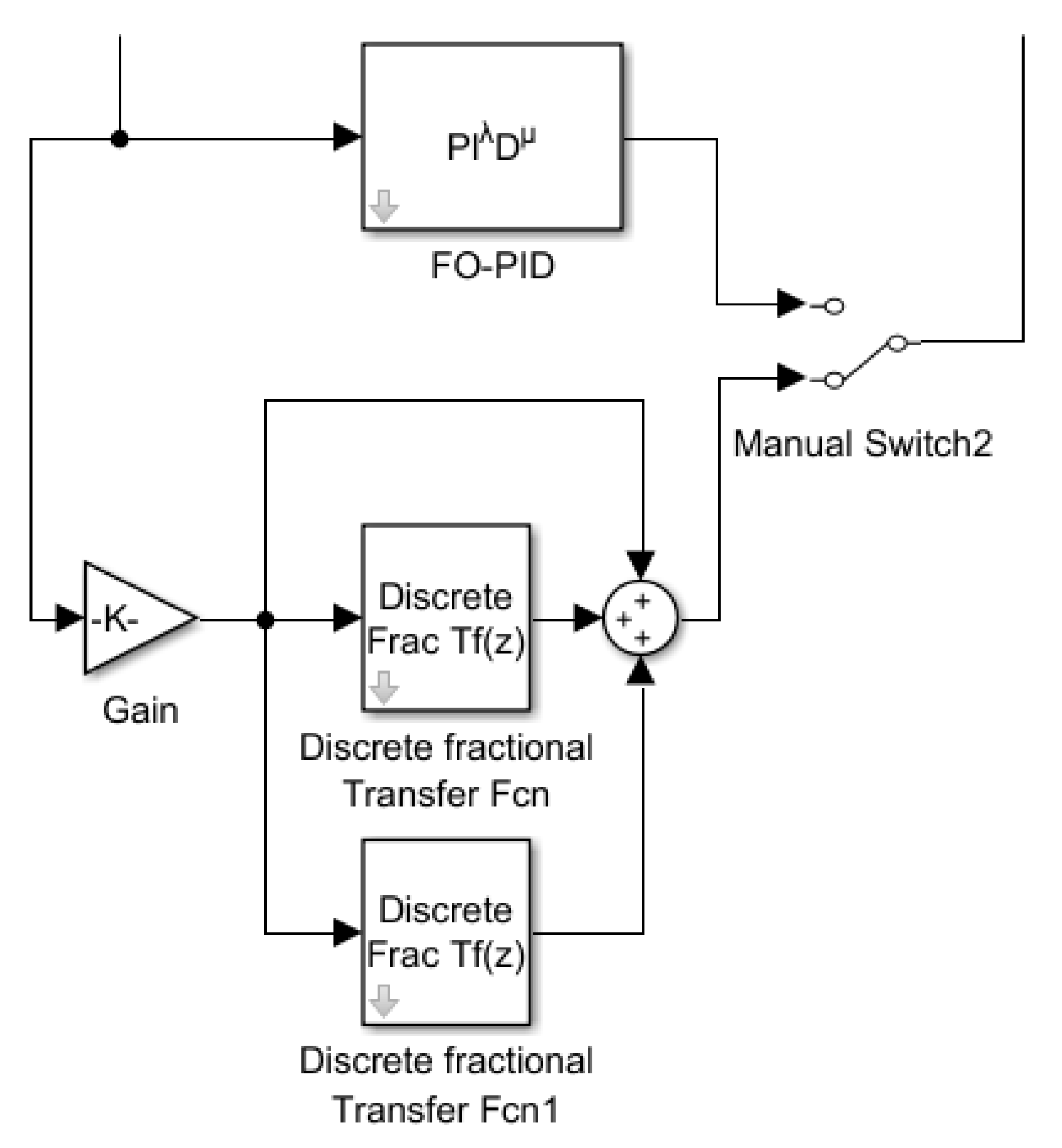
5.4. Closed-Loop Control System
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Barbosa, R.S.; Machado, J.A.T. Implementation of discrete-time fractional-order controllers based on LS approximations. Acta Polytech. Hung. 2006, 3, 5–22. [Google Scholar]
- Vinagre, B.M.; Chen, Y.Q.; Petráš, I. Two direct Tustin discretization methods for fractional-order differentiator/integrator. J. Frankl. Inst. 2003, 340, 349–362. [Google Scholar] [CrossRef]
- David, S.A.; Linares, J.L.; Pallone, E.M.J.A. Fractional order calculus: Historical apologia, basic concepts and some applications. Rev. Bras. Ensino Física 2011, 33, 4302. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature, 1st ed.; W. H. Freeman and Company: San Francisco, CA, USA, 1982. [Google Scholar]
- Lu, Y.; Tang, Y.; Zhang, X.; Wang, S. Parameter identification of fractional order systems with nonzero initial conditions based on block pulse functions. Measurement 2020, 158, 107684. [Google Scholar] [CrossRef]
- Tustin, A.; Allanson, J.T.; Layton, J.M.; Jakeways, R.J. The design of systems for automatic control of the position of massive objects. Proc. IEE Part C Monogr. 1958, 105, 1. [Google Scholar] [CrossRef]
- Manage, S. The Non-integer Integral and its Application to Control Systemes. J. Inst. Electr. Eng. Jpn. 1960, 80, 589–597. [Google Scholar] [CrossRef]
- Dogruer, T.; Tan, N. Design of PI Controller using Optimization Method in Fractional Order Control Systems. IFAC Papers OnLine 2018, 51, 841–846. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1998. [Google Scholar]
- Oziablo, P.; Mozyrska, D.; Wyrwas, M. Discrete-Time Fractional, Variable-Order PID Controller for a Plant with Delay. Entropy 2020, 22, 771. [Google Scholar] [CrossRef]
- Yaghi, M.; Efe, M.O. H2/H∞-Neural-Based FOPID Controller Applied for Radar-Guided Missile. IEEE Trans. Ind. Electron. 2020, 67, 4806–4814. [Google Scholar] [CrossRef]
- Wang, N.; Wang, J.; Li, Z.; Tang, X.; Hou, D. Fractional-Order PID Control Strategy on Hydraulic-Loading System of Typical Electromechanical Platform. Sensors 2018, 18, 3024. [Google Scholar] [CrossRef]
- Acharya, D.S.; Mishra, S.K. A multi-agent based symbiotic organisms search algorithm for tuning fractional order PID controller. Measurement 2020, 155, 107559. [Google Scholar] [CrossRef]
- Dziedzic, K.; Oprzędkiewicz, K. The Quickly Adjustable Digital FOPID Controller. In Advances in Intelligent Systems and Computing; Springer Nature Switzerland AG: Cham, Switzerland, 2020; pp. 847–856. [Google Scholar] [CrossRef]
- Ayas, M.S.; Sahin, E. FOPID controller with fractional filter for an automatic voltage regulator. Comput. Electr. Eng. 2020, 106895. [Google Scholar] [CrossRef]
- Pradhan, R.; Majhi, S.K.; Pradhan, J.K.; Pati, B.B. Optimal fractional order PID controller design using Ant Lion Optimizer. Ain Shams Eng. J. 2020, 11, 281–291. [Google Scholar] [CrossRef]
- Asgharnia, A.; Jamali, A.; Shahnazi, R.; Maheri, A. Load mitigation of a class of 5-MW wind turbine with RBF neural network based fractional-order PID controller. ISA Trans. 2020, 96, 272–286. [Google Scholar] [CrossRef]
- Radwan, A.G.; Emira, A.A.; AbdelAty, A.M.; Azar, A.T. Modeling and analysis of fractional order DC-DC converter. ISA Trans. 2018, 82, 184–199. [Google Scholar] [CrossRef]
- Yang, Z.Z.; Zhou, J.L. An Improved Design for the IIR-Type Digital Fractional Order Differential Filter. In Proceedings of the 2008 International Seminar on Future BioMedical Information Engineering, Wuhan, China, 18 December 2008. [Google Scholar] [CrossRef]
- Zhang, C.; Zhu, Z.; Zhu, S.; He, Z.; Zhu, D.; Liu, J.; Meng, S. Nonlinear Creep Damage Constitutive Model of Concrete Based on Fractional Calculus Theory. Materials 2019, 12, 1505. [Google Scholar] [CrossRef]
- Magin, R.L. Fractional calculus models of complex dynamics in biological tissues. Comput. Math. Appl. 2010, 59, 1586–1593. [Google Scholar] [CrossRef]
- Wiora, J.; Wiora, A. Inaccuracies Revealed During the Analysis of Propagation of Measurement Uncertainty Through a Closed-Loop Fractional-Order Control System. In Lecture Notes in Electrical Engineering; Springer Nature Switzerland AG: Cham, Switzerland, 2019; pp. 213–226. [Google Scholar] [CrossRef]
- Macias, M.; Sierociuk, D. Modeling of electrical drive system with flexible shaft based on fractional calculus. In Proceedings of the 14th International Carpathian Control Conference (ICCC), Rytro, Poland, 26–29 May 2013. [Google Scholar] [CrossRef]
- Viola, J.; Angel, L.; Sebastian, J.M. Design and robust performance evaluation of a fractional order PID controller applied to a DC motor. IEEE/CAA J. Autom. Sin. 2017, 4, 304–314. [Google Scholar] [CrossRef]
- Kumar, S.; Ghosh, A. Identification of fractional order model for a voltammetric E-tongue system. Measurement 2020, 150, 107064. [Google Scholar] [CrossRef]
- Freeborn, T.J.; Maundy, B.; Elwakil, A.S. Fractional-order models of supercapacitors, batteries and fuel cells: A survey. Mater. Renew. Sustain. Energy 2015, 4. [Google Scholar] [CrossRef]
- Zou, C.; Zhang, L.; Hu, X.; Wang, Z.; Wik, T.; Pecht, M. A review of fractional-order techniques applied to lithium-ion batteries, lead-acid batteries, and supercapacitors. J. Power Sources 2018, 390, 286–296. [Google Scholar] [CrossRef]
- Lenzi, E.K.; Ribeiro, H.V.; Zola, R.S.; Evangelista, L.R. Fractional Calculus in Electrical Impedance Spectroscopy: Poisson–Nernst–Planck model and Extensions. Int. J. Electrochem. Sci. 2017, 11677–11691. [Google Scholar] [CrossRef]
- Hu, M.; Li, Y.; Li, S.; Fu, C.; Qin, D.; Li, Z. Lithium-ion battery modeling and parameter identification based on fractional theory. Energy 2018, 165, 153–163. [Google Scholar] [CrossRef]
- Zou, C.; Hu, X.; Dey, S.; Zhang, L.; Tang, X. Nonlinear Fractional-Order Estimator with Guaranteed Robustness and Stability for Lithium-Ion Batteries. IEEE Trans. Ind. Electron. 2017, 1. [Google Scholar] [CrossRef]
- Lu, X.; Li, H.; Chen, N. An indicator for the electrode aging of lithium-ion batteries using a fractional variable order model. Electrochim. Acta 2019, 299, 378–387. [Google Scholar] [CrossRef]
- Allagui, A.; Freeborn, T.J.; Elwakil, A.S.; Fouda, M.E.; Maundy, B.J.; Radwan, A.G.; Said, Z.; Abdelkareem, M.A. Review of fractional-order electrical characterization of supercapacitors. J. Power Sources 2018, 400, 457–467. [Google Scholar] [CrossRef]
- Krishnan, G.; Das, S.; Agarwal, V. An Online Identification Algorithm to Determine the Parameters of the Fractional-Order Model of a Supercapacitor. IEEE Trans. Ind. Appl. 2020, 56, 763–770. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, G.; Li, X.; Chen, Z. A fractional-order model-based state estimation approach for lithium-ion battery and ultra-capacitor hybrid power source system considering load trajectory. J. Power Sources 2020, 449, 227543. [Google Scholar] [CrossRef]
- Kumar, S.; Ghosh, A. An Improved Fractional-Order Circuit Model for Voltammetric Taste Sensor System With Infused Tea as Analyte. IEEE Sens. J. 2020, 20, 7792–7800. [Google Scholar] [CrossRef]
- Alimisis, V.; Gourdouparis, M.; Dimas, C.; Sotiriadis, P.P. Implementation of Fractional-order Model of Nickel-Cadmium Cell using Current Feedback Operational Amplifiers. In Proceedings of the 2020 European Conference on Circuit Theory and Design (ECCTD), Sofia, Bulgaria, 7–10 September 2020. [Google Scholar] [CrossRef]
- Sarathi, V.P.; Uma, G.; Umapathy, M. Realization of Fractional order Inductive Transducer. IEEE Sens. J. 2018, 1. [Google Scholar] [CrossRef]
- Tian, A.; Zhao, J.; Xiong, H.; Gan, S.; Fu, C. Application of Fractional Differential Calculation in Pretreatment of Saline Soil Hyperspectral Reflectance Data. J. Sens. 2018, 2018, 1–12. [Google Scholar] [CrossRef]
- Gerolymatou, E.; Vardoulakis, I.; Hilfer, R. Modelling infiltration by means of a nonlinear fractional diffusion model. J. Phys. D: Appl. Phys. 2006, 39, 4104–4110. [Google Scholar] [CrossRef]
- Agrawal, N.; Kumar, A.; Bajaj, V.; Singh, G.K. Design of Bandpass and Bandstop Infinite Impulse Response Filters Using Fractional Derivative. IEEE Trans. Ind. Electron. 2019, 66, 1285–1295. [Google Scholar] [CrossRef]
- Prommee, P.; Pienpichayapong, P.; Manositthichai, N.; Wongprommoon, N. OTA-based tunable fractional-order devices for biomedical engineering. AEU Int. J. Electron. Commun. 2021, 128, 153520. [Google Scholar] [CrossRef]
- Kawala-Janik, A.; Zolubak, M.; Bauer, W.; Nazimek, B.; Sobolewski, T.; Martinek, R.; Sowa, M.; Pelc, M. Implementation of Non-Integer Order Filtering for the Purpose of Disparities Detection in Beta Frequencies—A Pilot Study. In Proceedings of the 2018 23rd International Conference on Methods & Models in Automation & Robotics (MMAR), Międzyzdroje, Poland, 27–30 August 2018. [Google Scholar] [CrossRef]
- Alimisis, V.; Dimas, C.; Pappas, G.; Sotiriadis, P.P. Analog Realization of Fractional-Order Skin-Electrode Model for Tetrapolar Bio-Impedance Measurements. Technologies 2020, 8, 61. [Google Scholar] [CrossRef]
- Miljković, N.; Popović, N.; Djordjević, O.; Konstantinović, L.; Šekara, T.B. ECG artifact cancellation in surface EMG signals by fractional order calculus application. Comput. Methods Programs Biomed. 2017, 140, 259–264. [Google Scholar] [CrossRef] [PubMed]
- Ren, H.; Yin, A.; Zhang, Q. Vibration signal denoising using partial differential equations of arbitrary order. Measurement 2019, 148, 106917. [Google Scholar] [CrossRef]
- Wu, C.; Yang, J.; Huang, D.; Liu, H.; Hu, E. Weak signal enhancement by fractional-order system resonance and its application in bearing fault diagnosis. Meas. Sci. Technol. 2019, 30, 035004. [Google Scholar] [CrossRef]
- Tolba, M.F.; AbdelAty, A.M.; Soliman, N.S.; Said, L.A.; Madian, A.H.; Azar, A.T.; Radwan, A.G. FPGA implementation of two fractional order chaotic systems. AEU Int. J. Electron. Commun. 2017, 78, 162–172. [Google Scholar] [CrossRef]
- Boukamp, B.A. Derivation of a Distribution Function of Relaxation Times for the (fractal) Finite Length Warburg. Electrochim. Acta 2017, 252, 154–163. [Google Scholar] [CrossRef]
- Jakubiec, B. Fuzzy logic controller for robot manipulator control system. In Proceedings of the 2018 Applications of Electromagnetics in Modern Techniques and Medicine (PTZE), Racławice, Poland, 9–12 September 2018. [Google Scholar] [CrossRef]
- Tepljakov, A.; Petlenkov, E.; Belikov, J. FOMCOM: A MATLAB toolbox for fractional-order system identification and control. Int. J. Microelectron. Comput. Sci. 2011, 2, 51–62. [Google Scholar]
- Xue, D.; FOTF Toolbox. MATLAB Central File Exchange. Available online: https://www.mathworks.com/matlabcentral/fileexchange/60874-fotf-toolbox (accessed on 12 October 2020).
- Ashwin Pajankar, S.C. GNU Octave by Example; Apress: New York City, NY, USA, 2020. [Google Scholar]
- Chen, Y.; Petras, I.; Xue, D. Fractional order control-A tutorial. In Proceedings of the 2009 American Control Conference, St. Louis, MO, USA, 10–12 June 2009. [Google Scholar] [CrossRef]
- Caputo, M.C.; Torres, D.F. Duality for the left and right fractional derivatives. Signal Process. 2015, 107, 265–271. [Google Scholar] [CrossRef]
- Ortigueira, M.D. Fractional Calculus for Scientists and Engineers; Springer Science+Business Media B.V.: Dordrecht, The Netherlands, 2011. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Vinagre, B.M.; Podlubny, I.; Hernandez, A.; Feliu, V. Some approximations of fractional order operators used in control theory and applications. Fract. Calc. Appl. Anal. 2000, 3, 231–248. [Google Scholar]
- Atherton, D.P.; Tan, N.; Yüce, A. Methods for computing the time response of fractional-order systems. IET Control Theory Appl. 2015, 9, 817–830. [Google Scholar] [CrossRef]
- Ionescu, C.; Machado, J.T.; Keyser, R.D. Fractional-order impulse response of the respiratory system. Comput. Math. Appl. 2011, 62, 845–854. [Google Scholar] [CrossRef]
- Baranowski, J.; Bauer, W.; Zagorowska, M.; Dziwinski, T.; Piatek, P. Time-domain Oustaloup approximation. In Proceedings of the 2015 20th International Conference on Methods and Models in Automation and Robotics (MMAR), Międzyzdroje, Poland, 24–27 August 2015. [Google Scholar] [CrossRef]
- Xue, D.; Zhao, C.; Chen, Y. A Modified Approximation Method of Fractional Order System. In Proceedings of the 2006 International Conference on Mechatronics and Automation, Luoyang, China, 25–28 June 2006. [Google Scholar] [CrossRef]
- Xue, D.; Chen, Y.; Atherton, D.P. Linear Feedback Control: Analysis and Design with MATLAB; SIAM: Philadelphia, PA, USA, 2007. [Google Scholar]
- Krajewski, W.; Viaro, U. A method for the integer-order approximation of fractional-order systems. J. Frankl. Inst. 2014, 351, 555–564. [Google Scholar] [CrossRef]
- Gluskin, E. Let us teach this generalization of the final-value theorem. Eur. J. Phys. 2003, 24, 591–597. [Google Scholar] [CrossRef]
- Bialkowski, S.E. Real-time digital filters: finite impulse response filters. Anal. Chem. 1988, 60, 355A–361A. [Google Scholar] [CrossRef]
- Reade, J.B. Calculus with Complex Numbers; Taylor & Francis: London, UK, 2003. [Google Scholar]
- Oprzędkiewicz, K. Discrete Transfer Function Models for Non Integer Order Inertial System. In Advances in Intelligent Systems and Computing; Springer International Publishing: Cham, Switzerland, 2018; pp. 14–25. [Google Scholar] [CrossRef]
- Wiora, J.; Wiora, A. Measurement Uncertainty Evaluation of Results Provided by Transducers Working in Control Loops. In Proceedings of the 2018 23rd International Conference on Methods & Models in Automation & Robotics (MMAR), Międzyzdroje, Poland, 27–30 August 2018. [Google Scholar] [CrossRef]

| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Inertia | Oustaloup Approximation | ||
| k | 2 | 0 or 5 | |
| T | 10 s | 0.001 rad/s | |
| 0.9 or 0.6 | 1000 rad/s | ||
| f | Hz | b | 10 |
| d | 9 | ||
| Frequency | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Hz | % | % | % | ||||||
| Model | Oustaloup | Ref. Oust. | Xue’s Oust. | ||||||
| 0.00100 | −1.38 | 0.203 | 0.118 | 0.516 | 0.0180 | −0.00590 | |||
| 0.00158 | −1.28 | 0.229 | 0.300 | 0.765 | 0.0104 | −0.00532 | |||
| 0.00251 | −1.16 | 0.268 | 0.643 | 1.11 | 0.0149 | −0.000791 | |||
| 0.00398 | −1.01 | 0.300 | 1.26 | 1.53 | 0.0147 | −0.00860 | |||
| 0.00631 | −0.831 | 0.335 | 2.28 | 1.98 | −0.00200 | −0.00126 | |||
| 0.0100 | −0.584 | 0.343 | 3.82 | 2.30 | 0.0219 | −0.00143 | |||
| 0.0158 | −0.384 | 0.298 | 5.58 | 2.30 | −0.00670 | −0.0129 | |||
| 0.0251 | −0.214 | 0.259 | 7.19 | 2.04 | −0.000391 | 0.00989 | |||
| 0.0398 | −0.0883 | 0.178 | 8.37 | 1.58 | 0.0195 | −0.0112 | |||
| 0.0631 | −0.0749 | 0.135 | 9.04 | 1.15 | −0.0247 | −0.00247 | |||
| 0.100 | −0.0134 | 0.118 | 9.47 | 0.815 | 0.0171 | 0.0101 | |||
| 0.158 | −0.0141 | 0.0860 | 9.67 | 0.537 | 0.00328 | −0.0161 | |||
| 0.251 | −0.0313 | 0.119 | 9.76 | 0.382 | −0.0216 | 0.00749 | |||
| 0.398 | 0.0126 | 0.149 | 9.88 | 0.258 | 0.0260 | 0.00192 | |||
| 0.631 | −0.0229 | 0.202 | 9.87 | 0.169 | −0.0122 | −0.0161 | |||
| 1.00 | −0.0149 | 0.340 | 9.90 | 0.149 | −0.0102 | 0.0105 | |||
| Frequency | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| 0.00100 | 16.8 | 9.8 | 1.2 | 1.3 | 1.7 | 1.6 | 1.5 | 1.5 |
| 0.0100 | 103.2 | −8.5 | 5.8 | 4.7 | 4.2 | 4.4 | 4.4 | 4.4 |
| 0.100 | 36.2 | 21.2 | 10.8 | 7.2 | 6.2 | 6.0 | 6.0 | 6.0 |
| 1.00 | −47.8 | −7.7 | 11.3 | 7.0 | 6.1 | 6.4 | 6.4 | 6.4 |
| Frequency | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Hz | % | % | % | ||||||
| Model | Oustaloup | Ref. Oust. | Xue’s Oust. | ||||||
| 0.00100 | −2.01 | 1.42 | 1.59 | 0.811 | 0.0530 | −0.0954 | |||
| 0.00158 | −1.44 | 1.16 | 2.08 | 0.907 | −0.00114 | −0.0506 | |||
| 0.00251 | −0.914 | 0.925 | 2.71 | 0.973 | 0.0616 | −0.0275 | |||
| 0.00398 | −0.595 | 0.666 | 3.29 | 0.937 | 0.00696 | −0.0559 | |||
| 0.00631 | −0.397 | 0.527 | 3.83 | 0.939 | −0.0182 | 0.0057 | |||
| 0.0100 | −0.157 | 0.364 | 4.45 | 0.846 | 0.0661 | −0.0208 | |||
| 0.0158 | −0.157 | 0.230 | 4.81 | 0.721 | −0.0484 | −0.0318 | |||
| 0.0251 | −0.0649 | 0.209 | 5.23 | 0.670 | 0.0106 | 0.0323 | |||
| 0.0398 | 0.0117 | 0.0950 | 5.59 | 0.503 | 0.0480 | −0.0360 | |||
| 0.0631 | −0.0854 | 0.0843 | 5.71 | 0.427 | −0.0737 | −0.00225 | |||
| 0.100 | 0.0330 | 0.0966 | 6.01 | 0.372 | 0.0527 | 0.0293 | |||
| 0.158 | −0.00155 | 0.0225 | 6.11 | 0.232 | 0.00784 | −0.0468 | |||
| 0.251 | −0.0629 | 0.0941 | 6.15 | 0.238 | −0.0642 | 0.0236 | |||
| 0.398 | 0.0629 | 0.0993 | 6.36 | 0.175 | 0.0779 | 0.00726 | |||
| 0.631 | −0.0466 | 0.101 | 6.30 | 0.099 | −0.0364 | −0.0465 | |||
| 1.00 | −0.0269 | 0.248 | 6.37 | 0.149 | −0.0314 | 0.0348 | |||
| k | ||||
|---|---|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wiora, J.; Wiora, A. Influence of Methods Approximating Fractional-Order Differentiation on the Output Signal Illustrated by Three Variants of Oustaloup Filter. Symmetry 2020, 12, 1898. https://doi.org/10.3390/sym12111898
Wiora J, Wiora A. Influence of Methods Approximating Fractional-Order Differentiation on the Output Signal Illustrated by Three Variants of Oustaloup Filter. Symmetry. 2020; 12(11):1898. https://doi.org/10.3390/sym12111898
Chicago/Turabian StyleWiora, Józef, and Alicja Wiora. 2020. "Influence of Methods Approximating Fractional-Order Differentiation on the Output Signal Illustrated by Three Variants of Oustaloup Filter" Symmetry 12, no. 11: 1898. https://doi.org/10.3390/sym12111898
APA StyleWiora, J., & Wiora, A. (2020). Influence of Methods Approximating Fractional-Order Differentiation on the Output Signal Illustrated by Three Variants of Oustaloup Filter. Symmetry, 12(11), 1898. https://doi.org/10.3390/sym12111898





