Numerical Analysis of Turbulent Heat Transfer in the Case of Minijets Array
Abstract
1. Introduction
2. Mathematical Model
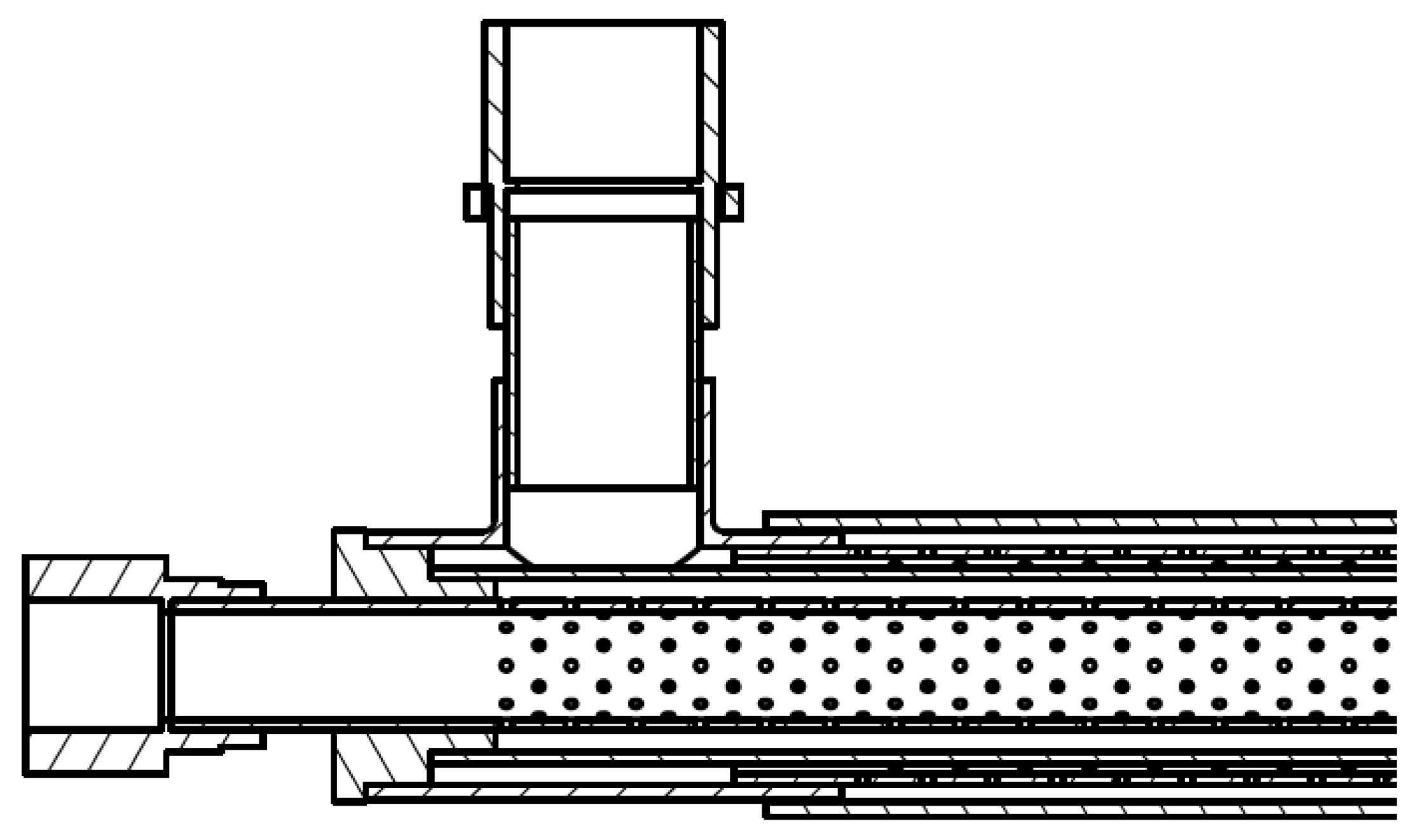
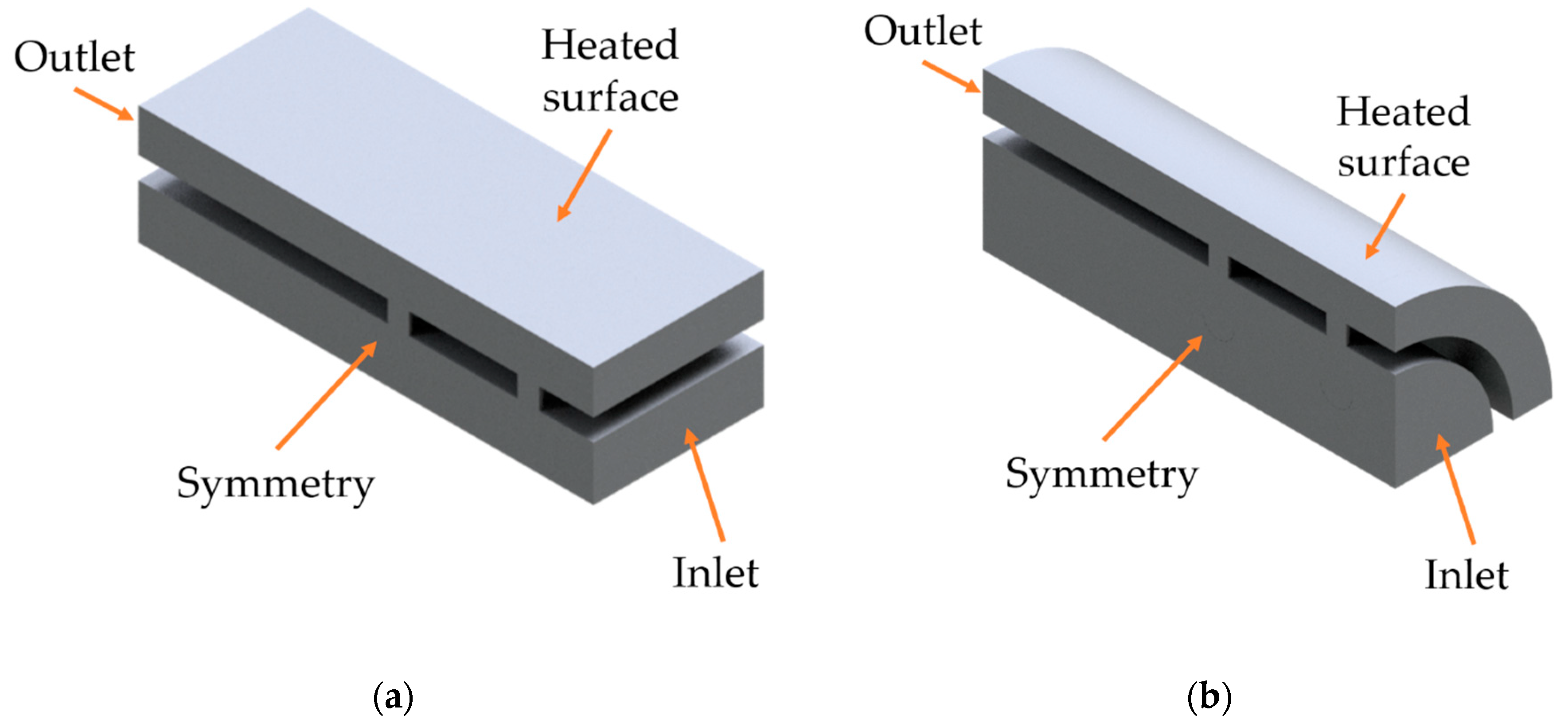
3. Jets Array
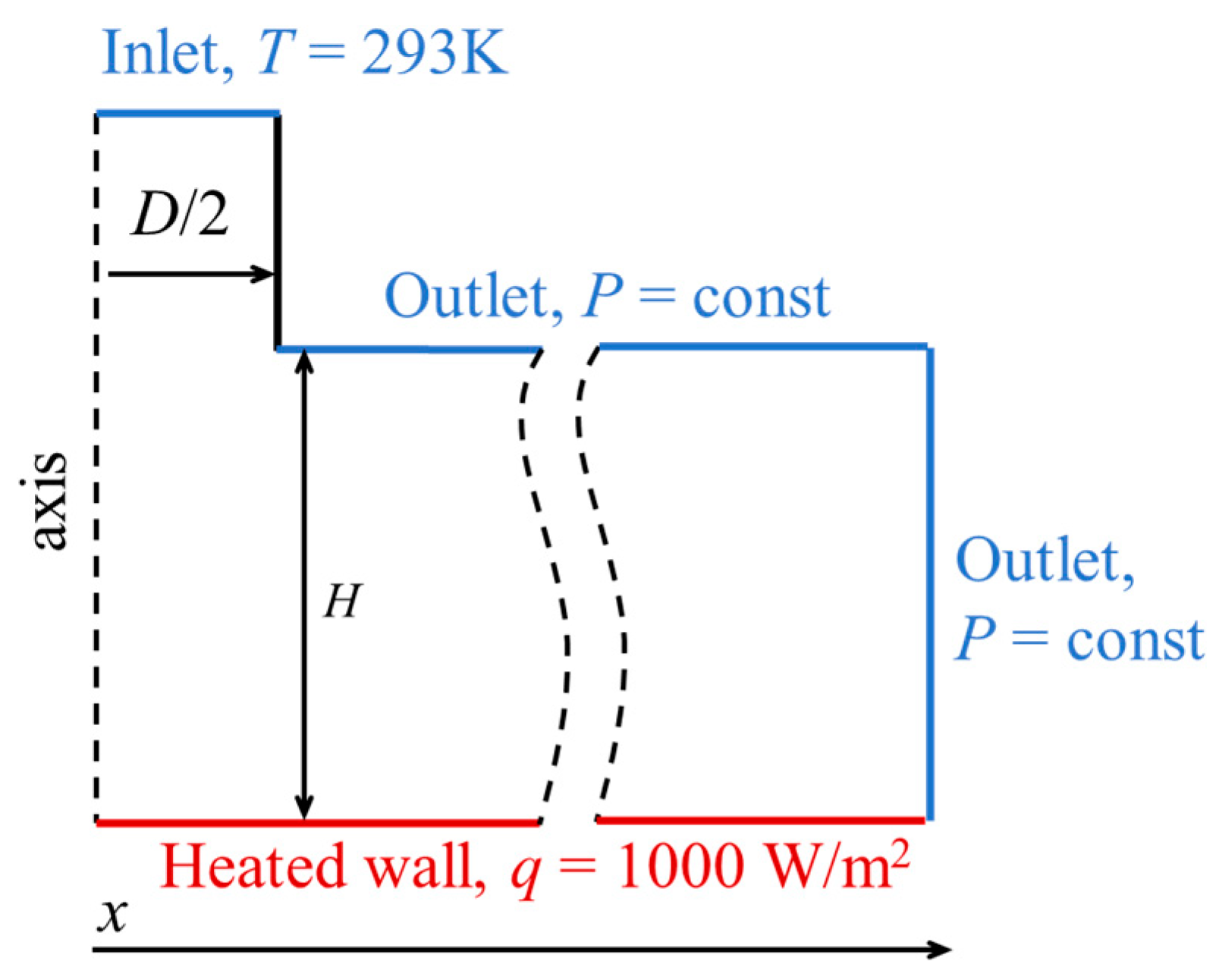
- incompressible flow
- constant material properties
- symmetry boundary condition
- all walls adiabatic except the heated surface
- fully developed inlet velocity profile with constant temperature
3.1. Mesh
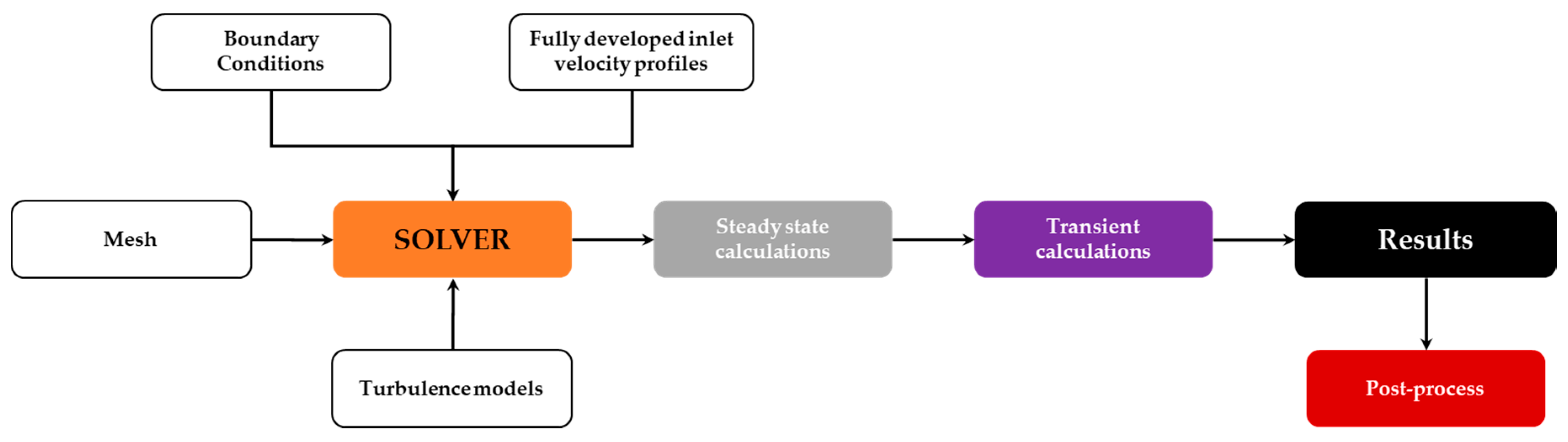
3.2. Numerical Procedure
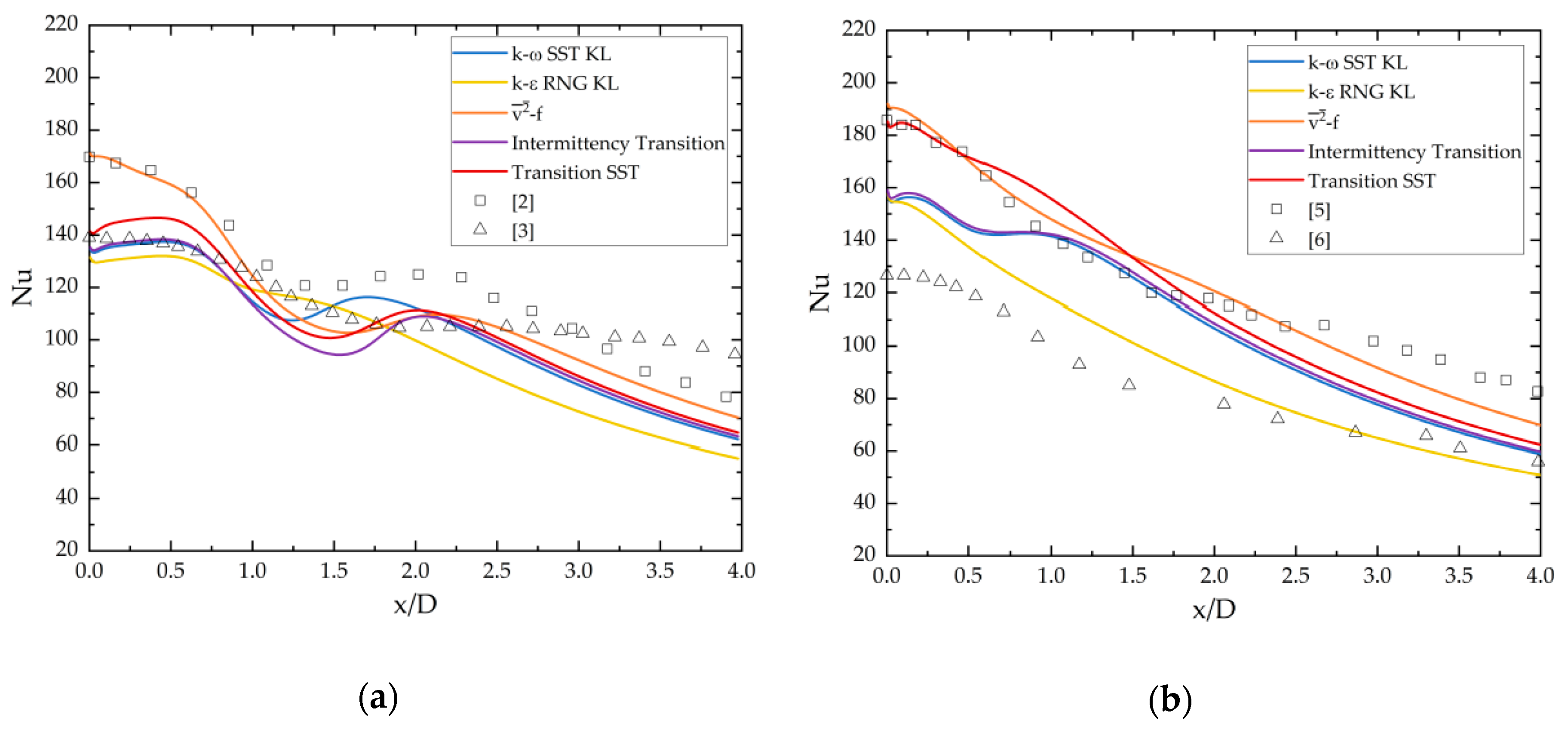
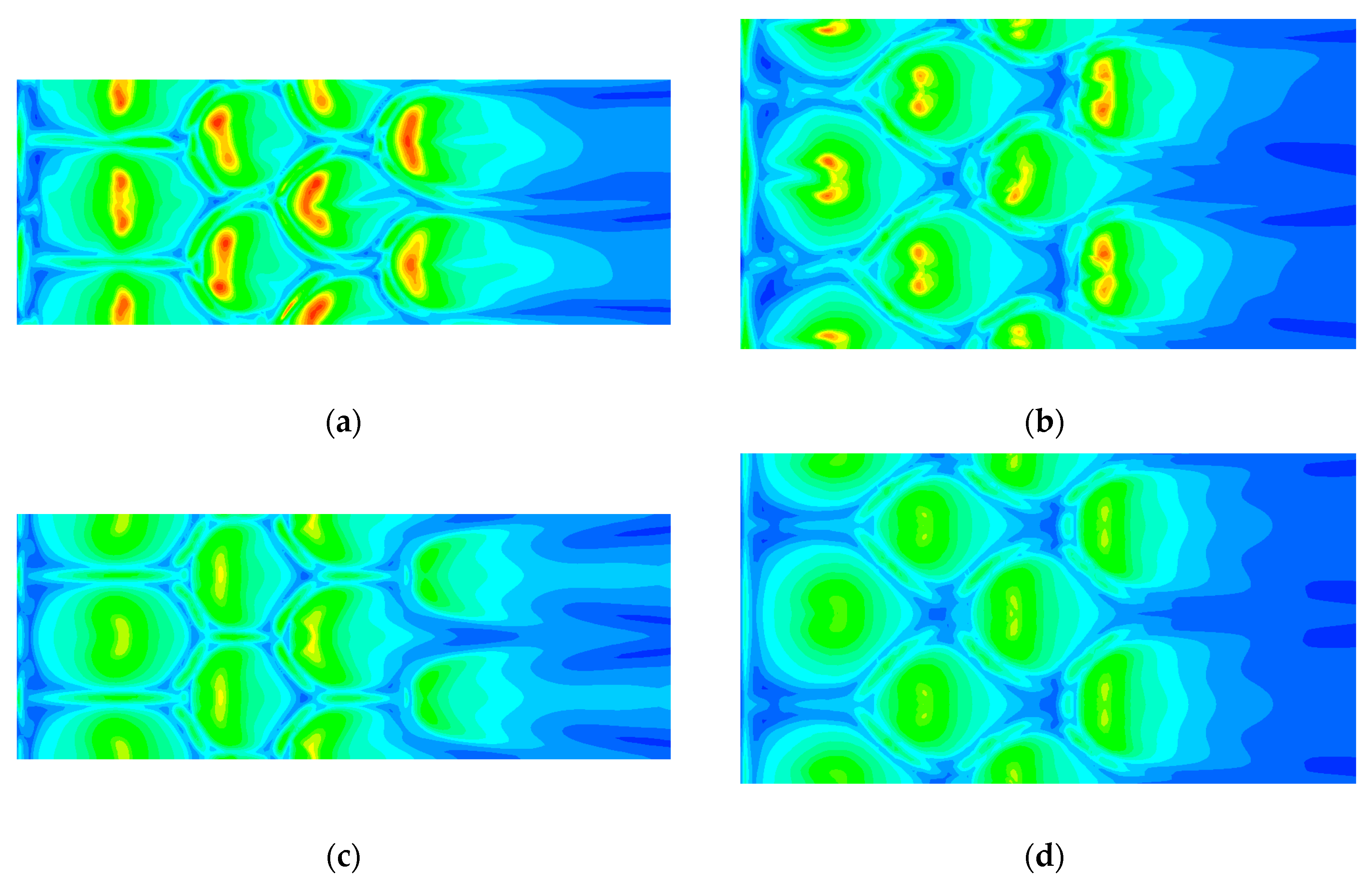
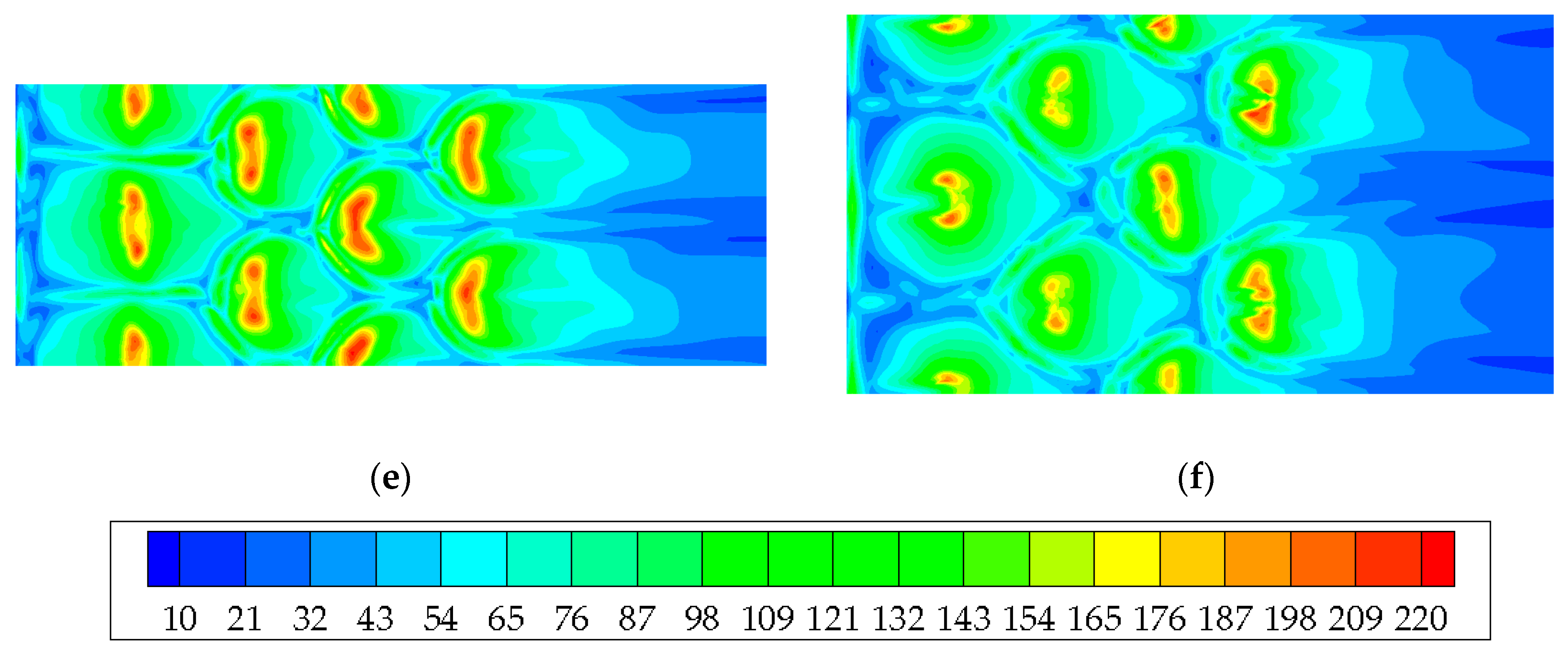
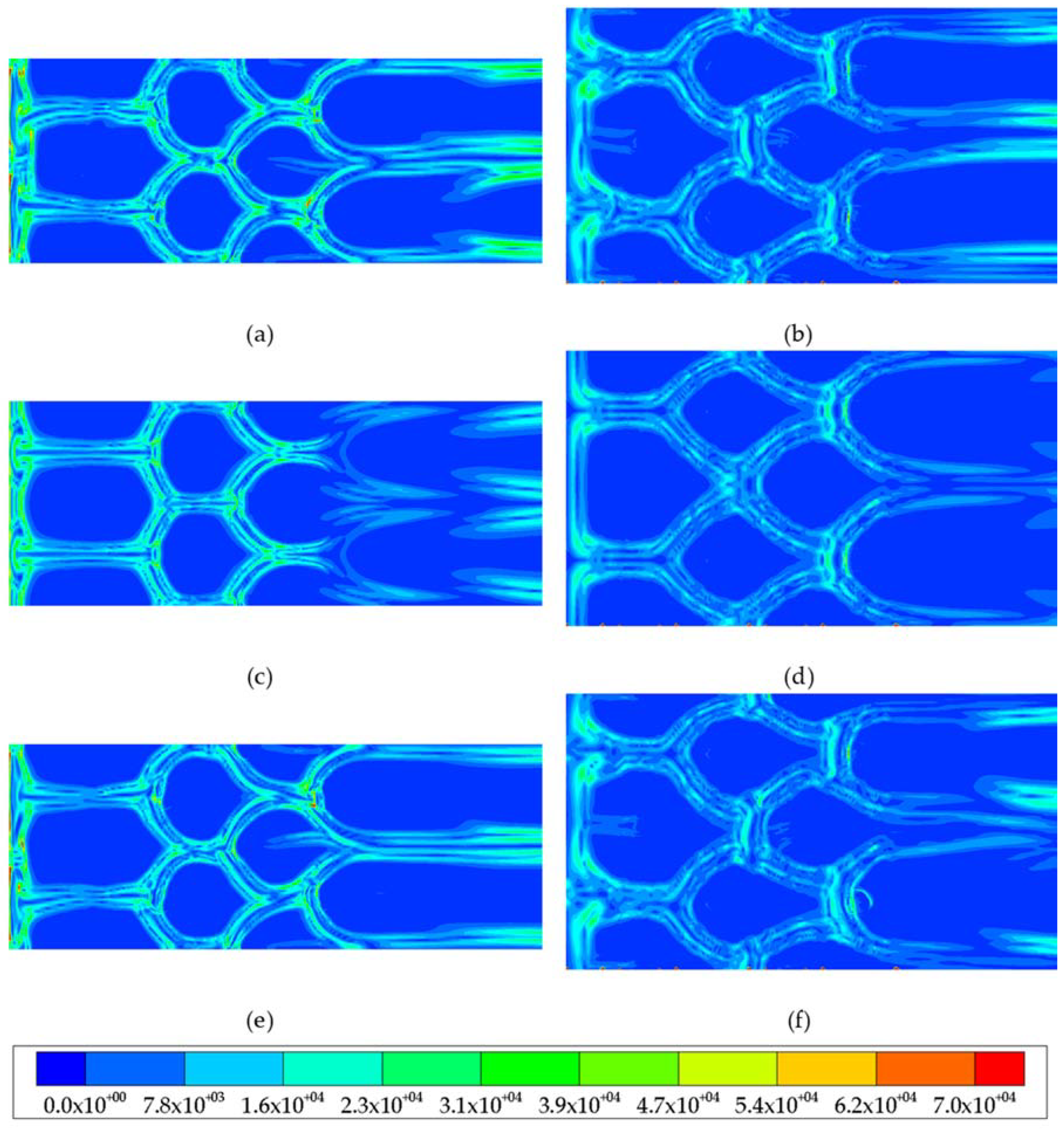
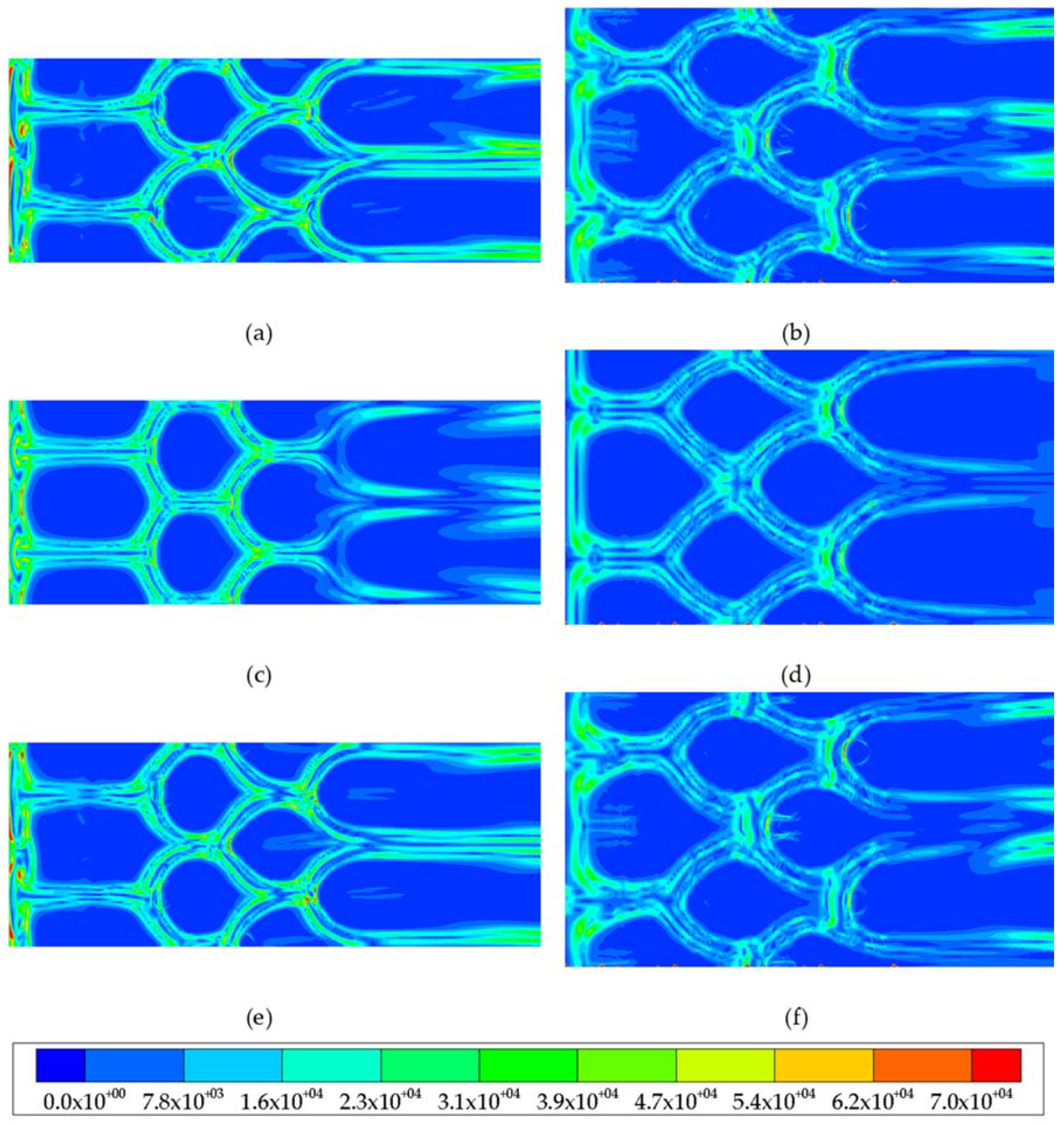
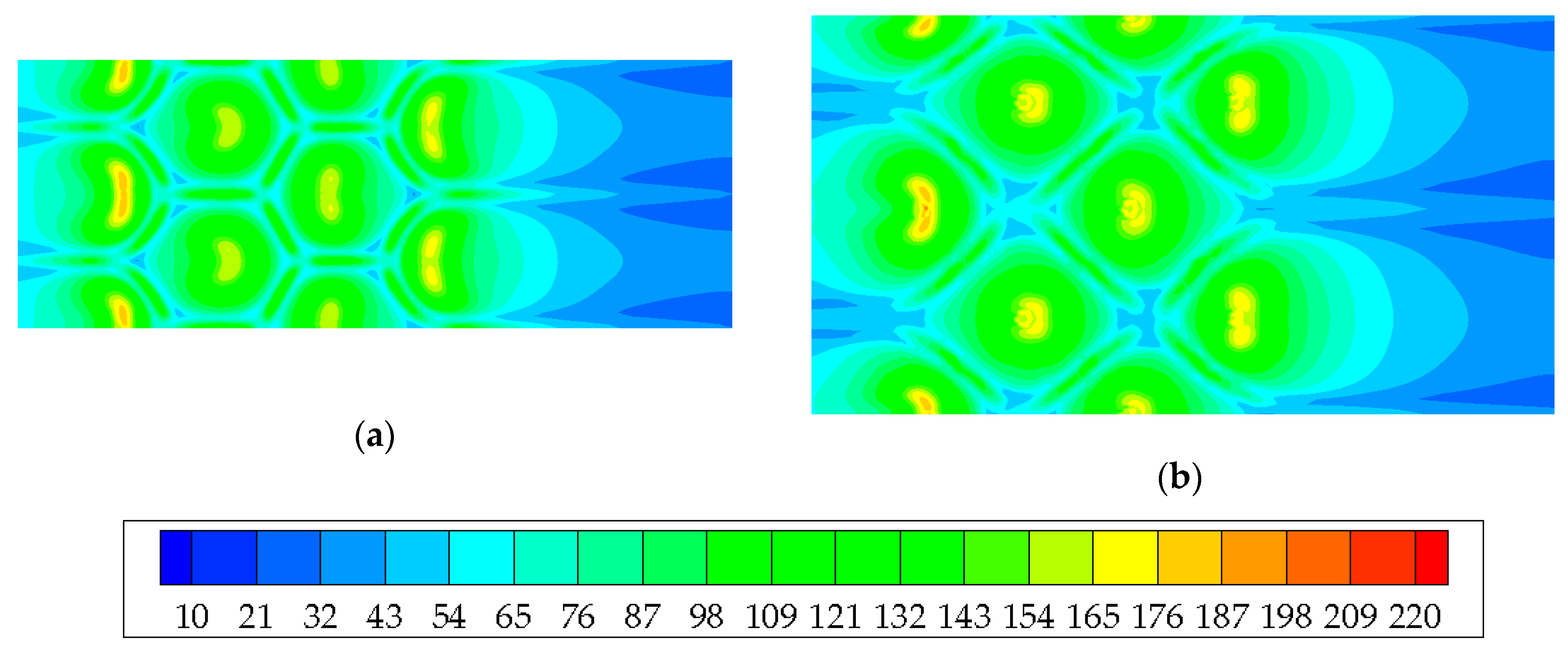
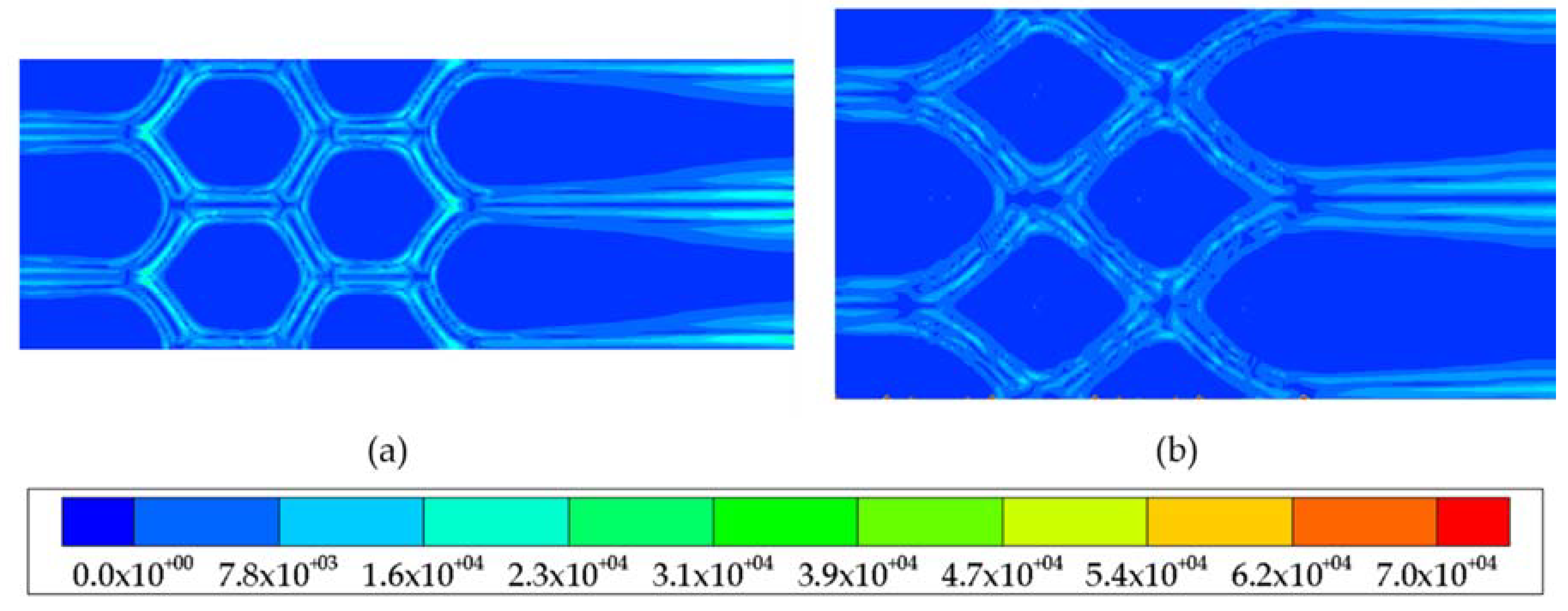
4. Results
5. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zuckerman, N.; Lior, N. Impingement heat transfer: Correlations and numerical modeling. J. Heat Transf. 2005, 127, 544–552. [Google Scholar] [CrossRef]
- Katti, V.; Prabhu, S.V. Experimental study and theoretical analysis of local heat transfer distribution between smooth flat surface and impinging air jet from a circular straight pipe nozzle. Int. J. Heat Mass Transf. 2008, 51, 4480–4495. [Google Scholar] [CrossRef]
- Gao, N.; Sun, H.; Ewing, D. Heat transfer to impinging round jets with triangular tabs. Int. J. Heat Mass Transf. 2003, 46, 2557–2569. [Google Scholar] [CrossRef]
- Lee, J.; Lee, S.J. Stagnation region heat transfer of a turbulent axisymmetric jet impingement. Exp. Heat Transf. 1999, 12, 137–156. [Google Scholar] [CrossRef]
- Lytle, D.; Webb, B.W. Air jet impingement heat transfer at low nozzle-plate spacings. Int. J. Heat Mass Transf. 1994, 37, 1687–1697. [Google Scholar] [CrossRef]
- Lee, D.H.; Song, J.; Jo, M.C. The effects of nozzle diameter on impinging jet heat transfer and fluid flow. J. Heat Transf. 2004, 126, 554–557. [Google Scholar] [CrossRef]
- Colucci, D.W.; Viskanta, R. Effect of nozzle geometry on local convective heat transfer to a confined impinging air jet. Exp. Therm. Fluid Sci. 1996, 13, 71–80. [Google Scholar] [CrossRef]
- Li, Z.X.; Khaled, U.; Al-Rashed, A.A.A.A.; Goodarzi, M.; Sarafraz, M.M.; Meer, R. Heat transfer evaluation of a micro heat exchanger cooling with spherical carbon-acetone nanofluid. Int. J. Heat Mass Transf. 2020, 149, 119124. [Google Scholar] [CrossRef]
- Wajs, J.; Mikielewicz, D.; Fornalik-Wajs, E. Cylindrical Jet Heat Exchanger Dedicated to Heat Recovery, Especially from Low Temperature Waste Sources. Patent PL224494, 8 July 2013. [Google Scholar]
- Wajs, J.; Mikielewicz, D.; Fornalik-Wajs, E.; Bajor, M. Recuperator with microjet technology as a proposal for heat recovery from low-temperature sources. Arch. Thermodyn. 2015, 36, 48–63. [Google Scholar] [CrossRef][Green Version]
- Tian, Z.; Abdollahi, A.; Shariati, M.; Amindoust, A.; Arasteh, H.; Karimipour, A.; Goodarzi, M.; Bach, Q.-V. Turbulent flows in a spiral double-pipe heat exchanger: Optimal performance conditions using an enhanced genetic algorithm. Int. J. Numer. Methods Heat Fluid Flow 2019, 30, 39–53. [Google Scholar] [CrossRef]
- Wajs, J.; Bochniak, R.; Golabek, A.; Kura, T. A new construction of shell-and-tube heat exchanger with impinging jets and minichannels technologies for heat recovery from gases—experimental analysis. In Proceedings of the 6th International Conference on Contemporary Problems of Thermal Engineering (CPOTE2020), Gliwice, Poland, 21–24 September 2020. [Google Scholar]
- Wajs, J.; Mikielewicz, D.; Fornalik-Wajs, E.; Bajor, M. High performance tubular heat exchanger with minijet heat transfer enhancement. Heat Transf. Eng. 2018, 40, 772–783. [Google Scholar] [CrossRef]
- Wajs, J.; Bajor, M.; Mikielewicz, D. Thermal-hydraulic studies on the shell-and-tube heat exchanger with minijets. Energies 2019, 12, 3276. [Google Scholar] [CrossRef]
- Kura, T.; Fornalik-Wajs, E.; Wajs, J.; Kenjeres, S. Local Nusselt number evaluation in the case of jet impingement. J. Phys. Conf. Ser. 2018, 1101, 012018. [Google Scholar] [CrossRef]
- Yang, B.; Chang, S.; Wu, H.; Zhao, Y.; Leng, M. Experimental and numerical investigation of heat transfer in an array of impingement jets on a concave surface. Appl. Therm. Eng. 2017, 127, 473–483. [Google Scholar] [CrossRef]
- Deng, Z.; Shen, J.; Dai, W.; Li, K.; Gong, W.; Dong, X.; Chen, G.; Gong, M. Numerical study on cooling of high-power laser diode arrays using slot jet array impingement. Appl. Therm. Eng. 2019, 160, 114061. [Google Scholar] [CrossRef]
- Sabato, M.; Fregni, A.; Stalio, E.; Brusiani, F.; Tranchero, M.; Baritaud, T. Numerical study of submerged impinging jets for power electronics cooling. Int. J. Heat Mass Transf. 2019, 141, 707–718. [Google Scholar] [CrossRef]
- Draksler, M.; Končar, B.; Cizelj, L. On the accuracy of Large Eddy Simulation of multiple impinging jets. Int. J. Heat Mass Transf. 2019, 133, 596–605. [Google Scholar] [CrossRef]
- Kura, T.; Fornalik-Wajs, E.; Wajs, J. Thermal and hydraulic phenomena in boundary layer of minijets impingement on curved surfaces. Arch. Thermodyn. 2018, 39, 147–166. [Google Scholar] [CrossRef]
- ANSYS Fluent Theory Guide. Available online: http://www.pmt.usp.br/academic/martoran/notasmodelosgrad/ANSYS%20Fluent%20Theory%20Guide%2015.pdf (accessed on 28 September 2020).
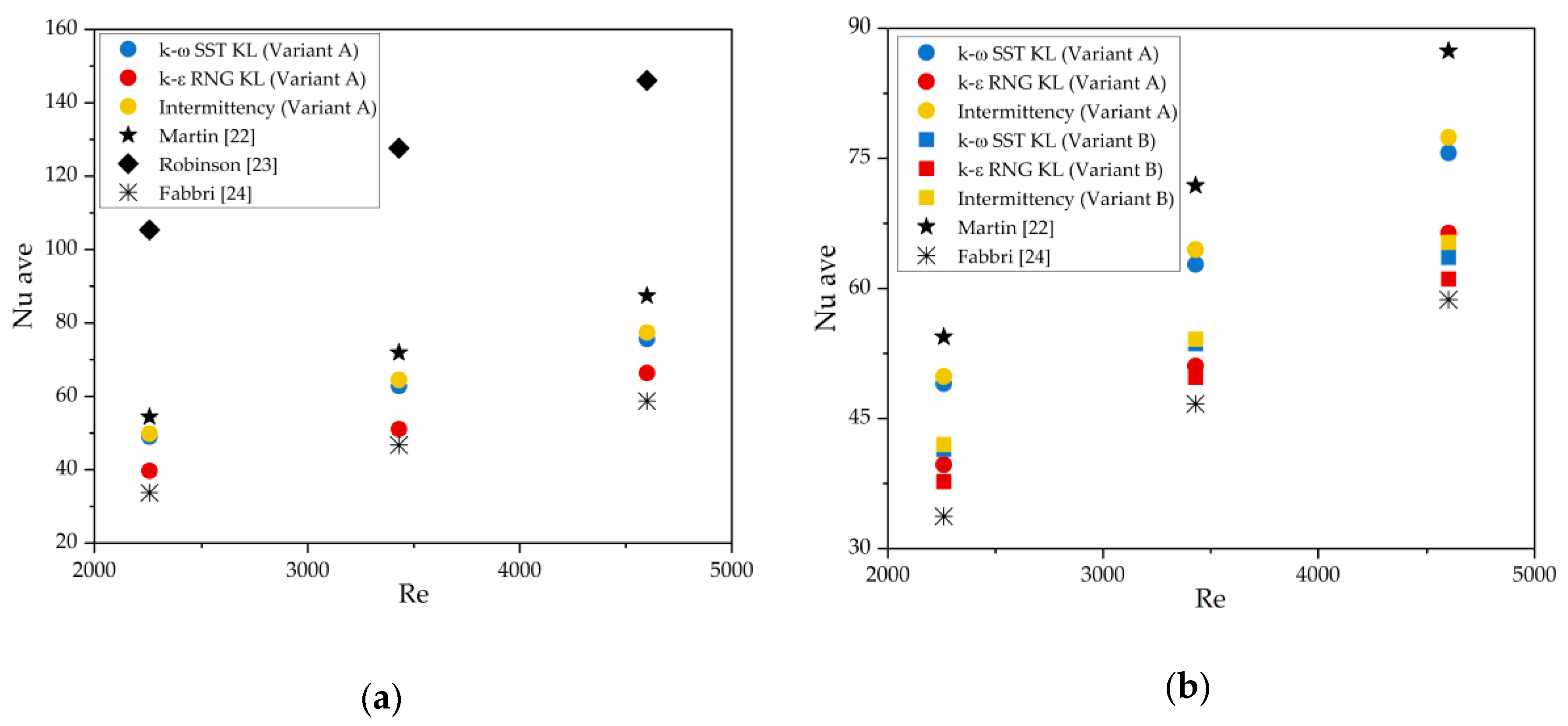
- Martin, H. Heat and mass transfer between impinging gas jets and solid surfaces. Adv. Heat Transf. 1977, 13, 1–60. [Google Scholar] [CrossRef]
- Robinson, A.J.; Schnitzler, E. An experimental investigation of free and submerged miniature liquid jet array impingement heat transfer. Exp. Therm. Fluid Sci. 2007, 32, 1–13. [Google Scholar] [CrossRef]
- Fabbri, M.; Dhir, V.K. Optimized heat transfer for high power electronic cooling using arrays of microjets. J. Heat Transf. 2005, 127, 760–769. [Google Scholar] [CrossRef]




| Inlet Volume Flow Rate, L/h | Inlet Water Temperature, K | Heat Flux at the Surface, W/m2 | Outlet | ||
|---|---|---|---|---|---|
| 50 | 75 | 100 | 293 | 150,000 | Constant pressure |
| Average Reynolds number in the orifice | |||||
| 2260 | 3430 | 4600 | |||
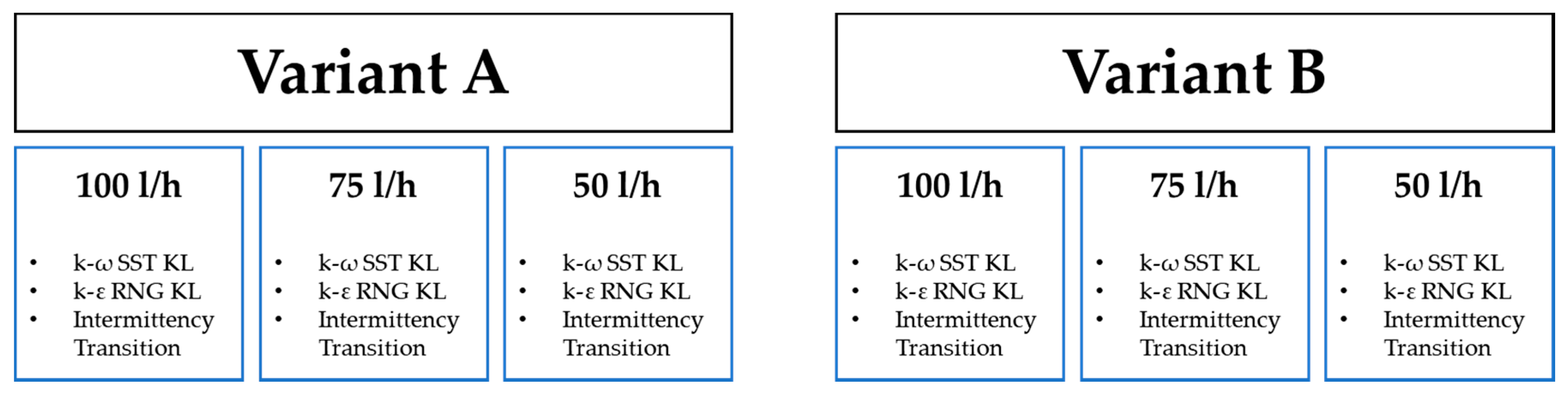
| Variant A | Variant B | |
|---|---|---|
| Number of elements | ~4.9 M | ~4.9 M |
| Average y+ on the heated surface (for 100 L/h case) | 0.34 | 0.32 |
| Maximum y+ on the heated surface (for 100 L/h case) | 0.84 | 1.12 |
| Mesh Version | Number of Elements | Average Nusselt Number |
|---|---|---|
| v1 | 2.7 M | 74.37 |
| v2 | 4.5 M | 75.35 |
| v3 | 4.9 M | 75.63 |
| v4 | 5.4 M | 76.11 |
| v5 | 6.4 M | 75.97 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gurgul, S.; Kura, T.; Fornalik-Wajs, E. Numerical Analysis of Turbulent Heat Transfer in the Case of Minijets Array. Symmetry 2020, 12, 1785. https://doi.org/10.3390/sym12111785
Gurgul S, Kura T, Fornalik-Wajs E. Numerical Analysis of Turbulent Heat Transfer in the Case of Minijets Array. Symmetry. 2020; 12(11):1785. https://doi.org/10.3390/sym12111785
Chicago/Turabian StyleGurgul, Sebastian, Tomasz Kura, and Elzbieta Fornalik-Wajs. 2020. "Numerical Analysis of Turbulent Heat Transfer in the Case of Minijets Array" Symmetry 12, no. 11: 1785. https://doi.org/10.3390/sym12111785
APA StyleGurgul, S., Kura, T., & Fornalik-Wajs, E. (2020). Numerical Analysis of Turbulent Heat Transfer in the Case of Minijets Array. Symmetry, 12(11), 1785. https://doi.org/10.3390/sym12111785





