A Novel Numerical Algorithm to Estimate the Subdivision Depth of Binary Subdivision Schemes
Abstract
1. Introduction
2. Preliminaries Results
2.1. Univariate Case
2.2. Bivariate Case
3. Subdivision Depth for Binary Subdivision Curves
Application for Univariate Case
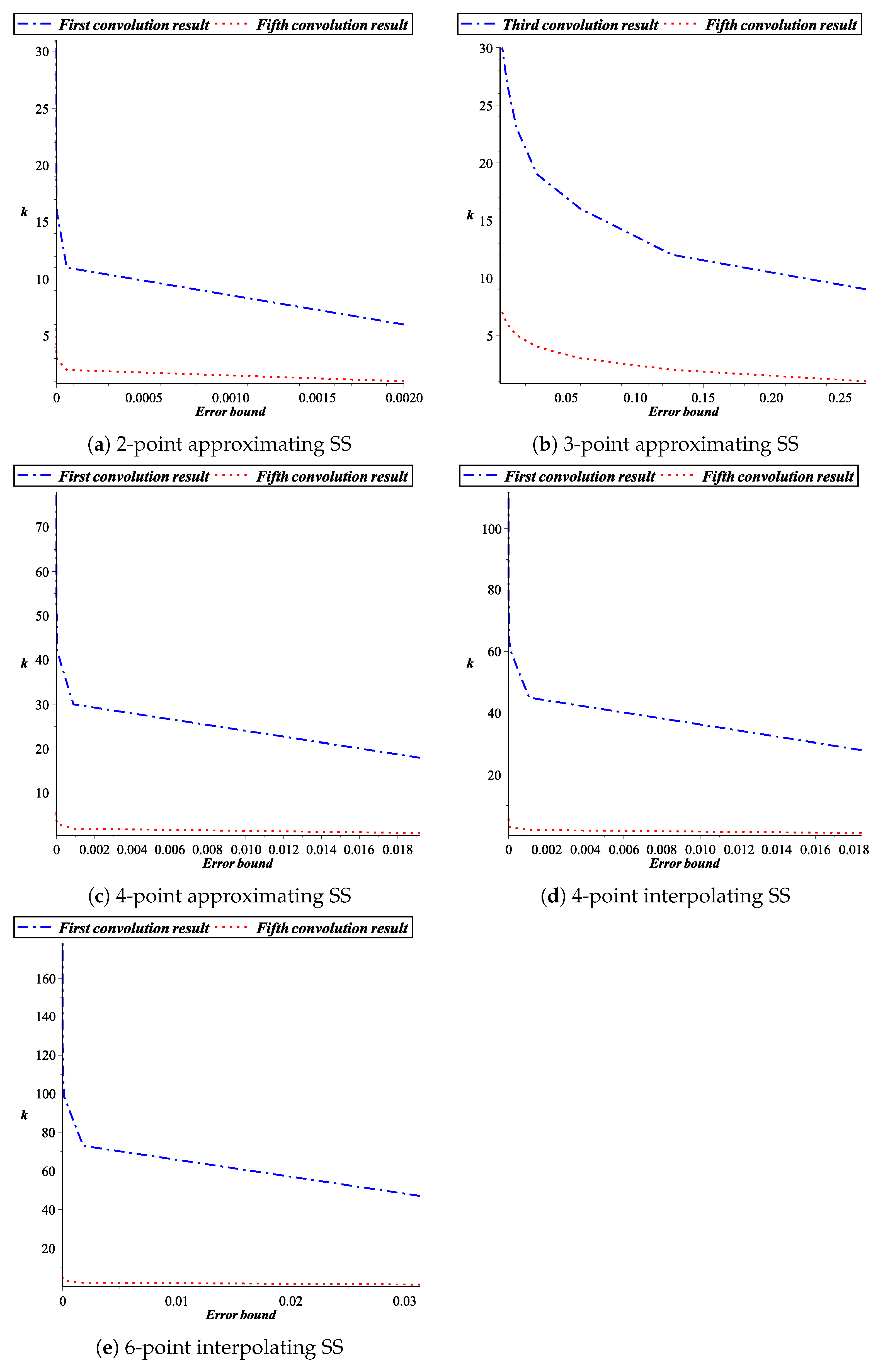
4. Subdivision Depth for Binary Subdivision Surfaces
Application for Bivariate Case
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Barnhill, R.E.; Riesenfeld, R.F. Computer Aided Geometric Design; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Faux, I.; Pratt, M. Computational Geometry for Design and Manufacture; Ellis Horwood: New York, NY, USA, 1979. [Google Scholar]
- Huawei, W.; Youjiang, G.; Kaihuai, Q. Error estimation for Doo-Sabin surfaces. Prog. Nat. Sci. 2002, 12, 697–700. [Google Scholar]
- Mustafa, G.; Chen, F.; Deng, J. Estimating error bounds for binary subdivision curves/surfaces. J. Comput. Appl. Math. 2006, 193, 596–613. [Google Scholar] [CrossRef][Green Version]
- Mustafa, G.; Hashmi, S.; Faheem, K. Estimating error bounds for non-stationary binary subdivision curves/surfaces. J. Inf. Comput. Sci. 2007, 2, 179–190. [Google Scholar]
- Mustafa, G.; Deng, J. Estimating error bounds for ternary subdivision curve/surfaces. J. Comput. Math. 2007, 25, 473–484. [Google Scholar]
- Mustafa, G.; Hashmi, S. Estimating error bounds for quaternary subdivision schemes. J. Math. Anal. Appl. 2009, 358, 159–167. [Google Scholar]
- Mustafa, G.; Hashmi, S.; Noshi, N.A. Estimating error bounds for tensor product binary subdivision volumetric model. Int. J. Comput. Math. 2006, 83, 879–903. [Google Scholar] [CrossRef]
- Mustafa, G.; Hashmi, S.; Faheem, K. Error bounds for subdivision surfaces. J. Univ. Sci. Technol. China 2009, 39, 1–9. [Google Scholar]
- Mustafa, G.; Hashmi, S.; Faheem, K. Subdivision depth for triangular surfaces. Alex. Eng. J. 2016, 55, 1647–1653. [Google Scholar] [CrossRef]
- Mustafa, G.; Hashmi, S. Subdivision depth computation for n-ary subdivision curves/surfaces. J. Vis. Comput. 2010, 26, 841–851. [Google Scholar] [CrossRef]
- Moncayo, M.; Amat, S. Error bounds for a class of subdivision schemes based on the two-scale refinement equation. J. Comput. Appl. Math. 2011, 236, 265–278. [Google Scholar] [CrossRef][Green Version]
- Dyn, N.; Gregory, A.; Levin, D. Analysis of uniform binary subdivision scheme for curve design. Constr. Approx. 1991, 7, 127–147. [Google Scholar] [CrossRef]
- Chaikin, G.M. An algorithm for high speed curve generation. Comput. Graph. Image Process. 1974, 3, 346–349. [Google Scholar] [CrossRef]
- Dyn, N.; Levin, D.; Micchelli, C.A. Using parameters to increase smoothness of curves and surfaces generated by subdivision. Comput. Aided Geom. Des. 1990, 7, 129–140. [Google Scholar] [CrossRef]
- Dyn, N.; Floater, M.S.; Hormann, K. A four-point subdivision scheme with fourth order accuracy and its extensions. In Mathematical Methods for Curves and Surfaces: Modern Methods in Mathematics; Springer: Troms, Norway, 2004; pp. 145–156. [Google Scholar]
- Dyn, N.; Levin, D.; Gregory, J.A. A 4-Point Interpolatory SS for Curve Design. Comput. Aided Geom. Des. Acad. Press. 1987, 4, 257–268. [Google Scholar] [CrossRef]
- Weissman, A. A 6-Point Interpolatory Subdivision Scheme for Curve Design. Master’s Thesis, Tel Aviv University, Tel Aviv-Yafo, Israel, 1990. [Google Scholar]
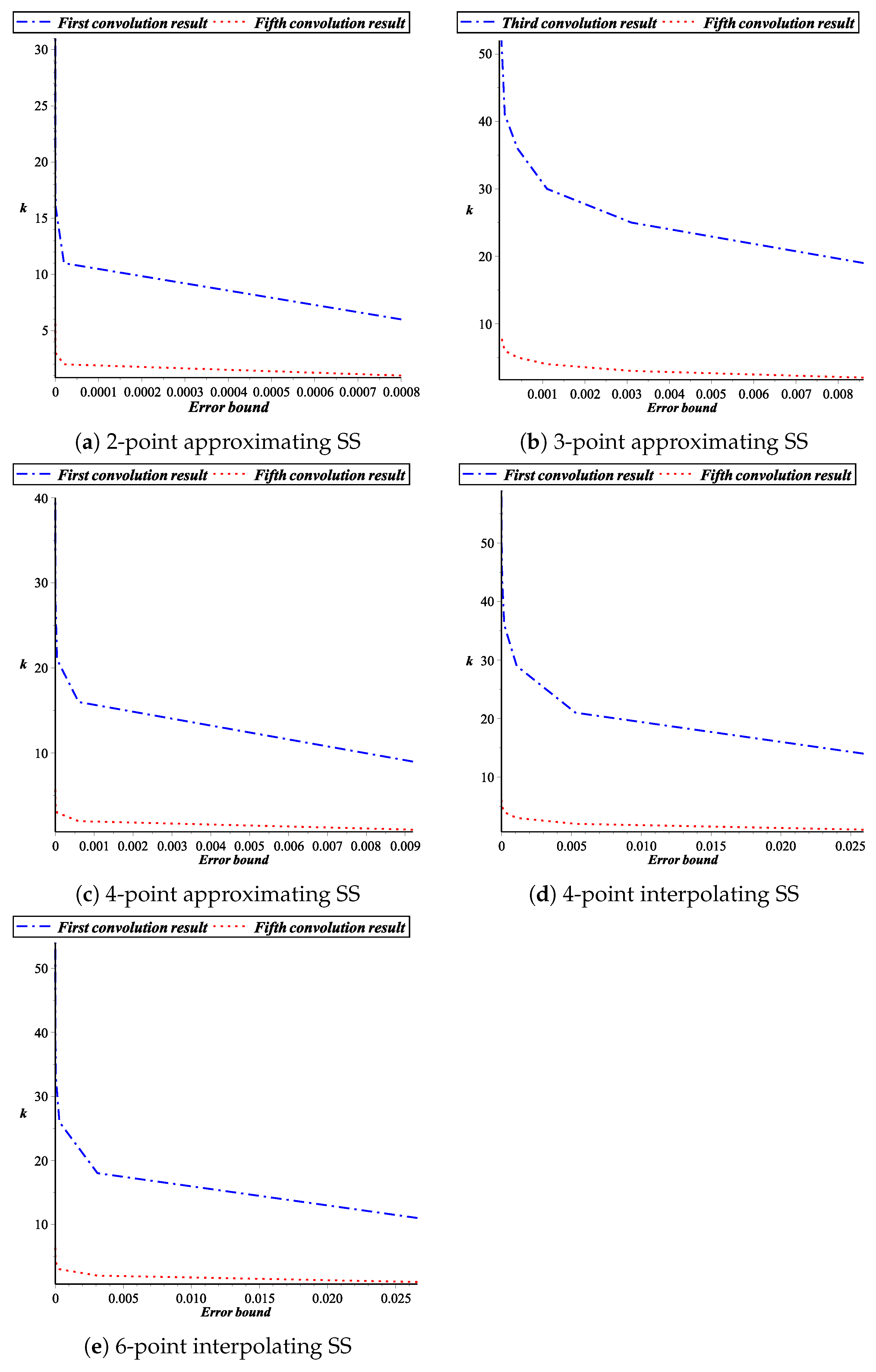
| Scheme/ | |||||
|---|---|---|---|---|---|
| 2-point scheme [14] | 0.50000 | 0.25000 | 0.12500 | 0.06250 | 0.03125 |
| 3-point scheme [15] | 1.50000 | 1.03125 | 0.83203 | 0.52685 | 0.36584 |
| 4-point scheme [16] | 0.65625 | 0.36829 | 0.21610 | 0.12153 | 0.06912 |
| 4-point scheme [17] | 0.80800 | 0.55800 | 0.40343 | 0.28765 | 0.20595 |
| 6-point scheme [18] | 0.74200 | 0.44218 | 0.28589 | 0.18321 | 0.11768 |
| / | 0.0008 | 0.00002 | ||||
|---|---|---|---|---|---|---|
| 6 | 11 | 16 | 21 | 26 | 31 | |
| 3 | 5 | 8 | 10 | 13 | 15 | |
| 1 | 3 | 5 | 7 | 8 | 10 | |
| 1 | 3 | 4 | 5 | 6 | 8 | |
| 1 | 2 | 3 | 4 | 5 | 6 |
| / | 0.0086 | 0.0031 | 0.0011 | 0.0004 | 0.0001 | ||
|---|---|---|---|---|---|---|---|
| 19 | 25 | 30 | 36 | 41 | 47 | 52 | |
| 4 | 5 | 7 | 9 | 10 | 12 | 13 | |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| / | 0.0092 | 0.0006 | ||||
|---|---|---|---|---|---|---|
| 9 | 16 | 21 | 28 | 34 | 40 | |
| 3 | 6 | 8 | 11 | 14 | 16 | |
| 2 | 4 | 5 | 7 | 9 | 11 | |
| 1 | 3 | 4 | 5 | 6 | 8 | |
| 1 | 2 | 3 | 4 | 5 | 6 |
| / | 0.0259 | 0.0053 | 0.00109 | 0.0002 | |||
|---|---|---|---|---|---|---|---|
| 14 | 21 | 29 | 36 | 44 | 51 | 59 | |
| 4 | 6 | 9 | 12 | 15 | 17 | 20 | |
| 2 | 4 | 6 | 7 | 9 | 11 | 12 | |
| 1 | 3 | 4 | 5 | 6 | 8 | 9 | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| / | 0.0266 | 0.0031 | 0.0003 | ||||
|---|---|---|---|---|---|---|---|
| 11 | 18 | 26 | 33 | 40 | 47 | 54 | |
| 3 | 6 | 8 | 11 | 14 | 16 | 19 | |
| 2 | 4 | 5 | 7 | 9 | 10 | 12 | |
| 1 | 3 | 4 | 5 | 6 | 8 | 9 | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Scheme/ | |||||
|---|---|---|---|---|---|
| 2-point scheme [14] | 0.50000 | 0.25000 | 0.12500 | 0.06250 | 0.03125 |
| 3-point scheme [15] | 1.50000 | 1.00000 | 0.81250 | 0.60937 | 0.47265 |
| 4-point scheme [16] | 0.77930 | 0.40902 | 0.20020 | 0.09959 | 0.04953 |
| 4-point scheme [17] | 0.84500 | 0.43741 | 0.22635 | 0.11557 | 0.05801 |
| 6-point scheme [18] | 0.89780 | 0.45218 | 0.23205 | 0.11764 | 0.05902 |
| / | 0.0020 | 0.00006 | ||||
|---|---|---|---|---|---|---|
| 6 | 11 | 16 | 21 | 26 | 31 | |
| 3 | 5 | 8 | 10 | 13 | 15 | |
| 2 | 3 | 5 | 7 | 8 | 10 | |
| 1 | 3 | 4 | 5 | 6 | 8 | |
| 1 | 2 | 3 | 4 | 5 | 6 |
| / | 0.2688 | 0.1270 | 0.06007 | 0.0283 | 0.0134 | 0.0063 | 0.0029 |
|---|---|---|---|---|---|---|---|
| 9 | 12 | 16 | 19 | 23 | 27 | 30 | |
| 2 | 4 | 5 | 7 | 8 | 10 | 11 | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| / | 0.0192 | 0.0009 | ||||
|---|---|---|---|---|---|---|
| 18 | 30 | 42 | 54 | 66 | 78 | |
| 4 | 7 | 10 | 14 | 17 | 21 | |
| 2 | 4 | 6 | 8 | 9 | 11 | |
| 1 | 3 | 4 | 5 | 7 | 8 | |
| 1 | 2 | 3 | 4 | 5 | 6 |
| / | 0.0184 | 0.00107 | ||||
|---|---|---|---|---|---|---|
| 28 | 45 | 61 | 78 | 95 | 112 | |
| 4 | 7 | 11 | 14 | 18 | 21 | |
| 2 | 4 | 6 | 8 | 10 | 12 | |
| 1 | 3 | 4 | 5 | 7 | 8 | |
| 1 | 2 | 3 | 4 | 5 | 6 |
| / | 0.0313 | 0.0018 | 0.0001 | |||
|---|---|---|---|---|---|---|
| 47 | 73 | 99 | 126 | 152 | 178 | |
| 4 | 8 | 11 | 15 | 18 | 22 | |
| 2 | 4 | 6 | 8 | 10 | 12 | |
| 1 | 3 | 4 | 5 | 7 | 8 | |
| 1 | 2 | 3 | 4 | 5 | 6 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shahzad, A.; Khan, F.; Ghaffar, A.; Mustafa, G.; Nisar, K.S.; Baleanu, D. A Novel Numerical Algorithm to Estimate the Subdivision Depth of Binary Subdivision Schemes. Symmetry 2020, 12, 66. https://doi.org/10.3390/sym12010066
Shahzad A, Khan F, Ghaffar A, Mustafa G, Nisar KS, Baleanu D. A Novel Numerical Algorithm to Estimate the Subdivision Depth of Binary Subdivision Schemes. Symmetry. 2020; 12(1):66. https://doi.org/10.3390/sym12010066
Chicago/Turabian StyleShahzad, Aamir, Faheem Khan, Abdul Ghaffar, Ghulam Mustafa, Kottakkaran Sooppy Nisar, and Dumitru Baleanu. 2020. "A Novel Numerical Algorithm to Estimate the Subdivision Depth of Binary Subdivision Schemes" Symmetry 12, no. 1: 66. https://doi.org/10.3390/sym12010066
APA StyleShahzad, A., Khan, F., Ghaffar, A., Mustafa, G., Nisar, K. S., & Baleanu, D. (2020). A Novel Numerical Algorithm to Estimate the Subdivision Depth of Binary Subdivision Schemes. Symmetry, 12(1), 66. https://doi.org/10.3390/sym12010066








