Abstract
The aim of the present analysis is to provide local similarity solutions of Casson fluid over a non-isothermal cylinder subject to suction/blowing. The cylinder is placed inside a porous medium and stretched in a nonlinear way. Further, the impact of chemical reaction, viscous dissipation, and heat generation/absorption on flow fields is also investigated. Similarity transformations are employed to convert the nonlinear governing equations to nonlinear ordinary differential equations, and then solved via the Keller box method. Findings demonstrate that the magnitude of the friction factor and mass transfer rate are suppressed with increment in Casson parameter, whereas heat transfer rate is found to be intensified. Increase in the curvature parameter enhanced the flow field distributions. The magnitude of wall shear stress is noticed to be higher with an increase in porosity and suction/blowing parameters.
1. Introduction
Boundary layer flow on linear or nonlinear stretching surfaces has a wide range of engineering and industrial applications, and has been used in many manufacturing processes, such as extrusion of plastic sheets, glass fiber production, crystal growing, hot rolling, wire drawing, metal and polymer extrusion, and metal spinning. The viscous flow past a stretching surface was first developed by Crane [1]. Later on, this pioneering work was extended by Gupta and Gupta [2] and Chen and Char [3], and the suction/blowing effects on heat transfer flow over a stretching surface were investigated. Gorla and Sidawi [4] analyzed three-dimensional free convection flow over permeable stretching surfaces. Motivated by this, the two-dimensional heat transfer flow of viscous fluid due to a nonlinear stretching sheet was investigated by Vajravelu [5]. The similarity solutions for viscous flow over a nonlinear stretching sheet was obtained by Vajravelu and Cannon [6]. On the other hand, Bachok and Ishak [7] studied the prescribed surface heat flux characteristics on boundary layer flow generated by a stretching cylinder. Hayat et al. [8] analyzed the heat and mass transfer features on two-dimensional flow due to a stretching cylinder placed through a porous media in the presence of convective boundary conditions. The heat transfer analysis in ferromagnetic viscoelastic fluid flow over a stretching sheet was discussed by Majeed et al. [9].
The study of magnetohydrodynamic (MHD) boundary layer flow towards stretching surface has gained considerable attention due to its important practical and engineering applications, such as MHD power generators, cooling or drying of papers, geothermal energy extraction, solar power technology, cooling of nuclear reactors, and boundary layer flow control in aerodynamics. Vyas and Ranjan [10] investigated two-dimensional flow over a nonlinear stretching sheet in the presence of thermal radiation and viscous dissipation. They predicted that stronger radiation boosts the fluid temperature field. The effect of magnetic field on incompressible viscous flow generated due to stretching cylinder was analyzed by Mukhopadhyay [11], and it was observed that a larger curvature parameter allowed more fluid to flow. Fathizadeh et al. [12] studied the MHD effect on viscous fluid due to a sheet stretched in a nonlinear way. Akbar et al. [13] developed laminar boundary layer flow induced by a stretching surface in the presence of a magnetic field. They noticed that the intensity of the magnetic field offered resistance to the fluid flow, because of which, skin friction was enhanced. In another study, Ellahi [14] demonstrated the effects of magnetic field on non-Newtonian nanofluid through a pipe.
The momentum slip at a stretching surface plays an important role in the manufacturing processes of several products, including emulsion, foams, suspensions, and polymer solutions. In recent years, researchers have avoided no-slip conditions and take velocity slip at the wall. The reason is that it has been proven through experiments that momentum slip at the boundary can enhance the heat transfer. Fang et al. [15] obtained the exact solution for two-dimensional slip flow due to stretching surface. The slip effects on stagnation point flow past a stretching sheet were numerically analyzed by Bhattacharyya et al. [16]. The slip effect on viscous flow generated due to a nonlinear stretching surface in the presence of first order chemical reaction and magnetic field was developed by Yazdi et al. [17]. They concluded that velocity slip at the wall reduced the friction factor. Hayat et al. [18] investigated the impact of hydrodynamic slip on incompressible viscous flow over a porous stretching surface under the influence of a magnetic field and thermal radiation. They predicted that suction and slip parameters have the same effect on fluid velocity. Seini and Makinde [19] analyzed the hydromagnetic boundary layer flow of a viscous fluid under the influence of velocity slip at the wall. They noticed that wall shear stress enhanced with the growth of the magnetic parameter. Motivated by this, Rahman et al. [20] discussed the slip mechanisms in boundary layer flow of Jeffery nanofluid through an artery, and the solutions were achieved by the homotopy perturbation method.
In the recent years, the analysis of non-Newtonian fluid past stretching surfaces has gained the attention of investigators due to its wide range practical applications in several industries, for instance, food processes, ground water pollution, crude oil extraction, production of plastic materials, cooling of nuclear reactors, manufacturing of electronic chips, etc. Due to the complex nature of these fluids, different models have been proposed. Among other non-Newtonian model, the Casson fluid model is one of them. The Casson fluid model was originally developed by Casson [21] for the preparation of printing inks and silicon suspensions. Casson fluid has important applications in polymer industries and biomechanics [22]. The Casson fluid model is also suggested as the best rheological model for blood and chocolate [23,24]. For this reason, many authors have considered Casson fluid for different geometries. Shawky [25] analyzed the heat and mass transfer mechanisms in MHD flow of Casson fluid over a linear stretching sheet saturated in a porous medium. Mukhopadhyay [26] and Medikare et al. [27] investigated heat transfer effects on Casson fluid over a nonlinear stretching sheet in the absence and presence of viscous dissipation, respectively. Mythili and Sivaraj [28] considered the geometry of cone and flat plate and studied the impact of chemical reaction on Casson fluid flow with thermal radiation. The impact of magnetic field and heat generation/absorption on heat transfer flow of Casson fluid through a porous medium was presented by Ullah et al. [29]. Imtiaz et al. [30] developed the mixed convection flow of Casson fluid due to a linear stretching cylinder filled with nanofluid with convective boundary conditions.
The above discussion and its engineering applications is the source of motivation to investigate the electrically conductive flow of Casson fluid due to a porous cylinder being stretched in a nonlinear way. It is also clear from the published articles that the mixed convection slip flow of Casson fluid for the geometry of a nonlinear stretching cylinder saturated in a porous medium in the presence of thermal radiation, viscous dissipation, joule heating, and heat generation/absorption has not yet been analyzed. It is worth mentioning that the current problem can be reduced to the flow over a flat plate ( and ), linear stretching sheet ( and ), nonlinear stretching sheet (), and linear stretching cylinder (). Local similarity transformations are applied to transform the governing equations. The obtained system of equations are then computed numerically using the Keller box method [31] via MATLAB. The variations of flow fields for various pertinent parameters are discussed and displayed graphically. Comparison of the friction factor is made with previous literature results and close agreement is noted. The accuracy achieved has developed our confidence that the present MATLAB code is correct and numerical results are accurate.
2. Mathematical Formulation
Consider a steady, two-dimensional, incompressible mixed convection slip flow of Casson fluid generated due to a nonlinear stretching cylinder in a porous medium in the presence of chemical reaction, slip, and convective boundary conditions. The cylinder is stretched with the velocity of , where , ( represents linear stretching and corresponds to nonlinear stretching) are constants. The x-axis is taken along the axis of the cylinder and the r-axis is measured in the radial direction (see Figure 1). It is worth mentioning here that the momentum boundary layer develops when there is fluid flow over a surface; a thermal boundary layer must develop if the bulk temperature differs from the surface temperature and a concentration boundary layer develops above the surfaces of species in the flow regime.
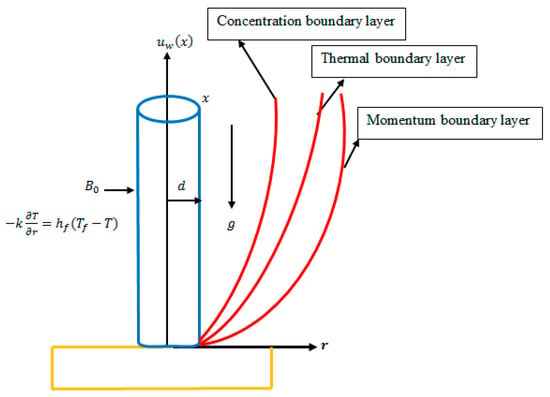
Figure 1.
Coordinate system and physical model.
A transverse magnetic field is applied in the radial direction with constant . Further, it is also assumed that surface of cylinder is heated by temperature , in which is a reference temperature. Concentration is , where is the reference concentration. The temperature and concentration at free stream are and , respectively.
The rheological equation of state for an isotropic and incompressible flow of a Casson fluid is
Here, and is the component of the deformation rate, is the product of the component of deformation rate with itself, is a critical value of this product based on the non-Newtonian model, is the plastic dynamic viscosity of the non-Newtonian fluid, and is the yield stress of the fluid.
Under the above assumption, the governing equations for Casson fluid along with the continuity equation are given as
In the above expressions and denote the velocity components in and direction, respectively, is kinematic viscosity, is the electrically conductivity, is the Casson parameter, is the fluid density, is the porosity, is the variable permeability of porous medium, is the gravitational force due to acceleration, is the volumetric coefficient of thermal expansion, the coefficient of concentration expansion, is the thermal diffusivity of the Casson fluid, is the thermal conductivity of fluid, is the heat capacity of the fluid, is the radiation parameter, is heat generation/absorption coefficient, is the coefficient of mass diffusivity, is the variable rate of chemical reaction, is a constant reaction rate and is the reference length along the flow.
The corresponding boundary conditions are written as follows
Here represents velocity slip with constant , and represents the convective heat and mass transfer with , being constants,
Now introduce the stream function , a similar variable and the following similarity transformations;
Equation (1) is identically satisfied by the introduction of the equation
The system of Equations (2)–(4) will take the form
The associated boundary conditions in Equations (5) and (6) are transformed as
In the above expressions, , , , , , ( corresponds to suction and indicates blowing), , Pr, , ( is for heat generation and denotes heat absorption), , , , and ( corresponds to destructive chemical reaction and represents no chemical reaction) are the curvature parameter, magnetic parameter, porosity parameter, thermal Grashof number, mass Grashof number, suction/blowing parameter, slip parameter, Prandtl number, Eckert number, heat generation/absorption parameter, Schmidt number, Biot numbers and chemical reaction parameter, and are defined as
The wall skin friction, wall heat flux, and wall mass flux, respectively, are defined by
The dimensionless skin friction coefficient , the local Nusselt number and local Sherwood number on the surface along —direction, local Nusselt number and Sherwood number are given by
where is the local Reynold number.
3. Results and Discussion
The system of Equations (9)–(11) are solved numerically by using the Keller-box method [31] and numerical computations are carried out for different values of physical parameters including curvature parameter , Casson fluid parameter , nonlinear stretching cylinder parameter , magnetic parameter , porosity parameter , Grashof number , mass Grashof number , Prandtl number , radiation parameter , Eckert number , heat generation/absorption parameter , Schmidt number , chemical reaction parameter , slip parameter , and Biot numbers , . In order to validate the algorithm developed in MATLAB software for the present method, the numerical results for skin friction coefficient are compared with the results of Akbar et al. [13], Fathizadeh et al. [12], Fang et al. [15], and Imtiaz et al. [30], and presented in Table 1. Comparison revealed a close agreement with them.

Table 1.
Comparison of skin friction coefficient for different values of with , , , and .
Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 are depicted to see the physical behavior of , , , , , , , , and on velocity profile. Figure 2 exhibits the variation of on fluid velocity for (linear stretching) and (nonlinear stretching). It is noticed that fluid velocity is higher for increasing values of . Since the increase in leads to reduction in the radius of curvature, it also reduces cylinder area. Thus, the cylinder experiences less resistance from the fluid particles and fluid velocity is enhanced. It can also be seen that the momentum boundary layer is thicker with increased when . The influence of on velocity profile for different values of is depicted in Figure 3. In all cases, the fluid velocity is a decreasing function of . The reason is that the fluid becomes more viscous with the growth of . Therefore, more resistance is offered which reduces the momentum boundary layer thickness. Figure 4 elucidates the effect of on velocity profile for and . It is evident that increasing values of enhance the fluid velocity. Also, this enhancement is more pronounced when . The momentum boundary layer is thicker when .
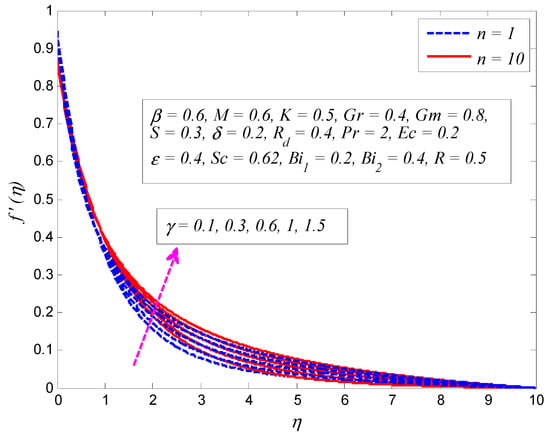
Figure 2.
Effect of curvature parameter on velocity for linear and nonlinear stretching parameter.
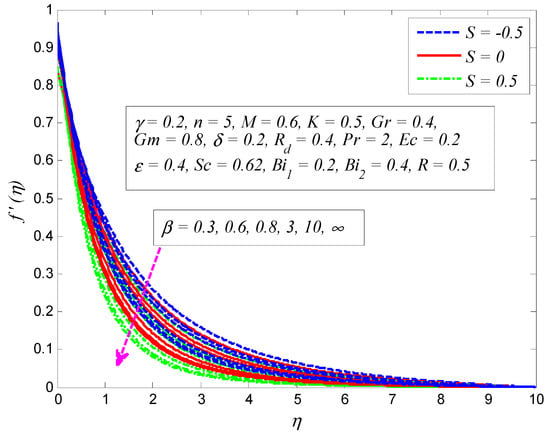
Figure 3.
Effect of Casson fluid parameter on velocity profile for different values of suction/blowing parameter .
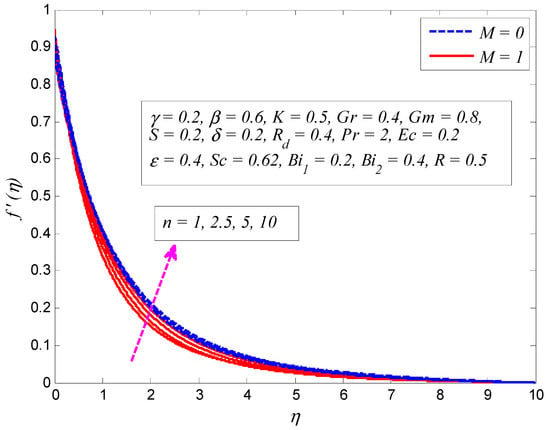
Figure 4.
Effect of nonlinear stretching parameter on velocity profile in the presence and absence of magnetic parameter .
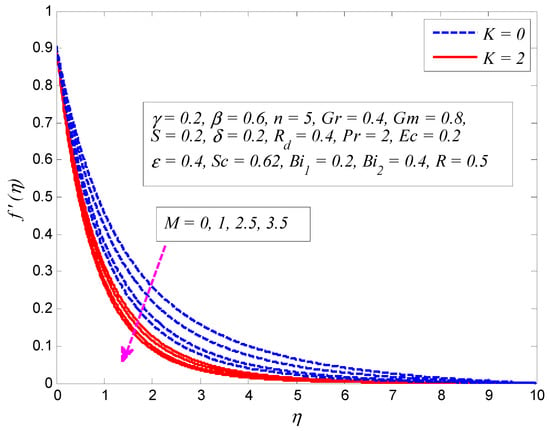
Figure 5.
Effect of magnetic parameter on velocity profile in the presence and absence of porosity parameter .
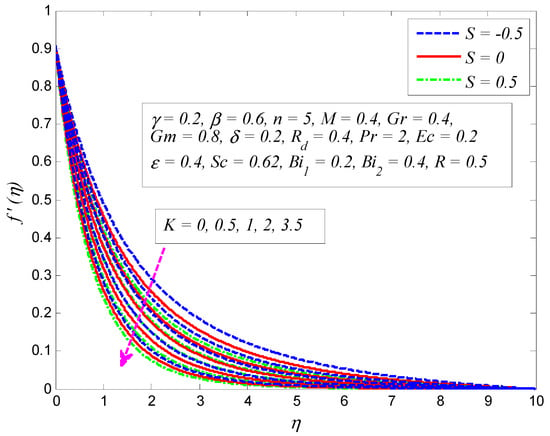
Figure 6.
Effect of porosity parameter on velocity profile for different values of suction/blowing parameter .
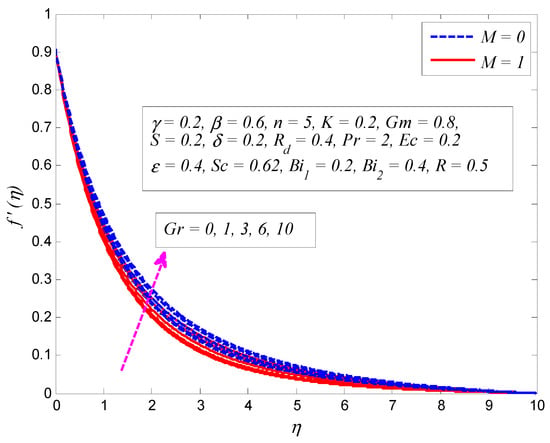
Figure 7.
Effect of Grashof number on velocity profile in the presence and absence of magnetic parameter .
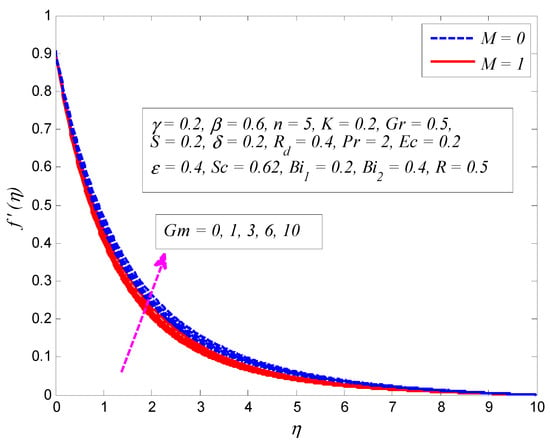
Figure 8.
Effect of mass Grashof number on velocity profile in the presence and absence of magnetic parameter .
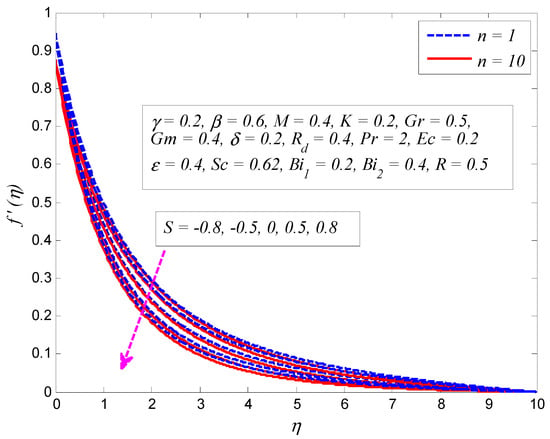
Figure 9.
Effect of suction/blowing parameter on velocity profile for nonlinear stretching parameter .
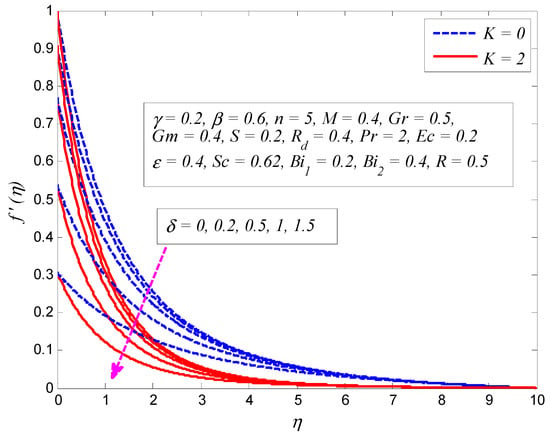
Figure 10.
Effect of slip parameter on velocity profile in the presence and absence of porosity parameter .
The variation of for and on the velocity profile is presented in Figure 5. As expected, the strength of the magnetic field lowers the fluid flow. It is an agreement with the fact that increase in produces Lorentz force that provides resistance to the flow, and apparently thins the momentum boundary layer across the boundary. It can also be seen that the fluid velocity is more influenced with when . A similar kind of variation is observed on velocity profile for different values of , as displayed in Figure 6. Since the porosity of porous medium provides resistance to the flow, fluid motion slows down and produces larger friction between the fluid particles and the cylinder surface. The impact of for and on velocity profile is depicted in Figure 7. The convection inside the fluid rises as the temperature difference enhances due to the growth of . In addition, increase in leads to stronger buoyancy force, in which case, the momentum boundary layer becomes thicker. The same kind of physical explanation can be given for the effect of on velocity profile (see Figure 8). The variation of on velocity profile for both and is portrayed in Figure 9. Clearly, the fluid velocity declines when , whereas a reverse trend is noted when . Physically, stronger blowing forces the hot fluid away from the surface, in which case the viscosity reduces and the fluid gets accelerated. On the other hand, wall suction exerts a drag force at the surface and hence thinning of the momentum boundary layer. Figure 10 demonstrates the effect of on velocity profile for and . It can be easily seen that fluid velocity falls with increase in . Since the resistance between the cylinder surface and the fluid particles rises with increase in , the momentum boundary layer become thinner.
Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20 and Figure 21 are plotted to get insight on the variation of , , , , , , , , , , and on the temperature profile. Figure 11 illustrates the variation of on dimensionless temperature profile for (Newtonian fluid) and (Casson fluid). It is noticed that temperature rises with increment in . A thermal boundary layer thickness is also noted. Figure 12 displays the influence of on temperature profile for various values of . It is noticeable that fluid temperature declines with the increase in for all the three cases of . The reason is that increase in implies a reduction in yield stress, and consequently the thickness of the thermal boundary layer reduces. The effect of on temperature profile for and is examined in Figure 13. It is clear from this figure that temperature is a decreasing function of . It is also noticed that the fluid temperature thermal boundary layer is thicker for a linear stretching cylinder () as compared to nonlinear stretching of the cylinder (). Figure 14 shows the variation of on temperature profile for different values of . It is noticeable that stronger magnetic field rises the fluid temperature in the vicinity of stretching cylinder. Because increasing enhances the Lorentz force, this force makes the thermal boundary layer thicker. The same kind of behavior is noticed for the effect of on dimensionless temperature profile for and , as presented in Figure 15.
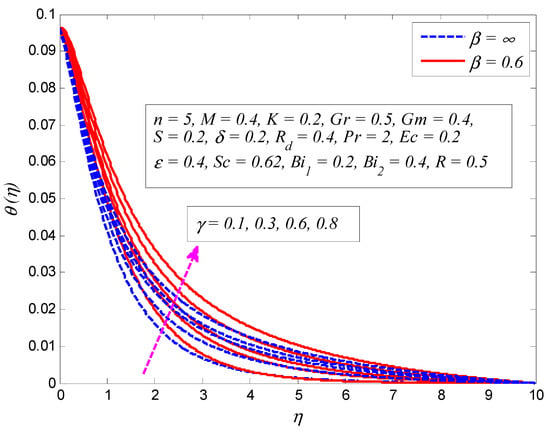
Figure 11.
Effect of curvature parameter on temperature profile for Newtonian fluid and Casson fluid .
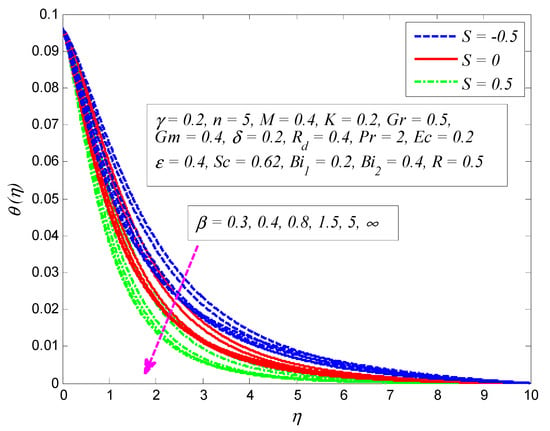
Figure 12.
Effect of Casson fluid parameter on temperature profile for different values of suction/blowing parameter .
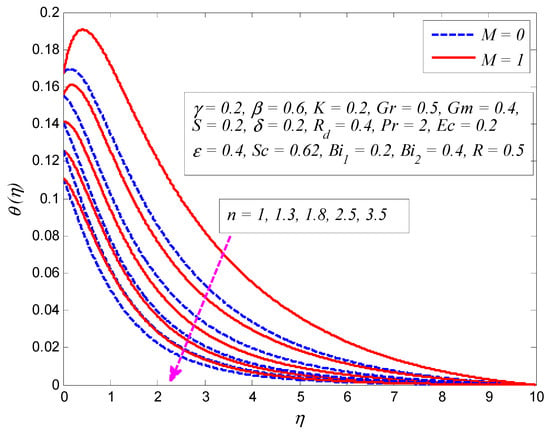
Figure 13.
Effect of nonlinear stretching parameter on temperature profile in the presence and absence of magnetic parameter .
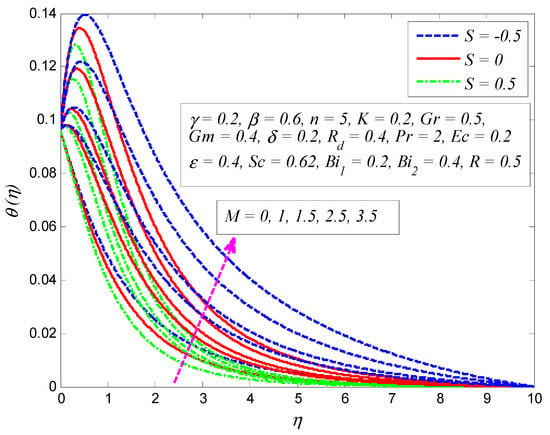
Figure 14.
Effect of magnetic parameter on temperature profile for different values of suction/blowing parameter .
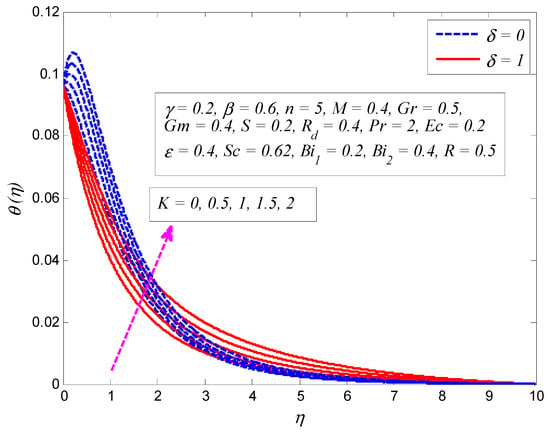
Figure 15.
Effect of porosity parameter on temperature profile in the presence and absence of slip parameter .
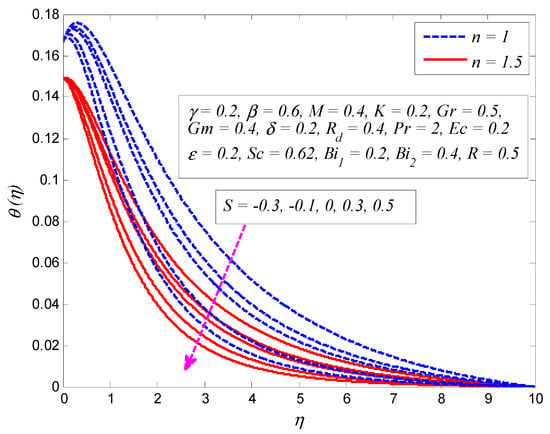
Figure 16.
Effect of suction/blowing parameter on temperature profile for different values of nonlinear stretching parameter .
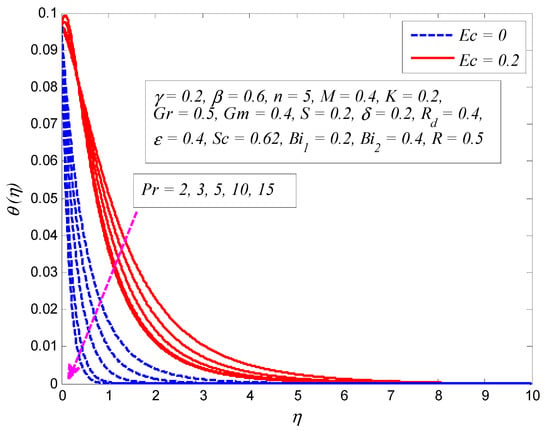
Figure 17.
Effect of Prandtl number on temperature profile in the presence and absence of Eckert number .
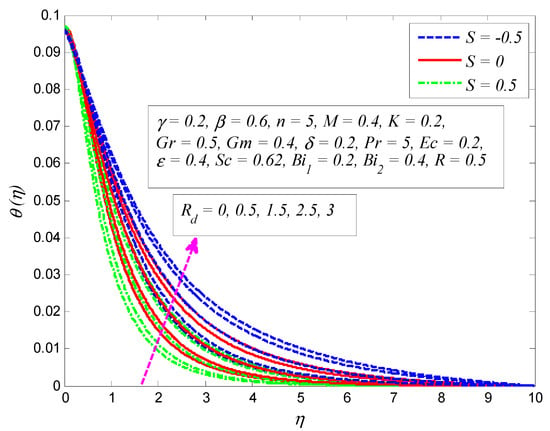
Figure 18.
Effect of radiation parameter on temperature profile for different values of suction/blowing parameter .
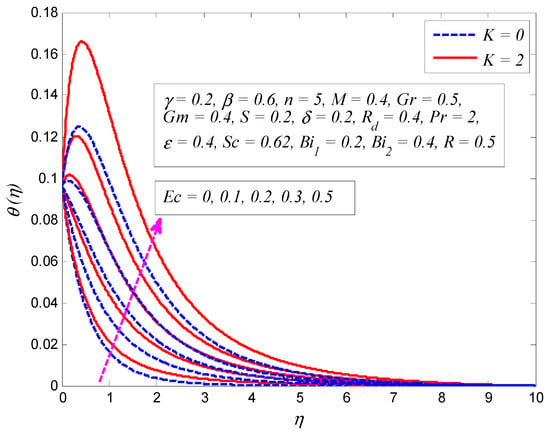
Figure 19.
Effect of Eckert number on temperature profile in the presence and absence of porosity parameter .
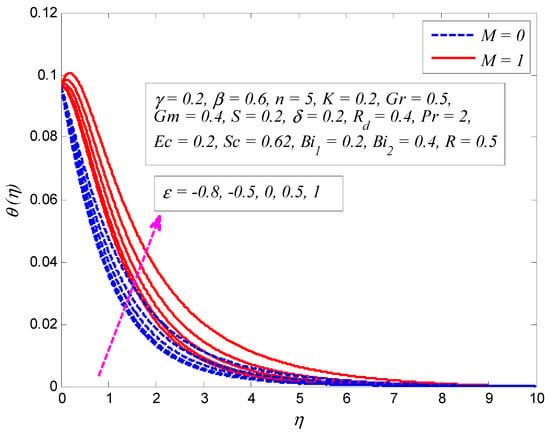
Figure 20.
Effect of heat generation/absorption parameter on temperature profile in the presence and absence of magnetic parameter .
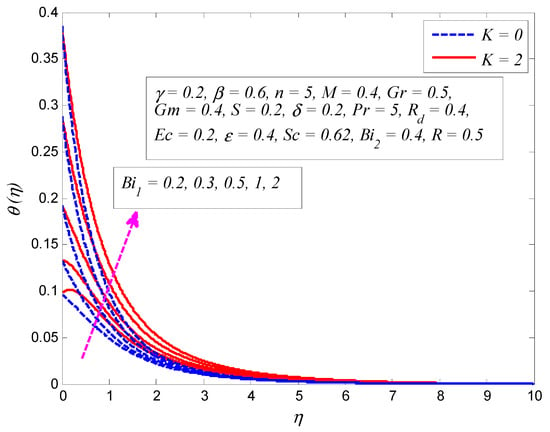
Figure 21.
Effect of Biot number on temperature profile in the presence and absence of porosity parameter .
Figure 16 reveals the influence of on temperature profile for (linear stretching) and (nonlinear stretching). Clearly, fluid temperature falls when , whereas it rises when . Since the wall suction offers resistance to fluid flow, the thermal boundary layer becomes thinner, and the opposite occurs when . The variation of Pr on dimensionless temperature profile for and is depicted in Figure 17. The Prandtl number is defined as the ratio of momentum diffusivity to thermal diffusivity. As expected, fluid temperature drops with the growth of Pr. It is a well-known fact that higher thermal conductivities are associated with lower Prandtl fluids, therefore heat diffuses quickly from the surface as compared to higher Prandtl fluids. Thus, Pr can be utilized to control the rate of cooling in conducting flows. Figure 18 exhibits the effect of on the temperature profile for different values of . It is noticeable that the strength of boosts the temperature. The larger surface heat flux corresponds to larger values of , causing the fluid to be warmer.
Figure 19 illustrates the influence of on the temperature profile for and . It is noted that the temperature is higher for higher values of . Physically this is true, because viscous dissipation generates heat energy due to friction between fluid particles and thereby thickens the thermal boundary layer structure. It is also observed from this figure that in the presence of porous medium, the strength of effectively enhances the fluid temperature. The influence of on temperature profile for and is displayed in Figure 20. It is clear from this graph that the temperature is enhanced when (heat generation), whereas the opposite trend is observed when (heat absorption). Internal heat generation causes the heat energy to be enhanced. Consequently, the heat transfer rate rises and thickens the thermal boundary layer. Besides, the heat absorption causes a reverse effect, i.e. the heat transfer rate and the thermal boundary layer thickness are reduced. Figure 21 reveals the variation of on the dimensionless temperature profile for and . The Biot number is the ratio of the internal thermal resistance of a solid to the boundary layer thermal resistance. It is noticed that fluid temperature is higher for larger values of . The reason is that increment in keeps the convection heat transfer higher and the cylinder thermal resistance lower. It is worth mentioning here that when , the internal resistance to heat transfer is negligible, representing that the value of is much larger than , and the internal thermal resistance is noticeably lower than the surface resistance. On the other hand, when the higher Biot number intends that the external resistance to heat transfer reduces, indicating that the surface and the surroundings temperature difference is minor and a noteworthy contribution of temperature to the center comes from the surface of the stretching cylinder.
Figure 22, Figure 23, Figure 24, Figure 25, Figure 26, Figure 27, Figure 28, Figure 29, Figure 30 and Figure 31 display the variation of , , , , , , , , , and on concentration profile, respectively. Figure 22 elucidates the effect of on concentration profile for (Newtonian fluid) and (Casson fluid). It is found that increasing values of enhances the fluid concentration and associated boundary layer thickness. Figure 23 demonstrates the influence of on concentration profile for and . It is noted that fluid concentration is higher as grows. The viscosity of the fluid increases with increasing , in which case the concentration rises and the concentration boundary layer becomes thicker. The opposite behavior is noticed for the effect of on concentration profile for various values of (see Figure 24). It is also observed that thickness of concentration boundary layer shortens for large . Figure 25 determines the variation of on the dimensionless concentration profile for and . It is seen that fluid concentration is higher for higher values of . As mentioned earlier for velocity and temperature profiles, fluid motion reduces due to magnetic field and results in an enhancement in thermal and concentration boundary layer thicknesses. A similar trend is observed for the effect of and on the concentration profile, as plotted in Figure 26 and Figure 27, respectively. The growth of both parameters offers resistance to the fluid particles and the concentration boundary layer becomes thicker. Figure 28 shows that fluid concentration reduces when , while it is enhanced when . Indeed, when mass suction occurs, some of the fluid is sucked through the wall which thins the boundary layer; on the contrary, blowing thickens the concentration boundary layer structure.
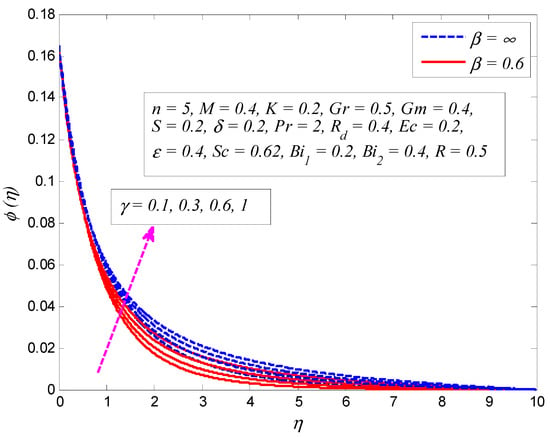
Figure 22.
Effect of curvature parameter on concentration profile for Newtonian fluid and Casson fluid .
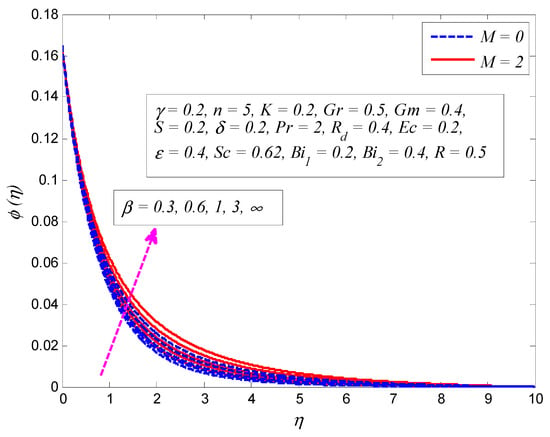
Figure 23.
Effect of Casson parameter on concentration profile in the presence and absence of magnetic parameter .
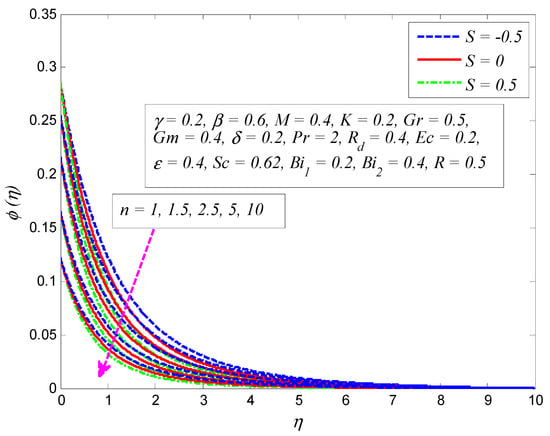
Figure 24.
Effect of nonlinear stretching parameter on concentration profile for different values of suction/blowing parameter .
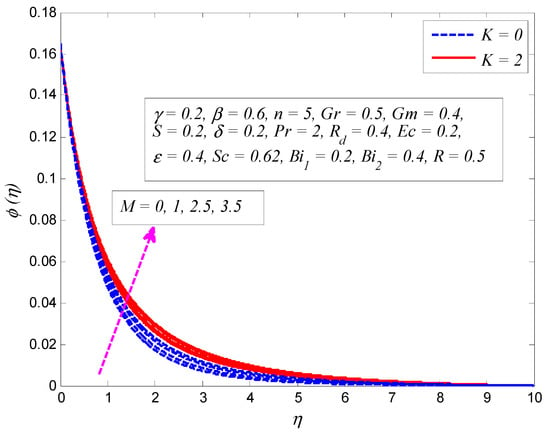
Figure 25.
Effect of magnetic parameter on concentration profile in the presence and absence of porosity parameter .
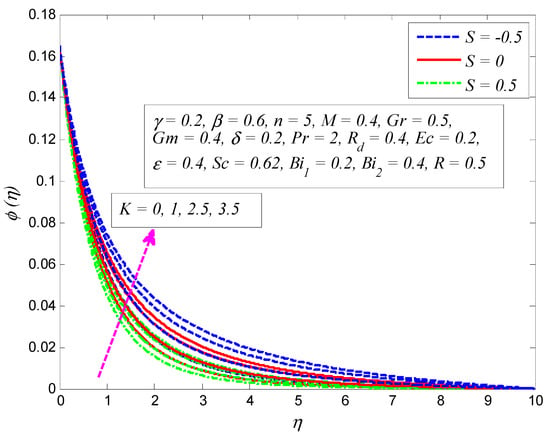
Figure 26.
Effect of porosity parameter on concentration profile for different values of suction/blowing parameter .
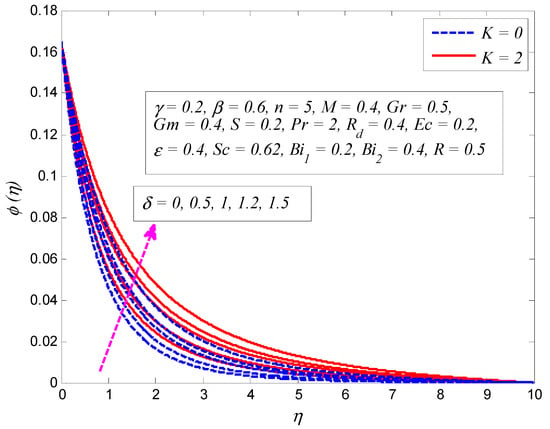
Figure 27.
Effect of slip parameter on concentration profile in the presence and absence of porosity parameter .
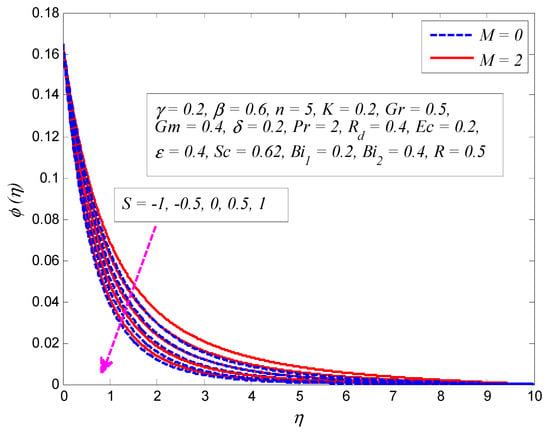
Figure 28.
Effect of suction/blowing parameter on concentration profile in the presence and absence of magnetic parameter .
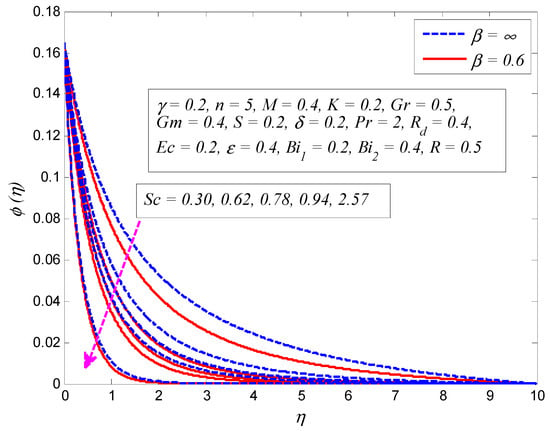
Figure 29.
Effect of Schmidt number on concentration profile for Newtonian fluid and Casson fluid .

Figure 30.
Effect of chemical reaction parameter on concentration profile for different values of suction/blowing parameter .
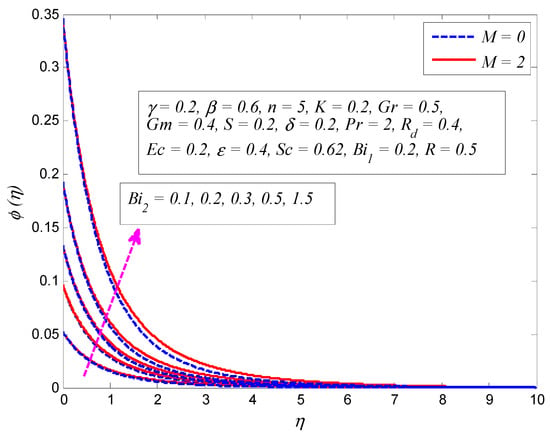
Figure 31.
Effect of Biot number on concentration profile in the presence and absence of magnetic parameter .
Figure 29 examines the variation of (Sc = 0.30, 0.62, 0.78, 0.94, 2.57 corresponds to hydrogen, helium, water vapor, hydrogen sulphide, and propyl Benzene) on the dimensionless concentration profile when (Newtonian fluid) and (Casson fluid). For both fluids, an increase in reduces the fluid concentration. Since higher values of lead to higher mass transfer rate, the thickness of the concentration boundary layer declines. The effect of on the concentration distribution for different values of is depicted in Figure 30. It is clear that fluid concentration drops with the growth of . Physically this makes sense, because the decomposition rate of reactant species enhances in the destructive chemical reaction (). Consequently, the mass transfer rate grows and thickens the concentration boundary layer. Figure 31 exhibits the variation of on concentration distribution for and . It is noticeable that fluid concentration rises with increasing . As increase in Biot number enhances the temperature field, the concentration field excites, making the solutal boundary layer thicker.
Figure 32, Figure 33, Figure 34 and Figure 35 depict the effect of the skin friction coefficient, Nusselt number, and Sherwood number for different values of , , , , , , , and , respectively. Figure 32 reveals the variation of wall shear stress for various values of , , and . It is noted that the absolute values of wall shear stress increase as and increase, whereas the opposite is observed for the effect of . It is also noticeable that the values of friction factor are negative, which shows that the stretching cylinder experiences a drag force from the fluid particles. Moreover, the effect of on wall shear stress is more pronounced for Casson fluid. The effect of , , and on dimensionless skin friction coefficient is examined in Figure 33. This figure shows that friction factor absolute values decline as , , and increase. Figure 34 portrays the variation of Nusselt number for various values of , , and . It is shown that heat transfer rate drops as and increase, whereas they increase for larger values of . However, the heat transfer rate is more influenced for Casson fluid. It is also noted that heat transfer rate is negative for higher values of . These negative values show that heat is transferred from the working fluid to the stretching surface. Finally, the effect of Sherwood number for various , , and is illustrated in Figure 35. It is found that the mass transfer rate is an increasing function of and and a decreasing function of .
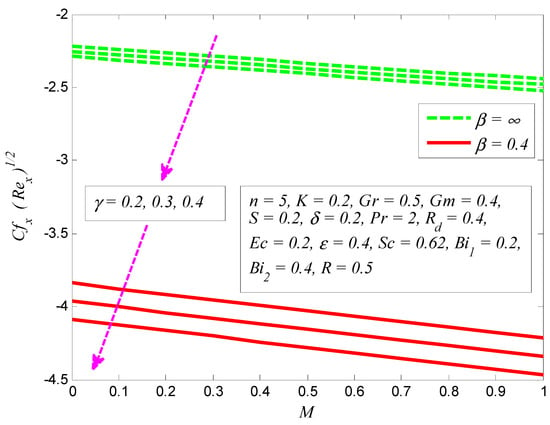
Figure 32.
Variation of skin friction coefficient for various values of Casson fluid parameter , curvature parameter , and magnetic parameter .
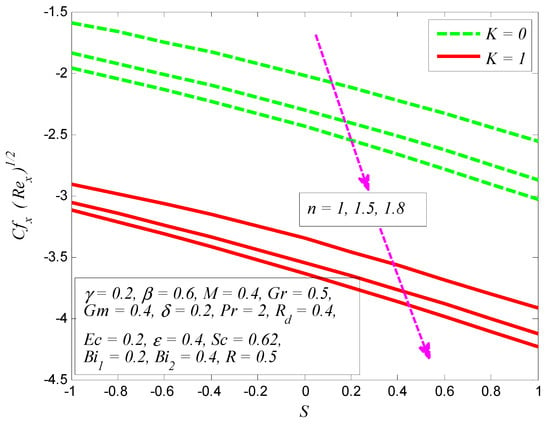
Figure 33.
Variation of skin friction coefficient for various values of nonlinear stretching parameter , porosity parameter , and suction/blowing parameter .
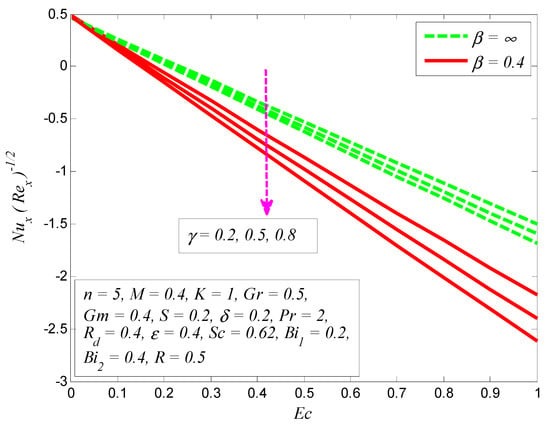
Figure 34.
Variation of Nusselt number for various values of Casson parameter , curvature parameter , and Eckert number .
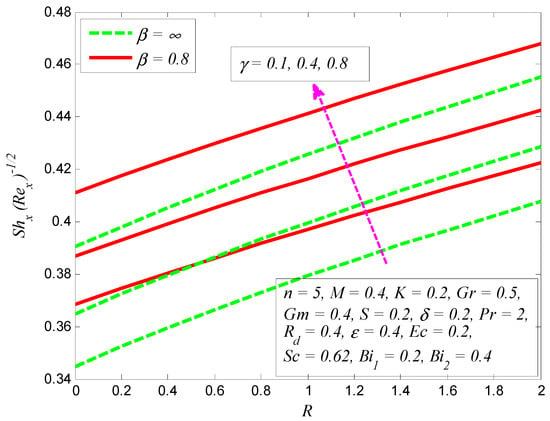
Figure 35.
Variation of Sherwood number for various values of Casson fluid parameter , curvature parameter , and chemical reaction parameter .
4. Conclusions
In the present study, the influence of chemical reaction on MHD slip flow of Casson fluid due to nonlinear cylinder stretching was investigated numerically. Similarity solutions for velocity, temperature, and concentration distributions are achieved via the Keller box method. The numerical results of wall shear stress and heat transfer rate are also compared as a limiting case. The effect of physical parameters, namely, unsteadiness parameter , Casson parameter , nonlinear stretching parameter , magnetic parameter , porosity parameter , thermal Grashof number , mass Grashof number , Prandtl number Pr, radiation parameter , Eckert number , heat generation/absorption parameter , Schmidt number , chemical reaction parameter , suction/blowing parameter , slip parameter , and Biot numbers , are discussed and displayed graphically. Some interesting observations from the present analysis are as follow:
- The fluid velocity, temperature, and concentration are found to increase with .
- The magnitude of wall shear stress and mass transfer rate increase with the growth of , whereas the heat transfer rate is enhanced.
- The effect of on fluid velocity is more pronounced when (nonporous medium).
- The temperature field is more influenced with increasing when .
- The velocity, temperature, and concentration distributions decrease when , while the reverse trend is seen when .
- The concentration boundary layer is observed to be thinner during destructive chemical reaction.
Author Contributions
Conceptualization, I.U. and I.K.; methodology, I.U. and I.K.; software, I.U.; validation, I.U., I.K. and S.S.; formal analysis, I.U., O.D.M., T.A.A., S.S. and K.S.N.; investigation, I.U., T.A.A., K.S.N. and O.D.M; resources, I.U., I.K., and S.S; data curation, I.U.; writing—original draft preparation, I.U. and O.D.M.; writing—review and editing, I.U.; visualization, T.A.A., K.S.N., I.U. and I.K.; supervision, I.U. and S.S.
Funding
This research received no external funding.
Acknowledgments
The authors would like to thank the reviewers and editor for their constructive and insightful comments in relation to this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Crane, L.J. Flow past a stretching plate. Z. Angew. Math. Phys. 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Gupta, P.S.; Gupta, A.S. Heat and mass transfer on a stretching sheet with suction or blowing. Can. J. Chem. Eng. 1977, 55, 744–746. [Google Scholar] [CrossRef]
- Chen, C.K.; Char, M.I. Heat transfer of a continuous, stretching surface with suction or blowing. J. Math. Anal. Appl. 1988, 135, 568–580. [Google Scholar] [CrossRef]
- Gorla, I.; Sidawi, R.S.R. Free Convection on a Vertical Stretching Surface with Suction and Blowing. Appl. Sci. Res. 1994, 52, 247–257. [Google Scholar] [CrossRef]
- Vajravelu, K. Viscous flow over a nonlinearly stretching sheet. Appl. Math. Comput. 2001, 124, 281–288. [Google Scholar] [CrossRef]
- Vajravelu, K.; Cannon, J.R. Fluid flow over a nonlinearly stretching sheet. Appl. Math. Comput. 2006, 181, 609–618. [Google Scholar] [CrossRef]
- Bachok, N.; Ishak, A. Flow and heat transfer over a stretching cylinder with prescribed surface heat flux. Malays. J. Math. Sci. 2010, 4, 159–169. [Google Scholar]
- Hayat, T.; Saeed, Y.; Asad, S.; Alsaedi, A. Convective heat and mass transfer in flow by an inclined stretching cylinder. J. Mol. Liq. 2016, 220, 573–580. [Google Scholar] [CrossRef]
- Majeed, A.; Zeeshan, A.; Alamri, S.Z.; Ellahi, R. Heat transfer analysis in ferromagnetic viscoelastic fluid flow over a stretching sheet with suction. Neur. Comp. Appl. 2018, 30, 1947–1955. [Google Scholar] [CrossRef]
- Vyas, A.; Ranjan, P. Dissipative mhd boundary layer flow in a porous medium over a sheet stretching nonlinearly in the presence of radiation. Appl. Math. Sci. 2010, 4, 3133–3142. [Google Scholar]
- Mukhopadhyay, S. MHD boundary layer flow along a stretching cylinder. Ain Shams Eng. J. 2013, 4, 317–324. [Google Scholar] [CrossRef]
- Fathizadeh, M.; Madani, M.; Khan, Y.; Faraz, N.; Yildirim, A.; Tutkun, S. An effective modification of the homotopy perturbation method for MHD viscous flow over a stretching sheet. J. King Saud Univ. Sci. 2013, 25, 107–113. [Google Scholar] [CrossRef]
- Akbar, N.S.; Ebaid, A.; Khan, Z.H. Numerical analysis of magnetic field effects on Eyring-Powell fluid flow towards a stretching sheet. J. Magn. Magn. Mater. 2015, 382, 355–358. [Google Scholar] [CrossRef]
- Ellahi, R. The effects of MHD and temperature dependent viscosity on the flow of non-Newtonian nanofluid in a pipe: Analytical solutions. Appl. Math. Model. 2013, 37, 1451–1467. [Google Scholar] [CrossRef]
- Fang, T.; Zhang, J.; Yao, S. Slip MHD viscous flow over a stretching sheet—An exact solution. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 3731–3737. [Google Scholar] [CrossRef]
- Bhattacharyya, K.; Mukhopadhyay, S.; Layek, G.C. Slip effects on an unsteady boundary layer stagnation-point flow and heat transfer towards a stretching sheet. Chin. Phys. Lett. 2011, 28, 094702. [Google Scholar] [CrossRef]
- Yazdi, M.H.; Abdullah, S.; Hashim, I.; Sopian, K. Slip MHD liquid flow and heat transfer over non-linear permeable stretching surface with chemical reaction. Int. J. Heat Mass Transf. 2011, 54, 3214–3225. [Google Scholar] [CrossRef]
- Hayat, T.; Qasim, M.; Mesloub, S. MHD flow and heat transfer over permeable stretching sheet with slip conditions. Int. J. Numer. Methods Fluids 2011, 66, 963–975. [Google Scholar] [CrossRef]
- Seini, I.Y.; Makinde, O.D. Boundary layer flow near stagnation-points on a vertical surface with slip in the presence of transverse magnetic field. Int. J. Numer. Methods Heat Fluid Flow 2014, 24, 643–653. [Google Scholar] [CrossRef]
- Rahman, S.U.; Ellahi, R.; Nadeem, S.; Zia, Q.Z. Simultaneous effects of nanoparticles and slip on Jeffrey fluid through tapered artery with mild stenosis. J. Mol. Liq. 2016, 218, 484–493. [Google Scholar] [CrossRef]
- Casson, N. A Flow Equation for Pigment-Oil Suspensions of the Printing Ink Type; Mill, C.C., Ed.; Rheol. Disperse Syst. Pergamon Press: Oxford, UK, 1959; pp. 84–104. [Google Scholar]
- Nandy, S.K. Analytical Solution of MHD Stagnation-Point Flow and Heat Transfer of Casson Fluid over a Stretching Sheet with. Thermodynamics 2013. [Google Scholar] [CrossRef]
- Singh, S. Clinical significance of aspirin on blood flow through stenotic blood vessels. J. Biomim. Biomater. Tissue Eng. 2011, 10, 17–24. [Google Scholar]
- Mukhopadhyay, S.; Bhattacharyya, K.; Hayat, T. Exact solutions for the flow of Casson fluid over a stretching surface with transpiration and heat transfer effects. Chin. Phys. B 2013, 22, 114701. [Google Scholar] [CrossRef]
- Shawky, H.M. Magnetohydrodynamic Casson fluid flow with heat and mass transfer through a porous medium over a stretching sheet. J. Porous Media 2012, 15, 393–401. [Google Scholar] [CrossRef]
- Mukhopadhyay, S. Casson fluid flow and heat transfer over a nonlinearly stretching surface. Chin. Phys. B 2013, 22, 074701. [Google Scholar] [CrossRef]
- Medikare, M.; Joga, S.; Chidem, K.K. MHD Stagnation Point Flow of a Casson Fluid over a Nonlinearly Stretching Sheet with Viscous Dissipation. Am. J. Comput. Math. 2016, 37–48. [Google Scholar] [CrossRef]
- Mythili, D.; Sivaraj, R. Influence of higher order chemical reaction and non-uniform heat source/sink on Casson fluid flow over a vertical cone and flat plate. J. Mol. Liq. 2016, 216, 466–475. [Google Scholar] [CrossRef]
- Ullah, I.; Khan, I.; Shafie, S. Hydromagnetic Falkner-Skan flow of Casson fluid past a moving wedge with heat transfer. Alex. Eng. J. 2016, 55, 2139–2148. [Google Scholar] [CrossRef]
- Imtiaz, M.; Hayat, T.; Alsaedi, A. Mixed convection flow of Casson nanofluid over a stretching cylinder with convective boundary conditions. Adv. Powder Technol. 2016, 27, 2245–2256. [Google Scholar] [CrossRef]
- Cebeci, T.; Bradshaw, P. Physical and Computational Aspects of Convective Heat Transfer, 1st ed.; Springer: New York, NY, USA, 1988. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).