Numerical Inverse Laplace Transform for Solving a Class of Fractional Differential Equations

Abstract

This paper discusses the applications of numerical inversion of the Laplace transform method based on the Bernstein operational matrix to find the solution to a class of fractional differential equations. By the use of Laplace transform, fractional differential equations are firstly converted to system of algebraic equations then the numerical inverse of a Laplace transform is adopted to find the unknown function in the equation by expanding it in a Bernstein series. The advantages and computational implications of the proposed technique are discussed and verified in some numerical examples by comparing the results with some existing methods. We have also combined our technique to the standard Laplace Adomian decomposition method for solving nonlinear fractional order differential equations. The method is given with error estimation and convergence criterion that exclude the validity of our method.

1. Introduction

Over the years, researchers have been attracted to study the scientific problems modelled in fractional differential equations due to their constant appearance in the different disciplines of mathematical sciences and engineering such as fluid mechanics, viscoelasticity, mathematical physics, mathematical biology, system identification, control theory, electrochemistry and signal processing [1,2,3,4,5,6]. Several analytical and numerical techniques have been developed to solve such kind of equations in the literature. Among these methods, Li and Sun [7] derived the generalized block pulse operational matrix to find the solution of fractional differential equations in terms of block pulse function. A truncated Legendre series together with generalized Legendre operational matrix is used to solve fractional differential equations by Saadatmandi and Dehgan in [8] and they also have presented shifted Legendre-tau method for finding the solution of fractional diffusion equations with variable coefficients in [9]. Doha et al. [10] used the shifted Jacobi operational matrix of fractional derivatives applied together with spectral tau-method for solving fractional differential equations. Kazem et al. [11] constructed an orthogonal fractional order Legendre function based on Legendre polynomials to solve fractional differential equations. Mokhtary et al. [12] provided the operational tau method based on Muntz–Legendre polynomials for solving fractional differential equations. Bernoulli wavlet operational matrix of fractional order integration has been derived to approximate the numerical solution of fractional differential equations in [13]. Fractional-order Lagrange polynomials have been proposed to solve the fractional differential equations in [14]. Albadarneh et al. [15] adopted the fractional finite difference method for solving linear and nonlinear fractional differential equations. Garrappa [16] provided a detailed survey on the two methods, i.e., product integration rules (PI) and Lubich’s fractional linear multi step methods (FLMMs) for solving fractional differential equations. Dehghan et al. [17] adopted homotopy analysis method to solve linear fractional partial differential equations, a meshless approximation strategy for solving fractional partial differential equations based on radial basis function is used in [18]. Haar wavlets have been employed to obtain the solutions of boundary value problems for linear fractional partial differential equations by Rehman and Khan [19]. Li et al. [20] solved the linear fractional partial differential equations based on operational matrix of fractional Bernstein polynomials. Yang et al. [21] discussed the solution of fractional order diffusion equations within the negative Prabhakar kernel comprise with the Laplace transform and the series solutions in terms of general Mittag–Leffler functions. In [22], a new factorization technique has been adopted for nonlinear differential equations involving local fractional derivatives and found the exact solutions for nonlinear local fractional FitzHugh–Nagumo and Newell–Whitehead equations. Cesarano [23] proposed the Hermite polynomials based operational method to solve fractional diffusive equations. From the last few decades, the Laplace transform method has become popular and adopted by many researchers to solve differential and integral equations. Since then it is necessary to find the inverse Laplace transform for finding the solution in its original domain. There exist a number of analytical and numerical methods for inverting a Laplace transform. For details one can refer [24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41]. The Laplace transform method reduces the differential or integral equation into a system of algebraic equations due to the Heaviside’s operational method. Further, Hasio and Chen [42] extended the idea of Heaviside’s operational method to operational matrix of integration. In the literature, few papers reported the use of operational matrices for inversion of Laplace transform: Chen et al. [39] obtained the walsh operational matrices and applied to distributed system, Wu et al. [40] adopted Haar wavlet operational matrices for numerical inverse Laplace transform of certain functions, Aznam and Hussin [38] modified Haar wavlet operational matrices by using generalized block pulse functions, Babolian and Shamloo [24] used operational matrices based on piecewise-constant block pulse function to invert the Laplace transform and solved Volterra integral equations, Maleknejad and Nouri [25] improved the operational matrices based on block pulse functions and Shamloo et al. [41] adopted this method to solve first kind of integral equations. The main purpose of using an operational matrix is that it converts the differential or integral equations into a system of algebraic equations that is simple and easy to solve.

Bernstein polynomials and its operational matrix is used to solve many differential, integral and integro-differential equations [43,44,45,46,47,48,49]. But these are not adopted with Laplace transform for inverting the Laplace transform. A Bernstein operational matrix of integration has been developed to find the numerical inverse Laplace transform of certain functions in our paper [50]. The proposed method expresses the solution of equations in terms of truncated Bernstein expansion and then using its operational matrix of integration, numerical inverse Laplace transform is obtained. The operational matrix of integration of Bernstein polynomials is easily calculated using a single formula of integration rather than Haar or block pulse function where the order of matrix is taken too large, i.e., $8,16,128$. Here in our method, we achieve the accuracy using a matrix of order 6 or 7. In the present research, our aim is to find the numerical solutions of linear fractional ordinary and partial differential equations, nonlinear fractional differential equations and system of fractional differential equations using numerical inverse Laplace transform method based on Bernstein operational matrix of integration developed in [50]. At first, for linear problems, we transform the fractional differential equations to system of linear algebraic equations using Laplace transform then the numerical approach for calculating the inverse Laplace transform is used to retrieve the time-domain. Here, we extend our numerical approach to solve some nonlinear fractional differential equations together with a well-known iterative method, i.e., a Laplace Adomian decomposition method [51] (briefly explained in the Section 4). One more advantage of using our proposed method is that there is no need of any fractional order matrix of integration for numerical inversion to solve fractional order differential equations.

The paper is organized as follows: In Section 2, some necessary definitions and preliminaries of the fractional calculus theory and Laplace transform are given. Section 3 reveals the basics of Bernstein polynomials, derivation of operational matrix of integration and function approximation in Bernstein polynomials. In Section 4, the proposed method is explained and presented the application to a class of fractional differential equations. Section 5 represents the error estimation and convergence analysis. 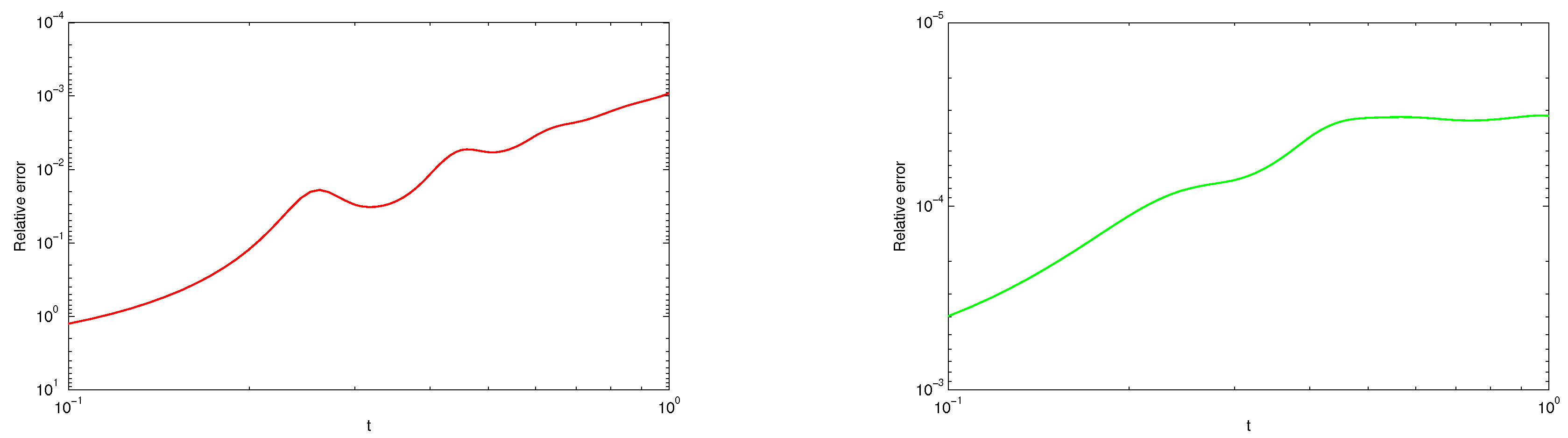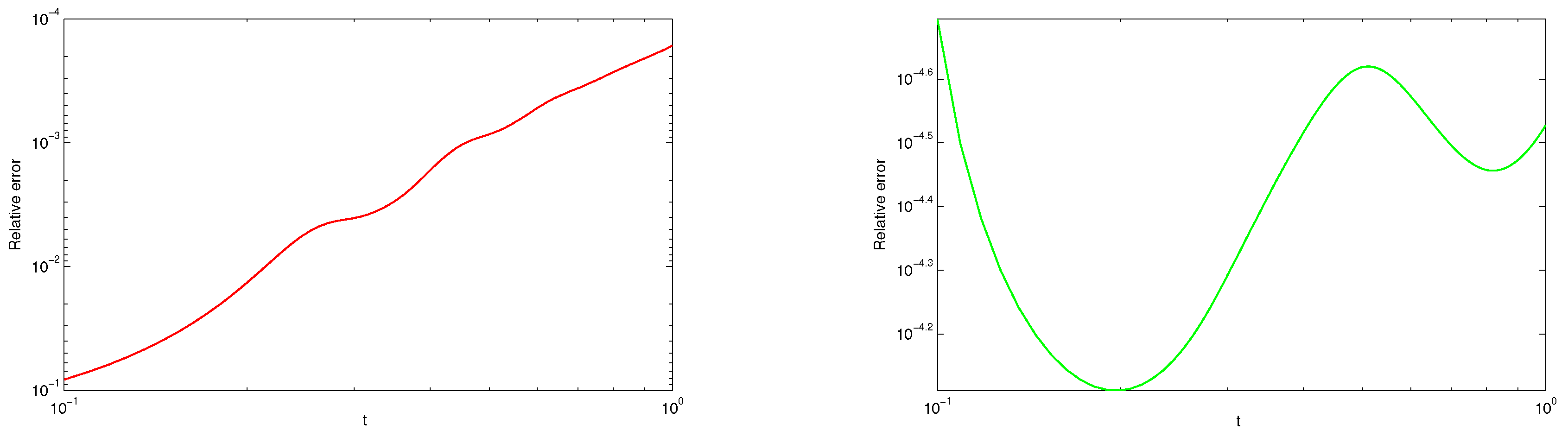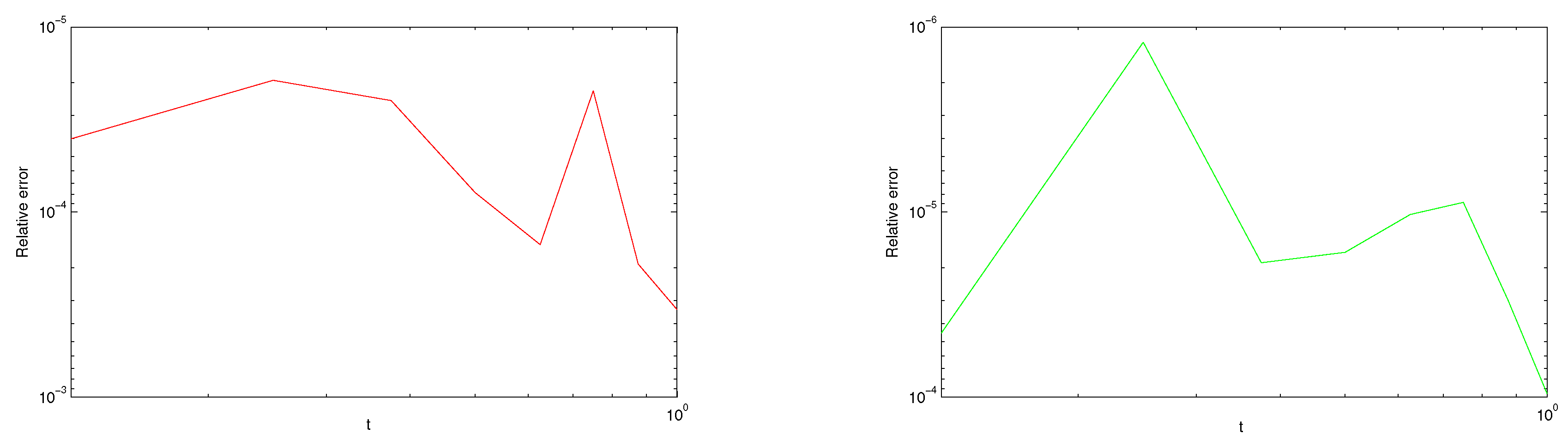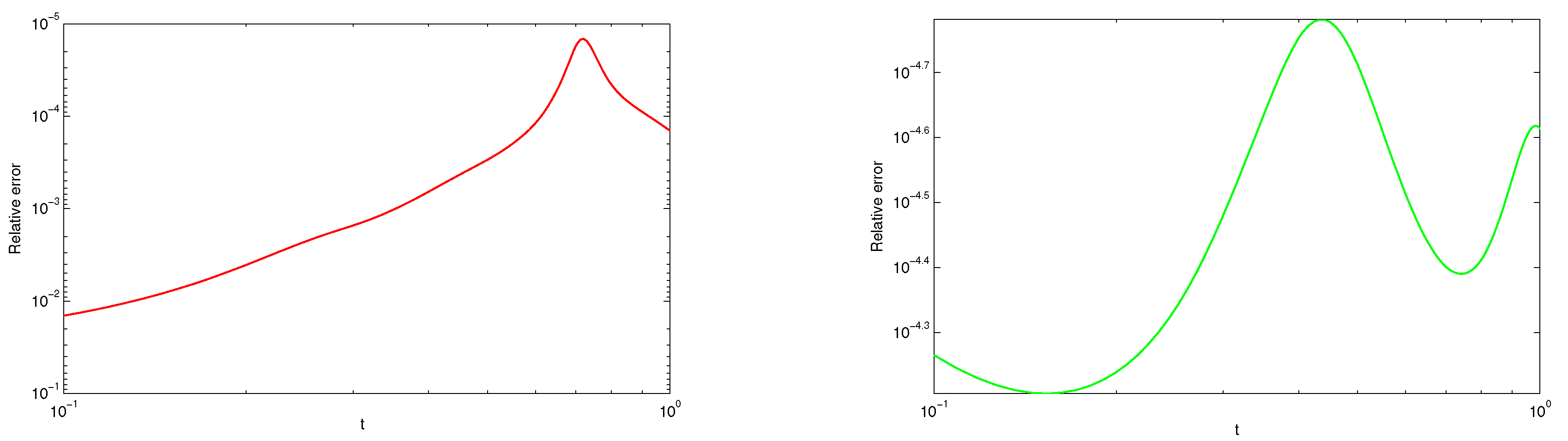In Section 6 the illustrative examples are given to show the applicability of the method. Section 7 is refers to conclusions.

2. Preliminaries

In this section, we give some basic definitions and properties of a Laplace transform [36] and fractional calculus as follows [1,2,4]:

Definition 1.

The Laplace transform of a continuous or piecewise continuous function $f\left(t\right)$ in $[0,\infty )$ is defined as

$$L\left(f\left(t\right)\right)=F\left(s\right)={\int }_0^{\infty }{e}^{-st}f\left(t\right)dt,$$

(1)

where s is known as Laplace variable.

Definition 2.

A real function $f\left(t\right)$, $t>0$ is said to be in the space $C_{\mu }$ if $\mu \in \mathbb{R}$, there exists a real number $p>\mu$ and the function $f_1\left(t\right)\in C[0,\infty )$ such that $f\left(t\right)=t^p{f}_1\left(t\right)$. Moreover, if $f^{\left(n\right)}\in C_{\mu }$ then $f\left(t\right)$ is said to be in the space $C_{\mu }^n$, $n\in N$.

Definition 3.

The Riemann–Liouville fractional integral of order $\alpha \ge 0$ for a function $f\left(t\right)$ is defined as

$$J^{\alpha }f\left(t\right)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{\Gamma \left(\alpha \right)}{\int }_0^t{(t-\tau )}^{\alpha -1}f\left(\tau \right)d\tau }\hfill & ,\alpha >0\hfill \\ f\left(t\right)\hfill & ,\alpha =0,\hfill \end{array}\right.$$

where $\Gamma (.)$ denotes the Gamma function.

Definition 4.

The Riemann–Liouville fractional derivative of order $\alpha >0$ for a function $f\left(t\right)$ is defined as

$$D^{\alpha }f\left(t\right)=\frac{d^n}{d{t}^n}{J}^{n-\alpha }f\left(t\right),n\in N,n-1<\alpha \le n.$$

(2)

Definition 5.

The Caputo fractional derivative of order $\alpha >0$ is defined as

$$D^{\alpha }f\left(t\right)=\left\{\begin{array}{cc}{\displaystyle \frac{d^{n}f\left(t\right)}{d{t}^n}}\hfill & ,\alpha =n,n\in N\hfill \\ {\displaystyle \frac{1}{\Gamma (n-\alpha )}{\int }_0^t\frac{f^{\left(n\right)}\left(\tau \right)}{{(t-\tau )}^{\alpha -n+1}}d\tau }\hfill & ,0\le n-1<\alpha <n,\hfill \end{array}\right.$$

where n is an integer, $t>0$, and $f\left(t\right)\in C_1^n$.

Definition 6.

The Laplace transform of a function $f(x,t)$, denoted as $F(x,s)$, $t⩾0$ is defined by

$$L\left(f(x,t)\right)=F(x,s)={\int }_0^{\infty }{e}^{-st}f(x,t)dt,$$

where s is the transformed parameter.

Definition 7.

The Caputo fractional partial derivative operator of order $\alpha >0$ is defined as

$$\frac{{\partial }^{\alpha }f(x,t)}{\partial t^{\alpha }}=\left\{\begin{array}{cc}{\displaystyle \frac{{\partial }^{n}f(x,t)}{\partial t^n}}\hfill & ,\alpha =n,n\in N\hfill \\ {\displaystyle \frac{1}{\Gamma (n-\alpha )}{\int }_0^t\frac{\frac{{\partial }^{n}f(x,\tau )}{\partial t^n}}{{(t-\tau )}^{\alpha -n+1}}d\tau }\hfill & ,0\le n-1<\alpha <n,\hfill \end{array}\right.$$

where n is an integer, $t>0$.

Property 1.

The Laplace transform of the Caputo fractional derivative ${\mathcal{D}}^{\alpha }f\left(t\right)$ can be found as

$$L\left({\mathcal{D}}^{\alpha }f\left(t\right)\right)=\frac{1}{s^{m-\alpha }}\left(s^{m}L\left(f\left(t\right)\right)-s^{m-1}f\left(0\right)-s^{m-2}{f}^{\prime }\left(0\right)-\dots -f^{(m-1)}\left(0\right)\right).$$

3. Bernstein Polynomials and Function Approximation

To explain the operational matrices of Bernstein polynomials, we need to give some basic definitions and properties following [52].

Definition 8.

The Bernstein basis polynomials of degree n are defined over the interval $[0,1]$:

$$b_{i,n}\left(t\right)=\left(\genfrac{}{}{0pt}{}{n}{i}\right)t^i{(1-t)}^{n-i},i=0,1,\dots ,n.$$

(3)

Some useful results of Bernstein polynomials are as follows:

• $b_{i,n}\left(t\right)=0$, if $i<0$ or $i>n$.
• $b_{i,n}\left(t\right)\ge 0$ for $t\in [0,1]$.
• The Bernstein polynomials form a partition of unity i.e., ${\sum }_{i=0}^n{b}_{i,n}\left(t\right)=1$.

Bernstein polynomials have one more important property that these polynomials are not orthogonal therefore to conquer this difficulty Bernstein polynomials of degree n are orthonormailized using Gram–Schmidt orthonormalization procedure and denoted as $B_{i,n}\left(t\right),i=0.,1\dots n$.

We can find the function approximation based on Bernstein polynomials. A function $f\left(t\right)$, $f\left(t\right)\in L^2[0,1]$ can be expressed in terms of orthonormal Bernstein polynomials [47]:

$$f\left(t\right)=\underset{n\to \infty }{lim}\sum _{i=0}^n{c}_i{B}_{i,n}\left(t\right),$$

(4)

where $c_i=\langle f,B_{i,n}\rangle$ and $\langle .,.\rangle$ denotes the standard inner product.

If the infinite series is truncated at $n=k$, then the approximate solution can be expressed as

$$f_k\left(t\right)=\sum _{i=0}^k{c}_i{B}_{i,k}\left(t\right)=C^{T}B\left(t\right),$$

(5)

where $C={\left[\begin{array}{ccccc}{c}_0& c_1& c_2& \dots & c_k\end{array}\right]}^T$ and $B\left(t\right)={\left[\begin{array}{ccccc}{B}_{0,k}\left(t\right)& B_{1,k}\left(t\right)& B_{2,k}\left(t\right)& \dots & B_{k,k}\left(t\right)\end{array}\right]}^T$.

Here, the operational matrix of integration of orthonormal Bernstein polynomials is introduced which depends on the integral property of basis vector, i.e., suppose we have a column vector $\varphi \left(t\right)=[{\varphi }_0\left(t\right),{\varphi }_1\left(t\right),\dots {\varphi }_k\left(t\right)]$ where ${\varphi }_0\left(t\right),{\varphi }_1\left(t\right),\dots {\varphi }_k\left(t\right)$ are the basis functions orthogonal on some interval $[a,b]$, then the property states that

$${\int }_a^t\dots {\int }_a^t\varphi \left(x\right){\left(dx\right)}^m=A_{k+1}^m\varphi \left(t\right),$$

(6)

where $A_{k+1}^m$ is the operational matrix of integration of $\varphi \left(t\right)$ which is a constant matrix of order $(k+1)\times (k+1)$. Now adopting this property on vector $B\left(t\right)$, we get

$${\int }_0^{t}B\left(x\right)dx=I_{k+1}B\left(t\right),$$

(7)

where $I_{k+1}$ is the operational matrix of integration of Bernstein polynomials defined as

$${\int }_0^t{B}_{i,k}\left(x\right)dx={\alpha }_i=\sum _{j=0}^k{a}_{jk}^i{B}_{j,k},i=0,1,\dots ,k,0\le t<1.$$

(8)

Therefore

$$I_{k+1}=\left(a_{jk}^i\right)=\langle {\alpha }_i,B_{j,k}\rangle ,i,j=0,1,\dots ,k.$$

(9)

4. The Method for Numerical Inverse Laplace Transform

In this section, we describe the algorithm proposed in [50] by considering the linear time varying system

$$f^{\prime }\left(t\right)+\alpha f\left(t\right)=u\left(t\right),f\left(0\right)=0$$

(10)

where $u\left(t\right)$ is the unit step function.

Here, we convert this differential equation to integral equation

$$f\left(t\right)+{\int }_0^t\alpha f\left(x\right)dx={\int }_0^{t}u\left(x\right)dx,f\left(0\right)=0.$$

(11)

Performing Laplace transform on both sides of (11), we get

$$F\left(s\right)=\frac{1}{s(s+\alpha )}.$$

(12)

We can rewrite (12) as

$$F\left(s\right)=\frac{\frac{1}{s^2}}{(1+\frac{\alpha }{s})}=\overline{F}\left(\frac{1}{s}\right).$$

(13)

Here, we use result from Laplace theory [36]: if $L\left(f\right(t\left)\right)=F\left(s\right)$, then

$$L\left({\int }_0^{t}f\left(x\right)dx\right)=\frac{1}{s}F\left(s\right).$$

(14)

This result can be explained as the integration in time-domain is corresponding to multiplication of $1/s$ in $s-domain$.

We can say that here three domains are introduced: one is time-domain, by performing Laplace transform we move from time-domain, $f\left(t\right)$ to $s-domain$$F\left(s\right)$, or $\overline{F}\left(\frac{1}{s}\right)$, and then to matrix domain where we define the functional $\tilde{F}\left(I_{k+1}\right)$ (say) defined on the space of matrices.

The integration in time domain of the inverse Laplace function is corresponding to the definition of the functional $\tilde{F}$ defined onto the space of Bernstein operational matrices. Therefore (13) becomes

$$\tilde{F}\left(I_{k+1}\right)=I_{k+1}^2{(I+\alpha I_{k+1})}^{-1}.$$

(15)

To solve the integral Equation (11), we approximate

$${\int }_0^t{f}_k\left(x\right)dx=C^T{I}_{k+1}B\left(t\right)$$

(16)

Also

$${\int }_0^{t}u\left(x\right)dx=d^T{I}_{k+1}B\left(t\right),$$

(17)

where $d={\left[\begin{array}{ccccc}{d}_0& d_1& d_2& \dots & d_k\end{array}\right]}^T$ defined by

$$d_i={\int }_0^t{B}_{i,k}\left(t\right)dt,i=0,1,2\dots ,k,0\le t<1.$$

(18)

Therefore, the integral Equation (11) becomes

$$C^{T}B\left(t\right)+\alpha C^T{I}_{k+1}B\left(t\right)=d^T{I}_{k+1}B\left(t\right)$$

$$C^T=d^T{I}_{k+1}(I+\alpha I_{k+1}){)}^{-1}$$

$$C^T=d^T{I}_{k+1}^{-1}\tilde{F}\left(I_{k+1}\right).$$

(19)

Thus, the unknown vector $C^T$ is calculated, where $\tilde{F}\left(I_{k+1}\right)$ can be taken from Equation (15). Consequently, the approximate solution $f_k\left(t\right)$ can be obtained in terms of Bernstein polynomials by substituting the unknown vector $C^T$ into (5).

In all these computations for finding the solution, we used simple algebraic operations of matrices, which have been computed using MATLAB R2014a on Intel® Core™ i3 processor (2328M)(2nd Gen.).

4.1. Application to a Class of Fractional Differential Equations

Here, we present the fundamental importance of proposed method by applying it to linear fractional differential equations, linear partial fractional differential equations and nonlinear fractional differential equations.

4.1.1. Application to Linear Fractional Differential Equations

Consider the linear ordinary fractional differential equation

$${\mathcal{D}}^{\alpha }f\left(t\right)=M\left(f\left(t\right)\right)+g\left(t\right),$$

(20)

with initial conditions $f^{\left(i\right)}\left(0\right)=f_i$, $i=0,1,\dots ,m-1$.

Here ${\mathcal{D}}^{\alpha }$ denotes the Caputo fractional order derivative and $M\left(f\right(t\left)\right)$ represents the linear operator, and may also contain the other derivatives than order $\alpha$.

To solve the initial problem, Laplace transform is applied to Equation (20) and we attain

$$\frac{1}{s^{m-\alpha }}\left[s^{m}L\left(f\left(t\right)\right)-s^{m-1}f\left(0\right)-s^{m-2}{f}^{\prime }\left(0\right)\dots -f^{(m-1)}\left(0\right)\right]=L[M\left(f\left(t\right)\right)+g\left(t\right)]=G\left(s\right)$$

$$L\left(f\left(t\right)\right)=\frac{1}{s^m}\left[s^{m-\alpha }G\left(s\right)+s^{m-1}f\left(0\right)+s^{m-2}{f}^{\prime }\left(0\right)\dots +f^{(m-1)}\left(0\right)\right].$$

(21)

Therefore, $f\left(t\right)=L^{-1}\left(H\left(s\right)\right)$, where $H\left(s\right)=\frac{1}{s^m}\left[s^{m-\alpha }G\left(s\right)+s^{m-1}f\left(0\right)+s^{m-2}{f}^{\prime }\left(0\right)\dots +f^{(m-1)}\left(0\right)\right]$. Hence, $f\left(t\right)$, i.e., the solution can be obtained by finding the inverse Laplace transform of $H\left(s\right)$ using the above described procedure.

4.1.2. Application to Linear Partial Fractional Differential Equations

Consider the linear partial fractional differential equation of the form

$$\frac{{\partial }^{\alpha }f}{\partial t^{\alpha }}+A\left(x\right)\frac{\partial f}{\partial x}+B\left(x\right)\frac{{\partial }^{2}f}{\partial x^2}+C\left(x\right)f=g(x,t),$$

(22)

with initial condition $\frac{{\partial }^{k}f}{\partial t^k}(x,0)=h_k\left(x\right),k=0,1,\dots m-1$.

Taking Laplace transform to both sides of Equation (22), we have

$$\begin{array}{c}\frac{1}{s^{m-\alpha }}\left[s^{m}F(x,s)-s^{m-1}{h}_0\left(x\right)-s^{m-2}{h}_1\left(x\right)\dots -h_{m-1}\left(x\right)\right]+\hfill \\ \hfill A\left(x\right)\frac{dF(x,s)}{dx}+B\left(x\right)\frac{d^{2}F(x,s)}{d{x}^2}+C\left(x\right)F(x,s)=G(x,s),\end{array}$$

where $F(x,s)$ and $G(x,s)$ denote the Laplace transform of $f(x,t)$ and $g(x,t)$ respectively. The above equation can be written as

$$\begin{array}{c}B\left(x\right)\frac{d^{2}F(x,s)}{d{x}^2}+A\left(x\right)\frac{dF(x,s)}{dx}+(s^{\alpha }+C\left(x\right))F(x,s)\hfill \\ \hfill =G(x,s)+\frac{1}{s^{m-\alpha }}\left[s^{m}F(x,s)+s^{m-1}{h}_0\left(x\right)+s^{m-2}{h}_1\left(x\right)\dots +h_{m-1}\left(x\right)\right].\end{array}$$

(23)

Now Equation (23) has become a second order ordinary differential equation in $F(x,s)$, that can be easily solved by any classical method for variable x, while keeping s as Laplace variable. The obtained solution $F(x,s)$ can be inverted to $f(x,t)$ using our developed technique.

4.1.3. Application to Nonlinear Fractional Differential Equations

In view to solve, nonlinear fractional order differential equations using standard Laplace adomian decomposition method, we briefly recall the Laplace adomian decomposition method here.

Consider the nonlinear fractional order differential equation

$${\mathcal{D}}^{\alpha }f\left(t\right)+M\left(f\left(t\right)\right)+N\left(f\left(t\right)\right)=g\left(t\right),m-1\le \alpha <m,$$

(24)

with initial condition $f^{\left(i\right)}\left(0\right)=f_i$, $i=0,1,\dots ,m-1$.

Here $M\left(f\right(t\left)\right)$ represents the linear operator which may include other derivatives than order $\alpha$ and $N\left(f\right(t\left)\right)$ be the nonlinear operator of $f\left(t\right)$.

The standard Laplace Adomian Decomposition Method (LADM) procedure begins with taking Laplace transform to this nonlinear equation and using the properties of Laplace transform, we have

$$\frac{1}{s^{m-\alpha }}\left[s^{m}L\left(f\left(t\right)\right)-s^{m-1}f\left(0\right)-s^{m-2}{f}^{\prime }\left(0\right)\dots -f^{(m-1)}\left(0\right)\right]+L\left(M\left(f\left(t\right)\right)\right)+L\left(N\left(f\left(t\right)\right)\right)=L\left(g\left(t\right)\right)$$

$$L\left(f\left(t\right)\right)=\frac{a}{s^{\alpha }}-\frac{1}{s^{\alpha }}L\left(M\left(f\left(t\right)\right)\right)-\frac{1}{s^{\alpha }}L\left(N\left(f\left(t\right)\right)\right)+\frac{1}{s^{\alpha }}L\left(g\left(t\right)\right),$$

(25)

where $a={\sum }_{i=0}^{m-1}{s}^{\alpha -i-1}{f}^{\left(i\right)}\left(0\right)$.

The method describes the series solution as

$$f\left(t\right)=\sum _{n=0}^{\infty }{f}_n\left(t\right).$$

(26)

Therefore, truncated series solution takes the form

$$f_m\left(t\right)=\sum _{n=0}^m{f}_n\left(t\right),$$

(27)

and the nonlinear term is decomposed as follows:

$$N\left(f\left(t\right)\right)=\sum _{n=0}^{\infty }{A}_n,$$

(28)

where $A_n$’s are the Adomian polynomials, given by

$$A_n=\frac{1}{n!}\frac{d^n}{d{\lambda }^n}{\left[N\left\{\sum _{i=0}^n{\lambda }^i\left(f_i\right)\right\}\right]}_{\lambda =0}.$$

(29)

Consequently, Equation (25) leads to following recurrence relation

$$f_0\left(t\right)=L^{-1}\left[\frac{a}{s^{\alpha }}-\frac{1}{s^{\alpha }}L\left\{M\left(f\left(t\right)\right)\right\}+\frac{1}{s^{\alpha }}L\left\{g\left(t\right)\right\}\right]$$

(30)

$$f_1\left(t\right)=L^{-1}\left[-\frac{1}{s^{\alpha }}L\left\{A_0\left(f_0\left(t\right)\right)\right\}\right].$$

(31)

In general

$$f_m\left(t\right)=L^{-1}\left[-\frac{1}{s^{\alpha }}L\left\{A_{m-1}(f_0\left(t\right),f_1\left(t\right)\dots f_{m-1}\left(t\right))\right\}\right].$$

(32)

The new development is that we find the values of $f_0\left(t\right)$, $f_1\left(t\right)\dots$ by finding inverse Laplace transform using our proposed technique, i.e., Bernstein operational matrix, as described above.

5. Error Estimation and Convergence Analysis

5.1. Error Estimation via RK45 Method

We have investigated error estimation of the proposed method [24]. The error function $e_k\left(t\right)$ of the truncated Bernstein expansion $f_k\left(t\right)$ is defined as

$$e_k\left(t\right)=f\left(t\right)-f_k\left(t\right).$$

(33)

From the following theorem the absolute error bound can be estimated:

Theorem 1.

Let $f\left(t\right)$ be the function defined on $[0,1]$, then the upper bound for the errors in truncated Bernstein expansion can be estimated.

Proof. 

Suppose that $f_k\left(t\right)$ and $f_{k+1}\left(t\right)$ are two consecutive approximate solutions of given differential equation. If the error sequence is increasing or decreasing, then we use the triangle inequality

$$|\parallel f\left(t\right)-f_{k_1}{\left(t\right)\parallel }_{\infty }-\parallel f\left(t\right)-f_{k_2}{\left(t\right)\parallel }_{\infty }|\le \parallel f_{k_1}\left(t\right)-f_{k_2}{\left(t\right)\parallel }_{\infty },$$

(34)

to the approximate solutions at k and $k+1$ and we achieve

$$|\parallel f\left(t\right)-f_{k+1}{\left(t\right)\parallel }_{\infty }-\parallel f\left(t\right)-f_k{\left(t\right)\parallel }_{\infty }|=\beta \parallel f\left(t\right)-f_m{\left(t\right)\parallel }_{\infty }\le {\parallel f_{k+1}\left(t\right)-f_k\left(t\right)\parallel }_{\infty },0\le \beta <1,$$

(35)

where

$$\parallel f\left(t\right)-f_m{\left(t\right)\parallel }_{\infty }=max\{\parallel f\left(t\right)-f_k{\left(t\right)\parallel }_{\infty },\parallel f\left(t\right)-f_{k+1}\left(t\right){\parallel }_{\infty }\}$$

and $\beta =\frac{\parallel f_{k+1}\left(t\right)-f_k{\left(t\right)\parallel }_{\infty }}{\parallel f\left(t\right)-f_m\left(t\right)\parallel }$.

Hence, it can be said that the error can be bounded from above. One of the absolute errors $e_k\left(t\right)$ or $e_{k+1}\left(t\right)$ are bounded by $\parallel f_{k+1}\left(t\right)-f_k{\left(t\right)\parallel }_{\infty }$, if the error sequence is monotone. The computable error bound is represented for $0\le \beta <1$. But, the solution diverges when the Bernstein series diverges for $\beta >1$. □

5.2. Convergence Analysis

In order to show the effectiveness of our method, a residual function of a linear time varying system in the Banach space for the values of k is adopted to interpret the convergence of the Bernstein polynomials solution as described in [47,53].

Suppose $f_k\left(t\right)$ are the approximate solution of (10), we write the residual function as

$$R_k\left(t\right)\simeq f_k^{\prime }\left(t\right)+\alpha f_k\left(t\right)-u\left(t\right),t\in [0,1].$$

(36)

The Bernstein polynomial-based numerical solution or the residual function can be expressed in terms of Taylor series expansion as:

$$R_k\left(t\right)=r_0+r_{1}t+r_2{t}^2\dots +r_k{t}^k=\sum _{j=0}^k{r}_j{t}^j.$$

(37)

Now, we desire to prove that the residual function sequence is convergent in Banach space and satisfying the condition: $\parallel R_{k+1}\parallel \le {\zeta }_k\parallel R_k\parallel$, for $0\le {\zeta }_k<1$.

For the convergence, we prove here that $\left\{R_{k+1}\left(t\right)\right\},k=0,1,\dots \infty$ is a Cauchy sequence.

Let us take that

$$\parallel R_{k+1}\left(t\right)\parallel =\parallel \sum _{j=0}^{k+1}{r}_j{t}^j\parallel \le sup\left\{\sum _{j=0}^{k+1}\parallel r_j{t}^j\parallel :t\in [a,b]\right\}=\left|R_{k+1}\left(b\right)\right|.$$

Therefore, the given condition can be written as

$$|R_{k+1}\left(b\right)|\le {\zeta }_k\left|R_k\left(b\right)\right|,$$

and this can be easily shown as follows. Let us write explicitly as functions of Bernstein polynomials

$$f_k^{\prime }\left(t\right)=\sum _{i=0}^{k}f\left(\frac{i}{k}\right)B_{i,k}^{\prime }\left(t\right)$$

(38)

$$f_k\left(t\right)=\sum _{i=0}^{k}f\left(\frac{i}{k}\right)B_{i,k}\left(t\right).$$

(39)

If we define

$$m_k=\underset{i=0,1,\dots k}{max}\left[f\left(\frac{i}{k}\right)\right],$$

(40)

we have

$$f_k^{\prime }\left(t\right)=m_k\sum _{i=0}^k{B}_{i,k}^{\prime }\left(t\right).$$

Here we used the following property of Bernstein polynomials

$$B_{i,k}^{\prime }\left(t\right)=k\left[B_{i-1,k-1}\left(t\right)-B_{i,k-1}\left(t\right)\right],$$

(41)

so that

$$f_k^{\prime }\left(t\right)<m_k\sum _{i=1}^{k-1}k\left[B_{i-1,k-1}\left(t\right)-B_{i,k-1}\left(t\right)\right].$$

From where, we get

$$f_k^{\prime }\left(t\right)<m_{k}k\left[B_{0,k-1}\left(t\right)-B_{k-1,k-1}\left(t\right)\right]$$

$$f_k^{\prime }\left(t\right)<m_{k}k\left[{(1-t)}^{k-1}-t^{k-1}\right].$$

Since the function in brackets is a decreasing function in $[-1,1]$, with ${max}_{t\in [0,1]}\left[{(1-t)}^{k-1}-t^{k-1}\right]=1$ there follows

$$f_k^{\prime }\left(t\right)<k{m}_k$$

(42)

Analogously, by using the properties of Bernstein polynomials, we can also estimate

$$f_k\left(t\right)<m_k\sum _{i=0}^k{B}_{i,k}\left(t\right),$$

and since Bernstein polynomials are partition of unit there follows

$$f_k\left(t\right)<m_k.$$

(43)

Let us combine Equation (36) with the condition in Equations (42) and (43), then we get

$$R_k<m_{k}k+\alpha m_k-u,$$

and analogously

$$R_{k+1}<m_{k+1}k+\alpha m_{k+1}-u.$$

This can be written as

$$R_{k+1}<\frac{m_{k+1}}{m_k}\left[m_{k}k+\alpha m_k-u\right]+\frac{m_{k+1}}{m_k}u-u$$

$$R_{k+1}<\frac{m_{k+1}}{m_k}{R}_k+\left[\frac{m_{k+1}}{m_k}u-u\right].$$

Here

$$\underset{k\to \infty }{lim}\frac{m_{k+1}}{m_k}=1,$$

which implies

$$\underset{k\to \infty }{lim}\left[\frac{m_{k+1}}{m_k}u-u\right]=0,$$

so that $R_{k+1}<{\zeta }_k{R}_k$, with ${\zeta }_k=\frac{m_{k+1}}{m_k},0<{\zeta }_k<1,{lim}_{k\to \infty }{\zeta }_k=1$.

Now, we begin from the above inequality

$$|R_{k+1}\left(b\right)|\le |R_{k+1}\left(b\right)-R_k\left(b\right)|\le ({\zeta }_k-1)\left|R_k\left(b\right)\right|.$$

Thus, we generalize the inequality and attain

$$\begin{array}{c}|R_{k+1}\left(b\right)-R_k\left(b\right)|\le ({\zeta }_k-1)|R_k\left(b\right)|\le ({\zeta }_k-1)({\zeta }_{k-1}-1)\left|R_{k-1}\left(b\right)\right|\dots \\ \le ({\zeta }_k-1)({\zeta }_{k-1}-1)\dots ({\zeta }_0-1)\left|R_0\left(b\right)\right|.\end{array}$$

(44)

For $k,s\in N$ and $k\ge s$, to prove that the sequence is Cauchy sequence, we take

$$\begin{array}{c}\hfill |R_k\left(b\right)-R_s\left(b\right)|\le |R_k\left(b\right)-R_{k-1}\left(b\right)+R_{k-1}\left(b\right)-R_{k-2}\left(b\right)+\dots R_{s+1}\left(b\right)-R_s\left(b\right)|\\ \hfill \le |R_k\left(b\right)-R_{k-1}\left(b\right)|+|R_{k-1}\left(b\right)-R_{k-2}\left(b\right)|+\dots |R_{s+1}\left(b\right)-R_s\left(b\right)|\\ \hfill \le {ϵ}_{k-1}|R_0\left(b\right)|+{ϵ}_{k-2}|R_0\left(b\right)|+\dots {ϵ}_{s+1}\left|R_0\left(b\right)\right|\\ \hfill \le ({ϵ}_{k-1}+{ϵ}_{k-2}\dots {ϵ}_{s+1})\left|R_0\left(b\right)\right|\\ \hfill \le \eta |R_0\left(b\right)|,\end{array}$$

(45)

where ${ϵ}_k={\prod }_{i=0}^k({\zeta }_i-1)$ and $\eta =({ϵ}_{k-1}+{ϵ}_{k-2}\dots {ϵ}_{s+1})$. Hence, for $0\le \eta <1$, $|R_k\left(b\right)-R_s\left(b\right)|\to 0$ as $k,s\to \infty$, that proves the residual function sequence is Cauchy sequence and convergent. Therefore the approximate solution is convergent.

6. Illustrative Examples

Here, we present some examples to demonstrate the applicability of the presented technique. The relative errors and $L_{\infty }$-errors are plotted at the different values of k. Also the error estimation is discussed in each example.

Example 1.

Consider the following fractional differential equation [12]

$$\mathcal{D}f\left(t\right)+{\mathcal{D}}^{0.25}f\left(t\right)+f\left(t\right)=t^{5/2}+\frac{5}{2}{t}^{3/2}+\frac{15}{8}\frac{\sqrt{\pi }}{\Gamma \left(13/4\right)}{t}^{9/4},f\left(0\right)=0,$$

(46)

with the exact solution $f\left(t\right)=t^2\sqrt{t}$.

The relative error for different values of k are plotted in Figure 1 which shows that the method is giving good results as compared to analytic solution. Using the error estimation method, we estimated the upper bound of errors and calculate

$$\begin{array}{ccc}\hfill \parallel e_6{\parallel }_{\infty }& =& 1.07\times {10}^{-3}\hfill \\ \hfill \parallel e_7{\parallel }_{\infty }& =& 6.00\times {10}^{-5}\hfill \\ \hfill \parallel f_6-f_7{\parallel }_{\infty }& =& 1.07\times {10}^{-3}.\hfill \end{array}$$

Therefore, it is clear from the data that the error is estimated and bounded above by $\parallel f_6-f_7{\parallel }_{\infty }$.

Example 2.

Consider the following fractional differential equation

$${\mathcal{D}}^{1.5}f\left(t\right)+3f\left(t\right)=3t^3+\frac{4}{\Gamma \left(1.5\right)}{t}^{1.5},f\left(0\right)=f^{\prime }\left(0\right)=0,$$

(47)

with exact solution $f\left(t\right)=t^3$.

The relative errors for different values of k are plotted in Figure 2. Using the error estimation method, we estimated the upper bound of errors and calculated

$$\begin{array}{ccc}\hfill \parallel e_6{\parallel }_{\infty }& =& 1.71\times {10}^{-3}\hfill \\ \hfill \parallel e_7{\parallel }_{\infty }& =& 3.21\times {10}^{-5}\hfill \\ \hfill \parallel f_6-f_7{\parallel }_{\infty }& =& 1.72\times {10}^{-3}.\hfill \end{array}$$

Hence, in this example $max\{\parallel e_6{\parallel }_{\infty },\parallel e_7{\parallel }_{\infty }\}\le \parallel f_6-f_7{\parallel }_{\infty }$ that justify the result of error analysis.

Example 3.

Consider the following fractional differential equation [15]

$${\mathcal{D}}^{0.5}f\left(t\right)+f\left(t\right)=t^2+\frac{2}{\Gamma \left(2.5\right)}{t}^{1.5},f\left(0\right)=0,$$

(48)

with the exact solution $f\left(t\right)=t^2$.

In Figure 3, we plotted the relative errors for $k=5$ and $k=6$. To show the efficiency, absolute errors compared to fractional finite difference method (FFDM) [15] are given in

Table 1. Comparison of absolute error in Example 3.

t	Present Method at k = 5	Present Method at k = 6	FFDM [15]
0.1	$8.17\times {10}^{-4}$	$2.02\times {10}^{-7}$	$1.16\times {10}^{-4}$
0.2	$5.36\times {10}^{-4}$	$3.09\times {10}^{-6}$	$1.56\times {10}^{-4}$
0.3	$3.64\times {10}^{-4}$	$4.59\times {10}^{-6}$	$1.81\times {10}^{-4}$
0.4	$2.65\times {10}^{-4}$	$4.87\times {10}^{-6}$	$2.00\times {10}^{-4}$
0.5	$2.13\times {10}^{-4}$	$6.01\times {10}^{-6}$	$2.15\times {10}^{-4}$
0.6	$1.88\times {10}^{-4}$	$9.61\times {10}^{-6}$	$2.27\times {10}^{-4}$
0.7	$1.77\times {10}^{-4}$	$1.56\times {10}^{-5}$	$2.37\times {10}^{-4}$
0.8	$1.72\times {10}^{-4}$	$2.23\times {10}^{-5}$	$2.46\times {10}^{-4}$
0.9	$1.68\times {10}^{-4}$	$2.73\times {10}^{-5}$	$2.54\times {10}^{-4}$
1	$1.64\times {10}^{-4}$	$2.97\times {10}^{-5}$	$2.61\times {10}^{-4}$

which clearly states that our method gives more accurate results. Using the error estimation method, we also estimate the upper bound of errors and calculate $\parallel e_6{\parallel }_{\infty }=8.17\times {10}^{-4}$, $\parallel e_7{\parallel }_{\infty }=2.97\times {10}^{-5}$ and $\parallel f_6-f_7{\parallel }_{\infty }=8.17\times {10}^{-4}$. Therefore $max\{\parallel e_6{\parallel }_{\infty },\parallel e_7{\parallel }_{\infty }\}\le \parallel f_6-f_7{\parallel }_{\infty }$ that follows the estimated upper bound of error.

Example 4.

Consider the following mathematical model, which is developed for a micro-electro mechanical system instrument, that has been designed to measure the viscosity of the fluids that are encountered during oil exploration [54]:

$${\mathcal{D}}^{2}f\left(t\right)+\beta \sqrt{\pi }{\mathcal{D}}^{1.5}f\left(t\right)+f\left(t\right)=0,f\left(0\right)=1,f^{\prime }\left(0\right)=0$$

(49)

In Figure 4, we plotted the relative errors for $k=5$ and $k=6$, taking $\beta =1$. To show the efficiency, absolute errors compared to cubic spline method [54] are given in

Table 2. Comparison of Absolute error in Example 4.

t	Present Method at k = 6	Cubic Spline Method [54]
0.125	4.49$\times {10}^{-5}$	1.24$\times {10}^{-3}$
0.250	1.18$\times {10}^{-6}$	5.12$\times {10}^{-3}$
0.375	1.80$\times {10}^{-5}$	1.39$\times {10}^{-2}$
0.500	1.53$\times {10}^{-5}$	2.61$\times {10}^{-2}$
0.625	9.29$\times {10}^{-6}$	4.04$\times {10}^{-2}$
0.75	7.63$\times {10}^{-6}$	5.58$\times {10}^{-2}$
0.875	2.47$\times {10}^{-5}$	7.15$\times {10}^{-2}$
1	7.43$\times {10}^{-5}$	8.72$\times {10}^{-2}$

which clearly states that our method gives more accurate results than the method in [54]. Using the error estimation method, we also estimate the upper bound of errors and calculate $\parallel e_6{\parallel }_{\infty }=2.61\times {10}^{-4}$, $\parallel e_7{\parallel }_{\infty }=7.43\times {10}^{-5}$ and $\parallel f_6-f_7{\parallel }_{\infty }=1.90\times {10}^{-4}$. Therefore $\parallel e_7{\parallel }_{\infty }\le {\parallel f_6-f_7\parallel }_{\infty }$ that follows the estimated upper bound of error.

Example 5.

Consider the following system of fractional differential equations [14,55]

$${\mathcal{D}}^{\alpha }{f}_1\left(t\right)=f_1\left(t\right)+f_2\left(t\right),$$

(50)

$${\mathcal{D}}^{\beta }{f}_2\left(t\right)=-f_1\left(t\right)+f_2\left(t\right),$$

(51)

subject to the conditions

$$f_1\left(0\right)=0,f_2\left(0\right)=1,$$

(52)

where the exact solution of system at $\alpha =\beta =1$ is $f_1\left(t\right)=e^{t}sint$ and $f_2\left(t\right)=e^{t}cost$.

The relative error for different values of k are plotted in Figure 5 and Figure 6. Using the error estimation method, we estimate the upper bound of errors for $f_1\left(t\right)$ and calculate

$$\begin{array}{ccc}\hfill \parallel e_6{\parallel }_{\infty }& =& 1.59\times {10}^{-3}\hfill \\ \hfill \parallel e_7{\parallel }_{\infty }& =& 6.18\times {10}^{-5}\hfill \\ \hfill \parallel f_6-f_7{\parallel }_{\infty }& =& 1.59\times {10}^{-3}\hfill \end{array}$$

We observe that the result $max\{\parallel e_6{\parallel }_{\infty },\parallel e_7{\parallel }_{\infty }\}\le \parallel f_6-f_7{\parallel }_{\infty }$ is satisfied here. Similarly for the function $f_2\left(t\right)$ the results are reported as

$$\begin{array}{ccc}\hfill \parallel e_6{\parallel }_{\infty }& =& 9.96\times {10}^{-4}\hfill \\ \hfill \parallel e_7{\parallel }_{\infty }& =& 2.98\times {10}^{-4}\hfill \\ \hfill \parallel f_6-f_7{\parallel }_{\infty }& =& 1.08\times {10}^{-3}.\hfill \end{array}$$

The numbers clearly show that the error is bounded from above, i.e., $max\{\parallel e_6{\parallel }_{\infty },\parallel e_7{\parallel }_{\infty }\}\le \parallel f_6-f_7{\parallel }_{\infty }$. To show the efficiency, absolute errors compared to variation iteration method (VIM) [55] are given in

Table 3. Comparison of Absolute errors in $f_1\left(t\right)$ in Example 5.

t	Present Method at k = 5	Present Method at k = 6	VIM [55]
0.1	1.59$\times {10}^{-3}$	5.99$\times {10}^{-6}$	1.66$\times {10}^{-4}$
0.2	9.84$\times {10}^{-4}$	1.40$\times {10}^{-5}$	1.32$\times {10}^{-3}$
0.3	6.08$\times {10}^{-4}$	1.32$\times {10}^{-5}$	4.39$\times {10}^{-3}$
0.4	3.80$\times {10}^{-4}$	1.02$\times {10}^{-5}$	1.02$\times {10}^{-2}$
0.5	2.34$\times {10}^{-4}$	1.53$\times {10}^{-5}$	1.93$\times {10}^{-2}$
0.6	1.22$\times {10}^{-4}$	3.16$\times {10}^{-5}$	3.21$\times {10}^{-2}$
0.7	2.24$\times {10}^{-5}$	5.15$\times {10}^{-5}$	4.86$\times {10}^{-2}$
0.8	7.21$\times {10}^{-5}$	6.18$\times {10}^{-5}$	6.81$\times {10}^{-2}$
0.9	1.73$\times {10}^{-4}$	5.60$\times {10}^{-5}$	8.95$\times {10}^{-2}$
1	3.29$\times {10}^{-4}$	5.56$\times {10}^{-5}$	1.11$\times {10}^{-1}$

and

Table 4. Comparison of Absolute errors in $f_2\left(t\right)$ in Example 5.

t	Present Method at k = 5	Present Method at k = 6	VIM [55]
0.1	1.33$\times {10}^{-4}$	4.81$\times {10}^{-5}$	1.79$\times {10}^{-4}$
0.2	2.89$\times {10}^{-4}$	1.31$\times {10}^{-5}$	1.54$\times {10}^{-4}$
0.3	4.07$\times {10}^{-4}$	1.74$\times {10}^{-5}$	5.57$\times {10}^{-3}$
0.4	5.09$\times {10}^{-4}$	3.42$\times {10}^{-7}$	1.41$\times {10}^{-2}$
0.5	6.02$\times {10}^{-4}$	7.26$\times {10}^{-5}$	2.94$\times {10}^{-2}$
0.6	6.85$\times {10}^{-4}$	1.45$\times {10}^{-4}$	5.40$\times {10}^{-2}$
0.7	7.64$\times {10}^{-4}$	1.25$\times {10}^{-4}$	9.11$\times {10}^{-2}$
0.8	8.44$\times {10}^{-4}$	2.68$\times {10}^{-5}$	1.44$\times {10}^{-1}$
0.9	9.28$\times {10}^{-4}$	1.53$\times {10}^{-4}$	2.17$\times {10}^{-1}$
1	9.96$\times {10}^{-4}$	2.98$\times {10}^{-4}$	3.13$\times {10}^{-1}$

which excludes that our method gives more accurate results than the method in [55].

Example 6.

Consider the following linear time fractional wave equation [18]

$$\frac{{\partial }^{\alpha }f}{\partial t^{\alpha }}=\frac{1}{2}{x}^2\frac{{\partial }^{2}f}{\partial x^2},$$

(53)

having $f(x,0)=x$, $\frac{\partial f(x,0)}{\partial t}=x^2$.

The exact solution is not known.

Here, we first convert the fractional partial differential equation to ordinary differential equation as described in Section 4, then the solution is obtained by our proposed method for $\alpha =1.5$, $k=6$ presented in

Table 5. Solution by proposed method for different values of x and t in Example 6.

x	t = 0	t = 0.06	t = 0.13	t = 0.29	t = 0.50
0.00	0.00	0.00	0.00	0.00	0.00
0.11	0.11	0.110729	0.111595	0.113677	0.116726
0.31	0.31	0.315791	0.322671	0.339207	0.363420
0.88	0.88	0.926665	0.982110	1.115365	1.310479
1.00	1.00	1.060260	1.131857	1.303932	1.555887

and have compared with the method VIM (

Table 6. Solution by variation iteration method (VIM) for different values of x and t in Example 6.

x	t = 0	t = 0.06	t = 0.13	t = 0.29	t = 0.50
0.00	0.00	0.00	0.00	0.00	0.00
0.11	0.11	0.110729	0.111595	0.113677	0.116726
0.31	0.31	0.315791	0.322670	0.339207	0.363419
0.88	0.88	0.926669	0.982101	1.115360	1.310469
1.00	1.00	1.060265	1.131845	1.303926	1.555874

) and Inverse Multiquadric-Radial Basis Functions (IMQ-RBF) (

Table 7. Solution by IMQ-RBF for different values of x and t in Example 6.

x	t = 0	t = 0.06	t = 0.13	t = 0.29	t = 0.50
0.00	0.00	0.00	0.00	0.00	0.00
0.11	0.11	0.110729	0.111595	0.113679	0.116710
0.31	0.31	0.315794	0.322675	0.339223	0.363298
0.88	0.88	0.926696	0.982140	1.115490	1.309495
1.00	1.00	1.060300	1.131896	1.304094	1.554617

) which shows that the solution is in good agreement with VIM and IMQ-RBF [18].

Example 7.

Consider the nonlinear fractional differential equation

$${\mathcal{D}}^{4}f\left(t\right)+{\mathcal{D}}^{7/2}f\left(t\right)+f^3\left(t\right)=t^9,f\left(0\right)=f^{\prime }\left(0\right)=f^{″}\left(0\right)=0,f^{‴}\left(0\right)=6,$$

(54)

with exact solution $f\left(t\right)=t^3$.

The relative error for different values of k are plotted in Figure 7 which show that our method gives a very close solution to the analytic solution. Using the error estimation method, we estimated the upper bound of errors and calculated

$$\begin{array}{ccc}\hfill \parallel e_6{\parallel }_{\infty }& =& 1.71\times {10}^{-3}\hfill \\ \hfill \parallel e_7{\parallel }_{\infty }& =& 7.72\times {10}^{-5}\hfill \\ \hfill \parallel f_6-f_7{\parallel }_{\infty }& =& 1.72\times {10}^{-3}.\hfill \end{array}$$

Hence, we can see that here $\parallel f_6-f_7{\parallel }_{\infty }$ bounds the error $\parallel e_6{\parallel }_{\infty }$.

We also analyzed the $L_{\infty }$-error at different values of k, i.e., $k=5,6,7,8$ for examples which clearly exclude that we achieve the best results at $k=6$, as shown in Figure 8, Figure 9, Figure 10, Figure 11.

7. Conclusions

Enormous efforts and advances have been conducted to obtain the numerical solutions of fractional differential equations. An operational matrix of orthonormal Bernstein polynomials is derived to find the inverse Laplace transform in [50]. Here, the practical use of our proposed method is discussed for finding the solutions of some fractional order ordinary differential equations including the mathematical model of instrument (MEMS) and partial differential equations (particularly wave equation) that converts the problem to system of linear algebraic equations. The accuracy of the method is illustrated while comparing the solutions with some existing methods like VIM, FFDM, cubic spline and IMQ-RBF. We have also combined our method with Laplace adomian decomposition method that is advantageous to solve nonlinear fractional differential equations. Finally, we have analyzed the solution of each illustrative example at different values of k, i.e., at $k=5,6,7,8$ and with the help of graphs relative errors are shown. It is also observed from the plots of supremum norm error that at $k=6$, we achieve the best accurate result compared to others.