Modeling and Optimization of Gaseous Thermal Slip Flow in Rectangular Microducts Using a Particle Swarm Optimization Algorithm
Abstract
1. Introduction
1.1. Rarefied Gas Flows
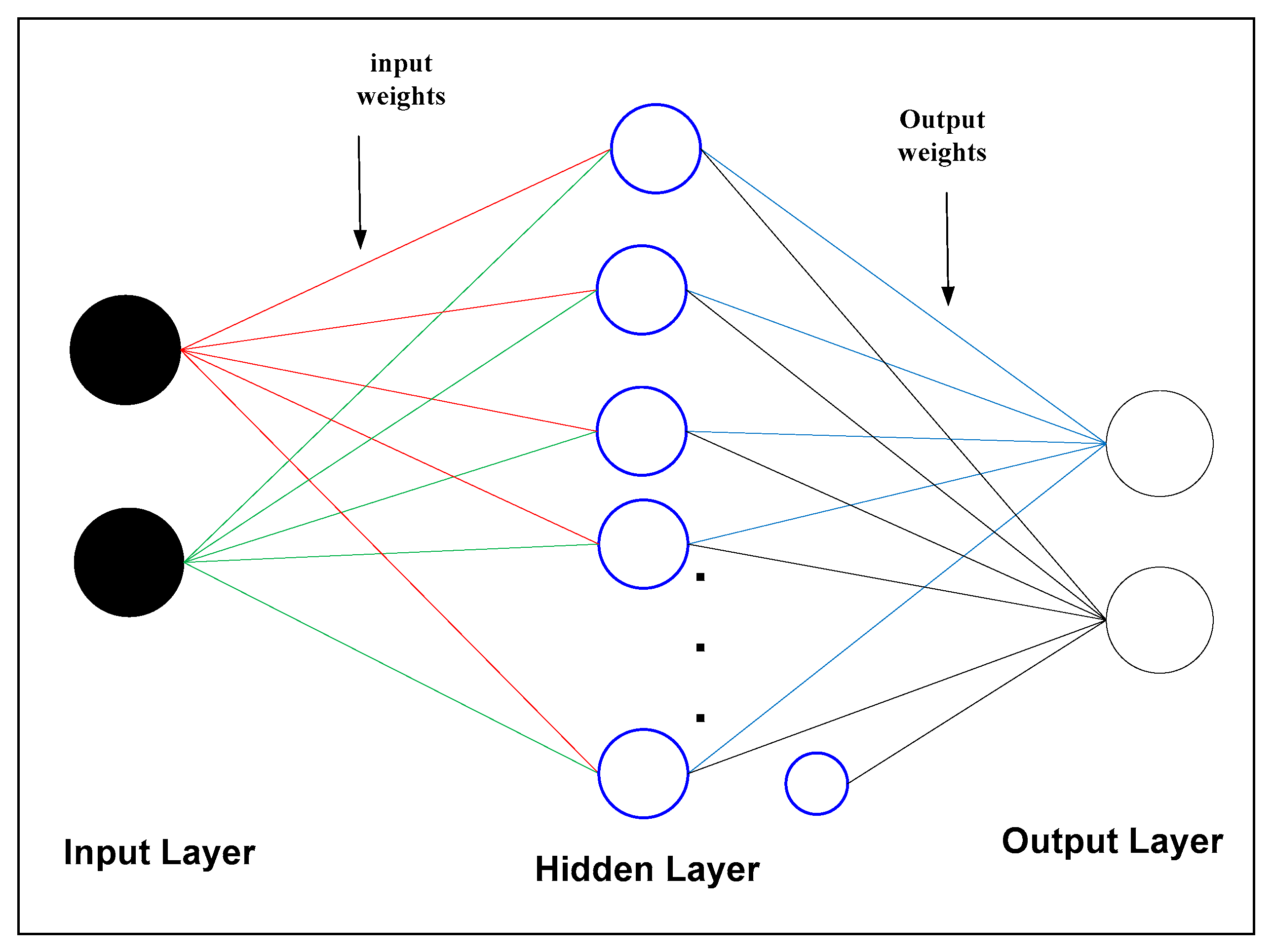
1.2. Artificial Neural Networks
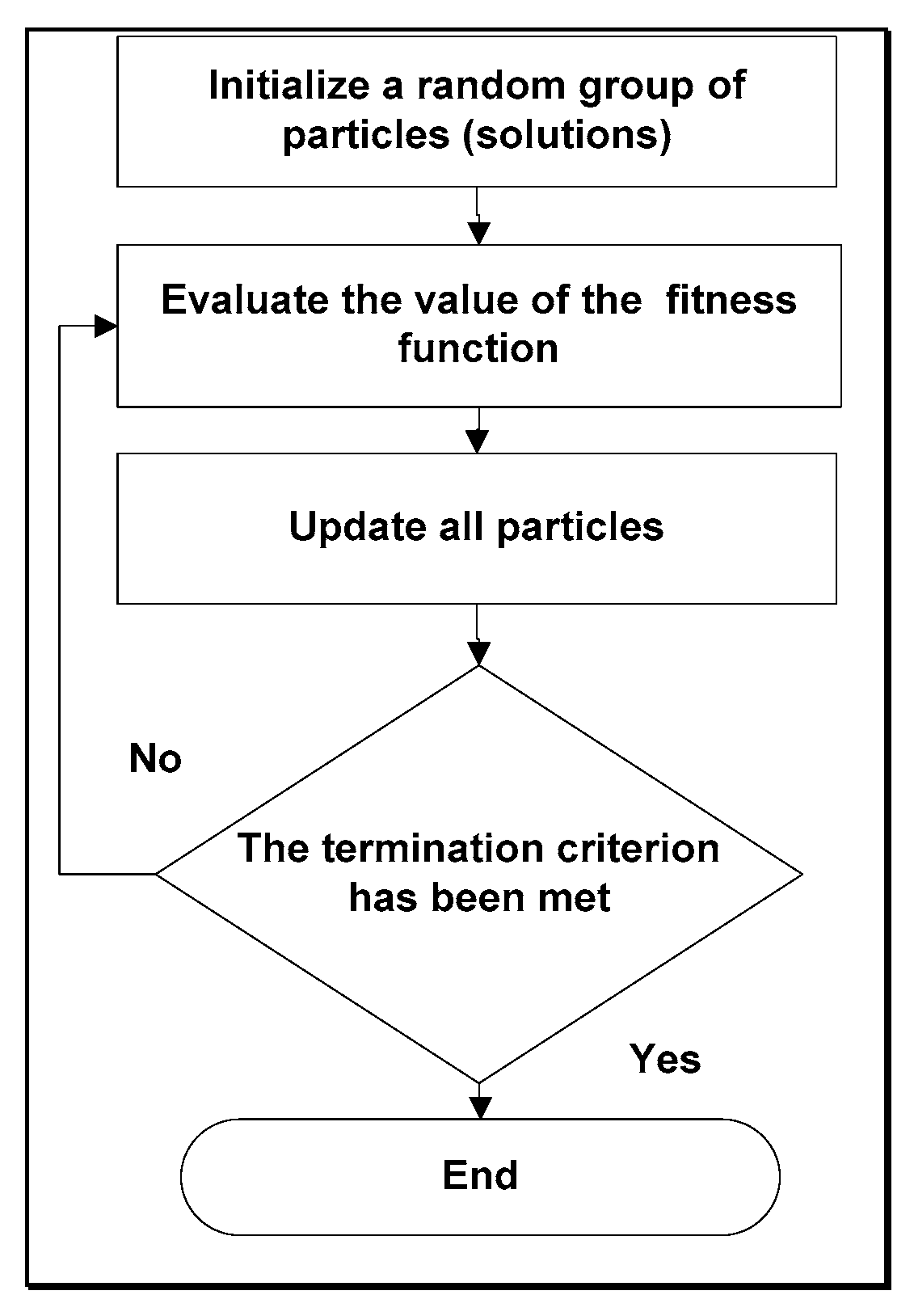
1.3. Particle Swarm Optimization Algorithm
2. Mathematical Model
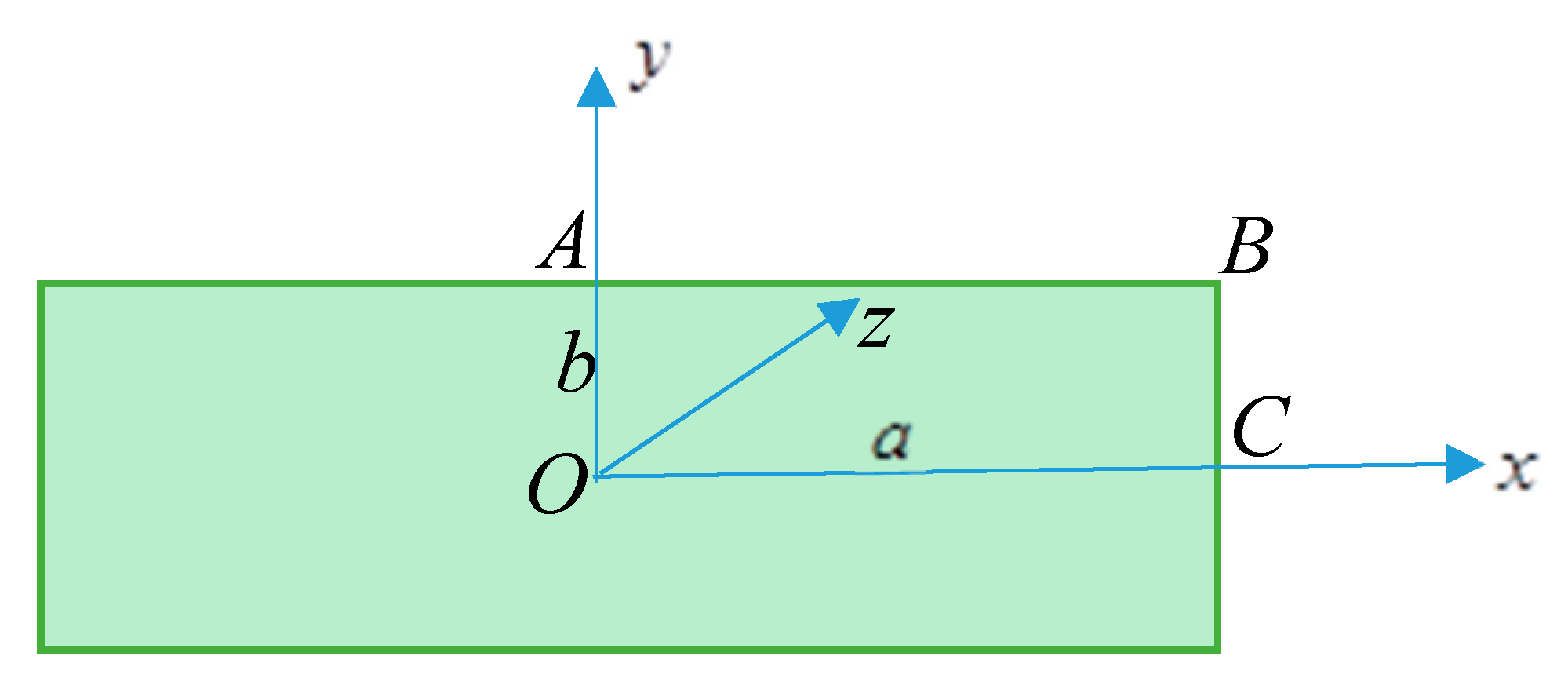
2.1. Hydrodynamic Analysis
2.2. Thermal Analysis
2.3. Solution Procedure
3. Results and Discussion
4. Conclusions
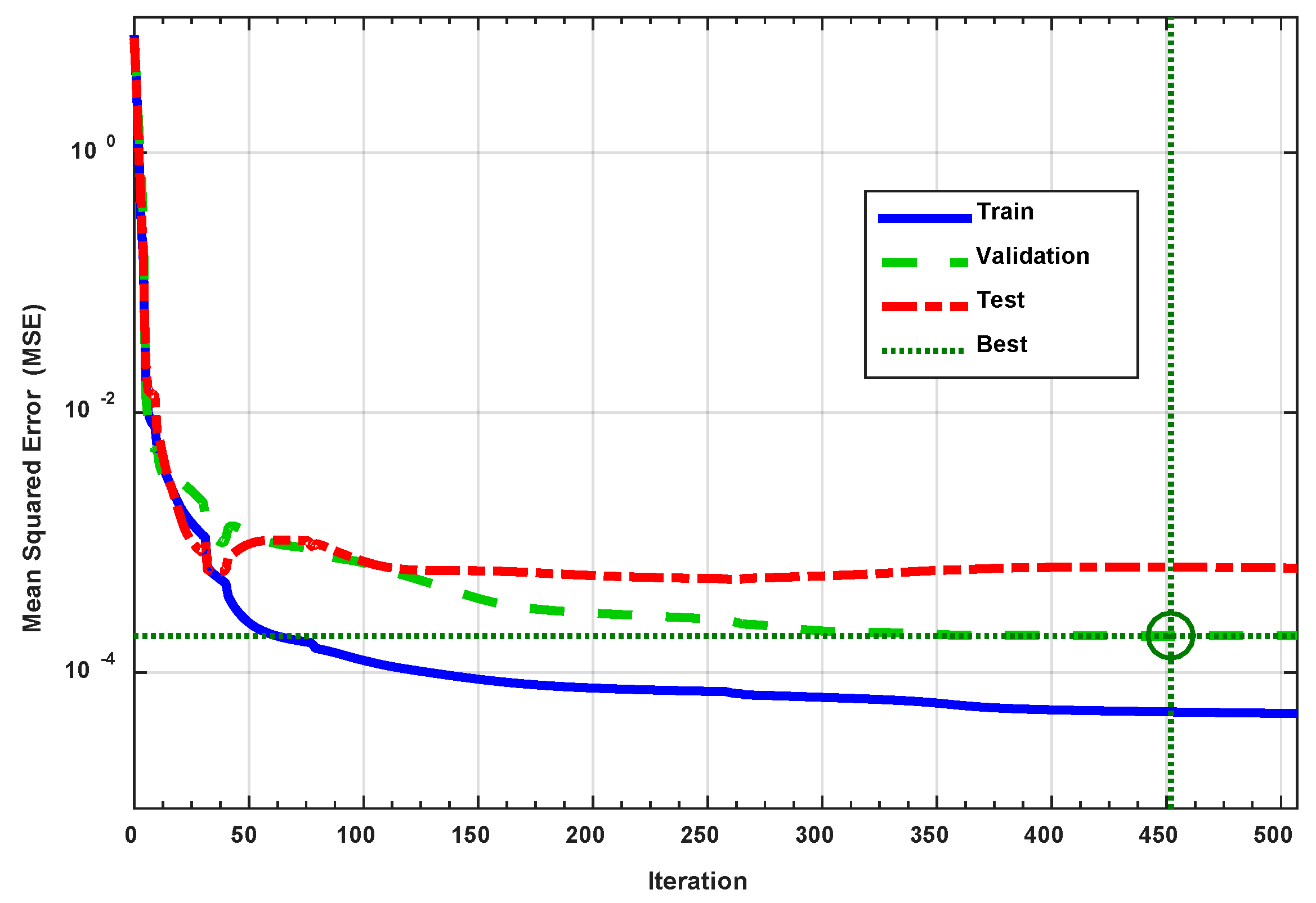
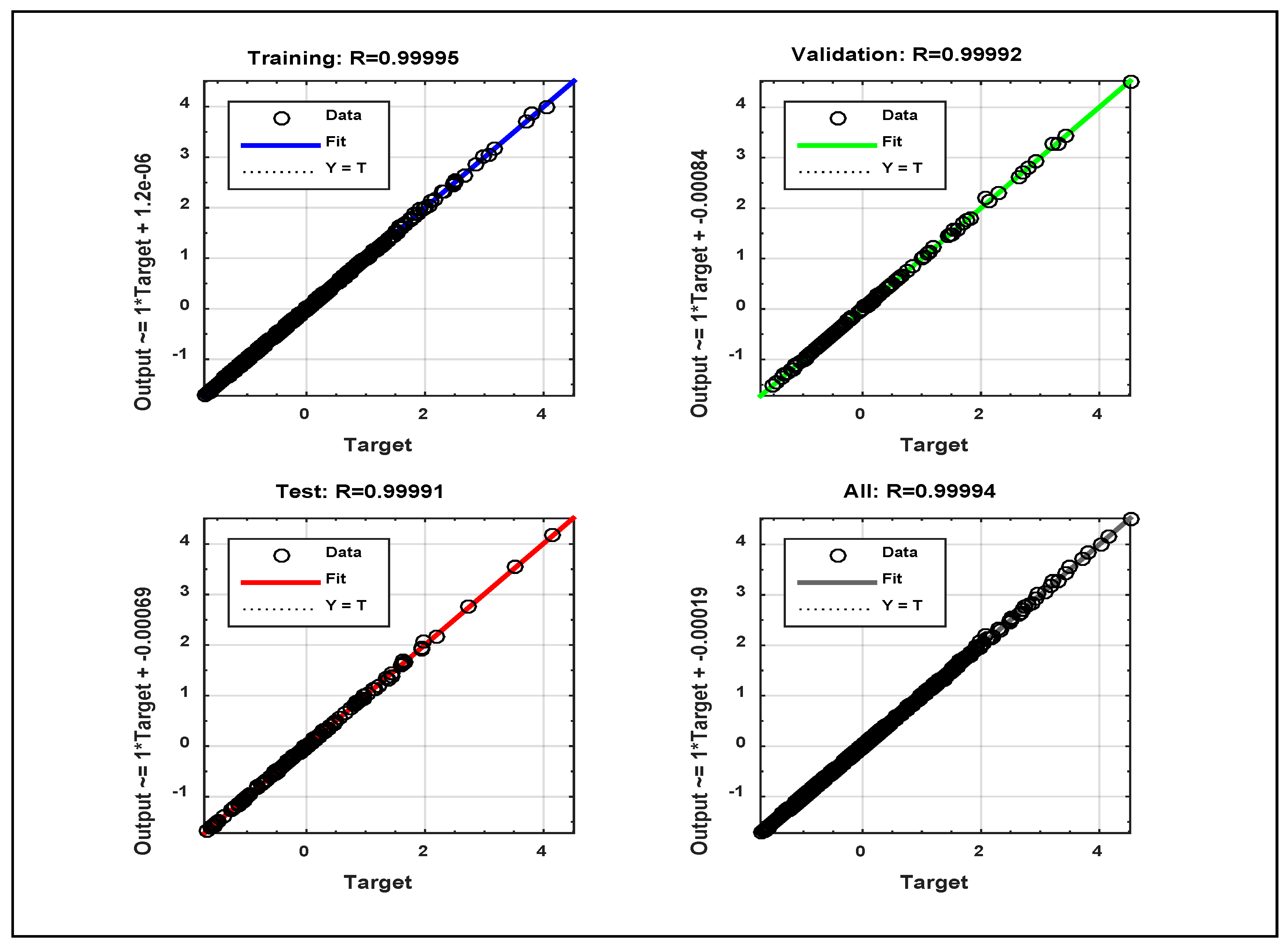
- The small tolerance values for the mean squared error function values and a very close correlation coefficient of 1 in the NN models proved that the NN models were suitable to use for predicting the Poiseuille Po and Nusselt Nu numbers.
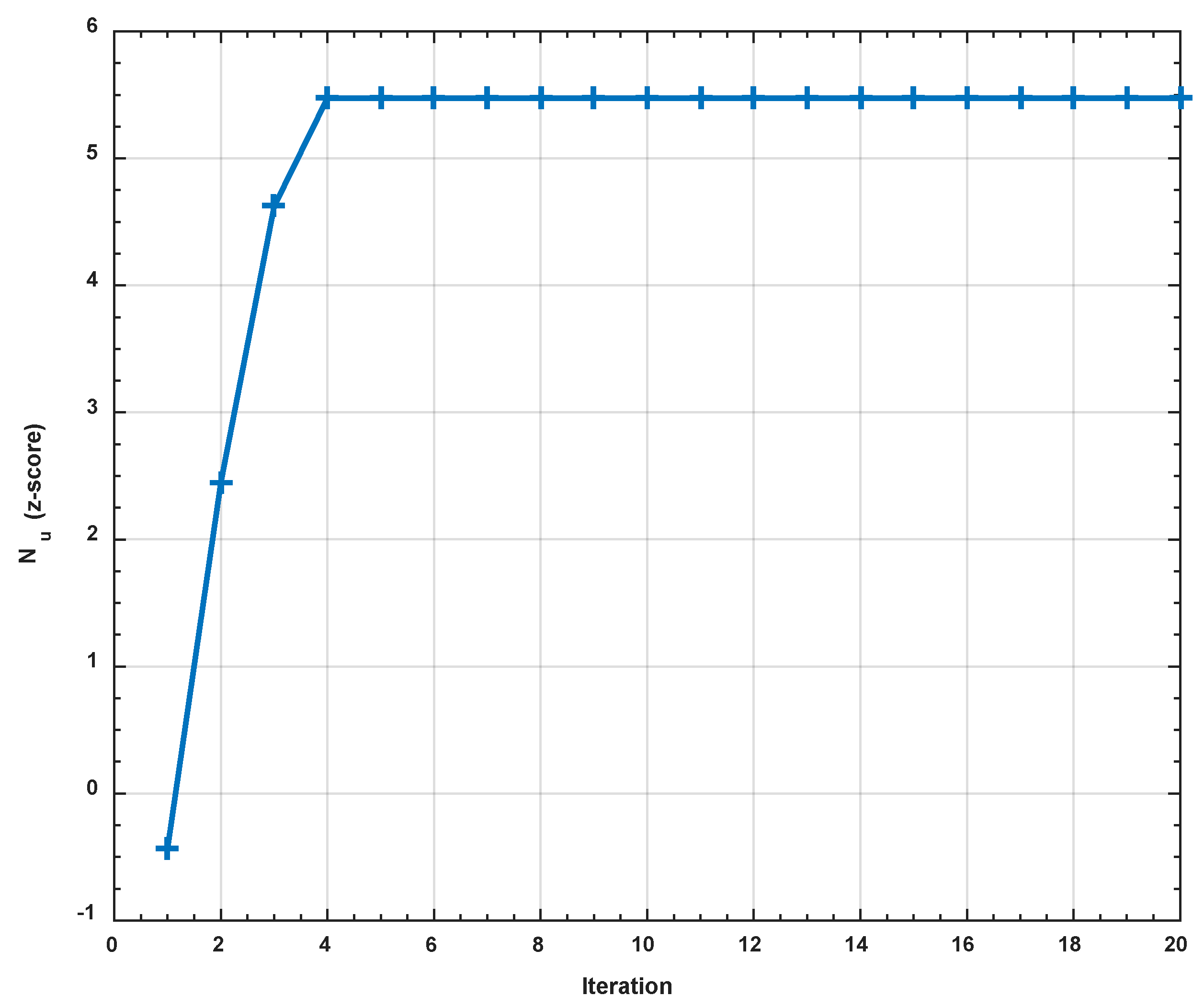
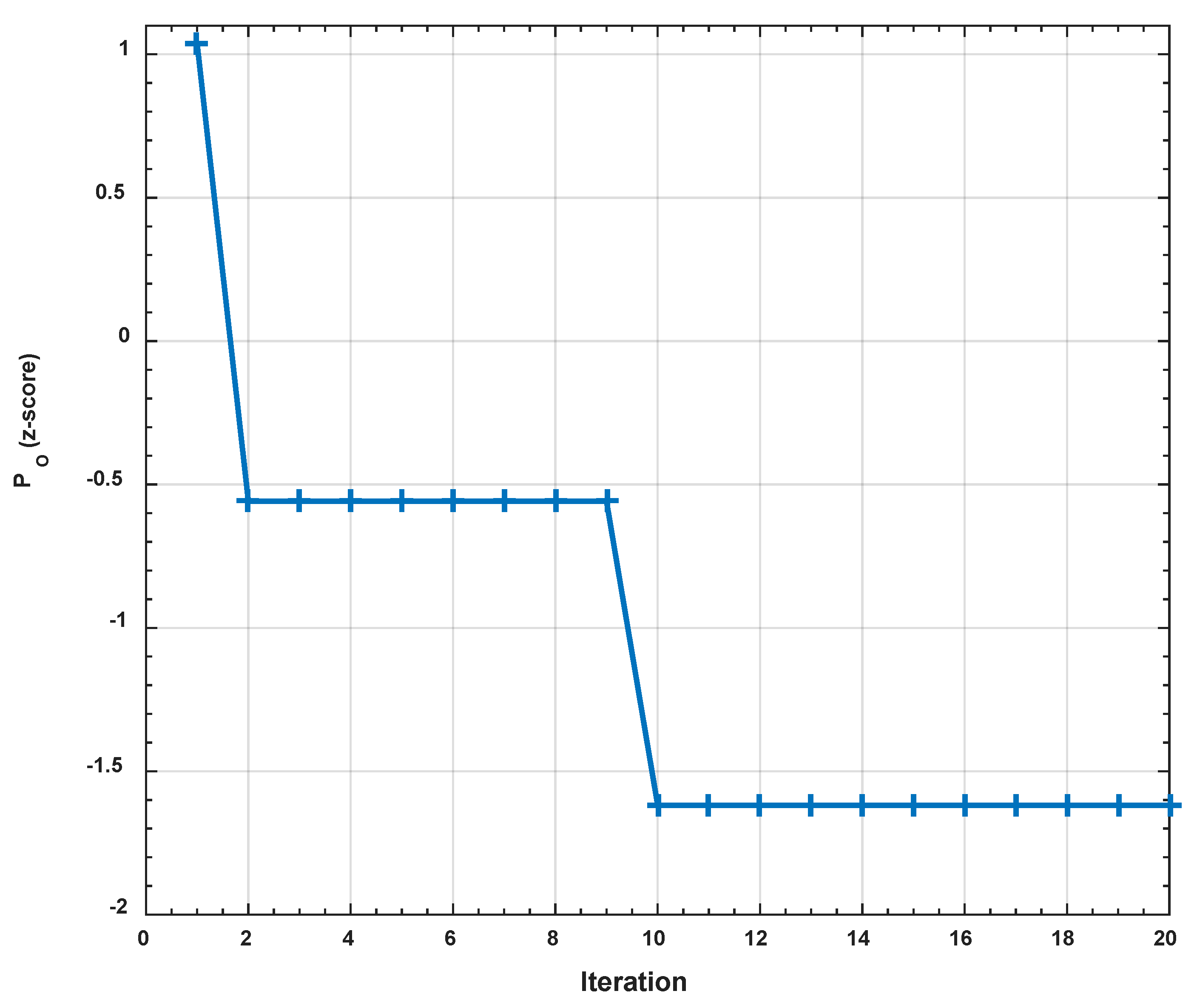
- Without going back to the numerical data, the proposed models were used with the PSO algorithm to find the optimal values of Po and Nu.
- The optimal values of Po and Nu are found when and .
- The correlation coefficient of the models was greater than 0.95.
- The optimal values of the curves were determined when the curves became stable.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liu, J.; Tai, Y.-C.; Pong, C.-M.H.-C. MEMS for pressure distribution studies of gaseous flows in microchannels. In Proceedings of the IEEE Micro Electro Mechanical Systems, Amsterdam, The Netherlands, 29 January–2 February 1995; p. 209. [Google Scholar]
- Arkilic, E.B. Gaseous Flow in Micro-channels, Application of Microfabrication to Fluid Mechanics. AsmeFed 1994, 197, 57–66. [Google Scholar]
- Ameel, T.A.; Wang, X.; Barron, R.F.; Warrington, R.O. Laminar forced convection in a circular tube with constant heat flux and slip flow. Microscale Thermophys. Eng. 1997, 1, 303–320. [Google Scholar]
- Zade, A.Q.; Renksizbulut, M.; Friedman, J. Heat transfer characteristics of developing gaseous slip-flow in rectangular microchannels with variable physical properties. Int. J. Heat Fluid Flow 2011, 32, 117–127. [Google Scholar] [CrossRef]
- Ghodoossi, L. Prediction of heat transfer characteristics in rectangular microchannels for slip flow regime and H1 boundary condition. Int. J. Therm. Sci. 2005, 44, 513–520. [Google Scholar] [CrossRef]
- Hettiarachchi, H.M.; Golubovic, M.; Worek, W.M.; Minkowycz, W. Three-dimensional laminar slip-flow and heat transfer in a rectangular microchannel with constant wall temperature. Int. J. Heat Mass Transf. 2008, 51, 5088–5096. [Google Scholar] [CrossRef]
- Yu, S.; Ameel, T.A. Slip-flow heat transfer in rectangular microchannels. Int. J. Heat Mass Transf. 2001, 44, 4225–4234. [Google Scholar] [CrossRef]
- Renksizbulut, M.; Niazmand, H.; Tercan, G. Slip-flow and heat transfer in rectangular microchannels with constant wall temperature. Int. J. Therm. Sci. 2006, 45, 870–881. [Google Scholar] [CrossRef]
- Tamayol, A.; Hooman, K. Slip-flow in microchannels of non-circular cross sections. J. Fluids Eng. 2011, 133, 091202. [Google Scholar] [CrossRef]
- Hooman, K. A superposition approach to study slip-flow forced convection in straight microchannels of uniform but arbitrary cross-section. Int. J. Heat Mass Transf. 2008, 51, 3753–3762. [Google Scholar] [CrossRef]
- Sadeghi, A.; Saidi, M.H. Viscous dissipation and rarefaction effects on laminar forced convection in microchannels. J. Heat Transf. 2010, 132, 072401. [Google Scholar] [CrossRef]
- Yovanovich, M.; Khan, W.A. Compact Slip Flow Models for Gas Flows in Rectangular, Trapezoidal and Hexagonal Microchannels. In Proceedings of the ASME 2015 International Technical Conference and Exhibition on Packaging and Integration of Electronic and Photonic Microsystems, San Francisco, CA, USA, 6–9 July 2015. [Google Scholar]
- Duan, Z.; Muzychka, Y. Slip flow in elliptic microchannels. Int. J. Therm. Sci. 2007, 46, 1104–1111. [Google Scholar] [CrossRef]
- Duan, Z.; Muzychka, Y. Slip flow in non-circular microchannels. Microfluid. Nanofluid. 2007, 3, 473–484. [Google Scholar] [CrossRef]
- Duan, Z.; Muzychka, Y. Slip flow in the hydrodynamic entrance region of circular and noncircular microchannels. J. Fluids Eng. 2010, 132, 011201. [Google Scholar] [CrossRef]
- Yovanovich, M.M.; Khan, W.A. Friction and Heat Transfer in Liquid and Gas Flows in Micro-and Nanochannels. Adv. Heat Transf. 2015, 47, 203–307. [Google Scholar]
- Ebert, W.; Sparrow, E.M. Slip flow in rectangular and annular ducts. J. Basic Eng. 1965, 87, 1018–1024. [Google Scholar] [CrossRef]
- Baghani, M.; Sadeghi, A.; Baghani, M. Gaseous slip flow forced convection in microducts of arbitrary but constant cross section. Nanoscale Microscale Thermophys. Eng. 2014, 18, 354–372. [Google Scholar] [CrossRef]
- Wang, C. Benchmark solutions for slip flow and H1 heat transfer in rectangular and equilateral triangular ducts. J. Heat Transf. 2013, 135, 021703. [Google Scholar] [CrossRef]
- Beskok, A.; Karniadakis, G.E. Report: A model for flows in channels, pipes, and ducts at micro and nano scales. Microscale Thermophys. Eng. 1999, 3, 43–77. [Google Scholar]
- Yovanovich, M.; Khan, W. Similarities of rarefied gas flows in elliptical and rectangular microducts. Int. J. Heat Mass Transf. 2016, 93, 629–636. [Google Scholar] [CrossRef]
- Klášterka, H.; Vimmr, J.; Hajžman, M. Contribution to the gas flow and heat transfer modelling in microchannels. Appl. Comput. Mech. 2009, 12, 63–74. [Google Scholar]
- Hamadneh, N.; Tilahun, S.; Sathasivam, S.; Choon, O.H. Prey-predator algorithm as a new optimization technique using in radial basis function neural networks. Res. J. Appl. Sci. 2013, 8, 383–387. [Google Scholar]
- Rakhshandehroo, G.R.; Vaghefi, M.; Aghbolaghi, M.A. Forecasting groundwater level in Shiraz plain using artificial neural networks. Arab. J. Sci. Eng. 2012, 37, 1871–1883. [Google Scholar] [CrossRef]
- Yeung, D.S.; Li, J.-C.; Ng, W.W.; Chan, P.P. MLPNN training via a multiobjective optimization of training error and stochastic sensitivity. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 978–992. [Google Scholar] [CrossRef] [PubMed]
- Mefoued, S. Assistance of knee movements using an actuated orthosis through subject’s intention based on MLPNN approximators. In Proceedings of the 2013 International Joint Conference on Neural Networks, Dallas, TX, USA, 4–9 August 2013; pp. 1–6. [Google Scholar]
- Shi, Y.; Eberhart, R.C. Empirical study of particle swarm optimization. In Proceedings of the 1999 Congress on Evolutionary Computation, Washington, DC, USA, 6–9 July 1999; pp. 1945–1950. [Google Scholar]
- Trelea, I.C. The particle swarm optimization algorithm: Convergence analysis and parameter selection. Inf. Process. Lett. 2003, 85, 317–325. [Google Scholar] [CrossRef]
- Liu, X. Radial basis function neural network based on PSO with mutation operation to solve function approximation problem. In Proceedings of the International Conference in Swarm Intelligence, Brussels, Belgium, 8–10 September 2010; pp. 92–99. [Google Scholar]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Shi, Y. Particle swarm optimization: Developments, applications and resources. In Proceedings of the 2001 Congress on Evolutionary Computation, Seoul, Korea, 27–30 May 2001; pp. 81–86. [Google Scholar]
- Marinke, R.; Araujo, E.; Coelho, L.S.; Matiko, I. Particle swarm optimization (PSO) applied to fuzzy modeling in a thermal-vacuum system. In Proceedings of the Fifth International Conference on Hybrid Intelligent Systems, Rio de Janeiro, Brazil, 6–9 November 2005; p. 6. [Google Scholar]
- Nenortaite, J.; Butleris, R. Application of particle swarm optimization algorithm to decision making model incorporating cluster analysis. In Proceedings of the 2008 Conference on Human System Interactions, Krakow, Poland, 25–27 May 2008; pp. 88–93. [Google Scholar]
- Hamadneh, N.; Khan, W.A.; Sathasivam, S.; Ong, H.C. Design optimization of pin fin geometry using particle swarm optimization algorithm. PLoS ONE 2013, 8, e66080. [Google Scholar] [CrossRef] [PubMed]
- Bai, Q. Analysis of particle swarm optimization algorithm. Comput. Inf. Sci. 2010, 3, 180. [Google Scholar] [CrossRef]
- Morini, G.L.; Spiga, M.; Tartarini, P. The rarefaction effect on the friction factor of gas flow in microchannels. Superlattices Microstruct. 2004, 35, 587–599. [Google Scholar] [CrossRef]
- Sadeghi, M.; Sadeghi, A.; Saidi, M.H. Gaseous slip flow mixed convection in vertical microducts of constant but arbitrary geometry. J. Thermophys. Heat Transf. 2014, 28, 771–784. [Google Scholar] [CrossRef]
- Shah, R.; London, A. Laminar Flow Forced Convection in Ducts, Advances in Heat Transfer; Academic Press: New York, NY, USA, 1978. [Google Scholar]


| Morini et al. [36] | Sadeghi et al. [37] | Present Results | |
|---|---|---|---|
| 0.2 | 9.46 | 9.464 | 9.519 |
| 0.4 | 8.65 | 8.654 | 8.721 |
| 0.6 | 8.25 | 8.248 | 8.331 |
| 0.8 | 8.08 | 8.076 | 8.178 |
| 1 | 8.04 | 8.033 | 8.159 |
| Numerical | Exact [38] | % Difference | |
|---|---|---|---|
| 0.001 | 24.031 | 23.7 | 1.3774 |
| 0.01 | 23.743 | 23.41 | 1.4025 |
| 0.02 | 23.432 | 22.24 | 5.0871 |
| 0.1 | 21.259 | 20.95 | 1.4535 |
| 0.2 | 19.182 | 18.89 | 1.5223 |
| 0.3 | 17.641 | 17.36 | 1.5929 |
| 0.4 | 16.514 | 16.24 | 1.6592 |
| 0.5 | 15.712 | 15.43 | 1.7948 |
| 0.6 | 15.164 | 14.87 | 1.9388 |
| 0.7 | 14.811 | 14.5 | 2.0998 |
| 0.8 | 14.608 | 14.28 | 2.2453 |
| 0.9 | 14.519 | 14.17 | 2.4037 |
| 1 | 14.514 | 14.14 | 2.5768 |
| Numerical | Exact [38] | % Difference | |
|---|---|---|---|
| 0.001 | 10.944 | 10.9 | 0.402 |
| 0.01 | 10.862 | 10.82 | 0.3867 |
| 0.02 | 10.773 | 10.47 | 2.8126 |
| 0.1 | 10.139 | 10.09 | 0.4833 |
| 0.2 | 9.519 | 9.46 | 0.6198 |
| 0.3 | 9.056 | 9 | 0.6184 |
| 0.4 | 8.721 | 8.66 | 0.6995 |
| 0.5 | 8.487 | 8.41 | 0.9073 |
| 0.6 | 8.331 | 8.25 | 0.9723 |
| 0.7 | 8.233 | 8.14 | 1.1296 |
| 0.8 | 8.178 | 8.08 | 1.1983 |
| 0.9 | 8.157 | 8.04 | 1.4344 |
| 1 | 8.159 | 8.04 | 1.4585 |
| 0.001 | 6.1658 | 1.4213 | 0.7164 |
| 0.25 | 5.1047 | 1.7625 | 1.0819 |
| 0.35 | 4.6786 | 1.8996 | 1.2287 |
| 0.5 | 4.0394 | 2.1051 | 1.4488 |
| 0.65 | 3.8048 | 2.1830 | 1.5590 |
| 0.75 | 3.6485 | 2.2348 | 1.6325 |
| 0.85 | 3.6156 | 2.2745 | 1.6816 |
| 1 | 3.5662 | 2.3341 | 1.7552 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamadneh, N.N.; Khan, W.A.; Khan, I.; Alsagri, A.S. Modeling and Optimization of Gaseous Thermal Slip Flow in Rectangular Microducts Using a Particle Swarm Optimization Algorithm. Symmetry 2019, 11, 488. https://doi.org/10.3390/sym11040488
Hamadneh NN, Khan WA, Khan I, Alsagri AS. Modeling and Optimization of Gaseous Thermal Slip Flow in Rectangular Microducts Using a Particle Swarm Optimization Algorithm. Symmetry. 2019; 11(4):488. https://doi.org/10.3390/sym11040488
Chicago/Turabian StyleHamadneh, Nawaf N., Waqar A. Khan, Ilyas Khan, and Ali S. Alsagri. 2019. "Modeling and Optimization of Gaseous Thermal Slip Flow in Rectangular Microducts Using a Particle Swarm Optimization Algorithm" Symmetry 11, no. 4: 488. https://doi.org/10.3390/sym11040488
APA StyleHamadneh, N. N., Khan, W. A., Khan, I., & Alsagri, A. S. (2019). Modeling and Optimization of Gaseous Thermal Slip Flow in Rectangular Microducts Using a Particle Swarm Optimization Algorithm. Symmetry, 11(4), 488. https://doi.org/10.3390/sym11040488






