Propagation of Blast Waves in a Non-Ideal Magnetogasdynamics
Abstract
:1. Introduction
2. Fundamental Equations
3. Similarity Transformation of Fundamental Equations
4. Construction of Solutions in Power Series of s
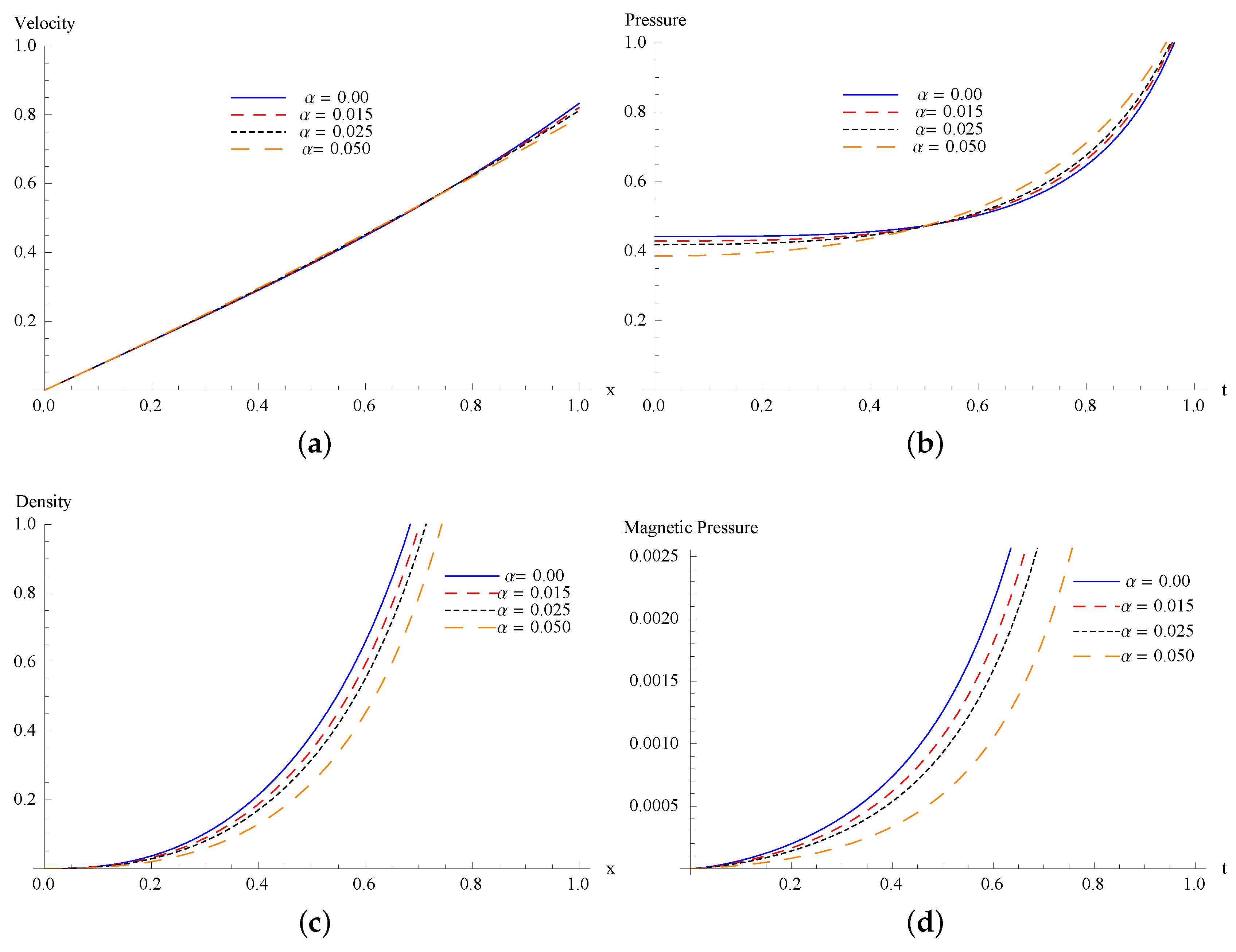
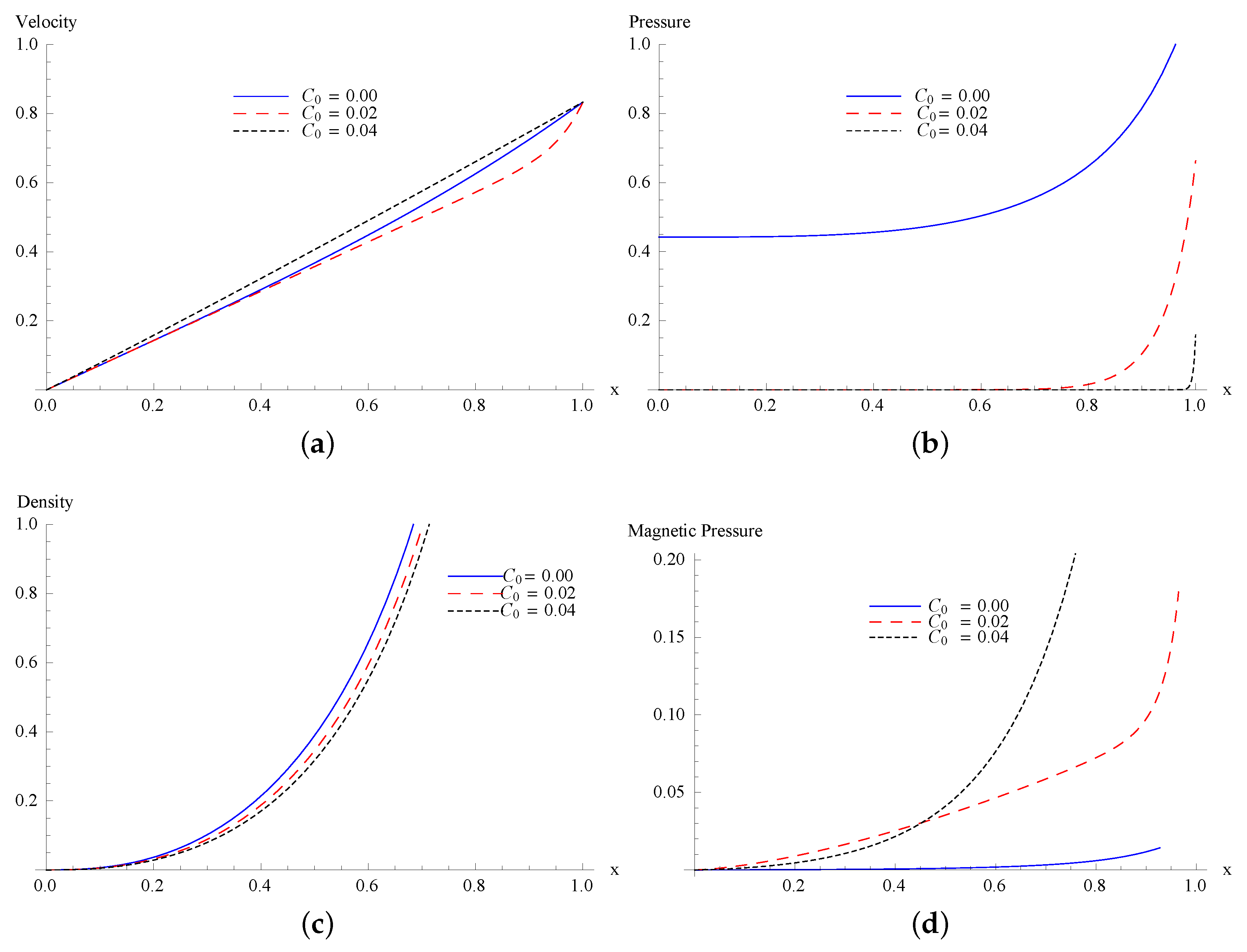
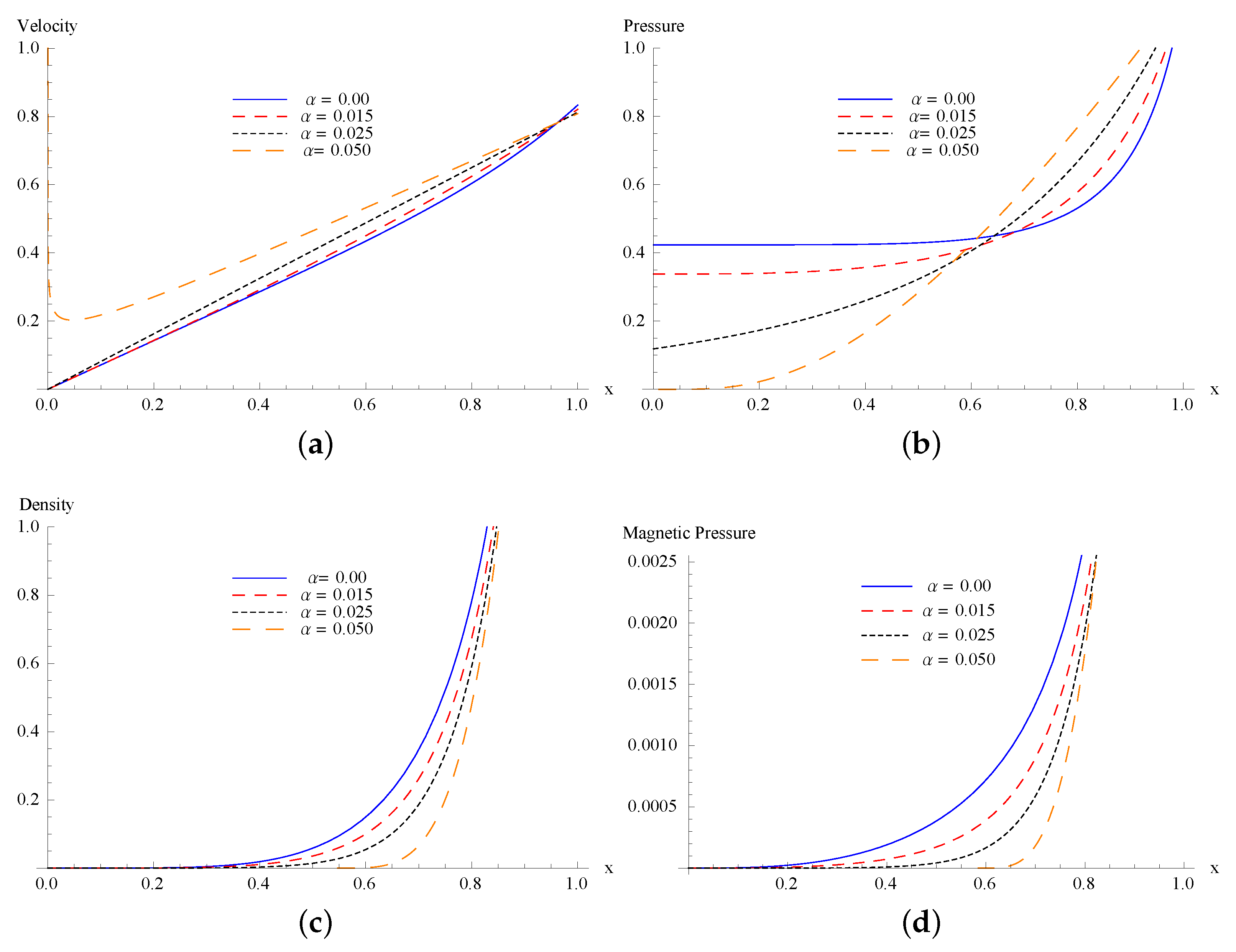
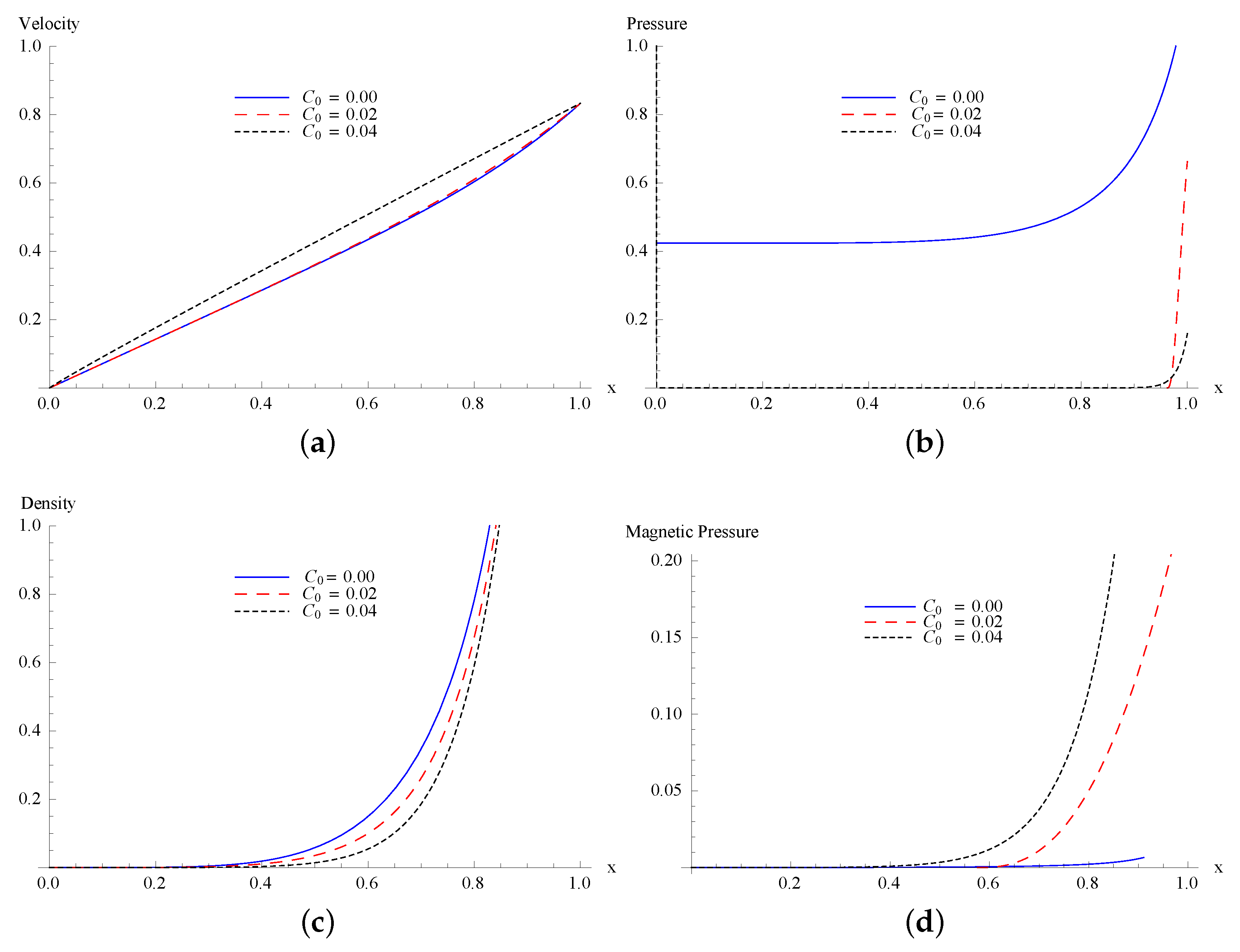
5. The First Approximation
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sedov, L. Propagation of strong shock waves. J. Appl. Math. Mech. 1946, 10, 241–250. [Google Scholar]
- Taylor, G. The formation of a blast wave by a very intense explosion. Proc. R. Soc. A 1950, 201, 159–174. [Google Scholar]
- Sakurai, A. On the propagation and structure of the blast wave, I. J. Phys. Soc. Japan 1953, 8, 662–669. [Google Scholar] [CrossRef]
- Sakurai, A. On the propagation and structure of a blast wave, II. J. Phys. Soc. Japan 1954, 9, 256–266. [Google Scholar] [CrossRef]
- Murata, S. New exact solution of the blast wave problem in gas dynamics. Chaos Solitons Fract. 2006, 28, 327–330. [Google Scholar] [CrossRef]
- Donato, A. Similarity analysis and non-linear wave propagation. Int. J. Non-Linear Mech. 1987, 22, 307–314. [Google Scholar] [CrossRef]
- Book, D.L. The Sedov self-similar point blast solutions in non-uniform media. Shock Waves 1994, 4, 1–10. [Google Scholar] [CrossRef]
- Lalicata, M.V.; Torrisi, M. Group analysis approach for a binary reacting mixture. Int. J. Non-Linear Mech. 1994, 29, 279–288. [Google Scholar] [CrossRef]
- Anisimov, S.; Spiner, O. Motion of an almost ideal gas in the presence of a strong point explosion. J. Appl. Math. Mech. 1972, 36, 883–887. [Google Scholar] [CrossRef]
- Lerche, I. Mathematical theory of cylindrical isothermal blast waves in a magnetic field. Aust. J. Phys. 1981, 34, 279–302. [Google Scholar] [CrossRef]
- Lerche, I. Mathematical theory of one-dimensional isothermal blast waves in a magnetic field. Aust. J. Phys. 1979, 32, 491–502. [Google Scholar] [CrossRef]
- Arora, R.; Yadav, S.; Siddiqui, M.J. Similarity method for the study of strong shock waves in magnetogasdynamics. Bound. Value Probl. 2014, 2014, 142. [Google Scholar] [CrossRef]
- Siddiqui, M.J.; Arora, R.; Kumar, A. Shock waves propagation under the influence of magnetic field. Chaos Solitons Fract. 2017, 97, 66–74. [Google Scholar] [CrossRef]
- Singh, L.; Husain, A.; Singh, M. On the evolution of weak discontinuities in radiative magnetogasdynamics. Acta Astronaut. 2011, 68, 16–21. [Google Scholar] [CrossRef]
- Singh, L.; Husain, A.; Singh, M. An analytical study of strong non-planar shock waves in magnetogasdynamics. Adv. Theor. Appl. Mech. 2010, 6, 291–297. [Google Scholar]
- Pandey, M.; Radha, R.; Sharma, V. Symmetry analysis and exact solutions of magnetogasdynamic equations. Q. J. Mech. Appl. Math. 2008, 61, 291–310. [Google Scholar] [CrossRef]
- Menon, V.; Sharma, V. Characteristic wave fronts in magnetohydrodynamics. J. Math. Anal. Appl. 1981, 81, 189–203. [Google Scholar] [CrossRef]
- Arora, R.; Siddiqui, M.J.; Singh, V. Similarity method for imploding strong shocks in a non-ideal relaxing gas. Int. J. Non-Linear Mech. 2013, 57, 1–9. [Google Scholar] [CrossRef]
- Siddiqui, M.J.; Arora, R.; Singh, V. Propagation of non-linear waves in a non-ideal relaxing gas. Int. J. Comput. Math. 2018, 95, 2330–2342. [Google Scholar] [CrossRef]
- Arora, R.; Siddiqui, M.J. Evolutionary behavior of weak shocks in a non-ideal gas. J. Theor. Appl. Phys. 2013, 7, 14. [Google Scholar] [CrossRef]
- Ramu, A.; Dunna, N.; Satpathi, D.K. Numerical study of shock waves in non-ideal magnetogasdynamics (MHD). J. Egypt. Math. Soc. 2016, 24, 116–124. [Google Scholar] [CrossRef]
- Whitham, G. Linear and nonlinear waves. Phys. Today 1975, 28, 55. [Google Scholar] [CrossRef]
- Zhuravskaya, T.; Levin, V. The propagation of converging and diverging shock waves under intense heat exchange conditions. J. Appl. Math. Mech. 1996, 60, 745–752. [Google Scholar] [CrossRef]
| x | Sakurai [3] | Sakurai [3] | Sakurai [3] | ||||
|---|---|---|---|---|---|---|---|
| 0.0 | 0.8333 | 6.000 | 1.167 | 0.8333 | 6.000 | 1.167 | |
| 1.0 | 0.015 | - | - | - | 0.8208 | 5.550 | 1.167 |
| 0.025 | - | - | - | 0.8125 | 5.250 | 1.167 | |
| 0.0 | 0.7170 | 3.096 | 0.815 | 0.7251 | 3.096 | 0.815 | |
| 0.9 | 0.015 | - | - | - | 0.7199 | 2.899 | 0.835 |
| 0.025 | 0.7159 | 2.767 | 0.848 | ||||
| 0.0 | 0.6151 | 1.785 | 0.647 | 0.6259 | 1.785 | 0.647 | |
| 0.8 | 0.015 | - | - | - | 0.6251 | 1.660 | 0.664 |
| 0.025 | - | - | - | 0.6240 | 1.577 | 0.677 | |
| 0.0 | 0.5239 | 1.080 | 0.556 | 0.5341 | 1.080 | 0.556 | |
| 0.7 | 0.015 | - | - | - | 0.5356 | 0.990 | 0.567 |
| 0.025 | - | - | - | 0.5362 | 0.931 | 0.575 | |
| 0.0 | 0.4405 | 0.658 | 0.504 | 0.4484 | 0.658 | 0.504 | |
| 0.6 | 0.015 | - | - | - | 0.4507 | 0.593 | 0.508 |
| 0.025 | - | - | - | 0.4521 | 0.551 | 0.515 | |
| 0.0 | 0.3624 | 0.389 | 0.473 | 0.3676 | 0.389 | 0.473 | |
| 0.5 | 0.015 | - | - | - | 0.3698 | 0.345 | 0.471 |
| 0.025 | - | - | - | 0.3712 | 0.317 | 0.471 | |
| 0.0 | 0.2877 | 0.214 | 0.456 | 0.2877 | 0.214 | 0.456 | |
| 0.4 | 0.015 | - | - | - | 0.2921 | 0.187 | 0.450 |
| 0.025 | - | - | - | 0.2933 | 0.170 | 0.446 | |
| 0.0 | 0.2148 | 0.102 | 0.447 | 0.2160 | 0.102 | 0.447 | |
| 0.3 | 0.015 | - | - | - | 0.2169 | 0.088 | 0.437 |
| 0.025 | - | - | - | 0.2177 | 0.079 | 0.431 | |
| 0.0 | 0.1430 | 0.037 | 0.443 | 0.1432 | 0.037 | 0.443 | |
| 0.2 | 0.015 | - | - | - | 0.1436 | 0.0316 | 0.432 |
| 0.025 | - | - | - | 0.1439 | 0.0282 | 0.423 | |
| 0.0 | 0.0714 | 0.006 | 0.442 | 0.0714 | 0.006 | 0.442 | |
| 0.1 | 0.015 | - | - | - | 0.0715 | 0.005 | 0.429 |
| 0.025 | - | - | - | 0.0716 | 0.005 | 0.419 | |
| 0.0 | 0.0000 | 0.000 | 0.442 | 0.0000 | 0.000 | 0.442 | |
| 0.0 | 0.015 | - | - | - | 0.0000 | 0.000 | 0.429 |
| 0.025 | - | - | - | 0.0000 | 0.000 | 0.419 |
| x | Sakurai [3] | Sakurai [3] | Sakurai [3] | ||||
|---|---|---|---|---|---|---|---|
| 0.0 | 0.8333 | 6.000 | 1.167 | 0.8333 | 6.000 | 1.167 | |
| 1.0 | 0.015 | - | - | - | 0.8208 | 5.550 | 1.167 |
| 0.025 | - | - | - | 0.8125 | 5.250 | 1.167 | |
| 0.0 | 0.7008 | 1.898 | 0.685 | 0.7072 | 1.898 | 0.684 | |
| 0.9 | 0.015 | - | - | - | 0.7196 | 1.767 | 0.767 |
| 0.025 | 0.7314 | 1.678 | 0.874 | ||||
| 0.0 | 0.5973 | 0.783 | 0.531 | 0.6038 | 0.783 | 0.531 | |
| 0.8 | 0.015 | - | - | - | 0.6246 | 0.713 | 0.577 |
| 0.025 | - | - | - | 0.6503 | 0.668 | 0.667 | |
| 0.0 | 0.5104 | 0.347 | 0.468 | 0.5141 | 0.346 | 0.468 | |
| 0.7 | 0.015 | - | - | - | 0.5351 | 0.309 | 0.474 |
| 0.025 | - | - | - | 0.5691 | 0.284 | 0.517 | |
| 0.0 | 0.4322 | 0.153 | 0.441 | 0.4346 | 0.150 | 0.441 | |
| 0.6 | 0.015 | - | - | - | 0.4503 | 0.131 | 0.414 |
| 0.025 | - | - | - | 0.4880 | 0.119 | 0.406 | |
| 0.0 | 0.3582 | 0.058 | 0.429 | 0.3592 | 0.0582 | 0.429 | |
| 0.5 | 0.015 | - | - | - | 0.3695 | 0.050 | 0.378 |
| 0.025 | - | - | - | 0.4077 | 0.045 | 0.323 | |
| 0.0 | 0.2859 | 0.019 | 0.425 | 0.2863 | 0.019 | 0.425 | |
| 0.4 | 0.015 | - | - | - | 0.2919 | 0.016 | 0.357 |
| 0.025 | - | - | - | 0.3255 | 0.014 | 0.260 | |
| 0.0 | 0.2140 | 0.005 | 0.424 | 0.2144 | 0.004 | 0.424 | |
| 0.3 | 0.015 | - | - | - | 0.2168 | 0.004 | 0.346 |
| 0.025 | - | - | - | 0.2443 | 0.003 | 0.211 | |
| 0.0 | 0.1429 | 0.001 | 0.424 | 0.1429 | 0.001 | 0.423 | |
| 0.2 | 0.015 | - | - | - | 0.1437 | 0.001 | 0.340 |
| 0.025 | - | - | - | 0.1630 | 0.000 | 0.173 | |
| 0.0 | 0.0714 | 0.000 | 0.424 | 0.0714 | 0.000 | 0.423 | |
| 0.1 | 0.015 | - | - | - | 0.0715 | 0.000 | 0.338 |
| 0.025 | - | - | - | 0.0815 | 0.000 | 0.143 | |
| 0.0 | 0.0000 | 0.000 | 0.424 | 0.0000 | 0.000 | 0.423 | |
| 0.0 | 0.015 | - | - | - | 0.0000 | 0.000 | 0.338 |
| 0.025 | - | - | - | 0.0000 | 0.000 | 0.118 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chauhan, A.; Arora, R.; Siddiqui, M.J. Propagation of Blast Waves in a Non-Ideal Magnetogasdynamics. Symmetry 2019, 11, 458. https://doi.org/10.3390/sym11040458
Chauhan A, Arora R, Siddiqui MJ. Propagation of Blast Waves in a Non-Ideal Magnetogasdynamics. Symmetry. 2019; 11(4):458. https://doi.org/10.3390/sym11040458
Chicago/Turabian StyleChauhan, Astha, Rajan Arora, and Mohd Junaid Siddiqui. 2019. "Propagation of Blast Waves in a Non-Ideal Magnetogasdynamics" Symmetry 11, no. 4: 458. https://doi.org/10.3390/sym11040458
APA StyleChauhan, A., Arora, R., & Siddiqui, M. J. (2019). Propagation of Blast Waves in a Non-Ideal Magnetogasdynamics. Symmetry, 11(4), 458. https://doi.org/10.3390/sym11040458





