Relationship between the Paradox of Enrichment and the Dynamics of Persistence and Extinction in Prey-Predator Systems
Abstract
:1. Introduction
2. Mathematical Systems
3. Occurrence of the Paradox of Enrichment
3.1. Occurrence of the Paradox of Enrichment with Holling Type I
3.2. Occurrence of the Paradox of Enrichment with Holling Type II
4. Theoretical Approach to Persistence and Extinction
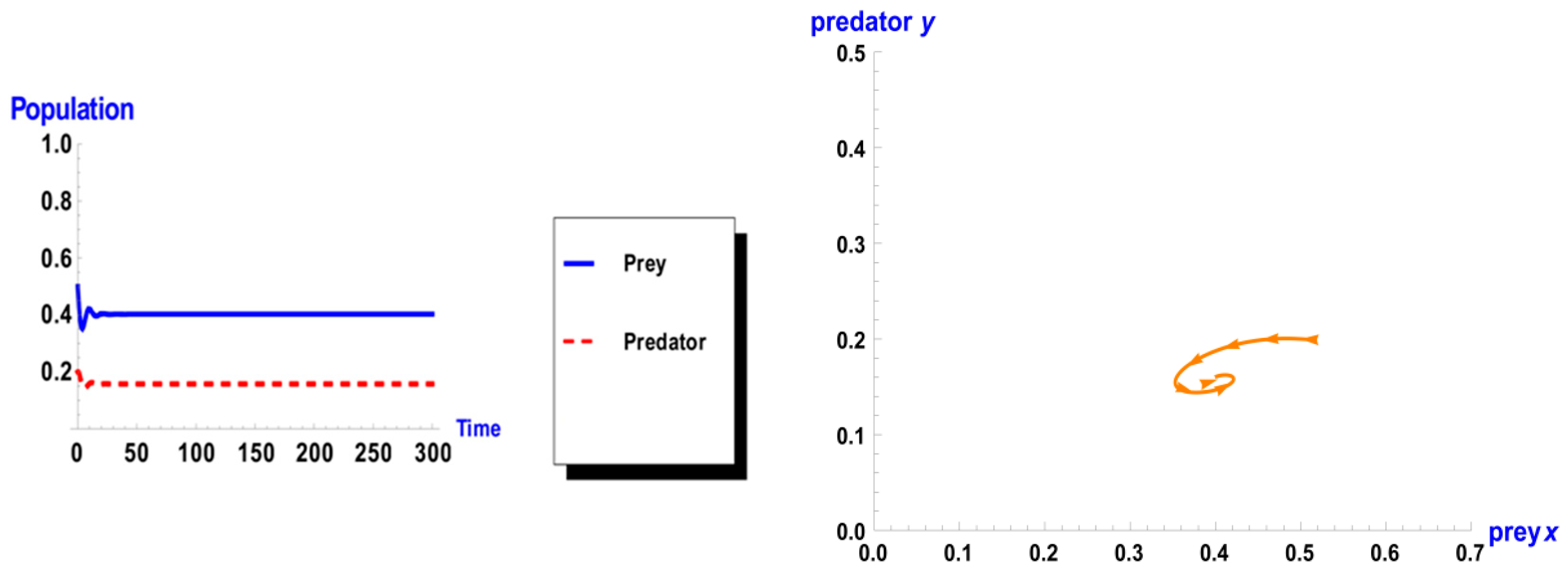
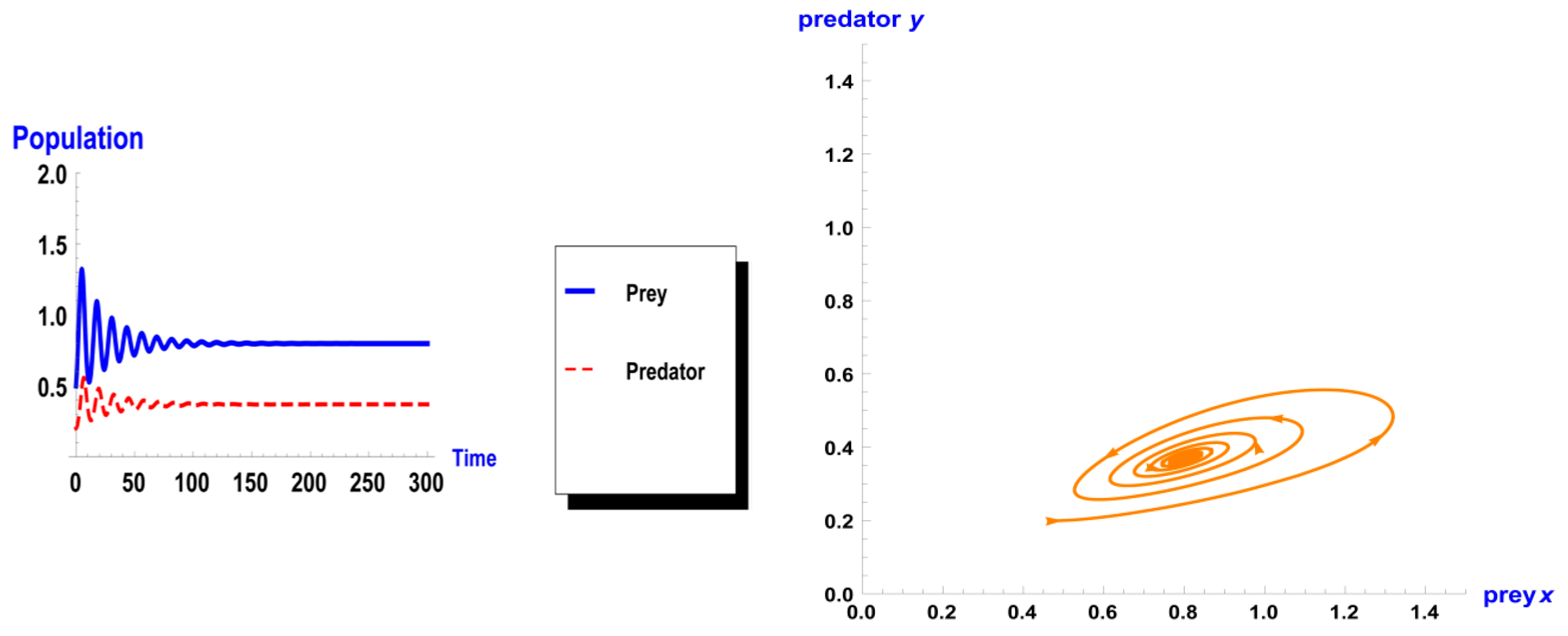
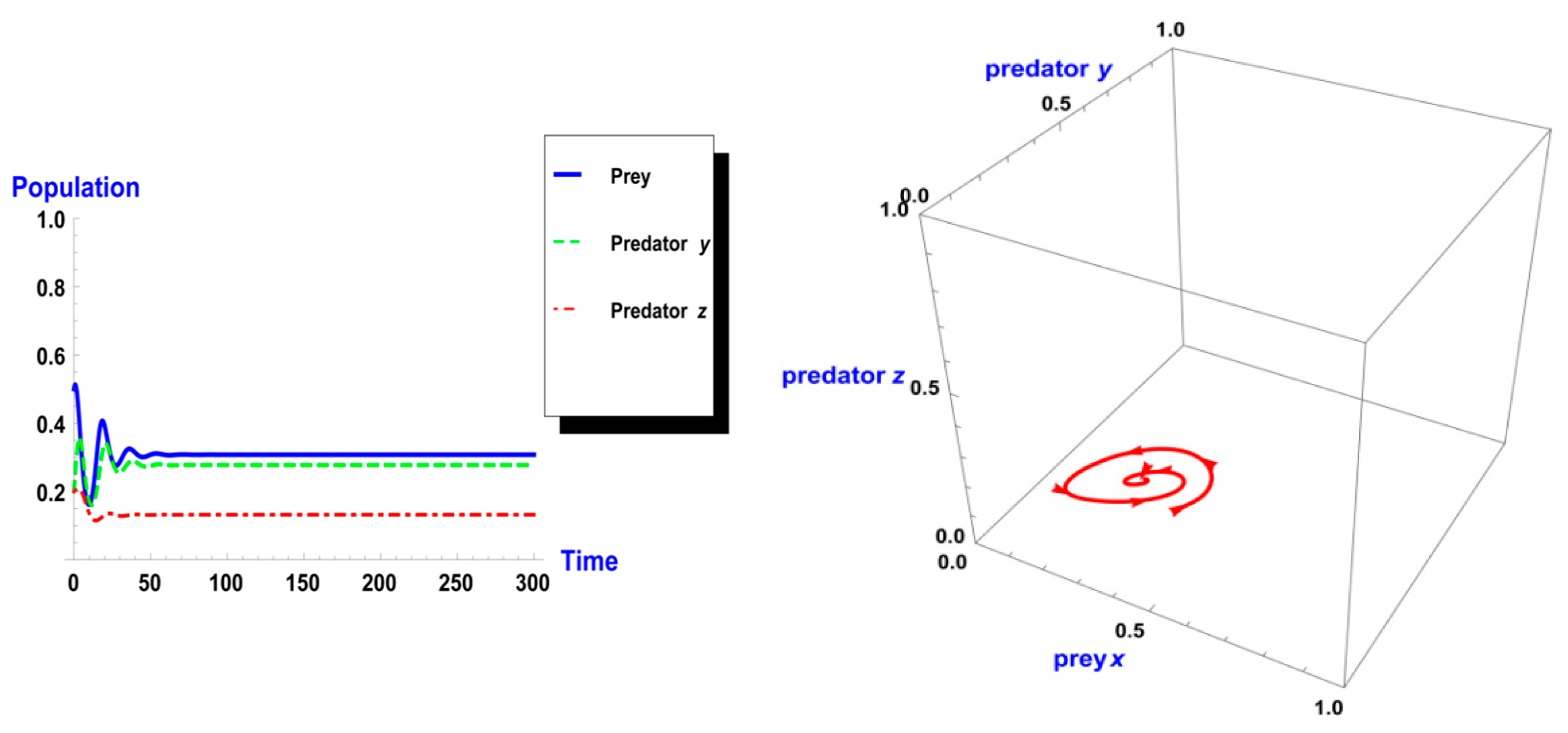
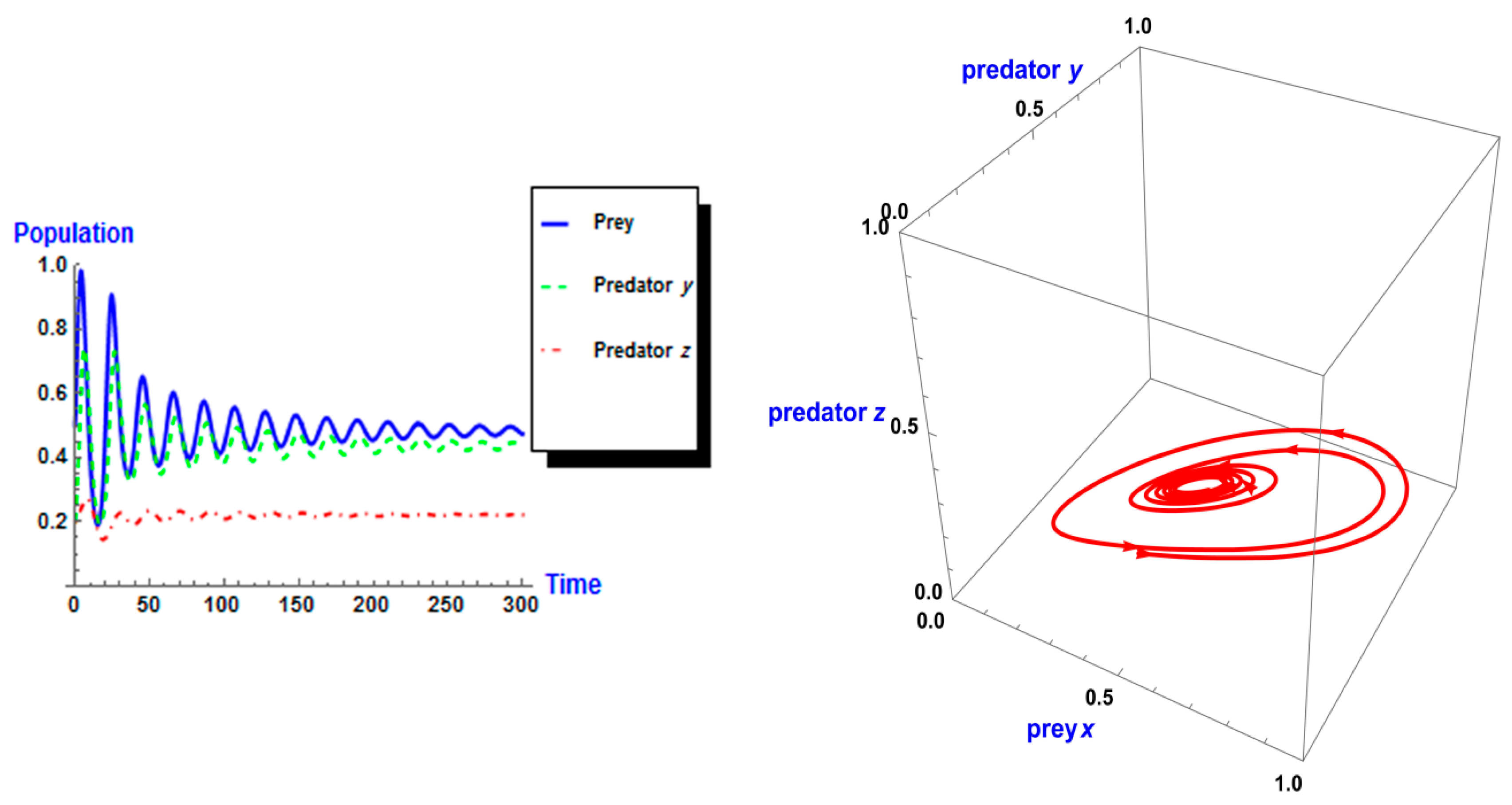
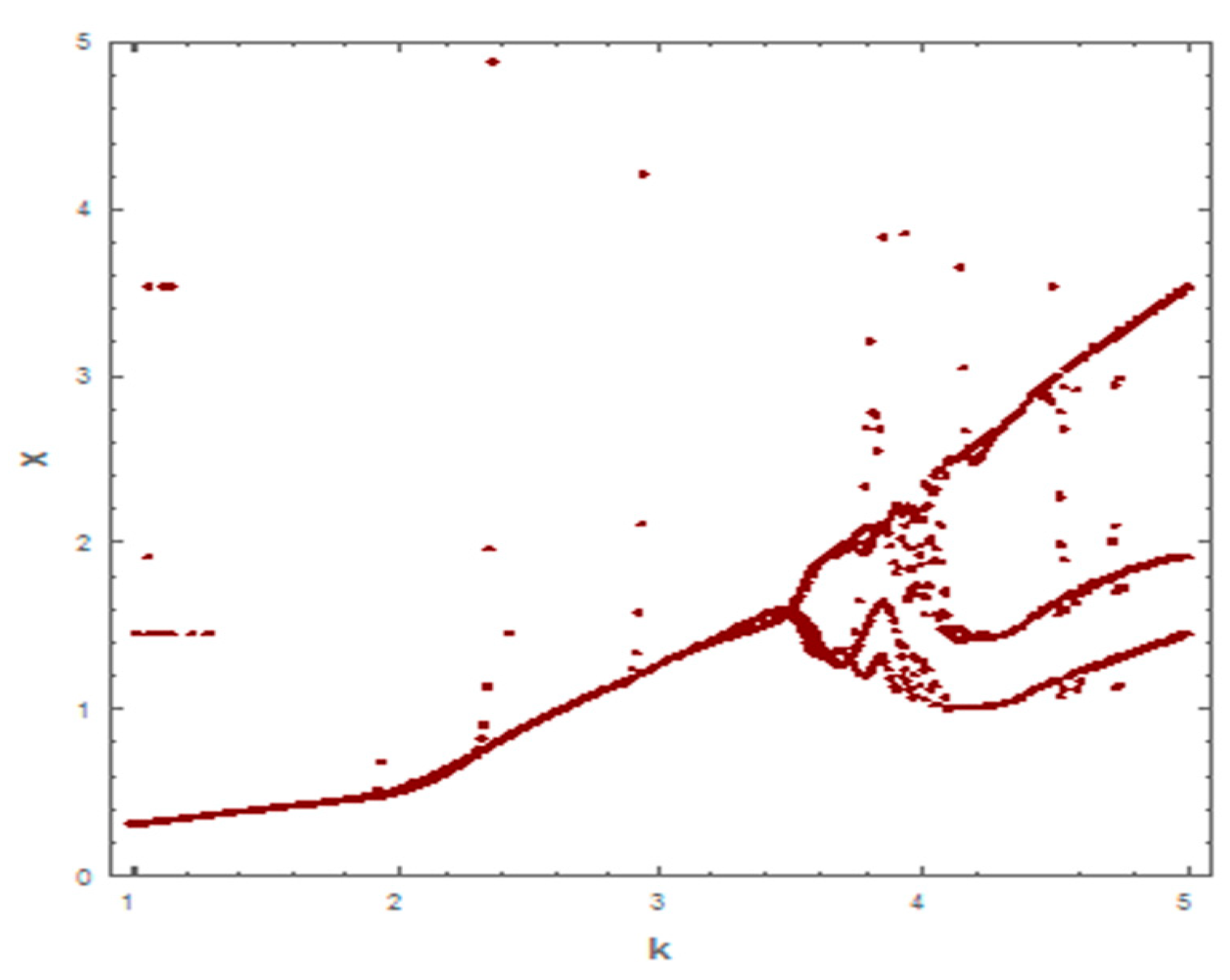
5. Numerical Simulation
6. Conclusions
Acknowledgments
Conflicts of Interest
References
- Liu, H.; Cheng, H. Dynamic analysis of a prey–predator model with state-dependent control strategy and square root response function. Adv. Differ. Equ. 2018, 2018, 63. [Google Scholar] [CrossRef] [Green Version]
- Gurubilli, K.K.; Srinivasu, P.D.N.; Banerjee, M. Global dynamics of a prey-predator model with Allee effect and additional food for the predators. Int. J. Dyn. Control 2017, 5, 903–916. [Google Scholar] [CrossRef]
- Keong, A.T.; Safuan, H.M.; Jacob, K. Dynamical behaviours of prey-predator fishery model with harvesting affected by toxic substances. Matematika 2018, 34, 143–151. [Google Scholar] [CrossRef]
- Heurich, M.; Zeis, K.; Küchenhoff, H.; Müller, J.; Belotti, E.; Bufka, L.; Woelfing, B. Selective predation of a stalking predator on ungulate prey. PLoS ONE 2016, 11, e0158449. [Google Scholar] [CrossRef] [PubMed]
- Gervasi, V.; Nilsen, E.B.; Sand, H.; Panzacchi, M.; Rauset, G.R.; Pedersen, H.C.; Kindberg, J.; Wabakken, P.; Zimmermann, B.; Odden, J.; et al. Predicting the potential demographic impact of predators on their prey: A comparative analysis of two carnivore–ungulate systems in Scandinavia. J. Anim. Ecol. 2012, 81, 443–454. [Google Scholar] [CrossRef] [PubMed]
- Mougi, A.; Iwasa, Y. Evolution towards oscillation or stability in a predator-prey system. Proc. Biol. Sci. 2010, 277, 3163–3171. [Google Scholar] [CrossRef] [PubMed]
- Nowak, E.M.; Theimer, T.C.; Schuett, G.W. Functional and numerical responses of predators: Where do vipers fit in the traditional paradigms? Biol. Rev. Camb. Philos. Soc. 2008, 83, 601–620. [Google Scholar] [CrossRef] [PubMed]
- Griffen, B.D.; Drake, J.M. Effects of habitat quality and size on extinction in experimental populations. Proc. R. Soc. B Biol. Sci. 2008, 275, 2251–2256. [Google Scholar] [CrossRef] [Green Version]
- Haberman, R. Mathematical Models Mechanical Vibrations, Population Dynamics, and Traffic Flow; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1998. [Google Scholar]
- Murray, J.D. Mathematical Biology; Springer: New York, NY, USA, 2002; Volume 2. [Google Scholar]
- Jensen, C.X.J.; Ginzburg, L.R. Paradoxes or theoretical failures? The jury is still out. Ecol. Model. 2005, 188, 3–14. [Google Scholar] [CrossRef]
- Rosenzweig, M.L. Paradox of enrichment—Destabilization of exploitation ecosystems in ecological time. Science 1971, 171, 385–387. [Google Scholar] [CrossRef] [PubMed]
- Walters, C.J.; Krause, E.; Neill, W.E.; Northcote, T.G. Equilibrium-models for seasonal dynamics of plankton biomass in 4 oligotrophic lakes. Can. J. Fish. Aquat. Sci. 1987, 44, 1002–1017. [Google Scholar] [CrossRef]
- McCauley, E.; Murdoch, W.W. Predator prey dynamics in environments rich and poor in nutrients. Nature 1990, 343, 455–457. [Google Scholar] [CrossRef]
- Persson, L.; Johansson, L.; Andersson, G.; Diehl, S.; Hamrin, S.F. Density dependent interactions in lake ecosystems—Whole lake perturbation experiments. Oikos 1993, 66, 193–208. [Google Scholar] [CrossRef]
- Mazumder, A. Patterns of algal biomass in dominant odd-link vs. even-link lake ecosystems. Ecology 1994, 75, 1141–1149. [Google Scholar] [CrossRef]
- Fussmann, G.F.; Ellner, S.P.; Shertzer, K.W.; Hairston, N.G., Jr. Crossing the hopf bifurcation in a live predator–prey system. Science 2000, 290, 1358–1360. [Google Scholar] [CrossRef] [PubMed]
- Cottingham, K.L.; Rusak, J.A.; Leavitt, P.R. Increased ecosystem variability and reduced predictability following fertilisation: Evidence from palaeolimnology. Ecol. Lett. 2000, 3, 340–348. [Google Scholar] [CrossRef]
- Meyer, K.M.; Vos, M.; Mooij, W.M.; Hol, W.H.G.; Termorshuizen, A.J.; van der Putten, W.H. Testing the Paradox of Enrichment along a Land Use Gradient in a Multitrophic Aboveground and Belowground Community. PLoS ONE 2012, 7, e49034. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Oksanen, L.; Fretwell, S.D.; Arruda, J.; Niemela, P. Exploitation ecosystems in gradients of primary productivity. Am. Nat. 1981, 118, 240–261. [Google Scholar] [CrossRef]
- Freedman, I. Deterministic Mathematical Models in Population Ecology; Marcel Dekker, Inc.: New York, NY, USA, 1980. [Google Scholar]
- Smith, H.L. Competitive coexistence in an oscillating chemostat. SIAM J. Appl. Math. 1981, 40, 498–522. [Google Scholar] [CrossRef]
- Hutson, V.; Vickers, G.A. Criterion for permanent coexistence of species, with an application to a two-prey one-predator system. Math. Biosci. 1983, 63, 253–269. [Google Scholar] [CrossRef]
- Freedman, H.; Waltman, P. Persistence in models of three interacting predator-prey populations. Math. Biosci. 1984, 68, 213–231. [Google Scholar] [CrossRef]
- Waltman, P. Coexistence in chemostat-like models. Rocky Mt. J. Math. 1990, 20, 777–807. [Google Scholar] [CrossRef]
- Ruan, S.; Freedman, H.I. Persistence in three-species food chain models with group defence. Math. Biosci. 1991, 107, 111–125. [Google Scholar] [CrossRef]
- Kuang, Y.; Beretta, E. Global qualitative analysis of a ratio-dependent predator-prey system. J. Math. Biol. 1998, 36, 389–406. [Google Scholar] [CrossRef]
- Kuang, Y. Basic properties of mathematical population models. J. Biomath. 2002, 17, 129–142. [Google Scholar]
- Hsu, S.-B.; Hwang, T.-W.; Kuang, Y. A ratio-dependent food chain model and its applications to biological control. Math. Biosci. 2003, 181, 55–83. [Google Scholar] [CrossRef] [Green Version]
- Dubey, B.; Upadhyay, R. Persistence and extinction of one-prey and two-predator system. Nonlinear Anal. 2004, 9, 307–329. [Google Scholar]
- Gakkhar, S.; Singh, B.; Naji, R.K. Dynamical behavior of two predators competing over a single prey. Biosystems 2007, 90, 808–817. [Google Scholar] [CrossRef] [PubMed]
- Naji, R.K.; Balasim, A.T. Dynamical behavior of a three species food chain model with beddington-deangelis functional response. Chaos Solitons Fractals 2007, 32, 1853–1866. [Google Scholar] [CrossRef]
- Upadhyay, R.K.; Naji, R.K. Dynamics of a three species food chain model with crowley-martin type functional response. Chaos Solitons Fractals 2009, 42, 1337–1346. [Google Scholar] [CrossRef]
- Huo, H.F.; Ma, Z.P.; Liu, C.Y. Persistence and stability for a generalized leslie-gower model with stage structure and dispersal. Abstr. Appl. Anal. 2009, 2009, 135843. [Google Scholar] [CrossRef]
- Kar, T.; Batabyal, A. Persistence and stability of a two prey one predator system. Int. J. Eng. Sci. Technol. 2010, 2, 174–190. [Google Scholar] [CrossRef]
- Tian, X.; Xu, R. Global dynamics of a predator-prey system with holling type II functional response. Nonlinear Anal. Model. Control 2011, 16, 242–253. [Google Scholar]
- Smith, H.L.; Thieme, H.R. Dynamical Systems and Population Persistence; Graduate Studies in Mathematics; AMS: Providence, RI, USA, 2011; Volume 118. [Google Scholar]
- Alebraheem, J.; Abu-Hassan, Y. The Effects of Capture Efficiency on the Coexistence of a Predator in a Two Predators-One Prey Model. J. Appl. Sci. 2011, 11, 3717–3724. [Google Scholar] [CrossRef]
- Alebraheem, J.; Abu-Hassan, Y. Persistence of Predators in a Two Predators-One Prey Model with Non-Periodic Solution. J. Appl. Sci. 2012, 6, 943–956. [Google Scholar]
- Alebraheem, J.; Abu-Hassan, Y. Efficient Biomass Conversion and its Effect on the Existence of Predators in a Predator-Prey System. Res. J. Appl. Sci. 2013, 8, 286–295. [Google Scholar]
- Alebraheem, J.; Abu-Hassan, Y. Dynamics of a two predator–one prey system. Comput. Appl. Math. 2014, 33, 767–780. [Google Scholar] [CrossRef]
- Alebraheem, J. Fluctuations in interactions of prey predator systems. Sci. Int. 2016, 28, 2357–2362. [Google Scholar]
- Hsu, S.B. On global stability of a predator-prey system. Math. Biosci. 1978, 39, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Ameixa, O.M.C.C.; Messelink, G.J.; Kindlmann, P. Nonlinearities Lead to Qualitative Differences in Population Dynamics of Predator-Prey Systems. PLoS ONE 2013, 8, e62530. [Google Scholar] [CrossRef] [PubMed]
- Abu-Hasan, Y.; Alebraheem, J. Functional and Numerical Response in Prey-Predator System. AIP Conf. Proc. 2015, 1651, 3. [Google Scholar] [CrossRef]
- Alebraheem, J.; Abu-Hassan, Y. Simulation of complex dynamical behaviour in prey predator model. In Proceedings of the 2012 International Conference on Statistics in Science, Business and Engineering, Langkawi, Malaysia, 10–12 September 2012. [Google Scholar]
- Smout, S.; Asseburg, C.; Matthiopoulos, J.; Fernández, C.; Redpath, S.; Thirgood, S.; Harwood, J. The Functional Response of a Generalist Predator. PLoS ONE 2010, 5, e10761. [Google Scholar] [CrossRef] [PubMed] [Green Version]



© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alebraheem, J. Relationship between the Paradox of Enrichment and the Dynamics of Persistence and Extinction in Prey-Predator Systems. Symmetry 2018, 10, 532. https://doi.org/10.3390/sym10100532
Alebraheem J. Relationship between the Paradox of Enrichment and the Dynamics of Persistence and Extinction in Prey-Predator Systems. Symmetry. 2018; 10(10):532. https://doi.org/10.3390/sym10100532
Chicago/Turabian StyleAlebraheem, Jawdat. 2018. "Relationship between the Paradox of Enrichment and the Dynamics of Persistence and Extinction in Prey-Predator Systems" Symmetry 10, no. 10: 532. https://doi.org/10.3390/sym10100532
APA StyleAlebraheem, J. (2018). Relationship between the Paradox of Enrichment and the Dynamics of Persistence and Extinction in Prey-Predator Systems. Symmetry, 10(10), 532. https://doi.org/10.3390/sym10100532



