In this section, we solve two numerical examples and compare outputs with other existing methods for verifying the applicability and superiority of the suggested method.
4.1. Numerical Example 1
In this example, the suggested approach is implemented on the benchmarking time series data of student enrollments at the University of Alabama from year 1971 to 1992 adopted from [
26]. The steps are as follows:
Step 1: Let the two proper positive numbers
and
be
and
, determined by the expert. By selecting the largest and the smallest observation from all available data which are presented in
Table 1, then
and
, respectively. Consequently, the universe of discourse U =
Step 2: Create a partition of the universe of discourse, to triangular neutrosophic numbers, as follows:
- -
Determine the suitable length () of available time series data:
- ○
From
Table 1, the average of absolute differences
- ○
The initial length
- ○
By using the base mapping table [
42], the base for length of intervals
, since it is located in the range
- ○
By rounding with regard to base , then the appropriate length of neutrosophic numbers = 300.
- -
Compute the number of triangular neutrosophic numbers
as follows:
Then, we can partition into triangular neutrosophic numbers with length
Step 3: According to the number of triangular neutrosophic numbers on the universe of discourse and determined length (
), begin to construct the triangular neutrosophic numbers as follows:
Step 4: Make a neutrosophication of the available time series data:
The first value of actual enrollments is 13,055 which is located only in the range of triangular neutrosophic number
, then the neutrosophication value of 13,055 is
as in
Table 1.
Also, the second value of actual enrollments (i.e., 13,563) locates in the range of triangular neutrosophic numbers and .
Then, we must select the highest score degree of 13,563 as follows:
The membership, indeterminacy, and non-membership degrees of this value are calculated by using Equations (1)–(3) as follows:
We must also calculate membership, indeterminacy, and non-membership degrees of
according to
as follows:
In this case, we must calculate the score degree of in both and and select the maximum value.
Since the score degree of
in
is greater than
, then the neutrosophication value of
is
, as in
Table 1.
We will apply the previous steps on the remaining data as follows:
The value 13867 locates in the range of , and .
So, the neutrosophication value of is
Also, the value of 14,696 locates in the range of
, then
So, the neutrosophication value of 14,696 is
The value 15,460 locates in the range of
and
, then
So, the neutrosophication value of is
The value of 15,311 locates in the range of
and
, then
So, the neutrosophication value of is
The value of 15,603 locates in the range of
and
, then
So, the neutrosophication value of is
The value of 15,861 locates in the range of
and
, then
So, the neutrosophication value of is .
The value of 16,807 locates in the range of then,
So, the neutrosophication value of is
The value of 16919 locates in the range of then
So, the neutrosophication value of is
The value of 16388 locates in the range of
, then
So, the neutrosophication value of is
The value of 15433 locates in the range of and , then
So, the neutrosophication value of is
The value of 15497 locates in the range of
and
then,
So, the neutrosophication value of is
The value of 15,145 locates in the range of
and
, then
So, the neutrosophication value of 15,145 is
The value of
locates in the range of
,
, then
So, the neutrosophication value of is
The value of
locates in the range of
, then
So, the neutrosophication value of is
The value of
locates in the range of
, then
So, the neutrosophication value of is
The value of
locates in the range of
, then
So, the neutrosophication value of is
The value of
locates in the range of
then
So, the neutrosophication value of is
The value of
locates in the range of
, then
So, the neutrosophication value of is
The value of
locates in the range of
then
So, the neutrosophication value of is
Finally, the value of
locates in the range of
, then
So, the neutrosophication value of is
Step 5: Construct the neutrosophic logical relationships (NLRs) as in
Table 2:
Step 6: Based on NLR, begin to establish the neutrosophic logical relationship groups (NLRGs) as in
Table 3.
Step 7: Calculate the forecasted values as in
Table 4:
To calculate the forecasted value of 13,055 in year 1971, do the following:
- -
Look at the neutrosophication value of 13055 in year 1971 which is
as it appears in
Table 1.
- -
Go to NLRG which is presented in
Table 3, and because
is the first neutrosophication value of data, then it is not caused by any other value (i.e.
) as in
Table 3.
Therefore, the forecasted value of 13,055 is—Which means leaving it empty, as we illustrated in Step 7, Rule 1 of the proposed algorithm.
Also, to calculate the forecasted value of 13,563 in year 1972, do the following:
- -
Look at the neutrosophication value of 13,563 in year 1972 which is
as it appears in
Table 1, and because
is caused by
(i.e.,
), then
- -
Go to
Table 3, and look at the NLRG which starts with
, and we noted that it is
Then the forecasted value of 13,563 is the middle value of
.
Another illustrating example for calculating the forecasted value of 18,876 in year 1992:
- -
Look at the neutrosophication value of 18,876 in year 1992 which is
as it appears in
Table 1. Since
is caused by
then
- -
Go to
Table 3, and look at the NLRG which starts with
(i.e.
). Then the forecasted value of 18876 is the average of the middle values of
,
, and it will equal 19,050.
The other forecasted values are calculated in the same manner.
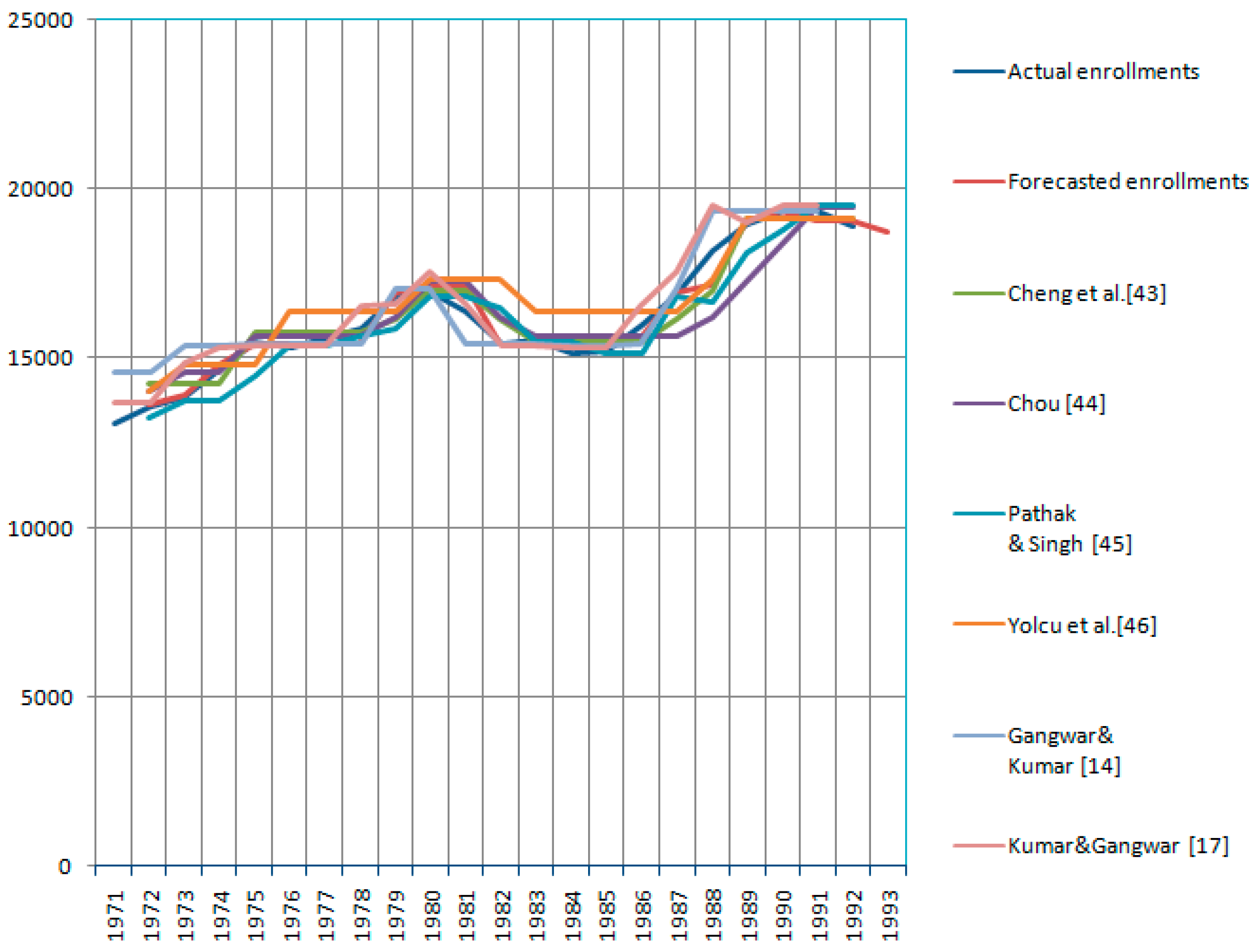
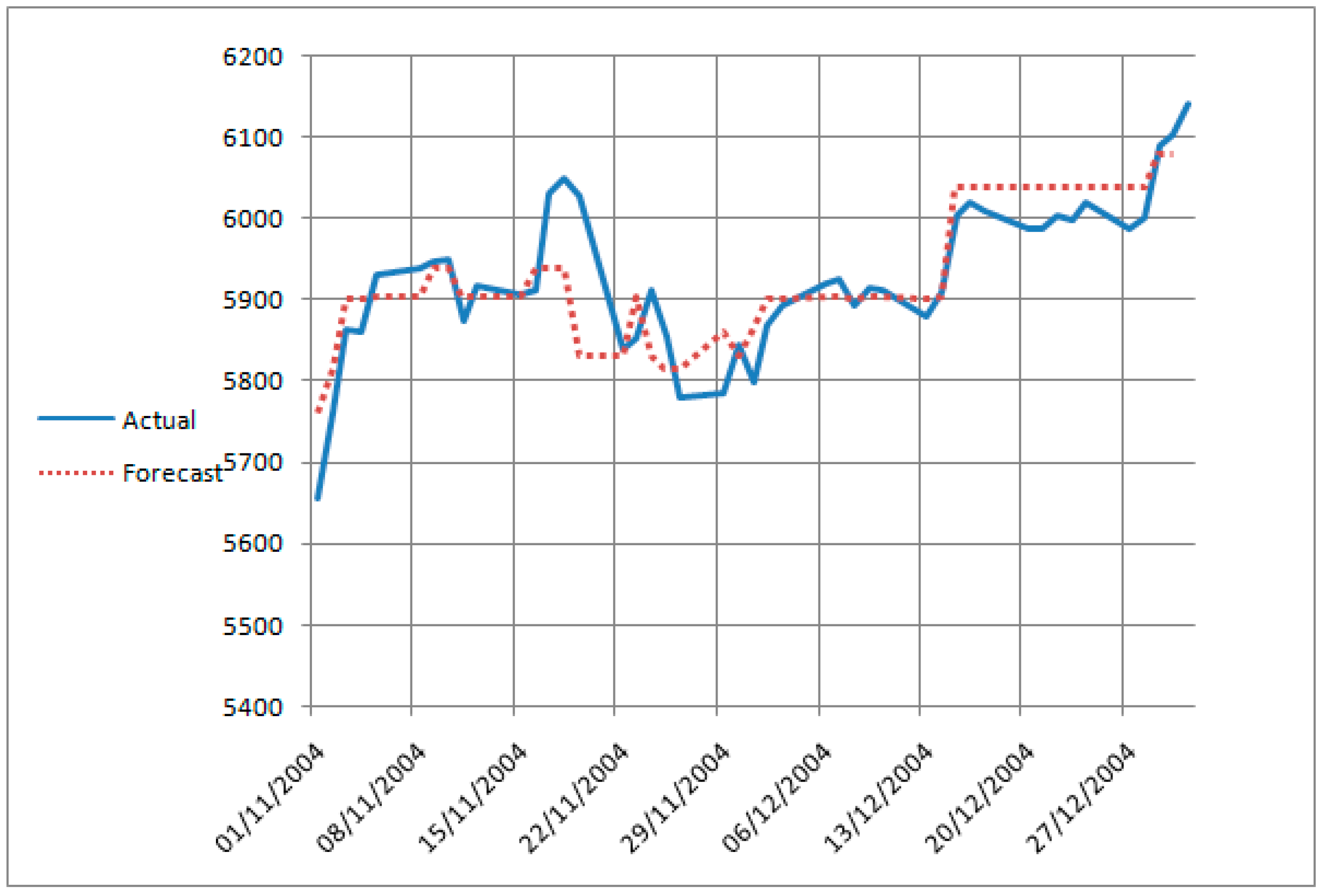
The actual and forecasted values of enrollments appear in
Figure 1.
The forecasted enrollment data obtained with the suggested method, along with the forecasted data obtained with the models in [
14,
17,
43,
44,
45,
46], are presented in
Table 5.
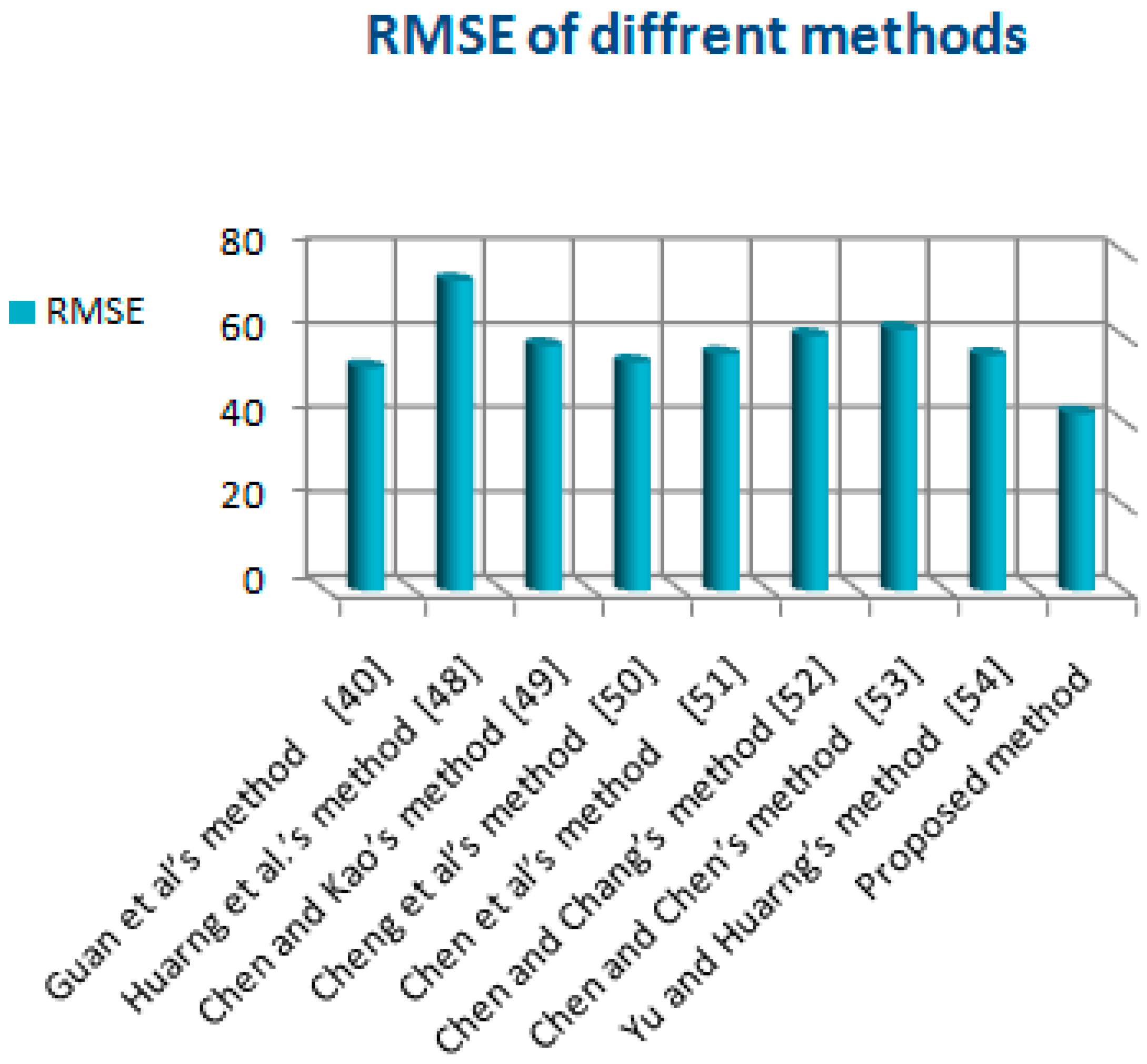
By comparing the proposed method with other existing methods in
Table 5, the RMSE and AFE tools confirm that the suggested method is better than others, as shown in
Table 6.
We combined forecasted values with respect to all methods in
Figure 2.
If we plan to find the second-order neutrosophic logical relationships of the previous example by applying the proposed method of forecasting based on the second-order NTS, they are as shown in
Table 7.
The second-order neutrosophic logical relationship groups of the previous example are as shown in
Table 8.
We compared forecasted values of enrollments based on the second order of neutrosophic logical relationship groups of the proposed method with the method of second order presented by Gautam and Singh [
47]. The results are shown in
Table 9.
The MSE and AFE of the two methods are presented in
Table 10.
From
Table 10, it appears that our proposed method of second order is also better than the proposed method of second order presented by Gautam and Singh [
47].
In addition, the third-order neutrosophic logical relationship groups of the previous example are constructed and shown in
Table 11.
We also compared the forecasted values of enrollments based on the third order of neutrosophic logical relationship groups of the proposed method with the proposed methods of third order presented by [
8,
9,
47], and the results are shown in
Table 12.
The MSE and AFE of the methods are presented in
Table 13.