Track Allocation Optimization in Multi-Direction High-Speed Railway Stations
Abstract
:1. Introduction
- Firstly, to our knowledge, there is litte research that directly pays attention to the track allocation optimization in a multi-direction high-speed railway station. We propose the track allocation problem in the multi-direction high-speed railway station for the first time.
- Secondly, the resources in the throat area are considered. Some researchers assumed that outbound and inbound trains are independent in the single-direction station and separated the track allocation plan into two parts. In this way, headway constraints in the train timetabling problem can make sure that no conflict exists between routes of the trains from the same line in a single-direction station. However, in the multi-direction station, trains’ arrival directions and departure directions are various. Train timetables of different lines are designed separately. The routes of trains from different lines may conflict with each other due to the layout of the throat area. Consequently, we cannot divide the track allocation plan into two independent parts based on their directions. The flexible track utilization rule is applied to this problem and all trains are allocated together. The restrictive resources of one multi-direction station are the switches in the throat area, and the track allocation plan is unfeasible if only the tracks near the platforms are considered. In this paper, the resources in the throat area and arrival-departure tracks are considered simultaneously and outbound and inbound trains are no longer independent in the station, which ensures the feasibility of the result.
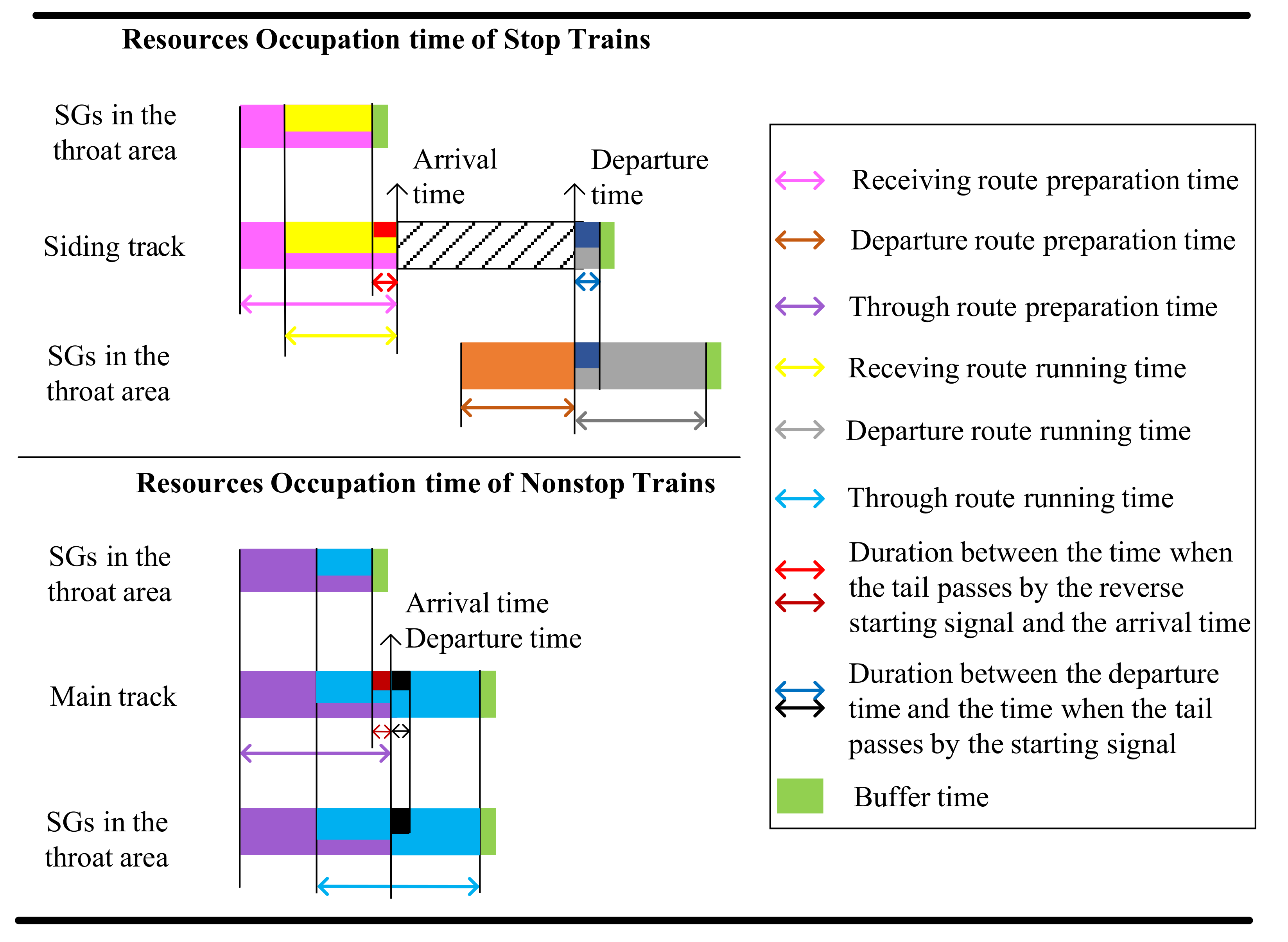
- Thirdly, the resources occupation times were not explained exhaustedly and correctly, which lead to a difficult expression of the constraints when solving the track allocation problem of multi-direction stations. We give a detailed analysis of the occupation times of resources in the throat area and arrival-departure tracks in this paper, which facilitates the construction of the complicated conflicting constraints.
2. Problem Description
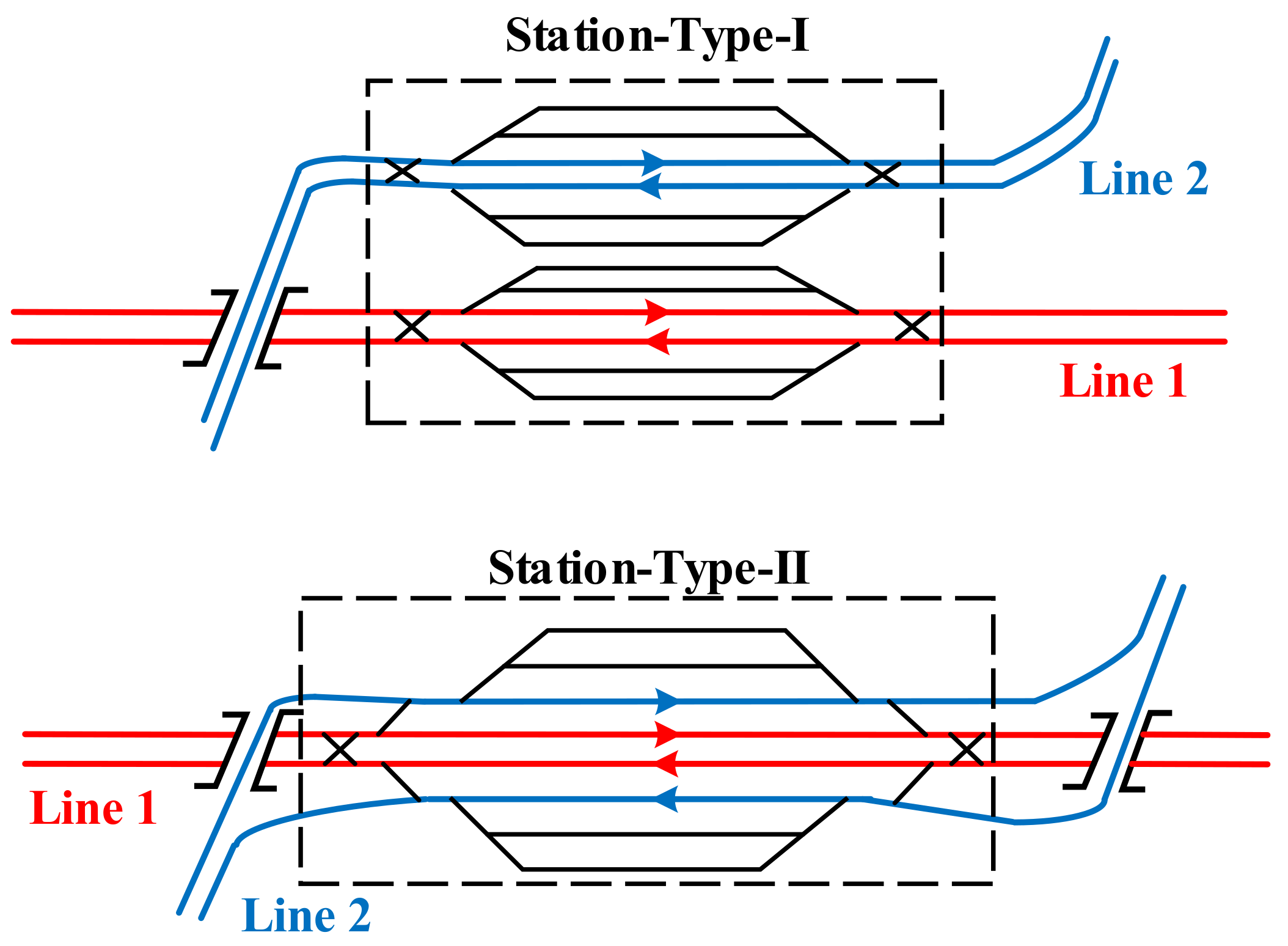
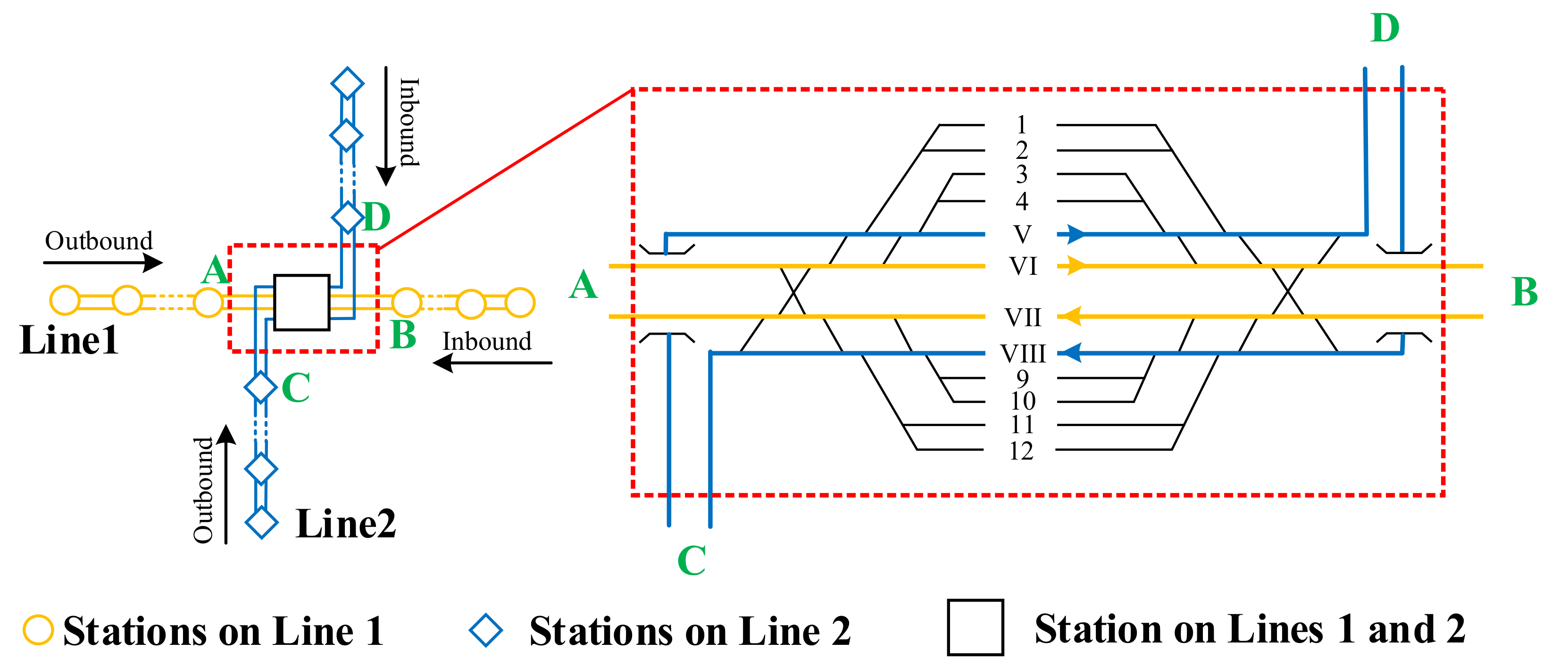
2.1. Multi-Direction Stations in a High-Speed Railway Network
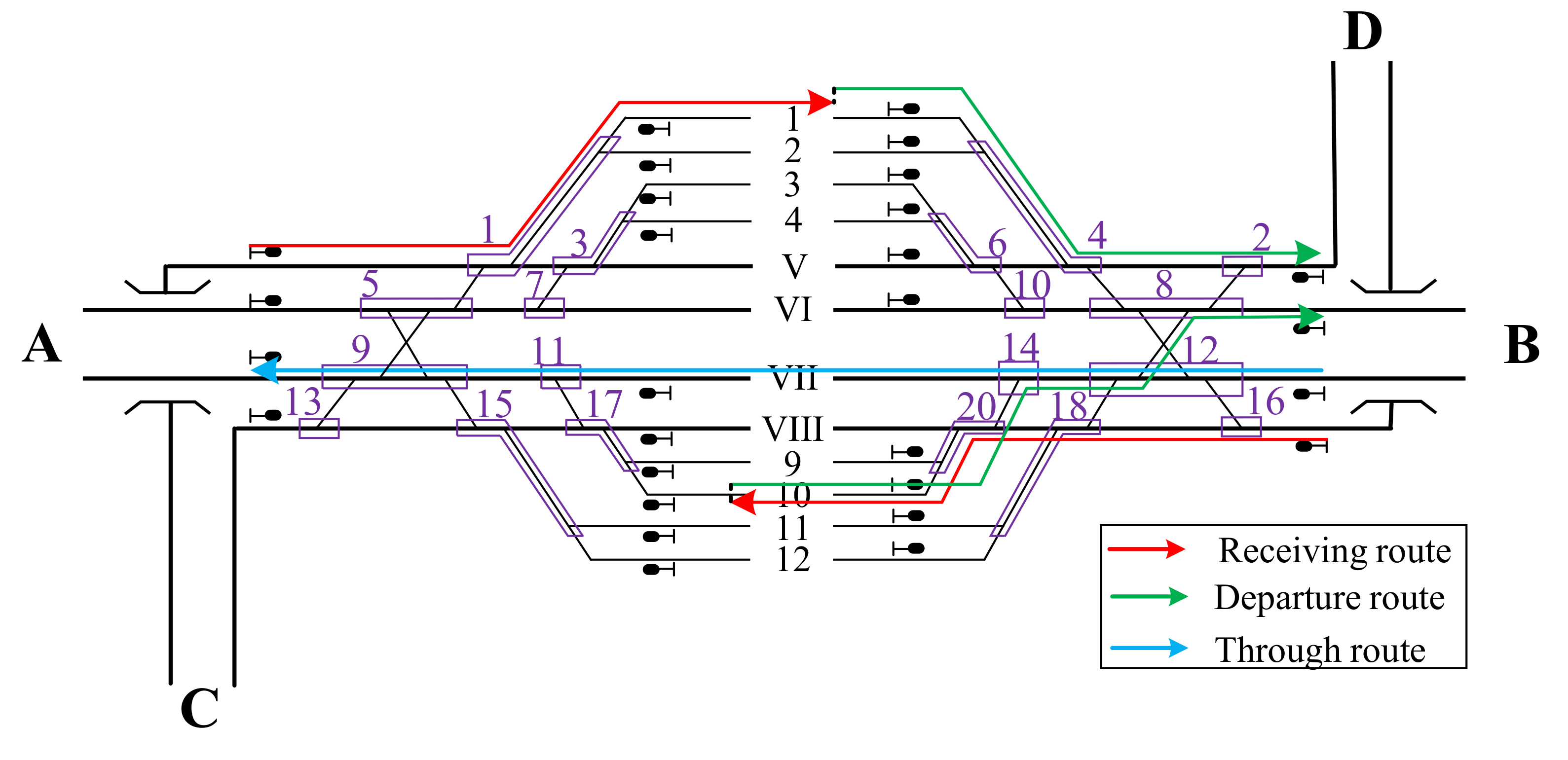
2.2. Occupation Time of Train Routes
2.3. Assumption
- The second type of the station layout mentioned above is discussed.
- Basic information of the station is given, including the minimum preparation time criterion and running time of different routes and the operations each track can provide.
- The speed differences in a station only exist between stop and nonstop trains. Because of the speed limitation in the station, the running time of nonstop trains are the same, regardless of the train types and the speed levels. The same assumption is applied to the stop trains.
- The train timetable and rolling stock plan are given, including the trains’ static operation in this multi-direction station.
- The basic receiving route from one arrival direction to one certain track is unique and fixed. Similarly, the basic departure route is also definite and unique.
3. Formulation of Optimization Model
3.1. Notations and Decision Variables
3.2. Objective Function
3.3. Constraints
3.3.1. Time Constraints
3.3.2. Safety Constraints
3.3.3. Operation Constraints
3.3.4. Domain Constraints
4. Computational Experiment
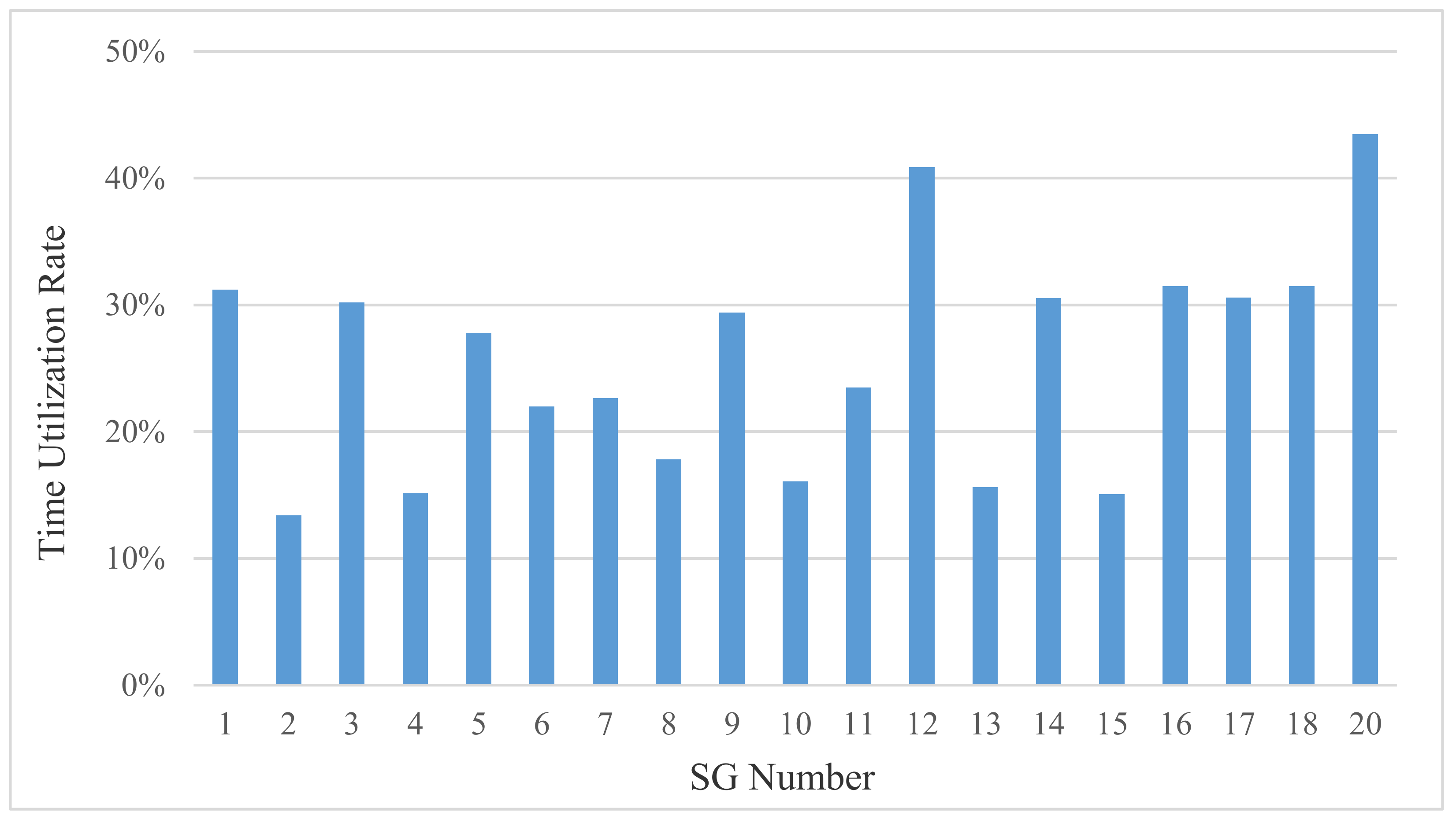
5. Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Woroniuk, C.; Aditjandra, P.T. A rail capacity framework: Making the case for rail freight evaluation in Indonesia. CSID J. Infrastruct. Dev. 2015, 1, 4–13. [Google Scholar] [CrossRef]
- Marinov, M.; Şahin, İ.; Ricci, S.; Vasic-Franklin, G. Railway operations, time-tabling and control. Res. Transp. Econ. 2013, 41, 59–75. [Google Scholar] [CrossRef]
- Meng, L.Y.; Zhou, X.S. Simultaneous train rerouting and rescheduling on an N-track network: A model reformulation with network-based cumulative flow variables. Transp. Res. Part B Methodol. 2014, 67, 208–234. [Google Scholar] [CrossRef]
- Gao, Y.; Kroon, L.; Yang, L.X.; Gao, Z.Y. Three-stage optimization method for the problem of scheduling additional trains on a high-speed rail corridor. Omega 2017, 80, 175–191. [Google Scholar] [CrossRef]
- Cardillo, D.D.L.; Mione, N. K L-list λ colouring of graphs. Eur. J. Oper. Res. 1998, 106, 160–164. [Google Scholar] [CrossRef]
- Billionnet, A. Using integer programming to solve the train-platforming problem. Transp. Sci. 2003, 37, 213–222. [Google Scholar] [CrossRef]
- Zwaneveld, P.J.; Kroon, L.G.; Van Hoesel, S.P.M. Routing trains through a railway station based on a node packing model. Eur. J. Oper. Res. 2001, 128, 14–33. [Google Scholar] [CrossRef]
- Lusby, R.; Larsen, J.; Ryan, D.; Ehrgott, M. Routing trains through railway junctions: A new set-packing approach. Transp. Sci. 2011, 45, 228–245. [Google Scholar] [CrossRef]
- Carey, M.; Carville, S. Scheduling and platforming trains at busy complex stations. Transp. Res. Part A Policy Pract. 2003, 37, 195–224. [Google Scholar] [CrossRef]
- Qiao, R. Research on Selection and Adjustment of Receiving Routes and Dispatching Routes in Passenger Dedicated Line Station. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2012. (In Chinese). [Google Scholar]
- Liu, W. Optimizing the Bottleneck Sections and Track Allocation Problems for Large Railway Passenger Stations under Abnormal Conditions. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2017. (In Chinese). [Google Scholar]
- Wu, J.J.; Kang, L.J.; Sun, H.J.; Jia, X.L. Track allocation optimization in railway station: Mean-variance model and case study. J. Transp. Eng. 2013, 139, 540–547. [Google Scholar] [CrossRef]
- Sels, P.; Vansteenwegen, P.; Dewilde, T.; Cattrysse, D.; Waquet, B.; Joubert, A. The train platforming problem: The infrastructure management company perspective. Transp. Res. Part B Methodol. 2014, 61, 55–72. [Google Scholar] [CrossRef]
- Qi, J.G.; Yang, L.X.; Gao, Y.; Li, S.K.; Gao, Z.Y. Integrated multi-track station layout design and train scheduling models on railway corridors. Transp. Res. Part C Emerg. Technol. 2016, 69, 91–119. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhu, X.N.; Wang, L. Track allocation optimization in high-speed railway stations from infrastructure management and service perspectives. Meas. Control 2018, 51, 243–259. [Google Scholar] [CrossRef]

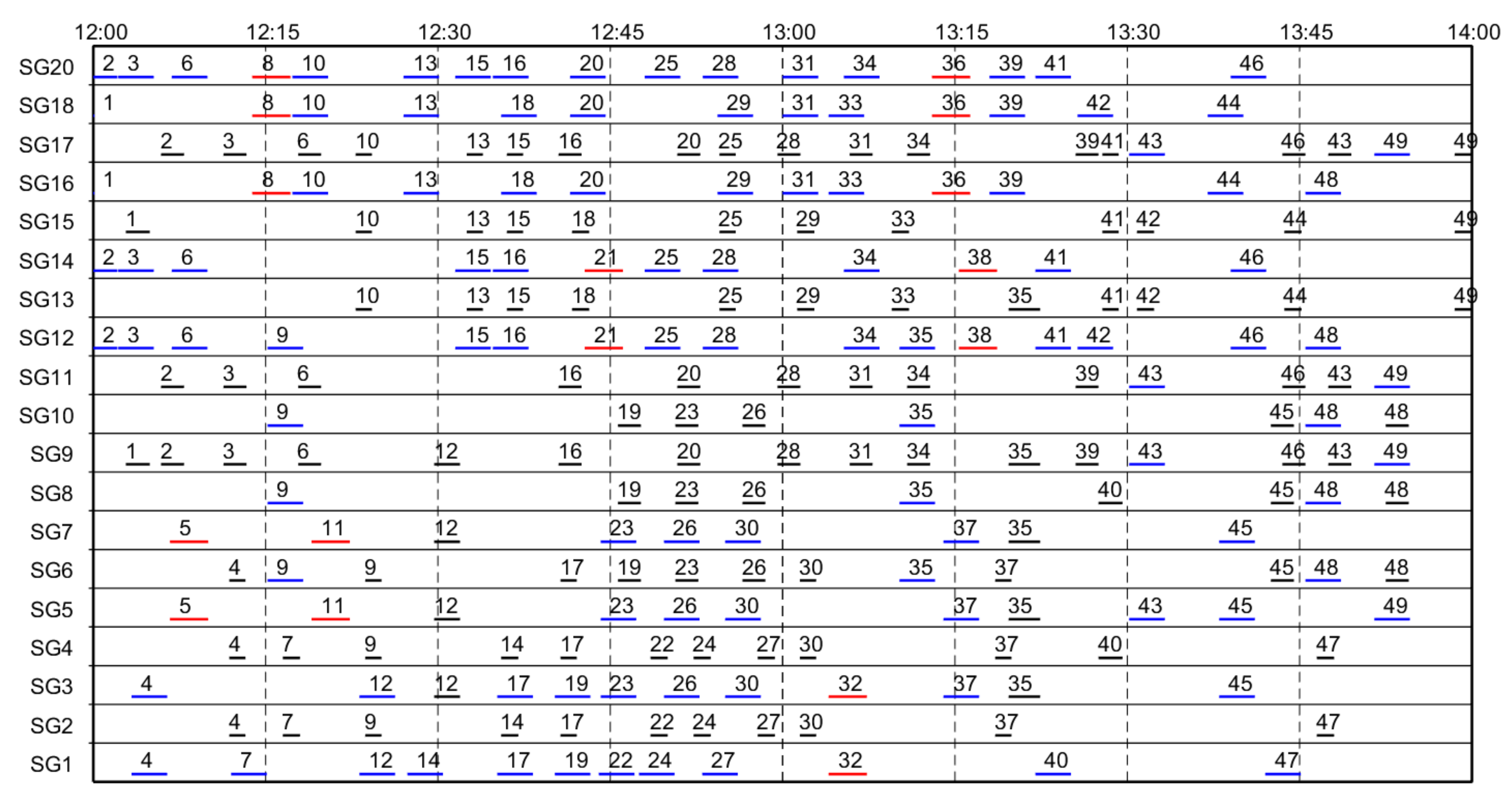

| Train ID | Arrival Direction | Departure Direction | Arrival Time | Departure Time | Stop (1) or Nonstop (0) |
|---|---|---|---|---|---|
| 1 | D | A | 12:00:00 | 12:03:20 | 1 |
| 2 | B | A | 12:02:00 | 12:06:24 | 1 |
| 3 | B | A | 12:05:10 | 12:11:50 | 1 |
| 4 | C | D | 12:06:20 | 12:12:20 | 1 |
| 5 | A | B | 12:09:40 | 12:09:40 | 0 |
| 6 | B | A | 12:09:50 | 12:18:20 | 1 |
| 7 | C | D | 12:15:00 | 12:17:00 | 1 |
| 8 | D | C | 12:16:50 | 12:16:50 | 0 |
| 9 | B | D | 12:18:10 | 12:24:10 | 1 |
| 10 | D | C | 12:20:20 | 12:23:20 | 1 |
| 11 | A | B | 12:22:00 | 12:22:00 | 0 |
| 12 | C | A | 12:26:10 | 12:30:10 | 1 |
| 13 | D | C | 12:30:00 | 12:33:00 | 1 |
| 14 | C | D | 12:30:20 | 12:36:00 | 1 |
| 15 | B | C | 12:34:30 | 12:36:30 | 1 |
| 16 | B | A | 12:37:47 | 12:41:00 | 1 |
| 17 | C | D | 12:38:10 | 12:41:10 | 1 |
| 18 | D | C | 12:38:30 | 12:42:10 | 1 |
| 19 | C | B | 12:43:10 | 12:46:10 | 1 |
| 20 | D | A | 12:44:30 | 12:51:20 | 1 |
| 21 | B | A | 12:45:46 | 12:45:46 | 0 |
| 22 | C | D | 12:47:00 | 12:49:00 | 1 |
| 23 | A | B | 12:47:10 | 12:51:10 | 1 |
| 24 | C | D | 12:50:30 | 12:52:45 | 1 |
| 25 | B | C | 12:51:00 | 12:55:00 | 1 |
| 26 | A | B | 12:52:40 | 12:57:00 | 1 |
| 27 | C | D | 12:56:00 | 12:58:20 | 1 |
| 28 | B | A | 12:56:03 | 13:00:03 | 1 |
| 29 | D | C | 12:57:20 | 13:01:46 | 1 |
| 30 | A | D | 12:58:00 | 13:02:00 | 1 |
| 31 | D | A | 13:03:00 | 13:06:20 | 1 |
| 32 | C | D | 13:07:00 | 13:07:00 | 0 |
| 33 | D | C | 13:07:00 | 13:10:00 | 1 |
| 34 | B | A | 13:08:20 | 13:11:20 | 1 |
| 35 | B | C | 13:13:10 | 13:20:10 | 1 |
| 36 | D | C | 13:16:00 | 13:16:00 | 0 |
| 37 | A | D | 13:17:00 | 13:19:00 | 1 |
| 38 | B | A | 13:18:20 | 13:18:20 | 0 |
| 39 | D | A | 13:21:00 | 13:26:00 | 1 |
| 40 | C | B | 13:25:00 | 13:28:00 | 1 |
| 41 | B | C | 13:25:00 | 13:28:20 | 1 |
| 42 | B | C | 13:28:40 | 13:31:20 | 1 |
| 43 | A | A | 13:36:10 | 13:48:00 | 1 |
| 44 | D | C | 13:40:00 | 13:44:10 | 1 |
| 45 | A | B | 13:41:00 | 13:43:00 | 1 |
| 46 | B | A | 13:42:00 | 13:44:00 | 1 |
| 47 | C | D | 13:45:00 | 13:47:00 | 1 |
| 48 | D | B | 13:48:40 | 13:53:00 | 1 |
| 49 | A | C | 13:54:30 | 13:59:00 | 1 |
| 180s | 30s | 2s | 4s | 8s | 10s | 10s |
| Arrival Direction | Track Number | Track Number | Departure Direction | ||
|---|---|---|---|---|---|
| A | 1/2 | 80 | 1/2 | A | 105 |
| A | 3/4 | 70 | 1/2 | B | 85 |
| A | 6 | 10 | 1/2 | C | 135 |
| A | 9/10 | 95 | 1/2 | D | 50 |
| A | 11/12 | 105 | 3/4 | A | 95 |
| B | 1/2 | 105 | 3/4 | B | 80 |
| B | 3/4 | 95 | 3/4 | C | 125 |
| B | 7 | 10 | 3/4 | D | 45 |
| B | 9/10 | 70 | 5 | B | 20 |
| B | 11/12 | 80 | 5 | D | 10 |
| C | 1/2 | 40 | 6 | B | 10 |
| C | 3/4 | 35 | 6 | D | 20 |
| C | 5 | 10 | 7 | A | 10 |
| D | 1/2 | 135 | 7 | C | 20 |
| D | 3/4 | 125 | 8 | A | 20 |
| D | 8 | 10 | 8 | C | 10 |
| D | 9/10 | 35 | 9/10 | A | 80 |
| D | 11/12 | 40 | 9/10 | B | 95 |
| - | - | - | 9/10 | C | 45 |
| - | - | - | 9/10 | D | 125 |
| - | - | - | 11/12 | A | 85 |
| - | - | - | 11/12 | B | 105 |
| - | - | - | 11/12 | C | 50 |
| - | - | - | 11/12 | D | 135 |
| Publication | Arri./Dep. Route 1 | Occupation Time Analysis 2 | Pre-acclaim 3 | Flexible Rules 4 | Multi-direction 5 | Rolling Stock Plan 6 |
|---|---|---|---|---|---|---|
| Meng and Zhou (2014) | N | N | N | - | - | N |
| Gao et al. (2017) | N | N | N | N | N | N |
| Billionnet (2003) | N | N | N | - | - | N |
| Sels et al. (2014) | Y | Y | N | - | - | N |
| Cardillo et al. (1998) | N | N | N | - | - | N |
| Zwaneveld et al. (2001) | Y | N | N | - | - | N |
| Qiao (2008) | Y | Y | N | N | N | N |
| Wu et al. (2013) | N | N | N | N | N | N |
| Zhang (2018) | Y | Y | Y | N | Y | N |
| This paper | Y | Y | Y | Y | Y | Y |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Zhu, X.; Wang, L. Track Allocation Optimization in Multi-Direction High-Speed Railway Stations. Symmetry 2019, 11, 459. https://doi.org/10.3390/sym11040459
Zhang Q, Zhu X, Wang L. Track Allocation Optimization in Multi-Direction High-Speed Railway Stations. Symmetry. 2019; 11(4):459. https://doi.org/10.3390/sym11040459
Chicago/Turabian StyleZhang, Qin, Xiaoning Zhu, and Li Wang. 2019. "Track Allocation Optimization in Multi-Direction High-Speed Railway Stations" Symmetry 11, no. 4: 459. https://doi.org/10.3390/sym11040459
APA StyleZhang, Q., Zhu, X., & Wang, L. (2019). Track Allocation Optimization in Multi-Direction High-Speed Railway Stations. Symmetry, 11(4), 459. https://doi.org/10.3390/sym11040459




