Propagation of Blast Waves in a Non-Ideal Magnetogasdynamics

Abstract

Blast waves are generated when an area grows abruptly with a supersonic speed, as in explosions. This problem is quite interesting, as a large amount of energy is released in the process. In contrast to the situation of imploding shocks in ideal gas, where a vast literature is available on the effect of magnetic fields, very little is known about blast waves propagating in a magnetic field. As this problem is highly nonlinear, there are very few techniques that may provide even an approximate analytical solution. We have considered a problem on planar and radially symmetric blast waves to find an approximate solution analytically using Sakurai’s technique. A magnetic field has been taken in the transverse direction. Gas particles are supposed to be propagating orthogonally to the magnetic field in a non-deal medium. We have further assumed that specific conductance of the medium is infinite. Using Sakurai’s approach, we have constructed the solution in a power series of ${(\mathit{C}/U)}^2$, where $\mathit{C}$ is the velocity of sound in an ideal gas and U is the velocity of shock front. A comparison of obtained results in the absence of a magnetic field within the published work of Sakurai has been made to generate the confidence in our results. Our results match well with the results reported by Sakurai for gas dynamics. The flow variables are computed behind the leading shock and are shown graphically. It is very interesting that the solution of the problem is obtained in closed form.

1. Introduction

The study of propagation of strong shock waves has always been given undivided attention by various research groups in the field of science. In particular, it is useful in nuclear science, plasma physics, geophysics, astrophysics, explosions, etc. Shocks are ubiquitary and quite useful in the generation of energy. Radially converging shocks are used to create a hot spot at the center in Inertial Confinement Fusion (ICF). The heat generated in the process is used to activate nuclear fission. After World War II, it becomes extremely important to understand explosion dynamics. Motivated by this, Sedov [1] first coined the idea of a similarity solution for the point explosion problem in an ideal medium. Soon, this solution became famous as the “Sedov Similarity Solution” among researchers due to its importance in blast wave theory. Taylor [2] found the analytical first approximate solution for the problem. These results of Sedov and Taylor showed a way to estimate the effects of nuclear or supernova explosions. Later, Sakurai [3,4] used this first approximate solution to find self-similar solutions to the problem. Murata [5] and Donato [6] obtained the exact solutions to blast wave problems in gas dynamics. Murata [5] assumed that change in density ahead of shock front is governed by the exponent of distance from the point (or axis) of ignition. The density ahead of the leading shock was assumed to vary as the power of the radial distance from the center of explosion in his study. Book [7] used Sedov formulas to find similarity solution of the point explosion problem. Lalicata and Torrisi [8] used the similarity method for reacting flow. Propagation of shock waves generated by sudden explosions within the presence of a magnetic field is very important because this phenomenon is well marked in the disassembled nature of the absorption of energy. Anisimov and Spiner [9] and Lerche [10] presented the theory of blast waves in magnetogasdynamics. A first comprehensive study on the effect of magnetic field on the exploding shocks was presented by Lerche [11] in 1979. There is an abrupt change in the entropy across an exploding shock and it releases a very high energy in the process. It is well known that after the explosion, the front of the blast wave is circumscribed by the surfaces of the shocks and propagates with decreasing velocity. Furthermore, a very high energy is released in the process. It raises the temperature of the surrounding. Therefore, the assumption of an ideal medium is not valid anymore, and one must consider the effect of non-deal medium on the blast waves. The gas particles are ionized due to the presence of high temperature at the center. These ionized gas particles generate the magnetic field. Therefore, the inclusion of a magnetic field on the study of blast waves is essential for capturing the physics of the process well. It has many applications in oceanography, astrophysics, aerodynamics, and atmospheric sciences.

Many research groups have worked afterwards on the topic to better understand the dynamics of shock waves in a magnetic field. Among the recent research on the topic, we wish to mention the work of Arora et al. [12], Siddiqui et al. [13], Singh et al. [14,15], and Pandey et al. [16]. Menon and Sharma [17] studied the flattening and steepening of the characteristics wave fronts in an ideal medium with magnetic field. Arora et al. [18] found a similar solution to the propagation of shocks in a non-ideal medium. Relaxation effects were also included in the study. Later, Siddiqui et al. [19] used asymptotic expansion of flow variables to find the solution to nonlinear waves far from the origin. The relaxation of gas particles has been taken into account in the study. Evolutionary behavior of weak shocks in real gas is presented by Arora and Siddiqui [20]. Despite there being vast literature available on imploding shocks in real gas, the behavior of shock front after ignition is still an open problem. In the present work, we have analyzed the flow variables after a blast in ignition by using the Sakurai analytical approach. The medium is considered to be real gases. Effects of a magnetic field have also been taken into account.

This paper is summarized as follows: Section 1 contains a brief introduction to the topic and historical background of earlier studies. Section 2 presents the fundamental equations governing the conservation laws. Rankine–Hugoniot (RH) jump conditions are also presented in this section. In Section 3, we introduce the new independent variables and transform the fundamental equations in the form of non-dimensional functions using the similarity analysis. In Section 4, power series solutions in terms of ${(C/U)}^2$ have been presented for the problem. In Section 5, the first approximation solutions are obtained which correspond to Taylor’s series solution. In Section 6, a brief conclusion is given about the whole study of this paper. Based on the study, we have concluded that the density and magnetic pressure of the particle decreases behind the leading shock. Charged particles are transported away by the magnetic field, and this gives an increase in the velocity of blast wind.

2. Fundamental Equations

The fundamental equations which govern unsteady planar ($m=0$) or cylindrically ($m=1$) symmetric flow in a non-ideal gas in the presence of transverse magnetic field can be expressed as [12,21]

$${\rho }_t+\rho u_x+u{\rho }_x+\frac{m\rho u}{x}=0,$$

(1)

$$u_t+u{u}_x+\frac{1}{\rho }(p_x+h_x)=0,$$

(2)

$$p_t+u{p}_x+a^2\rho \left(u_x+\frac{mu}{x}\right)=0,$$

(3)

$$h_t+u{h}_x+2h\left(u_x+\frac{mu}{x}\right)=0.$$

(4)

Here $\rho ,u,p$ and $h=\frac{\mu H^2}{2}$ denote the density, velocity, pressure, and magnetic pressure, respectively. $\mu$ denotes the magnetic permeability and H being used for transverse magnetic field. $a^2=\frac{\gamma p}{\rho (1-b\rho )}$ is speed of sound in real gases. $\gamma$ is the ratio the specific heats at constant pressure and volume of the gas. t and x represents the time and space variables, respectively. $m=0$ denotes to planar symmetry while m = 1 denotes cylindrical symmetry of the flow. It is assumed that electrical resistivity of the medium is zero and magnetic field is orthogonal to the radial motion of gas particles.

This system of Equations (1)–(4) is supplemented with the equation of state for real gas as follows

$$p=\frac{\rho RT}{(1-b\rho )}.$$

(5)

R, T represent the gas constant and temperature, respectively.

The position of leading shock at any time t is given by $\tilde{R}=\tilde{R}(t)$. Therefore, the velocity of shock front is ($\frac{d\tilde{R}}{dt}=C$). The conditions for flow variables ahead of shock are characterized by

$$\rho ={\rho }_0(x),u=0,p=p_0,h=h_0(x).$$

(6)

RH conditions at the leading shock $(x=\tilde{R}(t))$ are obtained by the conservation of laws that can be expressed in simplified form as follows [22]

$$\begin{array}{cc}\hfill {(\rho )}_{x=R}=& \frac{(\gamma +1)}{(\gamma -1)}{\rho }_0\left[1-\frac{2\alpha }{\gamma -1}-\frac{2}{\gamma -1}{\left(\frac{C}{U}\right)}^2\right],\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill {(u)}_{x=R}=& \frac{2}{(\gamma -1)}S\left[1-\alpha -{\left(\frac{V}{S}\right)}^2\right],\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill {(p)}_{x=R}=& \frac{2{\rho }_0{U}^2}{\gamma +1}\left[1-\alpha -\frac{\gamma -1}{2\gamma }{\left(\frac{C}{U}\right)}^2\right]-\frac{1}{2}{\left(\frac{\gamma +1}{\gamma -1}\right)}^2{C}_0{\rho }_0{U}^2\left[1-\frac{4\alpha }{\gamma -1}-\frac{4}{\gamma -1}{\left(\frac{C}{U}\right)}^2\right],\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill {(h)}_{x=R}=& \frac{1}{2}{\left(\frac{\gamma +1}{\gamma -1}\right)}^2{C}_0{\rho }_0{U}^2\left[1-\frac{4\alpha }{\gamma -1}-\frac{4}{\gamma -1}{\left(\frac{C}{U}\right)}^2\right],\hfill \end{array}$$

(10)

where $C_0=\frac{2h_0}{{\rho }_0{U}^2}$ is the shock cowling number, $C^2=\frac{\gamma p_0}{{\rho }_0}$ is the velocity of shock and $\alpha =(\gamma -1)b{\rho }_0$. The initial density ${\rho }_0$ is assumed to follow the power law given as

$${\rho }_0={\rho }_c{x}^{-\delta },$$

(11)

where x is the perpendicular distance of the point on leading shock from the point of explosion. ${\rho }_c$ is the constant density and $\delta$ is an exponent. Using the conservation of total energy, we get

$$E={\int }_0^{\tilde{R}}\left[\frac{1}{2}{u}^2+\frac{(1-b\rho )}{(\gamma -1)}\left(\frac{p}{\rho }-\frac{p_0}{{\rho }_0}\right)+\left(\frac{h}{\rho }-\frac{h_0}{{\rho }_0}\right)\right]\rho x^{m}dx,m=0,1,$$

(12)

where E denotes the surface energy carried by blast waves per unit of area. We obtain the following relation by the Lagrangian equation of continuity:

$${\int }_0^{\tilde{R}}\frac{\rho }{{\rho }_0}{x}^{m}dx=\frac{{\tilde{R}}^{m+1}}{m+1}.$$

(13)

We use the value of ${\int }_0^{\tilde{R}}\frac{\rho }{{\rho }_0}{x}^{m}dx$ from Equation (13) in Equation (12) to get the following expression

$$E={\int }_0^{\tilde{R}}\left[\frac{1}{2}\rho u^2+\frac{(1-b\rho )}{(\gamma -1)}p+h\right]x^{m}dx-\left\{\frac{(1-b\rho )p_0}{\gamma -1}+h_0\right\}\frac{{\tilde{R}}^{m+1}}{m+1}.$$

(14)

3. Similarity Transformation of Fundamental Equations

As the process is self-similar, $x=R(t)$ and $U=\frac{d\tilde{R}}{dt}$. It gives us the characteristic scale. We, therefore, introduce the following new independent non-dimensional variables in place of x and S:

$$x/\tilde{R}=r,{(C/U)}^2=s.$$

(15)

$x/\tilde{R}=r$ is known as similarity variable. Non-dimensional quantities $u/U$, $p/p_0$, $\rho /{\rho }_0$ and $h/(p_0{(U/C)}^2)$ are assumed to be equal to F, G, $\mathsf{\Pi }$, and H, respectively which are consistent with Equations (1)–(4). We, therefore, can take the similarity transformations as:

$$u=UF(r,s),$$

(16)

$$p=p_0{(U/C)}^{2}G(r,s),$$

(17)

$$\rho ={\rho }_0\mathsf{\Pi }(r,s),$$

(18)

$$h=p_0{(U/C)}^{2}H(r,s)=p_{0}H(r,s)/s.$$

(19)

Using the system of Equations (16)–(19), we obtain

$$\frac{\partial }{\partial x}=\frac{1}{\tilde{R}}\frac{\partial }{\partial r},$$

(20)

$$\frac{D}{Dt}=\frac{U}{\tilde{R}}\left[(F-r)\frac{\partial }{\partial r}+\lambda s\frac{\partial }{\partial s}\right],$$

(21)

where $\lambda =\lambda (s)=\tilde{R}(ds/d\tilde{R})/s$. Substituting (16)–(19) into the fundamental Equations (1)–(4), we obtain

$$(F-r){\mathsf{\Pi }}_r+\lambda s{\mathsf{\Pi }}_s+\mathsf{\Pi }\left(F_r+\frac{mF}{r}\right)=0,$$

(22)

$$\mathsf{\Pi }\left(-\frac{\lambda }{2}F+(F-r)F_r+\lambda s{F}_s\right)+\frac{1}{\gamma }(G_r+H_r)=0,$$

(23)

$$-\lambda G+(F-r)G_r+\lambda s{G}_s+\frac{\gamma G}{(1-\overline{b}\mathsf{\Pi })}\left(F_r+\frac{mF}{r}\right)=0,$$

(24)

$$-\lambda H+(F-r)H_r+\lambda s{H}_s+2H\left(F_r+\frac{mF}{r}\right)=0,$$

(25)

where $\overline{b}=b{\rho }_0$. Using Equation (14), we obtain

$$s{\left(\frac{{\tilde{R}}_0}{\tilde{R}}\right)}^{m+1}={\int }_0^1\left(\frac{1}{2}\gamma \mathsf{\Pi }{F}^2+\frac{(1-\overline{b}\mathsf{\Pi })G}{(\gamma -1)}+H\right)r^{m}dr-\frac{(1-\overline{b}\mathsf{\Pi })s}{(\gamma -1)(m+1)}-\frac{\gamma C_0}{2(m+1)},$$

(26)

where

$${\tilde{R}}_0={\left(\frac{E}{p_0}\right)}^{1/(m+1)}.$$

(27)

Using (16)–(19), RH conditions become

$$\mathsf{\Pi }(1,s)=\frac{(\gamma +1)}{(\gamma -1)}\left[1-\frac{2\alpha }{\gamma -1}-\frac{2}{\gamma -1}s\right],$$

(28)

$$F(1,s)=\frac{2}{\gamma +1}(1-\alpha -s),$$

(29)

$$G(1,s)=\frac{2\gamma }{\gamma +1}\left[1-\alpha -\frac{(\gamma -1)s}{2\gamma }\right]-\frac{1}{2}{\left(\frac{\gamma +1}{\gamma -1}\right)}^2{C}_0\gamma \left[1-\frac{4\alpha }{\gamma -1}-\frac{4s}{\gamma -1}\right],$$

(30)

$$H(1,s)=\frac{\gamma }{2}{C}_0{\left(\frac{\gamma +1}{\gamma -1}\right)}^2\left[1-\frac{4\alpha }{\gamma -1}-\frac{4s}{\gamma -1}\right].$$

(31)

Now differentiating Equation (26) regarding s, we obtain the expression for $\lambda$ as

$$\lambda =\frac{J(m+1)-\frac{(1-\overline{b}\mathsf{\Pi })s}{\gamma -1}-\frac{\gamma C_0}{2}}{J-s\frac{dJ}{ds}-\frac{\gamma C_0}{2(m+1)}}.$$

(32)

Here

$$J={\int }_0^1\left(\frac{1}{2}\gamma \mathsf{\Pi }{F}^2+\frac{(1-\overline{b}\mathsf{\Pi })G}{(\gamma -1)}+H\right)r^{m}dr.$$

(33)

The self-similar process of the explosion has clearly explained the power rule particularly in Equation (27).

4. Construction of Solutions in Power Series of s

As we are seeking solution for strong shocks, the velocity of leading shock front S is very large than the velocity of sound waves V in ideal gas. The quantity $s={(V/S)}^2$ is very small for strong shocks. We, therefore, expand the non-dimensional quantities F, G, $\mathsf{\Pi }$ and H in power series $s={(V/S)}^2$ as follows

$$\begin{array}{cc}\hfill F& =F^{(0)}+s{F}^{(1)}+s^2{F}^{(2)}+s^3{F}^{(3)}+\dots ,\hfill \\ \hfill G& =G^{(0)}+s{G}^{(1)}+s^2{G}^{(2)}+s^3{G}^{(3)}+\dots ,\hfill \\ \hfill \mathsf{\Pi }& ={\mathsf{\Pi }}^{(0)}+s{\mathsf{\Pi }}^{(1)}+s^2{\mathsf{\Pi }}^{(2)}+s^3{\mathsf{\Pi }}^{(3)}+\dots ,\hfill \\ \hfill H& =H^{(0)}+s{H}^{(1)}+s^2{H}^{(2)}+s^3{H}^{(3)}+\dots .\hfill \end{array}$$

(34)

Here $F^{(i)}$, $G^{(i)}$, ${\mathsf{\Pi }}^{(i)}$ and $H^{(i)}$ $(i=0,1,2,\dots )$ are either constants or functions of r. We use the power series expansions from Equation (34) in Equation (33) to obtain the value of J as

$$J=J_0(1+{\sigma }_{1}s+{\sigma }_2{s}^2+\dots ),$$

(35)

where

$$\begin{array}{ccc}\hfill J_0& =& {\int }_0^1\left[\frac{\gamma }{2}{\mathsf{\Pi }}^{(0)}{(F^{(0)})}^2+\frac{(1-b{\mathsf{\Pi }}^{(0)})}{\gamma -1}{G}^{(0)}+H^{(0)}\right]r^{m}dr,\hfill \\ \hfill {\sigma }_1{J}_0& =& {\int }_0^1\left[\frac{\gamma }{2}{\mathsf{\Pi }}^{(1)}{(F^{(0)})}^2+\gamma {\mathsf{\Pi }}^{(0)}{F}^{(0)}{F}^{(1)}+\frac{1}{\gamma -1}(G^{(1)}-b{\mathsf{\Pi }}^{(0)}{G}^{(1)}-b{\mathsf{\Pi }}^{(1)}{G}^{(0)})+H^{(1)}\right]r^{m}dr,\hfill \\ \hfill {\sigma }_2{J}_0& =& {\int }_0^1\left[\frac{\gamma }{2}{\mathsf{\Pi }}^{(2)}{(F^{(0)})}^2+\gamma {\mathsf{\Pi }}^{(0)}{F}^{(0)}{F}^{(2)}+\frac{\gamma }{2}{\mathsf{\Pi }}^{(0)}{(F^{(1)})}^2+2{\mathsf{\Pi }}^{(1)}{F}^{(1)}{F}^{(0)}+H^{(2)}\right]r^{m}dr\hfill \\ & +& {\int }_0^1\frac{1}{\gamma -1}[G^{(2)}-b{\mathsf{\Pi }}^{(2)}{G}^{(0)}-b{\mathsf{\Pi }}^{(1)}{G}^{(1)}-b{\mathsf{\Pi }}^{(0)}{G}^{(2)}]r^{m}dr,\hfill \\ & \dots & \end{array}$$

(36)

Using (35) in (26), we obtain

$$s{\left(\frac{{\tilde{R}}_0}{\tilde{R}}\right)}^{m+1}=J_0\left[\left(1-\frac{\gamma C_0}{2(m+1)J_0}\right)+\left({\sigma }_1-\frac{1}{(m+1)(\gamma -1)J_0}\right)s+{\sigma }_2{s}^2+\dots \right].$$

(37)

In view of (15), Equation (37) becomes

$${\left(\frac{V}{S}\right)}^2{\left(\frac{{\tilde{R}}_0}{\tilde{R}}\right)}^{m+1}=J_0\left[\left(1-\frac{\gamma C_0}{2(m+1)J_0}\right)+\left({\sigma }_1-\frac{1}{(m+1)(\gamma -1)J_0}\right){\left(\frac{V}{S}\right)}^2+{\sigma }_2{\left(\frac{V}{S}\right)}^4+\dots \right].$$

(38)

This equation provides a relation between shock velocity and its position at time t. We expand $\lambda$ by using Equations (32) and (35) as follows:

$$\lambda =(m+1)[1+{\sigma }_1^{\prime }s+2{\sigma }_2^{\prime }{s}^2+\dots ],$$

(39)

where

$$\begin{array}{cc}\hfill {\sigma }_1^{\prime }& =\frac{{\sigma }_1-\frac{1}{(m+1)(\gamma -1)J_0}}{1-\frac{\gamma C_0}{2(m+1)(\gamma -1)J_0}},\hfill \\ \hfill {\sigma }_2^{\prime }& =\frac{{\sigma }_2}{1-\frac{\gamma C_0}{2(m+1)J_0}},\hfill \\ \hfill {\sigma }_3^{\prime }& =\frac{{\sigma }_3}{1-\frac{\gamma C_0}{2(m+1)J_0}}.\hfill \end{array}$$

For simplification, let us consider ${\lambda }_1={\sigma }_1^{\prime }$, ${\lambda }_2=2{\sigma }_2^{\prime }$, ${\lambda }_3=3{\sigma }_3^{\prime }$,..., then the Equation (39) becomes

$$\lambda =(m+1)[1+{\lambda }_{1}s+{\lambda }_2{s}^2+\dots ].$$

(40)

We use the relations from Equations (34) and (40) in Equations (22)–(25). Comparing the likewise powers of s on both sides of an equation, we get relations in terms of Ordinary Differential Equations (ODEs). Comparing the terms free from s, we get

$$(F^{(0)}-r){\mathsf{\Pi }}_r^{(0)}+{\mathsf{\Pi }}^{(0)}\left(F_r^{(0)}+\frac{m{F}^{(0)}}{r}\right)=0,$$

(41)

$$(F^{(0)}-r){\mathsf{\Pi }}^{(0)}{F}_r^{(0)}+\frac{1}{\gamma }(G_x^{(0)}+H_x^{(0)})=\frac{(m+1)F^{(0)}{\mathsf{\Pi }}^{(0)}}{2},$$

(42)

$$-(m+1)G^{(0)}+(F^{(0)}-r)G_r^{(0)}+\frac{\gamma G^{(0)}}{(1-b{\mathsf{\Pi }}^{(0)})}\left(F_r^{(0)}+\frac{m{F}^{(0)}}{r}\right)=0,$$

(43)

$$-(m+1)H^{(0)}+(F^{(0)}-r)H_r^{(0)}+2H^{(0)}\left(F_r^{(0)}+\frac{m{F}^{(0)}}{r}\right)=0.$$

(44)

Equating the power s, we get

$$\begin{array}{c}(F^{(0)}-r){\mathsf{\Pi }}_r^{(1)}+F^{(1)}{\mathsf{\Pi }}_r^{(0)}+(m+1){\mathsf{\Pi }}^{(1)}+{\mathsf{\Pi }}^{(0)}\left(F_r^{(1)}+\frac{m{F}^{(1)}}{r}\right)\hfill \end{array}$$

$$\begin{array}{c}+{\mathsf{\Pi }}^{(1)}\left(F_r^{(0)}+\frac{m{F}^{(0)}}{r}\right)=0,\hfill \\ -\frac{{\mathsf{\Pi }}^{(0)}}{2}(m+1)[F^{(1)}+{\lambda }_1{F}^{(0)}]-\frac{(m+1){\mathsf{\Pi }}^{(1)}{F}^{(0)}}{2}+{\mathsf{\Pi }}^{(0)}[(F^{(0)}-r)F_r^{(1)}+F^{(1)}{F}_r^{(0)}]\hfill \end{array}$$

(45)

$$\begin{array}{c}+{\mathsf{\Pi }}^{(1)}(F^{(0)}-r)F_r^{(0)}+(m+1){\mathsf{\Pi }}^{(0)}{F}^{(1)}+\frac{1}{\gamma }[G_r^{(1)}+H_r^{(1)}]=0,\hfill \\ -\lambda G^{(1)}+F^{(1)}{G}_r^{(0)}+{\lambda }_1(G_r^{(0)}+G^{(1)})+F^{(0)}{G}_r^{(1)}+[1+b{\mathsf{\Pi }}^{(1)}{G}^{(0)}\hfill \end{array}$$

(46)

$$\begin{array}{c}+\{b{\mathsf{\Pi }}^{(0)}+{(b{\mathsf{\Pi }}^{(0)})}^2+\dots \}{G}^{(1)}][F^{(0)}+\frac{m{F}^{(0)}}{r}]=0,\hfill \\ -(m+1){\lambda }_1{H}^{(0)}+(F^{(0)}-r)H_r^{(1)}+F^{(1)}{H}_r^{(0)}+2H^{(0)}\left(F_r^{(1)}+\frac{m{F}^{(1)}}{r}\right)\hfill \end{array}$$

(47)

$$\begin{array}{c}+2H^{(1)}\left(F_r^{(0)}+\frac{m{F}^{(0)}}{r}\right)=0,\hfill \end{array}$$

(48)

From Equations (28)–(31) and (34), we have

$$\begin{array}{c}{F}^{(0)}(1)=\frac{2}{\gamma +1}(1-\alpha ),G^{(0)}(1)=\frac{2\gamma }{\gamma +1}(1-\alpha )-{\left(\frac{\gamma +1}{\gamma -1}\right)}^2\frac{\gamma C_0}{2}\left(1-\frac{4\alpha }{\gamma -1}\right),\hfill \\ {\mathsf{\Pi }}^{(0)}(1)=\frac{\gamma +1}{\gamma -1}\left(1-\frac{2\alpha }{\gamma -1}\right),H^{(0)}(1)={\left(\frac{\gamma +1}{\gamma -1}\right)}^2\frac{\gamma C_0}{2}\left(1-\frac{4\alpha }{\gamma -1}\right).\hfill \end{array}$$

(49)

$$\begin{array}{c}{F}^{(1)}(1)=-\frac{2}{\gamma +1},G^{(1)}(1)=-\frac{\gamma -1}{\gamma +1}+2\gamma C_0\frac{{(\gamma +1)}^2}{{(\gamma -1)}^3},\hfill \\ {\mathsf{\Pi }}^{(1)}(1)=-\frac{2(\gamma +1)}{(\gamma -1)},H^{(1)}(1)=-2\gamma C_0\frac{{(\gamma +1)}^2}{{(\gamma -1)}^3}.\hfill \end{array}$$

(50)

To get the first approximate solution, we determine $F^{(0)}$, $G^{(0)}$, ${\mathsf{\Pi }}^{(0)}$ and $H^{(0)}$ from the system of nonlinear ODEs (41)–(44) with the boundary conditions given in Equation (49). Finally, these values are used in Equation (36)₁ to get approximate solution as follows

$$\begin{array}{c}u=S{F}^{(0)}(r),p=p_0{(S/V)}^2{G}^{(0)}(r),\hfill \\ \rho ={\rho }_0{\mathsf{\Pi }}^{(0)}(r),h=p_0{(S/V)}^2{H}^{(0)}(r).\hfill \end{array}$$

(51)

To get the second approximation, we need to determine the values of $F^{(1)}$, $G^{(1)}$, ${\mathsf{\Pi }}^{(1)}$ and $H^{(1)}$ in Equation (45). $F^{(0)}$, $G^{(0)}$, ${\mathsf{\Pi }}^{(0)}$ and $H^{(0)}$ are used from the first approximation. $F^{(1)}$, $G^{(1)}$, ${\mathsf{\Pi }}^{(1)}$ and $H^{(1)}$ contain ${\lambda }_1$. We use these values in terms of ${\lambda }_1$ in Equation (36)₂ to finally obtain the value of ${\lambda }_1$. The obtained value of ${\lambda }_1$ is used to get the second approximate solution. The other steps involve the repetition of the above process to get higher order approximate solutions of the problem.

5. The First Approximation

The Equations (41)–(44) can be written in the following forms:

$$\frac{{\mathsf{\Pi }}_r^{(0)}}{{\mathsf{\Pi }}^{(0)}}=\left(F_r^{(0)}+\frac{m{F}^{(0)}}{r}\right)/(r-F^{(0)}),$$

(52)

$$(F^{(0)}-r){\mathsf{\Pi }}^{(0)}{F}_r^{(0)}+\frac{1}{\gamma }(G_r^{(0)}+H_r^{(0)})=\frac{(m+1)F^{(0)}{\mathsf{\Pi }}^{(0)}}{2},$$

(53)

$$\frac{G_r^{(0)}}{G^{(0)}}=\left[-(m+1)+\frac{\gamma }{(1-\overline{b}{\mathsf{\Pi }}^{(0)})}\left(F_r^{(0)}+\frac{m{F}^{(0)}}{r}\right)\right]/(r-F^{(0)}),$$

(54)

$$\frac{H_r^{(0)}}{H^{(0)}}=\left(2F_r^{(0)}+\frac{2m{F}^{(0)}}{r}-m-1\right)/(r-F^{(0)}).$$

(55)

We substitute the values $G_r^{(0)}$ and $H_r^{(0)}$ from Equations (54) and (55) in Equation (53) to get $F_r^{(0)}$ in the following form

$$F_r^{(0)}=\frac{\left[\frac{m+1}{\gamma }-\frac{m{F}^{(0)}}{(1-\overline{b}{\mathsf{\Pi }}^{(0)})r}+\left(\frac{m+1}{\gamma }-\frac{2m{F}^{(0)}}{\gamma r}\right)\frac{H^{(0)}}{G^{(0)}}+\frac{(m+1)F^{(0)}{\mathsf{\Pi }}^{(0)}(r-F^{(0)})}{2G^{(0)}}\right]}{\left[\frac{2H^{(0)}}{\gamma G^{(0)}}+\frac{1}{(1-\overline{b}{\mathsf{\Pi }}^{(0)})}-\frac{{\mathsf{\Pi }}^{(0)}(r-F^{(0)})}{G^{(0)}}\right]}.$$

(56)

Taylor [23] performed similarity transformation and presented the approximate solution for intense explosion. This approximation has been used by Sakurai [3] to produce analytical solution in gas dynamics. We, therefore, has assumed the first approximation $F^{(0)}$ as given in the work of Taylor [23]

$$F^{(0)}(r)=\frac{r}{\gamma }+A{r}^n.$$

(57)

We get the value of A in the following form using Equations (49) and (57),

$$A=\frac{\gamma (1-2\alpha )-1}{\gamma (\gamma +1)}.$$

(58)

We use Equations (56)–(58) to get n. After determining the values of A and n, we integrate Equations (52)–(55) with boundary conditions (49) to obtain

$${\mathsf{\Pi }}^{(0)}(r)=\frac{\gamma +1}{\gamma -1}\left(1-\frac{2\alpha }{\gamma -1}\right){\left[\frac{\gamma }{\gamma +1-r^{n-1}}\right]}^{\left(\frac{(n+m)(\gamma (1-2\alpha )-1)}{(n-1)(\gamma -1)}+\frac{m+1}{(n-1)(\gamma -1)}\right)}{r}^{(\frac{m+1}{\gamma -1})},$$

(59)

$$G^{(0)}(r)=\left\{\frac{2\gamma }{\gamma +1}(1-\alpha )-{\left(\frac{\gamma +1}{\gamma -1}\right)}^2\frac{\gamma C_0}{2}\left(1-\frac{4\alpha }{\gamma -1}\right)\right\}{\left[\frac{\gamma }{\gamma +1-r^{n-1}}\right]}^{(B)}{r}^{\frac{(\gamma +1)(m+1)\overline{b}(1-\frac{2\alpha }{\gamma -1})}{{(\gamma -1)}^2[1-\overline{b}\frac{\gamma +1}{\gamma -1}(1-\frac{2\alpha }{\gamma -1})]}},$$

(60)

where

$$B=\frac{\gamma (m+n)(\gamma (1-2\alpha )-1)+\gamma (m+1)\overline{b}(\gamma +1)(1-\frac{2\alpha }{\gamma -1})}{(n-1)(\gamma -1)\{1-\overline{b}(\frac{\gamma +1}{\gamma -1})(1-\frac{2\alpha }{\gamma -1})\}}.$$

and

$$H^{(0)}(r)=\frac{\gamma C_0}{2}{\left(\frac{\gamma +1}{\gamma -1}\right)}^2\left(1-\frac{4\alpha }{\gamma -1}\right){\left[\frac{\gamma }{\gamma +1-r^{n-1}}\right]}^{\left(\frac{2(m+n)(\gamma (1-2\alpha )-1)+(1+m)(2-\gamma )}{(n-1)(\gamma -1)}\right)}{r}^{\frac{(m+1)(2-\gamma )}{(\gamma -1)}}.$$

(61)

Dimensionless quantities $F^{(0)}$, ${\mathsf{\Pi }}^{(0)}$ and $G^{(0)}$ are computed in Table 1 and Table 2 for ($m=0,1$) in ideal gas (without magnetic field i.e., $C_0=0$). A comparison of the obtained results is presented with the published work of Sakurai [4] in gas dynamics. Schematic of dimensionless flow variables are depicted in Figure 1, Figure 2, Figure 3 and Figure 4.

Table 1. $F^{(0)}$, ${\mathsf{\Pi }}^{(0)}$ and $G^{(0)}$ for $m=0$, $\gamma =1.4$ and $C_0=0$.

x	$\mathit{\alpha }$	${\mathit{F}}^{(0)}$ Sakurai [3]	${\mathbf{\Pi }}^{(0)}$ Sakurai [3]	${\mathit{G}}^{(0)}$ Sakurai [3]	${\mathit{F}}^{(0)}$	${\mathbf{\Pi }}^{(0)}$	${\mathit{G}}^{(0)}$
	0.0	0.8333	6.000	1.167	0.8333	6.000	1.167
1.0	0.015	-	-	-	0.8208	5.550	1.167
	0.025	-	-	-	0.8125	5.250	1.167
	0.0	0.7170	3.096	0.815	0.7251	3.096	0.815
0.9	0.015	-	-	-	0.7199	2.899	0.835
	0.025				0.7159	2.767	0.848
	0.0	0.6151	1.785	0.647	0.6259	1.785	0.647
0.8	0.015	-	-	-	0.6251	1.660	0.664
	0.025	-	-	-	0.6240	1.577	0.677
	0.0	0.5239	1.080	0.556	0.5341	1.080	0.556
0.7	0.015	-	-	-	0.5356	0.990	0.567
	0.025	-	-	-	0.5362	0.931	0.575
	0.0	0.4405	0.658	0.504	0.4484	0.658	0.504
0.6	0.015	-	-	-	0.4507	0.593	0.508
	0.025	-	-	-	0.4521	0.551	0.515
	0.0	0.3624	0.389	0.473	0.3676	0.389	0.473
0.5	0.015	-	-	-	0.3698	0.345	0.471
	0.025	-	-	-	0.3712	0.317	0.471
	0.0	0.2877	0.214	0.456	0.2877	0.214	0.456
0.4	0.015	-	-	-	0.2921	0.187	0.450
	0.025	-	-	-	0.2933	0.170	0.446
	0.0	0.2148	0.102	0.447	0.2160	0.102	0.447
0.3	0.015	-	-	-	0.2169	0.088	0.437
	0.025	-	-	-	0.2177	0.079	0.431
	0.0	0.1430	0.037	0.443	0.1432	0.037	0.443
0.2	0.015	-	-	-	0.1436	0.0316	0.432
	0.025	-	-	-	0.1439	0.0282	0.423
	0.0	0.0714	0.006	0.442	0.0714	0.006	0.442
0.1	0.015	-	-	-	0.0715	0.005	0.429
	0.025	-	-	-	0.0716	0.005	0.419
	0.0	0.0000	0.000	0.442	0.0000	0.000	0.442
0.0	0.015	-	-	-	0.0000	0.000	0.429
	0.025	-	-	-	0.0000	0.000	0.419

Table 2. $F^{(0)}$, ${\mathsf{\Pi }}^{(0)}$ and $G^{(0)}$ for $m=1$, $\gamma =1.4$ and $C_0=0$.

x	$\mathit{\alpha }$	${\mathit{F}}^{(0)}$ Sakurai [3]	${\mathbf{\Pi }}^{(0)}$ Sakurai [3]	${\mathit{G}}^{(0)}$ Sakurai [3]	${\mathit{F}}^{(0)}$	${\mathbf{\Pi }}^{(0)}$	${\mathit{G}}^{(0)}$
	0.0	0.8333	6.000	1.167	0.8333	6.000	1.167
1.0	0.015	-	-	-	0.8208	5.550	1.167
	0.025	-	-	-	0.8125	5.250	1.167
	0.0	0.7008	1.898	0.685	0.7072	1.898	0.684
0.9	0.015	-	-	-	0.7196	1.767	0.767
	0.025				0.7314	1.678	0.874
	0.0	0.5973	0.783	0.531	0.6038	0.783	0.531
0.8	0.015	-	-	-	0.6246	0.713	0.577
	0.025	-	-	-	0.6503	0.668	0.667
	0.0	0.5104	0.347	0.468	0.5141	0.346	0.468
0.7	0.015	-	-	-	0.5351	0.309	0.474
	0.025	-	-	-	0.5691	0.284	0.517
	0.0	0.4322	0.153	0.441	0.4346	0.150	0.441
0.6	0.015	-	-	-	0.4503	0.131	0.414
	0.025	-	-	-	0.4880	0.119	0.406
	0.0	0.3582	0.058	0.429	0.3592	0.0582	0.429
0.5	0.015	-	-	-	0.3695	0.050	0.378
	0.025	-	-	-	0.4077	0.045	0.323
	0.0	0.2859	0.019	0.425	0.2863	0.019	0.425
0.4	0.015	-	-	-	0.2919	0.016	0.357
	0.025	-	-	-	0.3255	0.014	0.260
	0.0	0.2140	0.005	0.424	0.2144	0.004	0.424
0.3	0.015	-	-	-	0.2168	0.004	0.346
	0.025	-	-	-	0.2443	0.003	0.211
	0.0	0.1429	0.001	0.424	0.1429	0.001	0.423
0.2	0.015	-	-	-	0.1437	0.001	0.340
	0.025	-	-	-	0.1630	0.000	0.173
	0.0	0.0714	0.000	0.424	0.0714	0.000	0.423
0.1	0.015	-	-	-	0.0715	0.000	0.338
	0.025	-	-	-	0.0815	0.000	0.143
	0.0	0.0000	0.000	0.424	0.0000	0.000	0.423
0.0	0.015	-	-	-	0.0000	0.000	0.338
	0.025	-	-	-	0.0000	0.000	0.118

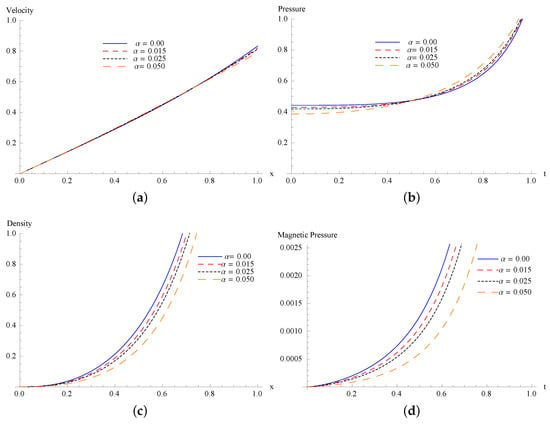
Figure 1. Schematic of non-dimensional velocity (a) $F^{(0)}$, (b) pressure $G^{(0)}$, (c) density ${\mathsf{\Pi }}^{(0)}$ and (d) magnetic pressure $H^{(0)}$ for $\gamma =1.4$, $C_0=0$, $m=0$ and $\alpha =0.0,0.015,0.025,0.05$.

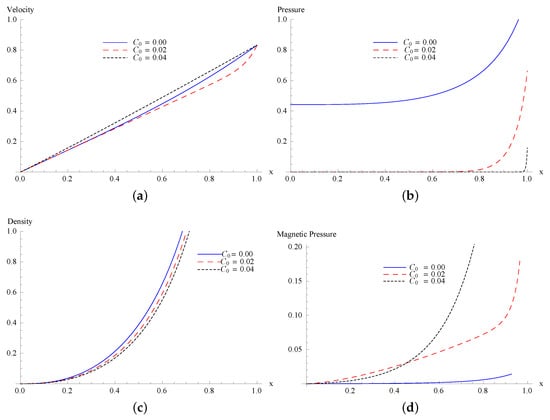
Figure 2. Schematic of non-dimensional (a) velocity $F^{(0)}$, (b) pressure $G^{(0)}$, (c) density ${\mathsf{\Pi }}^{(0)}$ and (d) magnetic pressure $H^{(0)}$ for $\gamma =1.4$, $\alpha =0$, $m=0$ and $C_0=0.00,0.02,0.04$.

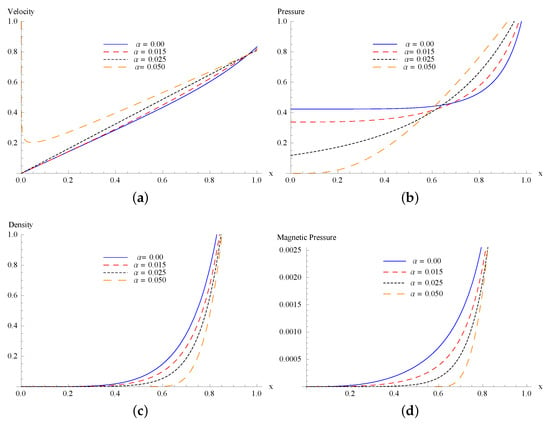
Figure 3. Schematic of non-dimensional (a) velocity $F^{(0)}$, (b) pressure $G^{(0)}$, (c) density ${\mathsf{\Pi }}^{(0)}$ and (d) magnetic pressure $H^{(0)}$ for $\gamma =1.4$, $C_0=0$, $m=1$ and $\alpha =0.0,0.015,0.025,0.05$.

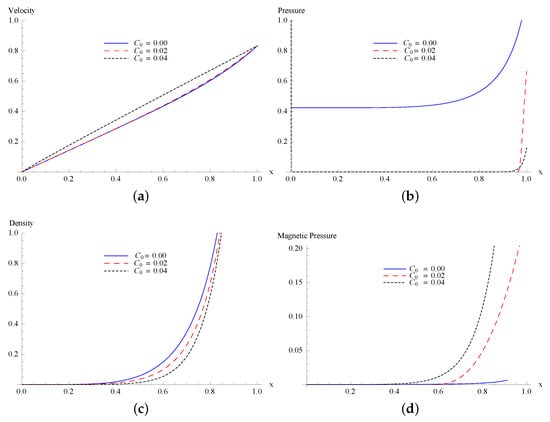
Figure 4. Schematic of non-dimensional (a) velocity $F^{(0)}$, (b) pressure $G^{(0)}$, (c) density ${\mathsf{\Pi }}^{(0)}$ and (d) magnetic pressure $H^{(0)}$ for $\gamma =1.4$, $\alpha =0$, $m=1$ and $C_0=0.00,0.02,0.04$.

6. Conclusions

In the present work, we have successfully used the Sakurai [4] approach to find the first-order approximate analytical solution of the planar and cylindrical symmetric flow under the presence of transverse magnetic field in a non-ideal medium. However, Sakurai [4] has obtained a solution in gas dynamics by using this method; there is no study afterwards that provides approximate analytical solution of the problem with magnetic field in non-ideal medium. We have tried to fill the gap by providing approximate analytical solutions of the problem with magnetic and non-ideal effects. These findings are quite useful for the groups working in the field of Magneto Hydrodynamics (MHD) or Computational Fluid Dynamics (CFD). To generate confidence in our results, we have recovered all results of Sakurai’s [4] published work as a particular case of our problem (i.e., $C_0=0$) in Table 1 and Table 2. The effects of non-ideal medium and transverse magnetic field on flow variables are depicted in Figure 1, Figure 2, Figure 3 and Figure 4.

Figure 1 consists of the profiles of velocity, density, pressure, and magnetic pressure for planar shocks ($m=0$) with $\gamma =1.4$, $C_0=0$, and $\alpha =0.00,0.015,0.025,0.050$. It is clearly seen from Figure 1 that the dimensionless profiles of flow variables decrease as value of parameter $\alpha$ increases except the pressure which increases with the small increase in the parameter $\alpha$. This is expected physically as gas particles will collide more frequently with the increase of non-idealness $\alpha$ which results in the rise in pressure with the increment of $\alpha$. In Figure 2, we observe that the pressure and density decrease as we increase the value of $C_0$, while the magnetic pressure increases for planar motion $(m=0)$ after a certain point. It is again an expected result as the charged particles will be transported away very quickly with the increase of $C_0$. It results in dropping in pressure after the blast. At the point of explosion, the process is not fully self-similar and therefore the initial dynamics is a bit off. It agrees with blast wave theory. It is well known that the phenomena are not self-similar at very near the center or axis of explosion. However, point explosions can be self-similar at considerable distance from the source (see Sakurai [3,4]). Figure 3 and Figure 4 display the profiles of the flow variables for cylindrically symmetric flow ($m=1$). From Figure 3a and Figure 4a, we observed that as we increase the value of $\alpha$ and $C_0$, velocity increases. Figure 3b shows that as the value of parameter $\alpha$ increases, pressure also increases after a certain point. This describes the physics of the post-shock process very well as increase in $\alpha$ makes the collision of the gas particles more frequent. Figure 4b shows that an increment in the value of $C_0$ causes a decrease in pressure for the cylindrically symmetric flow. It is attributed to the fact that the ionized gas molecules are carried away by a strong magnetic field. It is one of the reasons that the instabilities at the shock front can be suppressed under the presence of a magnetic field. Figure 4c shows that the density of the medium decreases as $C_0$ increases. Figure 4d shows that as the value of $C_0$ increases, magnetic pressure also increases.