m-Polar ( α , β ) -Fuzzy Ideals in BCK/BCI-Algebras

Abstract

Multi-polar vagueness in data plays a prominent role in several areas of the sciences. In recent years, the thought of m-polar fuzzy sets has captured the attention of numerous analysts, and research in this area has escalated in the past four years. Hybrid models of fuzzy sets have already been applied to many algebraic structures, such as $BCK/BCI$-algebras, lie algebras, groups, and symmetric groups. A symmetry of the algebraic structure, mathematically an automorphism, is a mapping of the algebraic structure onto itself that preserves the structure. This paper focuses on combining the concepts of m-polar fuzzy sets and m-polar fuzzy points to introduce a new notion called m-polar $(\alpha ,\beta )$-fuzzy ideals in $BCK/BCI$-algebras. The defined notion is a generalization of fuzzy ideals, bipolar fuzzy ideals, $(\alpha ,\beta )$-fuzzy ideals, and bipolar $(\alpha ,\beta )$-fuzzy ideals in $BCK/BCI$-algebras. We describe the characterization of m-polar $(\in ,\in \vee q)$-fuzzy ideals in $BCK/BCI$-algebras by level cut subsets. Moreover, we define m-polar $(\in ,\in \vee q)$-fuzzy commutative ideals and explore some pertinent properties.

1. Introduction

As a ramification of general algebra, $BCK/BCI$-algebras first appeared in the mathematics literature in 1966, in work by Imai and Iséki [1,2]. These ideas are created from two distinct approaches: propositional calculi and set theory. $BCK/BCI$-algebras are algebraic patterns of the $BCK/BCI$-system in combinatory logic. The name of $BCK/BCI$-algebras arises from the combinatories $B,C,K,I$ in combinatory logic. Various properties of $BCK/BCI$-algebras are explored within [3,4,5,6].

Bipolar fuzzy sets [7]—a generalization of Zadeh’s idea of the fuzzy set [8] which itself expands the classical set—are sets whose elements have positive and negative membership degrees. Hybrid models of fuzzy sets have been applied in many different sciences [9,10,11,12]. The first definition of fuzzy ideals in $BCK/BCI$-algebras was by Xi [13] in 1991. Bipolar information is applied in many algebraic structures—for instance, $BCK/BCI$-algebras [14,15,16,17], $BF$-algebras [18], $\mathsf{\Gamma }$-semihypergroups [19], and hemirings [20]. In many real-life issues, information sometimes comes from m factors $(m\ge 2)$, that is, multi-attribute data arise which cannot be handled using the existing ideals (e.g., fuzzy ideals, bipolar fuzzy ideals, etc.). For the time being, experts trust that the real world is proceeding to multipolarity. Multi-polar vagueness in information performs a crucial role in different areas of the sciences. In neurobiology, multi-polar neurons have numerous dendrites, permitting the integration of a great deal of data from different neurons. In technology, multi-polar technology can be utilized to build and perform large-scale IT structures.

In view of this inspiration, Chen et al. [21] introduced an m-polar fuzzy set (m-pF set, for short) in 2014, which was an extension of the bipolar fuzzy set. In an m-pF set, the degree of membership of an object ranges over ${[0,1]}^m$, which depicts m distinct characteristics of the object. The theory of m-pF sets was essentially created to deal with the absence of a mathematical method towards multi-attribute, multi-polar, and multi-index information. Since that time, m-pF sets have been utilized in mathematical theories such as graph theory [22,23,24] and matroid theory [25]. Additionally, m-pF sets have applications in real-life issues such as decision-making problems [26,27]. For the first time, Akram et al. [28] implemented the idea of m-pF sets into algebraic structures and gave the notion of m-pF lie subalgebras. In addition, Akram and Farooq [29] established m-pF lie ideals of lie subalgebras. Applying the idea of m-pF sets to group theory, Farooq et al. [30] initiated the concept of m-pF subgroups, and investigated some of their properties. Furthermore, Al-Masarwah and Ahmad [31] applied m-pF sets to $BCK/BCI$-algebras. They presented the concepts of m-pF subalgebras, m-pF ideals, and m-pF commutative ideals, and investigated related results.

In 1971, Rosenfeld [32] used fuzzy sets in the theory of groups and established the notion of fuzzy subgroups. In 1996, Bhakat and Das [33] generalized the idea of fuzzy subgroups to $(\alpha ,\beta )$-fuzzy subgroups by using the concept of fuzzy points and its “belongingness (∈)” and “quasi-coincidence (q)” with a fuzzy set. After that, Bhakat [34,35] studied this concept in detail. Actually, the notion of an $(\in ,\in \vee q)$-fuzzy subgroup is a fundamental and valuable generalization of the fuzzy subgroup. In $BCK/BCI$-algebras, $(\alpha ,\beta )$-fuzzy subalgebras were created and discussed by Jun [36,37], and further studied by Muhiuddin and Al-Roqi in [38]. Jun [39] and Zhan et al. [40] proposed and discussed a generalization of a fuzzy ideal in a $BCK/BCI$-algebra. As an extension of generalized fuzzy ideals in $BCK/BCI$-algebras, Ma et al. [41] considered $(\in ,\in \vee q)$-interval-valued fuzzy ideals and Jana et al. [42] proposed the concept of $(\in ,\in \vee q)$-bipolar fuzzy ideals. Recently, Ibrara et al. [43] proposed the $(\alpha ,\beta )$-bipolar fuzzy generalized bi-ideal in ordered semigroups. In hemirings, Abdullah [44] defined the concepts of N-dimensional $(\alpha ,\beta )$-fuzzy H-ideals.

Motivated by the previous studies, here we combine the notions of m-pF sets and m-pF points to introduce a new notion called m-polar $(\alpha ,\beta )$-fuzzy ideals in $BCK/BCI$-algebras. The defined concept is a generalization of fuzzy ideals, bipolar fuzzy ideals, $(\alpha ,\beta )$-fuzzy ideals, and $(\alpha ,\beta )$-bipolar fuzzy ideals. We prove that every m-polar $(\in ,\in )$-fuzzy ideal is an m-polar $(\in ,\in \vee q)$-fuzzy ideal, and every m-polar $(\in \vee q,\in \vee q)$-fuzzy ideal is an m-polar $(\in ,\in \vee q)$-fuzzy ideal. For the characterizations of $BCK/BCI$-algebras, we give a fundamental bridge between crisp ideals and m-polar $(\in ,\in \vee q)$-fuzzy ideals, since sometimes it is difficult to comprehend whether a particular ideal is an m-polar $(\in ,\in \vee q)$-fuzzy (resp., crisp) ideal or not. In this case, to provide the required information, we describe the characterization of m-polar $(\in ,\in \vee q)$-fuzzy ideals by level cut subsets. However, this technique has some gaps. One of them is that all outcomes have similarities in crisp ideals. In other words, m-polar $(\in ,\in \vee q)$-fuzzy ideals become a mirror of the crisp case. Moreover, we define m-polar $(\in ,\in \vee q)$-fuzzy commutative ideals and discuss some relevant properties. To show the novelty of this model, some contributions of several authors toward m-polar $(\alpha ,\beta )$-fuzzy ideals in $BCK/BCI$-algebras are analyzed in Table 1.

Table 1. Contributions of several authors toward m-polar $(\alpha ,\beta )$-fuzzy ideals.

Authors	Year	Contributions
Rosenfeld [32]	1971	Introduction of fuzzy subgroups.
Bhakat and Das [33]	1996	Generalization of fuzzy subgroups.
Xi [13]	1991	Introduction of fuzzy ideals.
Jun [39]	2004	Introduction of $(\alpha ,\beta )$-fuzzy ideals.
Lee [14]	2009	Introduction of bipolar fuzzy ideals.
Jana et al. [42]	2017	Generalization of bipolar fuzzy ideals.
Al-Masarwah and Ahmad [31]	2018	Introduction of m-pF ideals.
Al-Masarwah and Ahmad	This paper	Introduction of m-polar $(\alpha ,\beta )$-fuzzy ideals as a generalization of m-pF ideals.

2. Preliminaries

We recall basic concepts of $BCK/BCI$-algebras, m-pF sets, m-pF ideals, and m-pF commutative ideals. From now on, X stands for a $BCK/BCI$-algebra, unless something else is indicated.

A $BCI$-algebra is an algebraic structure $(X;\ast ,0)$ satisfying the axioms below: for all $x,y,z\in X,$

(I)

$((x\ast y)\ast (x\ast z))\ast (z\ast y)=0,$

(II)

$x\ast x=0,$

(III)

$(x\ast (x\ast y))\ast y=0,$

(IV)

$x\ast y=0$ and $y\ast x=0$ imply $x=y.$

A $BCI$-algebra X is called a $BCK$-algebra if $0\ast x=0$ for any $x\in X.$ In any $BCK/BCI$-algebra $X,$ the following hold: for all $x,y,z\in X,$

(1)

$x\ast 0=x,$

(2)

$x\ast y\le x,$

(3)

$(x\ast y)\ast z=(x\ast z)\ast y,$

(4)

$(x\ast y)\ast z\le (x\ast z)\ast (y\ast z),$

(5)

$x\le y\Rightarrow x\ast z\le y\ast z,$$z\ast y\le z\ast x,$

where $x\le y$ means $x\ast y=0.$

A non-empty subset J of X is said to be an ideal of X if for all $x,y\in X,$

• $0\in J,$
• $x\ast y\in J,y\in J\Rightarrow x\in J.$

A $BCK$-algebra X is called commutative if $y▽x=x▽y$ $\forall x,y\in X,$ where $y▽x=y\ast (y\ast x).$ A non-empty subset D of a $BCK$-algebra X is a commutative ideal of X (see [45]) if for all $x,y,z\in X,$

• $0\in D,$
• $(x\ast y)\ast z\in D,z\in D\Rightarrow x\ast (y▽x)\in D.$

Definition 1 

([21]). An m-pF set $\widehat{\mathcal{F}}$ on $X(\ne \varphi )$ is a function $\widehat{\mathcal{F}}:X\to {[0,1]}^m,$ where

$$\widehat{\mathcal{F}}(x)=(p_1\circ \widehat{\mathcal{F}}(x),p_2\circ \widehat{\mathcal{F}}(x),\dots ,p_m\circ \widehat{\mathcal{F}}(x))$$

is the membership value of every element $x\in X$ and $p_i\circ \widehat{\mathcal{F}}:{[0,1]}^m\to [0,1]$ is the i-th projection mapping for all $i=1,2,\dots ,m$. The values $\widehat{0}=(0,0,\dots ,0)$ and $\widehat{1}=(1,1,\dots ,1)$ are the smallest and largest values in ${[0,1]}^m,$ respectively.

Al-Masarwah and Ahmad [31] proposed m-pF ideals and m-pF commutative ideals as follows:

Definition 2 

([31]). An m-pF set $\widehat{\mathcal{F}}$ of X is said to be an m-pF ideal if the assertions below are valid: for all $x,y\in X,$

(J1) $\widehat{\mathcal{F}}(0)\ge \widehat{\mathcal{F}}(x),$

(J2) $\widehat{\mathcal{F}}(x)\ge inf\{\widehat{\mathcal{F}}(x\ast y),\widehat{\mathcal{F}}(y)\}.$

  That is,

(J1) $p_i\circ \widehat{\mathcal{F}}(0)\ge p_i\circ \widehat{\mathcal{F}}(x),$

(J2) $p_i\circ \widehat{\mathcal{F}}(x)\ge inf\{p_i\circ \widehat{\mathcal{F}}(x\ast y),p_i\circ \widehat{\mathcal{F}}(y)\}$

for all $i=1,2,\dots ,m.$

Definition 3 

([31]). An m-pF set $\widehat{\mathcal{F}}$ of a $BCK$-algebra X is said to be an m-pF commutative ideal of X if it satisfies $(J1)$ and for all $x,y,z\in X,$

(J3) $\widehat{\mathcal{F}}(x\ast (y▽x))\ge inf\{\widehat{\mathcal{F}}((x\ast y)\ast z),\widehat{\mathcal{F}}(z)\}.$

That is, (J3) $p_i\circ \widehat{\mathcal{F}}(x\ast (y▽x))\ge inf\{p_i\circ \widehat{\mathcal{F}}((x\ast y)\ast z),p_i\circ \widehat{\mathcal{F}}(z)\}$

for all $i=1,2,\dots ,m.$

For an m-pF set $\widehat{\mathcal{F}}$ of $X,$ the set

$${\widehat{\mathcal{F}}}_{\widehat{t}}=\{x\in X\mid \widehat{\mathcal{F}}(x)\ge \widehat{t}\}$$

for all $\widehat{t}\in {(0,1]}^m$ is called the level cut subset of $\widehat{\mathcal{F}}.$

An m-pF set $\widehat{\mathcal{F}}$ of X of the form

$$\begin{array}{c}\hfill \widehat{\mathcal{F}}(y)=\left\{\begin{array}{cc}\widehat{t}=(t_1,t_2,\dots ,t_m)\in {(0,1]}^m,\hfill & \mathrm{if}y=x\hfill \\ \widehat{0}=(0,0,\dots ,0),\hfill & \mathrm{if}y\ne x\hfill \end{array}\right.\end{array}$$

is called an m-pF point, denoted by $x_{\widehat{t}}$, with support x and value $(t_1,t_2,\dots ,t_m)=\widehat{t}.$

An m-pF point $x_{\widehat{t}}$

• Belongs to $\widehat{\mathcal{F}}$, denoted by $x_{\widehat{t}}\in \widehat{\mathcal{F}}$, if $\widehat{\mathcal{F}}(x)\ge \widehat{t}$, that is, $p_i\circ \widehat{\mathcal{F}}(x)\ge t_i$ for each $i=1,2,\dots ,m,$
• Is quasi-coincident with $\widehat{\mathcal{F}}$, denoted by $x_{\widehat{t}}q\widehat{\mathcal{F}}$, if $\widehat{\mathcal{F}}(x)+\widehat{t}>\widehat{1}$, that is, $p_i\circ \widehat{\mathcal{F}}(x)+t_i>\widehat{1}$ for each $i=1,2,\dots ,m.$

We say that

• $x_{\widehat{t}}\overline{\alpha }\widehat{\mathcal{F}}$ if $x_{\widehat{t}}\alpha \widehat{\mathcal{F}}$ does not hold,
• $x_{\widehat{t}}\in \vee q\widehat{\mathcal{F}}$ if $x_{\widehat{t}}\in \widehat{\mathcal{F}}$ or $x_{\widehat{t}}q\widehat{\mathcal{F}},$
• $x_{\widehat{t}}\in \wedge q\widehat{\mathcal{F}}$ if $x_{\widehat{t}}\in \widehat{\mathcal{F}}$ and $x_{\widehat{t}}q\widehat{\mathcal{F}}.$

3. $\mathit{m}$-Polar $(\mathit{\alpha },\mathit{\beta })$-Fuzzy Ideals

In this section, we propose and discuss m-polar $(\alpha ,\beta )$-fuzzy ideals, where

$$\alpha ,\beta \in \{\in ,q,\in \vee q,\in \wedge q\},\alpha \ne \in \wedge q.$$

Theorem 1.

For an m-pF set $\widehat{\mathcal{F}}$ of $X,$ the set ${\widehat{\mathcal{F}}}_{\widehat{t}}\ne \varphi$ for all $\widehat{t}\in {(0.5,1]}^m$ is an ideal of X if and only if $\widehat{\mathcal{F}}$ satisfies the assertions below: for all $x,y\in X,$

(1) 

$sup\{\widehat{\mathcal{F}}(0),\widehat{0.5}\}\ge \widehat{\mathcal{F}}(x),$

(2) 

$sup\{\widehat{\mathcal{F}}(x),\widehat{0.5}\}\ge inf\{\widehat{\mathcal{F}}(x\ast y),\widehat{\mathcal{F}}(y)\}.$

Proof. 

Let ${\widehat{\mathcal{F}}}_{\widehat{t}}\ne \varphi$ be an ideal of $X.$ Suppose that there exists $h\in X$ such that

$$sup\{\widehat{\mathcal{F}}(0),\widehat{0.5}\}<\widehat{\mathcal{F}}(h).$$

Then, $\widehat{\mathcal{F}}(h)\in {(0.5,1]}^m,$ and thus $h\in {\widehat{\mathcal{F}}}_{\widehat{\mathcal{F}}(h)}.$ But $\widehat{\mathcal{F}}(0)<\widehat{\mathcal{F}}(h),$ implies $0\notin {\widehat{\mathcal{F}}}_{\widehat{\mathcal{F}}(h)},$ a contradiction. Thus, (1) holds. Assume $sup\{\widehat{\mathcal{F}}(x),\widehat{0.5}\}<inf\{\widehat{\mathcal{F}}(x\ast y),\widehat{\mathcal{F}}(y)\}=\widehat{t}$ for some $x,y\in X.$ Then, $\widehat{t}\in {(0.5,1]}^m$ and $y,x\ast y\in {\widehat{\mathcal{F}}}_{\widehat{t}}.$ However, $x\notin {\widehat{\mathcal{F}}}_{\widehat{t}}$ since $\widehat{\mathcal{F}}(x)<\widehat{t},$ a contradiction. Thus, (2) holds.

Conversely, suppose that (1) and (2) hold. Let $\widehat{t}\in {(0.5,1]}^m$ be such that ${\widehat{\mathcal{F}}}_{\widehat{t}}\ne \varphi .$ For any $x\in {\widehat{\mathcal{F}}}_{\widehat{t}},$ we get

$$\widehat{0.5}<\widehat{t}\le \widehat{\mathcal{F}}(x)\le sup\{\widehat{\mathcal{F}}(0),\widehat{0.5}\}.$$

Thus, $\widehat{\mathcal{F}}(0)=sup\{\widehat{\mathcal{F}}(0),\widehat{0.5}\}\ge \widehat{t}.$ Therefore, $0\in {\widehat{\mathcal{F}}}_{\widehat{t}}.$ Let $x,y\in X$ be such that $x\ast y,y\in {\widehat{\mathcal{F}}}_{\widehat{t}}.$ This implies that

$$sup\{\widehat{\mathcal{F}}(x),\widehat{0.5}\}\ge inf\{\widehat{\mathcal{F}}(x\ast y),\widehat{\mathcal{F}}(y)\}\ge \widehat{t}>\widehat{0.5}.$$

Thus, $\widehat{\mathcal{F}}(x)=sup\{\widehat{\mathcal{F}}(x),\widehat{0.5}\}\ge \widehat{t},$ that is, $x\in {\widehat{\mathcal{F}}}_{\widehat{t}}.$ Hence, ${\widehat{\mathcal{F}}}_{\widehat{t}}$ is an ideal of $X.$ □

Definition 4.

An m-pF set $\widehat{\mathcal{F}}$ of X is called an m-polar $(\alpha ,\beta )$-fuzzy ideal of X if for all $x,y\in X$ and $\widehat{t},\widehat{s}\in {(0,1]}^m,$

(1) 

$x_{\widehat{t}}\alpha \widehat{\mathcal{F}}implies{0}_{\widehat{t}}\beta \widehat{\mathcal{F}},$

(2) 

${(x\ast y)}_{\widehat{t}}\alpha \widehat{\mathcal{F}}$ and $y_{\widehat{s}}\alpha \widehat{\mathcal{F}}imply{x}_{inf\{\widehat{t},\widehat{s}\}}\beta \widehat{\mathcal{F}}.$

Theorem 2.

Let $\widehat{\mathcal{F}}$ be an m-pF subset of X and J be an ideal of X such that

(1) 

$\widehat{\mathcal{F}}(x)=\widehat{0},$ for all $x\notin J,$

(2) 

$\widehat{\mathcal{F}}(x)\ge \widehat{0.5},$ for all $x\in J.$

Then, $\widehat{\mathcal{F}}$ is an m-polar $(\alpha ,\in \vee q)$-fuzzy ideal of $X.$

Proof. 

(a) (For $\alpha =q$) Let $x\in X$ and $\widehat{t}\in {(0,1]}^m$ be such that $x_{\widehat{t}}q\widehat{\mathcal{F}}.$ Then, $\widehat{\mathcal{F}}(x)+\widehat{t}>\widehat{1}.$ Since $0\in J,$ we have $\widehat{\mathcal{F}}(0)\ge \widehat{0.5}.$ If $\widehat{t}\le \widehat{0.5},$ then $\widehat{\mathcal{F}}(0)\ge \widehat{t}$ and we have $0_{\widehat{t}}\in \widehat{\mathcal{F}}.$ If $\widehat{t}>\widehat{0.5},$ then $\widehat{\mathcal{F}}(0)+\widehat{t}>\widehat{1}$ and we have $0_{\widehat{t}}q\widehat{\mathcal{F}}.$ Thus, $0_{\widehat{t}}\in \vee q\widehat{\mathcal{F}}.$ Let $x,y\in X$ and $\widehat{t},\widehat{s}\in {(0,1]}^m$ be such that ${(x\ast y)}_{\widehat{t}}q\widehat{\mathcal{F}}$ and $y_{\widehat{s}}q\widehat{\mathcal{F}}.$ Then,

$$\widehat{\mathcal{F}}(x\ast y)+\widehat{t}>\widehat{1}\mathrm{and}\widehat{\mathcal{F}}(y)+\widehat{s}>\widehat{1}.$$

This implies that $x\ast y,y\in J,$ and so $x\in J$. That is, $\widehat{\mathcal{F}}(x)\ge \widehat{0.5}.$ If $inf\{\widehat{t},\widehat{s}\}\le \widehat{0.5},$ then $\widehat{\mathcal{F}}(x)\ge \widehat{0.5}\ge inf\{\widehat{t},\widehat{s}\}$ and we have $x_{inf\{\widehat{t},\widehat{s}\}}\in \widehat{\mathcal{F}}.$ If $inf\{\widehat{t},\widehat{s}\}>\widehat{0.5},$ then $\widehat{\mathcal{F}}(x)+inf\{\widehat{t},\widehat{s}\}>\widehat{1}$ and we have $x_{inf\{\widehat{t},\widehat{s}\}}q\widehat{\mathcal{F}}.$ Therefore, $x_{inf\{\widehat{t},\widehat{s}\}}\in \vee q\widehat{\mathcal{F}}.$ Hence, $\widehat{\mathcal{F}}$ is an m-polar $(q,\in \vee q)$-fuzzy ideal of $X.$

(b) (For $\alpha =\in$) Let $x\in X$ and $\widehat{t}\in {(0,1]}^m$ be such that $x_{\widehat{t}}\in \widehat{\mathcal{F}}.$ Then, $\widehat{\mathcal{F}}(x)\ge \widehat{t}.$ This implies $x\in J$ and so $0\in J.$ Thus, $\widehat{\mathcal{F}}(0)\ge \widehat{0.5}.$ If $\widehat{t}\le \widehat{0.5},$ then $\widehat{\mathcal{F}}(0)\ge \widehat{0.5}\ge \widehat{t}$ and we have $0_{\widehat{t}}\in \widehat{\mathcal{F}}.$ If $\widehat{t}>\widehat{0.5},$ then $\widehat{\mathcal{F}}(0)+\widehat{t}>\widehat{1}$ and we have $0_{\widehat{t}}q\widehat{\mathcal{F}}.$ Hence, $0_{\widehat{t}}\in \vee q\widehat{\mathcal{F}}.$ Let $x,y\in X$ and $\widehat{t},\widehat{s}\in {(0,1]}^m$ be such that ${(x\ast y)}_{\widehat{t}}\in \widehat{\mathcal{F}}$ and $y_{\widehat{s}}\in \widehat{\mathcal{F}}.$ Then,

$$\widehat{\mathcal{F}}(x\ast y)\ge \widehat{t}\mathrm{and}\widehat{\mathcal{F}}(y)\ge \widehat{s}.$$

Thus $x\ast y,y\in J,$ and so $x\in J.$ That is, $\widehat{\mathcal{F}}(x)\ge \widehat{0.5}.$ If $inf\{\widehat{t},\widehat{s}\}\le \widehat{0.5},$ then $\widehat{\mathcal{F}}(x)\ge \widehat{0.5}\ge inf\{\widehat{t},\widehat{s}\}$ and we have $x_{inf\{\widehat{t},\widehat{s}\}}\in \widehat{\mathcal{F}}.$ If $inf\{\widehat{t},\widehat{s}\}>\widehat{0.5},$ then $\widehat{\mathcal{F}}(x)+inf\{\widehat{t},\widehat{s}\}>\widehat{1}$ and we have $x_{inf\{\widehat{t},\widehat{s}\}}q\widehat{\mathcal{F}}.$ Thus, $x_{inf\{\widehat{t},\widehat{s}\}}\in \vee q\widehat{\mathcal{F}}.$ Hence, $\widehat{\mathcal{F}}$ is an m-polar $(\in ,\in \vee q)$-fuzzy ideal of $X.$

(c) (For $\alpha =\in \vee q$) It follows from (a) and (b). □

The following example illustrates Theorem 2.

Example 1.

Let $X=\{0,1,2,a,b\}$ be a $BCI$-algebra which is defined in Table 2:

Table 2. The operation “$\ast$”.

$\ast$	0	1	2	a	b
0	0	0	0	a	a
1	1	0	1	b	a
2	2	2	0	a	a
a	a	a	a	0	0
b	b	a	b	1	0

Let $\widehat{\mathcal{F}}$ be a 3-pF set defined as:

$$\widehat{\mathcal{F}}(x)=\left\{\begin{array}{cc}(0.7,0.8,0.8),\hfill & ifx=0\hfill \\ (0.0,0.0,0.0),\hfill & ifx=1,b\hfill \\ (0.5,0.7,0.7),\hfill & ifx=2\hfill \\ (0.6,0.6,0.6),\hfill & ifx=a.\hfill \end{array}\right.$$

Then, $J=\{0,a,2\}$ is an ideal of $X.$ Therefore, $\widehat{\mathcal{F}}$ is a 3-polar $(\alpha ,\in \vee q)$-fuzzy ideal of $X.$

4. $\mathit{m}$-Polar $(\in ,\in \vee \mathit{q})$-Fuzzy Ideals

In this section, we define m-polar $(\in ,\in \vee q)$-fuzzy ideals of X as a special case of m-polar $(\alpha ,\beta )$-fuzzy ideals, and discuss several results.

Definition 5.

An m-pF set $\widehat{\mathcal{F}}$ of X is called an m-polar $(\in ,\in \vee q)$-fuzzy ideal of X if for all $x,y\in X$ and $\widehat{t},\widehat{s}\in {(0,1]}^m,$

(1) 

$x_{\widehat{t}}\in \widehat{\mathcal{F}}implies{0}_{\widehat{t}}\in \vee q\widehat{\mathcal{F}},$

(2) 

${(x\ast y)}_{\widehat{t}}\in \widehat{\mathcal{F}}$ and $y_{\widehat{s}}\in \widehat{\mathcal{F}}imply{x}_{inf\{\widehat{t},\widehat{s}\}}\in \vee q\widehat{\mathcal{F}}.$

Example 2.

Consider a $BCK$-algebra $X=\{0,a,b,c,d\}$ which is defined in Table 3:

Table 3. The operation “$\ast$”.

$\ast$	0	a	b	c	d
0	0	0	0	0	0
a	a	0	a	0	a
b	b	b	0	b	0
c	c	a	c	0	c
d	d	d	b	d	0

Let $\widehat{\mathcal{F}}$ be a 4-pF set defined as:

$$\widehat{\mathcal{F}}(x)=\left\{\begin{array}{cc}(0.6,0.7,0.7,0.6),\hfill & ifx=0\hfill \\ (0.3,0.4,0.3,0.3),\hfill & ifx=a,c\hfill \\ (0.1,0.2,0.2,0.1),\hfill & ifx=b,d.\hfill \end{array}\right.$$

Clearly, $\widehat{\mathcal{F}}$ is a 4-polar $(\in ,\in \vee q)$-fuzzy ideal of $X.$

Lemma 1.

For an m-pF set $\widehat{\mathcal{F}}$ of $X,$ the following conditions are equivalent for all $x\in X:$

(1) 

$x_{\widehat{t}}\in \widehat{\mathcal{F}}implies{0}_{\widehat{t}}\in \vee q\widehat{\mathcal{F}},$

(2) 

$\widehat{\mathcal{F}}(0)\ge inf\{\widehat{\mathcal{F}}(x),\widehat{0.5}\}.$

Proof. 

$(1)\Rightarrow (2)$ Let $\widehat{\mathcal{F}}$ be an m-pF set of X and $x\in X.$ Assume $\widehat{\mathcal{F}}(x)<\widehat{0.5}.$ If $\widehat{\mathcal{F}}(0)<\widehat{\mathcal{F}}(x),$ then

$$\widehat{\mathcal{F}}(0)<\widehat{t}\le \widehat{\mathcal{F}}(x)$$

for some $\widehat{0}<\widehat{t}<\widehat{0.5}.$ It follows that $x_{\widehat{t}}\in \widehat{\mathcal{F}}$ but $0_{\widehat{t}}\overline{\in }\widehat{\mathcal{F}}.$ Since $\widehat{\mathcal{F}}(0)+\widehat{t}<\widehat{1}$, we get $0_{\widehat{t}}\overline{q}\widehat{\mathcal{F}}.$ Therefore, $0_{\widehat{t}}\overline{\in \vee q}\widehat{\mathcal{F}},$ a contradiction to (1). Thus, $\widehat{\mathcal{F}}(0)\ge \widehat{\mathcal{F}}(x).$ If $\widehat{\mathcal{F}}(x)\ge \widehat{0.5},$ then $x_{\widehat{0.5}}\in \widehat{\mathcal{F}}$ and so $0_{\widehat{0.5}}\in \vee q\widehat{\mathcal{F}},$ which implies that $\widehat{\mathcal{F}}(0)\ge \widehat{0.5}$ or $\widehat{\mathcal{F}}(0)+\widehat{0.5}>\widehat{1}.$ Hence, $\widehat{\mathcal{F}}(0)\ge \widehat{0.5}.$ Otherwise, $\widehat{\mathcal{F}}(0)+\widehat{0.5}<\widehat{1},$ a contradiction. Therefore, $\widehat{\mathcal{F}}(0)\ge inf\{\widehat{\mathcal{F}}(x),\widehat{0.5}\}$ for all $x\in X.$

$(2)\Rightarrow (1)$ Let $x\in X$ and $\widehat{t}\in {(0,1]}^m$ be such that $x_{\widehat{t}}\in \widehat{\mathcal{F}}.$ Then, $\widehat{\mathcal{F}}(x)\ge \widehat{t}.$ Assume that $\widehat{\mathcal{F}}(0)<\widehat{t}.$ If $\widehat{\mathcal{F}}(x)<\widehat{0.5},$ then

$$\begin{array}{ccc}\hfill \widehat{\mathcal{F}}(0)& \ge & inf\{\widehat{\mathcal{F}}(x),\widehat{0.5}\}\hfill \\ & =& \widehat{\mathcal{F}}(x)\hfill \\ & \ge & \widehat{t}.\hfill \end{array}$$

This is a contradiction. Therefore, $\widehat{\mathcal{F}}(x)\ge \widehat{0.5},$ which implies that

$$\widehat{\mathcal{F}}(0)+\widehat{t}>2\widehat{\mathcal{F}}(0)\ge 2inf\{\widehat{\mathcal{F}}(x),\widehat{0.5}\}=\widehat{1}.$$

Thus, $0_{\widehat{t}}\in \vee q\widehat{\mathcal{F}}.$ □

Lemma 2.

For an m-pF set $\widehat{\mathcal{F}}$ of $X,$ the following conditions are equivalent for all $x,y\in X:$

(1) 

${(x\ast y)}_{\widehat{t}}\in \widehat{\mathcal{F}}$ and $y_{\widehat{s}}\in \widehat{\mathcal{F}}imply{x}_{inf\{\widehat{t},\widehat{s}\}}\in \vee q\widehat{\mathcal{F}},$

(2) 

$\widehat{\mathcal{F}}(x)\ge inf\{\widehat{\mathcal{F}}(x\ast y),\widehat{\mathcal{F}}(y),\widehat{0.5}\}.$

Proof. 

$(1)\Rightarrow (2)$ Let $\widehat{\mathcal{F}}$ be an m-pF set of X and $x,y\in X$ such that $\widehat{\mathcal{F}}(x)<inf\{\widehat{\mathcal{F}}(x\ast y),\widehat{\mathcal{F}}(y),\widehat{0.5}\}.$ If $inf\{\widehat{\mathcal{F}}(x\ast y),\widehat{\mathcal{F}}(y)\}<\widehat{0.5},$ then $\widehat{\mathcal{F}}(x)<inf\{\widehat{\mathcal{F}}(x\ast y),\widehat{\mathcal{F}}(y)\}.$ Choose $\widehat{t}\in {(0,0.5)}^m$ such that

$$\widehat{\mathcal{F}}(x)<\widehat{t}\le inf\{\widehat{\mathcal{F}}(x\ast y),\widehat{\mathcal{F}}(y)\}.$$

This implies that ${(x\ast y)}_{\widehat{t}}\in \widehat{\mathcal{F}}$ and $y_{\widehat{t}}\in \widehat{\mathcal{F}},$ but $x_{\widehat{t}}\overline{\in }\widehat{\mathcal{F}}$ and $\widehat{\mathcal{F}}(x)+\widehat{t}<2\widehat{t}<\widehat{1},$ that is, $x_{\widehat{t}}\overline{q}\widehat{\mathcal{F}},$ a contradiction. Thus, $\widehat{\mathcal{F}}(x)\ge inf\{\widehat{\mathcal{F}}(x\ast y),\widehat{\mathcal{F}}(y)\}$ whenever $inf\{\widehat{\mathcal{F}}(x\ast y),\widehat{\mathcal{F}}(y)\}<\widehat{0.5}.$ If $inf\{\widehat{\mathcal{F}}(x\ast y),\widehat{\mathcal{F}}(y)\}\ge \widehat{0.5},$ then ${(x\ast y)}_{\widehat{0.5}}\in \widehat{\mathcal{F}}$ and $y_{\widehat{0.5}}\in \widehat{\mathcal{F}}.$ It follows that by (1), $x_{\widehat{0.5}}=x_{inf\{\widehat{0.5},\widehat{0.5}\}}\in \vee q\widehat{\mathcal{F}},$ so that $\widehat{\mathcal{F}}(x)\ge \widehat{0.5}$ or $\widehat{\mathcal{F}}(x)+\widehat{0.5}>\widehat{1}.$ If $\widehat{\mathcal{F}}(x)<\widehat{0.5},$ then $\widehat{\mathcal{F}}(x)+\widehat{0.5}<\widehat{1},$ which is a contradiction. Therefore, $\widehat{\mathcal{F}}(x)\ge \widehat{0.5}.$ Consequently, $\widehat{\mathcal{F}}(x)\ge inf\{\widehat{\mathcal{F}}(x\ast y),\widehat{\mathcal{F}}(y),\widehat{0.5}\}$ for all $x,y\in X.$

$(2)\Rightarrow (1)$ For any $x,y\in X.$ Let $\widehat{t},\widehat{s}\in {(0,1]}^m$ be such that ${(x\ast y)}_{\widehat{t}},y_{\widehat{s}}\in \widehat{\mathcal{F}}.$ Then,

$$\widehat{\mathcal{F}}(x\ast y)\ge \widehat{t}\mathrm{and}\widehat{\mathcal{F}}(y)\ge \widehat{s}.$$

Suppose that $\widehat{\mathcal{F}}(x)<inf\{\widehat{t},\widehat{s}\}.$ If $inf\{\widehat{\mathcal{F}}(x\ast y),\widehat{\mathcal{F}}(y)\}<\widehat{0.5},$ then

$$\begin{array}{ccc}\hfill \widehat{\mathcal{F}}(x)& \ge & inf\{\widehat{\mathcal{F}}(x\ast y),\widehat{\mathcal{F}}(y),\widehat{0.5}\}\hfill \\ & =& inf\{\widehat{\mathcal{F}}(x\ast y),\widehat{\mathcal{F}}(y)\}\hfill \\ & \ge & inf\{\widehat{t},\widehat{s}\},\hfill \end{array}$$

a contradiction, so $inf\{\widehat{\mathcal{F}}(x\ast y),\widehat{\mathcal{F}}(y)\}\ge \widehat{0.5}.$ This implies that

$$\widehat{\mathcal{F}}(x)+inf\{\widehat{t},\widehat{s}\}>2\widehat{\mathcal{F}}(x)\ge 2inf\{\widehat{\mathcal{F}}(x\ast y),\widehat{\mathcal{F}}(y),\widehat{0.5}\}=\widehat{1}.$$

Hence, $x_{inf\{\widehat{t},\widehat{s}\}}\in \vee q\widehat{\mathcal{F}}.$ □

From Lemmas 1 and 2, we deduce that

Theorem 3.

An m-pF set $\widehat{\mathcal{F}}$ of X is an m-polar $(\in ,\in \vee q)$-fuzzy ideal of X if and only if for all $x,y\in X:$

(i) 

$\widehat{\mathcal{F}}(0)\ge inf\{\widehat{\mathcal{F}}(x),\widehat{0.5}\},$

(ii) 

$\widehat{\mathcal{F}}(x)\ge inf\{\widehat{\mathcal{F}}(x\ast y),\widehat{\mathcal{F}}(y),\widehat{0.5}\}.$

Theorem 4.

Any m-polar $(\in ,\in \vee q)$-fuzzy ideal $\widehat{\mathcal{F}}$ of X satisfies: for all $x,y,z\in X.$

(1) 

$x\le y\Rightarrow \widehat{\mathcal{F}}(x)\ge inf\{\widehat{\mathcal{F}}(y),\widehat{0.5}\},$

(2) 

$x\ast y\le z\Rightarrow \widehat{\mathcal{F}}(x)\ge inf\{\widehat{\mathcal{F}}(y),\widehat{\mathcal{F}}(z),\widehat{0.5}\}.$

Proof. 

(1) Suppose that $x\le y$ for all $x,y\in X.$ Then, $x\ast y=0.$ We have

$$\begin{array}{ccc}\hfill \widehat{\mathcal{F}}(x)& \ge & inf\{\widehat{\mathcal{F}}(x\ast y),\widehat{\mathcal{F}}(y),\widehat{0.5}\}\hfill \\ & =& inf\{\widehat{\mathcal{F}}(0),\widehat{\mathcal{F}}(y),\widehat{0.5}\}\hfill \\ & =& inf\{\widehat{\mathcal{F}}(y),\widehat{0.5}\}.\hfill \end{array}$$

(2) Assume that $x\ast y\le z$ hold in $X.$ Then,

$$\begin{array}{ccc}\hfill \widehat{\mathcal{F}}(x)& \ge & inf\{\widehat{\mathcal{F}}(x\ast y),\widehat{\mathcal{F}}(y),\widehat{0.5}\}\hfill \\ & \ge & inf\{inf\{\widehat{\mathcal{F}}(z),\widehat{0.5}\},\widehat{\mathcal{F}}(y),\widehat{0.5}\}\hfill \\ & =& inf\{\widehat{\mathcal{F}}(y),\widehat{\mathcal{F}}(z),\widehat{0.5}\}.\hfill \end{array}$$

This completes the proof. □

The next theorem gives the bridge between m-polar $(\in ,\in \vee q)$-fuzzy ideals and crisp ideals.

Theorem 5.

An m-pF set $\widehat{\mathcal{F}}$ of X is an m-polar $(\in ,\in \vee q)$-fuzzy ideal of X if and only if ${\widehat{\mathcal{F}}}_{\widehat{t}}\ne \varphi$ is an ideal of X for all $\widehat{t}\in {(0,0.5]}^m.$

Proof. 

Suppose $\widehat{\mathcal{F}}$ is an m-polar $(\in ,\in \vee q)$-fuzzy ideal of $X.$ Let $\widehat{t}\in {(0,0.5]}^m$ and $x\in {\widehat{\mathcal{F}}}_{\widehat{t}}.$ Then, $\widehat{\mathcal{F}}(x)\ge \widehat{t}.$ Using Theorem 3 (i) implies that

$$\widehat{\mathcal{F}}(0)\ge inf\{\widehat{\mathcal{F}}(x),\widehat{0.5}\}\ge \widehat{t}.$$

Thus, $0\in {\widehat{\mathcal{F}}}_{\widehat{t}}.$ Again, let $x\ast y,y\in {\widehat{\mathcal{F}}}_{\widehat{t}}.$ Then, $\widehat{\mathcal{F}}(x\ast y)\ge \widehat{t}$ and $\widehat{\mathcal{F}}(y)\ge \widehat{t}.$ Using Theorem 3 (ii), we have

$$\begin{array}{ccc}\hfill \widehat{\mathcal{F}}(x)& \ge & inf\{\widehat{\mathcal{F}}(x\ast y),\widehat{\mathcal{F}}(y),\widehat{0.5}\}\hfill \\ & \ge & inf\{\widehat{t},\widehat{0.5}\}\hfill \\ & =& \widehat{t}.\hfill \end{array}$$

Hence, $x\in {\widehat{\mathcal{F}}}_{\widehat{t}}.$ Therefore, ${\widehat{\mathcal{F}}}_{\widehat{t}}$ is an ideal of $X.$

Conversely, let ${\widehat{\mathcal{F}}}_{\widehat{t}}\ne \varphi$ be an ideal of X for all $\widehat{t}\in {(0,0.5]}^m.$ If there exists $h\in X$ such that $\widehat{\mathcal{F}}(0)<inf\{\widehat{\mathcal{F}}(h),\widehat{0.5}\},$ then $\widehat{\mathcal{F}}(0)<\widehat{t_h}\le inf\{\widehat{\mathcal{F}}(h),\widehat{0.5}\}$ for some $\widehat{t_h}\in {(0,0.5]}^m.$ It follows that $h\in {\widehat{\mathcal{F}}}_{\widehat{t_h}},$ but $0\notin {\widehat{\mathcal{F}}}_{\widehat{t_h}},$ a contradiction. Therefore, $\widehat{\mathcal{F}}(0)\ge inf\{\widehat{\mathcal{F}}(x),\widehat{0.5}\}$ for all $x\in X.$ Suppose there exist v, $w\in X$ such that

$$\widehat{\mathcal{F}}(v)<inf\{\widehat{\mathcal{F}}(v\ast w),\widehat{\mathcal{F}}(w),\widehat{0.5}\}.$$

Then, $\widehat{\mathcal{F}}(v)<\widehat{t_v}\le inf\{\widehat{\mathcal{F}}(v\ast w),\widehat{\mathcal{F}}(w),\widehat{0.5}\}$ for some $\widehat{t_v}\in {(0,0.5]}^m.$ It follows that $v\ast w\in {\widehat{\mathcal{F}}}_{\widehat{t_v}}$ and $w\in {\widehat{\mathcal{F}}}_{\widehat{t_v}},$ but $v\notin {\widehat{\mathcal{F}}}_{\widehat{t_v}},$ a contradiction. Thus,

$$\widehat{\mathcal{F}}(x)\ge inf\{\widehat{\mathcal{F}}(x\ast y),\widehat{\mathcal{F}}(y),\widehat{0.5}\}$$

for all $x,y\in X.$ Hence, $\widehat{\mathcal{F}}$ is an m-polar $(\in ,\in \vee q)$-fuzzy ideal of X by Theorem 3. □

Theorem 6.

An m-pF set $\widehat{\mathcal{F}}$ of X is an m-polar $(\in ,\in )$ fuzzy ideal of X if and only if $\widehat{\mathcal{F}}$ is an m-pF ideal of $X.$

Proof. 

Assume that $\widehat{\mathcal{F}}$ is an m-polar $(\in ,\in )$ fuzzy ideal of $X.$ Suppose that there exists $x\in X$ such that $\widehat{\mathcal{F}}(0)<\widehat{\mathcal{F}}(x).$ Select $\widehat{t}\in {(0,1]}^m$ such that

$$\widehat{\mathcal{F}}(0)<\widehat{t}\le \widehat{\mathcal{F}}(x).$$

Then, $x_{\widehat{t}}\in \widehat{\mathcal{F}}$ but $0_{\widehat{t}}\overline{\in }\widehat{\mathcal{F}},$ a contradiction. Thus, $\widehat{\mathcal{F}}(0)\ge \widehat{\mathcal{F}}(x)$ for all $x\in X.$ Assume there exist $x,y\in X$ such that $\widehat{\mathcal{F}}(x)<inf\{\widehat{\mathcal{F}}(x\ast y),\widehat{\mathcal{F}}(y)\}.$ Select $\widehat{t}\in {(0,1]}^m$ such that

$$\widehat{\mathcal{F}}(x)<\widehat{t}\le inf\{\widehat{\mathcal{F}}(x\ast y),\widehat{\mathcal{F}}(y)\}.$$

Then, ${(x\ast y)}_{\widehat{t}}\in \widehat{\mathcal{F}}$ and $y_{\widehat{t}}\in \widehat{\mathcal{F}}$ but $x_{\widehat{t}}\overline{\in }\widehat{\mathcal{F}},$ a contradiction. Thus, $\widehat{\mathcal{F}}(x)\ge inf\{\widehat{\mathcal{F}}(x\ast y),\widehat{\mathcal{F}}(y)\}$ for all $x,y\in X.$ Hence, $\widehat{\mathcal{F}}$ is an m-pF ideal of $X.$

Conversely, suppose $\widehat{\mathcal{F}}$ is an m-pF ideal of $X.$ Let $x_{\widehat{t}}\in \widehat{\mathcal{F}}$ for $\widehat{t}\in {(0,1]}^m.$ Then, $\widehat{\mathcal{F}}(x)\ge \widehat{t}.$ By hypothesis

$$\begin{array}{c}\hfill \widehat{\mathcal{F}}(0)\ge \widehat{\mathcal{F}}(x)\ge \widehat{t},\end{array}$$

that is, $0_{\widehat{t}}\in \widehat{\mathcal{F}}.$ Let ${(x\ast y)}_{\widehat{t}},y_{\widehat{s}}\in \widehat{\mathcal{F}}$ for $\widehat{t},\widehat{s}\in {(0,1]}^m.$ Then, $\widehat{\mathcal{F}}(x\ast y)\ge \widehat{t}\mathrm{and}\widehat{\mathcal{F}}(y)\ge \widehat{s}.$ By hypothesis

$$\begin{array}{c}\hfill \widehat{\mathcal{F}}(x)\ge inf\{\widehat{\mathcal{F}}(x\ast y),\widehat{\mathcal{F}}(y)\}\ge inf\{\widehat{t},\widehat{s}\}.\end{array}$$

This implies that $x_{inf\{\widehat{t},\widehat{s}\}}\in \widehat{\mathcal{F}}.$ Therefore, $\widehat{\mathcal{F}}$ is an m-polar $(\in ,\in )$ fuzzy ideal of $X.$ □

Remark 1.

The above theorem shows that m-polar $(\in ,\in )$ fuzzy ideals are the same as m-pF ideals of $X.$

Remark 2.

Every m-polar $(\in ,\in )$-fuzzy ideal is an m-polar $(\in ,\in \vee q)$-fuzzy ideal, but the converse may not be true, as shown in the next example.

Example 3.

Reconsider the $BCK$-algebra X given in Example 2. An m-pF set $\widehat{\mathcal{F}}$ of X defined by

$$\widehat{\mathcal{F}}(x)=\left\{\begin{array}{cc}(0.5,\dots ,0.5),\hfill & ifx=0\hfill \\ (0.3,\dots ,0.3),\hfill & ifx=a,c\hfill \\ (0.7,\dots ,0.7),\hfill & ifx=b\hfill \\ (0.2,\dots ,0.2),\hfill & ifx=d\hfill \end{array}\right.$$

is an m-polar $(\in ,\in \vee q)$-fuzzy ideal of X which is not an m-polar $(\in ,\in )$-fuzzy ideal of $X,$ since

$$b_{(0.6,\dots ,0.6)}={(d\ast b)}_{(0.6,\dots ,0.6)}\in \widehat{\mathcal{F}} and b_{(0.6,\dots ,0.6)}\in \widehat{\mathcal{F}}, but d_{(0.6,\dots ,0.6)}\overline{\in }\widehat{\mathcal{F}}.$$

We provide a condition for an m-polar $(\in ,\in \vee q)$-fuzzy ideal to be an m-polar $(\in ,\in )$-fuzzy ideal.

Theorem 7.

If $\widehat{\mathcal{F}}$ is an m-polar $(\in ,\in \vee q)$-fuzzy ideal of X and $\widehat{\mathcal{F}}(x)<\widehat{0.5}$ $\forall x\in X,$ then $\widehat{\mathcal{F}}$ is an m-polar $(\in ,\in )$-fuzzy ideal of $X.$

Proof. 

Let $\widehat{\mathcal{F}}$ be an m-polar $(\in ,\in \vee q)$-fuzzy ideal of X and $\widehat{\mathcal{F}}(x)<\widehat{0.5}$ $\forall x\in X.$ Let $x_{\widehat{t}}\in \widehat{\mathcal{F}}$ for $\widehat{t}\in {(0,1]}^m.$ Then, $\widehat{\mathcal{F}}(x)\ge \widehat{t}.$ Using Theorem 3 (i), we get

$$\widehat{\mathcal{F}}(0)\ge inf\{\widehat{\mathcal{F}}(x),\widehat{0.5}\}=\widehat{\mathcal{F}}(x)\ge \widehat{t}.$$

Therefore, $0_{\widehat{t}}\in \widehat{\mathcal{F}}.$ Now, let ${(x\ast y)}_{\widehat{t}},y_{\widehat{s}}\in \widehat{\mathcal{F}}$ for $\widehat{t},\widehat{s}\in {(0,1]}^m.$ Then, $\widehat{\mathcal{F}}(x\ast y)\ge \widehat{t}$ and $\widehat{\mathcal{F}}(y)\ge \widehat{s}.$ Using Theorem 3 (ii), we have

$$\begin{array}{ccc}\hfill \widehat{\mathcal{F}}(x)& \ge & inf\{\widehat{\mathcal{F}}(x\ast y),\widehat{\mathcal{F}}(y),\widehat{0.5}\}\hfill \\ & =& inf\{\widehat{\mathcal{F}}(x\ast y),\widehat{\mathcal{F}}(y)\}\hfill \\ & =& inf\{\widehat{t},\widehat{s}\}.\hfill \end{array}$$

Thus, $x_{inf\{\widehat{t},\widehat{s}\}}\in \widehat{\mathcal{F}}.$ Hence, $\widehat{\mathcal{F}}$ is an m-polar $(\in ,\in )$-fuzzy ideal of $X.$ □

Next, we discuss the relation between an m-polar $(\in \vee q,\in \vee q)$-fuzzy ideal and an m-polar $(\in ,\in \vee q)$-fuzzy ideal.

Theorem 8.

Every m-polar $(\in \vee q,\in \vee q)$-fuzzy ideal of X is an m-polar $(\in ,\in \vee q)$-fuzzy ideal of $X.$

Proof. 

Let $\widehat{\mathcal{F}}$ be an m-polar $(\in \vee q,\in \vee q)$-fuzzy ideal of $X.$ Let $x\in X$ and $\widehat{t}\in {(0,1]}^m$ be such that $x_{\widehat{t}}\in \widehat{\mathcal{F}}.$ Then, $x_{\widehat{t}}\in \vee q\widehat{\mathcal{F}}.$ It follows from Definition 4 (1) that $0_{\widehat{t}}\in \vee q\widehat{\mathcal{F}}.$ Let $x,y\in X$ and $\widehat{t},\widehat{s}\in {(0,1]}^m$ be such that ${(x\ast y)}_{\widehat{t}}\in \widehat{\mathcal{F}}$ and $y_{\widehat{s}}\in \widehat{\mathcal{F}}.$ Then, ${(x\ast y)}_{\widehat{t}}\in \vee q\widehat{\mathcal{F}}$ and $y_{\widehat{s}}\in \vee q\widehat{\mathcal{F}}.$ It is implied from Definition 4 (2) that $x_{inf\{\widehat{t},\widehat{s}\}}\in \vee q\widehat{\mathcal{F}}.$ Hence, $\widehat{\mathcal{F}}$ is an m-polar $(\in ,\in \vee q)$-fuzzy ideal of $X.$ □

The converse of the above theorem is not true in general.

Example 4.

Reconsider the $BCK$-algebra X given in Example 2. An m-pF set $\widehat{\mathcal{F}}$ of X defined by

$$\widehat{\mathcal{F}}(x)=\left\{\begin{array}{cc}(0.6,\dots ,0.6),\hfill & ifx=0\hfill \\ (0.7,\dots ,0.7),\hfill & ifx=a,c\hfill \\ (0.2,\dots ,0.2),\hfill & ifx=b,d\hfill \end{array}\right.$$

is an m-polar $(\in ,\in \vee q)$-fuzzy ideal of X which is not an m-polar $(\in \vee q,\in \vee q)$-fuzzy ideal of $X,$ since

$$b_{(0.82,\dots ,0.82)}={(b\ast a)}_{(0.82,\dots ,0.82)}\in \vee q\widehat{\mathcal{F}} and a_{(0.7,\dots ,0.7)}\in \vee q\widehat{\mathcal{F}},$$

but

$$b_{inf\{(0.82,\dots ,0.82),(0.7,\dots ,0.7)\}}=b_{(0.7,\dots ,0.7)}\overline{\in \vee q}\widehat{\mathcal{F}}.$$

Let $\widehat{\mathcal{F}}$ be an m-pF set of $X,$ we define the following sets for all $\widehat{t}\in {[0,1]}^m:$

$${⟨\widehat{\mathcal{F}}⟩}_{\widehat{t}}=\{x\in X\mid x_{\widehat{t}}q\widehat{\mathcal{F}}\}$$

and

$${[\widehat{\mathcal{F}}]}_{\widehat{t}}=\{x\in X\mid x_{\widehat{t}}\in \vee q\widehat{\mathcal{F}}\}.$$

The sets ${⟨\widehat{\mathcal{F}}⟩}_{\widehat{t}}$ and ${[\widehat{\mathcal{F}}]}_{\widehat{t}}$ are called q-level cut subset of $\widehat{\mathcal{F}}$ and $\in \vee q$-level cut subset of $\widehat{\mathcal{F}},$ respectively.

Obviously,

$${[\widehat{\mathcal{F}}]}_{\widehat{t}}={\widehat{\mathcal{F}}}_{\widehat{t}}\cup {⟨\widehat{\mathcal{F}}⟩}_{\widehat{t}}.$$

Theorem 9.

If $\widehat{\mathcal{F}}$ is an m-polar $(\in ,\in \vee q)$-fuzzy ideal of $X,$ then ${⟨\widehat{\mathcal{F}}⟩}_{\widehat{t}}\ne \varphi$ is an ideal of X for all $\widehat{t}\in {(0.5,1]}^m.$

Proof. 

Suppose $\widehat{\mathcal{F}}$ is an m-polar $(\in ,\in \vee q)$-fuzzy ideal of $X.$ Let $\widehat{t}\in {(0.5,1]}^m$ and $x\in {⟨\widehat{\mathcal{F}}⟩}_{\widehat{t}}.$ Then, $\widehat{\mathcal{F}}(x)+\widehat{t}>\widehat{1}.$ Using Theorem 3 (i), we have

$$\begin{array}{ccc}\hfill \widehat{\mathcal{F}}(0)& \ge & inf\{\widehat{\mathcal{F}}(x),\widehat{0.5}\}\hfill \\ & >& inf\{\widehat{1}-\widehat{t},\widehat{0.5}\}\hfill \\ & =& \widehat{1}-\widehat{t},\hfill \end{array}$$

i.e., $0_{\widehat{t}}q\widehat{\mathcal{F}}.$ Hence, $0\in {⟨\widehat{\mathcal{F}}⟩}_{\widehat{t}}.$ Again, let $x\ast y,y\in {⟨\widehat{\mathcal{F}}⟩}_{\widehat{t}}.$ Then, $\widehat{\mathcal{F}}(x\ast y)+\widehat{t}>\widehat{1}$ and $\widehat{\mathcal{F}}(y)+\widehat{t}>\widehat{1}.$ Using Theorem 3 (ii), we have

$$\begin{array}{ccc}\hfill \widehat{\mathcal{F}}(x)& \ge & inf\{\widehat{\mathcal{F}}(x\ast y),\widehat{\mathcal{F}}(y),\widehat{0.5}\}\hfill \\ & >& inf\{\widehat{1}-\widehat{t},\widehat{1}-\widehat{t},\widehat{0.5}\}\hfill \\ & =& \widehat{1}-\widehat{t},\hfill \end{array}$$

so that $x_{\widehat{t}}q\widehat{\mathcal{F}},$ that is, $x\in {⟨\widehat{\mathcal{F}}⟩}_{\widehat{t}}.$ Thus, ${⟨\widehat{\mathcal{F}}⟩}_{\widehat{t}}$ is an ideal of $X.$ □

Theorem 10.

An m-pF set $\widehat{\mathcal{F}}$ of X is an m-polar $(\in ,\in \vee q)$-fuzzy ideal of X if and only if ${[\widehat{\mathcal{F}}]}_{\widehat{t}}\ne \varphi$ is an ideal of X for all $\widehat{t}\in {(0,1]}^m.$

Proof. 

Suppose $\widehat{\mathcal{F}}$ is an m-polar $(\in ,\in \vee q)$-fuzzy ideal of $X.$ Let $\widehat{t}\in {(0,1]}^m$ and $x\in {[\widehat{\mathcal{F}}]}_{\widehat{t}}.$ Then, $x_{\widehat{t}}\in \vee q\widehat{\mathcal{F}},$ that is, $\widehat{\mathcal{F}}(x)\ge \widehat{t}\mathrm{or}\widehat{\mathcal{F}}(x)+\widehat{t}>\widehat{1}.$ Using Theorem 3 (i), we have

$$\widehat{\mathcal{F}}(0)\ge inf\{\widehat{\mathcal{F}}(x),\widehat{0.5}\}.$$

We consider two cases:

Case (1):$\widehat{\mathcal{F}}(x)\ge \widehat{t}.$

$$\begin{array}{ccc}\hfill \widehat{\mathcal{F}}(0)& \ge & inf\{\widehat{\mathcal{F}}(x),\widehat{0.5}\}\hfill \\ & \ge & inf\{\widehat{t},\widehat{0.5}\}\hfill \\ & =& \left\{\begin{array}{cc}\widehat{t},\hfill & \mathrm{if}\widehat{t}\le \widehat{0.5}\hfill \\ \widehat{0.5},\hfill & \mathrm{if}\widehat{t}>\widehat{0.5}.\hfill \end{array}\right.\hfill \end{array}$$

Hence, $\widehat{\mathcal{F}}(0)\ge \widehat{t}$ or $\widehat{\mathcal{F}}(0)+\widehat{t}\ge \widehat{0.5}+\widehat{t}>\widehat{0.5}+\widehat{0.5}=\widehat{1}.$ Therefore, $0_{\widehat{t}}\in \widehat{\mathcal{F}}$ or $0_{\widehat{t}}q\widehat{\mathcal{F}}.$ Thus, $0_{\widehat{t}}\in \vee q\widehat{\mathcal{F}}$, that is, $0\in {[\widehat{\mathcal{F}}]}_{\widehat{t}}.$

Case (2):$\widehat{\mathcal{F}}(x)+\widehat{t}>\widehat{1}.$

$$\begin{array}{ccc}\hfill \widehat{\mathcal{F}}(0)& \ge & inf\{\widehat{\mathcal{F}}(x),\widehat{0.5}\}\hfill \\ & >& inf\{\widehat{1}-\widehat{t},\widehat{0.5}\}\hfill \\ & =& \left\{\begin{array}{cc}\widehat{0.5},\hfill & \mathrm{if}\widehat{t}\le \widehat{0.5}\hfill \\ \widehat{1}-\widehat{t},\hfill & \mathrm{if}\widehat{t}>\widehat{0.5}.\hfill \end{array}\right.\hfill \end{array}$$

Hence, $\widehat{\mathcal{F}}(0)>\widehat{0.5}\ge \widehat{t}$ or $\widehat{\mathcal{F}}(0)+\widehat{t}>\widehat{1}.$ Therefore, $0_{\widehat{t}}\in \widehat{\mathcal{F}}$ or $0_{\widehat{t}}q\widehat{\mathcal{F}}.$ Thus, $0_{\widehat{t}}\in \vee q\widehat{\mathcal{F}}$, that is, $0\in {[\widehat{\mathcal{F}}]}_{\widehat{t}}.$ Hence, in any case, we get $0_{\widehat{t}}\in \vee q\widehat{\mathcal{F}}$, that is, $0\in {[\widehat{\mathcal{F}}]}_{\widehat{t}}.$ Suppose $x\ast y,y\in {[\widehat{\mathcal{F}}]}_{\widehat{t}}$ for $\widehat{t}\in {(0,1]}^m.$ Then,

$${(x\ast y)}_{\widehat{t}}\in \vee q\widehat{\mathcal{F}}\mathrm{and}{y}_{\widehat{t}}\in \vee q\widehat{\mathcal{F}}.$$

Thus, $\widehat{\mathcal{F}}(x\ast y)\ge \widehat{t}$ or $\widehat{\mathcal{F}}(x\ast y)+\widehat{t}>\widehat{1},$ and $\widehat{\mathcal{F}}(y)\ge \widehat{t}$ or $\widehat{\mathcal{F}}(y)+\widehat{t}>\widehat{1}.$ Using Theorem 3 (ii), we have

$$\widehat{\mathcal{F}}(x)\ge inf\{\widehat{\mathcal{F}}(x\ast y),\widehat{\mathcal{F}}(y),\widehat{0.5}\}.$$

We consider four cases:

Case (1):$\widehat{\mathcal{F}}(x\ast y)\ge \widehat{t}$ and $\widehat{\mathcal{F}}(y)\ge \widehat{t}.$

$$\begin{array}{ccc}\hfill \widehat{\mathcal{F}}(x)& \ge & inf\{\widehat{\mathcal{F}}(x\ast y),\widehat{\mathcal{F}}(y),\widehat{0.5}\}\hfill \\ & \ge & inf\{\widehat{t},\widehat{t},\widehat{0.5}\}\hfill \\ & =& \left\{\begin{array}{cc}\widehat{t},\hfill & \mathrm{if}\widehat{t}\le \widehat{0.5}\hfill \\ \widehat{0.5},\hfill & \mathrm{if}\widehat{t}>\widehat{0.5}.\hfill \end{array}\right.\hfill \end{array}$$

Hence, $\widehat{\mathcal{F}}(x)\ge \widehat{t}$ or $\widehat{\mathcal{F}}(x)+\widehat{t}\ge \widehat{0.5}+\widehat{t}>\widehat{0.5}+\widehat{0.5}=\widehat{1}.$ Therefore, $x_{\widehat{t}}\in \widehat{\mathcal{F}}$ or $x_{\widehat{t}}q\widehat{\mathcal{F}}.$ Thus, $x_{\widehat{t}}\in \vee q\widehat{\mathcal{F}}$, that is, $x\in {[\widehat{\mathcal{F}}]}_{\widehat{t}}.$

Case (2):$\widehat{\mathcal{F}}(x\ast y)\ge \widehat{t}$ and $\widehat{\mathcal{F}}(y)+\widehat{t}>\widehat{1}.$

$$\begin{array}{ccc}\hfill \widehat{\mathcal{F}}(x)& \ge & inf\{\widehat{\mathcal{F}}(x\ast y),\widehat{\mathcal{F}}(y),\widehat{0.5}\}\hfill \\ & \ge & inf\{\widehat{t},\widehat{1}-\widehat{t},\widehat{0.5}\}\hfill \\ & =& \left\{\begin{array}{cc}\widehat{t},\hfill & \mathrm{if}\widehat{t}\le \widehat{0.5}\hfill \\ \widehat{1}-\widehat{t},\hfill & \mathrm{if}\widehat{t}>\widehat{0.5}.\hfill \end{array}\right.\hfill \end{array}$$

Hence, $\widehat{\mathcal{F}}(x)\ge \widehat{t}$ or $\widehat{\mathcal{F}}(x)+\widehat{t}>\widehat{1}.$ Therefore, $x_{\widehat{t}}\in \widehat{\mathcal{F}}$ or $x_{\widehat{t}}q\widehat{\mathcal{F}}.$ Thus, $x_{\widehat{t}}\in \vee q\widehat{\mathcal{F}}$, that is, $x\in {[\widehat{\mathcal{F}}]}_{\widehat{t}}.$

Case (3):$\widehat{\mathcal{F}}(x\ast y)+\widehat{t}>\widehat{1}$ and $\widehat{\mathcal{F}}(y)\ge \widehat{t}.$ This is similar to Case (2).

Case (4):$\widehat{\mathcal{F}}(x\ast y)+\widehat{t}>\widehat{1}$ and $\widehat{\mathcal{F}}(y)+\widehat{t}>\widehat{1}.$

$$\begin{array}{ccc}\hfill \widehat{\mathcal{F}}(x)& \ge & inf\{\widehat{\mathcal{F}}(x\ast y),\widehat{\mathcal{F}}(y),\widehat{0.5}\}\hfill \\ & >& inf\{\widehat{1}-\widehat{t},\widehat{1}-\widehat{t},\widehat{0.5}\}\hfill \\ & =& \left\{\begin{array}{cc}\widehat{0.5},\hfill & \mathrm{if}\widehat{t}\le \widehat{0.5}\hfill \\ \widehat{1}-\widehat{t},\hfill & \mathrm{if}\widehat{t}>\widehat{0.5}.\hfill \end{array}\right.\hfill \end{array}$$

Hence, $\widehat{\mathcal{F}}(x)>\widehat{0.5}\ge \widehat{t}$ or $\widehat{\mathcal{F}}(x)+\widehat{t}>\widehat{1}.$ Therefore, $x_{\widehat{t}}\in \widehat{\mathcal{F}}$ or $x_{\widehat{t}}q\widehat{\mathcal{F}}.$ Thus, $x_{\widehat{t}}\in \vee q\widehat{\mathcal{F}}$, that is, $x\in {[\widehat{\mathcal{F}}]}_{\widehat{t}}.$ Therefore, in any case, we get $x_{\widehat{t}}\in \vee q\widehat{\mathcal{F}}$, that is, $x\in {[\widehat{\mathcal{F}}]}_{\widehat{t}}.$ Thus, ${[\widehat{\mathcal{F}}]}_{\widehat{t}}$ is an ideal of $X.$

Conversely, suppose $\widehat{\mathcal{F}}$ is an m-pF set of X and $\widehat{t}\in {(0,1]}^m$ such that ${[\widehat{\mathcal{F}}]}_{\widehat{t}}\ne \varphi$ is an ideal of $X.$ If there exists $h\in X$ such that $\widehat{\mathcal{F}}(0)<inf\{\widehat{\mathcal{F}}(h),\widehat{0.5}\},$ then

$$\widehat{\mathcal{F}}(0)<{\widehat{t}}_{\circ }\le inf\{\widehat{\mathcal{F}}(h),\widehat{0.5}\}$$

for some ${\widehat{t}}_{\circ }\in {(0,0.5]}^m.$ This implies that $h\in {\widehat{\mathcal{F}}}_{{\widehat{t}}_{\circ }}\subseteq {[\widehat{\mathcal{F}}]}_{{\widehat{t}}_{\circ }},$ but $0\notin {\widehat{\mathcal{F}}}_{{\widehat{t}}_{\circ }}.$ Additionally, $\widehat{\mathcal{F}}(0)+{\widehat{t}}_{\circ }<2{\widehat{t}}_{\circ }\le \widehat{1},$ and so $0_{{\widehat{t}}_{\circ }}\overline{q}\widehat{\mathcal{F}},$ that is, $0\notin {⟨\widehat{\mathcal{F}}⟩}_{{\widehat{t}}_{\circ }}.$ Therefore, $0\notin {[\widehat{\mathcal{F}}]}_{{\widehat{t}}_{\circ }},$ a contradiction. Thus, $\widehat{\mathcal{F}}(0)\ge inf\{\widehat{\mathcal{F}}(x),\widehat{0.5}\}$ for all $x\in X.$ Suppose that there exist $h,k\in X$ such that $\widehat{\mathcal{F}}(h)<inf\{\widehat{\mathcal{F}}(h\ast k),\widehat{\mathcal{F}}(k),\widehat{0.5}\}.$ Then,

$$\widehat{\mathcal{F}}(h)<{\widehat{t}}_h\le inf\{\widehat{\mathcal{F}}(h\ast k),\widehat{\mathcal{F}}(k),\widehat{0.5}\}$$

for some ${\widehat{t}}_h\in {(0,0.5]}^m.$ This implies that $h\ast k,k\in {\widehat{\mathcal{F}}}_{{\widehat{t}}_h}\subseteq {[\widehat{\mathcal{F}}]}_{{\widehat{t}}_h}.$ Since ${[\widehat{\mathcal{F}}]}_{{\widehat{t}}_h}$ is an ideal of $X,$ $h\in {[\widehat{\mathcal{F}}]}_{{\widehat{t}}_h}.$ Thus, $\widehat{\mathcal{F}}(h)\ge {\widehat{t}}_h$ or $\widehat{\mathcal{F}}(h)+{\widehat{t}}_h>\widehat{1},$ a contradiction. Therefore, $\widehat{\mathcal{F}}(x)\ge inf\{\widehat{\mathcal{F}}(x\ast y),\widehat{\mathcal{F}}(y),\widehat{0.5}\}$ for all $x,y\in X.$ Hence, $\widehat{\mathcal{F}}$ is an m-polar $(\in ,\in \vee q)$-fuzzy ideal of $X.$ □

5. $\mathit{m}$-Polar $(\in ,\in \vee \mathit{q})$-Fuzzy Commutative Ideals

In this section, we propose the notion of m-polar $(\in ,\in \vee q)$-fuzzy commutative ideals in $BCK$-algebras and discuss the related properties.

Definition 6.

An m-pF set $\widehat{\mathcal{F}}$ of a $BCK$-algebra X is called an m-polar $(\in ,\in \vee q)$-fuzzy commutative ideal of X if for all $x,y,z\in X$ and $\widehat{t},\widehat{s}\in {(0,1]}^m,$

(1) 

$x_{\widehat{t}}\in \widehat{\mathcal{F}}\mathrm{implies}{0}_{\widehat{t}}\in \vee q\widehat{\mathcal{F}},$

(2) 

${((x\ast y)\ast z)}_{\widehat{t}}\in \widehat{\mathcal{F}}$ and $z_{\widehat{s}}\in \widehat{\mathcal{F}}imply{(x\ast (y▽x))}_{inf\{\widehat{t},\widehat{s}\}}\in \vee q\widehat{\mathcal{F}}.$

Example 5.

Let $X=\{0,a,b,c\}$ be a $BCK$-algebra which is defined in Table 4:

Table 4. The operation “$\ast$”.

$\ast$	0	a	b	c
0	0	0	0	0
a	a	0	0	a
b	b	a	0	b
c	c	c	c	0

Let $\widehat{\mathcal{F}}$ be a 3-pF set defined as:

$$\widehat{\mathcal{F}}(x)=\left\{\begin{array}{cc}(0.9,0.9,0.9),\hfill & ifx=0\hfill \\ (0.7,0.8,0.8),\hfill & ifx=a,b\hfill \\ (0.6,0.6,0.6),\hfill & ifx=c.\hfill \end{array}\right.$$

Clearly, $\widehat{\mathcal{F}}$ is a 3-polar $(\in ,\in \vee q)$-fuzzy commutative ideal of $X.$

Theorem 11.

An m-pF set $\widehat{\mathcal{F}}$ of a $BCK$-algebra X is an m-polar $(\in ,\in \vee q)$-fuzzy commutative ideal of X if and only if for all $x,y,z\in X$:

(1) 

$\widehat{\mathcal{F}}(0)\ge inf\{\widehat{\mathcal{F}}(x),\widehat{0.5}\},$

(2) 

$\widehat{\mathcal{F}}(x\ast (y▽x))\ge inf\{\widehat{\mathcal{F}}((x\ast y)\ast z),\widehat{\mathcal{F}}(z),\widehat{0.5}\}.$

Proof. 

Assume $\widehat{\mathcal{F}}$ is an m-polar $(\in ,\in \vee q)$-fuzzy commutative ideal of a $BCK$-algebra $X.$ Let $x\in X$ and suppose that $\widehat{\mathcal{F}}(x)<\widehat{0.5}.$ If $\widehat{\mathcal{F}}(0)<\widehat{\mathcal{F}}(x),$ then

$$\widehat{\mathcal{F}}(0)<\widehat{t}\le \widehat{\mathcal{F}}(x)$$

for some $\widehat{0}<\widehat{t}<\widehat{0.5}.$ It follows that $x_{\widehat{t}}\in \widehat{\mathcal{F}}$, but $0_{\widehat{t}}\overline{\in }\widehat{\mathcal{F}}.$ Since $\widehat{\mathcal{F}}(0)+\widehat{t}<\widehat{1}$ we get $0_{\widehat{t}}\overline{q}\widehat{\mathcal{F}}.$ Therefore, $0_{\widehat{t}}\overline{\in \vee q}\widehat{\mathcal{F}},$ a contradiction. Thus, $\widehat{\mathcal{F}}(0)\ge \widehat{\mathcal{F}}(x)$ for all $x\in X.$ If $\widehat{\mathcal{F}}(x)\ge \widehat{0.5},$ then $x_{\widehat{0.5}}\in \widehat{\mathcal{F}}$ and so $0_{\widehat{0.5}}\in \vee q\widehat{\mathcal{F}},$ which implies that $0_{\widehat{0.5}}\in \vee q\widehat{\mathcal{F}}.$ Hence, $\widehat{\mathcal{F}}(0)\ge \widehat{0.5}.$ Otherwise, $\widehat{\mathcal{F}}(0)+\widehat{0.5}<\widehat{1},$ a contradiction. Hence, $\widehat{\mathcal{F}}(0)\ge inf\{\widehat{\mathcal{F}}(x),\widehat{0.5}\}$ for all $x\in X.$ Let $x,y,z\in X.$ Assume that

$$inf\{\widehat{\mathcal{F}}((x\ast y)\ast z),\widehat{\mathcal{F}}(z)\}<\widehat{0.5}.$$

Then,

$$\widehat{\mathcal{F}}(x\ast (y▽x))\ge inf\{\widehat{\mathcal{F}}((x\ast y)\ast z),\widehat{\mathcal{F}}(z)\}.$$

If not, then

$$\widehat{\mathcal{F}}(x\ast (y▽x))<\widehat{t}\le inf\{\widehat{\mathcal{F}}((x\ast y)\ast z),\widehat{\mathcal{F}}(z)\}$$

for some $\widehat{0}<\widehat{t}<\widehat{0.5}.$ This implies that ${((x\ast y)\ast z)}_{\widehat{t}}\in \widehat{\mathcal{F}}$ and $z_{\widehat{t}}\in \widehat{\mathcal{F}},$ but ${(x\ast (y▽x))}_{\widehat{t}}\overline{\in \vee q}\widehat{\mathcal{F}},$ a contradiction. Hence, $\widehat{\mathcal{F}}(x\ast (y▽x))\ge inf\{\widehat{\mathcal{F}}((x\ast y)\ast z),\widehat{\mathcal{F}}(z)\}$ whenever $inf\{\widehat{\mathcal{F}}((x\ast y)\ast z),\widehat{\mathcal{F}}(z)\}<\widehat{0.5}.$ If $inf\{\widehat{\mathcal{F}}((x\ast y)\ast z),\widehat{\mathcal{F}}(z)\}\ge \widehat{0.5},$ then

$${((x\ast y)\ast z)}_{\widehat{0.5}}\in \widehat{\mathcal{F}} \mathrm{and} z_{\widehat{0.5}}\in \widehat{\mathcal{F}}.$$

It follows that ${(x\ast (y▽x))}_{\widehat{0.5}}={(x\ast (y▽x))}_{inf\{\widehat{0.5},\widehat{0.5}\}}\in \vee q\widehat{\mathcal{F}}.$ Therefore, $\widehat{\mathcal{F}}(x\ast (y▽x))\ge \widehat{0.5}$ or $\widehat{\mathcal{F}}(x\ast (y▽x))+\widehat{0.5}>\widehat{1}.$ If $\widehat{\mathcal{F}}(x\ast (y▽x))<\widehat{0.5},$ then

$$\widehat{\mathcal{F}}(x\ast (y▽x))+\widehat{0.5}<\widehat{1},$$

a contradiction. Therefore, $\widehat{\mathcal{F}}(x\ast (y▽x))\ge inf\{\widehat{\mathcal{F}}((x\ast y)\ast z),\widehat{\mathcal{F}}(z),\widehat{0.5}\}$ for all $x,y,z\in X.$

Conversely, suppose that (1) and (2) hold. Let $x\in X$ and $\widehat{t}\in {(0,1]}^m$ be such that $x_{\widehat{t}}\in \widehat{\mathcal{F}}.$ Then, $\widehat{\mathcal{F}}(x)\ge \widehat{t}.$ Assume $\widehat{\mathcal{F}}(0)<\widehat{t}.$ If $\widehat{\mathcal{F}}(x)<\widehat{0.5},$ then

$$\begin{array}{ccc}\hfill \widehat{\mathcal{F}}(0)& \ge & inf\{\widehat{\mathcal{F}}(x),\widehat{0.5}\}\hfill \\ & =& \widehat{\mathcal{F}}(x)\ge \widehat{t},\hfill \end{array}$$

a contradiction. Therefore, $\widehat{\mathcal{F}}(x)\ge \widehat{0.5},$ which implies that

$$\begin{array}{ccc}\hfill \widehat{\mathcal{F}}(0)+\widehat{t}& >& 2\widehat{\mathcal{F}}(0)\hfill \\ & \ge & 2inf\{\widehat{\mathcal{F}}(x),\widehat{0.5}\}\hfill \\ & =& \widehat{1}.\hfill \end{array}$$

Thus, $0_{\widehat{t}}\in \vee q\widehat{\mathcal{F}}.$ Let $x,y,z\in X$ and $\widehat{t},\widehat{s}\in {(0,1]}^m$ be such that ${((x\ast y)\ast z)}_{\widehat{t}},z_{\widehat{s}}\in \widehat{\mathcal{F}}.$ Then,

$$\widehat{\mathcal{F}}((x\ast y)\ast z)\ge \widehat{t}\mathrm{and}\widehat{\mathcal{F}}(z)\ge \widehat{s}.$$

Suppose that $\widehat{\mathcal{F}}(x\ast (y▽x))<inf\{\widehat{t},\widehat{s}\}.$ If $inf\{\widehat{\mathcal{F}}((x\ast y)\ast z),\widehat{\mathcal{F}}(z)\}<\widehat{0.5},$ then

$$\begin{array}{ccc}\hfill \widehat{\mathcal{F}}(x\ast (y▽x))& \ge & inf\{\widehat{\mathcal{F}}((x\ast y)\ast z),\widehat{\mathcal{F}}(z),\widehat{0.5}\}\hfill \\ & =& inf\{\widehat{\mathcal{F}}((x\ast y)\ast z),\widehat{\mathcal{F}}(z)\}\hfill \\ & \ge & inf\{\widehat{t},\widehat{s}\},\hfill \end{array}$$

a contradiction. Hence, $inf\{\widehat{\mathcal{F}}((x\ast y)\ast z),\widehat{\mathcal{F}}(z)\ge \widehat{0.5}.$ This implies that

$$\begin{array}{ccc}\hfill \widehat{\mathcal{F}}(x\ast (y▽x))+inf\{\widehat{t},\widehat{s}\}& >& 2\widehat{\mathcal{F}}(x\ast (y▽x))\hfill \\ & \ge & 2inf\{\widehat{\mathcal{F}}((x\ast y)\ast z),\widehat{\mathcal{F}}(z),\widehat{0.5}\}\hfill \\ & =& \widehat{1}.\hfill \end{array}$$

So, ${(x\ast (y▽x))}_{inf\{\widehat{t},\widehat{s}\}}\in \vee q\widehat{\mathcal{F}}.$ Hence, $\widehat{\mathcal{F}}$ is an m-polar $(\in ,\in \vee q)$-fuzzy commutative ideal of $X.$ □

Theorem 12.

Every m-polar $(\in ,\in \vee q)$-fuzzy commutative ideal of a $BCK$-algebra X is an m-polar $(\in ,\in \vee q)$-fuzzy ideal of $X.$

Proof. 

Let $\widehat{\mathcal{F}}$ be an m-polar $(\in ,\in \vee q)$-fuzzy commutative ideal of a $BCK$-algebra $X.$ Let $x,y,z\in X$ and $\widehat{t},\widehat{s}\in {(0,1]}^m.$ Then, by taking $y=0$ in (2) of Definition 6, we have

$${((x\ast 0)\ast z)}_{\widehat{t}}\in \widehat{\mathcal{F}},z_{\widehat{s}}\in \widehat{\mathcal{F}}\mathrm{imply}{(x\ast (0▽x))}_{inf\{\widehat{t},\widehat{s}\}}\in \vee q\widehat{\mathcal{F}}.$$

Since for all $x\in X,0▽x=0\ast (0\ast x)=0\ast 0=0$ and $x\ast 0=x,$ so

$${(x\ast z)}_{\widehat{t}}\in \widehat{\mathcal{F}},z_{\widehat{s}}\in \widehat{\mathcal{F}}\mathrm{imply}{x}_{inf\{\widehat{t},\widehat{s}\}}\in \vee q\widehat{\mathcal{F}}.$$

Hence, $\widehat{\mathcal{F}}$ satisfies (2) of Definition 5. Combining with (1) of Definition 5 implies that $\widehat{\mathcal{F}}$ is an m-polar $(\in ,\in \vee q)$-fuzzy ideal of $X.$ □

In general, the converse of Theorem 12 is not true.

Example 6.

Let $X=\{0,1,2,a,b\}$ be a $BCK$-algebra which is defined in Table 5:

Table 5. The operation “$\ast$”.

$\ast$	0	1	2	a	b
0	0	0	0	0	0
1	1	0	1	0	0
2	2	2	0	0	0
a	a	a	a	0	0
b	b	b	b	a	0

A 3-pF set $\widehat{\mathcal{F}}$ defined by:

$$\widehat{\mathcal{F}}(x)=\left\{\begin{array}{cc}(0.5,0.5,0.5),\hfill & ifx=0\hfill \\ (0.4,0.4,0.4),\hfill & ifx=1\hfill \\ (0.3,0.3,0.3),\hfill & ifx=2,a,b\hfill \end{array}\right.$$

is a 3-polar $(\in ,\in \vee q)$-fuzzy ideal of X which is not a 3-polar $(\in ,\in \vee q)$-fuzzy commutative ideal of $X,$ since

$$\widehat{\mathcal{F}}(2\ast (a▽2))=(0.3,0.3,0.3)<inf\{\widehat{\mathcal{F}}((2\ast a)\ast 0),\widehat{\mathcal{F}}(0),\widehat{0.5}\}=(0.5,0.5,0.5).$$

Theorem 13.

If $\widehat{\mathcal{F}}$ is an m-polar $(\in ,\in \vee q)$-fuzzy ideal of a $BCK$-algebra X and

$$\widehat{\mathcal{F}}(x\ast (y▽x))\ge inf\{\widehat{\mathcal{F}}(x\ast y),\widehat{0.5}\}$$

for all $x,y\in X,$ then $\widehat{\mathcal{F}}$ is an m-polar $(\in ,\in \vee q)$-fuzzy commutative ideal of $X.$

Proof. 

Suppose $\widehat{\mathcal{F}}$ is an m-polar $(\in ,\in \vee q)$-fuzzy ideal of a $BCK$-algebra $X.$ Then,

$$\widehat{\mathcal{F}}(0)\ge inf\{\widehat{\mathcal{F}}(x),\widehat{0.5}\}$$

for all $x\in X.$ Also, by assumption and (ii) of Theorem 3, we have

$$\begin{array}{ccc}\hfill {\widehat{\mathcal{F}}}^{\ast }(x\ast (y▽x))& \ge & inf\{\widehat{\mathcal{F}}(x\ast y),\widehat{0.5}\}\hfill \\ & \ge & inf\{\widehat{\mathcal{F}}((x\ast y)\ast z),\widehat{\mathcal{F}}(z),\widehat{0.5},\widehat{0.5}\}\hfill \\ & \ge & inf\{\widehat{\mathcal{F}}((x\ast y)\ast z),\widehat{\mathcal{F}}(z),\widehat{0.5}\}.\hfill \end{array}$$

Hence, $\widehat{\mathcal{F}}$ is an m-polar $(\in ,\in \vee q)$-fuzzy commutative ideal of $X.$ □

The next theorem provides necessary and sufficient condition for the crisp commutative ideal to be an m-polar $(\in ,\in \vee q)$-fuzzy commutative ideal.

Theorem 14.

An m-pF set $\widehat{\mathcal{F}}$ of a $BCK$-algebra X is an m-polar $(\in ,\in \vee q)$-fuzzy commutative ideal of X if and only if ${\widehat{\mathcal{F}}}_{\widehat{t}}\ne \varphi$ is a commutative ideal of X for all $\widehat{t}\in {(0,0.5]}^m.$

Proof. 

Assume that $\widehat{\mathcal{F}}$ is an m-polar $(\in ,\in \vee q)$-fuzzy commutative ideal of $X.$ Let $\widehat{t}\in {(0,0.5]}^m$ and $x\in {\widehat{\mathcal{F}}}_{\widehat{t}}.$ Then, $\widehat{\mathcal{F}}(x)\ge \widehat{t}.$ Theorem 11 (1) implies that

$$\widehat{\mathcal{F}}(0)\ge inf\{\widehat{\mathcal{F}}(x),\widehat{0.5}\}=\widehat{t}.$$

Thus, $0\in {\widehat{\mathcal{F}}}_{\widehat{t}}.$ Again, let $(x\ast y)\ast z,z\in {\widehat{\mathcal{F}}}_{\widehat{t}}.$ Then, $\widehat{\mathcal{F}}((x\ast y)\ast z)\ge \widehat{t}$ and $\widehat{\mathcal{F}}(z)\ge \widehat{t}.$ Theorem 11 (2) implies that

$$\begin{array}{ccc}\hfill \widehat{\mathcal{F}}(x\ast (y▽x))& \ge & inf\{\widehat{\mathcal{F}}((x\ast y)\ast z),\widehat{\mathcal{F}}(z),\widehat{0.5}\}\hfill \\ & \ge & inf\{\widehat{t},\widehat{t},\widehat{0.5}\}\hfill \\ & =& \widehat{t}.\hfill \end{array}$$

Therefore, $x\ast (y▽x)\in {\widehat{\mathcal{F}}}_{\widehat{t}}.$ Thus, ${\widehat{\mathcal{F}}}_{\widehat{t}}$ is a commutative ideal of $X.$

Conversely, let $\widehat{\mathcal{F}}$ be an m-pF set of X be such that ${\widehat{\mathcal{F}}}_{\widehat{t}}\ne \varphi$ is a commutative ideal of X for all $\widehat{t}\in {(0,0.5]}^m.$ If there exists $h\in X$ such that $\widehat{\mathcal{F}}(0)<inf\{\widehat{\mathcal{F}}(h),\widehat{0.5}\},$ then

$$\widehat{\mathcal{F}}(0)<\widehat{t_{\circ }}\le inf\{\widehat{\mathcal{F}}(h),\widehat{0.5}\}$$

for some $\widehat{t_{\circ }}\in {(0,0.5]}^m.$ It follows that $h\in {\widehat{\mathcal{F}}}_{\widehat{t_{\circ }}},$ but $0\overline{\in }{\widehat{\mathcal{F}}}_{\widehat{t_{\circ }}},$ a contradiction. Therefore,

$$\widehat{\mathcal{F}}(0)\ge inf\{\widehat{\mathcal{F}}(x),\widehat{0.5}\}$$

for all $x\in X.$ Assume there exist $u,v,w\in X$ such that

$$\widehat{\mathcal{F}}(u\ast (v▽u))<inf\{\widehat{\mathcal{F}}((u\ast v)\ast w),\widehat{\mathcal{F}}(w),\widehat{0.5}\}.$$

Then, $\widehat{\mathcal{F}}(u\ast (v▽u))<\widehat{t_u}\le inf\{\widehat{\mathcal{F}}((u\ast v)\ast w),\widehat{\mathcal{F}}(w),\widehat{0.5}\}$ for some $\widehat{t_u}\in {(0,0.5]}^m.$ This implies that $(u\ast v)\ast w\in {\widehat{\mathcal{F}}}_{\widehat{t_u}}$ and $w\in {\widehat{\mathcal{F}}}_{\widehat{t_u}},$ but $u\ast (v▽u)\notin {\widehat{\mathcal{F}}}_{\widehat{t_u}}.$ This is impossible. Thus,

$$\widehat{\mathcal{F}}(x\ast (y▽x))\ge inf\{\widehat{\mathcal{F}}((x\ast y)\ast z),\widehat{\mathcal{F}}(z),\widehat{0.5}\}$$

for all $x,y,z\in X.$ Hence, $\widehat{\mathcal{F}}$ is an m-polar $(\in ,\in \vee q)$-fuzzy commutative ideal of X by Theorem 11. □

6. Insights of This Study

• m-pF points are defined.
• m-pF (commutative) ideals are modified and generalized.
• The concept of m-polar $(\alpha ,\beta )$-fuzzy ideals is introduced, and as a special case, an m-polar $(\in ,\in \vee q)$-fuzzy ideal is defined.
• The relations between an m-polar $(\in ,\in \vee q)$-fuzzy (commutative) ideal and the crisp (commutative) ideal are established.
• Conditions for an m-pF set to be an m-polar $(\alpha ,\in \vee q)$-fuzzy ideal are considered.
• Some results in this study are displayed in Figure 1.
  

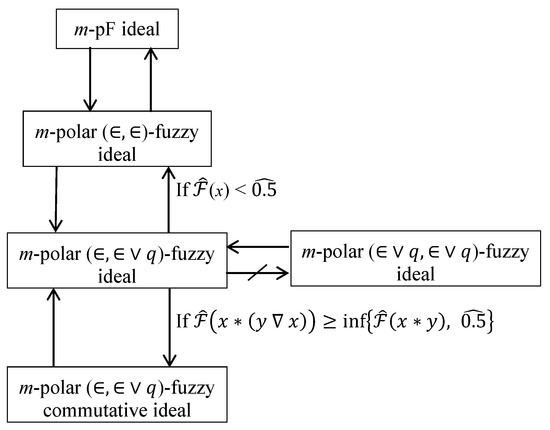  Figure 1. Some results in this study.
• The results in this paper are supported by suitable examples.

7. Conclusions

The idea of m-pF ideals plays a key role in the theory of a $BCK/BCI$-algebra. The m-pF points of a $BCK/BCI$-algebra X are crucial tools to designate the algebraic subsystems of $X.$ In this paper, we defined m-polar $(\alpha ,\beta )$-fuzzy ideals and investigated related results. We proved that every m-polar $(\in ,\in )$-fuzzy ideal is an m-polar $(\in ,\in \vee q)$-fuzzy ideal, and every m-polar $(\in \vee q,\in \vee q)$-fuzzy ideal is an m-polar $(\in ,\in \vee q)$-fuzzy ideal. We also obtained some characterization theorems of m-polar $(\in ,\in \vee q)$-fuzzy ideals in $BCK/BCI$-algebras. Finally, we defined m-polar $(\in ,\in \vee q)$-fuzzy commutative ideals in $BCK$-algebras and obtained some fundamental results.

The results of this study can be further expanded to various algebraic structures, such as $PF$-algebras, semigroups, $\mathsf{\Gamma }$-semihypergroups, and hemirings (see [18,19,44,46]). Furthermore, the notion of the m-pF set used in this work can be studied according to the thought in [47,48,49,50], which will be the way for much future research.