Evaluating the Efficiency of Different Regression, Decision Tree, and Bayesian Machine Learning Algorithms in Spatial Piping Erosion Susceptibility Using ALOS/PALSAR Data
Abstract
1. Introduction
2. Materials and Methods
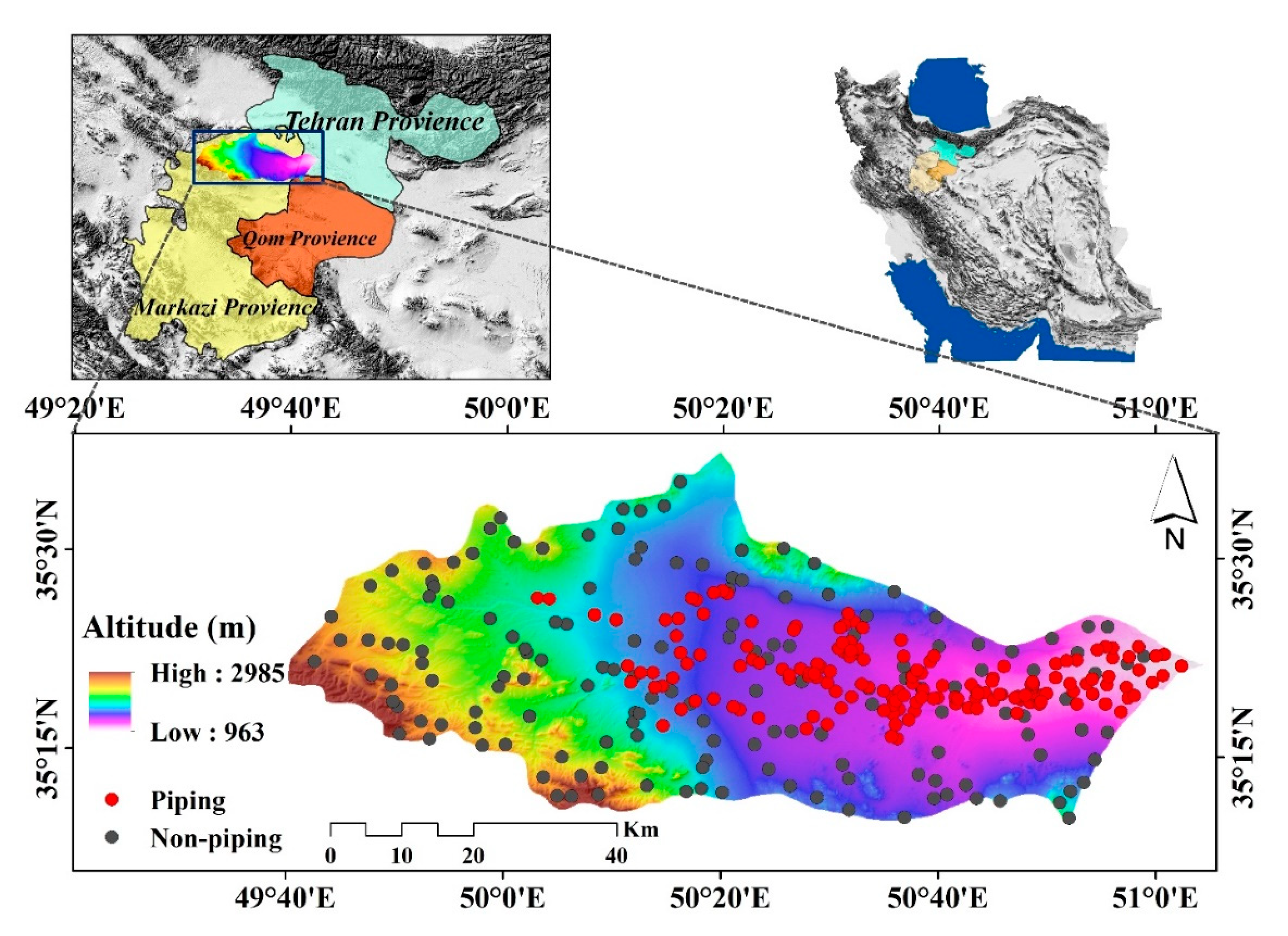
2.1. Description of the Study Area
2.2. Methods
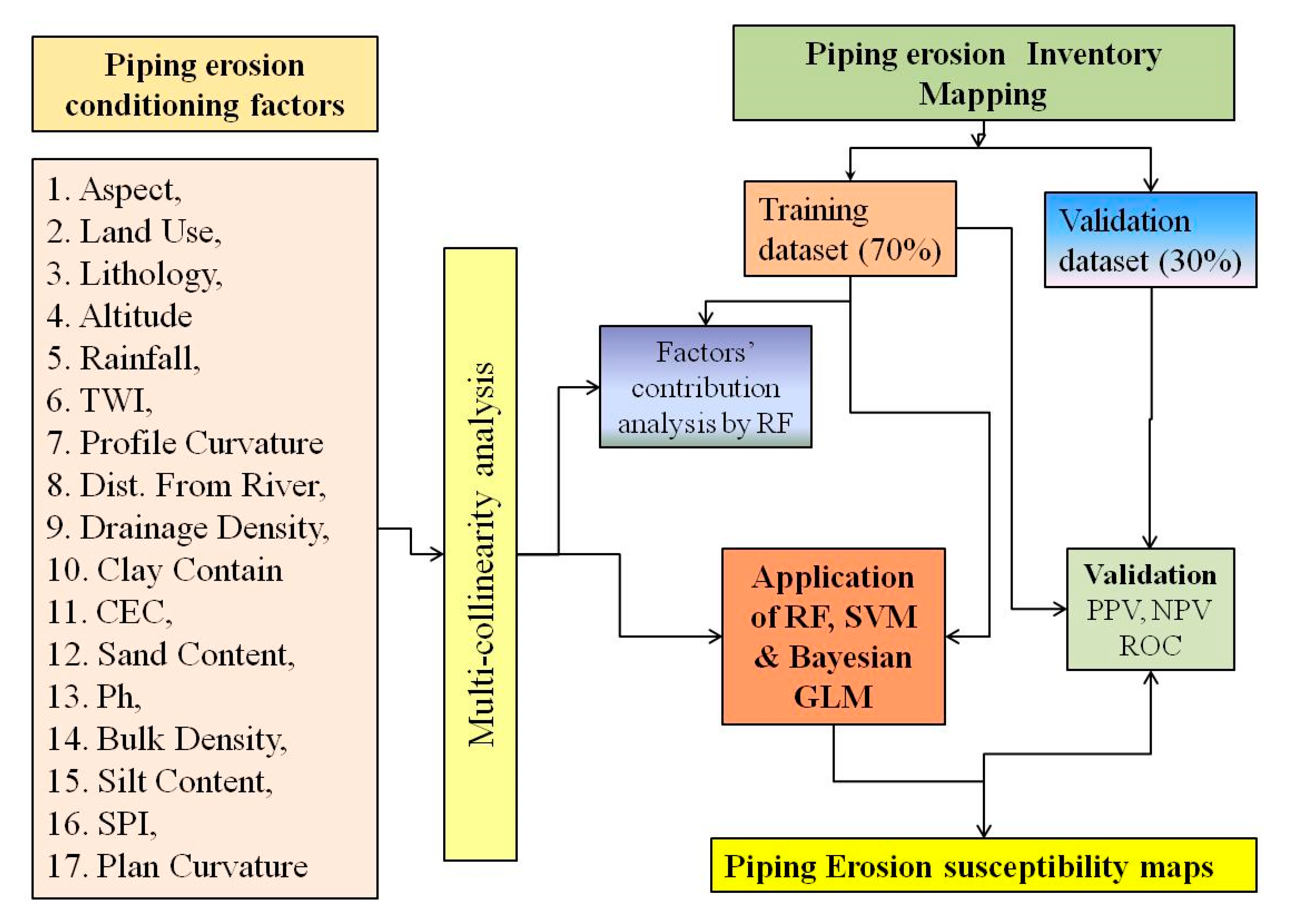
2.3. Dataset Preparation for Spatial Modeling
2.4. Multi-Collinearity Analysis
2.5. Machine Learning Method Used in Modeling the Piping Erosion
2.5.1. Random Forest (RF)
2.5.2. Support Vector Machine (SVM)
2.5.3. Bayesian Generalized Linear Models (Bayesian GLM)
2.6. Methods of Validation and Accuracy Assessment
3. Results
3.1. Multi-Collinearity Analysis
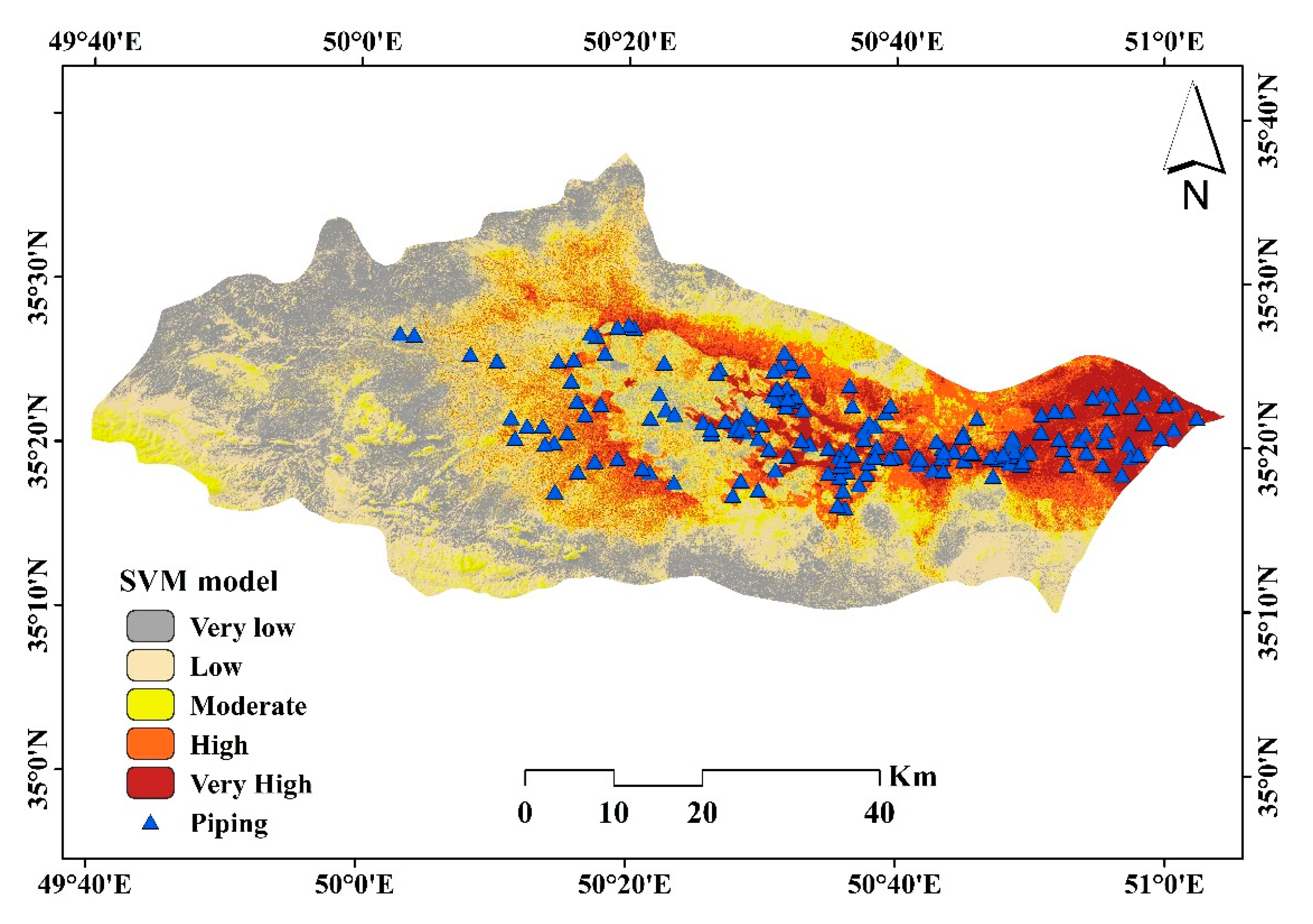
3.2. Piping Erosion Susceptibility Modeling
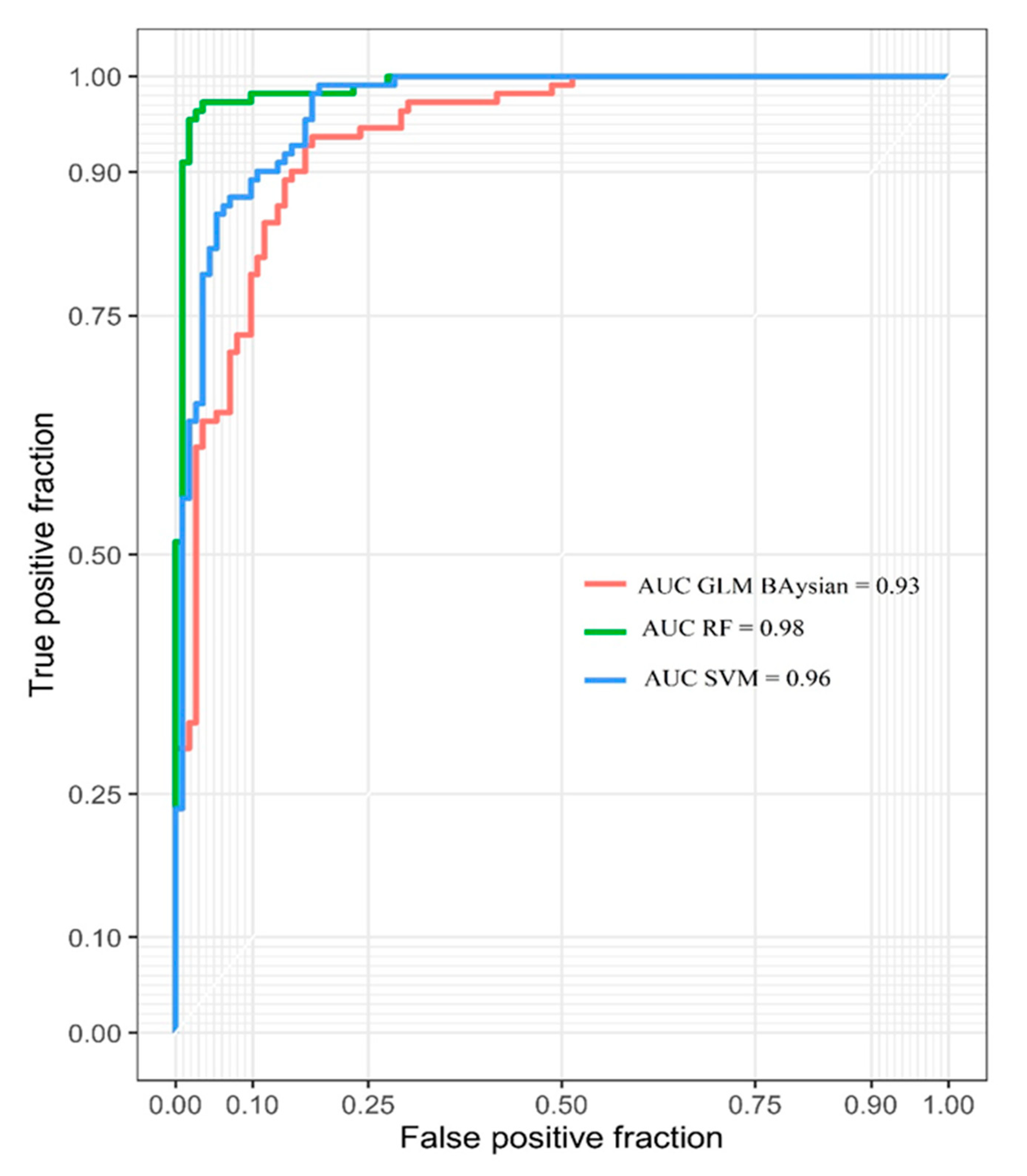
3.3. Validation of the Models
4. Discussion
4.1. Comparison of the Models
4.2. Variable Importance Analysis
4.3. Implications and Soil Erosion Control
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Poesen, J.; Vandaele, K.; Van Wesemael, B. Gully erosion: Importance and model implications. In Modelling Soil Erosion by Water; Springer: Berlin/Heidelberg, Germany, 1998; pp. 285–311. [Google Scholar]
- Chaplot, V. Impact of terrain attributes, parent material and soil types on gully erosion. Geomorphology 2013, 186, 1–11. [Google Scholar] [CrossRef]
- Cerdà, A. Seasonal and spatial variations in infiltration rates in badland surfaces under Mediterranean climatic conditions. Water Resour. Res. 1999, 35, 319–328. [Google Scholar] [CrossRef]
- Cerdà, A.; Garcia-Fayos, P. The influence of slope angle on sediment, water and seed losses on badland landscapes. Geomorphology 1997, 18, 77–90. [Google Scholar] [CrossRef]
- Karamage, F.; Shao, H.; Chen, X.; Ndayisaba, F.; Nahayo, L.; Kayiranga, A.; Omifolaji, J.K.; Liu, T.; Zhang, C. Deforestation effects on soil erosion in the Lake Kivu Basin, DR Congo-Rwanda. Forests 2016, 7, 281. [Google Scholar] [CrossRef]
- Nicu, I.C. Is overgrazing really influencing soil erosion. Water 2018, 10, 1077. [Google Scholar] [CrossRef]
- Gomiero, T. Soil degradation, land scarcity and food security: Reviewing a complex challenge. Sustainability 2016, 8, 281. [Google Scholar] [CrossRef]
- Keesstra, S.D.; Bouma, J.; Wallinga, J.; Tittonell, P.; Smith, P.; Cerdà, A.; Montanarella, L.; Quinton, J.N.; Pachepsky, Y.; Van Der Putten, W.H.; et al. The significance of soils and soil science towards realization of the United Nations Sustainable Development Goals. Soil 2016, 2, 111–128. [Google Scholar] [CrossRef]
- Rodrigo-Comino, J.; Senciales González, J.M.; Cerdà Bolinches, A.; Brevik, E.C. The multidisciplinary origin of soil geography: A review. Earth-Science Reviews. Earth Sci. Rev. 2018, 177, 114–123. [Google Scholar] [CrossRef]
- Keesstra, S.; Mol, G.; De Leeuw, J.; Okx, J.; De Cleen, M.; Visser, S. Soil-related sustainable development goals: Four concepts to make land degradation neutrality and restoration work. Land 2018, 7, 133. [Google Scholar] [CrossRef]
- Poesen, J.; Nachtergaele, J.; Verstraeten, G.; Valentin, C. Gully erosion and environmental change: Importance and research needs. Catena 2003, 50, 91–133. [Google Scholar] [CrossRef]
- Diaz, A.R.; Sanleandro, P.M.; Soriano, A.S.; Serrato, F.B.; Faulkner, H. The causes of piping in a set of abandoned agricultural terraces in southeast Spain. Catena 2007, 69, 282–293. [Google Scholar] [CrossRef]
- Kariminejad, N.; Hosseinalizadeh, M.; Pourghasemi, H.R.; Bernatek-Jakiel, A.; Alinejad, M. GIS-based susceptibility assessment of the occurrence of gully headcuts and pipe collapses in a semi-arid environment: Golestan Province, NE Iran. Land Degrad. Dev. 2019, 30, 2211–2225. [Google Scholar] [CrossRef]
- Bernatek-Jakiel, A.; Poesen, J. Subsurface erosion by soil piping: Significance and research needs. Earth Sci. Rev. 2018, 185, 1107–1128. [Google Scholar] [CrossRef]
- Faulkner, H. Piping hazard on collapsible and dispersive soils in Europe. Soil Eros. Eur. 2006, 537–562. [Google Scholar]
- Bonelli, S.; Brivois, O.; Borghi, R.; Benahmed, N. On the modelling of piping erosion. Comptes Rendus Mécanique 2006, 334, 555–559. [Google Scholar] [CrossRef]
- Farifteh, J.; Soeters, R. Factors underlying piping in the Basilicata region, southern Italy. Geomorphology 1999, 26, 239–251. [Google Scholar] [CrossRef]
- Jones, J.A.A.; Richardson, J.M.; Jacob, H.J. Factors controlling the distribution of piping in Britain: A reconnaissance. Geomorphology 1997, 20, 289–306. [Google Scholar] [CrossRef]
- Verachtert, E.; Van Den Eeckhaut, M.; Poesen, J.; Deckers, J. Factors controlling the spatial distribution of soil piping erosion on loess-derived soils: A case study from central Belgium. Geomorphology 2010, 118, 339–348. [Google Scholar] [CrossRef]
- Deng, Q.C.; Zhang, B.; Luo, J.; Shu, C.Q.; Qin, F.C.; Luo, M.L.; Lin, Y.B. Types and controlling factors of piping landform in Yuanmou dry-hot valley. J. Arid Land Resour. Environ. 2014, 28, 138–144. [Google Scholar]
- Garcia-Ruiz, J.; Lasanta, T.; Alberto, F. Soil erosion by piping in irrigated fields. Geomorphology 1997, 20, 269–278. [Google Scholar] [CrossRef]
- Jones, J.A.A. Soil piping and catchment response. Hydrol. Process. 2010, 24, 1548–1566. [Google Scholar] [CrossRef]
- Gutierrez, M.; Sancho, C.; Benito, G.; Sirvent, J.; Desir, G. Quantitative study of piping processes in badland areas of the Ebro Basin, NE Spain. Geomorphology 1997, 20, 237–253. [Google Scholar] [CrossRef]
- Hosseinalizadeh, M.; Kariminejad, N.; Alinejad, M. An application of different summary statistics for modelling piping collapses and gully headcuts to evaluate their geomorphological interactions in Golestan Province, Iran. Catena 2018, 171, 613–621. [Google Scholar] [CrossRef]
- Mirhasani, M.; Rostami, N.; Bazgir, M.; Tavakoli, M. Threshold friction velocity and soil loss across different land uses in arid regions: Iran. Arab. J. Geosci. 2019, 12, 91. [Google Scholar] [CrossRef]
- Zare, M.; Mohammady, M.; Pradhan, B. Modeling the effect of land use and climate change scenarios on future soil loss rate in Kasilian watershed of northern Iran. Environ. Earth Sci. 2017, 76, 305. [Google Scholar] [CrossRef]
- Zare, M.; Panagopoulos, T.; Loures, L. Simulating the impacts of future land use change on soil erosion in the Kasilian watershed, Iran. Land Use Policy 2017, 67, 558–572. [Google Scholar] [CrossRef]
- Nosrati, K.; Collins, A.L. A soil quality index for evaluation of degradation under land use and soil erosion categories in a small mountainous catchment, Iran. J. Mt. Sci. 2019, 16, 2577–2590. [Google Scholar] [CrossRef]
- Vaezi, A.R.; Abbasi, M.; Bussi, G.; Keesstra, S. Modeling sediment yield in semi-arid pasture micro-catchments, NW Iran. Land Degrad. Dev. 2017, 28, 1274–1286. [Google Scholar] [CrossRef]
- Vaezi, A.R.; Hasanzadeh, H.; Cerdà, A. Developing an erodibility triangle for soil textures in semi-arid regions, NW Iran. Catena 2016, 142, 221–232. [Google Scholar] [CrossRef]
- Arabameri, A.; Cerda, A.; Rodrigo-Comino, J.; Pradhan, B.; Sohrabi, M.; Blaschke, T.; Tien Bui, D. Proposing a novel predictive technique for gully erosion susceptibility mapping in arid and semi-arid regions (Iran). Remote Sens. 2019, 11, 2577. [Google Scholar] [CrossRef]
- Parhizkar, M.; Shabanpour, M.; Khaledian, M.; Cerdà, A.; Rose, C.W.; Asadi, H.; Lucas-Borja, M.E.; Zema, D.A. Assessing and Modeling Soil Detachment Capacity by Overland Flow in Forest and Woodland of Northern Iran. Forests 2020, 11, 65. [Google Scholar] [CrossRef]
- Ostovari, Y.; Ghorbani-Dashtaki, S.; Bahrami, H.-A.; Naderi, M.; Dematte, J.A.M.; Kerry, R. Modification of the USLE K factor for soil erodibility assessment on calcareous soils in Iran. Geomorphology 2016, 273, 385–395. [Google Scholar] [CrossRef]
- Vandenboer, K.; Celette, F.; Bezuijen, A. The effect of sudden critical and supercritical hydraulic loads on backward erosion piping: Small-scale experiments. Acta Geotech. 2019, 14, 783–794. [Google Scholar] [CrossRef]
- Pereyra, M.A.; Fernández, D.S.; Marcial, E.R.; Puchulu, M.E. Agricultural land degradation by piping erosion in Chaco Plain, Northwestern Argentina. Catena 2020, 185, 104295. [Google Scholar] [CrossRef]
- Gayen, A.; Pourghasemi, H.R.; Saha, S.; Keesstra, S.; Bai, S. Gully erosion susceptibility assessment and management of hazard-prone areas in India using different machine learning algorithms. Sci. Total Environ. 2019, 668, 124–138. [Google Scholar] [CrossRef]
- Chen, W.; Chai, H.; Zhao, Z.; Wang, Q.; Hong, H. Landslide susceptibility mapping based on GIS and support vector machine models for the Qianyang County, China. Environ. Earth Sci. 2016, 75, 474. [Google Scholar] [CrossRef]
- Mustafa, M.R.U.; Sholagberu, A.T.; Yusof, K.W.; Hashim, A.M.; Khan, M.W.A.; Shahbaz, M. SVM-Based Geospatial Prediction of Soil Erosion Under Static and Dynamic Conditioning Factors. MATEC Web Conf. 2018, 203, 4004. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Gayen, A.; Haque, S.M.; Bai, S. Gully Erosion Susceptibility Assessment Through the SVM Machine Learning Algorithm (SVM-MLA). In Gully Erosion Studies from India and Surrounding Regions; Springer: Berlin/Heidelberg, Germany, 2020; pp. 415–425. [Google Scholar]
- Amiri, M.; Pourghasemi, H.R.; Ghanbarian, G.A.; Afzali, S.F. Spatial Modeling of Gully Erosion Using Different Scenarios and Evidential Belief Function in Maharloo Watershed, Iran. In Advances in Remote Sensing and Geo Informatics Applications; Springer: Berlin/Heidelberg, Germany, 2019; pp. 253–256. [Google Scholar]
- Arabameri, A.; Rezaei, K.; Pourghasemi, H.R.; Lee, S.; Yamani, M. GIS-based gully erosion susceptibility mapping: A comparison among three data-driven models and AHP knowledge-based technique. Environ. Earth Sci. 2018, 77, 1–22. [Google Scholar] [CrossRef]
- Hosseinalizadeh, M.; Kariminejad, N.; Chen, W.; Pourghasemi, H.R.; Alinejad, M.; Mohammadian Behbahani, A.; Tiefenbacher, J.P. Spatial modelling of gully headcuts using UAV data and four best-first decision classifier ensembles (BFTree, Bag-BFTree, RS-BFTree, and RF-BFTree). Geomorphology 2019, 329, 184–193. [Google Scholar] [CrossRef]
- Avand, M.; Janizadeh, S.; Naghibi, S.A.; Pourghasemi, H.R.; Khosrobeigi Bozchaloei, S.; Blaschke, T. A Comparative Assessment of Random Forest and k-Nearest Neighbor Classifiers for Gully Erosion Susceptibility Mapping. Water 2019, 11, 2076. [Google Scholar] [CrossRef]
- Moradi, H.R.; Avand, M.T.; Janizadeh, S. Landslide susceptibility survey using modeling methods. In Spatial Modeling in GIS and R for Earth and Environmental Sciences; Elsevier: Amsterdam, The Netherlands, 2019; pp. 259–276. [Google Scholar]
- Arabameri, A.; Chen, W.; Loche, M.; Zhao, X.; Li, Y.; Lombardo, L.; Cerda, A.; Pradhan, B.; Bui, D.T. Comparison of machine learning models for gully erosion susceptibility mapping. Geosci. Front. 2019, 11, 1609–1620. [Google Scholar] [CrossRef]
- Amiri, M.; Pourghasemi, H.R.; Ghanbarian, G.A.; Afzali, S.F. Assessment of the importance of gully erosion effective factors using Boruta algorithm and its spatial modeling and mapping using three machine learning algorithms. Geoderma 2019, 340, 55–69. [Google Scholar] [CrossRef]
- Chen, W.; Yan, X.; Zhao, Z.; Hong, H.; Bui, D.T.; Pradhan, B. Spatial prediction of landslide susceptibility using data mining-based kernel logistic regression, naive Bayes and RBFNetwork models for the Long County area (China). Bull. Eng. Geol. Environ. 2019, 78, 247–266. [Google Scholar] [CrossRef]
- Javidan, N.; Kavian, A.; Pourghasemi, H.R.; Conoscenti, C.; Jafarian, Z. Gully Erosion Susceptibility Mapping Using Multivariate Adaptive Regression Splines—Replications and Sample Size Scenarios. Water 2019, 11, 2319. [Google Scholar] [CrossRef]
- Amiri, M.; Pourghasemi, H.R. Mapping and Preparing a Susceptibility Map of Gully Erosion Using the MARS Model. In Gully Erosion Studies from India and Surrounding Regions; Springer: Berlin/Heidelberg, Germany, 2020; pp. 405–413. [Google Scholar]
- Pourghasemi, H.R.; Yousefi, S.; Kornejady, A.; Cerdà, A. Performance assessment of individual and ensemble data-mining techniques for gully erosion modeling. Sci. Total Environ. 2017, 609, 764–775. [Google Scholar] [CrossRef]
- Gómez-Gutiérrez, Á.; Conoscenti, C.; Angileri, S.E.; Rotigliano, E.; Schnabel, S. Using topographical attributes to evaluate gully erosion proneness (susceptibility) in two mediterranean basins: Advantages and limitations. Nat. Hazards 2015, 79, 291–314. [Google Scholar] [CrossRef]
- Raja, N.B.; Çiçek, I.; Türkouglu, N.; Aydin, O.; Kawasaki, A. Landslide susceptibility mapping of the Sera River Basin using logistic regression model. Nat. Hazards 2017, 85, 1323–1346. [Google Scholar] [CrossRef]
- Arabameri, A.; Pradhan, B.; Pourghasemi, H.R.; Rezaei, K.; Kerle, N. Spatial modelling of gully erosion using GIS and R programing: A comparison among three data mining algorithms. Appl. Sci. 2018, 8, 1369. [Google Scholar] [CrossRef]
- Arabameri, A.; Cerda, A.; Tiefenbacher, J.P. Spatial pattern analysis and prediction of gully erosion using novel hybrid model of entropy-weight of evidence. Water 2019, 11, 1129. [Google Scholar] [CrossRef]
- Jenks, G.F. The data model concept in statistical mapping. Int. Yearb. Cartogr. 1967, 7, 186–190. [Google Scholar]
- Hair, J.F.; Black, W.C.; Babin, B.J.; Anderson, R.E.; Tatham, R.L. Multivariate Data Analysis; Prentice Hall: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- Saha, S. Groundwater potential mapping using analytical hierarchical process: A study on Md. Bazar Block of Birbhum District, West Bengal. Spat. Inf. Res. 2017, 25, 615–626. [Google Scholar]
- Roy, J.; Saha, S. GIS-based Gully Erosion Susceptibility Evaluation Using Frequency Ratio, Cosine Amplitude and Logistic Regression Ensembled with fuzzy logic in Hinglo River Basin, India. Remote Sens. Appl. Soc. Environ. 2019, 15, 100247. [Google Scholar]
- Roy, J.; Saha, S.; Arabameri, A.; Blaschke, T.; Bui, D.T. A Novel Ensemble Approach for Landslide Susceptibility Mapping (LSM) in Darjeeling and Kalimpong Districts, West Bengal, India. Remote Sens. 2019, 11, 2866. [Google Scholar]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar]
- Vapnik, V.N. The nature of statistical learning. In Theory; Elsevier: Amsterdam, The Netherlands, 1995. [Google Scholar]
- Burges, C.J.C. A tutorial on support vector machines for pattern recognition. Data Min. Knowl. Discov. 1998, 2, 121–167. [Google Scholar]
- Berry, D.A. Statistics: A Bayesian Perspective; Duxbury Press: Belmont, CA, USA, 1996. [Google Scholar]
- Bolstad, W.M.; Curran, J.M. Introduction to Bayesian Statistics; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Hoff, P.D. A First Course in Bayesian Statistical Methods; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Ly, H.-B.; Monteiro, E.; Le, T.-T.; Le, V.M.; Dal, M.; Régnier, G.; Pham, B.T. Prediction and sensitivity analysis of bubble dissolution time in 3D selective laser sintering using ensemble decision trees. Materials 2019, 12, 1544. [Google Scholar]
- Arabameri, A.; Pradhan, B.; Rezaei, K.; Lee, C.-W. Assessment of Landslide Susceptibility Using Statistical- and Artificial Intelligence-Based FR–RF Integrated Model and Multiresolution DEMs. Remote Sens. 2019, 11, 999. [Google Scholar] [CrossRef]
- Boucher, S.C. Field Tunnel Erosion, Its Characteristics and Amelioration; Department of Conservation and Environment, Land Protection Division: Oklahoma City, OK, USA, 1990.
- Carey, S.K.; Woo, M.-K. The role of soil pipes as a slope runoff mechanism, Subarctic Yukon, Canada. J. Hydrol. 2000, 233, 206–222. [Google Scholar]
- Putty, M.R.Y.; Prasad, R. Runoff processes in headwater catchments—An experimental study in Western Ghats, South India. J. Hydrol. 2000, 235, 63–71. [Google Scholar]
- George, C.M.; Anu, V.V. Predicting piping erosion susceptibility by statistical and artificial intelligence approaches-A review. Int. Res. J. Eng. Technol. 2018, 5, 239–243. [Google Scholar]
- Liu, D.; Liang, X.; Chen, H.; Zhang, H.; Mao, N. A quantitative assessment of comprehensive ecological risk for a loess erosion gully: A case study of Dujiashi Gully, Northern Shaanxi province, China. Sustainability 2018, 10, 3239. [Google Scholar] [CrossRef]
- Chowdhuri, I.; Pal, S.C.; Chakrabortty, R. Flood susceptibility mapping by ensemble evidential belief function and binomial logistic regression model on river basin of eastern India. Adv. Space Res. 2020, 65, 1466–1489. [Google Scholar] [CrossRef]
- Gayen, A.; Pourghasemi, H.R. Spatial Modeling of Gully Erosion: A New Ensemble of CART and GLM Data-Mining Algorithms. In Spatial Modeling in GIS and R for Earth and Environmental Sciences; Elsevier: Amsterdam, The Netherlands, 2019; pp. 653–669. [Google Scholar]
- Youssef, A.M.; Pourghasemi, H.R. Landslide susceptibility mapping using machine learning algorithms and comparison of their performance at Abha Basin, Asir Region, Saudi Arabia. Geosci. Front. 2020, 79, 1–18. [Google Scholar] [CrossRef]
- Hosseinalizadeh, M.; Kariminejad, N.; Rahmati, O.; Keesstra, S.; Alinejad, M.; Behbahani, A.M. How can statistical and artificial intelligence approaches predict piping erosion susceptibility. Sci. Total Environ. 2019, 646, 1554–1566. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chen, X.-W.; Liu, M. Prediction of protein—Protein interactions using random decision forest framework. Bioinformatics 2005, 21, 4394–4400. [Google Scholar] [CrossRef]
- Zhang, K.; Wu, X.; Niu, R.; Yang, K.; Zhao, L. The assessment of landslide susceptibility mapping using random forest and decision tree methods in the Three Gorges Reservoir area, China. Environ. Earth Sci. 2017, 76, 405. [Google Scholar] [CrossRef]
- Holden, J. Controls of soil pipe frequency in upland blanket peat. J. Geophys. Res. Earth Surf. 2005, 110. [Google Scholar] [CrossRef]
- Torri, D.; Colica, A.; Rockwell, D. Preliminary study of the erosion mechanisms in a biancana badland (Tuscany, Italy). Catena 1994, 23, 281–294. [Google Scholar] [CrossRef]
- Piccarreta, M.; Faulkner, H.; Bentivenga, M.; Capolongo, D. The influence of physico-chemical material properties on erosion processes in the badlands of Basilicata, Southern Italy. Geomorphology 2006, 81, 235–251. [Google Scholar] [CrossRef]
- Bernatek-Jakiel, A.; Vannoppen, W.; Poesen, J. Assessment of grass root effects on soil piping in sandy soils using the pinhole test. Geomorphology 2017, 295, 563–571. [Google Scholar] [CrossRef]
- Romero-Diaz, A.; Ruiz-Sinoga, J.D.; Belmonte-Serrato, F. Physical-chemical and mineralogical properties of parent materials and their relationship with the morphology of badlands. Geomorphology 2020, 354, 107047. [Google Scholar] [CrossRef]
- Castañeda, C.; Gracia, F.J.; Rodriguez-Ochoa, R.; Zarroca, M.; Roqué, C.; Linares, R.; Desir, G. Origin and evolution of Sariñena Lake (central Ebro Basin): A piping-based model. Geomorphology 2017, 290, 164–183. [Google Scholar] [CrossRef]
- Wang, F.; Okeke, A.C.-U.; Kogure, T.; Sakai, T.; Hayashi, H. Assessing the internal structure of landslide dams subject to possible piping erosion by means of microtremor chain array and self-potential surveys. Eng. Geol. 2018, 234, 11–26. [Google Scholar] [CrossRef]
- Masannat, Y.M. Development of piping erosion conditions in the Benson area, Arizona, USA. Q. J. Eng. Geol. Hydrogeol. 1980, 13, 53–61. [Google Scholar] [CrossRef]
- Parker, G.G. Piping: A Geomorphic Agent in Landform Development of the Drylands; International Association of Scientific Hydrology: Wallingford, UK, 1964. [Google Scholar]
- Parker, A.P. Assessment and Extension of an Analytical Formulation for Prediction of Residual Stress in Autofrettaged Thick Cylinders. In Proceedings of the ASME 2005 Pressure Vessels and Piping Conference, Denver, CO, USA, 17–21 July 2005; pp. 67–71. [Google Scholar]
- Seppälä, M. Piping causing thermokarst in permafrost, Ungava Peninsula, Quebec, Canada. Geomorphology 1997, 20, 313–319. [Google Scholar] [CrossRef]
- Carey, S.K.; Woo, M. Hydrogeomorphic relations among soil pipes, flow pathways, and soil detachments within a permafrost hillslope. Phys. Geogr. 2002, 23, 95–114. [Google Scholar] [CrossRef]
- Onda, Y.; Itakura, N. An experimental study on the burrowing activity of river crabs on subsurface water movement and piping erosion. Geomorphology 1997, 20, 279–288. [Google Scholar] [CrossRef]
- Onda, Y. Seepage erosion and its implication to the formation of amphitheatre valley heads: A case study at Obara, Japan. Earth Surf. Process. Landf. 1994, 19, 627–640. [Google Scholar] [CrossRef]
- Sannigrahi, S.; Zhang, Q.; Joshi, P.K.; Sutton, P.C.; Keesstra, S.; Roy, P.S.; Pilla, F.; Basu, B.; Wang, Y.; Jha, S.; et al. Examining effects of climate change and land use dynamic on biophysical and economic values of ecosystem services of a natural reserve region. J. Clean. Prod. 2020, 257, 120424. [Google Scholar] [CrossRef]
- Cerdà, A.; Rodrigo-Comino, J.; Yakupouglu, T.; Dindarouglu, T.; Terol, E.; Mora-Navarro, G.; Arabameri, A.; Radziemska, M.; Novara, A.; Kavian, A.; et al. Tillage Versus No-Tillage. Soil Properties and Hydrology in an Organic Persimmon Farm in Eastern Iberian Peninsula. Water 2020, 12, 1539. [Google Scholar] [CrossRef]
- Guadie, M.; Molla, E.; Mekonnen, M.; Cerdà, A. Effects of Soil Bund and Stone-Faced Soil Bund on Soil Physicochemical Properties and Crop Yield Under Rain-Fed Conditions of Northwest Ethiopia. Land 2020, 9, 13. [Google Scholar] [CrossRef]
- Cerdà, A.; Ackermann, O.; Terol, E.; Rodrigo-Comino, J. Impact of farmland abandonment on water resources and soil conservation in citrus plantations in eastern Spain. Water 2019, 11, 824. [Google Scholar] [CrossRef]
- Novara, A.; Keesstra, S.; Cerdà, A.; Pereira, P.; Gristina, L. Understanding the role of soil erosion on CO2-C loss using 13C isotopic signatures in abandoned Mediterranean agricultural land. Sci. Total Environ. 2016, 550, 330–336. [Google Scholar] [CrossRef]
- Moradi, E.; Rodrigo-Comino, J.; Terol, E.; Mora-Navarro, G.; da Silva, A.N.; Daliakopoulos, I.; Khosravi, H.; Pulido Fernández, M.; Cerdà, A. Quantifying Soil Compaction in Persimmon Orchards Using ISUM (Improved Stock Unearthing Method) and Core Sampling Methods. Agriculture 2020, 10, 266. [Google Scholar] [CrossRef]
- Rodrigo-Comino, J.; Ponsoda-Carreres, M.; Salesa, D.; Terol, E.; Gyasi-Agyei, Y.; Cerdà, A. Soil erosion processes in subtropical plantations (Diospyros kaki) managed under flood irrigation in Eastern Spain. Singap. J. Trop. Geogr. 2020, 41, 120–135. [Google Scholar] [CrossRef]
- Novara, A.; Pulido, M.; Rodrigo-Comino, J.; Di Prima, S.; Smith, P.; Gristina, L.; Giminez-Morera, A.; Terol, E.; Salesa, D.; Keesstra, S. Long-term organic farming on a citrus plantation results in soil organic carbon recovery. Cuad. Investig. Geográfica 2019, 45, 271–286. [Google Scholar] [CrossRef]
- López-Vicente, M.; Calvo-Seas, E.; Álvarez, S.; Cerdà, A. Effectiveness of cover crops to reduce loss of soil organic matter in a rainfed vineyard. Land 2020, 9, 230. [Google Scholar] [CrossRef]
- Visser, S.; Keesstra, S.; Maas, G.; De Cleen, M. Soil as a basis to create enabling conditions for transitions towards sustainable land management as a key to achieve the SDGs by 2030. Sustainability 2019, 11, 6792. [Google Scholar] [CrossRef]


| Parameters | Equations | Kernel Function |
|---|---|---|
| - | Linear kernel | |
| and | Polynomial kernel | |
| Radial basis function kernel |
| Row | Variables | VIF |
|---|---|---|
| 1 | Aspect | 1.13 |
| 2 | Altitude | 2.52 |
| 3 | Plan | 1.73 |
| 4 | Profile | 1.62 |
| 5 | Distance from river | 1.28 |
| 6 | Slope | 1.79 |
| 7 | TWI | 1.40 |
| 8 | Lithology | 1.49 |
| 9 | Land use | 1.41 |
| 10 | Rainfall | 3.62 |
| 11 | TPI | 1.51 |
| 12 | Silt | 2.58 |
| 13 | Sand | 1.89 |
| 14 | Clay | 3.93 |
| 15 | CEC | 1.88 |
| 16 | Bulk density | 2.96 |
| 17 | pH | 2.57 |
| Susceptibility Class | GLM Bayesian | SVM | RF | |||
|---|---|---|---|---|---|---|
| Area (Km2) | Area (%) | Area (Km2) | Area (%) | Area (Km2) | Area (%) | |
| Very Low | 196.67 | 5.48 | 904.50 | 25.18 | 1542.10 | 42.93 |
| Low | 510.74 | 14.22 | 1055.98 | 29.40 | 680.66 | 18.95 |
| Moderate | 876.75 | 24.41 | 694.27 | 19.33 | 537.86 | 14.97 |
| High | 1196.65 | 33.32 | 523.98 | 14.59 | 428.56 | 11.93 |
| Very High | 811.04 | 22.58 | 413.11 | 11.50 | 402.64 | 11.21 |
| Models | SVM | RF | GLM Bayesian | |||
|---|---|---|---|---|---|---|
| Evaluation Parameter | Test | Train | Test | Train | Test | Train |
| Sensitivity | 0.918 | 0.891 | 0.89 | 0.95 | 0.91 | 0.80 |
| Specificity | 0.702 | 0.893 | 0.74 | 0.97 | 0.70 | 0.89 |
| NPV | 0.891 | 0.893 | 0.87 | 0.95 | 0.89 | 0.82 |
| PPV | 0.762 | 0.891 | 0.78 | 0.97 | 0.76 | 0.88 |
| AUC | 0.88 | 0.96 | 0.90 | 0.98 | 0.87 | 0.93 |
| Variables | Importance |
|---|---|
| Aspect | 1.59 |
| Altitude | 9.29 |
| Plan curvature | 0.51 |
| Profile curvature | 0.84 |
| Distance from river | 4.47 |
| Slope | 1.76 |
| TWI | 2.76 |
| Lithology | 0.78 |
| Land use | 1.29 |
| Rain | 0.18 |
| TPI | 1.00 |
| Silt | 1.46 |
| Sand | 1.65 |
| Clay | 0.90 |
| CEC | 3.99 |
| Bulk density | 6.81 |
| pH | 8.80 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Band, S.S.; Janizadeh, S.; Saha, S.; Mukherjee, K.; Bozchaloei, S.K.; Cerdà, A.; Shokri, M.; Mosavi, A. Evaluating the Efficiency of Different Regression, Decision Tree, and Bayesian Machine Learning Algorithms in Spatial Piping Erosion Susceptibility Using ALOS/PALSAR Data. Land 2020, 9, 346. https://doi.org/10.3390/land9100346
Band SS, Janizadeh S, Saha S, Mukherjee K, Bozchaloei SK, Cerdà A, Shokri M, Mosavi A. Evaluating the Efficiency of Different Regression, Decision Tree, and Bayesian Machine Learning Algorithms in Spatial Piping Erosion Susceptibility Using ALOS/PALSAR Data. Land. 2020; 9(10):346. https://doi.org/10.3390/land9100346
Chicago/Turabian StyleBand, Shahab S., Saeid Janizadeh, Sunil Saha, Kaustuv Mukherjee, Saeid Khosrobeigi Bozchaloei, Artemi Cerdà, Manouchehr Shokri, and Amirhosein Mosavi. 2020. "Evaluating the Efficiency of Different Regression, Decision Tree, and Bayesian Machine Learning Algorithms in Spatial Piping Erosion Susceptibility Using ALOS/PALSAR Data" Land 9, no. 10: 346. https://doi.org/10.3390/land9100346
APA StyleBand, S. S., Janizadeh, S., Saha, S., Mukherjee, K., Bozchaloei, S. K., Cerdà, A., Shokri, M., & Mosavi, A. (2020). Evaluating the Efficiency of Different Regression, Decision Tree, and Bayesian Machine Learning Algorithms in Spatial Piping Erosion Susceptibility Using ALOS/PALSAR Data. Land, 9(10), 346. https://doi.org/10.3390/land9100346







