A Machine-Learning Approach Combining Wavelet Packet Denoising with Catboost for Weather Forecasting
Abstract
:1. Introduction
2. Materials and Methods
2.1. Problem Statement
2.2. Data Processing
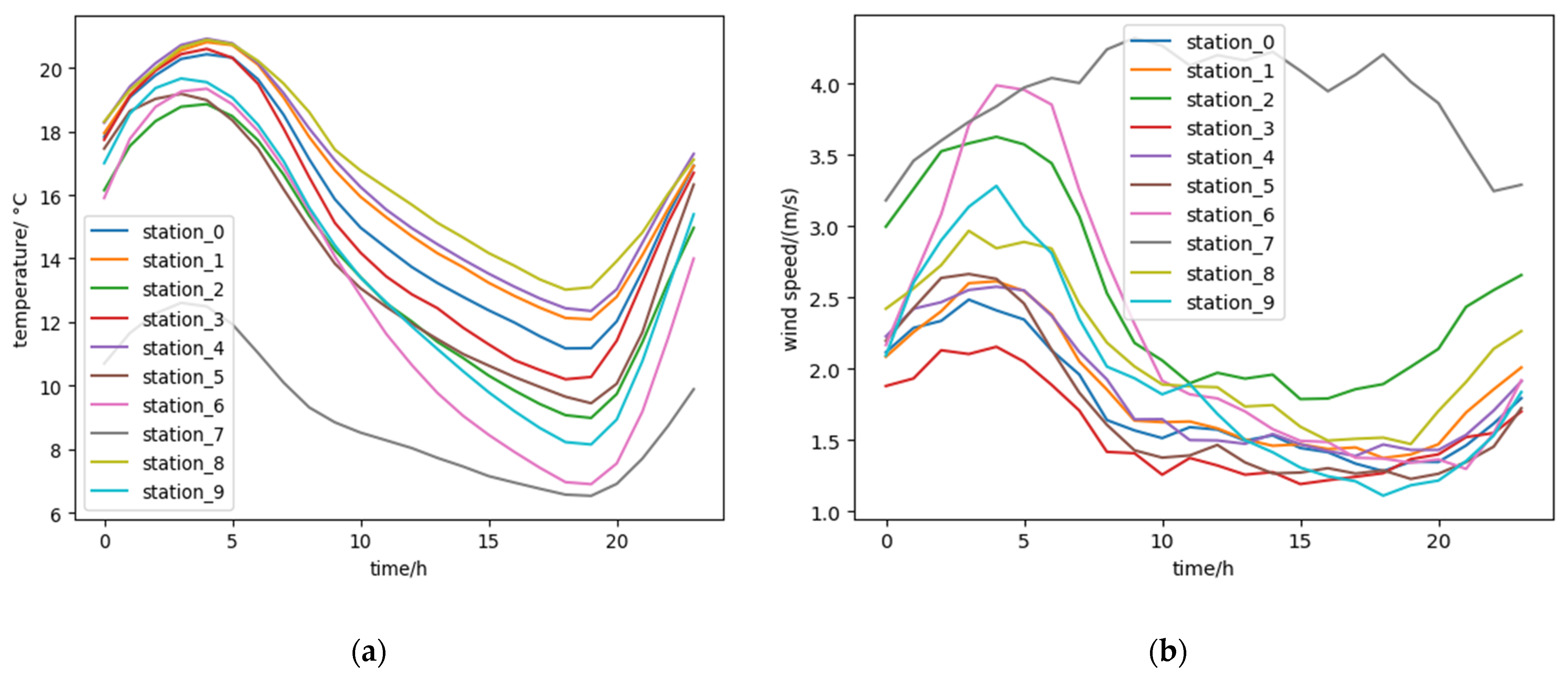
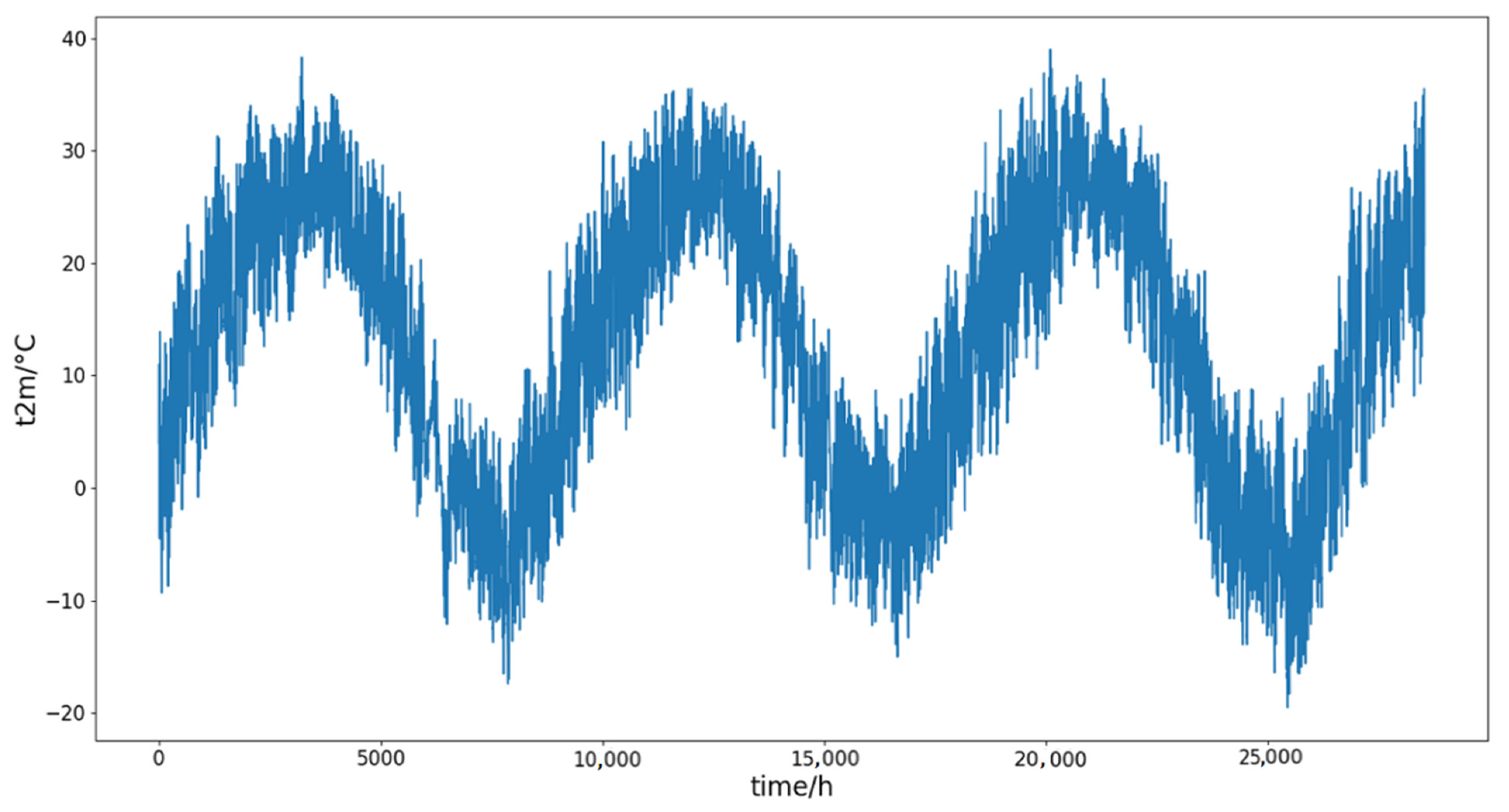
2.2.1. Missing Values
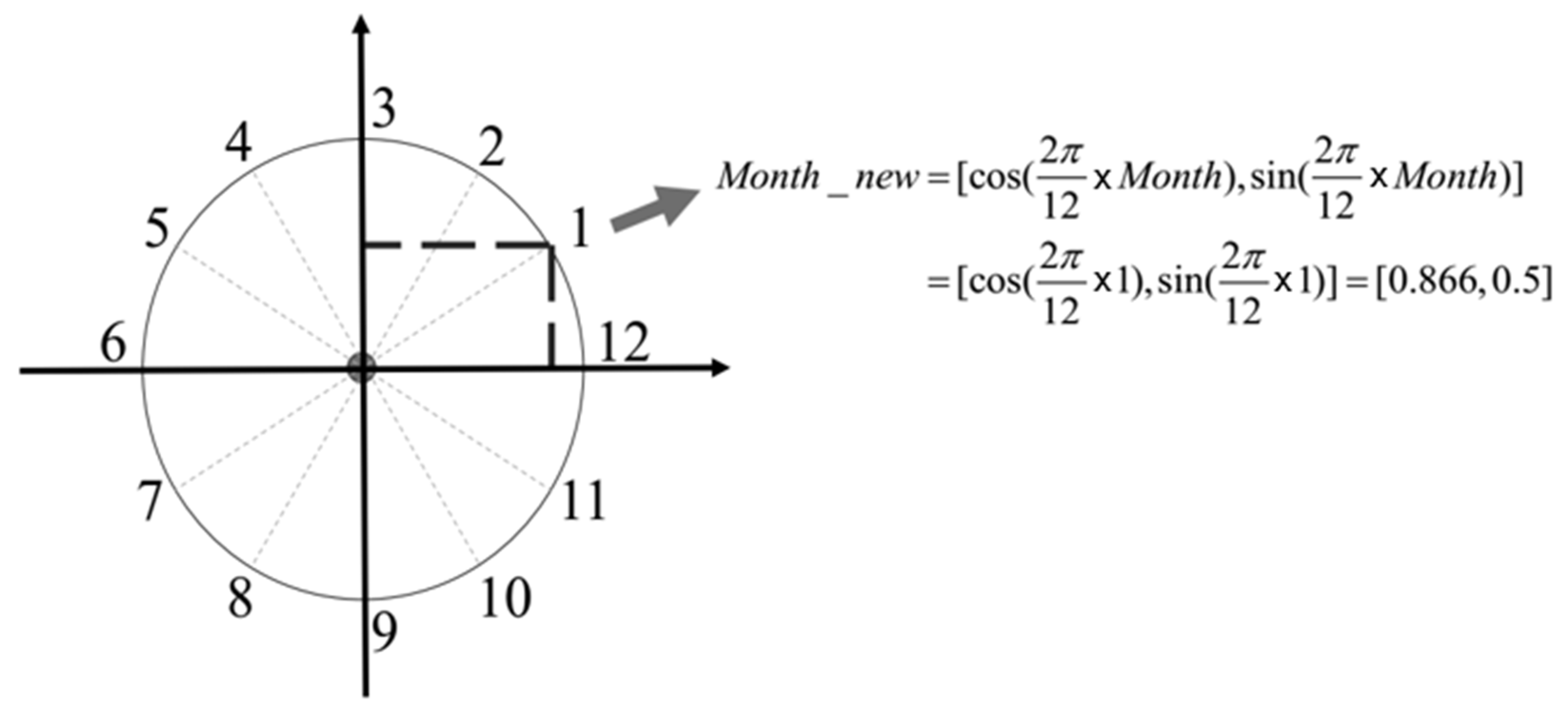
2.2.2. Additional Spatiotemporal Feathers
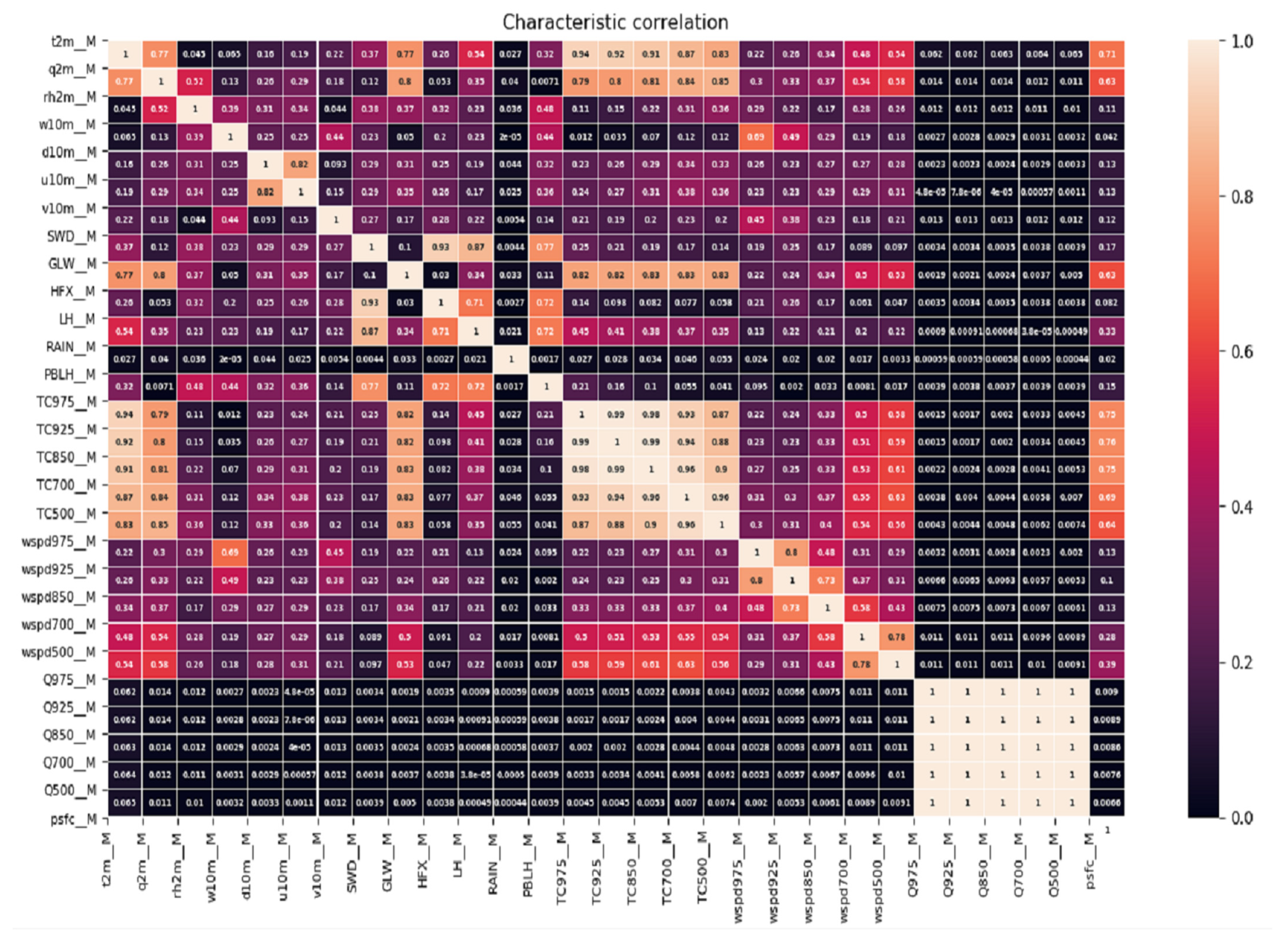
2.2.3. Feature Selection
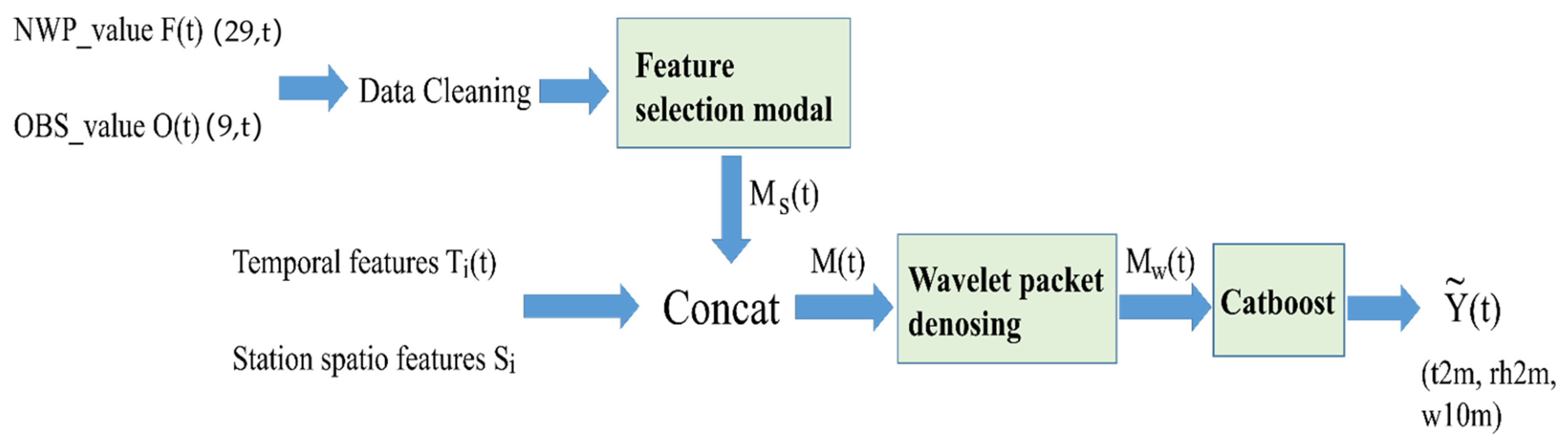
2.3. Model Architecture
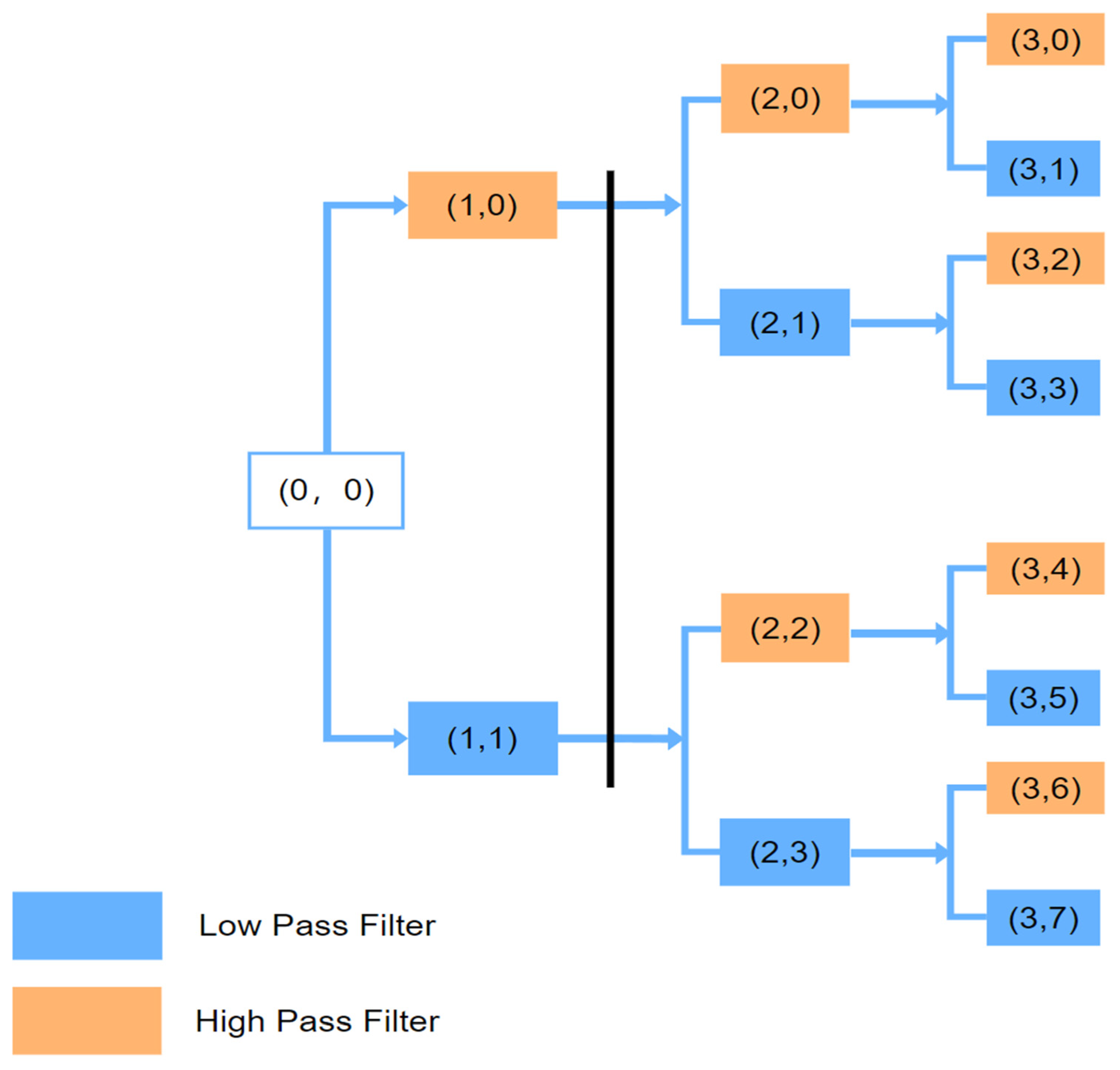
2.3.1. Wavelet Packet Denoising Principle
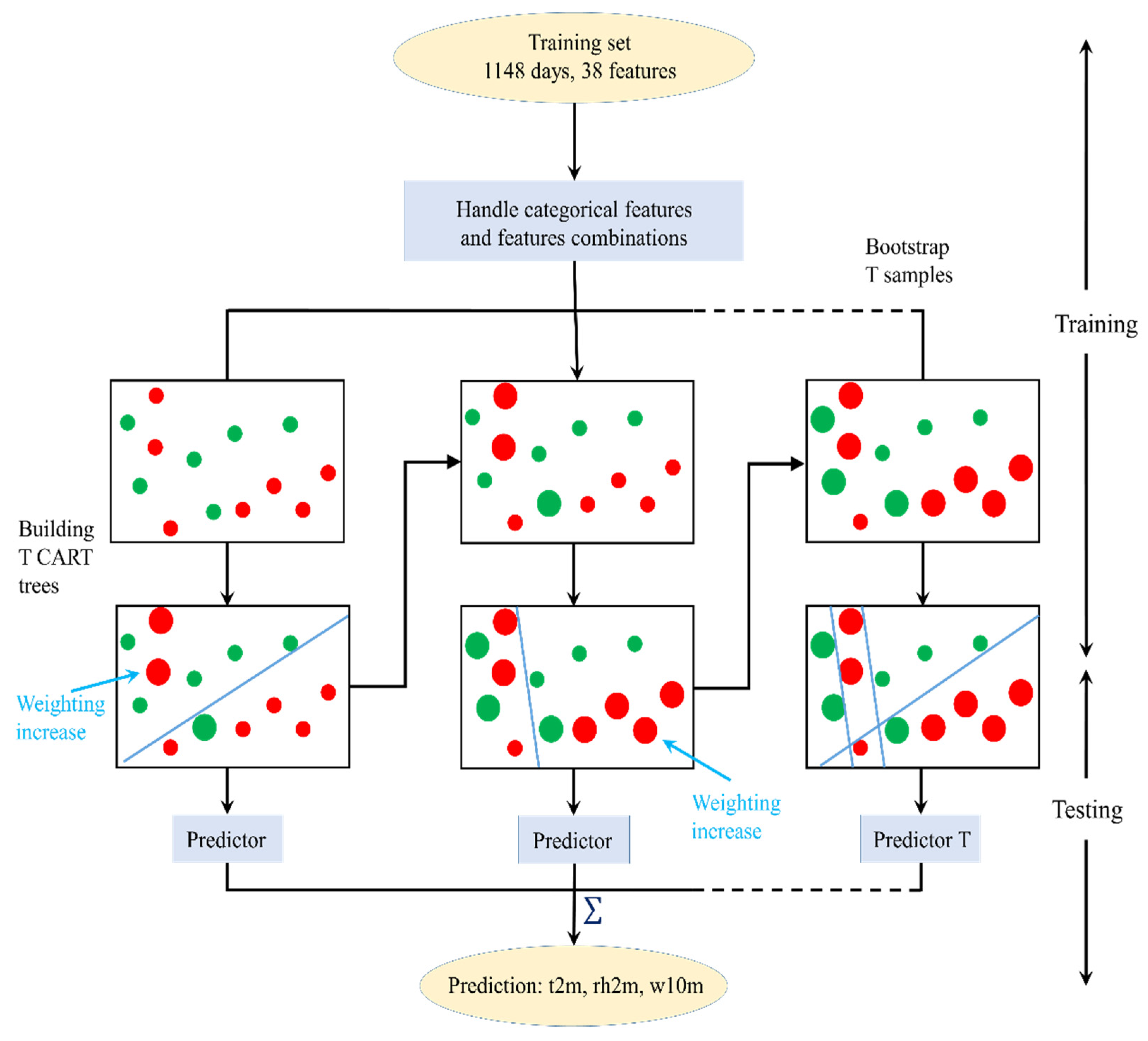
2.3.2. Learning Model: Categorical Boosting
3. Performance Analysis and Comparisons
3.1. Statistical Evaluation
3.2. Baselines and Experimental Settings
| Algorithm 1. Combining WPD and Catboost Method for Weather Forecasting |
| Input: Historical Observation Datasets , NWP Datasets , Ground Truth |
| Output: Prrediction |
| 1:Data Cleaning |
| 2: Feature Selection: |
| 3: Temproal Features: |
| 4: Spatio Features: |
| 5: Concat , , |
| 6: Wavelet Packet Denosing: |
| 7: Catboost: |
| 8:End |
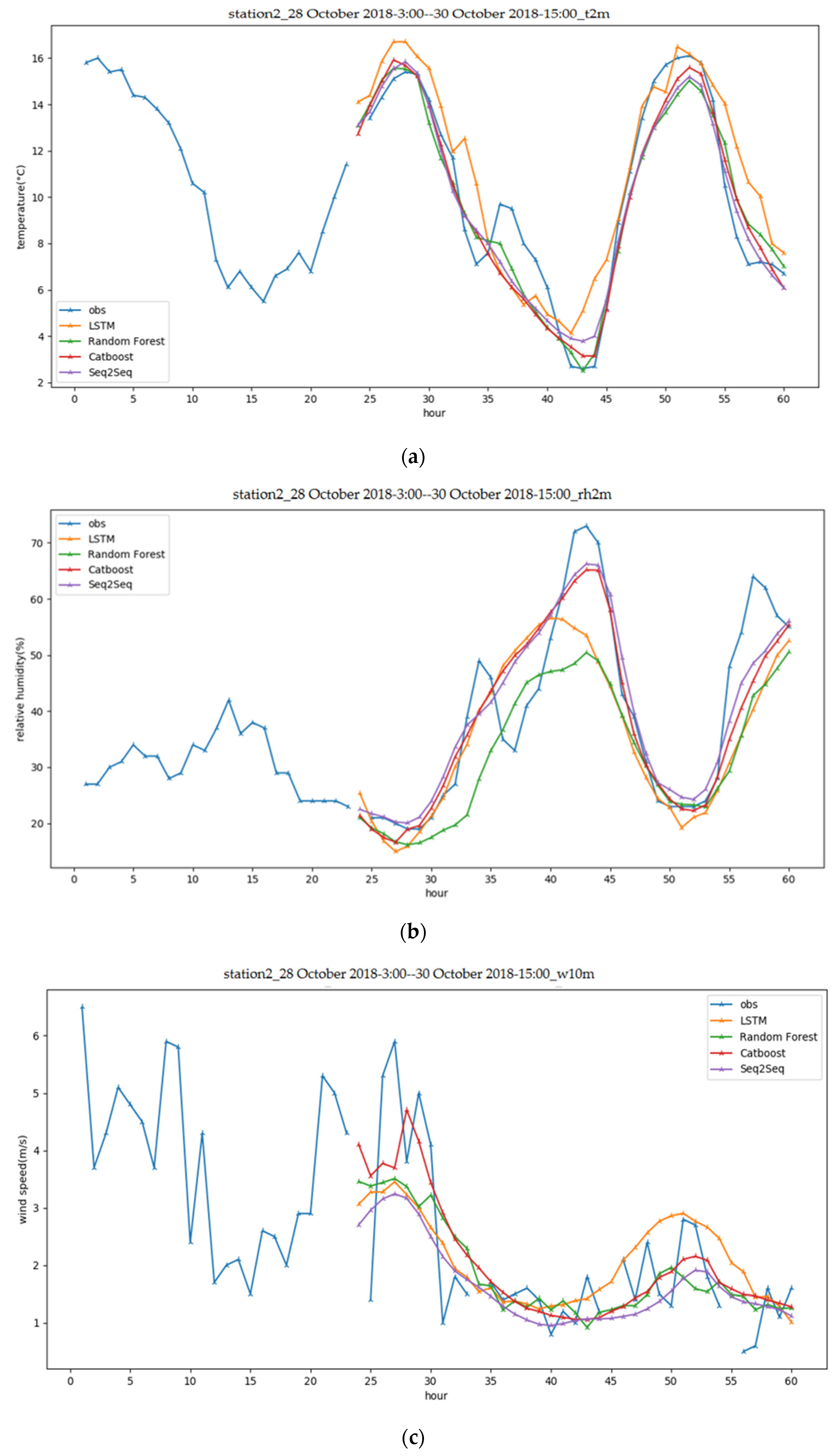
3.3. Performance Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gneiting, T.; Raftery, A.E. Weather forecasting with ensemble methods. Science 2005, 310, 248–249. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jones, N. Machine learning tapped to improve climate forecasts. Nature 2017, 548, 379–380. [Google Scholar] [CrossRef] [PubMed]
- Ham, Y.G.; Kim, J.H.; Luo, J.J. Deep learning for multi-year ENSO forecasts. Nature 2019, 573, 568–572. [Google Scholar] [CrossRef] [PubMed]
- Ravuri, S.; Lenc, K.; Willson, M.; Kangin, D.; Lam, R.; Mirowski, M. Skillful Precipitation Nowcasting using Deep Generative Models of Radar. Nature 2021, 597, 672–677. [Google Scholar] [CrossRef]
- Marchuk, G. Numerical Methods in Weather Prediction; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Tolstykh, M.A.; Frolov, A.V. Some current problems in numerical weather prediction. Izv. Atmos. Ocean. Phys. 2005, 41, 285–295. [Google Scholar]
- Juanzhen, S.; Ming, X.; James, W.W.; Zawadzki, I.; Ballard, S.P.; Onvlee-Hooimeyer, J.; Pinto, J. Use of NWP for nowcasting convective precipitation: Recent progress and challenges. Bull. Am. Meteorol. Soc. 2014, 95, 409–426. [Google Scholar]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.Y.; Wong, W.K.; Woo, W.C. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. In Proceedings of the 28th International Conference on Neural Information Processing Systems (NeurIPS), Montreal, QC, Canada, 7–10 December 2015; pp. 802–810. [Google Scholar]
- McGovern, A.; Elmore, K.L.; Gagne, D.J.; Haupt, S.E.; Karstens, C.D.; Lagerquist, R.; Williams, J.K. Using artificial intelligence to improve real-time decision-making for high-impact weather. Bull. Am. Meteorol. Soc. 2017, 98, 2073–2090. [Google Scholar] [CrossRef]
- Basha, C.Z.; Bhavana, N.; Bhavya, P.; Sowmya, V. Rainfall prediction using machine learning & deep learning techniques. In Proceedings of the International Conference on Electronics and Sustainable Communication Systems (ICESC), Coimbatore, India, 2–4 July 2020; pp. 92–97. [Google Scholar]
- Imam Cholissodin, S. Prediction of rainfall using improved deep learning with particle swarm optimization. Telkomnika 2020, 18, 2498–2504. [Google Scholar] [CrossRef]
- Khan, M.I.; Maity, R. Hybrid deep learning approach for multi-step-ahead daily rainfall prediction using GCM simulations. IEEE Access 2020, 8, 52774–52784. [Google Scholar] [CrossRef]
- Sapankevych, N.I.; Sankar, R. Time series prediction using support vector machines: A survey. IEEE Comput. Intell. Mag. 2009, 4, 24–38. [Google Scholar] [CrossRef]
- Ling, C.; Xu, L. Comparison between ARIMA and ANN models used in short-term wind speed forecasting. In Proceedings of the Power and Energy Engineering Conference (APPEEC), Wuhan, China, 25–28 March 2011; pp. 1–4. [Google Scholar]
- Cyril, V.; Marc, M.; Christophe, P.; Marie-Laure, N. Numerical weather prediction (NWP) and hybrid ARMA/ANN model to predict global radiation. Energy 2012, 39, 341–355. [Google Scholar]
- Chen, N.; Qian, Z.; Nabney, I.T.; Meng, X. Short-term wind power forecasting using gaussian processes. In Proceedings of the Twenty-Third International Joint Conference on Artificial Intelligence, Beijing, China, 3–9 August 2013. [Google Scholar]
- Grover, A.; Kapoor, A.; Horvitz, E. A deep hybrid model for weather forecasting. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, Australia, 10–13 August 2015; pp. 379–386. [Google Scholar]
- Hernández, E.; Sanchez-Anguix, V.; Julian, V.; Palanca, J.; Duque, N. Rainfall prediction: A deep learning approach. In Proceedings of the International Conference on Hybrid Artificial Intelligence Systems, Seville, Spain, 18–20 April 2016; pp. 151–162. [Google Scholar]
- Li, Y.; Lang, J.; Ji, L.; Zhong, J.; Wang, Z.; Guo, Y.; He, S. Weather forecasting using ensemble of spatial-temporal attention network and multi-layer perceptron. Asia-Pac. J. Atmos. Sci. 2021, 57, 533–546. [Google Scholar] [CrossRef]
- Salman, A. Single layer & multi-layer long short-term memory (LSTM) model with intermediate variables for weather forecasting. Procedia Comput. Sci. 2018, 135, 89–98. [Google Scholar]
- Fu, Q.; Niu, D.; Zang, Z.; Hao, H.; Li, D. Multi-stations’ weather prediction based on hybrid model using 1D CNN and Bi-LSTM. In Proceedings of the 2019 Chinese Control Conference, Guangzhou, China, 27–30 July 2019; pp. 3771–3775. [Google Scholar]
- Wang, B.; Lu, J.; Yan, Z.; Luo, H.; Li, T.; Zheng, Y.; Zhang, G. Deep uncertainty quantification: A machine learning approach Bashafor weather forecasting. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 2087–2095. [Google Scholar]
- Shi, X.; Gao, Z.; Lausen, L.; Wang, H.; Yeung, D.Y.; Wong, W.K.; Woo, W.C. Deep Learning for Precipitation Nowcasting: A Benchmark and A New Model. In Proceedings of the 30th International Conference on Neural Information Processing Systems (NeurIPS), Long Beach, CA, USA, 4–7 December 2017; pp. 5617–5627. [Google Scholar]
- Wang, Y.; Zhang, J.; Zhu, H. Memory in memory: A predictive neural network for learning higher-order non-stationarity from spatiotemporal dynamics. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 9154–9162. [Google Scholar]
- Wang, Y.; Long, M.; Wang, J.; Gao, Z.; Yu, P.S. Predrnn: Recurrent neural networks for predictive learning using spatiotemporal lstms. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–7 December 2017; pp. 879–888. [Google Scholar]
- Wang, Y.; Gao, Z.; Long, M.; Wang, J.; Philip, S.Y. Predrnn++: Towards a resolution of the deep-in-time dilemma in spatiotemporal predictive learning. In Proceedings of the International Conference on Machine Learning (PMLR), Stockholm, Sweden, 10–15 July 2018; pp. 5123–5132. [Google Scholar]
- Wang, C.; Wang, P.; Wang, P.; Xue, B.; Wang, D. Using Conditional Generative Adversarial 3D Convolutional Neural Network for Precise Radar Extrapolation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 5735–5749. [Google Scholar] [CrossRef]
- Liu, H.B.; Lee, I. MPL-GAN: Toward Realistic Meteorological Predictive Learning Using Conditional GAN. IEEE Access 2020, 8, 93179–93186. [Google Scholar] [CrossRef]
- Niu, D.; Huang, J.; Zang, Z.; Xu, L.; Che, H.; Tang, Y. Two-Stage Spatiotemporal Context Refinement Network for Precipitation Nowcasting. Remote Sens. 2021, 13, 4285. [Google Scholar] [CrossRef]
- Huang, G.; Wu, L.; Ma, X. Evaluation of CatBoost method for prediction of reference evapotranspiration in humid regions. J. Hydrol. 2019, 574, 1029–1041. [Google Scholar] [CrossRef]
- Karimi, S.; Shiri, J.; Marti, P. Supplanting missing climatic inputs in classical and random forest models for estimating reference evapotranspiration in humid coastal areas of Iran. Comput. Electron. Agric. 2020, 176, 105633. [Google Scholar] [CrossRef]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A. CatBoost: Unbiased boosting with categorical features. In Proceedings of the Advances in Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018; pp. 6638–6648. [Google Scholar]
- Wu, L.; Huang, G.; Fan, J. Potential of kernel-based nonlinear extension of Arps decline model and gradient boosting with categorical features support for predicting daily global solar radiation in humid regions. Energy Convers. Manag. 2019, 183, 280–295. [Google Scholar] [CrossRef]
- Chia, M.Y.; Huang, Y.F.; Koo, C.H. Recent advances in evapotranspiration estimation using artificial intelligence approaches with a focus on hybridization techniques—A review. Agronomy 2020, 10, 101. [Google Scholar] [CrossRef] [Green Version]
- Kang, P.; Lin, Z.; Teng, S. Catboost-based framework with additional user information for social media popularity prediction. In Proceedings of the the 27th ACM International Conference on Multimedia, Nice, France, 21–25 October 2019; pp. 2677–2681. [Google Scholar]
- März, A. CatBoostLSS-An extension of CatBoost to probabilistic forecasting. arXiv 2020, arXiv:2001.02121. [Google Scholar]
- Huang, X.; Zhang, L.; Wang, B. Feature clustering based support vector machine recursive feature elimination for gene selection. Appl. Intell. 2018, 48, 594–607. [Google Scholar] [CrossRef]
- Qian, H.; Ma, J.C. Research on fiber optic gyro signal de-noising based on wavelet packet soft-threshold. J. Syst. Eng. Electron. 2009, 20, 607–612. [Google Scholar]
- Wu, Y.J.; Gao, G.J.; Cui, C. Improved wavelet denoising by non-convex sparse regularization under double wavelet domains. IEEE Access 2019, 7, 30659–30671. [Google Scholar] [CrossRef]
- Pan, Y.; Zhang, L.M.; Wu, X.G.; Zhang, K.N.; Skibniewski, M.J. Structural health monitoring and assessment using wavelet packet energy spectrum. Saf. Sci. 2019, 120, 652–665. [Google Scholar] [CrossRef]

| Method | ||||||
|---|---|---|---|---|---|---|
| LSTM + FS | 0.0203 | 0.1112 | 0.0503 | 0.1303 | 0.3143 | 0.1253 |
| LSTM + FS + ST | 0.1000 | 0.2978 | 0.1821 | 0.2596 | 0.3488 | 0.2377 |
| RF + FS + ST | 0.1146 | 0.1962 | 0.3582 | 0.4270 | 0.3859 | 0.2964 |
| RF + FS + ST + WPD | 0.1821 | 0.2358 | 0.3990 | 0.4513 | 0.4553 | 0.3447 |
| Seq2Seq + FS + ST + WPD | 0.2587 | 0.3793 | 0.4606 | 0.5320 | 0.5102 | 0.4282 |
| Catboost + ST | 0.2933 | 0.3692 | 0.4610 | 0.5136 | 0.5406 | 0.4355 |
| Catboost + ST + FS | 0.2992 | 0.3921 | 0.4654 | 0.5175 | 0.5434 | 0.4435 |
| Catboost + ST + FS + WPD | 0.3273 | 0.4088 | 0.4908 | 0.5447 | 0.5530 | 0.4649 |
| Catboost + ST + FS + WPD + noNWP | 0.183 | 0.139 | 0.195 | 0.197 | 0.207 | 0.1842 |
| Catboost + ST + FS + WPD + noOBS | 0.016 | 0.314 | 0.343 | 0.396 | 0.401 | 0.294 |
| Method | ||||||
|---|---|---|---|---|---|---|
| LSTM + FS | 4.3167 | 4.5871 | 4.8221 | 5.1009 | 3.9671 | 4.5588 |
| LSTM + FS + ST | 2.4113 | 2.5097 | 2.6214 | 2.7719 | 2.6444 | 2.5917 |
| RF + FS + ST | 2.3121 | 2.3584 | 1.7002 | 1.4721 | 1.5651 | 1.8816 |
| RF + FS + ST + WPD | 2.1167 | 2.1871 | 1.6672 | 1.4323 | 1.5333 | 1.7873 |
| Seq2Seq + FS + ST + WPD | 1.7189 | 1.7228 | 1.2688 | 1.2554 | 1.4117 | 1.4755 |
| Catboost + ST | 1.1699 | 1.7337 | 1.2561 | 1.3019 | 1.1887 | 1.3300 |
| Catboost + ST + FS | 1.1642 | 1.6993 | 1.2343 | 1.2982 | 1.1832 | 1.3158 |
| Catboost + ST + FS + WPD | 1.0596 | 1.6738 | 1.0977 | 1.1276 | 1.1253 | 1.2168 |
| Catboost + ST + FS + WPD + noNWP | 2.1002 | 3.2278 | 2.5180 | 3.0988 | 4.4333 | 3.0756 |
| Catboost + ST + FS + WPD + noOBS | 4.9663 | 2.8534 | 2.1721 | 2.2564 | 1.5477 | 2.7592 |
| Method | ||||||
|---|---|---|---|---|---|---|
| LSTM + FS | 13.2332 | 13.8361 | 13.3123 | 14.5241 | 12.1123 | 13.4036 |
| LSTM + FS + ST | 11.7341 | 8.4723 | 8.2121 | 11.0852 | 9.4516 | 9.7910 |
| RF + FS + ST | 12.1946 | 12.1678 | 6.5207 | 9.0303 | 8.6171 | 9.7061 |
| RF + FS + ST + WPD | 11.1348 | 11.4681 | 6.2913 | 8.9234 | 8.4588 | 9.2553 |
| Seq2Seq + FS + ST + WPD | 9.9271 | 8.5661 | 5.7026 | 6.8698 | 7.3950 | 7.6921 |
| Catboost + ST | 9.4694 | 8.6883 | 6.6771 | 7.3775 | 7.0220 | 7.8469 |
| Catboost + ST + FS | 9.3367 | 8.3433 | 6.6651 | 7.3379 | 7.0112 | 7.7388 |
| Catboost + ST + FS + WPD | 9.2295 | 8.3106 | 6.4138 | 7.1386 | 6.9638 | 7.6113 |
| Catboost + ST + FS + WPD + noNWP | 10.4456 | 12.3314 | 8.0278 | 11.4123 | 12.9973 | 11.0429 |
| Catboost + ST + FS + WPD + noOBS | 13.4584 | 9.8877 | 7.7854 | 10.5543 | 8.5771 | 10.0526 |
| Method | ||||||
|---|---|---|---|---|---|---|
| LSTM + FS | 2.1244 | 1.3122 | 1.4667 | 1.1883 | 1.2671 | 1.47174 |
| LSTM + FS + ST | 1.6000 | 0.9260 | 0.9670 | 0.8750 | 0.8140 | 1.0364 |
| RF + FS + ST | 1.5527 | 1.0406 | 0.7638 | 0.8242 | 0.8862 | 1.0135 |
| RF + FS + ST + WPD | 1.5488 | 1.0091 | 0.7505 | 0.8009 | 0.8801 | 0.99788 |
| Seq2Seq + FS + ST + WPD | 1.5357 | 0.9507 | 0.7392 | 0.7340 | 0.8982 | 0.97156 |
| Catboost + ST | 1.4889 | 0.9355 | 0.7311 | 0.7502 | 0.8663 | 0.9544 |
| Catboost + ST + FS | 1.4019 | 0.9031 | 0.7229 | 0.7442 | 0.8547 | 0.92536 |
| Catboost + ST + FS + WPD | 1.3631 | 0.8883 | 0.7178 | 0.7365 | 0.8114 | 0.90342 |
| Catboost + ST + FS + WPD + noNWP | 1.5439 | 1.0218 | 0.9512 | 0.9338 | 1.3304 | 1.15622 |
| Catboost + ST + FS + WPD + noOBS | 2.2883 | 0.9802 | 0.8856 | 0.9117 | 0.8834 | 1.18984 |
| Method | |||||||
|---|---|---|---|---|---|---|---|
| LSTM + FS | 0.0992 | 0.2273 | 0.1372 | 0.1391 | 0.1335 | 0.1763 | 0.1521 |
| LSTM + FS + ST | 0.3109 | 0.2755 | 0.2859 | 0.2679 | 0.1677 | 0.2056 | 0.2522 |
| RF + FS + ST | 0.3771 | 0.3902 | 0.3561 | 0.2997 | 0.1984 | 0.2559 | 0.3129 |
| RF + FS + ST + WPD | 0.4358 | 0.4376 | 0.3997 | 0.3208 | 0.2110 | 0.3278 | 0.3555 |
| Seq2Seq + FS + ST + WPD | 0.5119 | 0.5005 | 0.4267 | 0.3329 | 0.2655 | 0.3792 | 0.4028 |
| Catboost + ST | 0.5134 | 0.5137 | 0.4215 | 0.3517 | 0.3287 | 0.4116 | 0.4234 |
| Catboost + ST + FS | 0.5264 | 0.5528 | 0.4293 | 0.3623 | 0.3319 | 0.4479 | 0.4418 |
| Catboost + ST + FS + WPD | 0.5672 | 0.5837 | 0.4370 | 0.3878 | 0.3536 | 0.4732 | 0.4671 |
| Catboost + ST + FS + WPD + noNWP | 0.449 | 0.341 | 0.269 | 0.188 | 0.109 | 0.165 | 0.2535 |
| Catboost + ST + FS + WPD + noOBS | 0.075 | 0.465 | 0.373 | 0.295 | 0.237 | 0.317 | 0.2937 |
| Method | ||||||
|---|---|---|---|---|---|---|
| 0.3109 | 0.3913 | 0.4755 | 0.5226 | 0.5337 | 0.4396 | |
| 0.3188 | 0.3991 | 0.4837 | 0.5316 | 0.5411 | 0.4549 | |
| 0.3229 | 0.4025 | 0.4869 | 0.5365 | 0.5469 | 0.4591 | |
| 0.3273 | 0.4088 | 0.4908 | 0.5447 | 0.553 | 0.4649 | |
| 0.3246 | 0.4053 | 0.4889 | 0.5414 | 0.5492 | 0.4619 | |
| 0.3238 | 0.4031 | 0.488 | 0.5377 | 0.5471 | 0.4599 |
| Method | Level 1 Dataset (1 Station) | Level 2 Dataset (5 Station) | Level 3 Dataset (10 Station) |
|---|---|---|---|
| RF | 39 s | 222 s | 724 s |
| LSTM | 1791 s | 8754 s | 37,774 s |
| Seq2Seq | 87,291 s | 897,654 s | 9,135,680 s |
| The proposed method | 37 s | 68 s | 118 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, D.; Diao, L.; Zang, Z.; Che, H.; Zhang, T.; Chen, X. A Machine-Learning Approach Combining Wavelet Packet Denoising with Catboost for Weather Forecasting. Atmosphere 2021, 12, 1618. https://doi.org/10.3390/atmos12121618
Niu D, Diao L, Zang Z, Che H, Zhang T, Chen X. A Machine-Learning Approach Combining Wavelet Packet Denoising with Catboost for Weather Forecasting. Atmosphere. 2021; 12(12):1618. https://doi.org/10.3390/atmos12121618
Chicago/Turabian StyleNiu, Dan, Li Diao, Zengliang Zang, Hongshu Che, Tianbao Zhang, and Xisong Chen. 2021. "A Machine-Learning Approach Combining Wavelet Packet Denoising with Catboost for Weather Forecasting" Atmosphere 12, no. 12: 1618. https://doi.org/10.3390/atmos12121618
APA StyleNiu, D., Diao, L., Zang, Z., Che, H., Zhang, T., & Chen, X. (2021). A Machine-Learning Approach Combining Wavelet Packet Denoising with Catboost for Weather Forecasting. Atmosphere, 12(12), 1618. https://doi.org/10.3390/atmos12121618





