Can the Aerosol Absorption Ångström Exponent Represent Aerosol Color in the Atmosphere: A Numerical Study
Abstract
1. Introduction
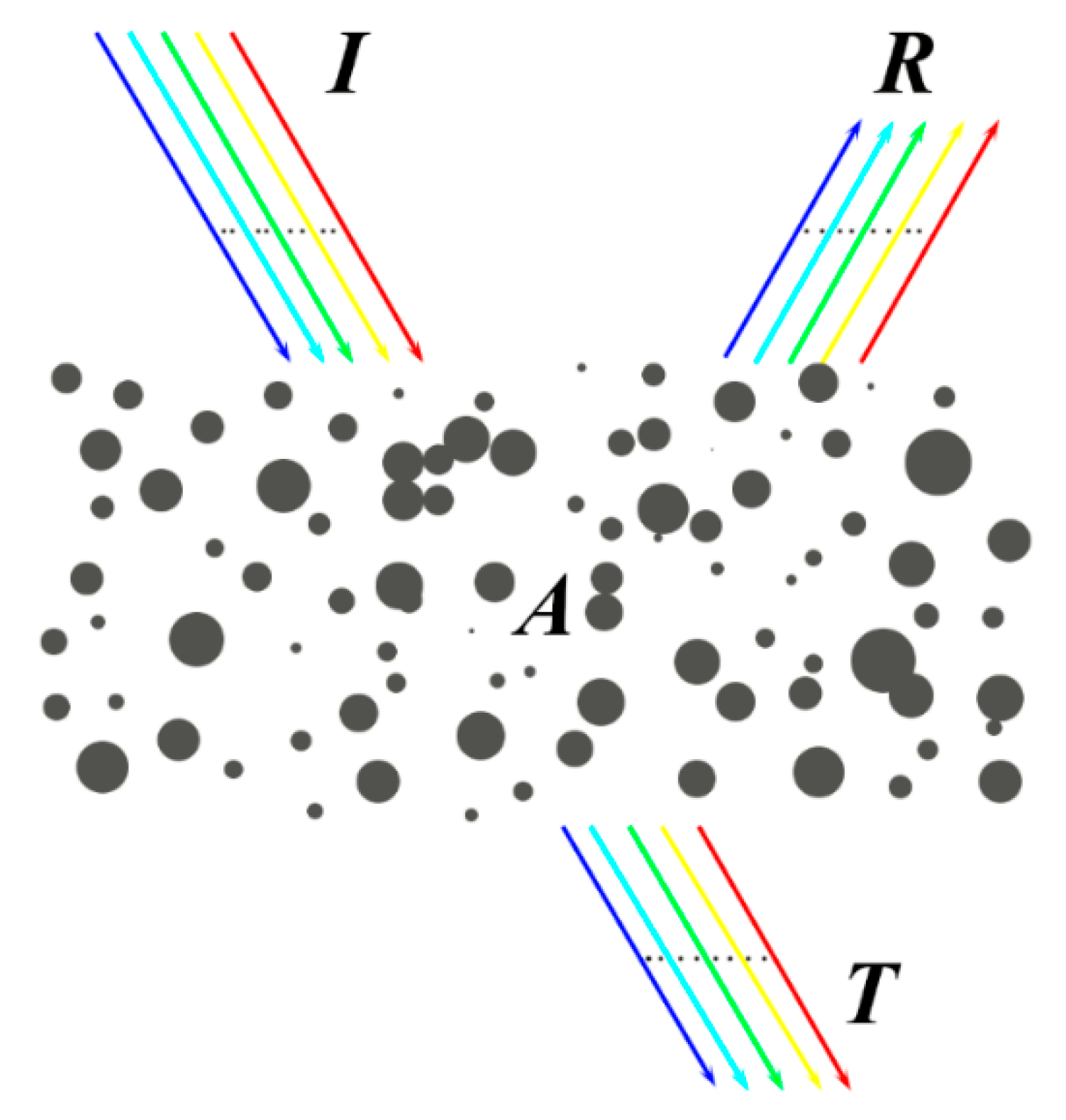
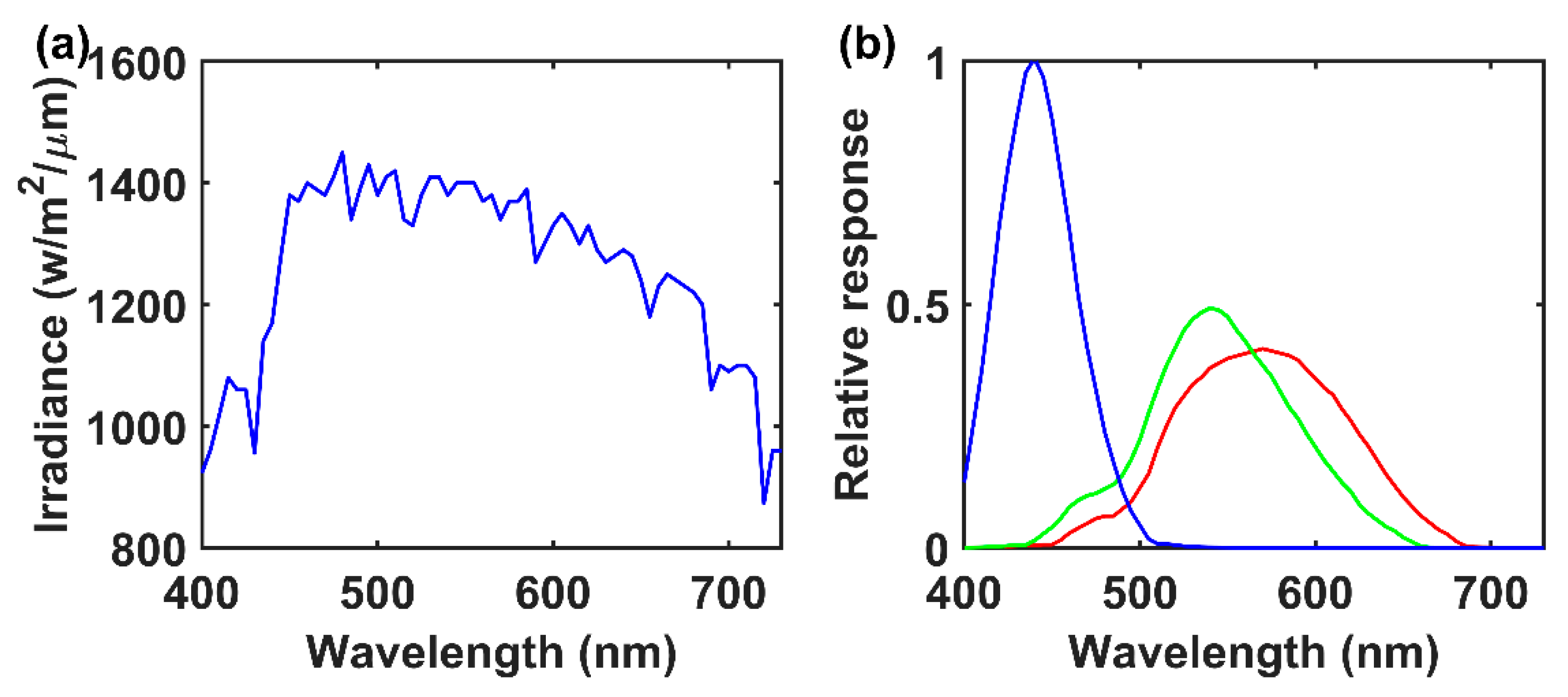
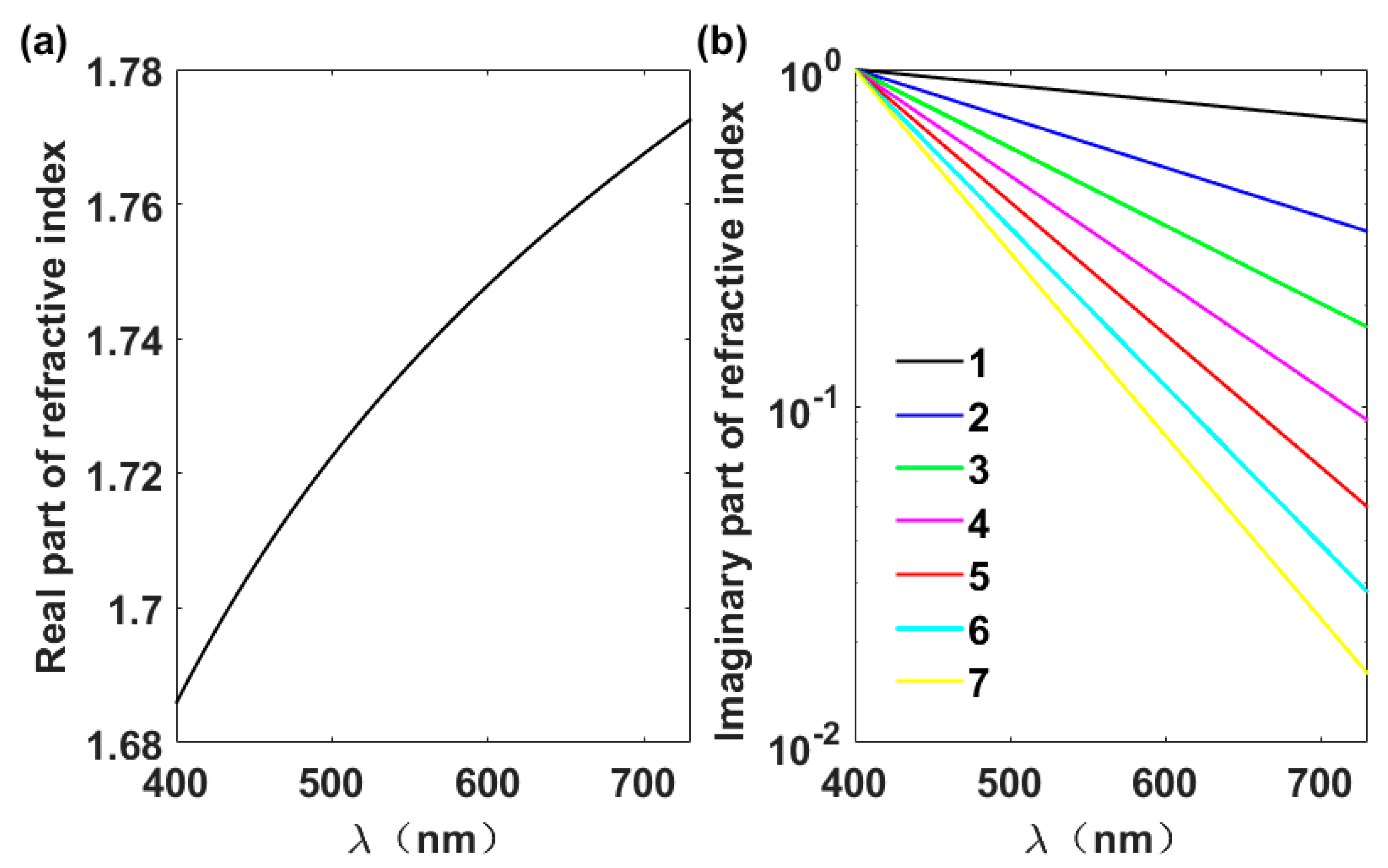
2. Improvement and Discussion of the Numerical Model for Color Simulation
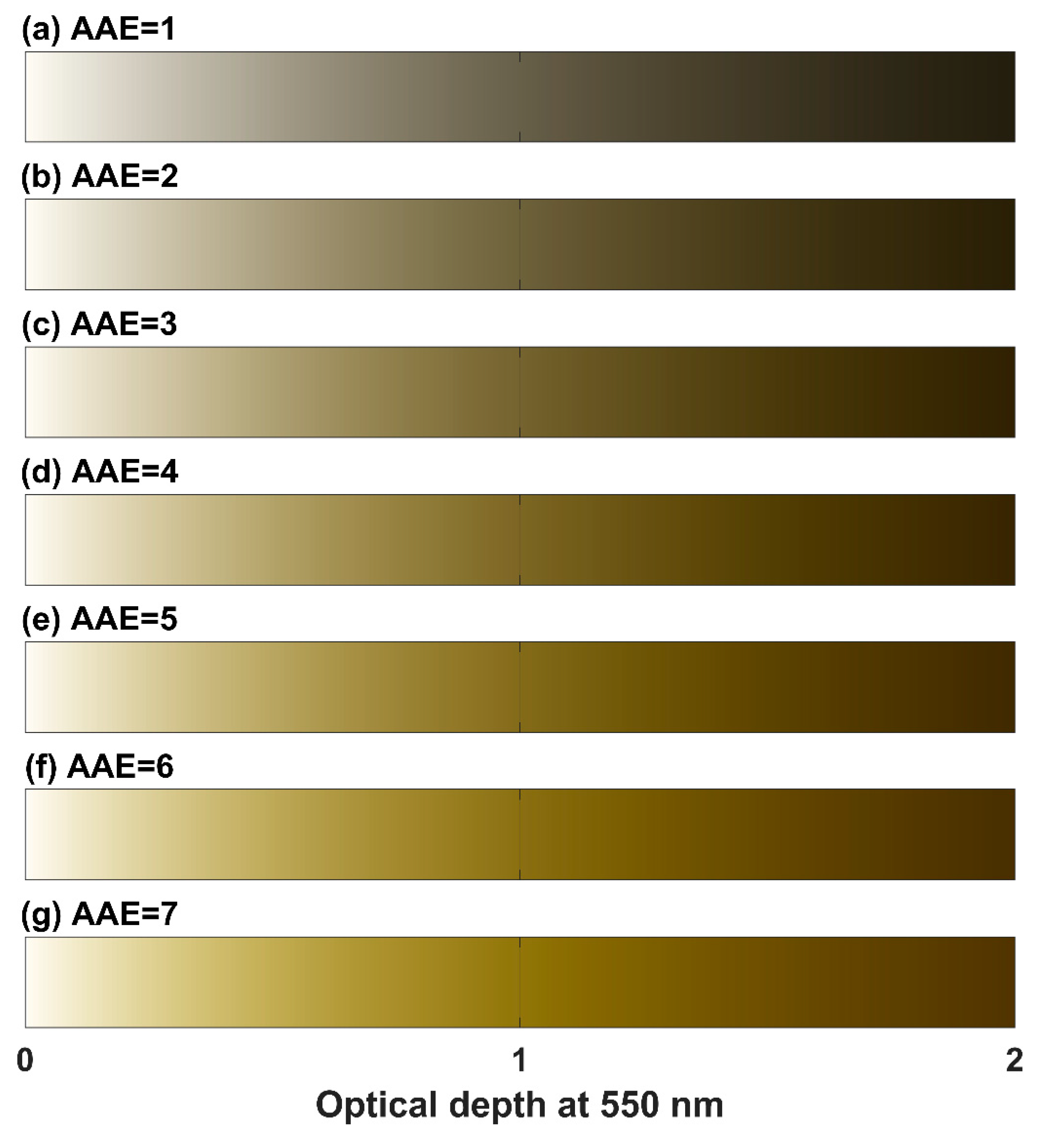
3. Is the AAE an Indicator of Aerosol Color?
4. Conclusions and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kaufman, Y.J.; Tanré, D.; Boucher, O. A satellite view of aerosols in the climate system. Nature 2002, 419, 215–223. [Google Scholar] [CrossRef] [PubMed]
- Twomey, S.A.; Piepgrass, M.; Wolfe, T.L. An assessment of the impact of pollution on global cloud albedo. Tellus B Chem. Phys. Meteorol. 2017, 36, 356–366. [Google Scholar] [CrossRef]
- Kirchstetter, T.W.; Novakov, T.; Hobbs, P.V. Evidence that the spectral dependence of light absorption by aerosols is affected by organic carbon. J. Geophys. Res. Atmos. 2004, 109, D21208. [Google Scholar] [CrossRef]
- Andreae, M.; Gelencsér, A. Black carbon or brown cabon? The nature of light-absorbing carbonaceous aerosols. Atmos. Chem. Phys. Discuss. 2006, 6, 3131–3148. [Google Scholar] [CrossRef]
- Sun, H.; Biedermann, L.; Bond, T.C. Color of brown carbon: A model for ultraviolet and visible light absorption by organic carbon aerosol. Geophys. Res. Lett. 2007, 34, 17. [Google Scholar] [CrossRef]
- Myhre, G. Consistency Between Satellite-Derived and Modeled Estimates of the Direct Aerosol Effect. Science 2009, 325, 187–190. [Google Scholar] [CrossRef]
- Russell, P.B.; Bergstrom, R.W.; Shinozuka, Y.; Clarke, A.D.; DeCarlo, P.F. Absorption Angstrom Exponent in AERONET and related data as an indicator of aerosol composition. Atmos. Chem. Phys. 2010, 10, 1155–1169. [Google Scholar] [CrossRef]
- Zhong, M.; Jang, M. Dynamic light absorption of biomass-burning organic carbon photochemically aged under natural sunlight. Atmos. Chem. Phys. 2014, 14, 1517–1525. [Google Scholar] [CrossRef]
- Liu, B.; Ma, Y.; Gong, W.; Zhang, M. Observations of aerosol color ratio and depolarization ratio over Wuhan. Atmos. Pollut. Res. 2017, 8, 1113–1122. [Google Scholar] [CrossRef]
- Oberlin, A. High-resolution TEM studies of carbonization and graphitization. Chem. Phys. Carbon. 1989, 22, 1. [Google Scholar]
- Dal Farra, A.; Kaspari, S.; Beach, J.; Bucheli, T.D.; Schaepman, M. Spectral signatures of submicron scale light-absorbing impurities in snow and ice using hyperspectral microscopy. J. Glaciol. 2018, 64, 377–386. [Google Scholar] [CrossRef]
- Schnaiter, M.; Linke, C.; Ibrahim, I.; Kiselev, A.; Waitz, F. Specifying the light-absorbing properties of aerosol particles in fresh snow samples, collected at the Environmental Research Station Schneefernerhaus (UFS), Zugspitze. Atmos. Chem. Phys. 2019, 19, 10829–10844. [Google Scholar] [CrossRef]
- Huang, J.; Fu, Q.; Zhang, W.; Wang, X.; Zhang, R. Dust and Black Carbon in Seasonal Snow Across Northern China. Bull. Am. Meteorol. Soc. 2011, 92, 175–181. [Google Scholar] [CrossRef]
- Liu, C.; Chung, C.E.; Zhang, F.; Yin, Y. The colors of biomass burning aerosols in the atmosphere. Sci. Rep. 2016, 6, 28267. [Google Scholar] [CrossRef] [PubMed]
- Jacobson, M.Z. Strong radiative heating due to the mixing state of black carbon in atmospheric aerosols. Nature 2001, 409, 695–697. [Google Scholar] [CrossRef] [PubMed]
- Bond, T.C.; Sun, H. Can Reducing Black Carbon Emissions Counteract Global Warming? Environ. Sci. Technol. 2005, 39, 5921–5926. [Google Scholar] [CrossRef]
- Ramanathan, V.; Carmichael, G.R. Global and regional climate changes due to black carbon. Nat. Geosci. 2008, 1, 221–227. [Google Scholar] [CrossRef]
- Scarnato, B.; Vahidinia, S.; Richard, D.; Kirchstetter, T. Effects of internal mixing and aggregate morphology on optical properties of black carbon using a discrete dipole approximation model. Atmos. Chem. Phys. 2013, 13, 5089–5101. [Google Scholar] [CrossRef]
- Dubovik, O.; Holben, B.; Eck, T.F.; Smirnov, A.; Kaufman, Y.J. Variability of absorption and optical properties of key aerosol types observed in worldwide locations. J. Atmos. Sci. 2002, 59, 590–608. [Google Scholar] [CrossRef]
- Soni, K.; Singh, S.; Bano, T.; Tanwar, R.S.; Nath, S. Wavelength Dependence of the Aerosol Angstrom Exponent and Its Implications Over Delhi, India. Aerosol Sci. Technol. 2011, 45, 1488–1498. [Google Scholar] [CrossRef]
- Toledano, C.; Cachorro, V.E.; Berjon, A.; Frutos, A.M.D.; Sorribas, M. Aerosol optical depth and Ångström exponent climatology at El Arenosillo AERONET site (Huelva, Spain). Q. J. R. Meteorol. Soc. 2010, 133, 795–807. [Google Scholar] [CrossRef]
- Reid, J.G.; Eck, T.F.; Christopher, S.A.; Hobbs, P.V.; Holben, B.N. Use of the Ångstrom exponent to estimate the variability of optical and physical properties of aging smoke particles in Brazil. J. Geophys. Res. 1999, 104, 27473–27489. [Google Scholar] [CrossRef]
- Chung, C.E.; Lee, K.; Muller, D. Effect of internal mixture on black carbon radiative forcing. Tellus B 2012, 64, 10925. [Google Scholar] [CrossRef]
- Liu, C.; Chung, C.E.; Yin, Y.; Schnaiter, M. The absorption Ångström exponent of black carbon: From numerical aspects. Atmos. Chem. Phys. 2018, 18, 6259–6273. [Google Scholar] [CrossRef]
- Chang, H.; Charalampopoulos, T.T. Determination of the Wavelength Dependence of Refractive Indices of Flame Soot. Proc. R. Soc. A Math. Phys. Eng. Sci. 1990, 430, 577–591. [Google Scholar]
- He, C.; Liou, K.-N.; Takano, Y.; Zhang, R.; Levy Zamora, M. Variation of the radiative properties during black carbon aging: Theoretical and experimental intercomparison. Atmos. Chem. Phys. 2015, 15, 11967–11980. [Google Scholar] [CrossRef]
- China, S.; Scarnato, B.; Owen, R.C.; Zhang, B.; Ampadu, M.T. Morphology and mixing state of aged soot particles at a remote marine free troposphere site: Implications for optical properties. Geophys. Res. Lett. 2015, 42, 1243–1250. [Google Scholar] [CrossRef]
- Mie, G. Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen. Ann. Phys. 1908, 330, 377–445. [Google Scholar] [CrossRef]
- Johnson, N.L.; Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions; Houghton Mifflin: Boston, MA, USA, 1970. [Google Scholar]
- Reddington, C.L.; McMeeking, G.; Mann, G.W.; Coe, H.; Frontoso, M.G. The mass and number size distributions of black carbon aerosol over Europe. Atmos. Chem. Phys. 2013, 13, 4917–4939. [Google Scholar] [CrossRef]
- Meador, W.; Weaver, W. Two-stream approximations to radiative transfer in planetary atmospheres: A unified description of existing methods and a new improvement. J. Atmos. Sci. 1980, 37, 630–643. [Google Scholar] [CrossRef]
- Ricchiazzi, P.; Yang, S.; Gautier, C.; Sowle, D. SBDART: A research and teaching software tool for plane-parallel radiative transfer in the Earth’s atmosphere. Bull. Am. Meteorol. Soc. 1998, 79, 2101–2114. [Google Scholar] [CrossRef]
- Young, T. The Bakerian lecture. On the mechanism of the eye. Philos. Trans. R. Soc. London 1801, 91, 23–88. [Google Scholar]
- Falk, D.R.; Brill, D.R.; Stork, D.G. Seeing the light: Optics in nature, photography, color, vision, and holography. In Seeing the Light: Optics in Nature, Photography, Color, Vision, and Holography; Falk, D.R., Brill, D.R., Stork, D.G., Eds.; Wiley-VCH: Weinheim, Germany, 1985; p. 480. ISBN 0-471-60385-6. [Google Scholar]
- Qin, S.; Tang, J.; Wen, Y. Black carbon and its importance in climate change studies. Meteorol. Mon. 2001, 27, 3–7. (In Chinese) [Google Scholar]
- Chakrabarty, R.K.; Moosmüller, H.; Garro, M.A.; Arnott, W.P.; Walker, J. Emissions from the laboratory combustion of wildland fuels: Particle morphology and size. J. Geophys. Res. Atmos. 2006, 111, D7. [Google Scholar] [CrossRef]
- Schmidt, A.F.; Finan, C. Linear regression and the normality assumption. J. Clin. Epidemiol. 2018, 98, 146–151. [Google Scholar] [CrossRef]
- Schnaiter, M.; Horvath, H.; Möhler, O.; Naumann, K.-H.; Saathoff, H. UV-VIS-NIR spectral optical properties of soot and soot-containing aerosols. J. Aerosol Sci. 2003, 34, 1421–1444. [Google Scholar] [CrossRef]
- D’Almeida, G.A.; Koepke, P.; Shettle, E.P. Atmospheric Aerosols: Global Climatology and Radiative Characteristics; A Deepak Pub: Hampton, VA, USA, 1991; p. 561. [Google Scholar]
- Liu, C.; Xu, X.; Yin, Y.; Schnaiter, M.; Yung, Y.L. Black carbon aggregates: A database for optical properties. J. Quant. Spectrosc. Radiat. Transf. 2019, 222, 170–179. [Google Scholar] [CrossRef]
- Lewis, K.; Arnott, W.P.; Moosmüller, H.; Wold, C.E. Strong spectral variation of biomass smoke light absorption and single scattering albedo observed with a novel dual-wavelength photoacoustic instrument. J. Geophys. Res. Atmos. 2008, 113, D16203. [Google Scholar] [CrossRef]
- Schuster, G.L.; Dubovik, O.; Holben, B.N. Angstrom exponent and bimodal aerosol size distributions. J. Geophys. Res. 2006, 111, D07207. [Google Scholar] [CrossRef]
- Li, J.; Liu, C.; Yin, Y.; Kumar, K.R. Numerical investigation on the Ångström exponent of black carbon aerosol. J. Geophys. Res. Atmos. 2016, 121, 3506–3518. [Google Scholar] [CrossRef]
- Dubovik, O.; Holben, B.; Kaufman, Y.; Yamasoe, M.; Smirnov, A. Single-scattering albedo of smoke retrieved from the sky radiance and solar transmittance measured from ground. J. Geophys. Res. Atmos. 1998, 103, 31903–31923. [Google Scholar] [CrossRef]
- Bond, T.C.; Bussemer, M.; Wehner, B.; Keller, S.; Charlson, R. Light absorption by primary particle emissions from a lignite burning plant. Environ. Sci. Technol. 1999, 33, 3887–3891. [Google Scholar] [CrossRef]
- Lawless, P.A.; Rodes, C.E.; Ensor, D.S. Multiwavelength absorbance of filter deposits for determination of environmental tobacco smoke and black carbon. Atmos. Environ. 2004, 38, 3373–3383. [Google Scholar] [CrossRef]
- Bond, T.C.; Bergstrom, R.W. Light absorption by carbonaceous particles: An investigative review. Aerosol Sci. Technol. 2006, 40, 27–67. [Google Scholar] [CrossRef]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Bergstrom, R. Extinction and absorption coefficients of the atmospheric aerosol as a function of particle size. Contr. Atmos. Phys. 1973, 46, 223–234. [Google Scholar]
- Schnaiter, M.; Schmid, O.; Petzold, A.; Fritzsche, L.; Klein, K. Measurement of wavelength-resolved light absorption by aerosols utilizing a UV-VIS extinction cell. Aerosol Sci. Technol. 2005, 39, 249–260. [Google Scholar] [CrossRef]
- Schmid, O.; Artaxo, P.; Arnott, W.; Chand, D.; Gatti, L.V. Spectral light absorption by ambient aerosols: Influenced by biomass burning in the Amazon Basin. I: Comparison and field calibration of absorption measurement techniques. Atmos Chem. Phys. 2006, 6, 3443–3462. [Google Scholar] [CrossRef]
- Lindberg, J.D.; Douglass, R.E.; Garvey, D.M. Carbon and the optical properties of atmospheric dust. Appl. Opt. 1993, 32, 6077–6081. [Google Scholar] [CrossRef]
- Hoffer, A.; Gelencsér, A.; Guyon, P.; Kiss, G.; Schmid, O. Optical properties of humic-like substances (HULIS) in biomass-burning aerosols. Atmos Chem. Phys. 2006, 6, 3563–3570. [Google Scholar] [CrossRef]
- Phillips, S.M.; Smith, G.D. Spectroscopic comparison of water-and methanol-soluble brown carbon particulate matter. Aerosol Sci. Technol. 2017, 51, 1113–1121. [Google Scholar] [CrossRef]
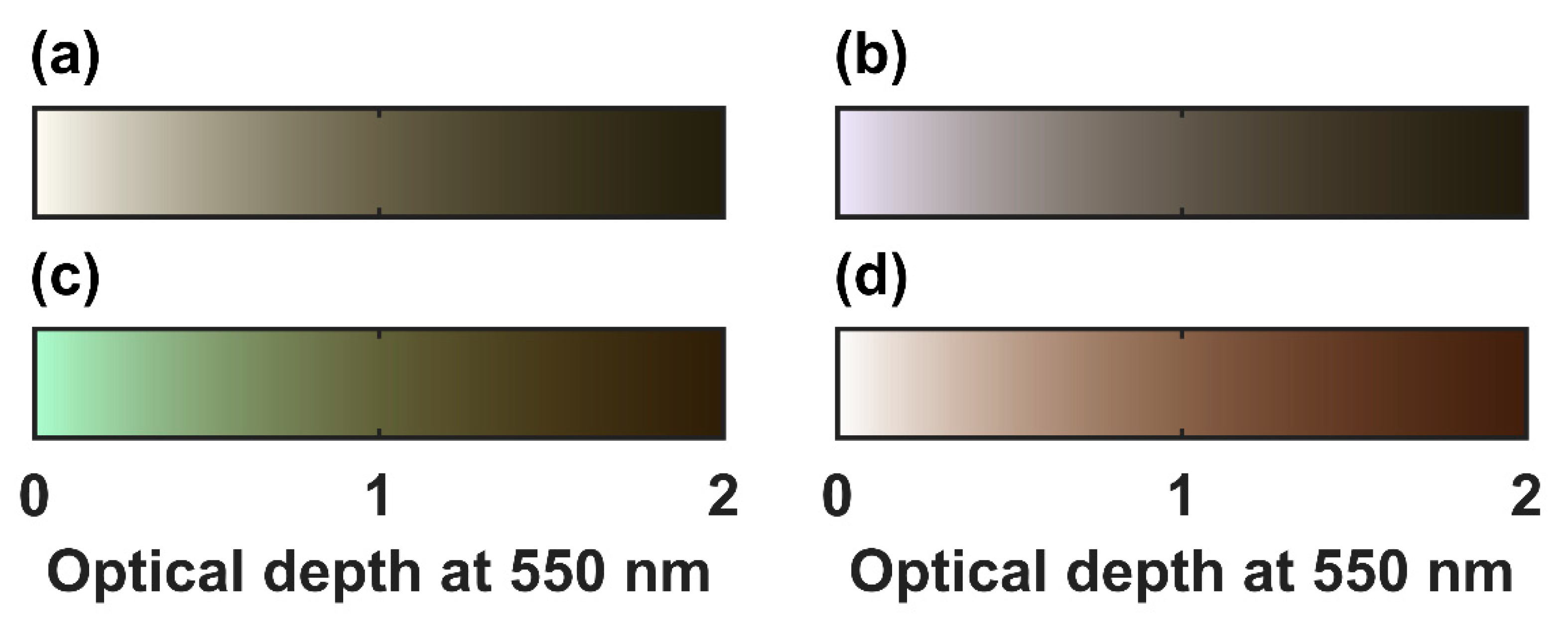
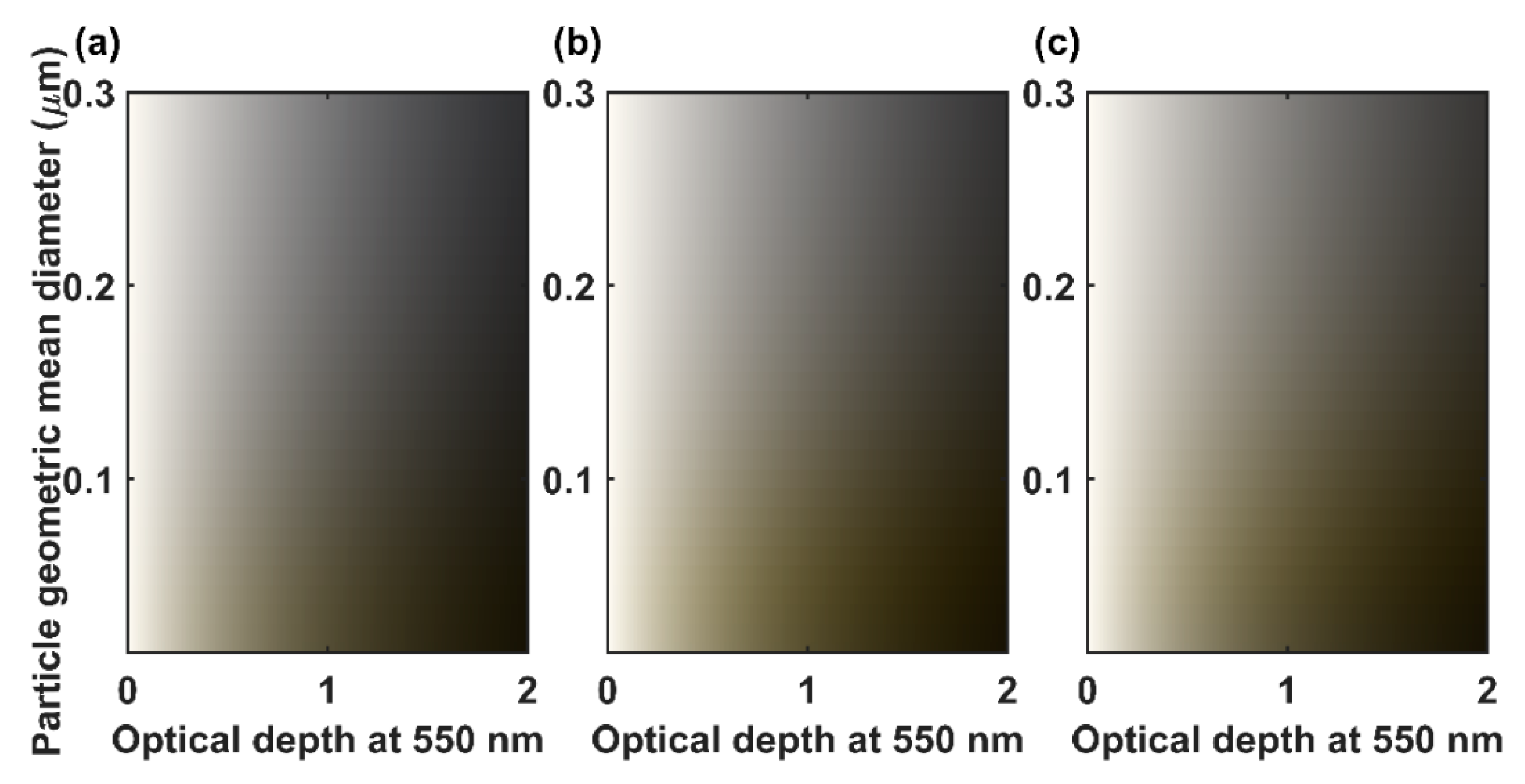
| Relation between (b) and (a) | Relation between (c) and (a) | Relation between (d) and (a) | |
|---|---|---|---|
| regression equation | R: β = 0.93, ε = 1 × 10−4 | R: β = 0.77, ε = 1 × 10−2 | R: β = 0.99, ε = 1 × 10−2 |
| G: β = 0.92, ε = 1 × 10−4 | G: β = 1.01, ε = −6 × 10−4 | G: β = 1.01, ε = −5 × 10−4 | |
| B: β = 1.04, ε = −1 × 10−4 | B: β = 0.84, ε = −6 × 10−4 | B: β = 1.04, ε = −8 × 10−4 |
| AAE | ||||||
|---|---|---|---|---|---|---|
| 1 | 0.20 | 0.90 | 0.83 | 0.42 | 0.09 | 0.23 |
| 2 | 0.20 | 1.20 | 0.83 | 0.32 | 0.17 | 0.44 |
| 3 | 0.18 | 1.30 | 0.85 | 0.30 | 0.21 | 0.58 |
| 4 | 0.16 | 1.45 | 0.87 | 0.27 | 0.23 | 0.68 |
| 5 | 0.13 | 1.55 | 0.90 | 0.27 | 0.23 | 0.74 |
| 6 | 0.10 | 1.60 | 0.93 | 0.27 | 0.20 | 0.78 |
| 7 | 0.09 | 1.65 | 0.94 | 0.29 | 0.20 | 0.80 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, D.; Yin, Y.; Liu, C.; Lu, C.; Xu, X. Can the Aerosol Absorption Ångström Exponent Represent Aerosol Color in the Atmosphere: A Numerical Study. Atmosphere 2020, 11, 187. https://doi.org/10.3390/atmos11020187
Zhao D, Yin Y, Liu C, Lu C, Xu X. Can the Aerosol Absorption Ångström Exponent Represent Aerosol Color in the Atmosphere: A Numerical Study. Atmosphere. 2020; 11(2):187. https://doi.org/10.3390/atmos11020187
Chicago/Turabian StyleZhao, Dapeng, Yan Yin, Chao Liu, Chunsong Lu, and Xiaofeng Xu. 2020. "Can the Aerosol Absorption Ångström Exponent Represent Aerosol Color in the Atmosphere: A Numerical Study" Atmosphere 11, no. 2: 187. https://doi.org/10.3390/atmos11020187
APA StyleZhao, D., Yin, Y., Liu, C., Lu, C., & Xu, X. (2020). Can the Aerosol Absorption Ångström Exponent Represent Aerosol Color in the Atmosphere: A Numerical Study. Atmosphere, 11(2), 187. https://doi.org/10.3390/atmos11020187






