iDMaTraj: Improved Diffusion Mamba Model for Stochastic Pedestrian Trajectory Prediction

Abstract

Trajectory prediction constitutes a key technology for intelligent systems to forecast future movements of dynamic agents, yet it faces significant challenges due to the uncertainty of motion behavior. We propose iDMa, a stochastic trajectory prediction framework that pioneers the integration of diffusion model with Mamba architecture to achieve high-precision and high-efficiency trajectory generation. Our approach introduces two key innovations: (1) a dual-parameter learning mechanism that optimizes noise estimation of mean and variance space, unlike conventional diffusion methods that employ fixed variance during the denoising process, so as to constrain the feasible domain more accurately; (2) a hybrid denoising backbone network that incorporates Transformer encoders and Mamba blocks. Compared to existing state-of-the-art methods, iDMa reduces the average displacement error (ADE) by 4.76% (0.20 vs. 0.21) on the ETH-UCY dataset and 1.85% (7.95 vs. 8.10) on the SDD dataset.

1. Introduction

Trajectory prediction is a critical task for understanding target motion intent, with wide applications in pedestrian  [1,2], vehicle [3,4] and drone [5] tracking scenarios. The accurate prediction of target future motion paths remains challenging, primarily due to the high uncertainty of movement intentions, which gives rise to multiple plausible trajectories, and the dynamic interaction between targets and their environment, which further amplifies trajectory randomness.

Over the past few decades, trajectory prediction methods have evolved from traditional statistical models [6,7,8] to deep learning-based approaches. Recurrent neural networks [9,10,11] excel at temporal dependency modeling but ignore spatial interactions, and while subsequent studies introduced attention mechanisms [12,13,14,15] to enhance spatial relationship capture, this improvement came with higher model complexity and computational overhead; graph-based methods [16,17,18,19,20,21,22] capture social interactions yet have limitations in capturing temporal dynamics. Generative models such as GANs [23,24,25,26,27] and VAEs [28,29,30] have made progress in multi-modality modeling, with GAN-based methods capable of generating diverse trajectories but suffering from unstable training processes, and VAE-based methods featuring more stable training while often struggling to ensure prediction accuracy for complex trajectories such as those with sharp curvature or highly nonlinear shapes.

In recent years, denoising diffusion probabilistic models (DDPMs) have offered a new direction for time series prediction due to their stable training process and powerful ability to generate samples. Studies like [31,32] are pioneers to introduce diffusion models into time series prediction tasks. Early works like MID [33], LED [34] and MLD [35] have applied diffusion models to trajectory prediction, but still struggle with high computational cost and limited ability to model dynamic interactions. Furthermore, the single-parameter mean estimation approach adopted by these methods struggles to characterize multimodal distribution patterns effectively. In scenarios with high uncertainty, they persistently generate deterministic mean trajectories, which can result in misjudgments for downstream decision-making tasks. To address these challenges, we propose a novel framework named Improved Diffusion Mamba (iDMa), which employs an enhanced diffusion modeling strategy. In particular, we introduce a dual-parameter learning mechanism that incorporates a variance branch, enabling explicit modeling of multimodal distributions and reliable uncertainty calibration. Moreover, the proposed framework integrates an advanced Mamba architecture as the backbone of the denoising model, further enhancing prediction performance.

Specifically, the proposed iDMa framework introduces an innovative dual-parameter learning mechanism in the Markov chain process. Unlike standard diffusion models that only predict the mean, this framework learns both mean and variance parameters at the same time during denoising. The variance learning strategy dynamically modulates the output variance based on the multimodal properties of observed trajectories. It elevates variance when multiple plausible future paths exist and maintains low variance for highly deterministic trajectories, thereby balancing multimodal coverage and prediction accuracy. For uncertainty calibration, the learned variance exhibits a positive correlation with actual prediction errors. Low variance corresponds to high-confidence scenarios while high variance signals ambiguous scenarios and quantifies elevated prediction risk. This design endows the iDMa framework with built-in uncertainty awareness, enabling it to self-assess prediction reliability. This capability is critical for stochastic trajectory prediction tasks, as it addresses core challenges related to multimodality and uncertainty quantification that standard diffusion models fail to resolve. To reduce model parameters while keeping good performance, and considering the selection mechanism in Mamba, we design a hybrid denoising backbone network called T-Mamba. By integrating a Transformer encoder with Mamba [36] block, the model significantly enhances its capability to model the noise distribution of trajectory data. Theoretical analysis demonstrates that the framework can stably converge to the optimal solution. Experiments on the ETH-UCY [37,38] and Stanford Drone (SDD) [39] datasets confirm that iDMa performs much better than existing top methods in short-term trajectory prediction tasks. All experimental data used is based on 2D trajectories taken from image sequences. This paper’s main contributions are as follows:

1.

Our iDMa framework introduces a new dual-parameter learning method during the diffusion process that fundamentally extends conventional diffusion models through simultaneous mean-variance optimization. This paradigm shift enables (1) probabilistically tighter trajectory bounds via KL-optimal noise matching, and (2) physically plausible prediction spaces through variance-constrained sampling;

2.

We design a hybrid denoising network for the denoising process that combines Transformer encoders with Mamba blocks, specifically engineered to capture both the fine-grained local details within the data and the broader, global connections between all points in a trajectory. The two components work together to create a more powerful representation of the path data.

2. Related Works

2.1. Stochastic Trajectory Prediction

Stochastic trajectory prediction aims to forecast an agent’s future motion trajectory based on its historical movement. Most current methods use an encoder–decoder framework. The encoder gathers multi-source information such as the target’s own history, interactive behaviors with neighbors even scene map [40]. For temporal modeling, models like RNNs [41], LSTMs [10], GRUs [42], and Transformers [13,43] are commonly used. As for social modeling, specialized networks like SGCN [18], STAR [16], Trajectron++ [9], and GroupNet [19] have been developed. Finally, the decoder integrates these encoded features to generate final trajectory predictions. However, this common framework has the following clear limitations in dealing with complex trajectory distributions: (1) The training process can be unstable [23,24], and (2) the generated samples may lack diversity [29,30]. In contrast, methods based on diffusion models can generate more diverse and realistic paths through a step-by-step noise removal process, while exhibiting better stability during training. This demonstrates the great potential of diffusion models for trajectory prediction.

2.2. Denoising Diffusion Probabilistic Models

Denoising Diffusion Probabilistic Models (DDPMs) [44,45,46] are inspired by the particle diffusion process in non-equilibrium thermodynamics. The core idea is to gradually add noise to the original data until it converges to a noise-dominated distribution, and then use a reparameterized Markov chain to reconstruct the data. By learning to remove the noise, the model captures underlying structural dependencies, enabling the generation of highly realistic and diverse samples. Methods such as MID [33], LED [34], and SingularTrajectory [47] follow the basic DDPM [45] framework to refine the initially uncertain feasible region into a deterministic trajectory distribution. However, these methods use a fixed variance strategy during denoising, overlooking its importance. Research [48] indicates that properly adjusting the variance, especially in the early stages of denoising, is crucial for accurate data reconstruction. Therefore, we propose a new dual-parameter training mechanism that dynamically adapts the variance throughout the denoising process, which is integrated into our framework to improve the quality of the generated trajectories.

2.3. Mamba in Trajectory Prediction

Mamba [36] is recognized for its ability to handle long-range dependencies, which relies on a structured State Space Model (SSM) [49] mechanism that offers excellent memory and computational efficiency, thereby improving both its practicality and performance. Hippo [50] represents a key contribution to SSMs, establishing their effectiveness in long-sequence modeling tasks. Subsequent research [51] further refined the underlying mechanisms of SSMs by introducing a selective mechanism, leading to significant performance improvements. In time series tasks, Mamba-based approaches [52,53] have shown clear advantages, providing a theoretical basis for the stochastic trajectory prediction method studied in this paper.

For trajectory prediction tasks, Mamba-based methods [54,55] focus more on modeling the long-range dependencies of individual trajectories, lacking an explicit mechanism to model global correlations between multiple trajectories. In complex scenes, using Mamba alone will make it difficult to accurately capture group social interaction patterns, resulting in predicted trajectories that violate social common sense. In contrast, the self-attention mechanism of Transformer can directly calculate the dependency weights between any two agents, thereby explicitly modeling the correlation between trajectories of different individuals. This feature provides indispensable global social constraints for the denoising process of DDPM [45], ensuring that the generated trajectories conform to group behavior logic. On the other hand, in terms of functionality, when the Transformer-based MID [33] method extracts trajectory spatiotemporal features, it is prone to introducing redundant social interaction noise. Although the attention stacking strategy it adopts can mitigate this defect, the resulting computational burden has become a new problem to be solved. To address the above issues, this paper adopts a Transformer-Mamba fusion strategy and proposes a T-Mamba block. First, the attention mechanism of Transformer is leveraged to capture social interactions among agents and local temporal dependencies of individual agents. Then, Mamba adaptively captures the long-range dependencies of trajectory sequences to filter out local noise, enhance temporal consistency, and reduce computational overhead, thus achieving complementary advantages between the two.

Notably, Mamba has not been fully explored in the field of pedestrian stochastic trajectory prediction. This paper integrates the diffusion model architecture with Mamba for stochastic trajectory prediction tasks, and systematic experiments demonstrate that the proposed method effectively improves prediction accuracy while maintaining computational efficiency.

3. Method

3.1. Architecture

Trajectory prediction refers to the task of inferring an object’s future trajectory given its observed historical trajectory within a known time window. Mathematically, given a set of target objects to be predicted, let the 2D coordinates of target i at time t be denoted as ${\mathbf{x}}_t^i\in {\mathbb{R}}^2$ For the observation period $t\in [1,T_{\mathrm{obs}}]$, the historical trajectory of target i is represented as ${\mathbf{X}}_{1:T_{\mathrm{obs}}}^i=\left[{\mathbf{x}}_1^i,{\mathbf{x}}_2^i,\dots ,{\mathbf{x}}_{T_{\mathrm{obs}}}^i\right]$, while the collective historical trajectories of N targets are denoted as ${\mathbf{X}}_{1:T_{\mathrm{obs}}}={\left\{{\mathbf{X}}_{1:T_{\mathrm{obs}}}^i\right\}}_{i=1}^N$. Correspondingly, for the future period $t\in \left[T_{\mathrm{obs}+1},T_{\mathrm{fut}}\right]$, the future trajectory of target i is expressed as ${\mathbf{Y}}_{T_{\mathrm{obs}}+1:T_{\mathrm{fut}}}^i=\left[{\mathbf{x}}_{T_{\mathrm{obs}}+1}^i,{\mathbf{x}}_{T_{\mathrm{obs}}+2}^i,\dots ,{\mathbf{x}}_{T_{\mathrm{fut}}}^i\right]$, and the future trajectories of all N targets are represented as ${\mathbf{Y}}_{T_{\mathrm{obs}}+1:T_{\mathrm{fut}}}={\left\{{\mathbf{Y}}_{T_{\mathrm{obs}}+1:T_{\mathrm{fut}}}^i\right\}}_{i=1}^N$. For notational simplicity, we hereafter use $\mathbb{X}$ and $\mathbb{Y}$ to denote the historical and future trajectories, respectively.

This paper proposes an iDMa framework for stochastic trajectory prediction, which conceptualizes the ambiguous future motion area as isotropic Gaussian noise and refines it step-by-step through a denoising process to generate deterministic trajectory distribution. The overall architecture is illustrated in Figure 1a. Within this framework, the model takes observed historical trajectory and target’s motion states as inputs, generating multiple trajectory samples during inference. The output samples $\widehat{\mathbb{Y}}={\left\{{\widehat{\mathbb{Y}}}^k\right\}}_{k=1}^K$ are guaranteed to include at least one sample that closely approximates the ground-truth (GT) future trajectory. The following sections provide detailed mathematical formulations of the forward noise diffusion process and the reverse denoising inference procedure in our framework.

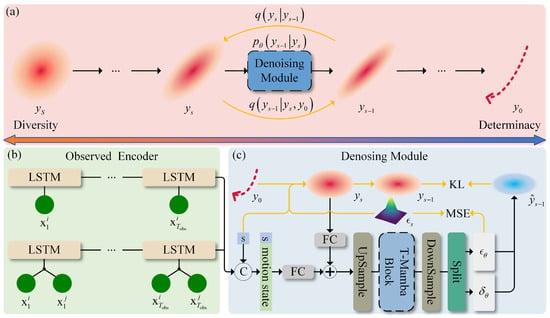
Figure 1. The iDMa framework. (a) Overall architecture; (b) Encoder: Target’s trajectory feature learning; (c) Decoder: Denoising at step s (training and inference). Yellow arrows indicate training-phase-only operations.

We formally describe the noise diffusion and denoising processes in the iDMa framework as follows. To model the uncertainty in future motion patterns, we formulate a progressive noise injection mechanism through a forward diffusion process q. This process gradually corrupts the GT future trajectory $y_0=\mathbb{Y}$ by adding isotropic Gaussian noise ${ϵ}_s\sim \mathcal{N}\left(\mathbf{0},{\beta }_s\mathbf{I}\right)$ according to a linear noise schedule [45], generating a sequence of latent variables $[y_1,y_2,\dots ,y_S]$. The diffusion process can be formally expressed as

$$\begin{array}{cc}\hfill q(y_S\mid y_0)& :=\prod _{s=1}^{S}q(y_s\mid y_{s-1}),\hfill \\ \hfill q(y_s\mid y_{s-1})& :=\mathcal{N}\left(y_s;\sqrt{1-{\beta }_s}{y}_{s-1},{\beta }_s\mathbf{I}\right)\hfill \end{array}$$

(1)

Leveraging the additive property of Gaussian distributions, we can derive a closed-form sampling equation for any step of the diffusion process:

$$q(y_s\mid y_0)=\mathcal{N}\left(y_s;\sqrt{{\overline{\alpha }}_s}{y}_0,(1-{\overline{\alpha }}_s)\mathbf{I}\right)$$

(2)

where ${\alpha }_s:=1-{\beta }_s$, ${\overline{\alpha }}_s:={\prod }_{\ell =0}^s{\alpha }_{\ell }$. Based on Bayesian theorem, we can derive the posterior distribution of the reverse process. Let $q\left(y_{s-1}\right|y_s,y_0)\sim \mathcal{N}\left(y_s-1;\tilde{\mu }(y_s,y_0),{\tilde{\beta }}_s\mathbf{I}\right)$ denote the posterior distribution of the latent variable at the previous step given the noisy motion region $y_s$ and the desired trajectory $y_0$. This posterior follows a Gaussian distribution, with its mean and variance expressed as

$$\begin{array}{cc}\hfill {\tilde{\mu }}_s(y_s,y_0)& ={\displaystyle \frac{\sqrt{{\overline{\alpha }}_{s-1}}{\beta }_s}{1-{\overline{\alpha }}_s}}{y}_0+{\displaystyle \frac{\sqrt{{\alpha }_s}(1-{\overline{\alpha }}_{s-1})}{1-{\overline{\alpha }}_s}}{y}_s,\hfill \\ \hfill {\tilde{\beta }}_s& ={\displaystyle \frac{1-{\overline{\alpha }}_{s-1}}{1-{\overline{\alpha }}_s}}{\beta }_s\hfill \end{array}$$

(3)

The derived posterior mean and variance establish a theoretical foundation for the denoising process, enabling the reparameterization of the posterior distribution through neural networks to progressively recover the desired motion trajectory from noise.

The mitigation of future motion uncertainty is conceptualized as the inverse process within diffusion models. Provided with an initial uncertain motion region $y_S$ and objective historical motion state information $\mathbf{f}$, the intended motion trajectory generation process is formally characterized as a Markov chain:

$$\begin{array}{cc}\hfill p_{\theta }(y_{0:S}\mid \mathbf{f})& :=p\left(y_S\right)\prod _{s=1}^S{p}_{\theta }(y_{s-1}\mid y_s,\mathbf{f}),\hfill \\ \hfill p_{\theta }(y_{s-1}\mid y_s,\mathbf{f})& :=\mathcal{N}\left(y_{s-1};{\mu }_{\theta }(y_s,\mathbf{f}),{\mathrm{\Sigma }}_{\theta }(y_s,\mathbf{f})\mathbf{I}\right)\hfill \end{array}$$

(4)

where $p\left(y_S\right)\sim \mathcal{N}(\mathbf{0},\mathbf{I})$ denotes the initial noise distribution and $\theta$ represents the learnable parameters of the diffusion model. During the denoising process, the mean ${\mu }_{\theta }$ and variance ${\mathrm{\Sigma }}_{\theta }$ of the predicted noise distribution at each step are derived via reparameterization, utilizing the noise ${ϵ}_{\theta }$ and the control variable ${\delta }_{\theta }$ generated by the deep learning backbone network, as follows:

$$\begin{array}{cc}\hfill {\mu }_{\theta }(y_s,\mathbf{f})& ={\displaystyle \frac{1}{\sqrt{{\alpha }_s}}}\left(y_s-{\displaystyle \frac{{\beta }_s}{\sqrt{1-{\overline{\alpha }}_s}}}{ϵ}_{\theta }(y_s,\mathbf{f})\right),\hfill \\ \hfill {\mathrm{\Sigma }}_{\theta }(y_s,\mathbf{f})& =exp\left({\delta }_{\theta }(y_s,\mathbf{f})log{\beta }_s+\left(1-{\delta }_{\theta }(y_s,\mathbf{f})\right)log{\tilde{\beta }}_s\right)\hfill \end{array}$$

(5)

3.2. Training Objective

To train an iDMa model for accurate modeling of future trajectory, we optimize the model parameters by minimizing the divergence between the latent distribution in the denoising process and the true posterior distribution. Specifically, we adopt a variational inference strategy to maximize the following evidence lower bound (ELBO):

$$\begin{array}{cc}\hfill {\mathcal{L}}_{\mathrm{vlb}}& :={\mathcal{L}}_0+{\mathcal{L}}_1+\cdots +{\mathcal{L}}_{S-1}+{\mathcal{L}}_S,\hfill \\ \hfill {\mathcal{L}}_0& :=-log{p}_{\theta }(y_0\mid y_1,\mathbf{f}),\hfill \\ \hfill {\mathcal{L}}_{s-1}& :=D_{\mathrm{KL}}\left(q(y_{s-1}\mid y_s,y_0)\parallel p_{\theta }({\widehat{y}}_{s-1}\mid y_s,\mathbf{f})\right),\hfill \\ \hfill {\mathcal{L}}_S& :=D_{\mathrm{KL}}\left(q(y_S\mid y_0)\parallel p\left(y_S\right)\right),\hfill \end{array}$$

(6)

where $D_{\mathrm{KL}}\left(·\right)$ represents the KL divergence between two Gaussian distributions. ${\mathcal{L}}_0$ serves as a reconstruction loss, preserving the fidelity of generated trajectories, while ${\mathcal{L}}_{s-1}$ regularizes the denoising process by aligning its distribution with the true posterior. Notably, when the diffusion step S is sufficiently large, $q\left(y_S\left|y_0\right.\right)$ converges to an isotropic Gaussian, making ${\mathcal{L}}_S$ negligible (i.e., approaching 0). This simplifies optimization by allowing the model to omit this term during training.

Given the critical influence of the variance term in the initial stage of the diffusion process on the quality of generated samples [48], we propose a mixed-loss training strategy that introduces a learnable variance control vector to guide the Gaussian transition in the denoising process. The training objective is formulated as

$$\mathcal{L}={\mathcal{L}}_{\mathrm{simple}}+\lambda {\mathcal{L}}_{\mathrm{vlb}}$$

(7)

where ${\mathcal{L}}_{\mathrm{simple}}={\mathbb{E}}_{{ϵ}_s,y_s,\mathbf{f}}\parallel {ϵ}_s-{ϵ}_{\theta }(y_s,\mathbf{f})\parallel$ is optimized via the L2 norm of the noise distribution, aligning with the conventional training objective [33,45]. Furthermore, we introduce a small manually tuned weighting coefficient $\lambda$ to ensure that ${\mathcal{L}}_{\mathrm{vlb}}$ effectively guides ${\mu }_{\theta }$ without compromising its primary role. This design preserves the simplicity of the original noise prediction framework while explicitly modeling the variance term to improve the model’s generative performance in pivotal diffusion stage. The complete training algorithm is detailed in Algorithm 1.

Algorithm 1 The Algorithm for Training

Input: $\mathbb{X}$ and $\mathbb{Y}$; Output: ${ϵ}_{\theta }$, ${\delta }_{\theta }$;   1: Compute Encoded vector $\mathbf{f} = f_{\mathrm{encoder}}\left(\mathbb{X}\right)$;   2: repeat   3:    $y_0\leftarrow \mathbb{Y}$;   4:    ${ϵ}_s\sim \mathcal{N}(\mathbf{0},{\beta }_s\mathbf{I})$;   5:    $y_s=\sqrt{{\overline{\alpha }}_s}{y}_0+(1-{\overline{\alpha }}_s){ϵ}_s$;   6:    ${ϵ}_{\theta },{\delta }_{\theta }=g_{\mathrm{decoder}}(y_s,\mathbf{f})$;   7:    Compute $\mathcal{L}$ according to Equation (7);   8:    Take gradient descent step on ${\nabla }_{\theta }\left(\mathcal{L}\right)$.   9: until convered

3.3. Inference Phase

The inference phase utilizes the trained noise predictor and the control variable, and performs S iterative Gaussian transition on an initial pure Gaussian noise distribution following the reparameterization in Equation (5), ultimately generating the predicted future trajectory. This phase is described in Algorithm 2. Below, we will elaborate on the deep learning model architecture employed for this generative framework, encompassing critical aspects such as network design, conditional fusion mechanisms, and other implementation details.

Algorithm 2 The Algorithm for Inference

Input: $\mathbb{X}$; Output: $\widehat{\mathbb{Y}}$;   1: Compute Encoded vector $\mathbf{f}=f_{\mathrm{encoder}}\left(\mathbb{X}\right)$;   2: for $k=1,2,\cdots ,K$ do   3:    $y_S^k\sim \mathcal{N}(\mathbf{0},\mathbf{I})$;   4:    for $s=S,S-1,\cdots ,1$ do   5:       if $s>1$ then   6:          $z\sim \mathcal{N}(\mathbf{0},\mathbf{I})$;   7:       else   8:          $z=\mathbf{0}$;   9:       end if  10:       ${ϵ}_{\theta },{\delta }_{\theta }=g_{\mathrm{decoder}}(y_s,\mathbf{f})$;  11:       ${\widehat{y}}_{s-1}^k={\displaystyle \frac{1}{\sqrt{{\overline{\alpha }}_s}}}\left(y_s^k-{\displaystyle \frac{1-{\alpha }_s}{\sqrt{1-{\overline{\alpha }}_s}}}{ϵ}_{\theta }(y_s^k,\mathbf{f})\right)+\sqrt{{\mathrm{\Sigma }}_{\theta }(y_s^k,\mathbf{f})}z$;  12:    end for, return ${\widehat{y}}_0^k$;  13: end for, return $\widehat{\mathbb{Y}}\leftarrow {\left\{{\widehat{y}}_0^k\right\}}_{k=1}^K$.

3.4. Denoising Module

We design a dedicated denoising module for the iDMa architecture tailored to the characteristics of trajectory data, as illustrated in Figure 1b,c. The module follows an encoder–decoder structure. Specifically, the encoder inherits partial encoding components from Trajectron++ [9], adopts hierarchical bidirectional LSTM modules to extract the temporal motion characteristics of the target and its social interaction features with neighboring entities from the input historical trajectory and then concatenates these two types of features to form a latent feature representation $\mathbf{f}$ that simultaneously encodes temporal dynamics and social correlations. The decoder consists of the proposed T-Mamba block (see Figure 2), which integrates the Transformer encoder and Mamba block. This design addresses the limitations of standard Transformer, where MLP components exhibit limited spatial relationship modeling capabilities between sequence elements. It also reduces the computational cost associated with stacked attention layers, while achieving stronger performance in capturing key positional dependencies in trajectory sequences.

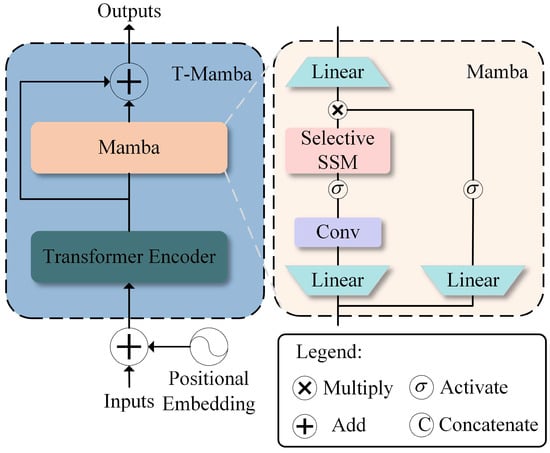
Figure 2. T-Mamba block.

The decoder takes three inputs: the current diffusion timestep s, the observed motion features $\mathbf{f}$, and the noisy motion region $y_s$ at s. We first compute the timestep embedding $Emb\left(s\right)$ and concatenate it with the motion features, forming a conditional vector $\left[Emb\left(s\right),\mathbf{f}\right]$. The region and the conditional vector are then passed through a fully-connected (FC) layer with upsampling. Their outputs are summed to form a fused feature representation ${\displaystyle \mathbf{\ae }}\in {\mathbb{R}}^{\left(T_{\mathrm{fut}}-T_{\mathrm{obs}}\right)\times N\times d_{{\displaystyle \mathbf{\ae }}}}$, which is fed into the T-Mamba block to learn complex spatiotemporal dependencies. Specifically, the input sequence ${\displaystyle \mathbf{\ae }}$ is initially processed by a Transformer encoder for local context modeling:

$${{\displaystyle \mathbf{\ae }}}^{\prime }=\mathrm{TransformerEncoder}({\displaystyle \mathbf{\ae }}+PE)$$

(8)

where PE denotes sinusoidal positional encoding, enhancing the model’s awareness of sequential order. Then, a Mamba block is applied to capture long-range dependencies efficiently via a discretized state-space model:

$$\begin{array}{cc}\hfill {\mathbf{h}}_t& =\overline{\mathbf{A}}{\mathbf{h}}_{t-1}+\overline{\mathbf{B}}{{\displaystyle \mathbf{\ae }}\prime }_{t-1},\hfill \\ \hfill {\mathbf{z}}_t& =\overline{\mathbf{C}}{\mathbf{h}}_t+\overline{\mathbf{D}}{{\displaystyle \mathbf{\ae }}\prime }_t\hfill \end{array}$$

(9)

where $\overline{\mathbf{A}}$, $\overline{\mathbf{B}}$, $\overline{\mathbf{C}}$, $\overline{\mathbf{D}}$ are learnable parameters and $\mathbf{h}$ denotes the hidden state. To combine the global perception of the Transformer with the efficient sequence modeling of Mamba, we apply a residual connection between the Transformer output and the Mamba output:

$$\mathbf{o}=Mamba\left({{\displaystyle \mathbf{\ae }}}^{\prime }\right)+{{\displaystyle \mathbf{\ae }}}^{\prime }$$

(10)

Finally, the output $\mathbf{o}$ of T-Mamba block undergoes dimensionality reduction through multiple FC layers, yielding the noise estimate ${ϵ}_{\theta }$ and the variance control vector ${\delta }_{\theta }$ for the current timestep. They guide the Gaussian transition process and the computation of the training loss.

4. Experiments

4.1. Experimental Setup

4.1.1. Datasets

The proposed method is evaluated on the ETH-UCY [37,38] and SDD [39] datasets, following the standards of existing studies [29,33,35,47], predicting future trajectory for the next 12 frames based on the trajectory of the past 8 frames. The ETH [38] and UCY [37] datasets are classic benchmarks for pedestrian trajectory prediction, containing five distinct scenes: ETH, HOTEL, UNIV, ZARA1, and ZARA2. These sub-datasets provide trajectories annotated with real-world coordinates, and we follow the standard leave-one-out evaluation strategy for assessment. The SDD dataset is a large-scale dataset collected from a bird’s-eye view, in which the trajectory coordinates of various targets such as pedestrians and bicycles are annotated in pixel coordinates.

4.1.2. Evaluation Metrics

We employ widely used Average Displacement Error (ADE) and Final Displacement Error (FDE) as evaluation metrics [9,23,24,47,56,57]. ADE calculates the mean Euclidean distance between the predicted trajectory and the GT trajectory at all timesteps, reflecting the overall prediction accuracy. FDE measures the Euclidean distance between the predicted final position and the GT final position, evaluating the model’s long-term forecasting capability. These metrics provide a comprehensive assessment of the model’s trajectory prediction performance. Their mathematical formulations are given below:

$$\begin{array}{cc}\hfill \mathrm{ADE}(\widehat{\mathbb{Y}},\mathbb{Y})& ={\displaystyle \frac{1}{T_{\mathrm{fut}}-T_{\mathrm{obs}}}}\sqrt{\sum _{t=T_{\mathrm{obs}}+1}^{T_{\mathrm{fut}}}{\left({\widehat{\mathbf{x}}}_t-{\mathbf{x}}_t\right)}^2},\hfill \\ \hfill \mathrm{FDE}(\widehat{\mathbb{Y}},\mathbb{Y})& =\sqrt{{\left({\widehat{\mathbf{x}}}_{T_{\mathrm{fut}}}-{\mathbf{x}}_{T_{\mathrm{fut}}}\right)}^2}\hfill \end{array}$$

(11)

4.1.3. Implementation Details

The proposed denoising module includes an upsampling block, T-Mamba block with a dimension of 512, and two downsampling blocks with dimensions halved at each stage. The T-Mamba block consists of single-layer Transformer encoder with 4 attention heads, and a Mamba layer featuring a state space dimension of 16 and convolutional kernel size of 4. During training, the model is trained for 150 epochs with an initial learning rate of 0.001 and a decay rate of 0.9. The weight factor for the loss function is set to 0.001. During inference, each prediction case generates $K=20$ random trajectories. All experiments are conducted on a single RTX 4070 GPU.

4.2. Ablation Studies

We conduct ablation studies on ETH-UCY and SDD to evaluate the effectiveness of the key components in our proposed method. As shown in Table 1, we focus on analyzing two main designs: (1) variance control in the diffusion model, and (2) the role of T-Mamba block. The experimental results reveal three key patterns: First, when the T-Mamba block is disabled, incorporating variance learning still leads to the improvement in prediction performance across both datasets. Second, in the scenario where variance learning is turned off, integrating the T-Mamba block yields even more significant enhancements in model performance on the two datasets, while also reducing the number of parameters and inference time. Third, when both the variance learning module and the T-Mamba block are activated simultaneously, the model attains its optimal performance with the fewest parameters and fastest inference, outperforming the baseline configurations on both ETH-UCY and SDD.

Table 1. The results of ablation studies for iDMa on ETH-UCY and SDD datasets using ADE/FDE, where ETH-UCY is measured in meters and SDD in pixels. Bold fonts represent the best, lower is better.

Variance Learing	Mamba Block	Parameters	Inference (ms)	ETH	HOTEL	UNIV	ZARA1	ZARA2	SDD
✗	✗	6.5 M	~914	0.43/0.75	0.15/0.28	0.22/0.44	0.21/0.38	0.15/0.28	8.24/15.63
✓	✗	6.5 M	~914	0.41/0.64	0.14/0.24	0.21/0.42	0.20/0.35	0.14/0.27	8.01/14.10
✗	✓	4.0 M	~621	0.39/0.62	0.14/0.22	0.23/0.42	0.19/0.32	0.15/0.27	7.99/13.69
✓	✓	4.0 M	~621	0.37/0.59	0.12/0.20	0.22/0.40	0.18/0.31	0.14/0.25	7.95/13.01

To clarify the contribution of each component, we compare ablation studies with MID in the ZARA2 scene (see Figure 3). From the analysis of visual comparison results, we find that the variance variable can indeed constrain the predicted trajectory points within a reasonable range during the late-stage denoising process of the model. Additionally, the T-Mamba block iteratively captures the noise distribution in the high-dimensional space during denoising.

Figure 3. Visualization of ablation experiments. (a) Standard Transformer denoising process; (b) only variance component; (c) only T-Mamba component; (d) Combination of variance and T-Mamba components.

Figure 4 clearly illustrates how T-Mamba denoising block shifts high-dimensional features from being noise-dominated to trajectory-semantics-dominated. In the initial state, the pure noise distribution shows a disordered mapping of color patches. As the denoising steps proceed, the high-dimensional mapping gradually exhibits consistent trends in time and increasingly approximates the high-dimensional mapping of real trajectory. These findings strongly validate the importance of variance control in the diffusion process and confirm Mamba’s effectiveness in capturing critical latent space features.

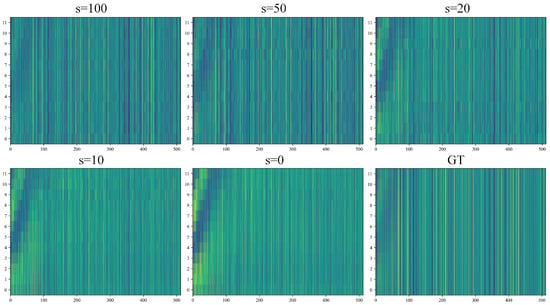
Figure 4. Visualization of noisy trajectory at different denoising timestamps in the high-dimensional state space, with brighter colors indicating larger values and the color variation represents the hidden-layer confidence of the model. Horizontal axis: high-dimensional representation of target coordinates at time t; Vertical axis: predicted duration.

Moreover, we investigated the impact of the number of denoising steps on model performance and computational efficiency. As shown in Table 2, the prediction performance and inference time of the Transformer-Only (TF-O, 3 layers), Mamba-Only (M-O, 3 layers), and our proposed T-Mamba baselines are compared across different denoising steps on the ETH-UCY and SDD datasets. A clear trend emerges from the results: as the number of steps increases, the prediction accuracy of all three models gradually improves and eventually converges. However, this improvement in accuracy is accompanied by a near-linear increase in inference time, indicating that gains in prediction performance come at the cost of substantially higher computational overhead. Compared to these two baselines, under the setting of S = 100, the hybrid architecture proposed in this paper achieves an improvement of 3.4% in ADE and 7.7% in FDE on the SDD dataset. Considering the trade-off between computational cost and performance, we set the timesteps to 100.

Table 2. Prediction performance and inference time comparison of Transformer-Only, Mamba-Only, and T-Mamba across different denoising steps on ETH-UCY and SDD datasets.

Baseline	S	ETH	HOTEL	UNIV	ZARA1	ZARA2	SDD	Inference (ms)
TF-O	10	1.02/1.72	0.62/1.40	0.71/1.50	0.49/0.88	0.52/1.22	31.50/46.20	~92
	20	0.68/1.30	0.47/0.88	0.49/0.70	0.36/0.58	0.26/0.65	22.10/35.50	~179
	50	0.45/0.80	0.16/0.31	0.24/0.57	0.22/0.39	0.18/0.32	11.80/16.95	~461
	100	0.42/0.75	0.15/0.28	0.22/0.45	0.20/0.38	0.15/0.28	8.23/15.28	~914
M-O	10	1.15/2.22	0.83/1.93	0.94/2.10	0.57/1.12	0.55/1.38	36.90/52.87	~61
	20	0.75/1.58	0.55/1.17	0.51/0.92	0.39/0.68	0.29/0.88	26.20/46.10	~125
	50	0.48/0.85	0.18/0.36	0.28/0.63	0.27/0.50	0.21/0.36	12.33/19.76	~306
	100	0.45/0.82	0.19/0.32	0.24/0.55	0.23/0.42	0.17/0.33	9.02/16.94	~613
T-Mamba	10	0.97/1.65	0.59/1.37	0.68/1.45	0.47/0.84	0.50/1.12	30.34/44.63	~62
	20	0.63/1.24	0.44/0.63	0.46/0.64	0.34/0.56	0.24/0.61	20.28/33.73	~124
	50	0.42/0.66	0.14/0.22	0.23/0.49	0.20/0.36	0.16/0.29	10.16/15.77	~311
	100	0.37/0.59	0.12/0.20	0.22/0.40	0.18/0.31	0.14/0.25	7.95/13.01	~621

Note: TF-O and M-O denote Transformer-Only and Mamba-Only respectively.

4.3. Quantitative Evaluation

As illustrated in Table 3, our method achieves notable improvement on the ETH-UCY dataset, reducing the ADE index from 0.21 to 0.20, which corresponds to a relative improvement of 4.76%. On the more challenging SDD dataset, our method also exhibits competitive performance, lowering the ADE from 8.10 to 7.95, representing a relative gain of 1.85%. Given the complexity of the dataset and the performance saturation observed in existing research, this progress holds practical importance. The consistent performance gains across diverse datasets demonstrate the robustness and generalization capability of the proposed method.

Table 3. Comparison with baseline models on ETH-UCY and SDD dataset using ADE/FDE, where ETH-UCY is measured in meters and SDD in pixels. AVG is the average over five tested scenes of ETH-UCY. Bold/underlined fonts represent the best/second-best result.

Methods	ETH	HOTEL	UNIV	ZARA1	ZARA2	AVG	SDD
SSA-GAN [26]	0.68/1.44	0.69/1.55	0.55/1.22	0.30/0.63	0.36/0.75	0.52/1.12	-
NMMP [58]	0.67/1.24	0.34/0.64	0.52/1.12	0.33/0.66	0.30/0.62	0.43/0.86	21.14/37.17
Social STGCNN [20]	0.78/1.31	0.44/0.75	0.47/0.85	0.37/0.61	0.36/0.59	0.48/0.82	-
TPPO [27]	0.75/1.27	0.36/0.70	0.39/0.74	0.22/0.37	0.23/0.45	0.39/0.71	-
InfoSTGCNN [59]	0.61/0.82	0.48/0.71	0.40/0.64	0.33/0.51	0.30/0.44	0.42/0.62	-
PECNet [40]	0.63/1.12	0.25/0.42	0.37/0.66	0.28/0.52	0.19/0.36	0.34/0.62	9.97/15.89
FlowChain [60]	0.55/0.99	0.20/0.35	0.29/0.54	0.22/0.40	0.20/0.34	0.29/0.52	9.93/17.71
Trajectron++[9]	0.54/0.95	0.18/0.28	0.28/0.55	0.21/0.41	0.16/0.31	0.27/0.50	10.00/17.15
GroupNet [19]	0.46/0.73	0.15/0.25	0.26/0.49	0.21/0.39	0.17/0.33	0.25/0.44	9.31/16.11
MID [33]	0.42/0.75	0.15/0.28	0.22/0.45	0.20/0.38	0.15/0.28	0.23/0.43	8.23/15.28
AgentFormer [13]	0.44/0.78	0.13/0.21	0.25/0.45	0.19/0.30	0.14/0.24	0.23/0.40	-
TP-EGT [61]	0.41/0.68	0.13/0.21	0.29/0.50	0.18/0.30	0.16/0.27	0.23/0.39	-
NPSN [62]	0.39/0.59	0.16/0.26	0.23/0.39	0.19/0.33	0.14/0.25	0.22/0.36	8.63/11.75
SocialVAE [29]	0.44/0.67	0.14/0.21	0.24/0.41	0.19/0.32	0.14/0.26	0.23/0.37	8.10/11.72
MGF [63]	0.40/0.59	0.15/0.25	0.23/0.41	0.17/0.29	0.14/0.24	0.22/0.35	9.13/15.42
EigenTraj [56]	0.38/0.61	0.12/0.19	0.26/0.46	0.20/0.36	0.14/0.25	0.22/0.37	8.12/13.10
LED [34]	0.39/0.58	0.11/0.17	0.26/0.43	0.18/0.26	0.13/0.27	0.21/0.34	8.48/11.66
SingularTraj [47]	0.35/0.44	0.13/0.22	0.25/0.44	0.19/0.33	0.15/0.26	0.21/0.33	-
Ours (iDMa)	0.37/0.59	0.12/0.20	0.22/0.40	0.18/0.31	0.14/0.25	0.20/0.35	7.95/13.01

4.4. Qualitative Evaluation

For a more intuitive evaluation of model performance, we conduct a visual comparison on the ETH-UCY dataset, comparing our method with several existing approaches: NPSN [62], EigenTrajectory [56], and SingularTrajectory [47]. As shown in Figure 5, the historical trajectories, GT future trajectories, and predicted trajectories are represented by green curves, red curves, and blue dashed lines, respectively. Notably, the blue dashed lines correspond to the optimal predicted trajectories selected from 20 generated samples, which exhibit the closest alignment with the GT trajectories. To highlight the performance differences more clearly, we select a representative sample from each scene for zoomed-in qualitative analysis.

Figure 5. Visualization comparison on ETH/UCY. We compare the best-of-20 predictions by our method against NPSN, EigenTrajectory, and SingularTrajectory. (green curves: Observed trajectories; red curves: GT future trajectories; sky-blue dashed lines: Best-of-20 predictions).

The visual results demonstrate that the trajectories predicted by our method are more consistent with GT trajectories in both overall trend and local fine-grained details. More importantly, under challenging scenes, such as the densely crowded and complex interaction scene in the zoomed-in UNIV sample, our method maintains high prediction accuracy and outperforms the compared benchmarks significantly. This advantage stems from our model’s unique design of a diffusion model framework with dual-parameter learning, combined with a denoising module that fuses T-Mamba, which effectively addresses the limitations of existing methods. In contrast, our dual-parameter learning enables adaptive quantification of motion randomness by explicitly modeling the central tendency (mean) of trajectory distributions and trajectory boundary convergence (variance). This characteristic compensates for the deficiency of NPSN’s static sampling by dynamically responding to real-time interaction changes, while preserving subtle motion fluctuations through variance modeling to alleviate the loss of fine-grained details in EigenTrajectory. Meanwhile, the T-Mamba denoising module fully leverages Transformer’s strength in capturing local spatiotemporal dependencies and utilizes Mamba’s efficient selective state update mechanism to capture global temporal dynamic interaction cues. This synergy not only resolves SingularTrajectory’s trade-off dilemma between generalization and specificity but also ensures the model retains global consistency while responding to local interaction dynamics, thereby generating more realistic and accurate trajectories.

5. Discussion

The proposed iDMa framework exclusively takes the target’s location information as input and dispenses with pixel-level data such as maps. This characteristic endows the method with broad applicability in trajectory prediction tasks across diverse scenarios, transcending the limitation to pedestrian targets alone. Despite its favorable performance in relevant tasks, the framework still exhibits certain inherent constraints. Firstly, the iterative denoising process demands substantial computational resources, which poses a significant obstacle to real-time deployment in practical applications. Secondly, the model encounters difficulties in accurately characterizing complex trajectories, especially those involving abrupt curvatures or sharp turns, indicating inadequacies in capturing highly nonlinear motion patterns. Additionally, it is worth noting that its performance degrades markedly in highly interactive and crowded scenes. The mutual interference between multiple moving targets elevates motion complexity, and the absence of pixel-level environmental information impairs the model’s ability to infer target collision avoidance behaviors. Additionally, the model is sensitive to such key hyperparameters as diffusion steps and loss weights. Reducing diffusion steps accelerates inference but drastically compromises prediction accuracy, while tuning loss weights leads to performance fluctuations across datasets.

6. Conclusions

In this paper, we propose a novel stochastic trajectory prediction framework based on diffusion model. The framework integrates a dual-parameter learning mechanism for mean and variance, thereby enhancing the accuracy of noise estimation. Additionally, a hybrid denoising backbone is designed by combining Transformer and Mamba architectures, which not only reduces parameter overhead effectively but also strengthens the model’s capability to capture complex noise distributions. Experimental results validate that the iDMa framework achieves superior performance in trajectory prediction tasks, generating predictions with high accuracy and motion consistency while maintaining remarkable computational efficiency. Looking ahead, we will focus on optimizing real-time inference performance and further improving the models ability to predict highly nonlinear motion patterns, so as to expand its practical application scenarios.