Comprehensive Die Shear Test of Silicon Packages Bonded by Thermocompression of Al Layers with Thin Sn Capping or Insertions
Abstract
:1. Introduction
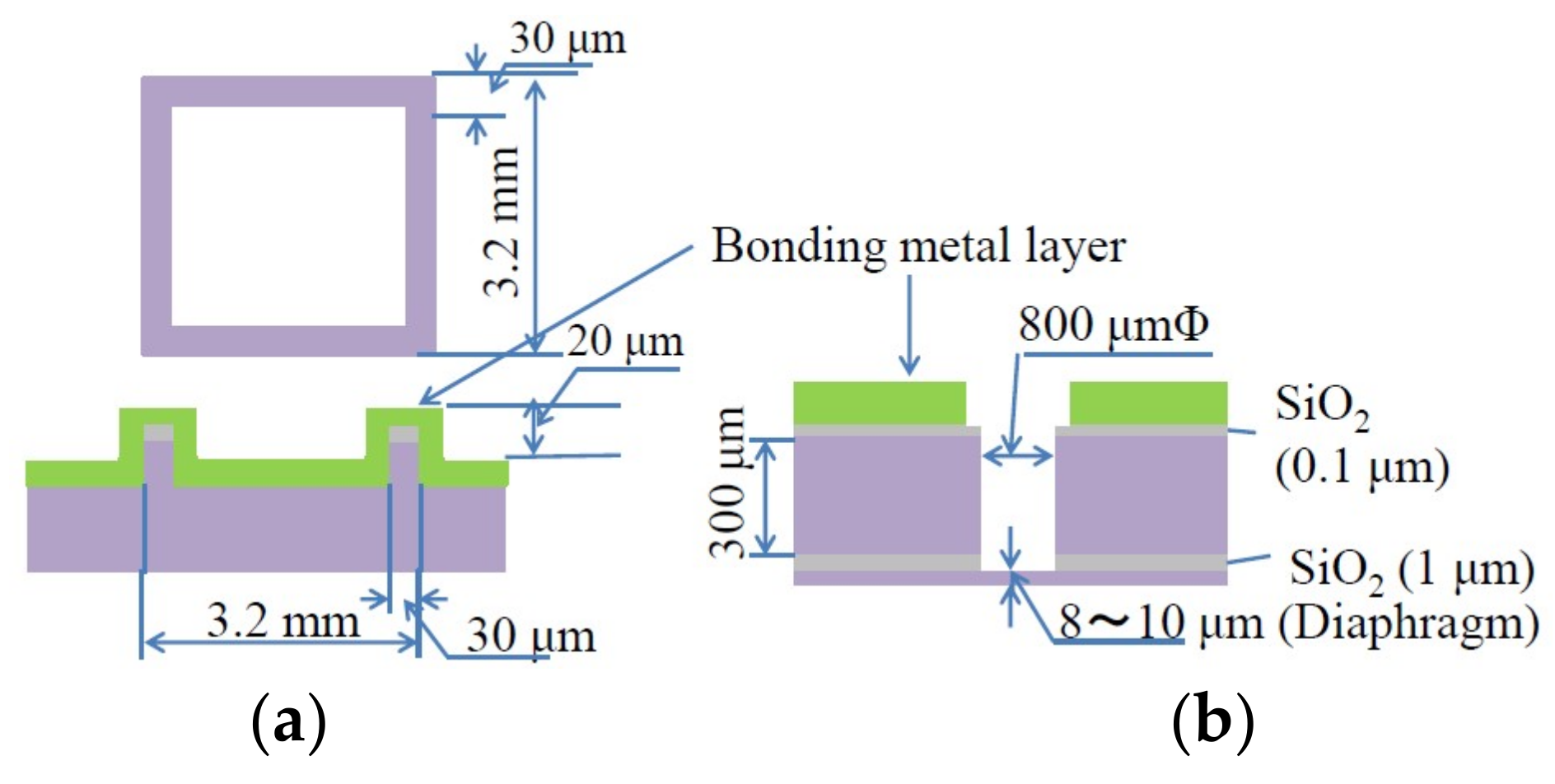
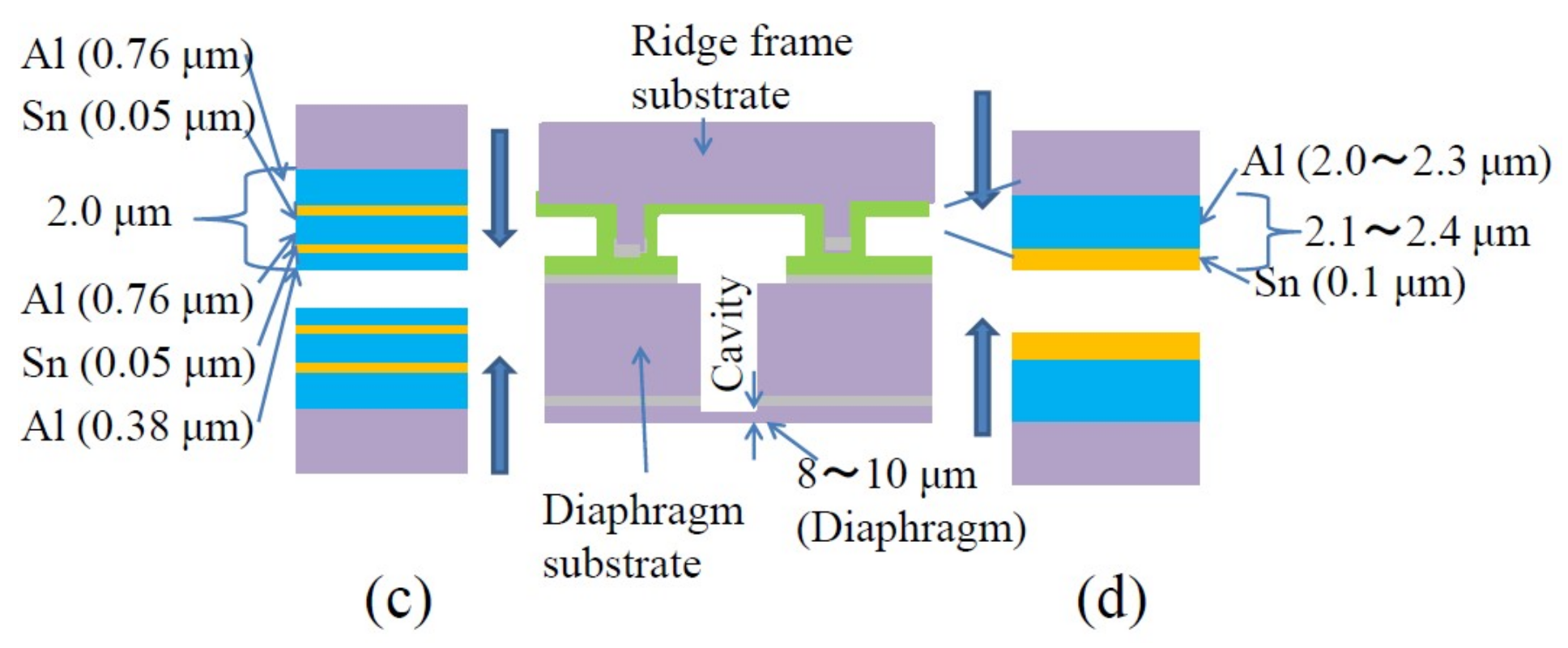
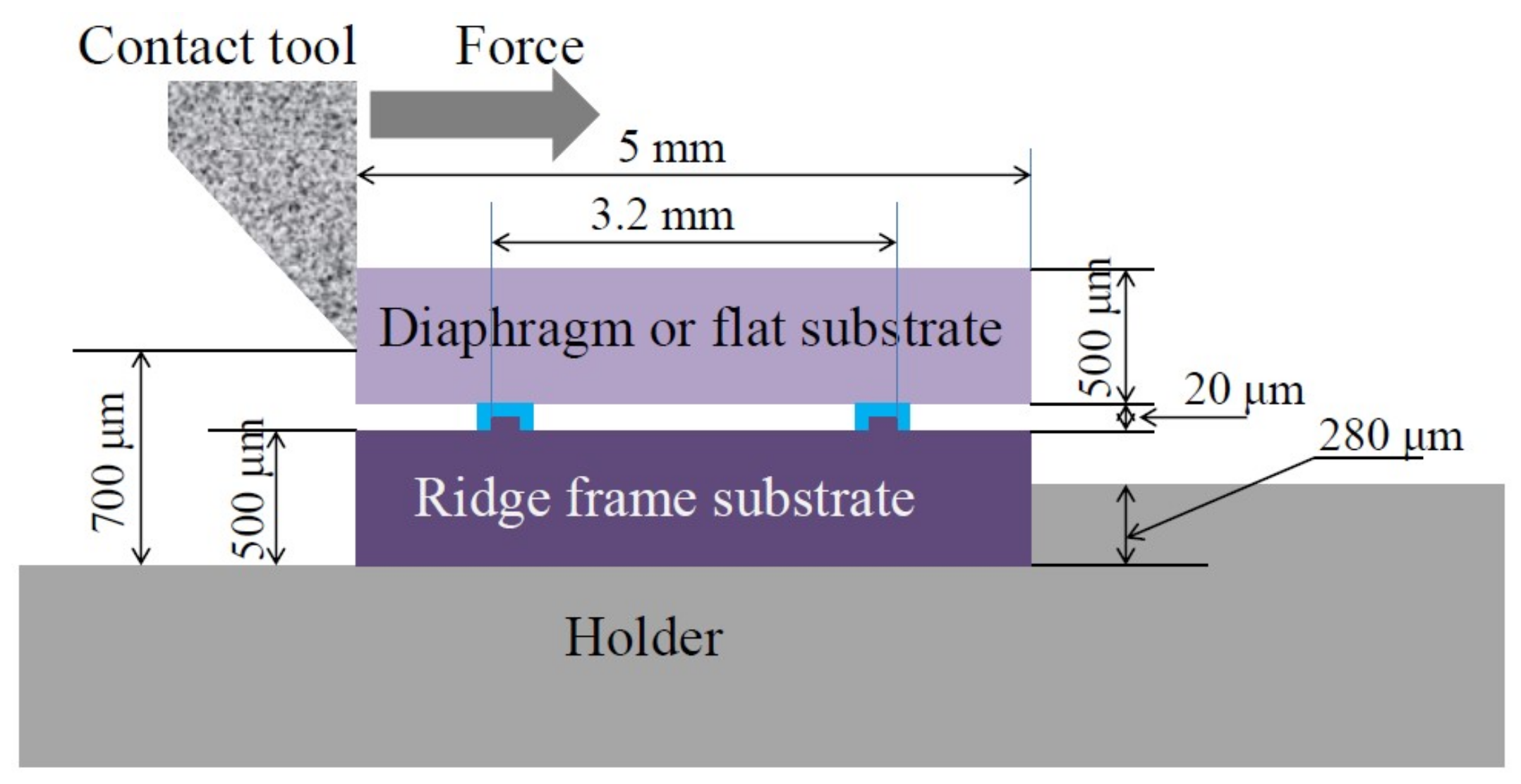
2. Materials and Methods
3. Results
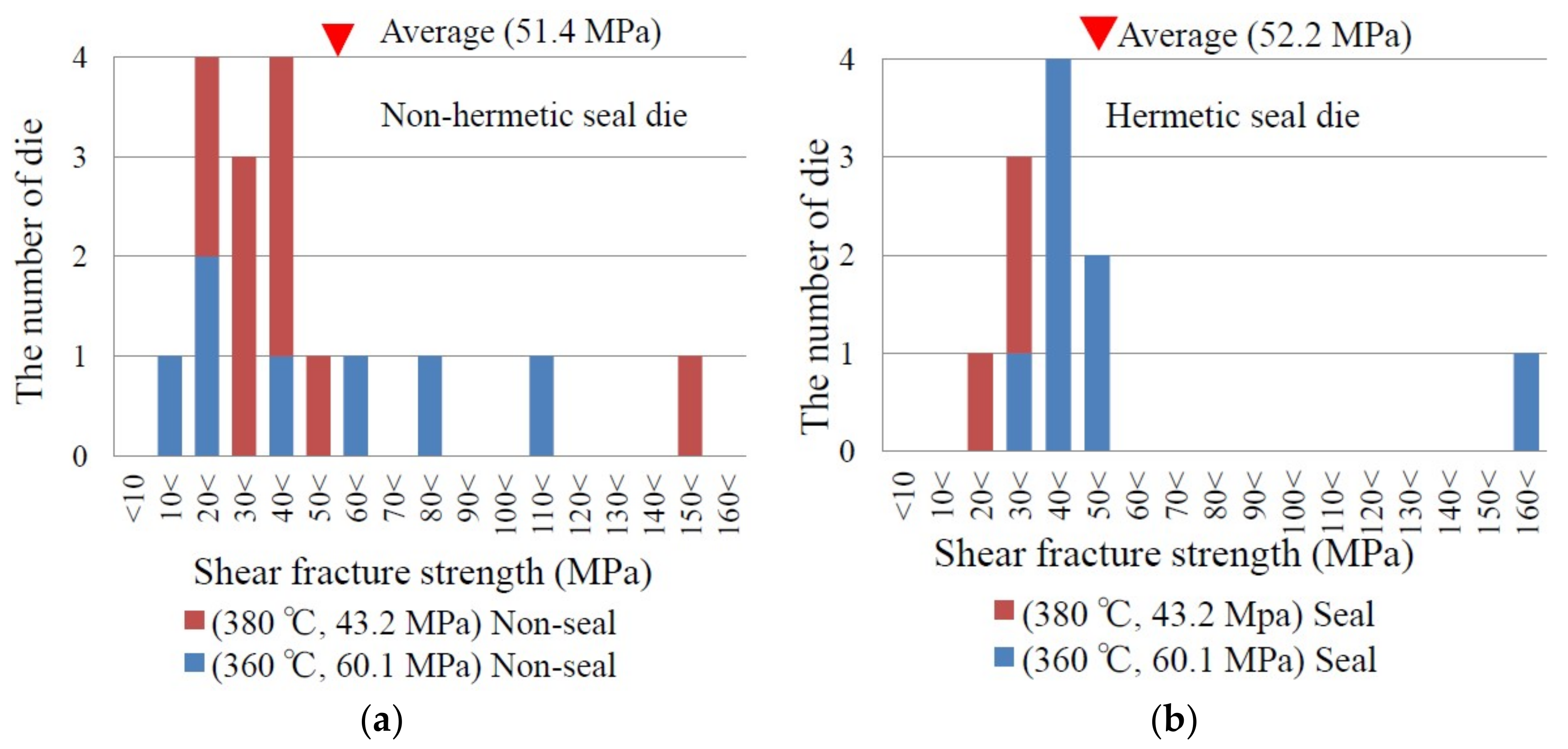
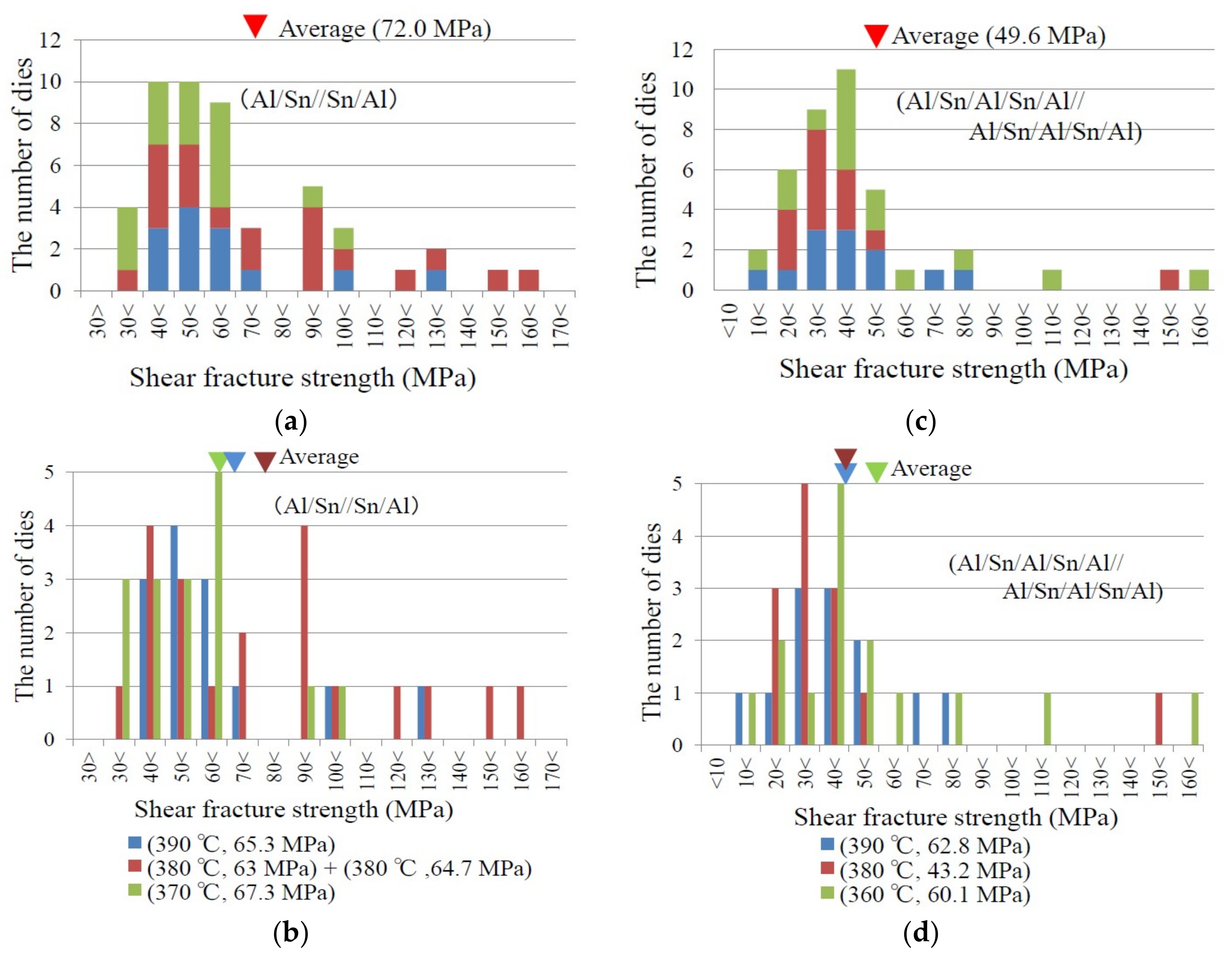
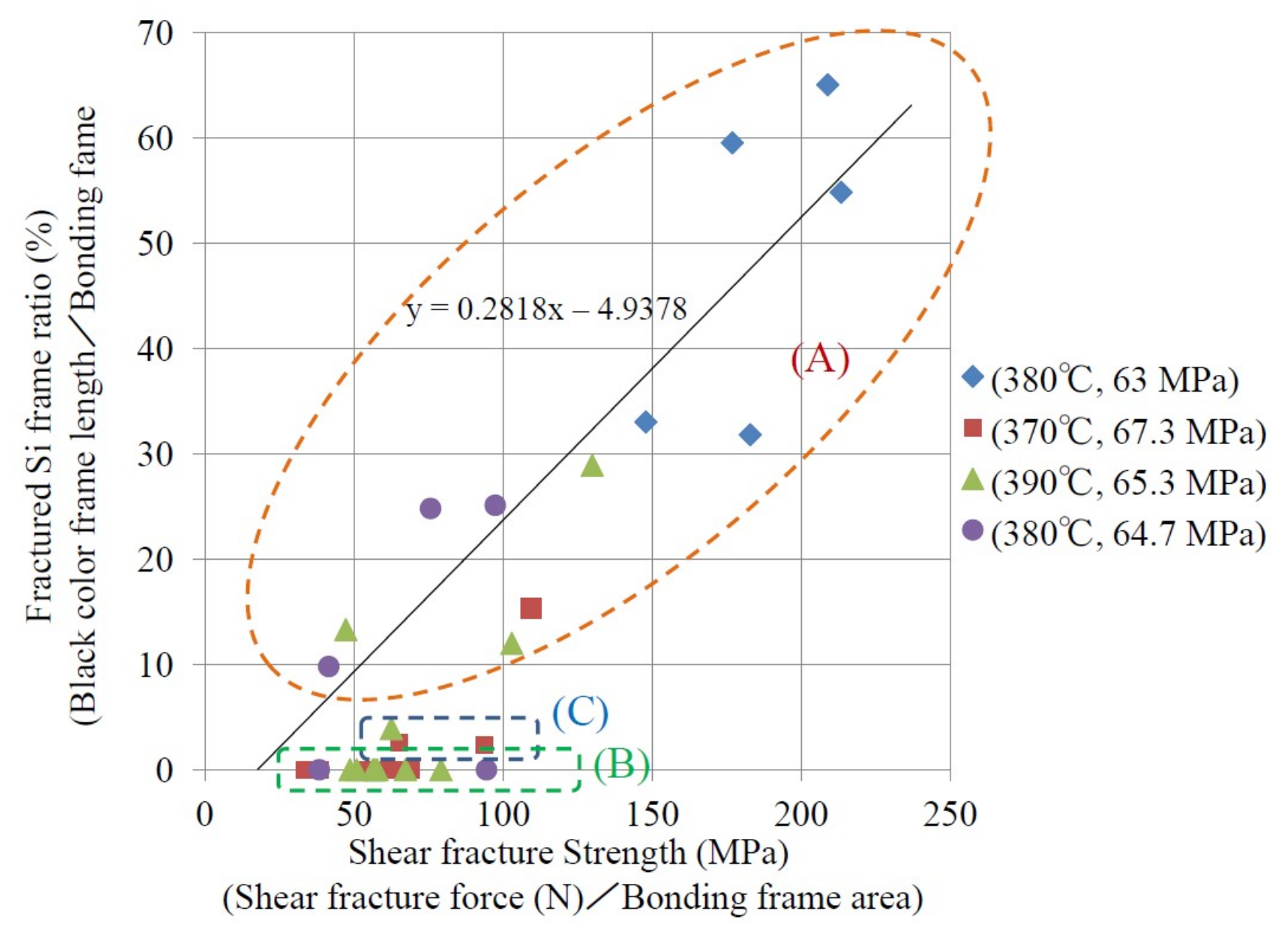
3.1. Shear Fracture Strength
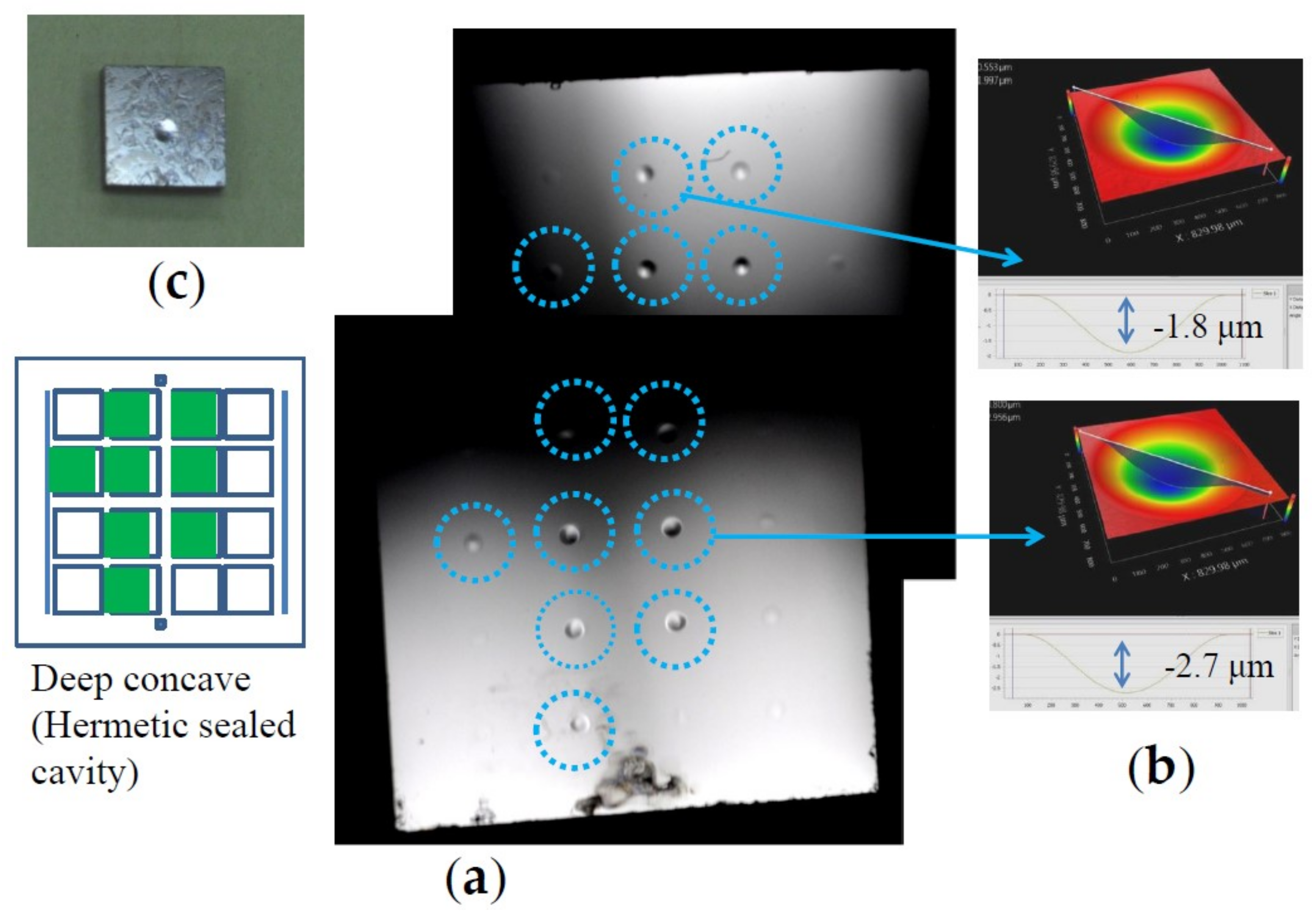
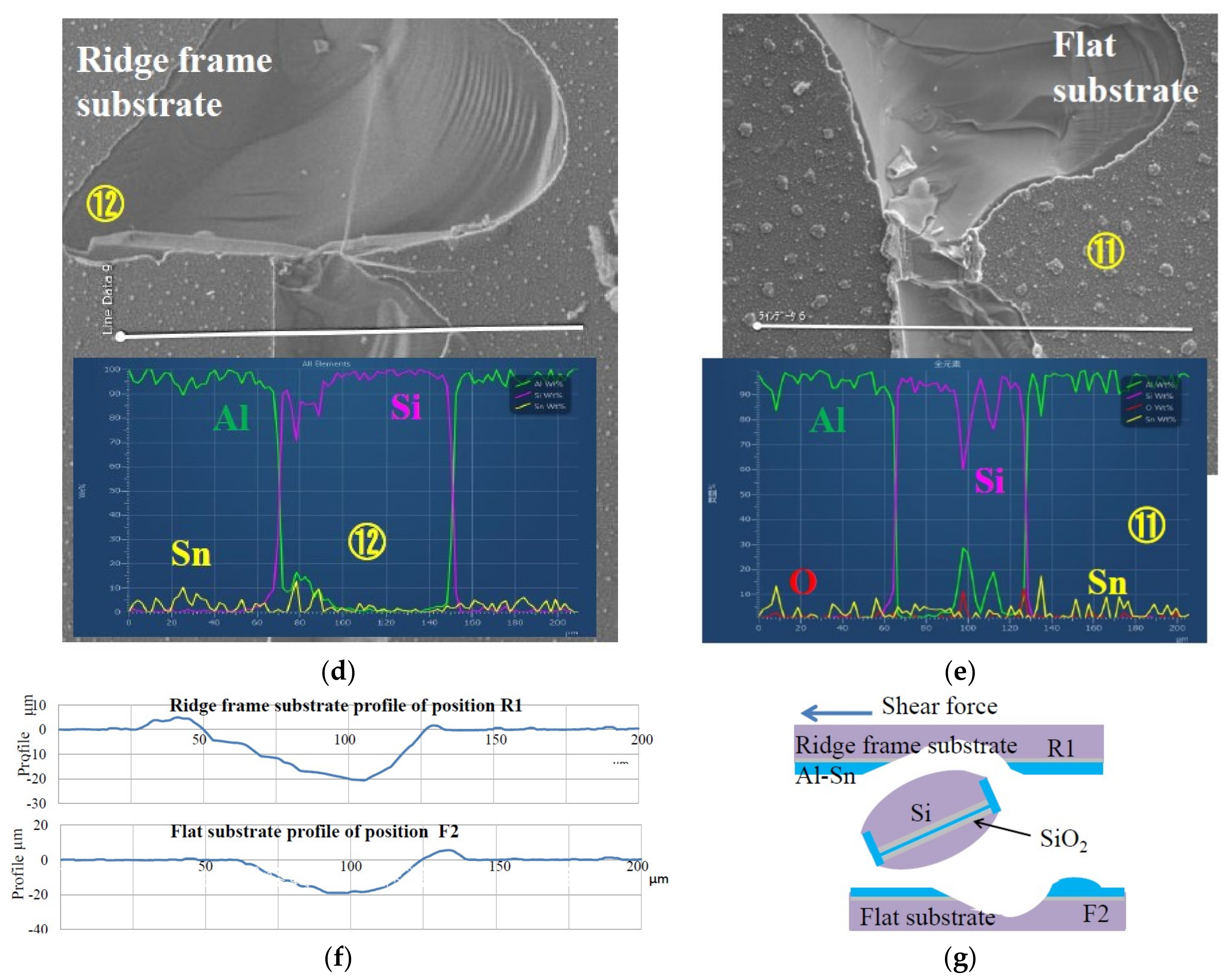
3.2. Observation Results of Shear-Fractured Surface
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Knechtel, R. Glass frit bonding: An universal technology for wafer level encapsulation and packaging. Microsyst. Technol. 2005, 12, 63–68. [Google Scholar] [CrossRef]
- Steven, S.; Flannery, A.F., Jr. Method of Fabrication of a Al/Ge Bonding in a Wafer Packaging Environment and a Produced Therefrom. WO 2006/101769 A2, 28 September 2006. [Google Scholar]
- Martin, J. Wafer capping of MEMS with fab-friendly metals. In Proceedings of the SPIE, San Jose, CA, USA, 19 January 2007; Volume 6463, pp. M-1–M-6. [Google Scholar]
- Yun, C.H.; Martin, J.R.; Winbigler, J.T. Al to Al wafer bonding for MEMS encapsulation and 3-D interconnect. In Proceedings of the IEEE MEMS, Tucson, AZ, USA, 13–17 January 2008; pp. 13–17. [Google Scholar]
- Malik, N.; Schjolberg-Henriksen, K.; Poppe, E.; Visser Taklo, M.M.; Finstad, T.G. Al-Al thermocompression bonding for wafer-level MEMS sealing. Sens. Actuators A 2014, 211, 115–120. [Google Scholar] [CrossRef]
- Satoh, S.; Fukushi, H.; Esashi, M.; Tanaka, S. Low-temperature aluminum thermo-compression wafer bonding with tin antioxidation layer for hermetic sealing of MEMS. In Proceedings of the IEEE MEMS, Shanghai, China, 24–28 January 2016; pp. 581–584. [Google Scholar]
- Satoh, S.; Fukushi, H.; Esashi, M.; Tanaka, S. Low temperature hermetic sealing by aluminum thermocompression bonding using tin intermediate layer. In Proceedings of the IEEE Electron Technology and Manufacturing Conference, Toyama, Japan, 28 February–2 March 2017; pp. 219–221. [Google Scholar]
- Satoh, S.; Fukushi, H.; Esashi, M.; Tanaka, S. Low temperature Al-Al thermo-compression bonding with sn oxidation protect layer for wafer-level hermetic sealing. IEEJ Trans. Sens. Micromach. 2016, 136, 237–243. [Google Scholar] [CrossRef]
- Tanaka, S.; Mohri, M.; Ogashima, T.; Fukushi, H.; Tanaka, K.; Nakamura, D.; Nishimori, T.; Esashi, M. Electrical Interconnection in anodic bonding of silicon wafer to LTCC wafer using highly compliant porous bumps made from submicron gold particles. Sens. Actuators A 2012, 188, 198–202. [Google Scholar] [CrossRef]
- Itoh, I.; Otoguro, Y.; Samata, Y. Diffusion welding of Al-Sn alloy in the atmosphere. Keikinzoku 1992, 42, 383–388. [Google Scholar] [CrossRef]
- Nakajima, H.; Kawamura, N.; Kurishita, H.; Yoshinaga, H. Work-hardening and recovery rates in pure aluminum single crystals during high-temperature deformation. J. Jpn. Inst. Metals 1986, 50, 441–448. [Google Scholar]
- Yi, T.; Li, L.; Kim, C.J. Microscale material testing of single crystalline silicon: process effects on surface morphology and tensile strength. Sens. Actuators 2000, 83, 172–178. [Google Scholar] [CrossRef]
- Isono, Y.; Namazu, T.; Terayama, N.; Tanaka, T. Mechanical characterization of sub-micrometer thick DLC films by AFM tensile testing for surface modification in MEMS. In Proceedings of the IEEE MEMS, Las Vegas, NV, USA, 24 January 2002; pp. 431–434. [Google Scholar]
- Schweitz, J.A.; Ericson, F. Evaluation of mechanical materials properties by means of surface micromachined structures. Sens. Actuators 1999, 74, 126–133. [Google Scholar] [CrossRef]
- Mazza, E.; Dual, J. Mechanical behavier of a μm-sized single crystal silicon structure with sharp notches. J. Mech. Phys. Solid 1999, 47, 1795–1821. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Satoh, S.; Fukushi, H.; Esashi, M.; Tanaka, S. Comprehensive Die Shear Test of Silicon Packages Bonded by Thermocompression of Al Layers with Thin Sn Capping or Insertions. Micromachines 2018, 9, 174. https://doi.org/10.3390/mi9040174
Satoh S, Fukushi H, Esashi M, Tanaka S. Comprehensive Die Shear Test of Silicon Packages Bonded by Thermocompression of Al Layers with Thin Sn Capping or Insertions. Micromachines. 2018; 9(4):174. https://doi.org/10.3390/mi9040174
Chicago/Turabian StyleSatoh, Shiro, Hideyuki Fukushi, Masayoshi Esashi, and Shuji Tanaka. 2018. "Comprehensive Die Shear Test of Silicon Packages Bonded by Thermocompression of Al Layers with Thin Sn Capping or Insertions" Micromachines 9, no. 4: 174. https://doi.org/10.3390/mi9040174
APA StyleSatoh, S., Fukushi, H., Esashi, M., & Tanaka, S. (2018). Comprehensive Die Shear Test of Silicon Packages Bonded by Thermocompression of Al Layers with Thin Sn Capping or Insertions. Micromachines, 9(4), 174. https://doi.org/10.3390/mi9040174




