Method of Measuring the Mismatch of Parasitic Capacitance in MEMS Accelerometer Based on Regulating Electrostatic Stiffness
Abstract
:1. Introduction
2. Method of Measuring the Mismatch of Parasitic Capacitance
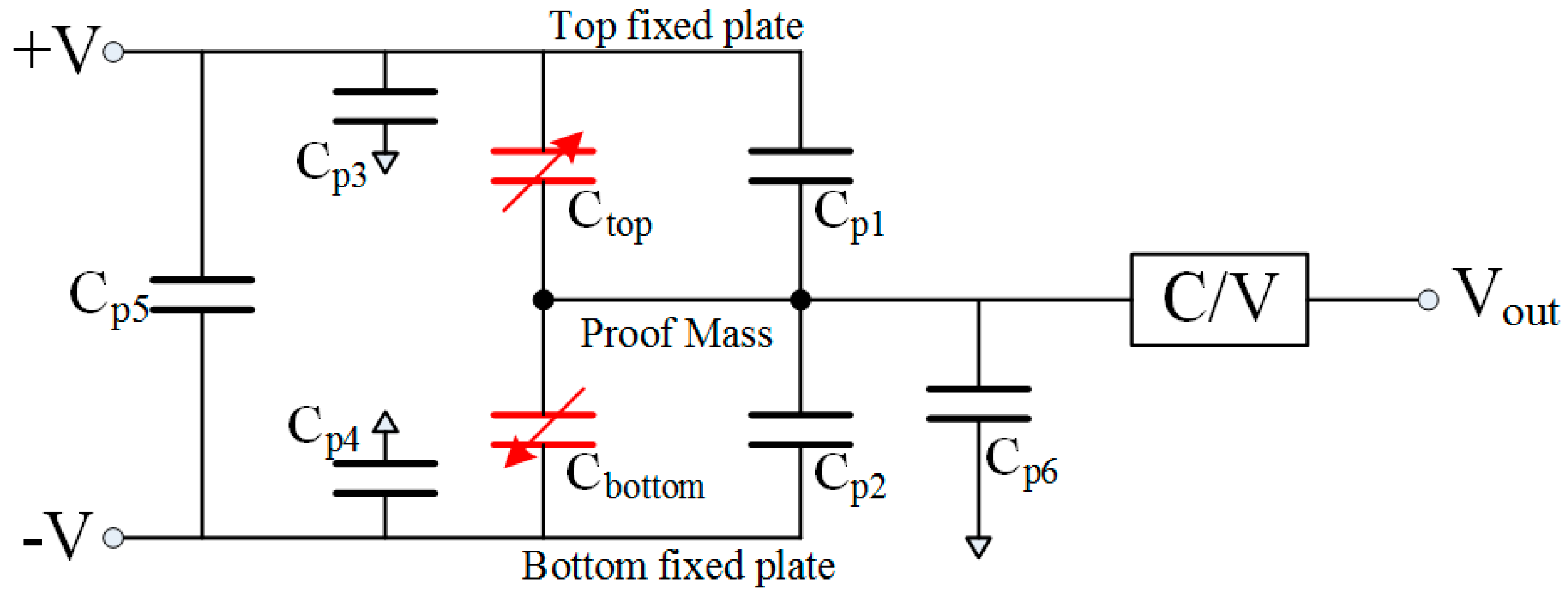
2.1. Influence of Parasitic Capacitance
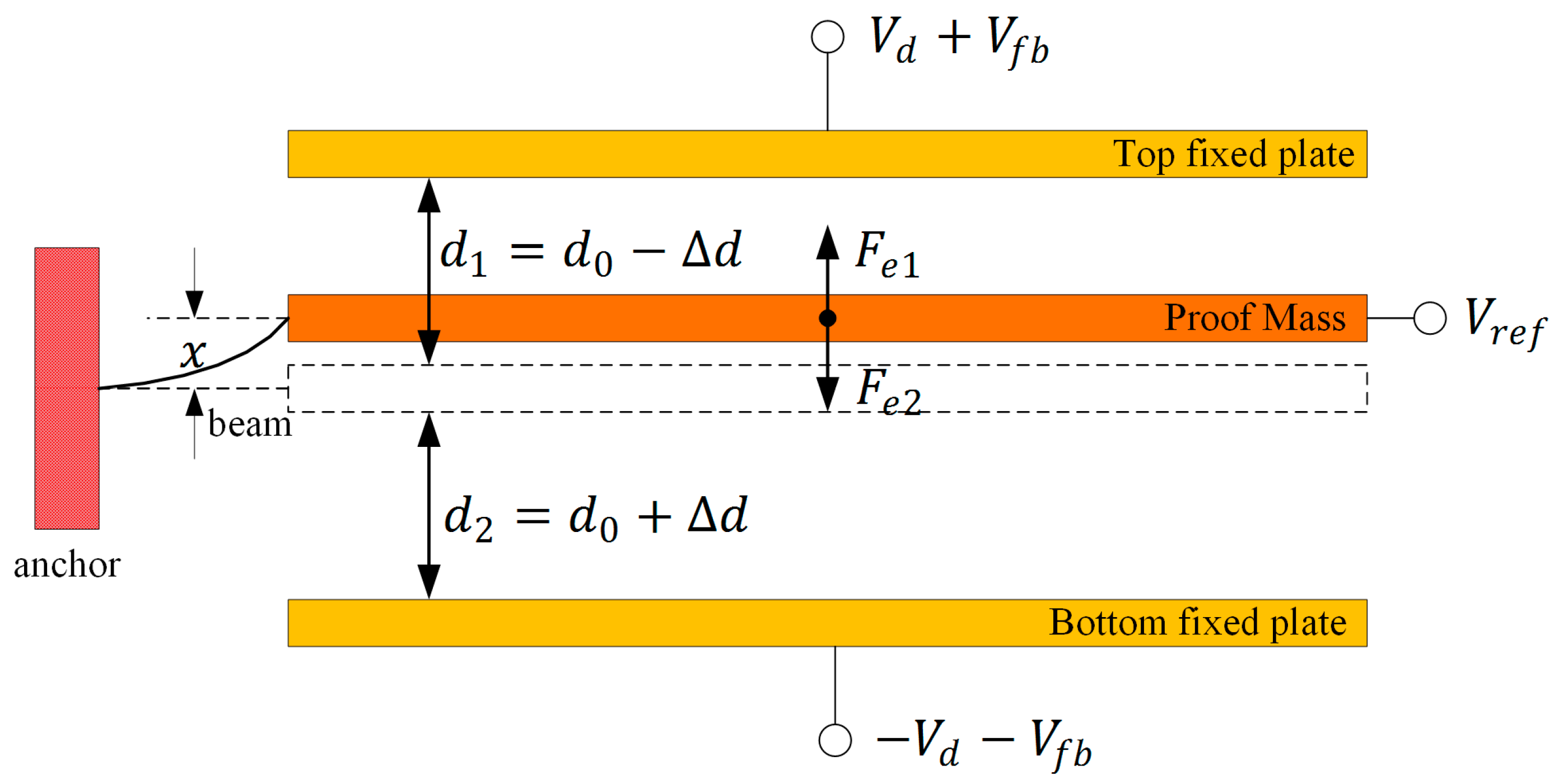
2.2. Theory of Measuring the Mismatch
3. Measurement Results and Discussion
3.1. Measurement Results
3.1.1. Verification Experiment and Results
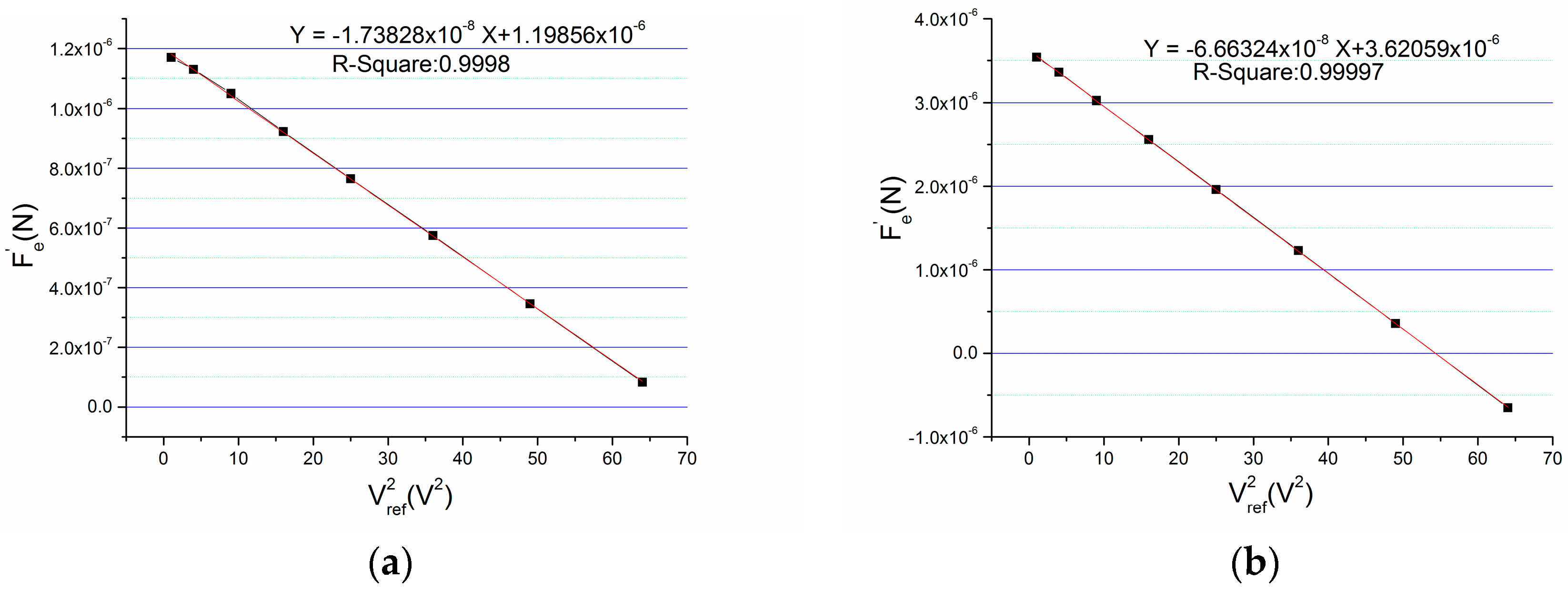
3.1.2. Applications and Results
3.2. Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Dong, Y.; Zwahlen, P.; Nguyen, A.M.; Frosio, R.; Rudolf, F. Ultra-high precision MEMS accelerometer. In Proceedings of the 16th International Conference on Solid-State Sensors, Actuators and Microsystems, Beijing, China, 5–9 June 2011. [Google Scholar]
- Ullah, P.; Ragot, V.; Zwahlen, P.; Rudolf, F. A new high performance sigma-delta MEMS accelerometer for inertial navigation. In Proceedings of the 2015 Dgon Inertial Sensors and Systems Symposium, Karlsruhe, Germany, 22–23 September 2015. [Google Scholar]
- Yazdi, N.; Kulah, H.; Najafi, K. Precision readout circuits for capacitive microaccelerometers. In Proceedings of the IEEE Sensors 2004, Vienna, Austria, 24–27 October 2004. [Google Scholar]
- Zhu, Z.Y.; Liu, Y.D.; Jin, Z.H. The parasitic capacitance’s influence on noise in a MEMS accelerometer sensor. Chin. J. Sens. Actuators 2013, 26, 17–20. [Google Scholar]
- He, J.B.; Xie, J.; He, X.P.; Du, L.M.; Zhou, W. Research on nonlinear error of micro-accelerometers considering the fringe and parasitic capacitance. Mech. Sci. Technol. Aerosp. Eng. 2016, 35, 752–757. [Google Scholar]
- Jeong, Y.; Ayazi, F. A novel offset calibration method to suppress capacitive mismatch in MEMS accelerometer. In Proceedings of the Samsung Electro-Mechanics Best Paper Award, Seoul, Korea, 13 November 2013. [Google Scholar]
- Lajevardi, P.; Petkov, V.P.; Murmann, B. A delta sigma interface for MEMS accelerometers using electrostatic spring constant modulation for cancellation of bondwire capacitance drift. IEEE J. Solid-State Circ. 2016, 48, 265–275. [Google Scholar] [CrossRef]
- Xiong, X.X.; Wu, Y.L.; Jone, W.B. Control circuitry for self-repairable MEMS accelerometers. In Technological Developments in Education and Automation, 1st ed.; Iskander, M., Kapila, V., Karim, M.A., Eds.; Springer: Berlin, Germany, 2010; pp. 265–270. [Google Scholar]
- Ko, H. Highly configurable capacitive interface circuit for tri-axial MEMS microaccelerometer. Int. J. Electron. 2012, 99, 945–955. [Google Scholar] [CrossRef]
- Liu, M.J.; Dong, J.X. Compensation for bias in capacitive micro accelerometer. J. Chin. Inert. Technol. 2008, 16, 86–89. [Google Scholar]
- Zhou, H.Y.; Shen, T.Y.; Li, L.R.; Xu, F.Y.; Hu, J.W.; Xie, Y.H. Study on the measurement of micro-capacitance based on RLC series resonance and increment. In Proceedings of the International Conference on Mechanical, Electronic and Information Technology Engineering, Chongqing, China, 21–22 May 2016. [Google Scholar]
- Dascher, D.J. Measuring parasitic capacitance and inductance using TDR. Hewlett-Packard J. 1996, 47, 83–96. [Google Scholar]
- Li, J.; Dong, J.X.; Liu, Y.F.; Wu, T.Z. Effects of preload voltage on performance of force-rebalance micro silicon accelerometer. J. Transducer Technol. 2004, 23, 35–40. [Google Scholar]
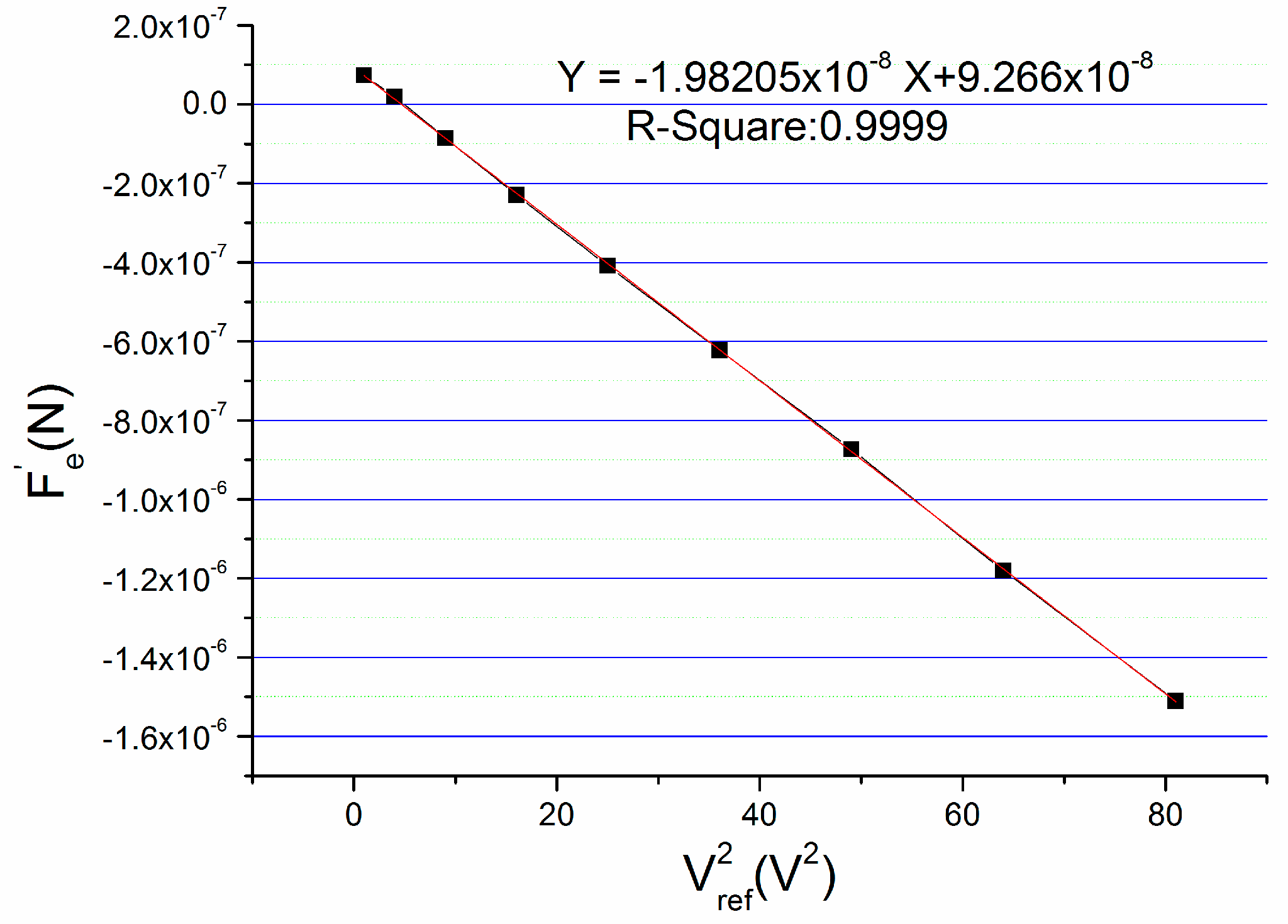
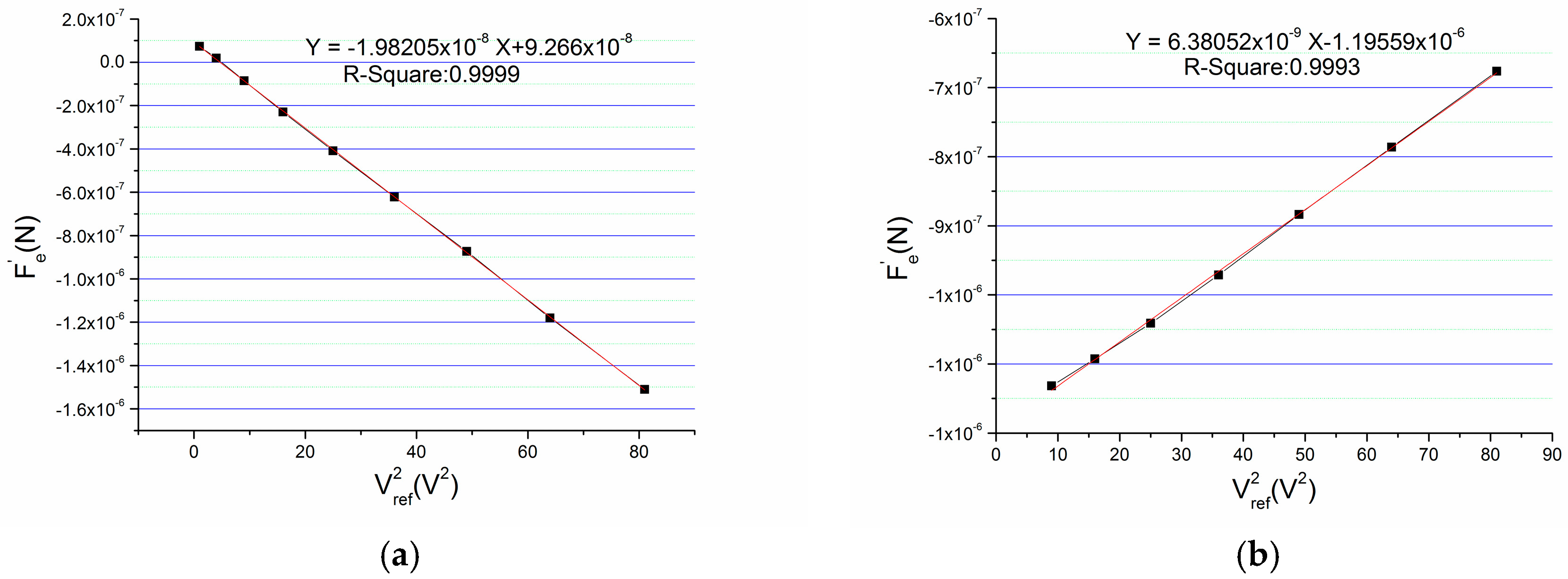
| 1.00 | 5058 | 137,837 | 1.00 | 7.33 × 10−8 |
| 2.00 | 1526 | 68,051 | 4.00 | 1.96 × 10−8 |
| 3.00 | −49 | 45,092 | 9.00 | −8.48 × 10−8 |
| 4.00 | −1079 | 33,768 | 16.00 | −2.29 × 10−7 |
| 5.00 | −1946 | 26,993 | 25.00 | −4.09 × 10−7 |
| 6.00 | −2651 | 22,491 | 36.00 | −6.22 × 10−7 |
| 7.00 | −3329 | 19,253 | 49.00 | −8.73 × 10−7 |
| 8.00 | −4043 | 16,811 | 64.00 | −1.18 × 10−6 |
| 9.00 | −4682 | 14,942 | 81.00 | −1.51 × 10−6 |
| Sensor | X2 (m) | Mismatch/fF |
|---|---|---|
| 1 | −1.12 × 10−8 | −57.64 |
| 2 | −0.99 × 10−8 | −50.95 |
| 3 | −0.98 × 10−8 | −50.43 |
| 4 | −1.14 × 10−8 | −58.67 |
| 5 | −1.17 × 10−8 | −60.21 |
| 6 | −1.18 × 10−8 | −60.73 |
| average | −1.10 × 10−8 | −56.44 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, X.; Yang, S.; Zhu, J.; En, Y.; Huang, Q. Method of Measuring the Mismatch of Parasitic Capacitance in MEMS Accelerometer Based on Regulating Electrostatic Stiffness. Micromachines 2018, 9, 128. https://doi.org/10.3390/mi9030128
Dong X, Yang S, Zhu J, En Y, Huang Q. Method of Measuring the Mismatch of Parasitic Capacitance in MEMS Accelerometer Based on Regulating Electrostatic Stiffness. Micromachines. 2018; 9(3):128. https://doi.org/10.3390/mi9030128
Chicago/Turabian StyleDong, Xianshan, Shaohua Yang, Junhua Zhu, Yunfei En, and Qinwen Huang. 2018. "Method of Measuring the Mismatch of Parasitic Capacitance in MEMS Accelerometer Based on Regulating Electrostatic Stiffness" Micromachines 9, no. 3: 128. https://doi.org/10.3390/mi9030128
APA StyleDong, X., Yang, S., Zhu, J., En, Y., & Huang, Q. (2018). Method of Measuring the Mismatch of Parasitic Capacitance in MEMS Accelerometer Based on Regulating Electrostatic Stiffness. Micromachines, 9(3), 128. https://doi.org/10.3390/mi9030128




