Design, Fabrication, and Performance Characterization of LTCC-Based Capacitive Accelerometers
Abstract
1. Introduction
2. Structure Design and Process Optimization
3. Signal Processing Methods
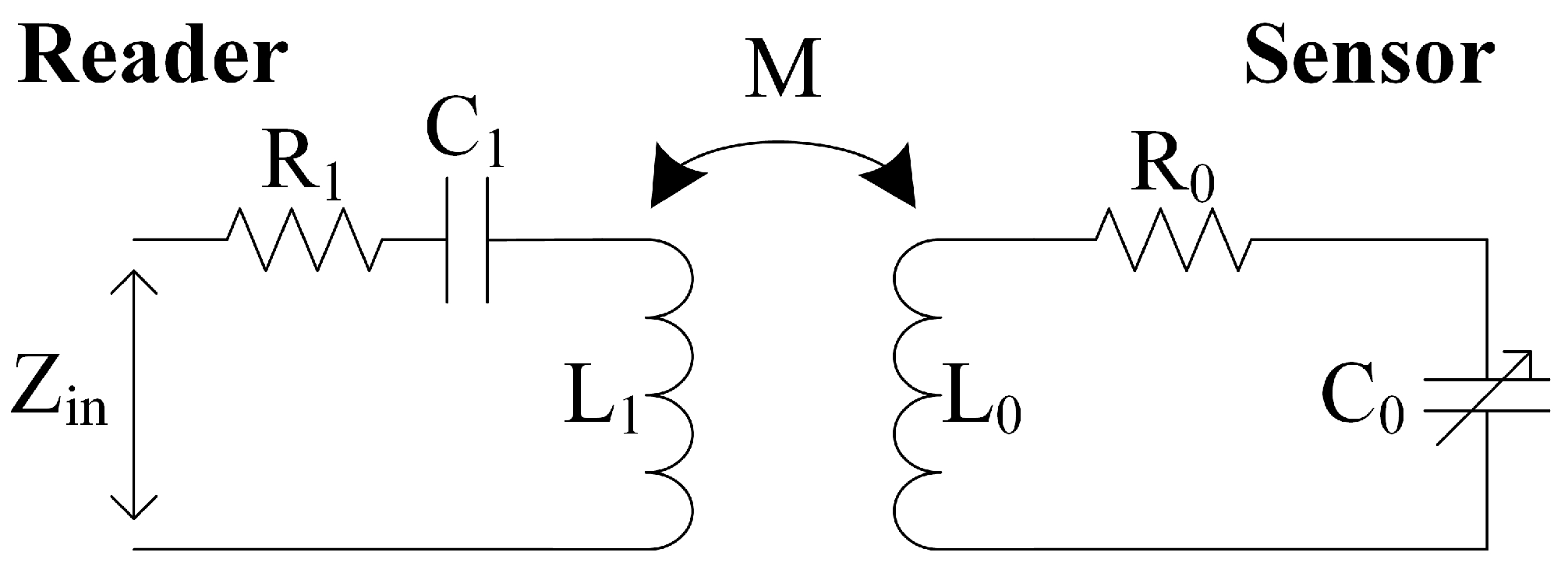
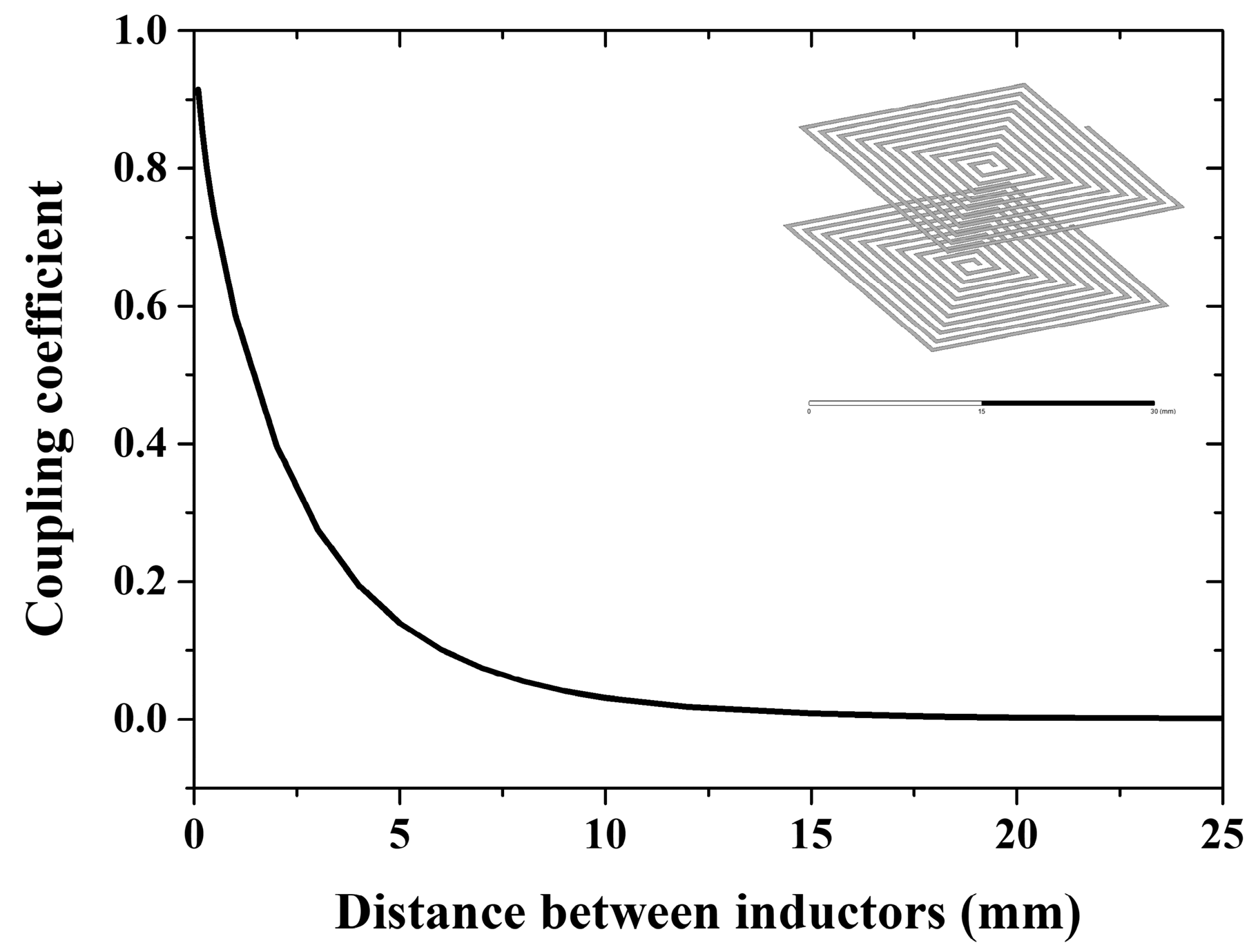
3.1. Coupling Resonance Frequency Sensing
3.2. Differential Capacitive Sensing
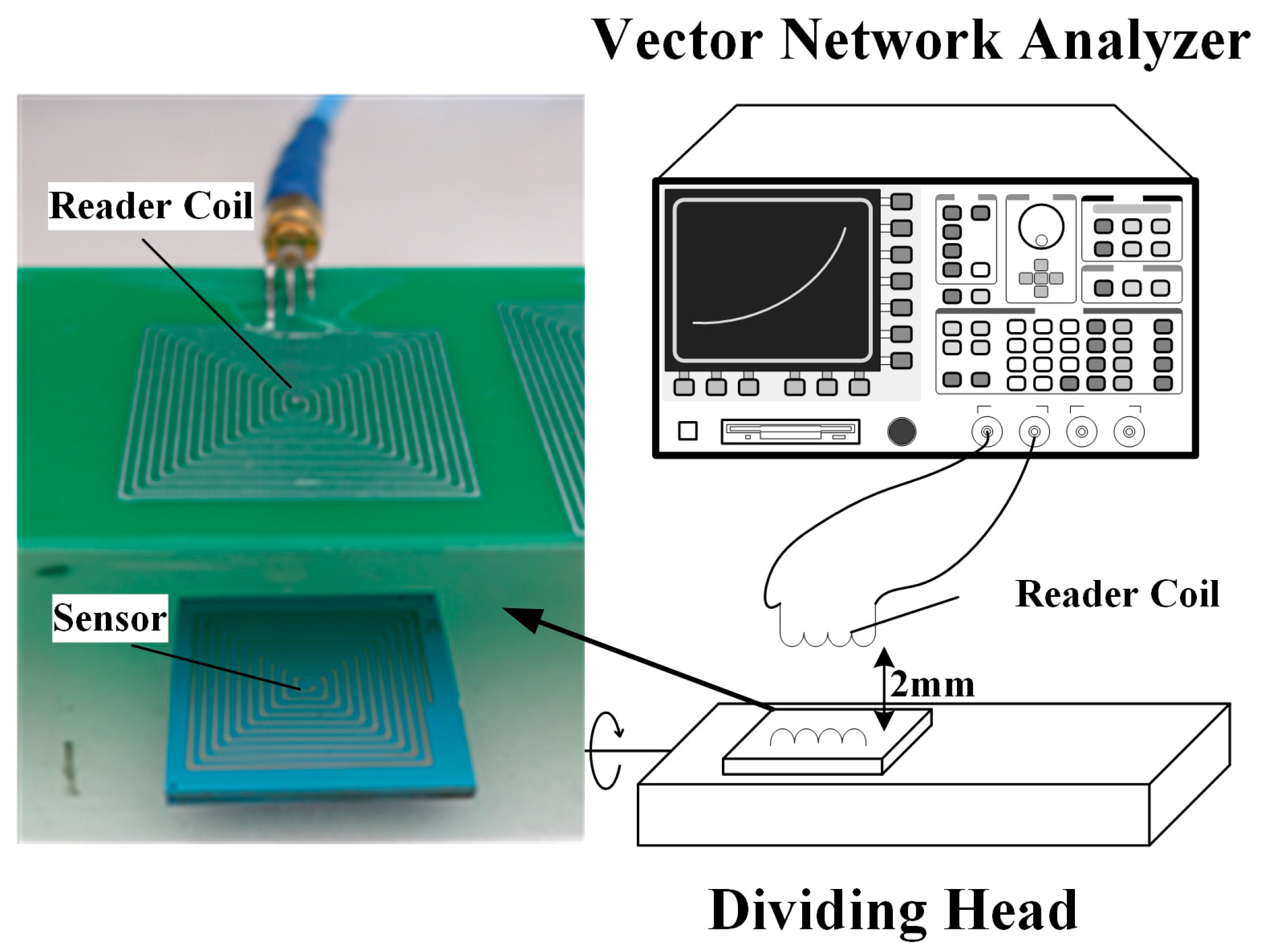
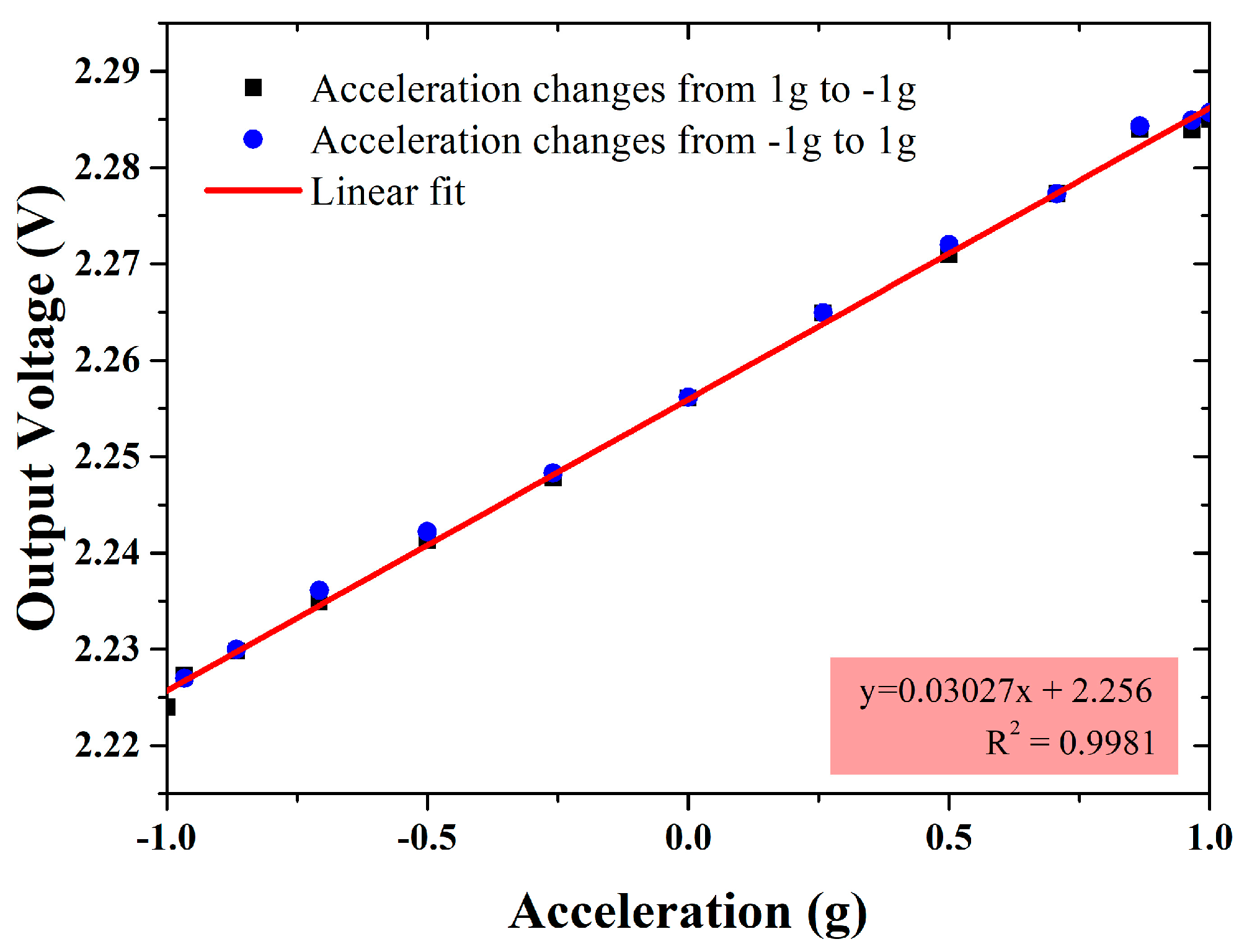
4. Performance Characterization
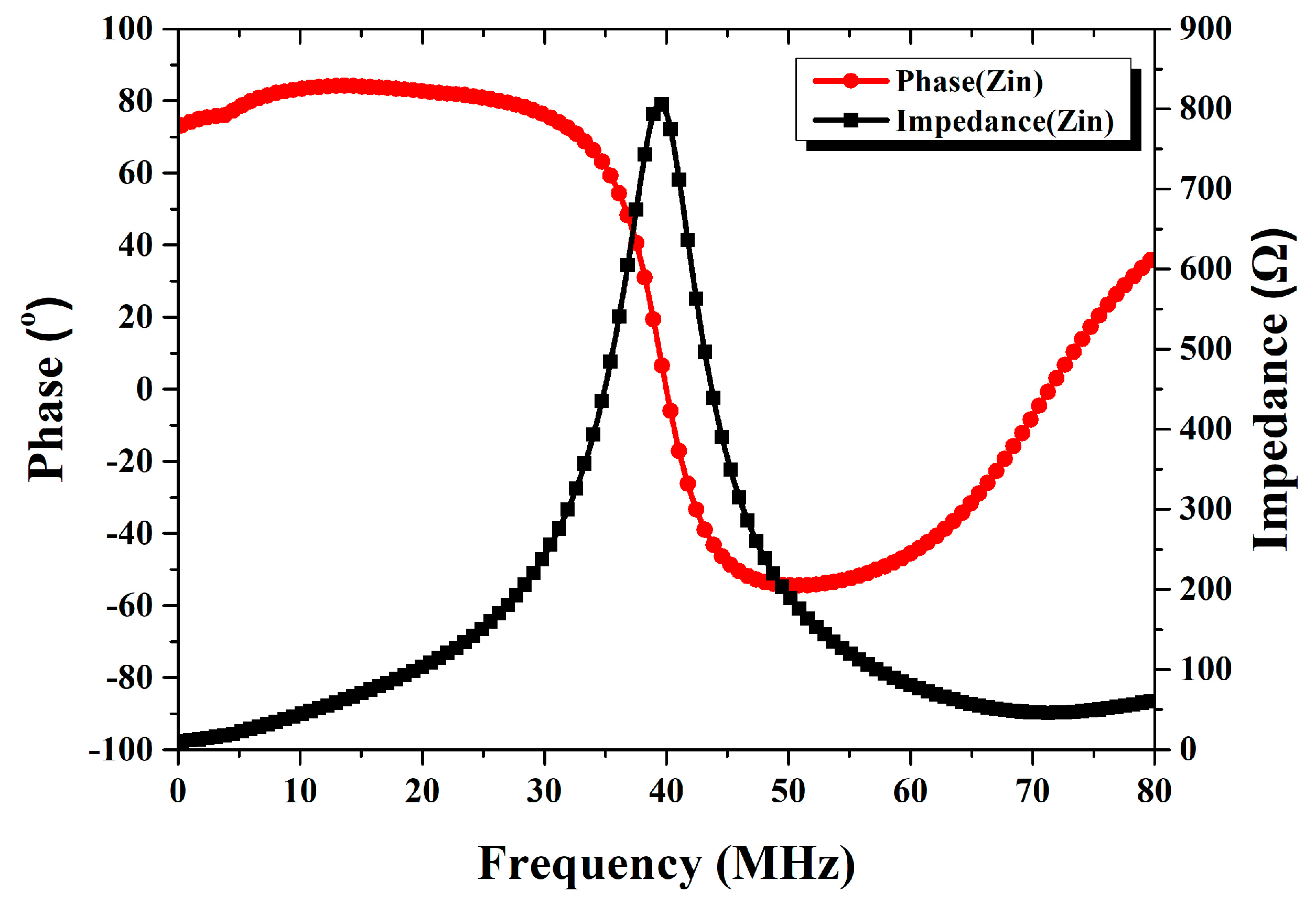
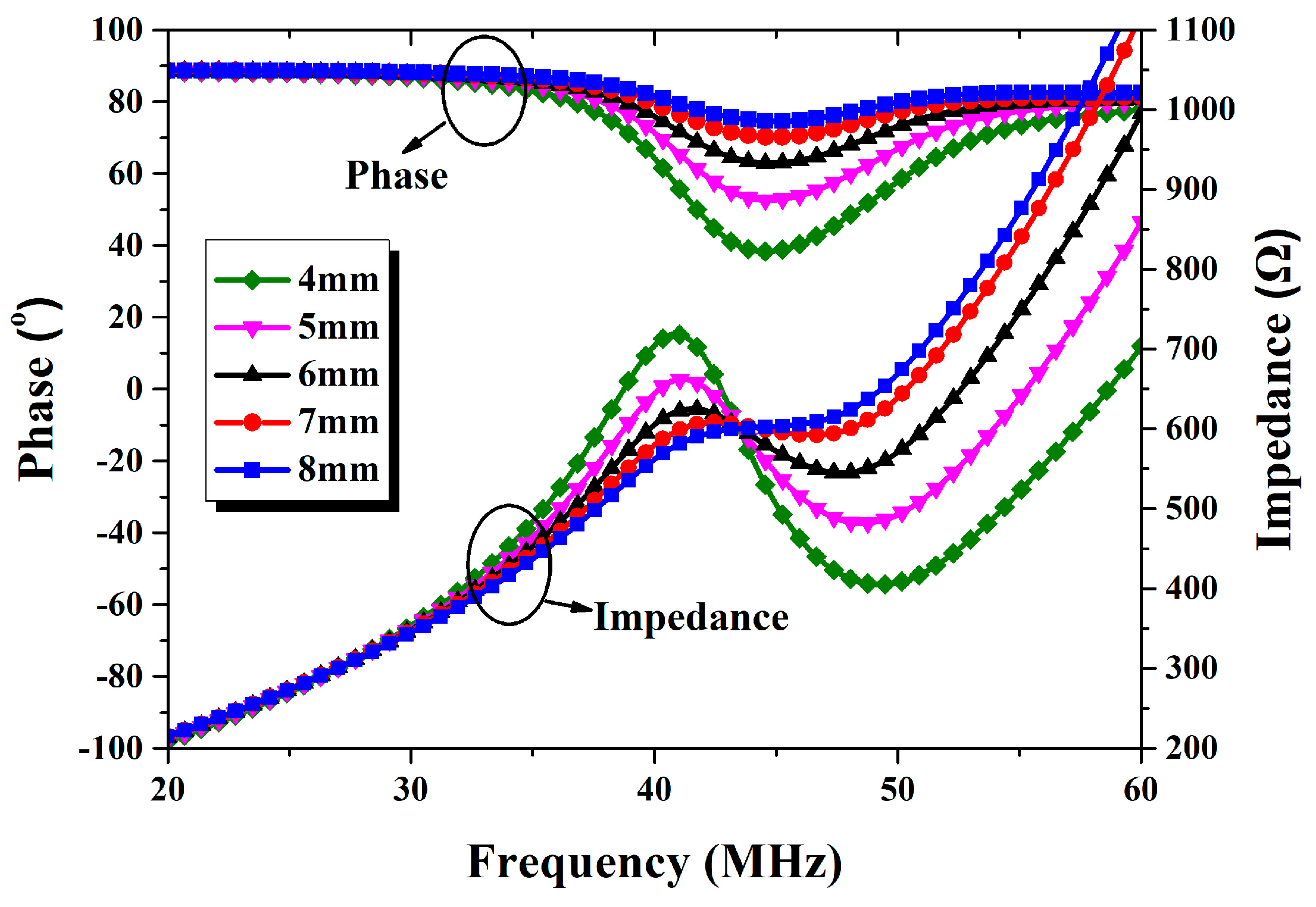
4.1. LC Resonant Accelerometer
4.2. Differential Capacitive Accelerometer
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ko, Y.-J.; Park, J.Y.; Ryu, J.-H.; Lee, K.-H.; Bu, J.U. A miniaturized LTCC multi-layered front-end module for dual band WLAN (802.11 a/b/g) applications. In Proceedings of the 2004 IEEE MTT-S International Microwave Symposium Digest, Fort Worth, TX, USA, 6–11 June 2004; pp. 563–566. [Google Scholar]
- Ponchak, G.E.; Chun, D.H.; Yook, J.G.; Katehi, L.P.B. The use of metal filled via holes for improving isolation in LTCC RF and wireless multichip packages. IEEE Trans. Adv. Packag. 2000, 23, 88–99. [Google Scholar] [CrossRef]
- Miao, M.; Jin, Y.F.; Fang, R.N.; Mu, F.Q.; Guo, S.C.; Zhang, X.Q.; Zhang, Y.; Hu, D.W.; Li, Z.S.; Xiang, W. Investigation of Micromachined LTCC Functional Modules for High-density 3D SIP based on LTCC Packaging Platform. In Proceedings of the IEEE 63rd Electronic Components and Technology Conference (ECTC), Las Vegas, NV, USA, 28–31 May 2014; pp. 1815–1822. [Google Scholar]
- Darko, E.; Thurbide, K.B.; Gerhardt, G.C.; Michienzi, J. Characterization of Low-Temperature Cofired Ceramic Tiles as Platforms for Gas Chromatographic Separations. Anal. Chem. 2013, 85, 5376–5381. [Google Scholar] [CrossRef] [PubMed]
- Goldbacha, M.; Axthelm, H.; Keusgen, M. LTCC-based microchips for the electrochemical detection of phenolic compounds. Sens. Actuator B-Chem. 2006, 120, 346–351. [Google Scholar] [CrossRef]
- Malecha, K.; Remiszewska, E.; Pijanowska, D.G. Technology and application of the LTCC-based microfluidic module for urea determination. Microelectron. Int. 2015, 32, 126–132. [Google Scholar] [CrossRef]
- Sadler, D.J.; Changrani, R.; Roberts, P.; Chou, C.F.; Zenhausern, F. Thermal management of BioMEMS: Temperature control for ceramic-based PCR and DNA detection devices. IEEE Trans. Compon. Packag. Technol. 2003, 26, 309–316. [Google Scholar] [CrossRef]
- Xu, W.; Yang, J.; Xie, G.; Wang, B.; Qu, M.; Wang, X.; Liu, X.; Tang, B. Design and Fabrication of a Slanted-Beam MEMS Accelerometer. Micromachines 2017, 8, 77. [Google Scholar] [CrossRef]
- Li, W.; Song, Z.; Li, X.; Che, L.; Wang, Y. A novel sandwich capacitive accelerometer with a double-sided 16-beam-mass structure. Microelectron. Eng. 2014, 115, 32–38. [Google Scholar] [CrossRef]
- Li, Z.; Wu, W.J.; Zheng, P.P.; Liu, J.Q.; Fan, J.; Tu, L.C. Novel Capacitive Sensing System Design of a Microelectromechanical Systems Accelerometer for Gravity Measurement Applications. Micromachines 2016, 7, 167. [Google Scholar] [CrossRef]
- Neubert, H.; Partsch, U.; Fleischer, D.; Gruchow, M.; Kamusella, A.; Pham, T.-Q. Thick Film Accelerometers in LTCC Technology—Design Optimization, Fabrication, and Characterization. JMEP 2008, 5, 150–155. [Google Scholar] [CrossRef][Green Version]
- Jurkow, D.; Dabrowski, A.; Golonka, L.; Zawada, T. Preliminary Model and Technology of Piezoelectric Low Temperature Co-fired Ceramic (LTCC) Uniaxial Accelerometer. Int. J. Appl. Ceram. Technol. 2013, 10, 395–404. [Google Scholar] [CrossRef]
- Jurkow, D. Three axial low temperature cofired ceramic accelerometer. Microelectron. Int. 2013, 30, 125–133. [Google Scholar] [CrossRef]
- Hua, G.; Yufeng, J.; Min, M.; Xin, S. A novel LTCC capacitive accelerometer embedded in LTCC packaging substrate. In Proceedings of the 2011 6th IEEE International Conference on Nano/Micro Engineered and Molecular Systems (NEMS 2011), Kaohsiung, Taiwan, 20–23 February 2011; pp. 796–799. [Google Scholar]
- Imanaka, Y. Multilayered Low Temperature Cofired Ceramics (LTCC) Technology, 1st ed.; Springer: New York, NY, USA, 2005. [Google Scholar]
- Technical Datasheet of 951 Low Temperature Ceramic System. Available online: http://www.dupont.com/content/dam/dupont/products-and-services/electronic-and-electrical-materials/documents/prodlib/951.pdf (accessed on 20 December 2017).
- Birol, H.; Maeder, T.; Ryser, P. Processing of graphite-based sacrificial layer for microfabrication of low temperature co-fired ceramics (LTCC). Sens. Actuator A Phys. 2006, 130, 560–567. [Google Scholar] [CrossRef]
- Khoong, L.E.; Tan, Y.M.; Lam, Y.C. Overview on fabrication of three-dimensional structures in multi-layer ceramic substrate. J. Eur. Ceram. Soc. 2010, 30, 1973–1987. [Google Scholar] [CrossRef]
- Xiong, J.J.; Li, Y.; Hong, Y.P.; Zhang, B.Z.; Cui, T.H.; Tan, Q.L.; Zheng, S.J.; Liang, T. Wireless LTCC-based capacitive pressure sensor for harsh environment. Sens. Actuator A Phys. 2013, 197, 30–37. [Google Scholar] [CrossRef]
- Tan, Q.L.; Yang, M.L.; Luo, T.; Liu, W.; Li, C.; Xue, C.Y.; Liu, J.; Zhang, W.D.; Xiong, J.J. A Novel Interdigital Capacitor Pressure Sensor Based on LTCC Technology. J. Sens. 2014, 431503. [Google Scholar] [CrossRef]
- Sardini, E.; Serpelloni, M. High-temperature measurement system with wireless electronics for harsh environments. In Proceedings of the 2011 IEEE Sensors Applications Symposium (SAS), San Antonio, TX, USA, 22–24 February 2011; pp. 256–261. [Google Scholar]
- Radosavljevic, G. Wireless LTCC sensors for monitoring of pressure, temperature and moisture. Inf. MIDEM-J. Microelectron. Electron. Compon. Mater. 2012, 42, 272–281. [Google Scholar]
- Nopper, R.; Niekrawietz, R.; Reindl, L. Wireless Readout of Passive LC Sensors. IEEE Trans. Instrum. Meas. 2010, 59, 2450–2457. [Google Scholar] [CrossRef]
- Mohan, S.S.; Hershenson, M.D.; Boyd, S.P.; Lee, T.H. Simple accurate expressions for planar spiral inductances. IEEE J. Solid-State Circuit 1999, 34, 1419–1424. [Google Scholar] [CrossRef]
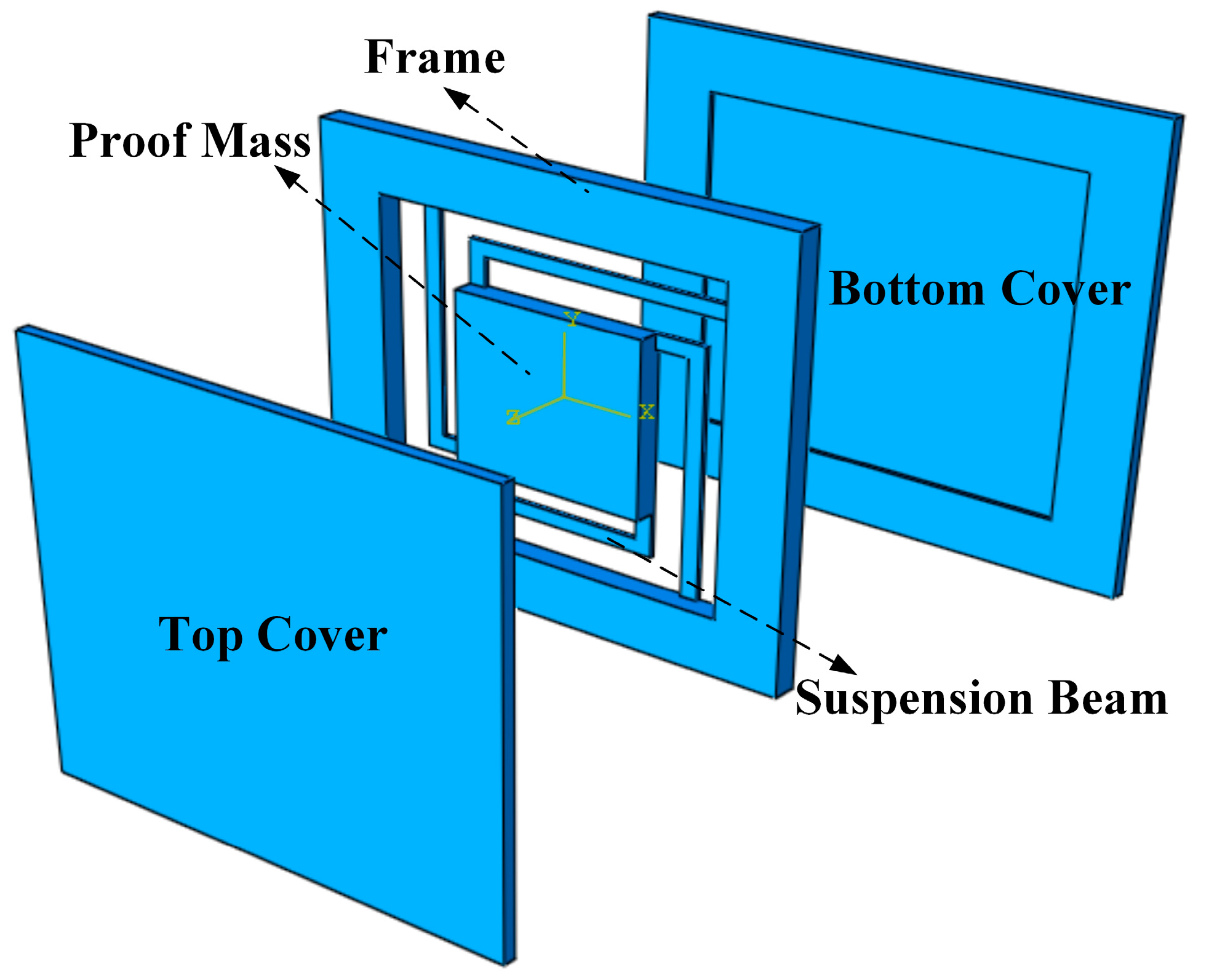
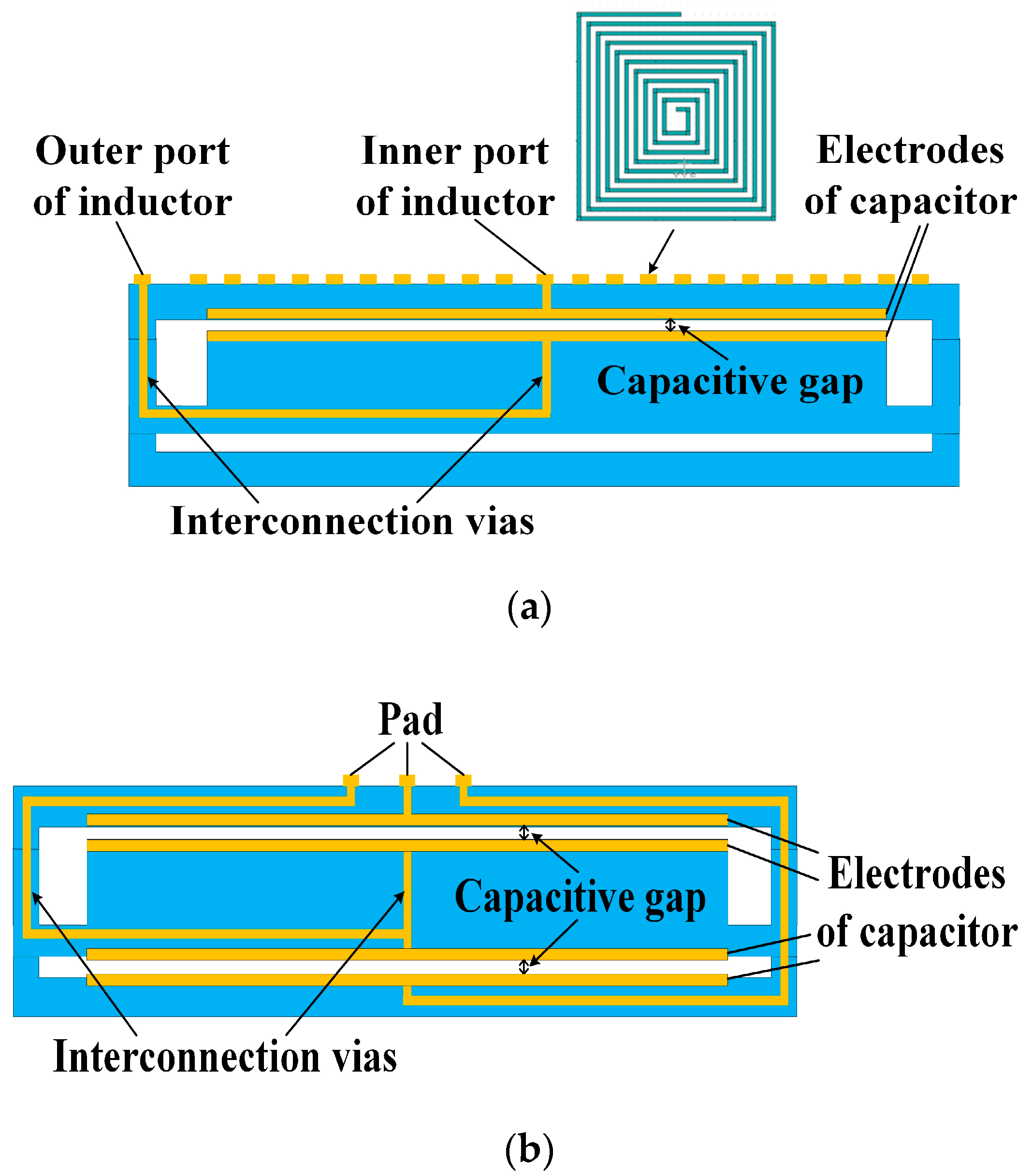

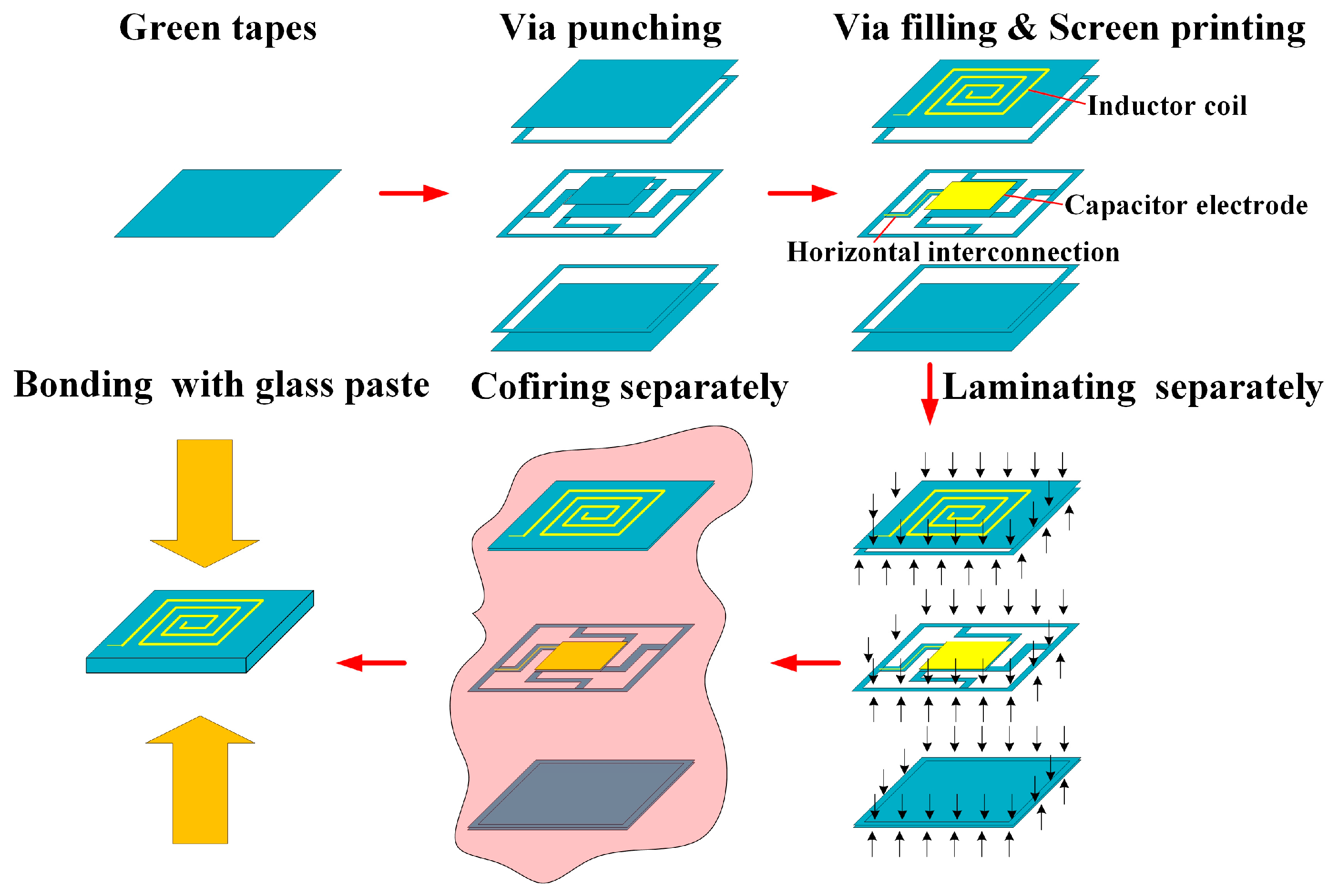





| Dimension Parameters | Value |
|---|---|
| Middle frame/top cover/bottom cover | 30 mm × 30 mm × 1.5 mm/0.4 mm/0.4 mm |
| Cavity | 22 mm × 22 mm × 1.7 mm |
| Proof mass | 12 mm × 12 mm × 1.5 mm |
| L-shapedd beam | 16 mm × 1 mm × 0.3 mm |
| Z-shapedd beam | 6 mm × 1 mm × 0.3 mm |
| Anchor of Z-shapedd beam | 3 mm × 3 mm × 0.3 mm |
| Capacitive gap | 0.1 mm |
| Parameters | L-Shaped Beams | Z-Shaped Beams |
|---|---|---|
| Displacement sensitivity | 2.99 μm/g | 0.321 μm/g |
| First resonance frequency | 291 Hz | 885 Hz |
| Second resonance frequency | 634 Hz | 1549 Hz |
| Third resonance frequency | 634 Hz | 1549 Hz |
| Parameters | Value |
|---|---|
| Inner diameter of inductor coil | 2.5 mm |
| Outer diameter of inductor coil | 25.3 mm |
| Number of turns | 10 |
| Line width of coil | 0.5 mm |
| Line spacing of coil | 0.7 mm |
| Capacitor dimension | 12 mm × 12 mm |
| Gap between capacitor electrodes | 0.1 mm |
| Parameters | LC Resonant Accelerometer | Differential Capacitive Accelerometer |
|---|---|---|
| Type of beams | L-shaped beams | Z-shaped beams |
| Sensitivity | 375 kHz/g (1.88 μm/g) | 30.27 mV/g (0.844 μm/g) |
| Full scale range | 1 g | 10 g |
| Zero offset | 40.12 MHz | 2.255 V |
| Nonlinearity | Less than 6% | Less than 1% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Fang, R.; Miao, M.; Zhang, Y.; Yan, Y.; Tang, X.; Lu, H.; Jin, Y. Design, Fabrication, and Performance Characterization of LTCC-Based Capacitive Accelerometers. Micromachines 2018, 9, 120. https://doi.org/10.3390/mi9030120
Liu H, Fang R, Miao M, Zhang Y, Yan Y, Tang X, Lu H, Jin Y. Design, Fabrication, and Performance Characterization of LTCC-Based Capacitive Accelerometers. Micromachines. 2018; 9(3):120. https://doi.org/10.3390/mi9030120
Chicago/Turabian StyleLiu, Huan, Runiu Fang, Min Miao, Yichuan Zhang, Yingzhan Yan, Xiaoping Tang, Huixiang Lu, and Yufeng Jin. 2018. "Design, Fabrication, and Performance Characterization of LTCC-Based Capacitive Accelerometers" Micromachines 9, no. 3: 120. https://doi.org/10.3390/mi9030120
APA StyleLiu, H., Fang, R., Miao, M., Zhang, Y., Yan, Y., Tang, X., Lu, H., & Jin, Y. (2018). Design, Fabrication, and Performance Characterization of LTCC-Based Capacitive Accelerometers. Micromachines, 9(3), 120. https://doi.org/10.3390/mi9030120






