Low Phase Noise, Dual-Frequency Pierce MEMS Oscillators with Direct Print Additively Manufactured Amplifier Circuits
Abstract
1. Introduction
2. Materials and Methods
2.1. Phase Noise
2.2. Piezoelectric ZnO-on-SOI MEMS Resonators
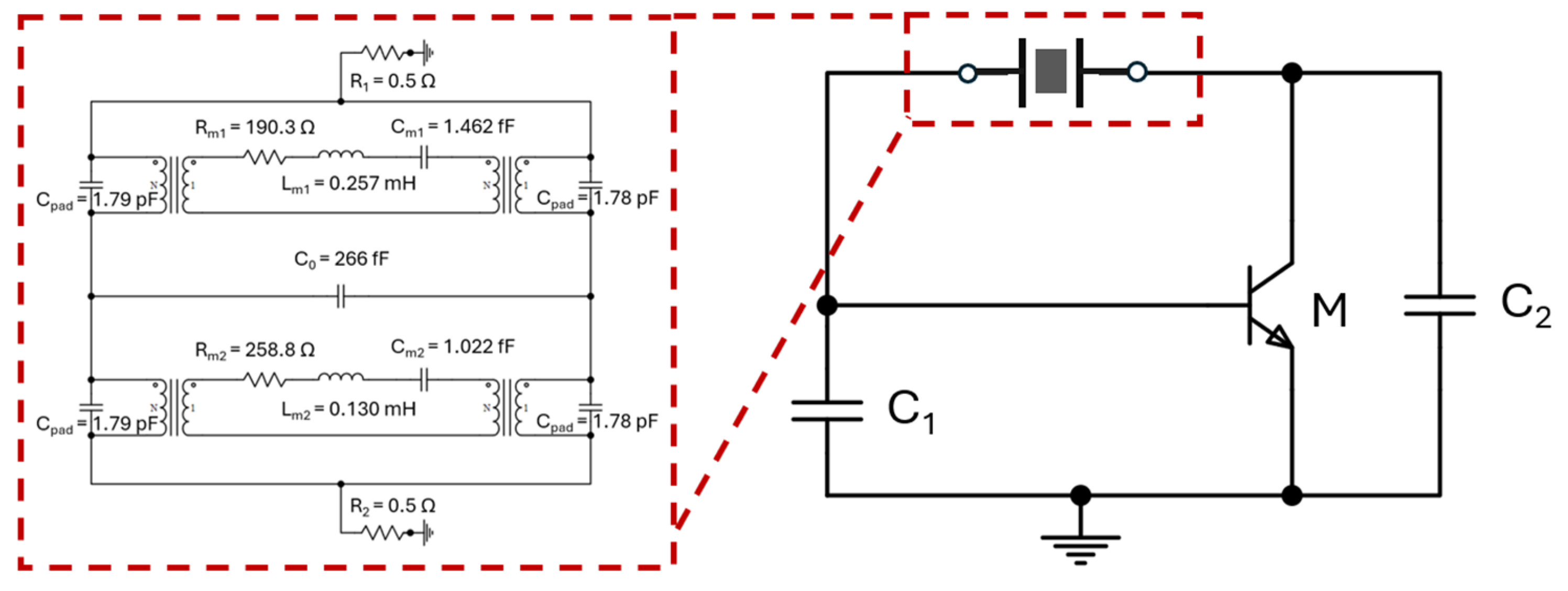
2.3. Customized Pierce Oscillator Circuit for Selected Transistors
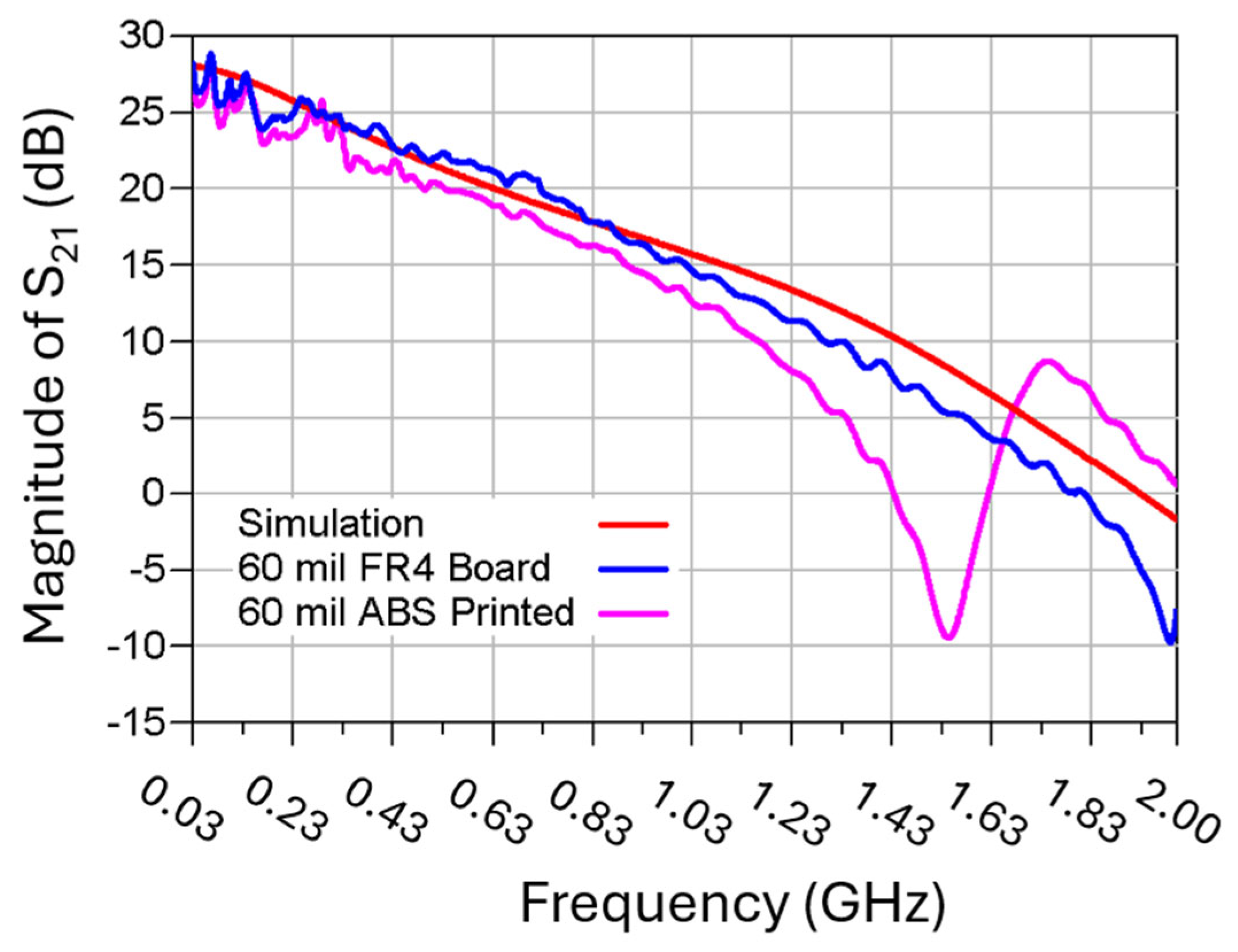
2.4. 3D-Printing Process
3. Results and Discussion
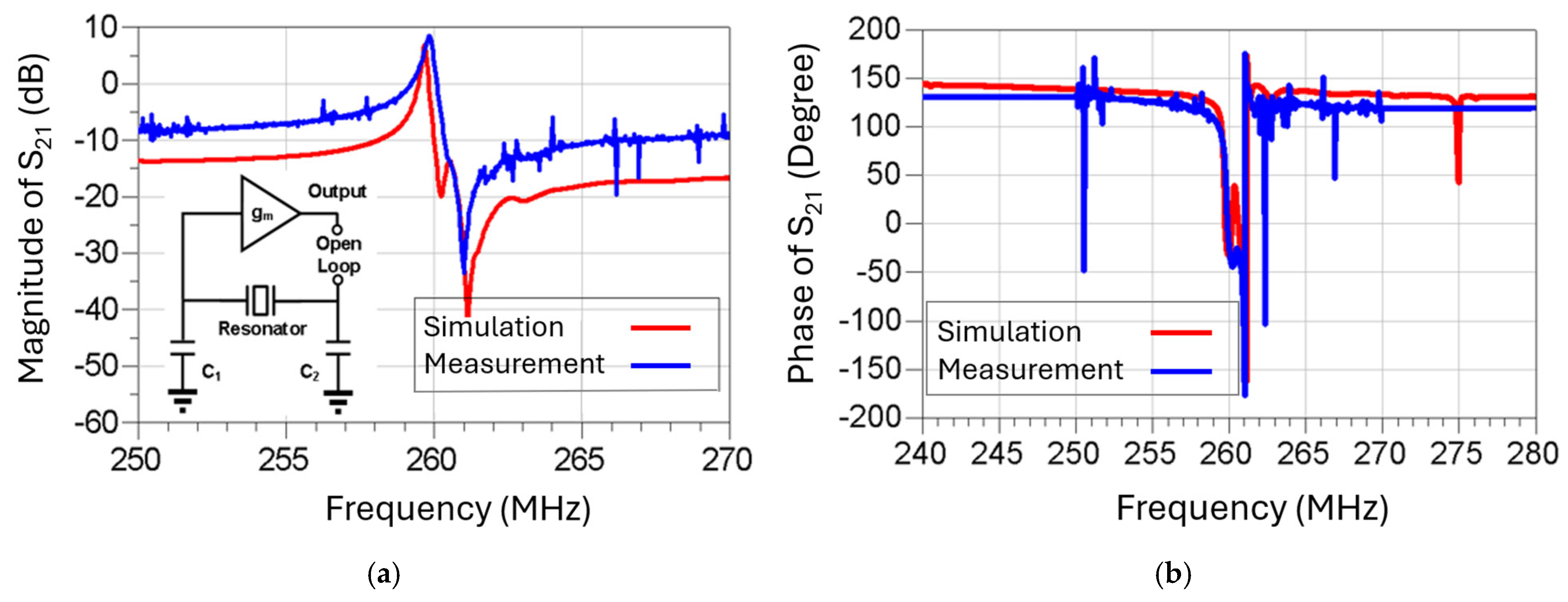
3.1. Piezoelectric ZnO-on-SOI MEMS Resonators
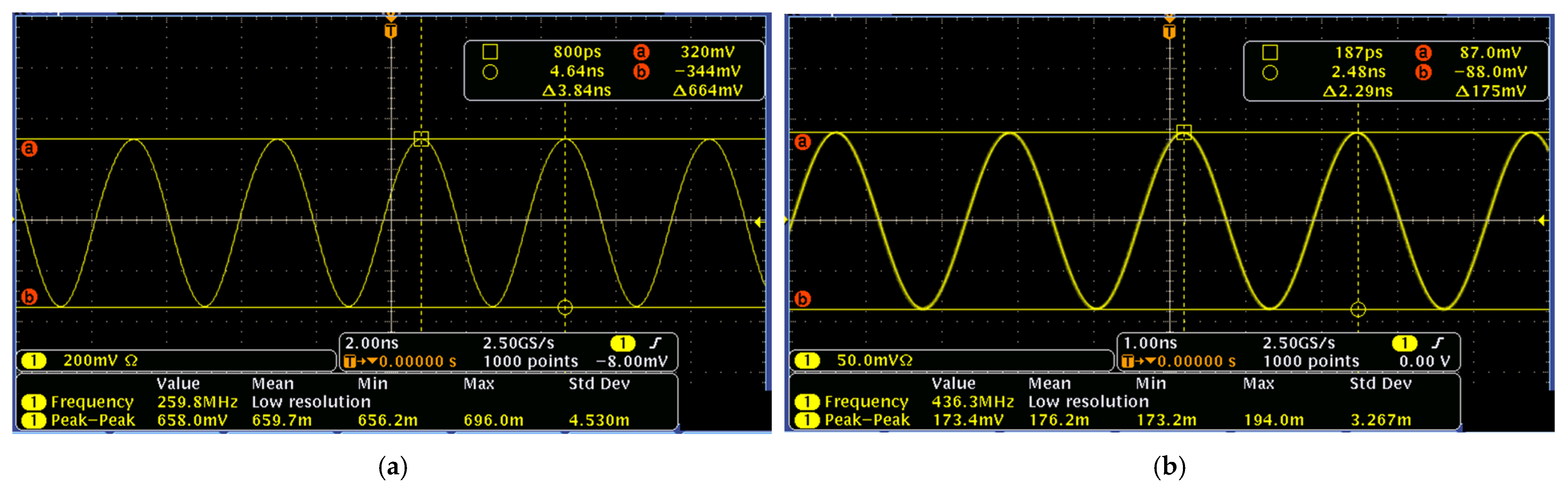
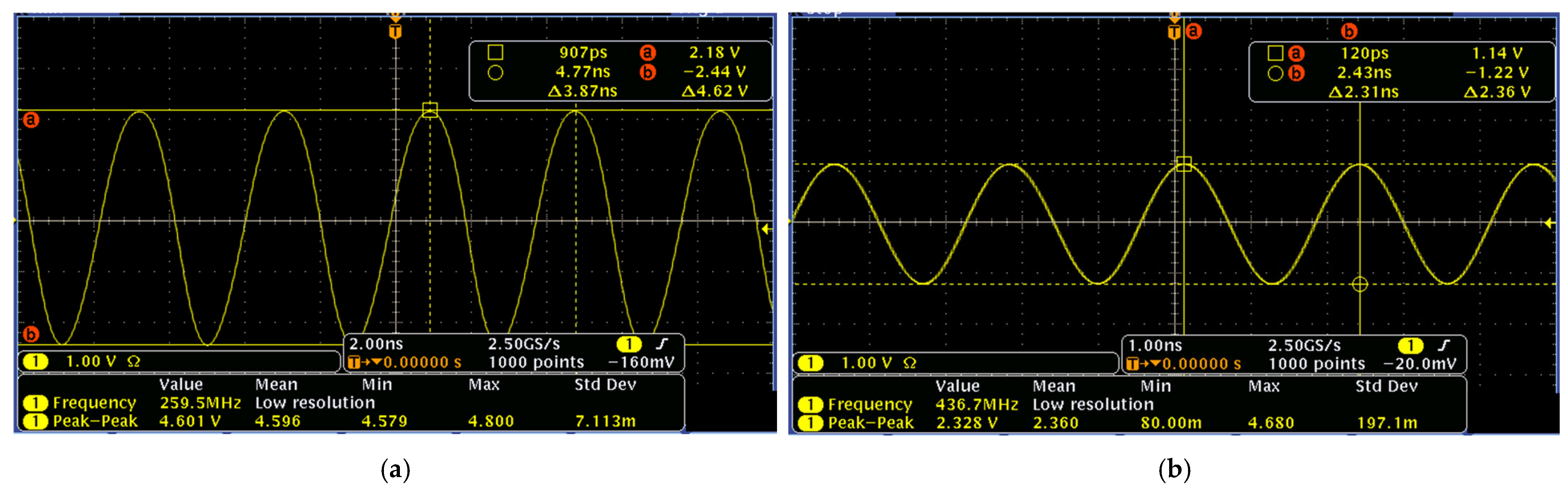
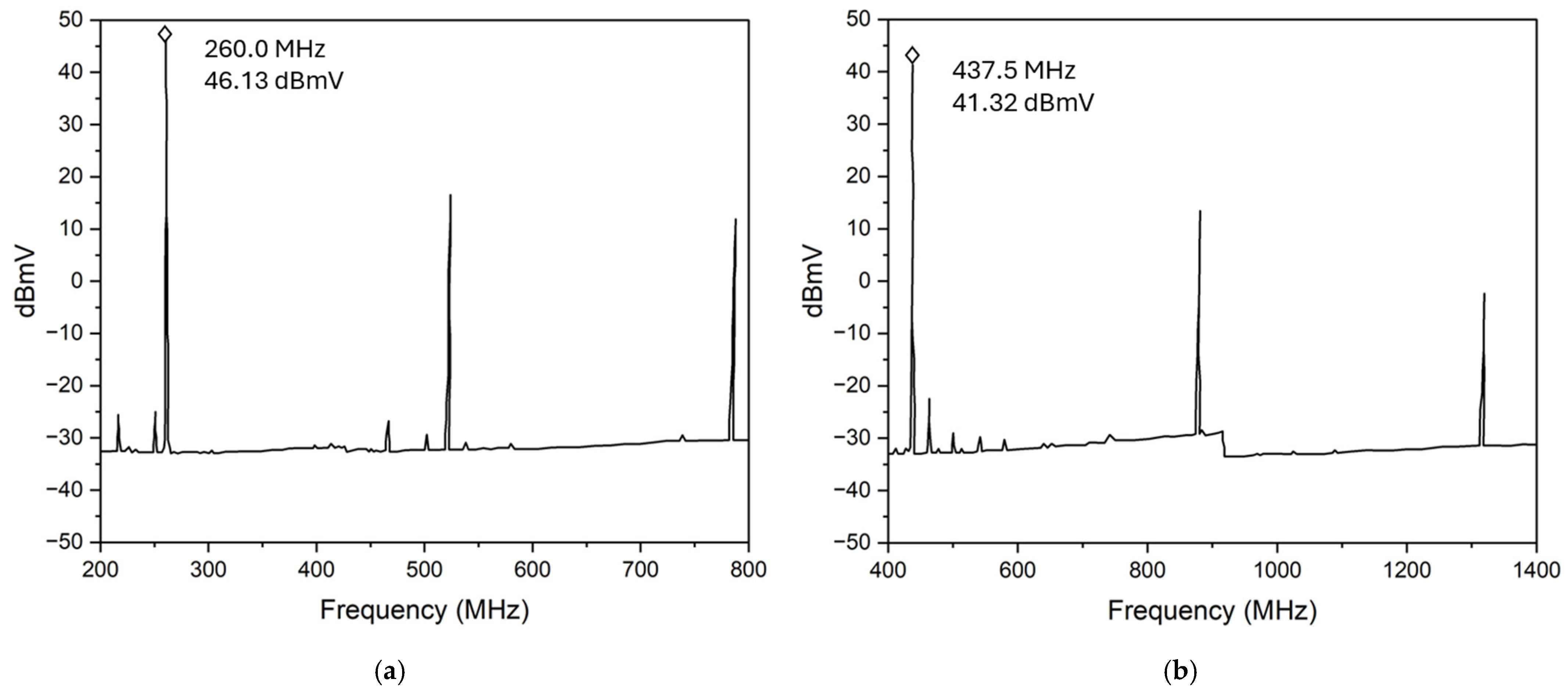
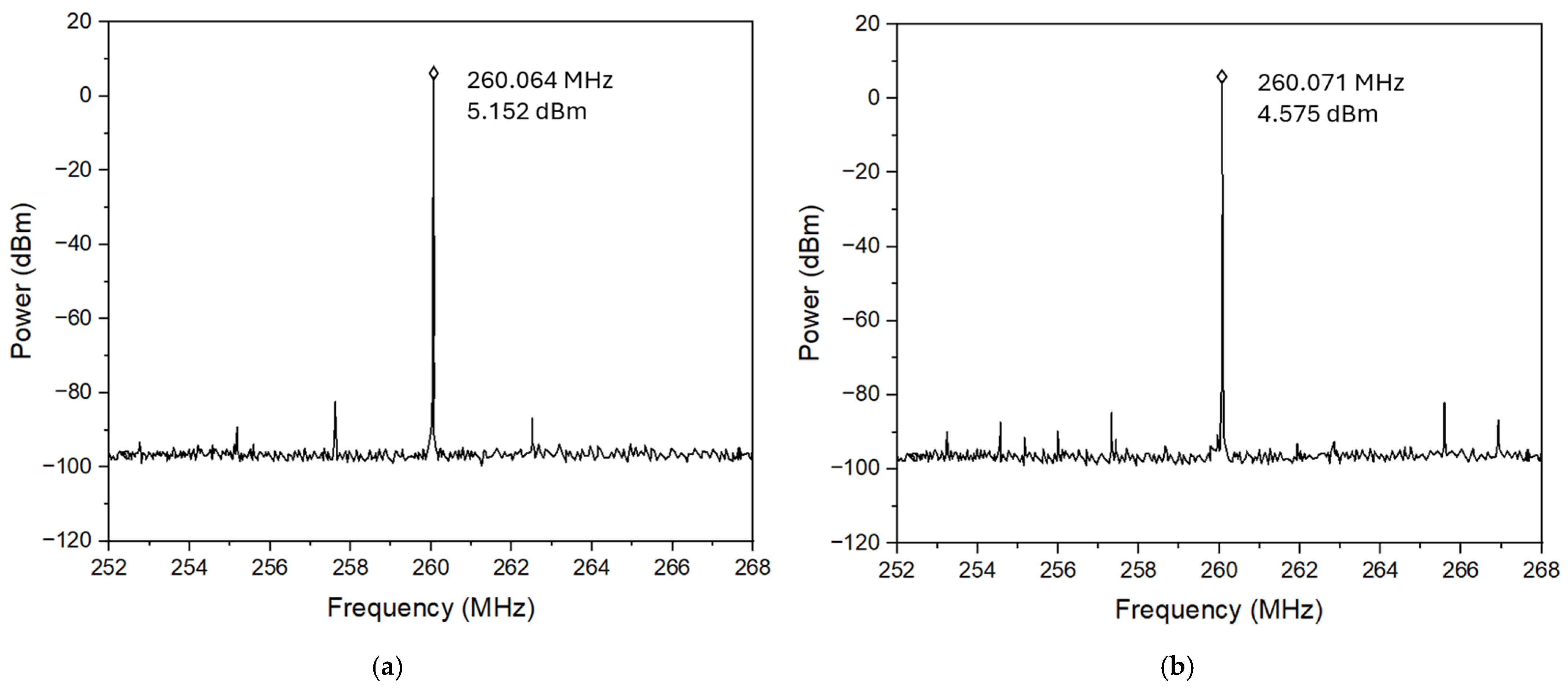
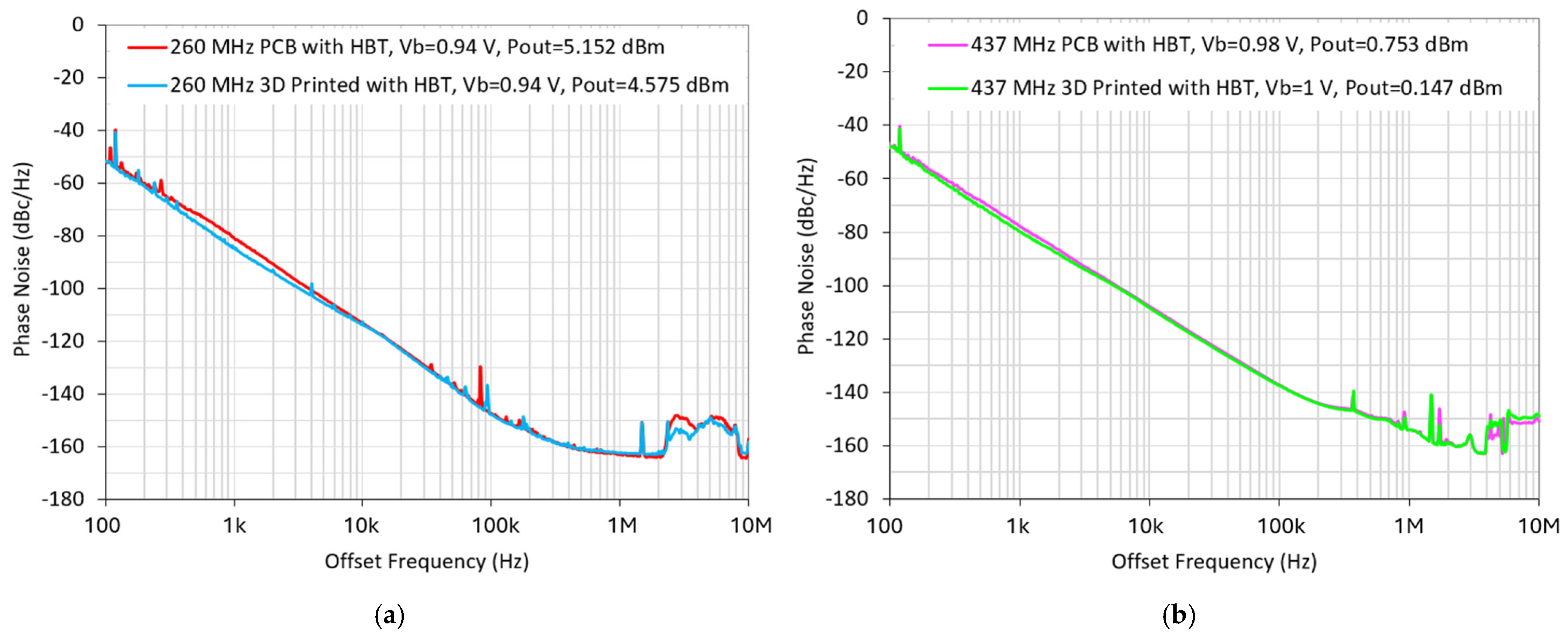
3.2. Pierce Oscillator with Selected Transistors
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nguyen, C.T.-C. MEMS Technology for Timing and Frequency Control. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2007, 54, 251–270. [Google Scholar] [CrossRef]
- Wu, G.; Xu, J.; Ng, E.J.; Chen, W. MEMS Resonators for Frequency Reference and Timing Applications. J. Microelectromech. Syst. 2020, 29, 1137–1166. [Google Scholar] [CrossRef]
- Lam, C.S. A review of the recent development of MEMS and crystal oscillators and their impacts on the frequency control products industry. In Proceedings of the IEEE International Ultrasonics Symposium (IUS), Beijing, China, 2–5 November 2008. [Google Scholar]
- Lavasani, H.M.; Abdolvand, R.; Ayazi, F. A 500MHz Low Phase-Noise AlN-on-Silicon Reference Oscillator. In Proceedings of the IEEE Custom Integrated Circuits Conference, San Jose, CA, USA, 16–19 September 2007. [Google Scholar]
- Kira, A.; Elsayed, M.Y.; Allidina, K.; Chodavarapu, V.P.; El-Gamal, M.N. A 6.7 μW Low-Noise, Compact PLL with an Input MEMS-Based Reference Oscillator Featuring a High-Resolution Dead/Blind Zone-Free PFD. Sensors 2024, 24, 7963. [Google Scholar] [CrossRef]
- Hsu, W. Vibrating RF MEMS for Timing and Frequency References. In Proceedings of the IEEE MTT-S International Microwave Symposium Digest, San Francisco, CA, USA, 11–16 June 2006. [Google Scholar]
- Van Beek, J.; Puers, R. A review of MEMS oscillators for frequency reference and timing applications. J. Micromech. Microeng. 2012, 22, 013001. [Google Scholar] [CrossRef]
- Zaman, A.; Guneroglu, U.; Alsolami, A.; Wang, J. Piezoelectrically and Capacitively Transduced Hybrid MEMS Resonator with Superior RF Performance and Enhanced Parasitic Mitigation by Low-Temperature Batch Fabrication. Appl. Sci. 2024, 14, 8166. [Google Scholar] [CrossRef]
- Chen, H.-Y.; Li, S.-S.; Li, M.-H. A Low Impedance CMOS-MEMS Capacitive Resonator Based on Metal-Insulator-Metal (MIM) Capacitor Structure. IEEE Electron Device Lett. 2021, 42, 1045–1048. [Google Scholar] [CrossRef]
- Feng, T.; Yuan, Q.; Yu, D.; Wu, B.; Wang, H. Concepts and Key Technologies of Microelectromechanical Systems Resonators. Micromachines 2022, 13, 2195. [Google Scholar] [CrossRef]
- Chen, H.-Y.; Shih, P.-I.; Li, M.-H.; Li, S.-S. 5V-Bias Cmos-Mems Capacitive Resonator with RM <5KΩ Based On Metal-Insulator-Metal (Mim) Capacitor. In Proceedings of the IEEE 35th International Conference on Micro Electro Mechanical Systems Conference (MEMS), Tokyo, Japan, 9–13 January 2022. [Google Scholar]
- Liu, W.; Lu, Y.; Chen, Z.; Jia, Q.; Zhao, J.; Niu, B.; Wang, W.; Hao, Y.; Zhu, Y.; Yang, J.; et al. A GHz Silicon-Based Width Extensional Mode MEMS Resonator with Q over 10,000. Sensors 2023, 23, 3808. [Google Scholar] [CrossRef]
- Piazza, G.; Stephanou, P.J.; Pisano, A.P. Piezoelectric Aluminum Nitride Vibrating Contour-Mode MEMS Resonators. J. Microelectromech. Syst. 2006, 15, 1406–1418. [Google Scholar] [CrossRef]
- Zuo, C.; Van Der Spiegel, J.; Piazza, G. 1.05-GHz CMOS oscillator based on lateral- field-excited piezoelectric AlN contour- mode MEMS resonators. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2010, 57, 82–87. [Google Scholar] [CrossRef]
- Kaisar, T.; Yousuf, S.M.E.H.; Lee, J.; Qamar, A.; Rais-Zadeh, M.; Mandal, S.; Feng, P.X.-L. Five Low-Noise Stable Oscillators Referenced to the Same Multimode AlN/Si MEMS Resonator. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2023, 70, 1213–1228. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.-W.; Lee, S.; Li, S.-S.; Xie, Y.; Ren, Z.; Nguyen, C.T.-C. Series-resonant VHF micromechanical resonator reference oscillators. IEEE J. Solid-State Circuits 2004, 39, 2477–2491. [Google Scholar] [CrossRef]
- Zampetti, E.; Pantalei, S.; Macagnanoa, A.; Proietti, E.; Di Natale, C.; D’Amico, A. Use of a Multiplexed Oscillator in a Miniaturized Electronic Nose based on a Multichannel Quartz Crystal Microbalance. Sens. Actuators B Chem. 2008, 131, 159–166. [Google Scholar] [CrossRef]
- Wang, J.; Ren, Z.; Nguyen, C.T.-C. 1.156-GHz self-aligned vibrating micromechanical disk resonator. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2004, 51, 1607–1628. [Google Scholar] [CrossRef]
- Naing, T.L.; Rocheleau, T.O.; Ren, Z.; Li, S.-S.; Nguyen, C.T.-C. High-Q UHF Spoke-Supported Ring Resonators. J. Microelectromech. Syst. 2016, 25, 11–29. [Google Scholar] [CrossRef]
- Alameh, A.H.; Bouchami, A.; Nabki, F. A wide voltage range charge pump in 0.13 μm CMOS for biasing of MEMS resonators. In Proceedings of the IEEE International Conference on Electronics, Circuits and Systems (ICECS), Monte Carlo, Monaco, 11–14 December 2016. [Google Scholar]
- Huang, L.; Feng, Z.; Xiao, Y.; Sun, F.; Xu, J. High-Q and Low-Motional Impedance Piezoelectric mems Resonator through Mechanical Mode Coupling. In Proceedings of the IEEE 36th International Conference on Micro Electro Mechanical Systems (MEMS), Munich, Germany, 15–19 January 2023. [Google Scholar]
- Jin, H.; Zhou, J.; He, X.; Wang, W.; Guo, H.; Dong, S.; Wang, D.; Xu, Y.; Geng, J.; Luo, J.; et al. Flexible surface acoustic wave resonators built on disposable plastic film for electronics and lab-on-a-chip applications. Sci. Rep. 2013, 3, 2140. [Google Scholar] [CrossRef]
- Ali, W.R.; Prasad, M. Piezoelectric MEMS based acoustic sensors: A review. Sens. Actuators A Phys. 2020, 301, 111756. [Google Scholar] [CrossRef]
- Joshi, P.K.; Latwe, K.R.; Hasamnis, M.A. Analysis and Enhancement of Q-Factor in Thin-Film Bulk Acoustic Wave Resonator (FBAR). J. Phys. Conf. Ser. 2022, 2273, 012010. [Google Scholar] [CrossRef]
- Niro, G.; Marasco, I.; Rizzi, F.; D’Orazio, A.; Grande, M.; De Vittorio, M. Design and Fabrication of a Flexible Gravimetric Sensor Based on a Thin-Film Bulk Acoustic Wave Resonator. Sensors 2023, 23, 1655. [Google Scholar] [CrossRef]
- Perelló-Roig, R.; Verd, J.; Barceló, J.; Bota, S.; Segura, J. A 0.35-μm CMOS-MEMS Oscillator for High-Resolution Distributed Mass Detection. Micromachines 2018, 9, 484. [Google Scholar] [CrossRef]
- Perelló-Roig, R.; Verd, J.; Bota, S.; Segura, J. A Tunable-Gain Transimpedance Amplifier for CMOS-MEMS Resonators Characterization. Micromachines 2021, 12, 82. [Google Scholar] [CrossRef] [PubMed]
- Zuo, C.; Sinha, N.; Van der Spiegel, J.; Piazza, G. Multi-frequency pierce oscillators based on piezoelectric AlN contour-mode MEMS resonators. In Proceedings of the IEEE International Frequency Control Symposium, Honolulu, HI, USA, 19–21 May 2008. [Google Scholar]
- Nguyen, C.T.-C.; Howe, R.T. An integrated CMOS micromechanical resonator high-Q oscillator. IEEE J. Solid-State Circuits 1999, 34, 440–455. [Google Scholar] [CrossRef]
- Abdin, M.M.; Johnson, W.J.D.; Wang, J.; Weller, T.M. W-Band MMIC Chip Assembly Using Laser-Enhanced Direct Print Additive Manufacturing. IEEE Trans. Microw. Theory Tech. 2021, 69, 5381–5392. [Google Scholar] [CrossRef]
- Ketterl, T.P.; Vega, Y.; Arnal, N.C.; Stratton, J.W.I.; Rojas-Nastrucci, E.A.; Córdoba-Erazo, M.F.; Abdin, M.M.; Perkowski, C.W.; Deffenbaugh, P.I.; Church, K.H.; et al. A 2.45 GHz Phased Array Antenna Unit Cell Fabricated Using 3-D Multi-Layer Direct Digital Manufacturing. IEEE Trans. Microw. Theory Tech. 2015, 63, 4382–4394. [Google Scholar] [CrossRef]
- Wang, H.; Ma, J.; Yang, Y.; Gong, M.; Wang, Q. A Review of System-in-Package Technologies: Application and Reliability of Advanced Packaging. Micromachines 2023, 14, 1149. [Google Scholar] [CrossRef]
- Liang, M.; Yu, X.; Shemelya, C.; MacDonald, E.; Xin, H. 3D printed multilayer microstrip line structure with vertical transition toward integrated systems. In Proceedings of the IEEE MTT-S International Microwave Symposium, Phoenix, AZ, USA, 17–22 May 2015. [Google Scholar]
- Hozdić, E. Characterization and Comparative Analysis of Mechanical Parameters of FDM- and SLA-Printed ABS Materials. Appl. Sci. 2024, 14, 649. [Google Scholar] [CrossRef]
- Church, K.H.; Crane, N.B.; Deffenbaugh, P.I.; Ketterl, T.P.; Neff, C.G.; Nesbitt, P.B.; Nussbaum, J.T.; Perkowski, C.; Tsang, H.; Castro, J.; et al. Multimaterial and Multilayer Direct Digital Manufacturing of 3-D Structural Microwave Electronics. Proc. IEEE 2017, 105, 688–701. [Google Scholar] [CrossRef]
- Khosravani, M.R.; Schüürmann, J.; Berto, F.; Reinicke, T. On the Post-Processing of 3D-Printed ABS Parts. Polymers 2021, 13, 1559. [Google Scholar] [CrossRef]
- Stephenson, J.A. A Study of RF/Microwave Components Using Fused Deposition Modeling and Micro-Dispensing. Master’s Thesis, University of South Florida, Tampa, FL, USA, 2017. [Google Scholar]
- Ramirez, R.A.; Rojas-Nastrucci, E.A.; Weller, T.M. 3D tag with improved read range for UHF RFID applications using Additive Manufacturing. In Proceedings of the IEEE 16th Annual Wireless and Microwave Technology Conference (WAMICON), Cocoa Beach, FL, USA, 13–15 April 2015. [Google Scholar]
- Chan, Y.L.; Widodo, R.T.; Ming, L.C.; Khan, A.; Abbas, S.A.; Ping, N.Y.; Sofian, Z.M.; Kanakal, M.M. Review on 3D Printing Filaments Used in Fused Deposition Modeling Method for Dermatological Preparations. Molecules 2025, 30, 2411. [Google Scholar] [CrossRef]
- Castro, J.; Rojas, E.; Ross, A.; Weller, T.; Wang, J. High-k and low-loss thermoplastic composites for Fused Deposition Modeling and their application to 3D-printed Ku-band antennas. In Proceedings of the IEEE MTT-S International Microwave Symposium (IMS), San Francisco, CA, USA, 22–27 May 2016. [Google Scholar]
- Elhadad, A.A.; Rosa-Sainz, A.; Cañete, R.; Peralta, E.; Begines, B.; Balbuena, M.; Alcudia, A.; Torres, Y. Applications and multidisciplinary perspective on 3D printing techniques: Recent developments and future trends. Mater. Sci. Eng. R Rep. 2023, 156, 100760. [Google Scholar] [CrossRef]
- Lan, D.; Dewdney, J.; Wu, I.; Rivera, I.; Avila, A.; Wang, J. Dual-frequency MEMS based Oscillator using a single ZnO-on-SOI Resonator. In Proceedings of the 48th Annual International Symposium on Microelectronics, Orlando, FL, USA, 26–29 October 2015. [Google Scholar]
- Ramirez, R.A.; Lan, D.; Wang, J.; Weller, T.M. MMIC packaging and on-chip low-loss lateral interconnection using additive manufacturing and laser machining. In Proceedings of the IEEE MTT-S International Microwave Symposium (IMS), Honololu, HI, USA, 4–9 June 2017. [Google Scholar]
- Lan, D. Development of 3-D Printed Hybrid Packaging for GaAs-MEMS Oscillators Based on Piezoelectrically-Transduced ZnO-on-SOI Micromechanical Resonators. Ph.D. Thesis, University of South Florida, Tampa, FL, USA, 2018. [Google Scholar]
- Naing, T.L.; Rocheleau, T.O.; Alon, E.; Nguyen, C.T.-C. Low-Power MEMS-Based Pierce Oscillator Using a 61-MHz Capacitive-Gap Disk Resonator. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2020, 67, 1377–1391. [Google Scholar] [CrossRef]
- Lin, Y.-W.; Li, S.-S.; Ren, Z.; Nguyen, C.T.-C. Low phase noise array-composite micromechanical wine-glass disk oscillator. In Proceedings of the IEEE International Electron Devices Meeting, IEDM Technical Digest, Washington, DC, USA, 5 December 2005. [Google Scholar]
- Galliou, S.; Goryachev, M.; Abbe, P.; Vacheret, X.; Tobar, M.E.; Bourquin, R. Quality Factor Measurements of Various Types of Quartz Crystal Resonators Operating Near 4 K. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2016, 63, 975–980. [Google Scholar] [CrossRef]
- Lim, M.K.; M’Closkey, R.T.; Kirby, D.; Kubena, R.; Vig, J.R.; Ballato, A.; Yong, Y.K. 3-D modeling of high-Q quartz resonators for VHF-UHF applications. In Proceedings of the IEEE International Frequency Control Symposium and PDA Exhibition Jointly with the 17th European Frequency and Time Forum, Tampa, FL, USA, 4–8 May 2003. [Google Scholar]
- Zaman, A.; Alsolami, A.; Rivera, I.F.; Wang, J. Thin-Piezo on Single-Crystal Silicon Reactive Etched RF MEMS Resonators. IEEE Access 2020, 8, 139266–139273. [Google Scholar] [CrossRef]
- Dewdney, J. Low Loss VHF and UHF Filters for Wireless Communications Based on Piezoelectrically-Transduced Mircomechanical Resonators. Ph.D. Thesis, University of South Florida, Tampa, FL, USA, 2012. [Google Scholar]
- Liu, T.H.; Han, X.; Pastrana, J.; Sepúlveda, N.; Wang, J. Piezoelectric Lateral-Extensional Mode Resonators with Reconfigurable Electrode and Resonance Mode-Switching Behavior Enabled by a VO2 Thin-Film. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2022, 69, 2512–2525. [Google Scholar] [CrossRef]
- Guneroglu, U.; Zaman, A.; Alsolami, A.; Rivera, I.F.; Wang, J. Study of Frequency Trimming Ability and Performance Enhancement of Thin-Film Piezoelectric-on-Silicon MEMS Resonators by Joule Heating via Localized Annealing. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2025, 72, 686–696. [Google Scholar] [CrossRef] [PubMed]
- Wei, M.; Avila, A.; Rivera, I.; Baghelani, M.; Wang, J. ZnO on nickel RF micromechanical resonators for monolithic wireless communication applications. J. Micromech. Microeng. 2017, 27, 055006. [Google Scholar] [CrossRef]
- Zuo, C.; Van der Spiegel, J.; Piazza, G. Dual-Mode Resonator and Switchless Reconfigurable Oscillator Based on Piezoelectric AlN MEMS Technology. IEEE Trans. Electron. Devices 2011, 58, 3599–3603. [Google Scholar] [CrossRef]
- Rai, S.; Su, Y.; Pang, W.; Ruby, R.; Otis, B. A digitally compensated 1. 5 GHz CMOS/FBAR frequency reference. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2010, 57, 552–561. [Google Scholar] [CrossRef]
- Yuan, Q.; Peng, B.; Luo, W.; Zhao, J.; Yang, J.; Yang, F. Frequency stability of RF oscillator with MEMS-based encapsulated resonator. In Proceedings of the 18th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS), Anchorage, AK, USA, 21–25 June 2015. [Google Scholar]
- Hsu, W.-H.; Chen, H.-Y.; Lin, Z.-W.; Li, S.-S. A Novel Electrostatic Frequency Tuning Mechanism Based On A Vertically Coupled Cmos-Mems Resonator. In Proceedings of the IEEE 38th International Conference on Micro Electro Mechanical Systems (MEMS), Kaohsiung, China, 19–23 January 2025. [Google Scholar]
- Luo, H.; Zhang, M.; Gong, Y.; Ning, Y.; Chen, X.; Li, Q.; Pang, W. Piezoelectric MEMS Oscillators Based on Flexural Mode Membrane Resonator Array for Resonant Sensors. In Proceedings of the 22nd International Conference on Solid-State Sensors, Actuators and Microsystems (Transducers), Kyoto, Japan, 25–29 June 2023. [Google Scholar]
- Atashbar, H.; Majd, Y.; Hasan, T.; Mahdavi, H.; Mansoorzare, H.; Abdolvand, R. Advancing Precision Timing: A Thermally Stable Lithium Tantalate MEMS Oscillator with low Phase Noise. In Proceedings of the IEEE Ultrasonics, Ferroelectrics, and Frequency Control Joint Symposium (UFFC-JS), Taipei, China, 22–26 September 2024. [Google Scholar]
- Lo, P.-C.; Lin, W.; Li, S.-S. A Low Phase Noise Piezoelectric MEMS Oscillator with Low Power Consumption. In Proceedings of the International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 9–13 December 2023. [Google Scholar]
- Lin, Y.-T.; Chang, C.-Y.; Li, S.-S. High-Performance Piezoelectric Mems Resonators And Oscillators Leveraging Advanced High-Order Support Transducer Topologies. In Proceedings of the IEEE 38th International Conference on Micro Electro Mechanical Systems (MEMS), Kaohsiung, China, 19–23 January 2025. [Google Scholar]
- Everard, J.; Burtichelov, T.; Ng, K. Ultralow Phase Noise 10-MHz Crystal Oscillators. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2019, 66, 181–191. [Google Scholar] [CrossRef]
- Qiu, X.; Zhu, J.; Oiler, J.; Yu, C.; Wang, Z.; Yu, H. Film Bulk Acoustic-Wave Resonator (FBAR) based ultraviolet sensor. In Proceedings of the International Solid-State Sensors, Actuators and Microsystems Conference (TRANSDUCERS), Denver, CO, USA, 21–25 June 2009. [Google Scholar]
- Jia, Z.; Miao, J.; Lu, H.B.; Habibi, D.; Zhang, W.C.; Zhang, L.C. Photocatalytic degradation and absorption kinetics of cibacron brilliant yellow 3G-P by nanosized ZnO catalyst under simulated solar light. J. Taiwan Inst. Chem. E 2016, 60, 267–274. [Google Scholar] [CrossRef]
- Soni, R.K.; Navas, M.P. ZnO/Polyethylene-Glycol and ZnO/Au Nanocomposites for Enhanced Photocatalytic Degradation of Organic Dye. J. Nanoeng. Nanomanuf. 2013, 3, 348–352. [Google Scholar] [CrossRef]
- Pintupimol, P.; Sinornate, W.; Pecharapa, W. Investigation on Optically Ultraviolet Response of Low-dimensional ZnO Structures Prepared by Chemical Processes. IOP Conf. Ser. Mater. Sci. Eng. 2023, 1286, 012007. [Google Scholar] [CrossRef]
- Boonyarattanakalin, K.; Sinornate, W.; Mimura, H.; Mekprasart, W.; Pecharapa, W. Ultraviolet response of ZnO nanorod/Sb-doped ZnO thin film homojunction structure prepared by all-chemically wet process. Radiat. Phys. Chem. 2025, 227, 112240. [Google Scholar] [CrossRef]









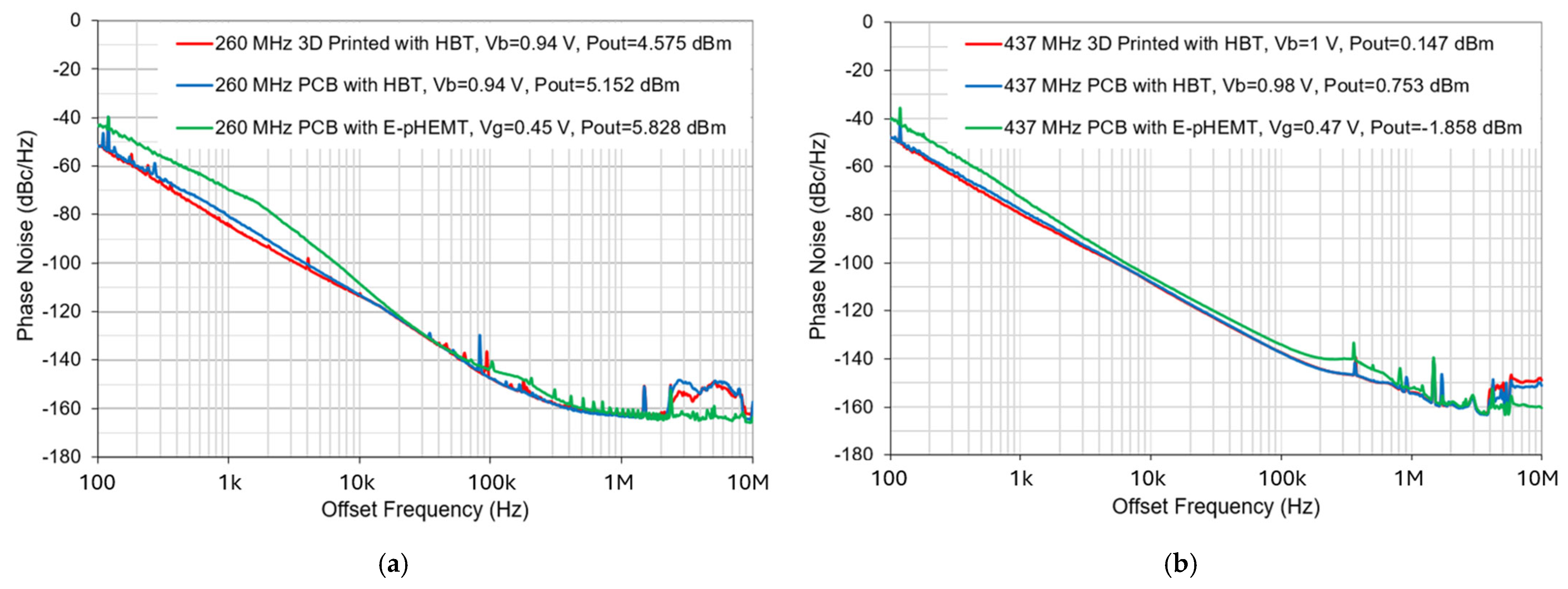
| PCB with SiGe HBT | PCB with E-pHEMT | |||
|---|---|---|---|---|
| Offset Frequency (Hz) | @ 260 MHz dBc/Hz | @ 437 MHz dBc/Hz | @ 260 MHz dBc/Hz | @ 437 MHz dBc/Hz |
| 1 k | −80.9 | −77.8 | −69.8 | −72.8 |
| 10 k | −113.1 | −107.9 | −108.4 | −106.1 |
| 100 k | −147.4 | −137.4 | −142.7 | −134.14 |
| 1 M | −163.1 | −154.3 | −161.4 | −152.4 |
| PCB with SiGe HBT | 3D-Printed ABS with SiGe HBT | |||
|---|---|---|---|---|
| Offset Frequency (Hz) | @ 260 MHz dBc/Hz | @ 437 MHz dBc/Hz | @ 260 MHz dBc/Hz | @ 437 MHz dBc/Hz |
| 1 k | −80.9 | −77.8 | −84.2 | −79.9 |
| 10 k | −113.1 | −107.9 | −112.5 | −108.3 |
| 100 k | −147.4 | −137.4 | −147.7 | −137.4 |
| 1 M | −163.1 | −154.3 | −162.4 | −154.2 |
| Reference | f0 (MHz) | Q | FOM (f0 × Q) | P0 (dBm) | Phase Noise (dBc/Hz) | Technology |
|---|---|---|---|---|---|---|
| This work | 260 437 | 1171.3 689.2 | 0.305 × 1012 0.301 × 1012 | 4.575 0.147 | −84.2 @ 1 kHz and −162.4 @ 1 MHz −79.8 @ 1 kHz and −154.2 @ 1 MHz | Dual-Mode ZnO MEMS Pierce Oscillator with 3D-Printed ABS Chip-Carrier Substrate |
| [28] | 176 222 307 482 | 1500 2100 1400 850 | 0.264 × 1012 0.466 × 1012 0.430 × 1012 0.410 × 1012 | −4.7 −4.8 −6.7 −13.6 | −79 @ 1 kHz and −153 @ 1 MHz −88 @ 1 kHz and −160 @ 1 MHz −84 @ 1 kHz and −151 @ 1 MHz −68 @ 1 kHz and −145 @ 1 MHz | AlN Contour-Mode MEMS Oscillator AMIS 0.5 μm 5 V CMOS |
| [54] | 472 1900 | 1800 600 | 0.850 × 1012 1.140 × 1012 | −6.5 −16 | −82 @ 1 kHz and −160 @ 1 MHz −69 @ 1 kHz and −153 @ 1 MHz | Dual-Mode AlN MEMS 0.5-µm CMOS |
| [55] | 1500 | 1573 | 2.360 × 1012 | −14 | −86 @ 1 kHz and −147 @ 1 MHz | Temperature-Compensated FBAR 0.35 µm CMOS |
| [56] | 150 | 10000 | 1.500 × 1012 | −9 | −96 @ 1 kHz and −128 @ 1 MHz | Disk MEMS Oscillator Encapsulated with AGC Module |
| [57] | 5.996 | 590 | 0.004 × 1012 | −25 | −80 @ 1 kHz and −115 @ 100 kHz | FC and CC Beam Capacitive Resonator 0.18 µm CMOS |
| [58] | 3.25 | 115 | 0.004 × 1011 | 24 | −115 @ 1 kHz and −145 @ 1 MHz | Flexural-Mode MEMS Two-Port Resonator Array |
| [59] | 283 | 1100 | 0.311 × 1012 | N/A | −102.6 @ 1 kHz and −164.6 @ 1 MHz | MEMS Lamb Wave Resonator on X-cut Lithium Tantalate |
| [60] | 17.55 | 5000 | 0.088 × 1012 | −3.64 | −137 @ 1 kHz and −158 @ 1 MHz | AlN-Si WE TSMC 0.18 μm CMOS |
| [61] | 16.75 | 5550 | 0.093 × 1012 | N/A | −124.4 @ 1 kHz and −160.4 @ 1 MHz | AlN WE-Mode MEMS Based on STT |
| [62] | 10 | 491580 | 4.916 × 1012 | −6 | −156 @ 1 kHz and −161 @ 1 MHz | SC-cut Crystal Oscillator with Transformer-Coupled Differential Amplifier |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Lan, D.; Han, X.; Liu, T.; Dewdney, J.; Zaman, A.; Guneroglu, U.; Martinez, C.M.; Wang, J. Low Phase Noise, Dual-Frequency Pierce MEMS Oscillators with Direct Print Additively Manufactured Amplifier Circuits. Micromachines 2025, 16, 755. https://doi.org/10.3390/mi16070755
Li L, Lan D, Han X, Liu T, Dewdney J, Zaman A, Guneroglu U, Martinez CM, Wang J. Low Phase Noise, Dual-Frequency Pierce MEMS Oscillators with Direct Print Additively Manufactured Amplifier Circuits. Micromachines. 2025; 16(7):755. https://doi.org/10.3390/mi16070755
Chicago/Turabian StyleLi, Liguan, Di Lan, Xu Han, Tinghung Liu, Julio Dewdney, Adnan Zaman, Ugur Guneroglu, Carlos Molina Martinez, and Jing Wang. 2025. "Low Phase Noise, Dual-Frequency Pierce MEMS Oscillators with Direct Print Additively Manufactured Amplifier Circuits" Micromachines 16, no. 7: 755. https://doi.org/10.3390/mi16070755
APA StyleLi, L., Lan, D., Han, X., Liu, T., Dewdney, J., Zaman, A., Guneroglu, U., Martinez, C. M., & Wang, J. (2025). Low Phase Noise, Dual-Frequency Pierce MEMS Oscillators with Direct Print Additively Manufactured Amplifier Circuits. Micromachines, 16(7), 755. https://doi.org/10.3390/mi16070755






