Prediction of Surface Roughness as a Function of Temperature for SiO2 Thin-Film in PECVD Process
Abstract
:1. Introduction
1.1. Linear Regression
1.2. Cubic Regression
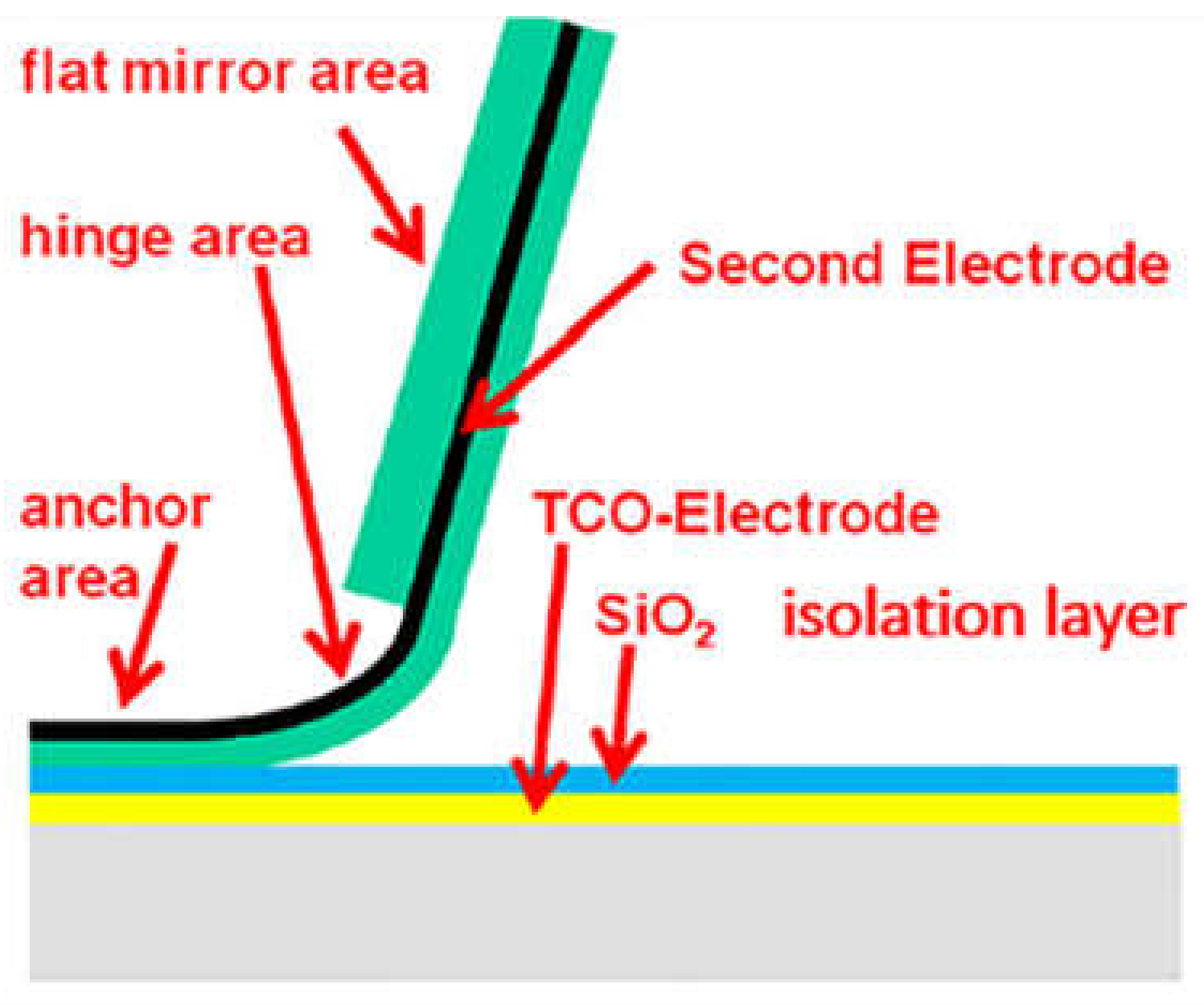
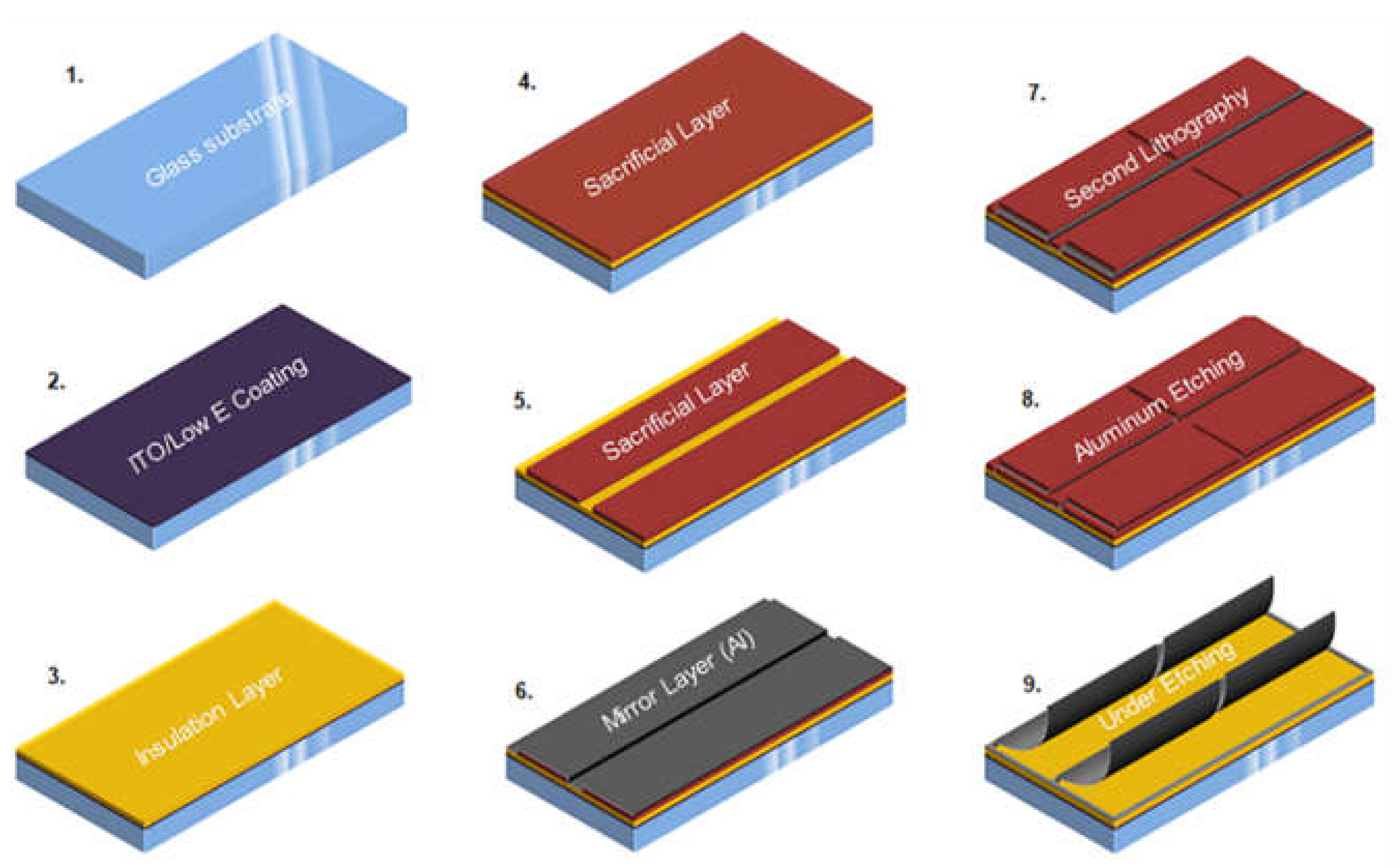
2. Experiment
3. Results and Discussion
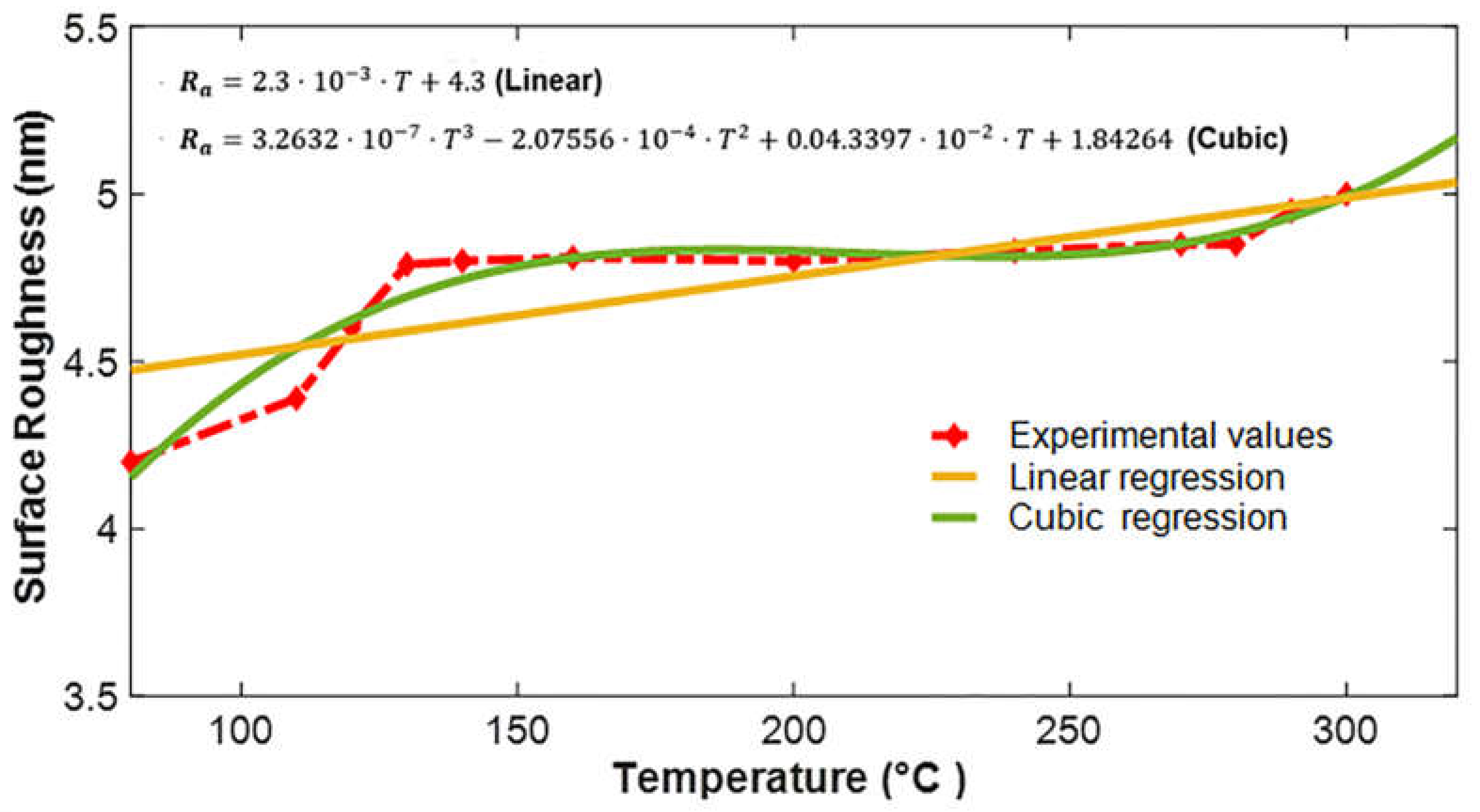
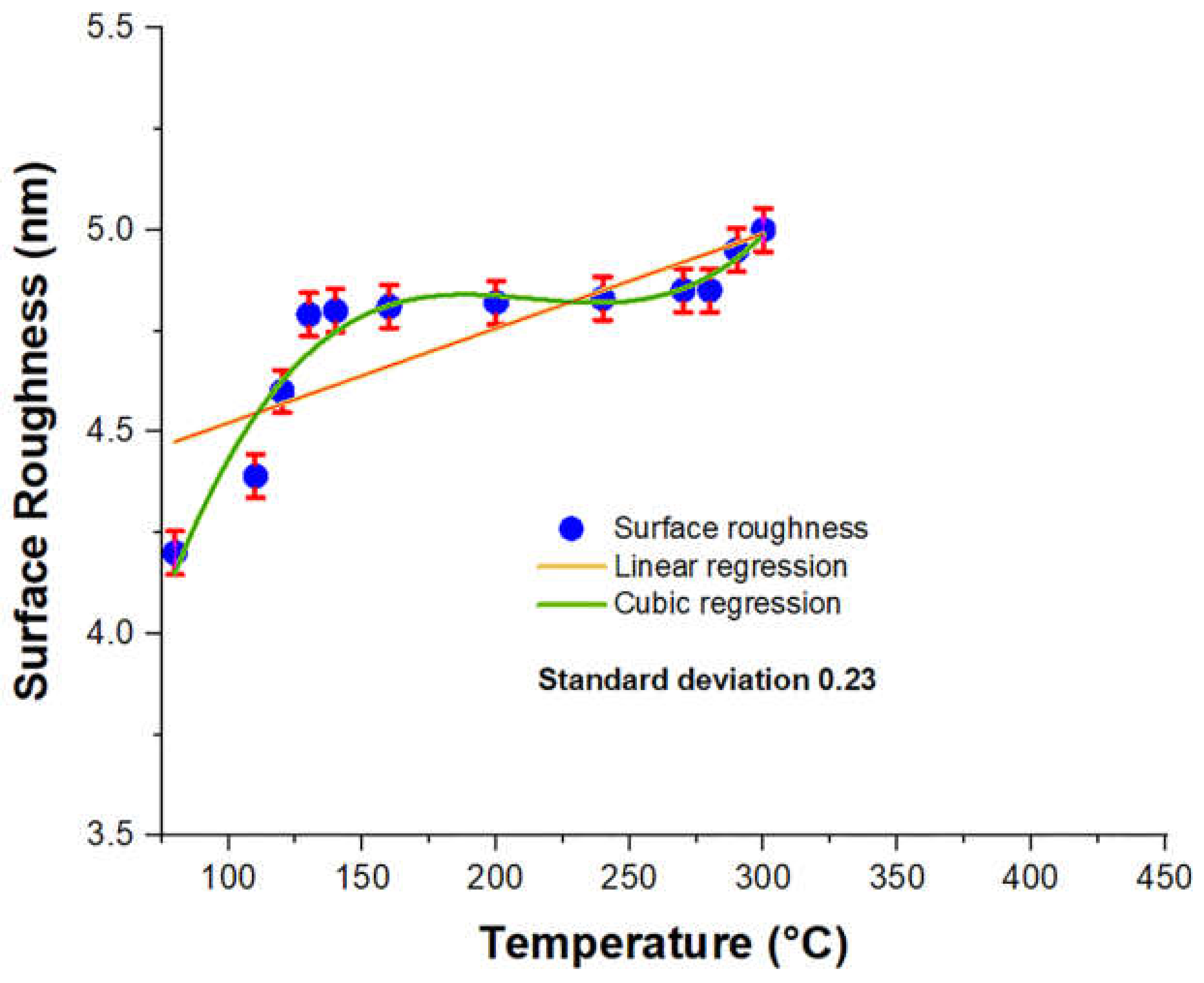
3.1. Linear Regression-Based Prediction Model
3.2. Cubic Regression-Based Prediction Model
3.3. The Proposed Analytical Model
3.4. Error Bars and Correlation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Song, P.; Si, C.; Zhang, M.; Zhao, Y.; He, Y.; Liu, W.; Wang, X. A Novel Piezoresistive MEMS Pressure Sensors Based on Temporary Bonding Technology. Sensors 2020, 20, 337. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Berndt, D.; Muggli, J.; Wittwer, F.; Langer, C.; Heinrich, S.; Knittel, T.; Schreiner, R. MEMS-based thermal conductivity sensor for hydrogen gas detection in automotive applications. Sens. Actuators A Phys. 2020, 305, 111670. [Google Scholar] [CrossRef]
- Kaya, O.; Köse, T.; Azgın, K. A Dual-Resonator Temperature Sensing Approach with Time Base Error Suppression. IEEE Sens. J. 2020, 20, 707–714. [Google Scholar] [CrossRef]
- Ren, Z.; Chang, Y.; Ma, Y.; Shih, K.; Dong, B.; Lee, C. Leveraging of MEMS Technologies for Optical Metamaterials Applications: A review. Adv. Opt. Mater. 2019, 8, 1900653. [Google Scholar] [CrossRef]
- Su, J.; Niekiel, F.; Fichtner, S.; Thormaehlen, L.; Kirchhof, C.; Meyners, D.; Quandt, E.; Wagner, B.; Lofink, F. AlScN-based MEMS Magnetoelectric Sensor. Appl. Phys. Lett. 2020, 117, 132903. [Google Scholar] [CrossRef]
- Amirzada, M.R.; Tatzel, A.; Viereck, V.; Hillmer, H. Surface roughness analysis of SiO2 for PECVD, PVD and IBD on different substrates. Appl. Nanosci. 2015, 6, 215–222. [Google Scholar] [CrossRef] [Green Version]
- Amirzada, M.R.; Li, Q.; Hillmer, H. Development of optical MEMS-based micromirror arrays on flexible substrate for curvilinear surfaces. Opt. Quantum Electron. 2021, 53, 210. [Google Scholar] [CrossRef]
- Alisaraei, E.A.; Hashemi, R.; Rahmatabadi, D.; Sommitsch, C. Experimental Study of Forming Limit Diagram and Mechanical Properties of Aluminum Foils Processed by the Accumulative Roll Bonding. Mater. Res. Express 2020, 7, 126511. [Google Scholar] [CrossRef]
- Li, D.; Tong, L. Direct Growth of Carbon Nanotubes on Aluminum Foil by Atmospheric Pressure Microwave Plasma Chemical Vapor Deposition. Processes 2020, 9, 36. [Google Scholar] [CrossRef]
- Semaltianos, N. Thermally evaporated aluminium thin films. Appl. Surf. Sci. 2001, 183, 223–229. [Google Scholar] [CrossRef]
- Lindahl, N.; Bitenc, J.; Dominko, R.; Johansson, P. Aluminum Metal–Organic Batteries with Integrated 3D Thin Film Anodes. Adv. Funct. Mater. 2020, 30, 2004573. [Google Scholar] [CrossRef]
- Yang, D.; Laforgue, A. Laser Surface Roughening of Aluminum Foils for Supercapacitor Current Collectors. J. Electrochem. Soc. 2019, 166, A2503–A2512. [Google Scholar] [CrossRef]
- Kumar, A.; Ashudeep; Bansal, D.; Kumar, P.; Anuroop; Khushbu; Rangra, K. Post-release deformation and curvature correction of an electrothermally actuated MEMS bilayer platform. Microelectron. Eng. 2020, 221, 111192. [Google Scholar] [CrossRef]
- Reddy, J.W.; Lassiter, M.; Chamanzar, M. Parylene photonics: A flexible, broadband optical waveguide platform with integrated micromirrors for biointerfaces. Microsyst. Nanoeng. 2020, 6, 85. [Google Scholar] [CrossRef]
- Garcia, I.S.; Ferreira, C.; Santos, J.D.; Martins, M.; Dias, R.A.; Aguiam, D.E.; Cabral, J.; Gaspar, J. Fabrication of a MEMS Micromirror Based on Bulk Silicon Micromachining Combined With Grayscale Lithography. J. Microelectromech. Syst. 2020, 29, 734–740. [Google Scholar] [CrossRef]
- Khara, S.; Singh, R.; Mandal, S.K. Review on Fabrication Technologies and Actuation Principles of Optical MEMS or MoEMS Devices. J. Crit. Rev. 2020, 7, 1388–1392. [Google Scholar]
- Xu, Y.; Hu, X.; Kundu, S.; Nag, A.; Afsarimanesh, N.; Sapra, S.; Mukhopadhyay, S.C.; Han, T. Silicon-Based Sensors for Biomedical Applications: A Review. Sensors 2019, 19, 2908. [Google Scholar] [CrossRef] [Green Version]
- Gopalakrishnan, S.; Dasgupta, A.; Nair, D.R. Study of the Effect of Surface Roughness on the Performance of RF MEMS Capacitive Switches through 3-D Geometric Modeling. IEEE J. Electron Devices Soc. 2016, 4, 451–458. [Google Scholar] [CrossRef]
- Tang, H.; Ma, S.; Lv, Y.; Li, Z.; Shen, W. Optimization of rear surface roughness and metal grid design in industrial bifacial PERC solar cells. Sol. Energy Mater. Sol. Cells 2020, 216, 110712. [Google Scholar] [CrossRef]
- Werner, J.; Boyd, C.C.; Moot, T.; Wolf, E.J.; France, R.M.; Johnson, S.A.; van Hest, M.F.A.M.; Luther, J.M.; Zhu, K.; Berry, J.J.; et al. Learning from existing photovoltaic technologies to identify alternative perovskite module designs. Energy Environ. Sci. 2020, 13, 3393–3403. [Google Scholar] [CrossRef]
- Newkirk, J.M.; Nayshevsky, I.; Sinha, A.; Law, A.M.; Xu, Q.; To, B.; Ndione, P.F.; Schelhas, L.T.; Walls, J.M.; Lyons, A.M.; et al. Artificial linear brush abrasion of coatings for photovoltaic module first-surfaces. Sol. Energy Mater. Sol. Cells 2021, 219, 110757. [Google Scholar] [CrossRef]
- Lin, P.-C.; Hsieh, C.-T.; Liu, X.; Chang, F.-C.; Chen, W.-C.; Yu, J.; Chueh, C.-C. Fabricating efficient flexible organic photovoltaics using an eco-friendly cellulose nanofibers/silver nanowires conductive substrate. Chem. Eng. J. 2021, 405, 126996. [Google Scholar] [CrossRef]
- Khandelwal, R.; Singh, A.P.; Kapoor, A.; Grigorescu, S.; Miglietta, P.; Stankova, N.E.; Perrone, A. Effects of deposition temperature on the structural and morphological properties of SnO2 films fabricated by pulsed laser deposition. Opt. Laser Technol. 2008, 41, 89–93. [Google Scholar] [CrossRef]
- Yartaşı, Y.; Karaman, M. Plasma Enhanced Chemical Vapor Deposition of Poly(Cyclohexyl Methacrylate) as a Sacrificial Thin Film. Plasma Chem. Plasma Process. 2020, 40, 357–369. [Google Scholar] [CrossRef]
- Su, J.; Li, C. Effect of plasma-enhanced chemical vapor deposition (PECVD) graphene content on the properties of EPDM/graphene composites. J. Mater. Sci. Mater. Electron. 2021, 32, 9065–9073. [Google Scholar] [CrossRef]
- Bute, A.; Jena, S.; Kedia, S.; Udupa, D.; Singh, K.; Bhattacharya, D.; Modi, M.; Chand, N.; Sinha, S. Boron carbide thin films deposited by RF-PECVD and PLD technique: A comparative study based on structure, optical properties, and residual stress. Mater. Chem. Phys. 2021, 258, 123860. [Google Scholar] [CrossRef]
- Wuu, D.; Lo, W.; Chiang, C.; Lin, H.; Chang, L.; Horng, R.; Huang, C.; Gao, Y. Plasma-deposited silicon oxide barrier films on polyethersulfone substrates: Temperature and thickness effects. Surf. Coat. Technol. 2005, 197, 253–259. [Google Scholar] [CrossRef]
- Elam, J.W.; Sechrist, Z.A.; George, S.M. ZnOyAl2O3 Nanolaminates Fabricated by Atomic Layer Deposition: Growth and Surface Roughness Measurements. Thin Solid Film. 2002, 414, 43–55. [Google Scholar] [CrossRef]
- Cotta, M.A.; Hamm, R.A.; Staley, T.W.; Chu, S.N.G.; Harriott, L.R.; Panish, M.B.; Temkin, H. Kinetic surface roughening in molecular beam epitaxy of InP. Phys. Rev. Lett. 1993, 70, 4106–4109. [Google Scholar] [CrossRef]
- Morkoc, H. Influence of mbe growth conditions on the properties of AlxGa1-xAs/GaAs heterostructures. J. Phys. Colloq. 1982, 43, C5-209. [Google Scholar] [CrossRef]
- Zhang, W. Surface Roughness Prediction with Machine Learning. In Proceedings of the Journal of Physics: Conference Series; IOP Publishing: Zhuhai, China, 2021; Volume 1856, p. 012040. [Google Scholar]
- Patel, D.R.; Kiran, M.B.; Vakharia, V. Modeling and prediction of surface roughness usingmultiple regressions: A noncontact approach. Eng. Rep. 2020, 2, e12119. [Google Scholar]
- Khan, Y.; Samad, A.; Iftikhar, U.; Kumar, S.; Ullah, N.; Sultan, J.; Ali, H.; Haider, M.L. Mathematical Modeling of Photonic Crystal based Optical Filters using Machine Learning. In Proceedings of the 2018 International Conference on Computing, Electronic and Electrical Engineering (ICE Cube), Quetta, Pakistan, 12–13 November 2018; pp. 1–5. [Google Scholar]
- Alpaydin, E. Introduction to Machine Learning; The MIT Press: Cambridge, MA, USA, 2020. [Google Scholar]
- Sizemore, N.E.; Nogueira, M.L.; Greis, N.P.; Davies, M.A. Application of Machine Learning to the Prediction of Surface Roughness in Diamond Machining. Procedia Manuf. 2020, 48, 1029–1040. [Google Scholar] [CrossRef]
- Nalbanta, M.; Gökkaya, H.G.; Toktas, I.; Sur, G. The Experimental Investigation of the Effects of Uncoated PVD and CVD Coated Cemented Carbide inserts and Cutting Parameters on Surface Roughness in CNC turning and its Prediction Using Artificial Neural Networks. Robot. Comput.-Integr. Manuf. 2009, 25, 211–223. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, F.; Shenoy, V.B.; Tang, M.; Lou, J. Towards controlled synthesis of 2D crystals by chemical vapor deposition (CVD). Mater. Today 2020, 40, 132–139. [Google Scholar] [CrossRef]
- Brownlee, J. Linear Regression for Machine Learning [Online]. Available online: https://machinelearningmastery.com/linear-regression-for-machine-learning (accessed on 7 February 2022).
- Nadir, Z.; Ahmad, M.I. Pathloss Determination Using Okumura-Hata Model and Cubic Regression for Missing Data for Oman. In Proceedings of the International MultiConference of Engineers and Computer Scientists, Hong Kong, China, 17–19 March 2010. [Google Scholar]
- Voigtlander, B. Atomic Force Microscopy; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Xiang, W.; Tian, Y.; Liu, X. Dynamic analysis of tapping mode atomic force microscope (AFM) for critical dimension measurement. Precis. Eng. 2020, 64, 269–279. [Google Scholar] [CrossRef]
- Putnam, J.; Damircheli, M.; Eslami, B. Effects of laser spot positioning with optical beam deflection method on tapping mode and bimodal AFM. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2020, 234, 675–690. [Google Scholar] [CrossRef]
- Kolahdoozan, M.; Kiani, A.; Heidari, P.; Oveissi, S. Investigating the effect of varying coating thickness on the surface roughness and adhesion forces of MEMS surfaces utilizing a theoretical and experimental approach. Appl. Surf. Sci. 2019, 481, 531–539. [Google Scholar] [CrossRef]


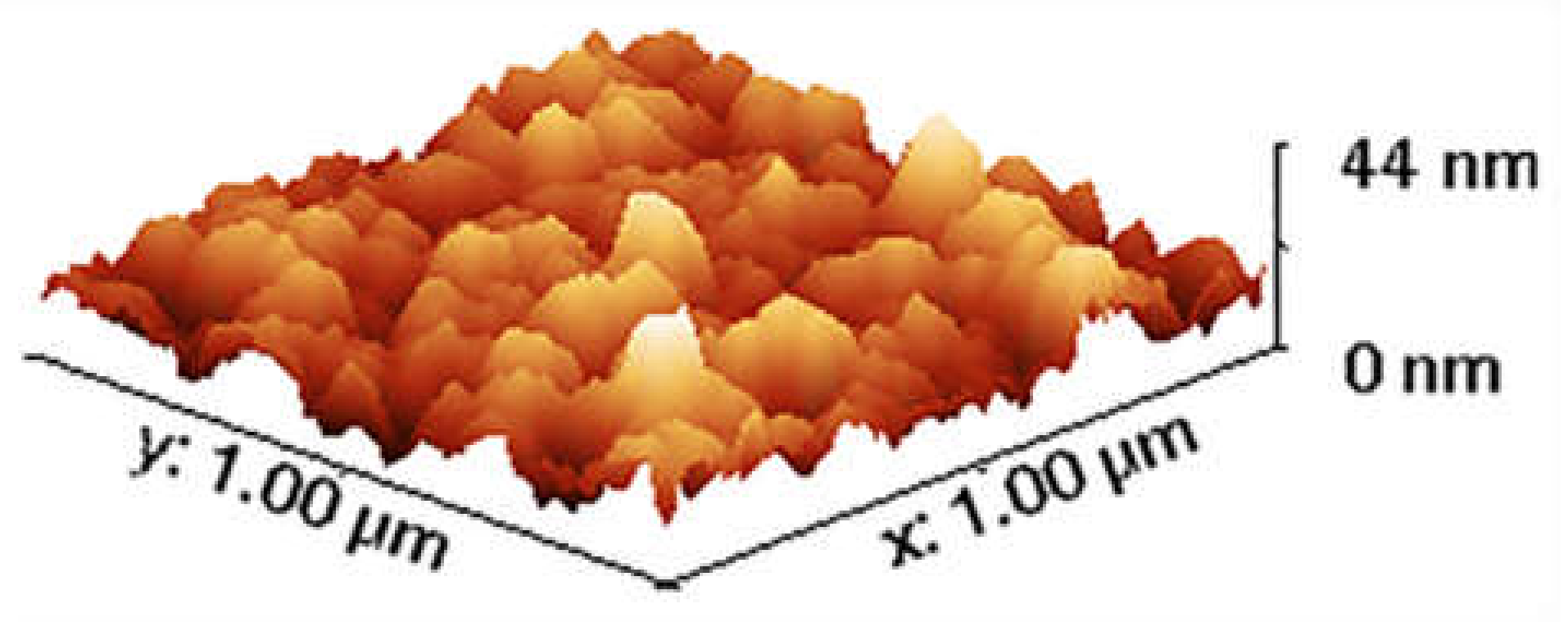
| Parameters | Values |
|---|---|
| (sccm) | 430 |
| (sccm) | 710 |
| (sccm) | 0 |
| power (watt) | 20 |
| power (watt) | 20 |
| (torr) | 1 |
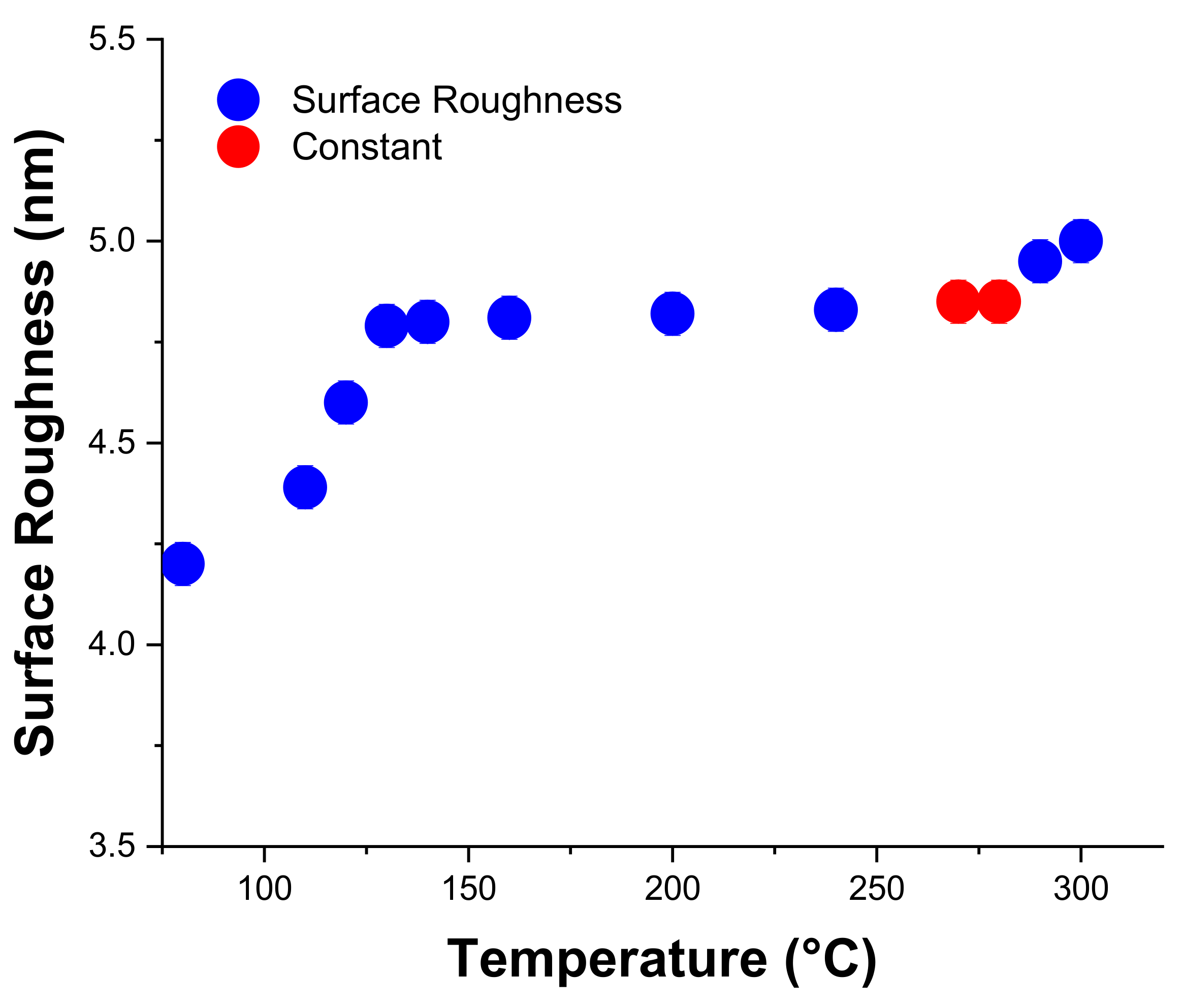
| Temp vs. Surface Roughness of SiO2 Layers Using PECVD Process | ||
|---|---|---|
| Sr. No. | Temperature (°C) | Surface Roughness (nm) |
| 1 | 80.00 | 4.20 |
| 2 | 110.00 | 4.39 |
| 3 | 120.00 | 4.60 |
| 4 | 130.00 | 4.79 |
| 5 | 140.00 | 4.80 |
| 6 | 160.00 | 4.81 |
| 7 | 200.00 | 4.80 |
| 8 | 240.00 | 4.83 |
| 9 | 270.00 | 4.85 |
| 10 | 280.00 | 4.85 |
| 11 | 290.00 | 4.95 |
| 12 | 300.00 | 5.00 |
| Temperature (T) | Surface Roughness | |||||
|---|---|---|---|---|---|---|
| 80 | 4.20 | −113.33 | −0.539 | 61.087 | 12,844.369 | 0.291 |
| 110 | 4.39 | −83.333 | −0.349 | 29.083 | 6944.389 | 0.122 |
| 120 | 4.60 | −73.333 | −0.139 | 10.193 | 5377.729 | 0.019 |
| 130 | 4.79 | −63.333 | 0.051 | −3.238 | 4011.069 | 0.003 |
| 140 | 4.80 | −53.333 | 0.061 | −3.253 | 2844.409 | 0.004 |
| 160 | 4.81 | −33.333 | 0.071 | 2.367 | 1111.089 | 0.005 |
| 200 | 4.80 | 6.667 | 0.061 | 0.407 | 44.449 | 0.004 |
| 240 | 4.83 | 46.667 | 0.091 | 4.247 | 2177.809 | 0.008 |
| 270 | 4.85 | 76.667 | 0.111 | 8.510 | 5877.829 | 0.012 |
| 280 | 4.85 | 86.667 | 0.111 | 9.620 | 7511.169 | 0.012 |
| 290 | 4.95 | 96.667 | 0.211 | 20.397 | 9344.509 | 0.045 |
| 300 | 5.00 | 106.66 | 0.261 | 27.840 | 11,377.849 | 0.068 |
| =193.333 | = 4.739 | - | - |
| Linear Correlation (r2) | Cubic Correlation (r2) |
|---|---|
| 0.64008 | 0.9321 |
| Moderate correlation | Strong correlation |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amirzada, M.R.; Khan, Y.; Ehsan, M.K.; Rehman, A.U.; Jamali, A.A.; Khatri, A.R. Prediction of Surface Roughness as a Function of Temperature for SiO2 Thin-Film in PECVD Process. Micromachines 2022, 13, 314. https://doi.org/10.3390/mi13020314
Amirzada MR, Khan Y, Ehsan MK, Rehman AU, Jamali AA, Khatri AR. Prediction of Surface Roughness as a Function of Temperature for SiO2 Thin-Film in PECVD Process. Micromachines. 2022; 13(2):314. https://doi.org/10.3390/mi13020314
Chicago/Turabian StyleAmirzada, Muhammad Rizwan, Yousuf Khan, Muhammad Khurram Ehsan, Atiq Ur Rehman, Abdul Aleem Jamali, and Abdul Rafay Khatri. 2022. "Prediction of Surface Roughness as a Function of Temperature for SiO2 Thin-Film in PECVD Process" Micromachines 13, no. 2: 314. https://doi.org/10.3390/mi13020314
APA StyleAmirzada, M. R., Khan, Y., Ehsan, M. K., Rehman, A. U., Jamali, A. A., & Khatri, A. R. (2022). Prediction of Surface Roughness as a Function of Temperature for SiO2 Thin-Film in PECVD Process. Micromachines, 13(2), 314. https://doi.org/10.3390/mi13020314







