A Designed Broadband Absorber Based on ENZ Mode Incorporating Plasmonic Metasurfaces
Abstract
:1. Introduction
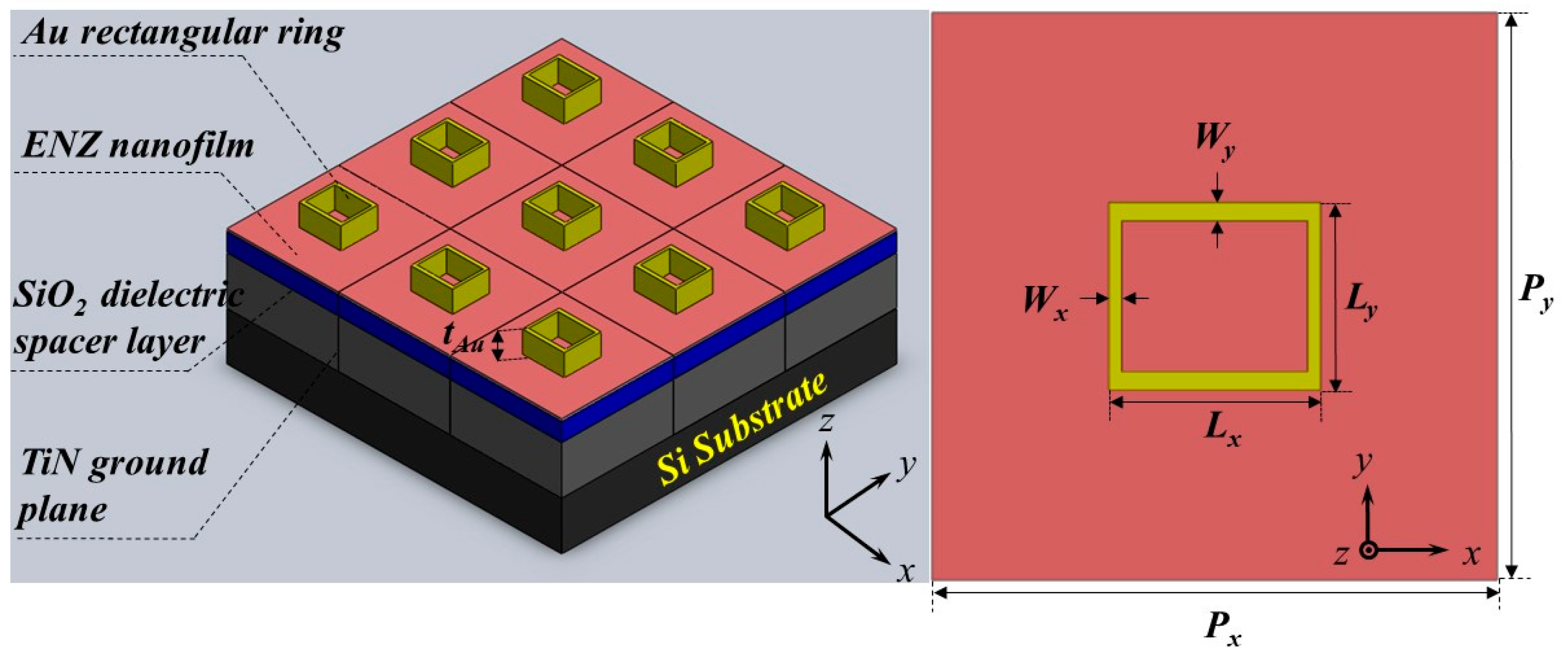
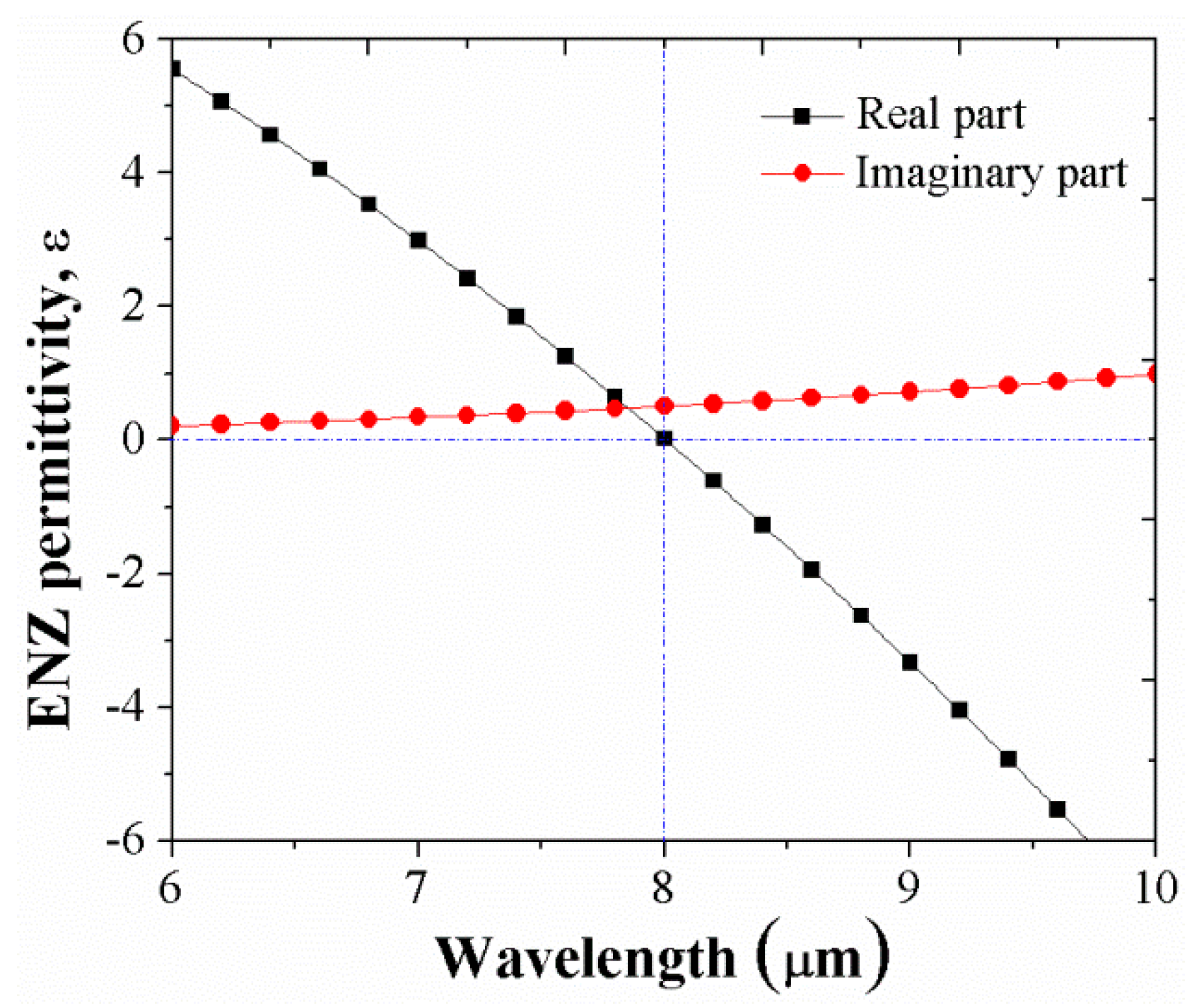
2. Absorber Structure and Simulation Details
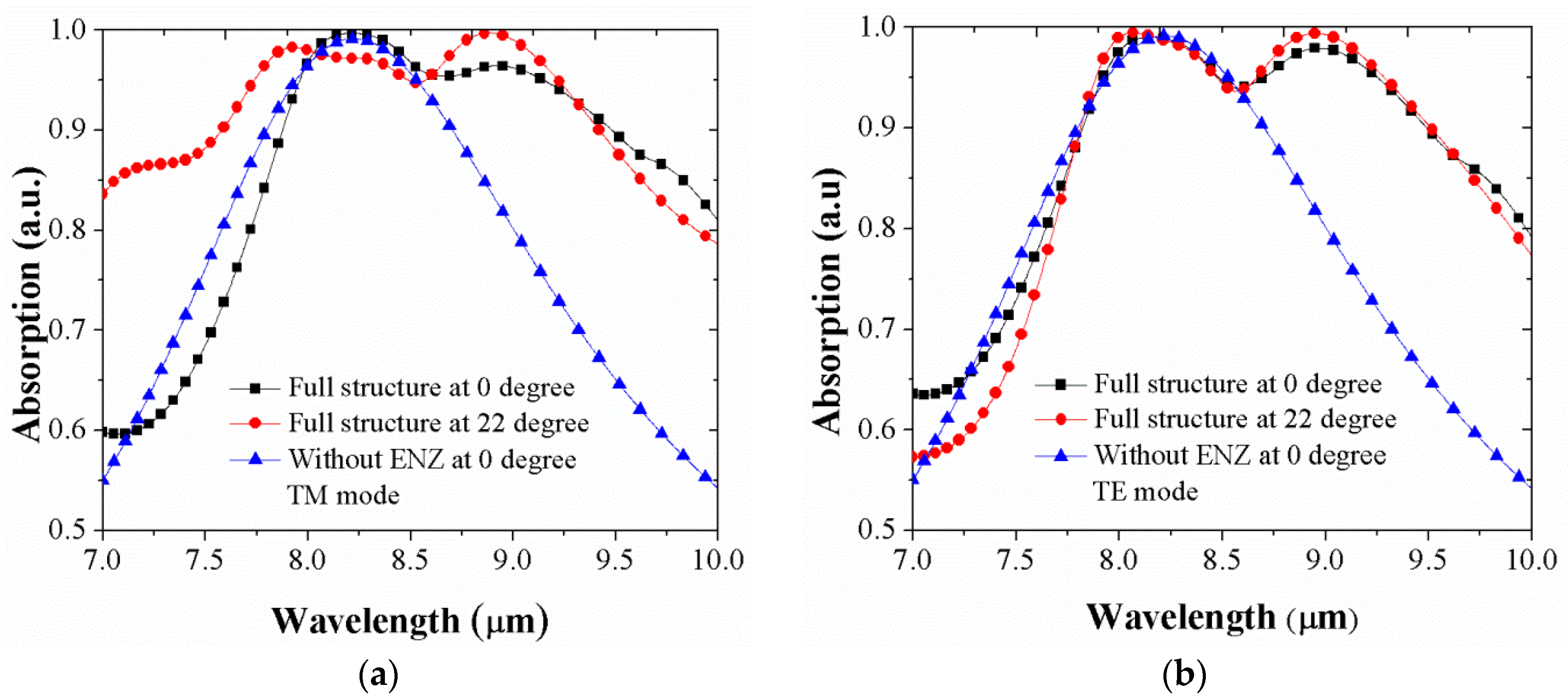
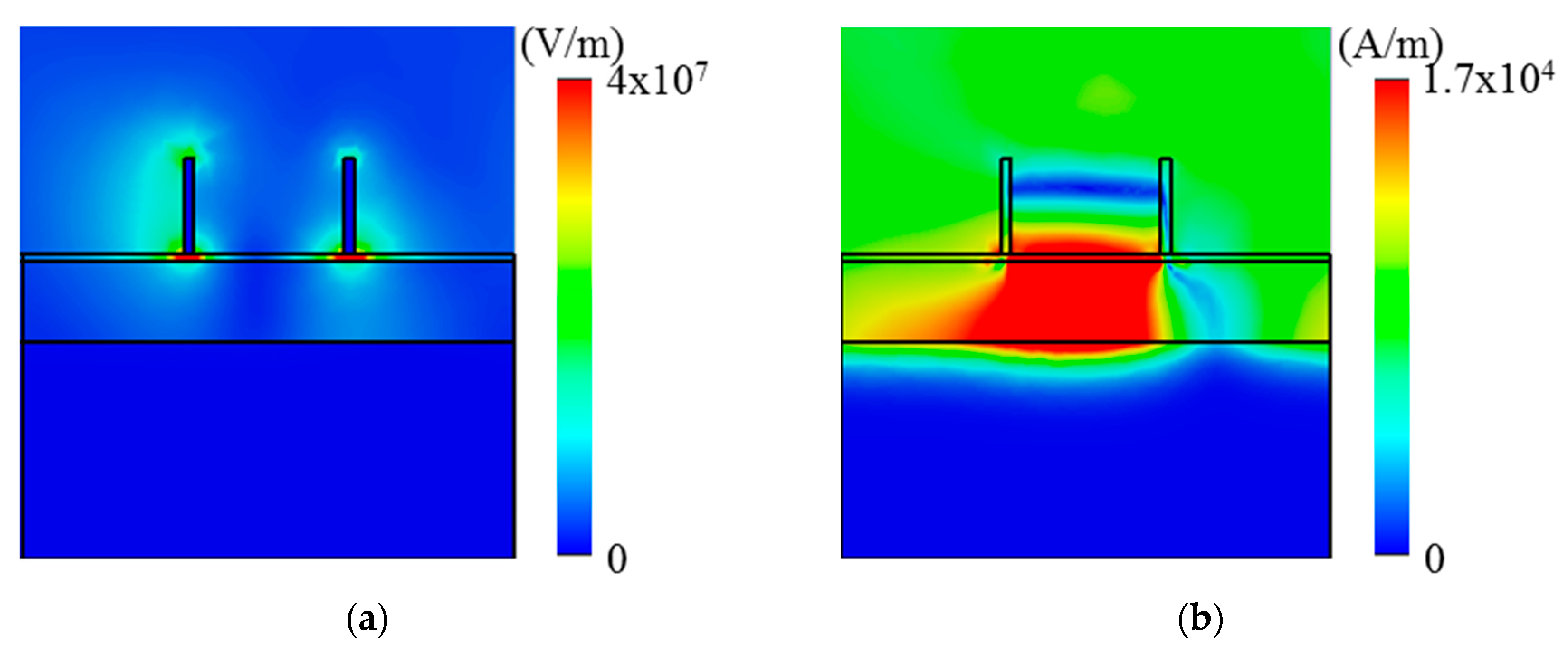
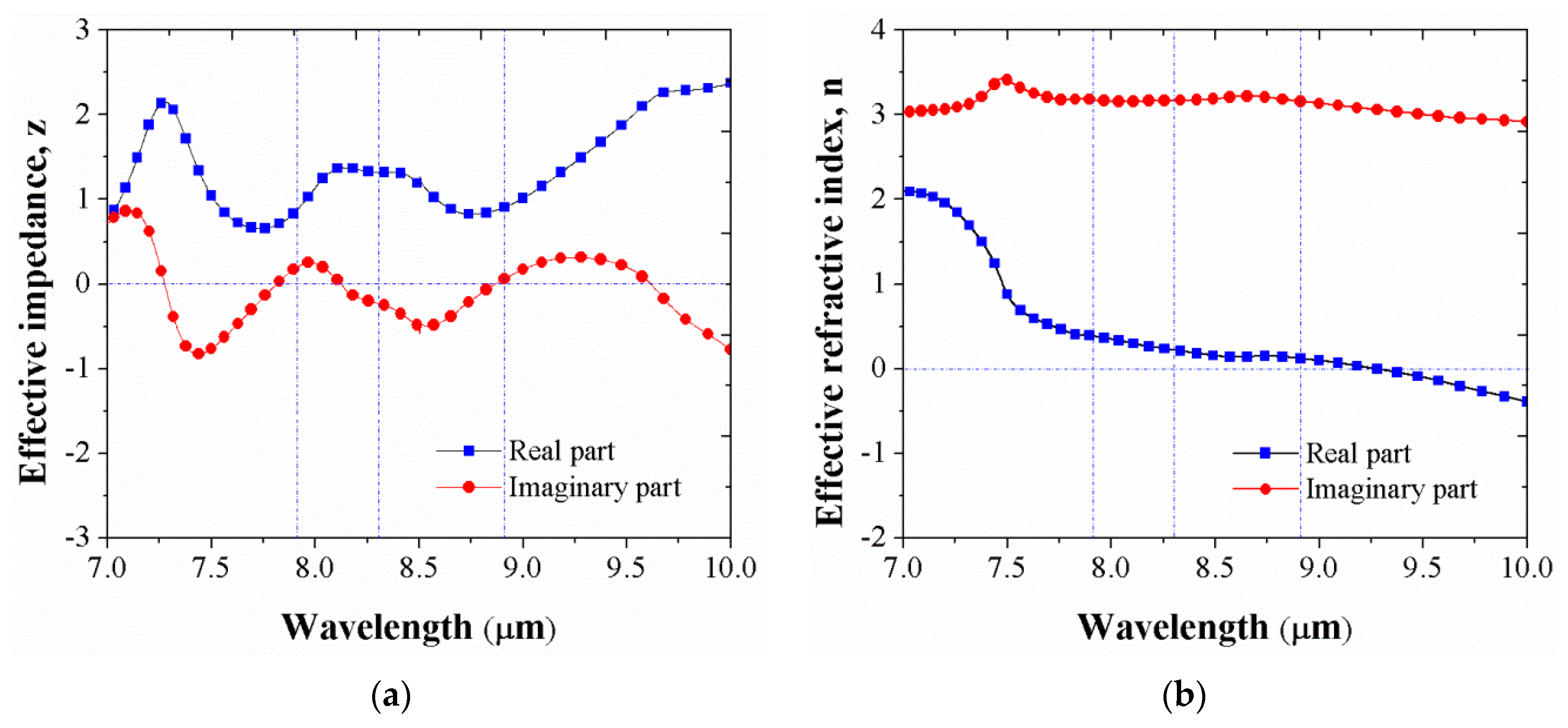
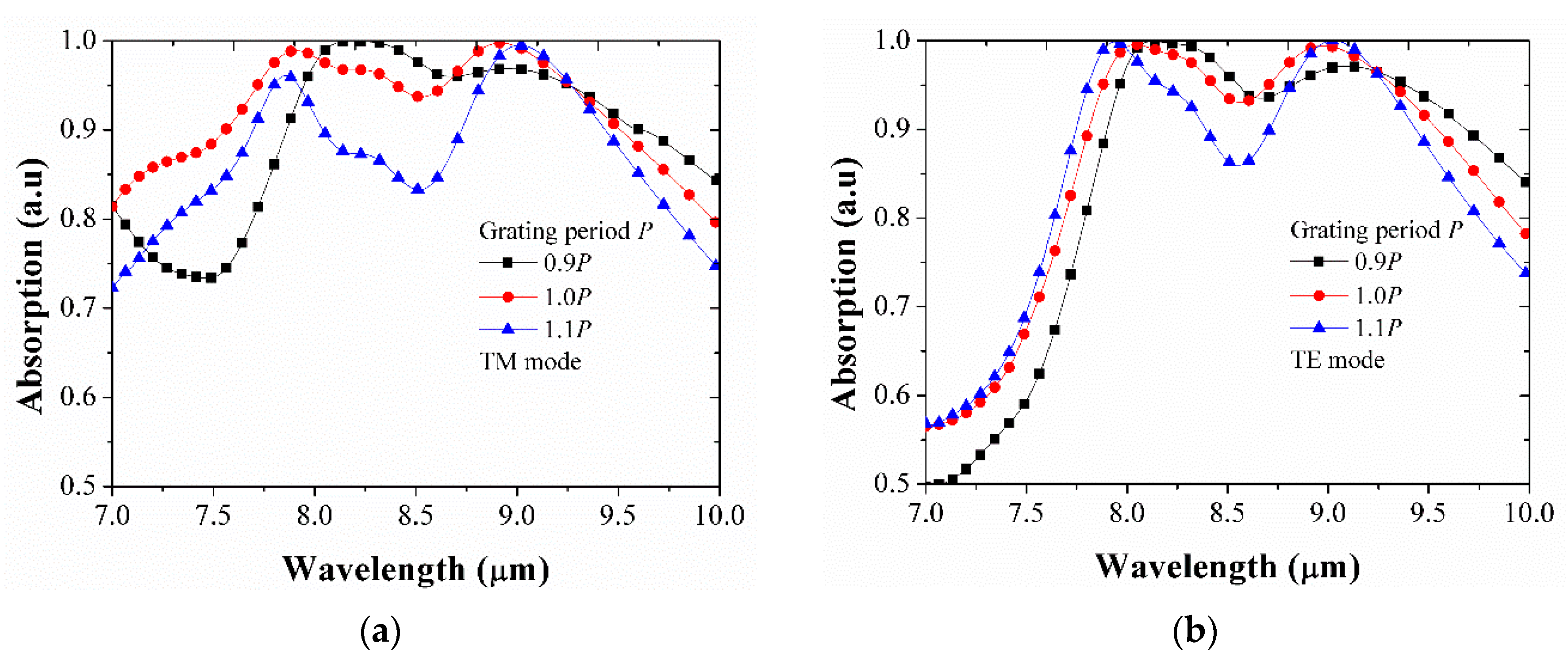
3. Results
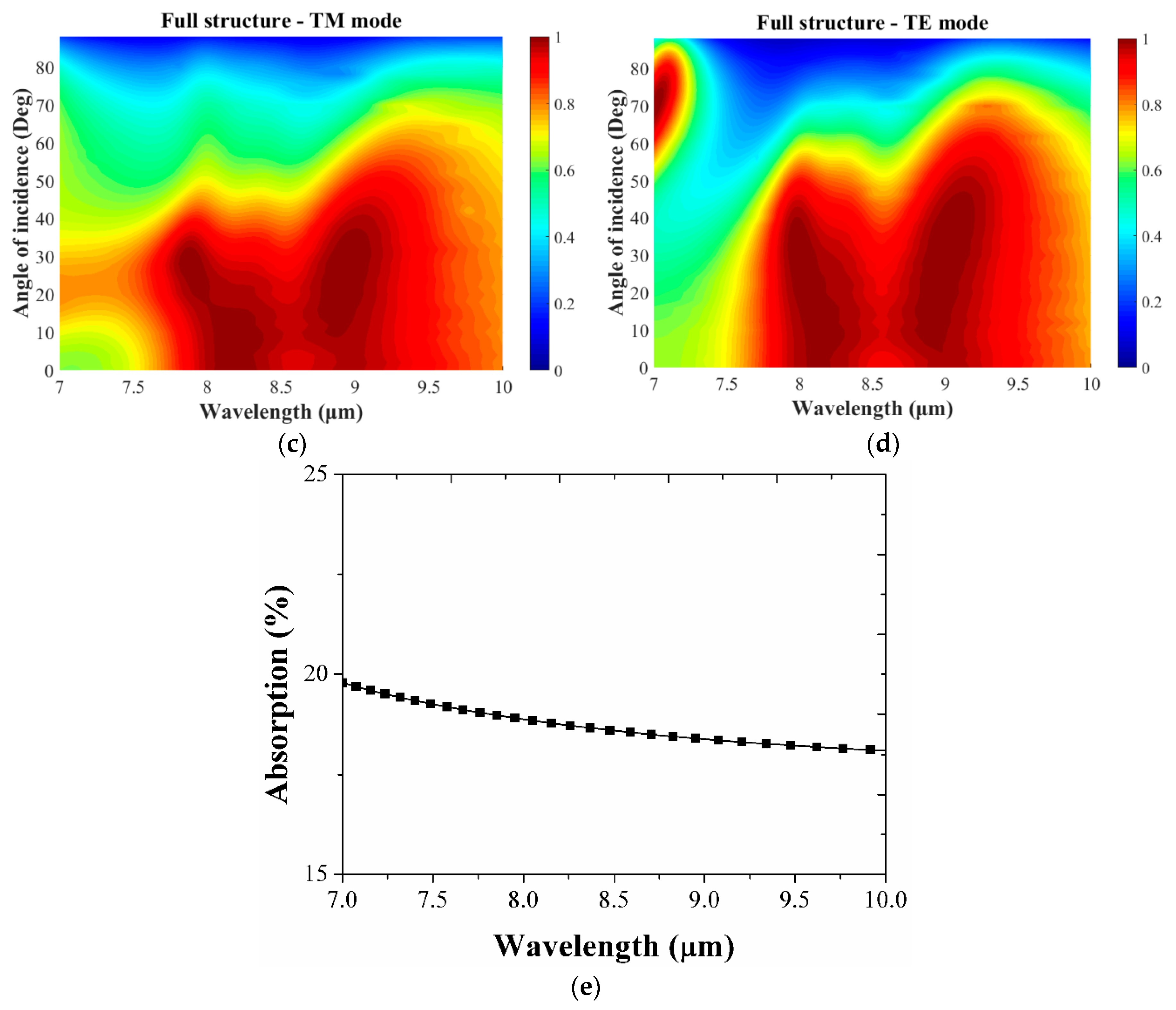
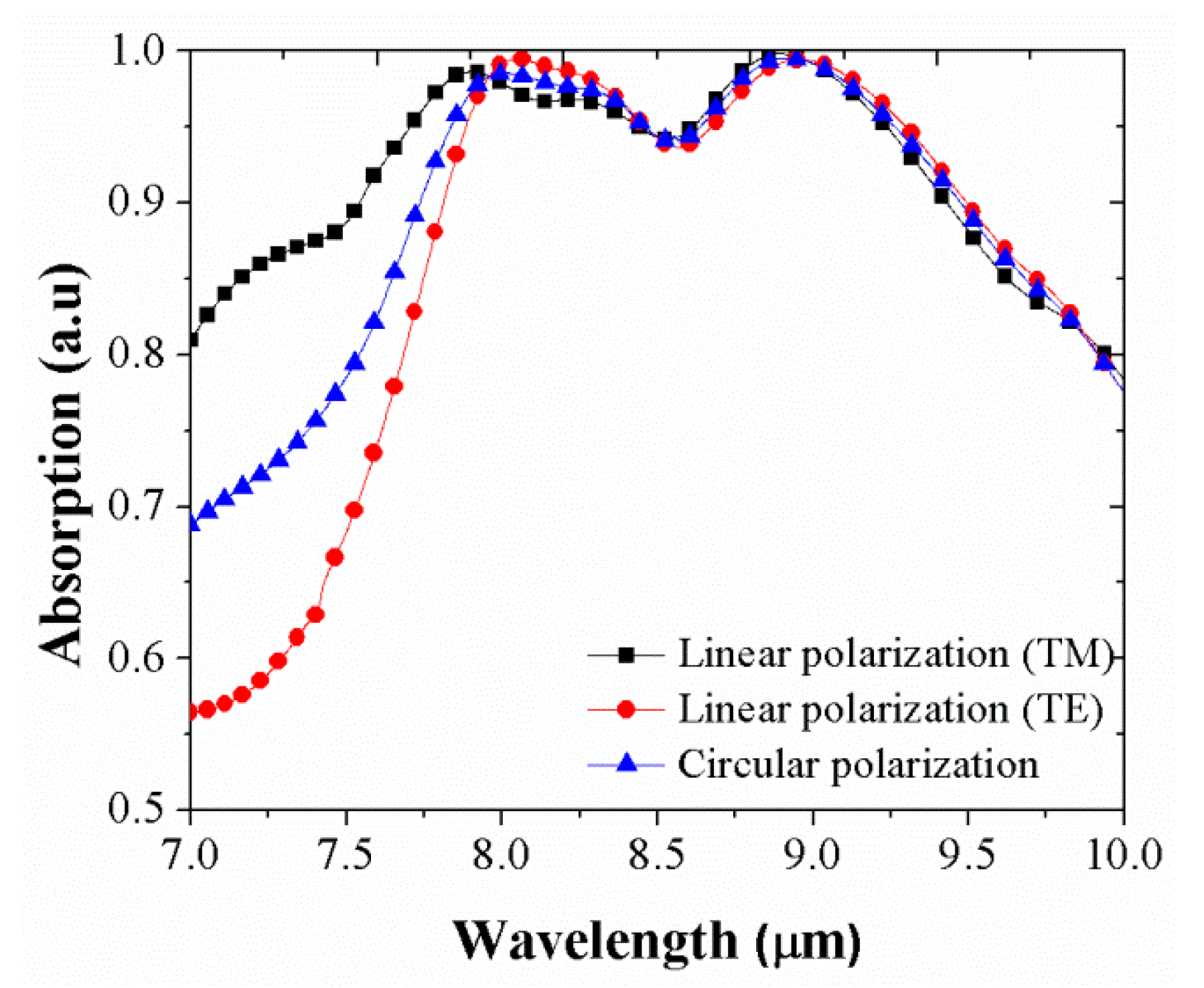
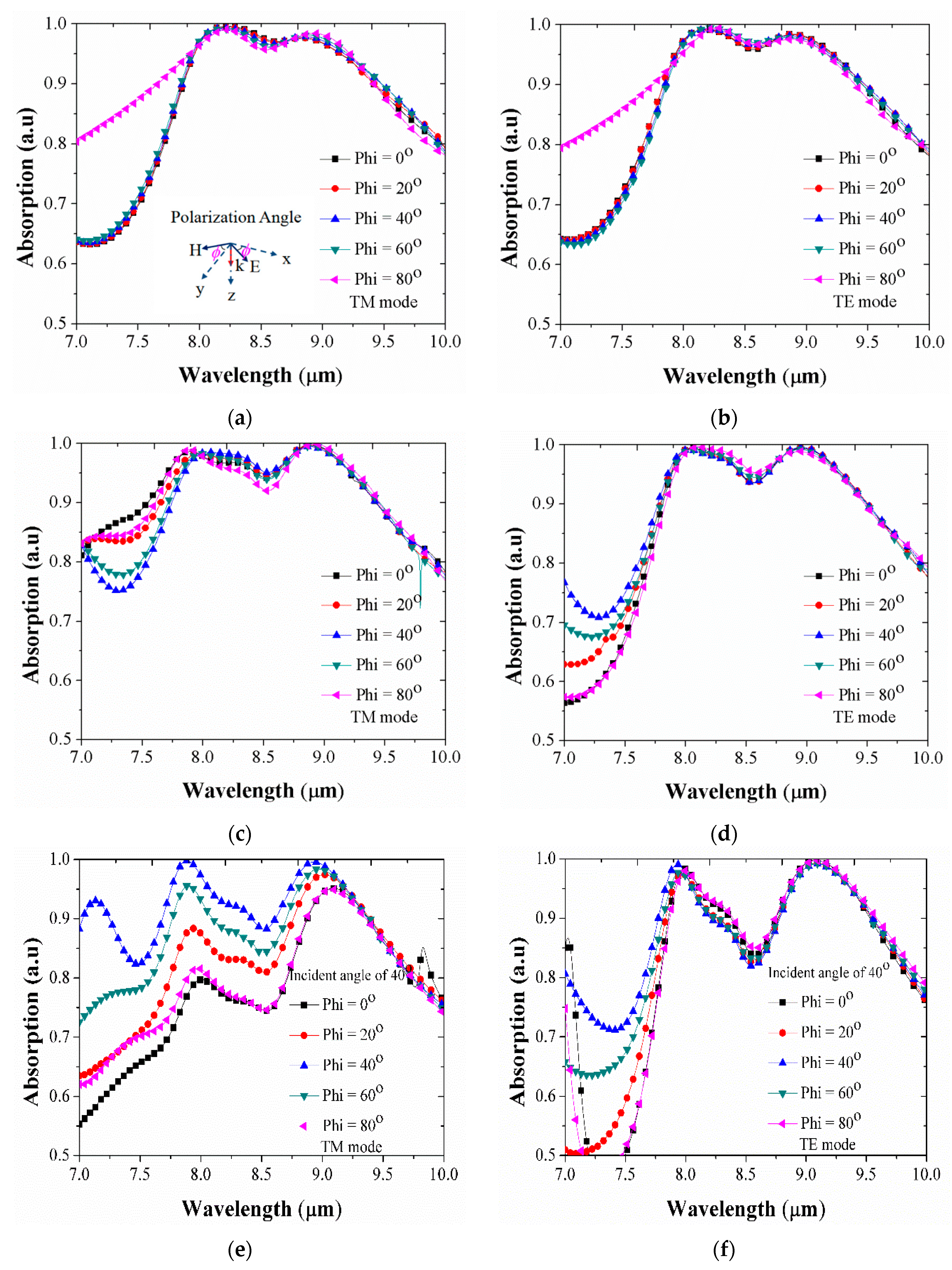
4. The Absorptivity as a Function of Polarization angle
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fu, P.; Liu, F.; Ren, G.J.; Su, F.; Li, D.; Yao, J.Q. A broadband metamaterial absorber based on multi-layer graphene in the terahertz region. Opt. Commun. 2018, 417, 62–66. [Google Scholar] [CrossRef]
- Landy, N.I.; Sajuyigbe, S.; Mock, J.J.; Smith, D.R.; Padilla, W.J. Perfect metamaterial absorber. Phys. Rev. Lett. 2008, 100, 207402. [Google Scholar] [CrossRef] [PubMed]
- Tang, J.; Xiao, Z.; Xu, K.; Liu, D. A polarization insensitive and broadband metamaterial absorber based on three-dimensional structure. Opt. Commun. 2016, 372, 64–70. [Google Scholar] [CrossRef]
- Sturmberg, B.C.P.; Chong, T.K.; Choi, D.-Y.; White, T.P.; Botten, L.C.; Dossou, K.B.; Poulton, C.G.; Catchpole, K.R.; McPhedran, R.C.; De Sterke, C.M. Total absorption of visible light in ultrathin weakly absorbing semiconductor gratings. Optica 2016, 3, 556–562. [Google Scholar] [CrossRef]
- Safaei, A.; Chandra, S.; Leuenberger, M.N.; Chanda, D. Wide Angle Dynamically Tunable Enhanced Infrared Absorption on Large-Area Nanopatterned Graphene. ACS Nano 2019, 13, 421–428. [Google Scholar] [CrossRef] [PubMed]
- Thongrattanasiri, S.; Koppens, F.H.L.; Javier Garcı´a de Abajo, F. Complete Optical Absorption in Periodically Patterned Graphene. Phys. Rev. Lett. 2012, 108, 047401. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, T.K.; Dang, P.T.; Park, I.; Le, K.Q. Broadband THz radiation through tapered semiconductor grating on high-index substrate. J. Opt. Soc. Am. B 2017, 34, 583–589. [Google Scholar] [CrossRef]
- Cleary, J.W.; Nader, N.; Leedy, K.D.; Soref, R. Tunable short- to mid-infrared perfectly absorbing thin films utilizing conductive zinc oxide on metal. Opt. Mater. Express 2015, 9, 1898–1909. [Google Scholar] [CrossRef]
- Zhao, Y.; Huang, Q.; Cai, H.; Lin, X.; Lu, Y. A broadband and switchable VO2-based perfect absorber at the THz frequency. Opt. Commun. 2018, 426, 443–449. [Google Scholar] [CrossRef]
- Badsha, M.A.; Jun, Y.C.; Hwangbo, C.K. Admittance matching analysis of perfect absorption in unpatterned thin films. Opt. Commun. 2014, 332, 206–213. [Google Scholar] [CrossRef]
- Yang, Y.; Kelley, K.; Sachet, E.; Campione, S.; Luk, T.S.; Maria, J.-P.; Sinclair, M.B.; Brenner, I. Femtosecond optical polarization switching using a cadmium oxide-based perfect absorber. Nat. Photonics 2017, 11, 390–395. [Google Scholar] [CrossRef]
- Rensberg, J.; Zhou, Y.; Richter, S.; Wan, C.; Zhang, S.; Schoppe, P.; Schmidt-Grund, R.; Ramanathan, S.; Capasso, F.; Kats, M.A.; et al. Epsilon-near-zero substrate engineering for ultrathin-film perfect absorbers. Phys. Rev. Appl. 2017, 8, 014009. [Google Scholar] [CrossRef]
- Hendrickson, J.; Guo, J.; Zhang, B.; Buchwald, W.; Soref, R. Wideband perfect light absorber at mid-wave infrared using multiplexed metal structures. Opt. Lett. 2012, 37, 371–373. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Hendrickson, J.; Guo, J. Multi-spectral near perfect metamaterial absorbers using spatially multiplexed plasmon resonance metal square structures. J. Opt. Soc. Am. B 2013, 30, 656–662. [Google Scholar] [CrossRef]
- Dang, P.T.; Pham, T.T.; Le, K.Q.; Nguyen, T.K. Epsilon-near-zero enhanced plasmonic Brewster transmission through subwavelength tapered metallic gratings. J. Korean Phys. Soc. 2018, 72, 38–44. [Google Scholar] [CrossRef]
- Feng, S.; Halterman, K. Coherent perfect absorption in epsilon-near-zero metamaterials. Phys. Rev. B 2012, 86, 165103. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, T.; Paude, T.; Zhang, Y.; Ren, Z.; Kempa, K. Metamaterial-plasmonic absorber structure for high efficiency amorphous silicon solar cells. Nano Lett. 2012, 12, 440–445. [Google Scholar] [CrossRef]
- Nakayama, K.; Tanabe, K.; Atwater, H.A. Plasmonic nanoparticle enhanced light absorption in GaAs solar cells. Appl. Phys. Lett. 2008, 93, 121904. [Google Scholar] [CrossRef] [Green Version]
- Jin, Y.; Feng, J.; Zhang, X.L.; Xu, M.; Bi, Y.G.; Chen, Q.D.; Wang, H.Y.; Sun, H.B. Surface-plasmon enhanced absorption in organic solar cells by employing a periodically corrugated metallic electrode. Appl. Phys. Lett. 2012, 101, 163303. [Google Scholar] [CrossRef]
- Argyropoulos, C.; Le, K.Q.; Mattiucci, N.; D’Aguanno, G.; Alú, A. Broadband absorbers and selective emitters based on plasmonic Brewster metasurfaces. Phys. Rev. B 2013, 87, 205112. [Google Scholar] [CrossRef]
- Hendrickson, J.R.; Vangala, S.; Dass, C.; Gibson, R.; Goldsmith, J.; Leedy, K.; Walker, D.E., Jr.; Cleary, J.W.; Kim, W.; Guo, J. Coupling of epsilon-near-zero mode to gap plasmon mode for flat-top wideband perfect light absorption. ACS Photonics 2018, 5, 776–781. [Google Scholar] [CrossRef]
- Vassant, S.; Hugonin, J.P.; Marquier, F.; Greffet, J.J. Berreman mode and epsilon near zero mode. Opt. Expr. 2012, 20, 23971–23977. [Google Scholar] [CrossRef] [PubMed]
- Campione, S.; de Ceglia, D.; Vincenti, M.A.; Scalora, M.; Capolino, F. Electric field enhancement in ɛ-near-zero slabs under TM-polarized oblique incidence. Phys. Rev. B 2013, 87, 035120. [Google Scholar] [CrossRef]
- Vincenti, M.A.; de Ceglia, D.; Scalora, M. Nonlinear dynamics in low permittivity media: The impact of losses. Opt. Exp. 2013, 21, 29949–29954. [Google Scholar] [CrossRef]
- de Ceglia, D.; Campione, S.; Vincenti, M.A.; Capolino, F.; Scalora, M. Low-damping epsilon-near-zero slabs: Nonlinear and nonlocal optical properties. Phys. Rev. B 2013, 87, 155140. [Google Scholar] [CrossRef]
- Campione, S.; Brener, I.; Marquier, F. Theory of epsilon-near-zero modes in ultrathin films. Phys. Rev. B 2015, 91, 121408(R). [Google Scholar] [CrossRef]
- Adams, D.C.; Inampudi, S.; Ribaudo, T.; Slocum, D.; Vangala, S.; Kuhta, N.A.; Goodhue, W.D.; Podolskiy, V.A.; Wasserman, D. Funneling light through a subwavelength aperture with epsilon-near-zero materials. Phys. Rev. Lett. 2011, 107, 133901. [Google Scholar] [CrossRef]
- Naik, G.V.; Shalaev, V.M.; Boltasseva, A. Alternative plasmonic materials: Beyond gold and silver. Adv. Mater. 2013, 25, 3264–3294. [Google Scholar] [CrossRef]
- Kinsey, N.; Devault, C.; Kim, J.; Ferrera, M.; Shalaev, V.M.; Boltasseva, A. Epsilon-near-zero Al-doped ZnO for ultrafast switching at telecom wavelengths. Optica 2015, 2, 616–622. [Google Scholar] [CrossRef]
- Kliewer, K.L.; Fuchs, R. Optical modes of vibration in an ionic crystal slab including retardation. II. Radiative region. Phys. Rev. 1966, 150, 573. [Google Scholar] [CrossRef]
- Sarid, D. Long-range surface-plasma waves on very thin metal films. Phys. Rev. Lett. 1981, 47, 1927–1930. [Google Scholar] [CrossRef]
- Chikkaraddy, R.; de Nijs, B.; Benz, F.; Barrow, S.J.; Scherman, O.A.; Rosta, E.; Demetriadou, A.; Fox, P.; Hess, O.; Baumberg, J. Single-molecule strong coupling at room temperature in plasmonic nanocavities. Nature 2016, 535, 127–130. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hao, J.; Wang, J.; Liu, X.; Padilla, W.J.; Zhou, L.; Qiu, M. High performance optical absorber based on a plasmonic metamaterial. Appl. Phys. Lett. 2010, 96, 251104. [Google Scholar] [CrossRef]
- Hendrickson, J.R.; Vangala, S.; Dass, C.K.; Gibson, R.; Leedy, K.; Walker, D.; Cleary, J.W.; Luk, T.S.; Guo, J. Experimental Observation of Strong Coupling Between an Epsilon-Near-Zero Mode in a Deep Subwavelength Nanofilm and a Gap Plasmon Mode. Available online: https://arxiv.org/abs/1801.03139 (accessed on 9 January 2018).
- Palik, E.D. Handbook of Optical Constants of Solids, 1st ed.; Academic Press: Cambridge, MA, USA, 1991. [Google Scholar]
- CST Microwave Studio, CST GmbH. Available online: http://cst.com (accessed on 1 January 2016).
- Chen, X.; Grzegorczyk, T.M.; Wu, B.-I.; Pacheco, J., Jr.; Kong, J.A. Robust method to retrieve the constitutive effective parameters of metamaterials. Phys. Rev. E 2004, 70, 016608. [Google Scholar] [CrossRef] [PubMed]
- Tao, H.; Landy, N.I.; Bingham, C.M.; Zhang, X.; Averitt, R.D.; Padilla, W.J. A metamaterial absorber for the terahertz regime: Design, fabrication and characterization. Opt. Expr. 2008, 16, 7181–7188. [Google Scholar] [CrossRef] [PubMed]
- Tittl, A.; Harats, M.G.; Walter, R.; Yin, X.; Schäferling, M.; Liu, N.; Rapaport, R.; Giessen, H. Quantitative angle-resolved small-spot refectance measurements on plasmonic perfect absorbers: Impedance matching and disorder efects. ACS Nano 2014, 8, 10885–10892. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dang, P.T.; Le, K.Q.; Lee, J.-H.; Nguyen, T.K. A Designed Broadband Absorber Based on ENZ Mode Incorporating Plasmonic Metasurfaces. Micromachines 2019, 10, 673. https://doi.org/10.3390/mi10100673
Dang PT, Le KQ, Lee J-H, Nguyen TK. A Designed Broadband Absorber Based on ENZ Mode Incorporating Plasmonic Metasurfaces. Micromachines. 2019; 10(10):673. https://doi.org/10.3390/mi10100673
Chicago/Turabian StyleDang, Phuc Toan, Khai Q. Le, Ji-Hoon Lee, and Truong Khang Nguyen. 2019. "A Designed Broadband Absorber Based on ENZ Mode Incorporating Plasmonic Metasurfaces" Micromachines 10, no. 10: 673. https://doi.org/10.3390/mi10100673
APA StyleDang, P. T., Le, K. Q., Lee, J.-H., & Nguyen, T. K. (2019). A Designed Broadband Absorber Based on ENZ Mode Incorporating Plasmonic Metasurfaces. Micromachines, 10(10), 673. https://doi.org/10.3390/mi10100673





