Individual-Tree Segmentation from UAV–LiDAR Data Using a Region-Growing Segmentation and Supervoxel-Weighted Fuzzy Clustering Approach
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Data
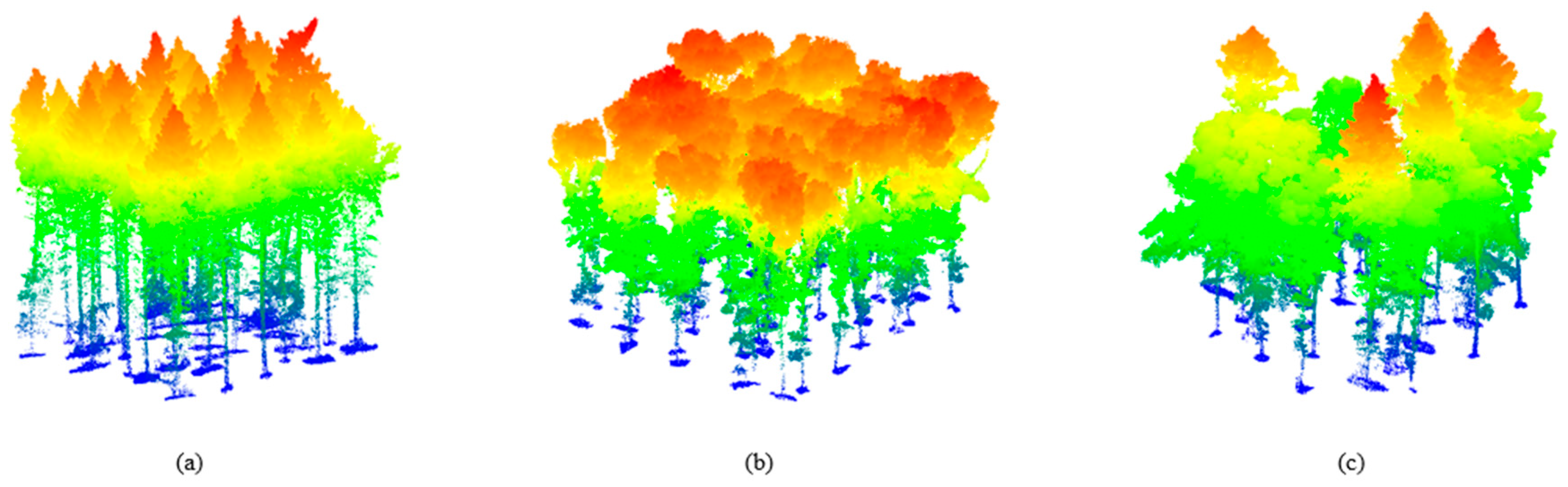
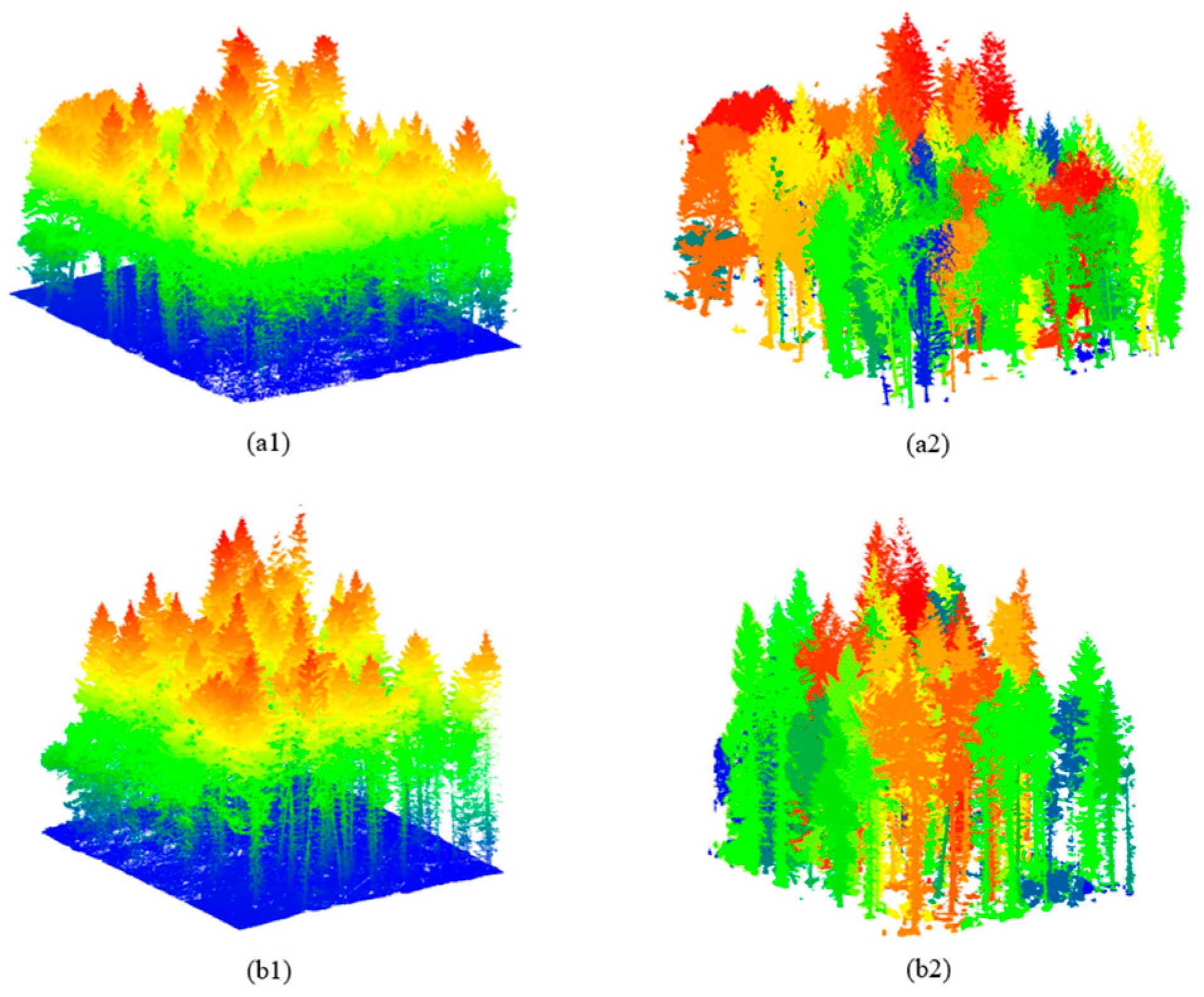
2.1.1. Synthetic Dataset
2.1.2. Real UAV–LiDAR Dataset
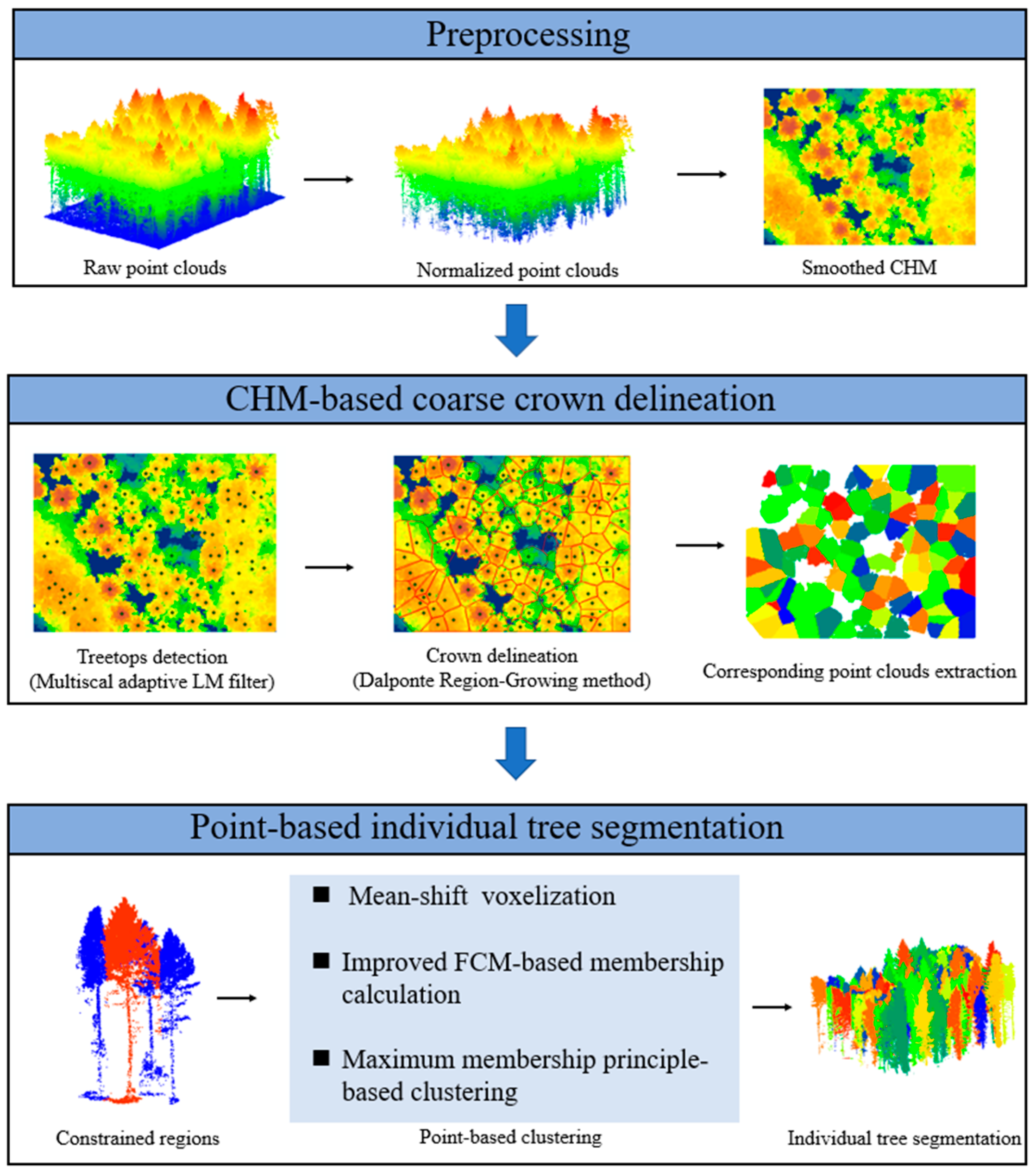
2.2. Methodology
2.2.1. Preprocessing
2.2.2. Treetop Detection
2.2.3. CHM-Based Crown Delineation
2.2.4. Point-Based Individual-Tree Segmentation
- Constrained region extraction: First, a zone method was used because of the computational complexity for large-scale point clouds. This method also eliminated the effect of the distance on the clustering because the tree-crown sizes varied, and the tree distributions were uneven, which would restrict the distance-based cluster methods. Other hybrid methods defined each coarse crown derived from the CHM as a constrained region, and point-based treetop reidentification and clustering were conducted in such regions. However, these methods worked only when there was under-segmentation of subdominant trees because they did not consider the neighboring region. In this study, new constrained regions were defined with the use of a neighbor-searching method. For each tree, the constrained region comprised its k-nearest neighbor crowns and itself, and a distance threshold was applied to remove the far-neighbor crowns. Then, the point clouds in constrained regions were extracted, and further clustering was conducted in the region;
- Mean-shift voxelization: A mean-shift voxelization method was applied to obtain supervoxels. Relative to traditional voxel-based methods, which transform point clouds into cubic voxels at a fixed resolution, mean-shift voxelization is more robust and flexible [30] and groups points by iteratively shifting each point to the density maxima via a kernel. Considering the various point cloud densities in different constrained regions, a bandwidth estimation technique was used to choose the appropriate bandwidth for each region;
- Maximum membership degree principle-based supervoxel clustering: Given the boundary’s ambiguity, for each coarse single-tree point cloud and its neighbors, an FCM was adopted to complete the fine segmentation [49]. Fuzzy c-means is a data-clustering technique where each data point belongs to a cluster to a degree that is specified by a membership grade. Because the supervoxels aggregated different quantities of points, in this study, a sample weight for each supervoxel was introduced to the objective function of the FCM (Equation (2)).where is the membership of the supervoxel, , and for each supervoxel, the membership in all the clusters adds to 1. is the number of supervoxels in a constrained region, is the number of clusters, is a weighting exponent, is the centroid of cluster , is a weight for the number of points in each supervoxel, and is the Euclidian distance between and . The optimization problem of J could be solved with the use of a Lagrange multiplier (Equation (3)). Then, by calculating the first derivatives of and for the constraint function and setting them equal to zero, two optimal parameters were obtained (Equations (4) and (5), respectively). After an iterative process, the objective function, J, was minimized until the centroid distance was less than a low threshold.
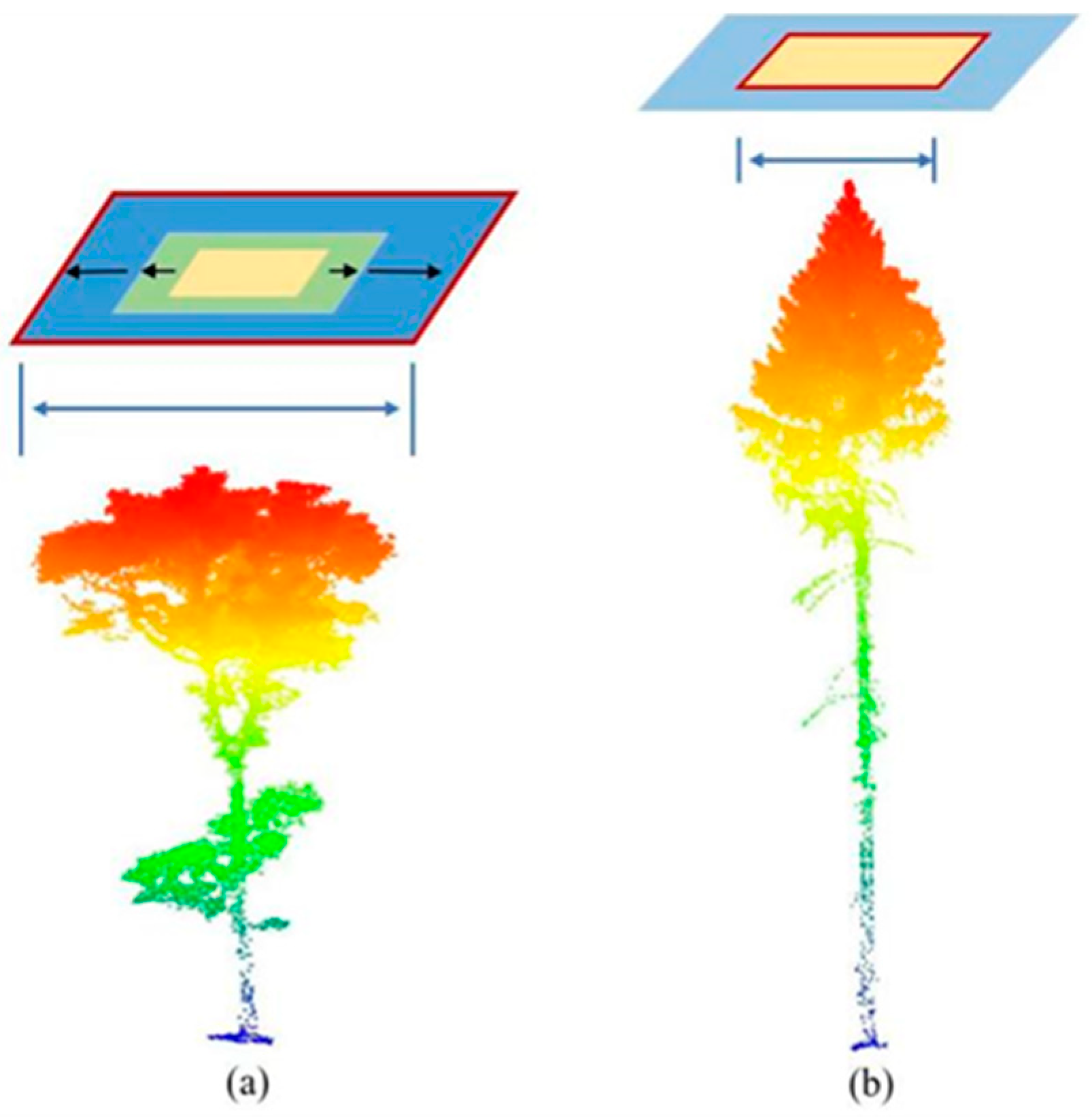
2.2.5. Accuracy Assessment
3. Results
3.1. Treetop Detection
3.2. Individual-Tree Segmentation
3.3. Results for the Accuracy of the Remotely Sensed Biophysical Observation and Retrieval (ARBOR) Framework
3.4. Comparison with Existing Methods
| Plot | Method | |||||||
|---|---|---|---|---|---|---|---|---|
| Proposed Method | Li 2012 | Dalponte | Watershed | |||||
| AMPS | DSS | AMPS | DSS | AMPS | DSS | AMPS | DSS | |
| Coniferous plots (L) | 0.8237 | 0.7547 | 0.8054 | 0.7245 | 0.7824 | 0.7044 | 0.7940 | 0.7213 |
| Coniferous plots (H) | 0.7498 | 0.6679 | 0.6775 | 0.4905 | 0.6536 | 0.5322 | 0.5943 | 0.6626 |
| Broadleaved plots (L) | 0.7033 | 0.5542 | 0.6626 | 0.4875 | 0.6844 | 0.4873 | 0.6797 | 0.4417 |
| Broadleaved plots (H) | 0.6399 | 0.6073 | 0.6132 | 0.5470 | 0.5530 | 0.5814 | 0.5926 | 0.5458 |
| Mixed plots | 0.6603 | 0.5294 | 0.6936 | 0.5013 | 0.6546 | 0.4864 | 0.6700 | 0.4345 |
| Real plot1 | 0.6469 | 0.6449 | 0.6512 | 0.5273 | 0.6223 | 0.6170 | 0.6711 | 0.5857 |
| Real plot2 | 0.7080 | 0.6667 | 0.7024 | 0.4366 | 0.6935 | 0.5970 | 0.6987 | 0.5735 |
4. Discussion
4.1. Parameter Analysis
4.2. Synthetic Dataset Compared with Actual LiDAR Dataset
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, W.; Guo, W.-Y.; Pasgaard, M.; Niu, Z.; Wang, L.; Chen, F.; Qin, Y.; Svenning, J.-C. Human Fingerprint on Structural Density of Forests Globally. Nat. Sustain. 2023, 6, 368–379. [Google Scholar] [CrossRef]
- Pan, Y.; Birdsey, R.A.; Fang, J.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A Large and Persistent Carbon Sink in the World’s Forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef]
- Hao, Y.; Widagdo, F.R.A.; Liu, X.; Liu, Y.; Dong, L.; Li, F. A Hierarchical Region-Merging Algorithm for 3-d Segmentation of Individual Trees Using UAV-LiDAR Point Clouds. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5701416. [Google Scholar] [CrossRef]
- Liang, X.; Wang, Y.; Pyörälä, J.; Lehtomäki, M.; Yu, X.; Kaartinen, H.; Kukko, A.; Honkavaara, E.; Issaoui, A.E.; Nevalainen, O.; et al. Forest in Situ Observations Using Unmanned Aerial Vehicle as an Alternative of Terrestrial Measurements. For. Ecosyst. 2019, 6, 20. [Google Scholar] [CrossRef]
- Bai, J.; Niu, Z.; Gao, S.; Bi, K.; Wang, J.; Huang, Y.; Sun, G. An Exploration, Analysis, and Correction of the Distance Effect on Terrestrial Hyperspectral LiDAR Data. ISPRS J. Photogramm. Remote Sens. 2023, 198, 60–83. [Google Scholar] [CrossRef]
- Kotivuori, E.; Kukkonen, M.; Mehtätalo, L.; Maltamo, M.; Korhonen, L.; Packalen, P. Forest Inventories for Small Areas Using Drone Imagery without In-Situ Field Measurements. Remote Sens. Environ. 2020, 237, 111404. [Google Scholar] [CrossRef]
- Li, W.; Niu, Z.; Shang, R.; Qin, Y.; Wang, L.; Chen, H. High-Resolution Mapping of Forest Canopy Height Using Machine Learning by Coupling ICESat-2 LiDAR with Sentinel-1, Sentinel-2 and Landsat-8 Data. Int. J. Appl. Earth Obs. Geoinf. 2020, 92, 102163. [Google Scholar] [CrossRef]
- Wang, Y.; Lehtomäki, M.; Liang, X.; Pyörälä, J.; Kukko, A.; Jaakkola, A.; Liu, J.; Feng, Z.; Chen, R.; Hyyppä, J. Is Field-Measured Tree Height as Reliable as Believed–A Comparison Study of Tree Height Estimates from Field Measurement, Airborne Laser Scanning and Terrestrial Laser Scanning in a Boreal Forest. ISPRS J. Photogramm. Remote Sens. 2019, 147, 132–145. [Google Scholar] [CrossRef]
- Zhen, Z.; Yang, L.; Ma, Y.; Wei, Q.; Jin, H.I.; Zhao, Y. Upscaling Aboveground Biomass of Larch (Larix Olgensis Henry) Plantations from Field to Satellite Measurements: A Comparison of Individual Tree-Based and Area-Based Approaches. GIScience Remote Sens. 2022, 59, 722–743. [Google Scholar] [CrossRef]
- Du, L.; Pang, Y.; Wang, Q.; Huang, C.; Bai, Y.; Chen, D.; Lu, W.; Kong, D. A LiDAR Biomass Index-Based Approach for Tree-and Plot-Level Biomass Mapping over Forest Farms Using 3D Point Clouds. Remote Sens. Environ. 2023, 290, 113543. [Google Scholar] [CrossRef]
- Brede, B.; Terryn, L.; Barbier, N.; Bartholomeus, H.M.; Bartolo, R.; Calders, K.; Derroire, G.; Moorthy, S.M.K.; Lau, A.; Levick, S.R.; et al. Non-Destructive Estimation of Individual Tree Biomass: Allometric Models, Terrestrial and UAV Laser Scanning. Remote Sens. Environ. 2022, 280, 113180. [Google Scholar] [CrossRef]
- Mielcarek, M.; Stereńczak, K.; Khosravipour, A. Testing and Evaluating Different LiDAR-Derived Canopy Height Model Generation Methods for Tree Height Estimation. Int. J. Appl. Earth Obs. Geoinf. 2018, 71, 132–143. [Google Scholar] [CrossRef]
- Vega, C.; Hamrouni, A.; El Mokhtari, S.; Morel, J.; Bock, J.; Renaud, J.-P.; Bouvier, M.; Durrieu, S. PTrees: A Point-Based Approach to Forest Tree Extraction from Lidar Data. Int. J. Appl. Earth Obs. Geoinf. 2014, 33, 98–108. [Google Scholar] [CrossRef]
- Wu, B.; Yu, B.; Wu, Q.; Huang, Y.; Chen, Z.; Wu, J. Individual Tree Crown Delineation Using Localized Contour Tree Method and Airborne LiDAR Data in Coniferous Forests. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 82–94. [Google Scholar] [CrossRef]
- Dralle, K.; Rudemo, M. Stem Number Estimation by Kernel Smoothing of Aerial Photos. Can. J. For. Res. 1996, 26, 1228–1236. [Google Scholar] [CrossRef]
- Koch, B.; Heyder, U.; Weinacker, H. Detection of Individual Tree Crowns in Airborne Lidar Data. Photogramm. Eng. Remote Sens. 2006, 72, 357–363. [Google Scholar] [CrossRef]
- Wulder, M.; Niemann, K.O.; Goodenough, D.G. Local Maximum Filtering for the Extraction of Tree Locations and Basal Area from High Spatial Resolution Imagery. Remote Sens. Environ. 2000, 73, 103–114. [Google Scholar] [CrossRef]
- Popescu, S.C.; Wynne, R.H.; Nelson, R.F. Estimating Plot-Level Tree Heights with Lidar: Local Filtering with a Canopy-Height Based Variable Window Size. Comput. Electron. Agric. 2002, 37, 71–95. [Google Scholar] [CrossRef]
- Yin, D.; Wang, L. Individual Mangrove Tree Measurement Using UAV-Based LiDAR Data: Possibilities and Challenges. Remote Sens. Environ. 2019, 223, 34–49. [Google Scholar] [CrossRef]
- Falkowski, M.J.; Smith, A.M.; Hudak, A.T.; Gessler, P.E.; Vierling, L.A.; Crookston, N.L. Automated Estimation of Individual Conifer Tree Height and Crown Diameter via Two-Dimensional Spatial Wavelet Analysis of Lidar Data. Can. J. Remote Sens. 2006, 32, 153–161. [Google Scholar] [CrossRef]
- Barnes, C.; Balzter, H.; Barrett, K.; Eddy, J.; Milner, S.; Suárez, J.C. Individual Tree Crown Delineation from Airborne Laser Scanning for Diseased Larch Forest Stands. Remote Sens. 2017, 9, 231. [Google Scholar] [CrossRef]
- Persson, A.; Holmgren, J.; Soderman, U. Detecting and Measuring Individual Trees Using an Airborne Laser Scanner. Photogramm. Eng. Remote Sens. 2002, 68, 925–932. [Google Scholar]
- Liu, H.; Dong, P.; Wu, C.; Wang, P.; Fang, M. Individual Tree Identification Using a New Cluster-Based Approach with Discrete-Return Airborne LiDAR Data. Remote Sens. Environ. 2021, 258, 112382. [Google Scholar] [CrossRef]
- Dalponte, M.; Coomes, D.A. Tree-Centric Mapping of Forest Carbon Density from Airborne Laser Scanning and Hyperspectral Data. Methods Ecol. Evol. 2016, 7, 1236–1245. [Google Scholar] [CrossRef] [PubMed]
- Duncanson, L.; Cook, B.; Hurtt, G.; Dubayah, R. An Efficient, Multi-Layered Crown Delineation Algorithm for Mapping Individual Tree Structure across Multiple Ecosystems. Remote Sens. Environ. 2014, 154, 378–386. [Google Scholar] [CrossRef]
- Liu, T.; Im, J.; Quackenbush, L.J. A Novel Transferable Individual Tree Crown Delineation Model Based on Fishing Net Dragging and Boundary Classification. ISPRS J. Photogramm. Remote Sens. 2015, 110, 34–47. [Google Scholar] [CrossRef]
- Yun, T.; Jiang, K.; Li, G.; Eichhorn, M.P.; Fan, J.; Liu, F.; Chen, B.; An, F.; Cao, L. Individual Tree Crown Segmentation from Airborne LiDAR Data Using a Novel Gaussian Filter and Energy Function Minimization-Based Approach. Remote Sens. Environ. 2021, 256, 112307. [Google Scholar] [CrossRef]
- Pang, Y.; Wang, W.; Du, L.; Zhang, Z.; Liang, X.; Li, Y.; Wang, Z. Nyström-Based Spectral Clustering Using Airborne LiDAR Point Cloud Data for Individual Tree Segmentation. Int. J. Digit. Earth 2021, 14, 1452–1476. [Google Scholar] [CrossRef]
- Morsdorf, F.; Meier, E.; Allgöwer, B.; Nüesch, D. Clustering in Airborne Laser Scanning Raw Data for Segmentation of Single Trees. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2003, 34, W13. [Google Scholar]
- Ferraz, A.; Saatchi, S.; Mallet, C.; Meyer, V. Lidar Detection of Individual Tree Size in Tropical Forests. Remote Sens. Environ. 2016, 183, 318–333. [Google Scholar] [CrossRef]
- du Toit, F.; Coops, N.C.; Ratcliffe, B.; El-Kassaby, Y.A.; Lucieer, A. Modelling Internal Tree Attributes for Breeding Applications in Douglas-Fir Progeny Trials Using RPAS-ALS. Sci. Remote Sens. 2023, 7, 100072. [Google Scholar] [CrossRef]
- Li, W.; Guo, Q.; Jakubowski, M.K.; Kelly, M. A New Method for Segmenting Individual Trees from the Lidar Point Cloud. Photogramm. Eng. Remote Sens. 2012, 78, 75–84. [Google Scholar] [CrossRef]
- Sačkov, I.; Hlásny, T.; Bucha, T.; Juriš, M. Integration of Tree Allometry Rules to Treetops Detection and Tree Crowns Delineation Using Airborne Lidar Data. Iforest-Biogeosciences For. 2017, 10, 459. [Google Scholar] [CrossRef]
- Paris, C.; Valduga, D.; Bruzzone, L. A Hierarchical Approach to Three-Dimensional Segmentation of LiDAR Data at Single-Tree Level in a Multilayered Forest. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4190–4203. [Google Scholar] [CrossRef]
- Zhang, J.; Sohn, G.; Brédif, M. A Hybrid Framework for Single Tree Detection from Airborne Laser Scanning Data: A Case Study in Temperate Mature Coniferous Forests in Ontario, Canada. ISPRS J. Photogramm. Remote Sens. 2014, 98, 44–57. [Google Scholar] [CrossRef]
- Hu, B.; Li, J.; Jing, L.; Judah, A. Improving the Efficiency and Accuracy of Individual Tree Crown Delineation from High-Density LiDAR Data. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 145–155. [Google Scholar] [CrossRef]
- Harikumar, A.; Bovolo, F.; Bruzzone, L. A Local Projection-Based Approach to Individual Tree Detection and 3-D Crown Delineation in Multistoried Coniferous Forests Using High-Density Airborne LiDAR Data. IEEE Trans. Geosci. Remote Sens. 2018, 57, 1168–1182. [Google Scholar] [CrossRef]
- Yang, J.; Kang, Z.; Cheng, S.; Yang, Z.; Akwensi, P.H. An Individual Tree Segmentation Method Based on Watershed Algorithm and Three-Dimensional Spatial Distribution Analysis from Airborne LiDAR Point Clouds. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1055–1067. [Google Scholar] [CrossRef]
- Beland, M.; Parker, G.; Sparrow, B.; Harding, D.; Chasmer, L.; Phinn, S.; Antonarakis, A.; Strahler, A. On Promoting the Use of Lidar Systems in Forest Ecosystem Research. For. Ecol. Manag. 2019, 450, 117484. [Google Scholar] [CrossRef]
- Wallace, L.; Lucieer, A.; Watson, C.S. Evaluating Tree Detection and Segmentation Routines on Very High Resolution UAV LiDAR Data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7619–7628. [Google Scholar] [CrossRef]
- Murray, J.; Gullick, D.; Blackburn, G.A.; Whyatt, J.D.; Edwards, C. ARBOR: A New Framework for Assessing the Accuracy of Individual Tree Crown Delineation from Remotely-Sensed Data. Remote Sens. Environ. 2019, 231, 111256. [Google Scholar] [CrossRef]
- Weiser, H.; Schäfer, J.; Winiwarter, L.; Krašovec, N.; Fassnacht, F.E.; Höfle, B. Individual Tree Point Clouds and Tree Measurements from Multi-Platform Laser Scanning in German Forests. Earth Syst. Sci. Data 2022, 14, 2989–3012. [Google Scholar] [CrossRef]
- Brede, B.; Lau, A.; Bartholomeus, H.M.; Kooistra, L. Comparing RIEGL RiCOPTER UAV LiDAR Derived Canopy Height and DBH with Terrestrial LiDAR. Sensors 2017, 17, 2371. [Google Scholar] [CrossRef] [PubMed]
- Wang, D. Unsupervised Semantic and Instance Segmentation of Forest Point Clouds. ISPRS J. Photogramm. Remote Sens. 2020, 165, 86–97. [Google Scholar] [CrossRef]
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An Easy-to-Use Airborne LiDAR Data Filtering Method Based on Cloth Simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- Popescu, S.C.; Wynne, R.H. Seeing the Trees in the Forest. Photogramm. Eng. Remote Sens. 2004, 70, 589–604. [Google Scholar] [CrossRef]
- Popescu, S.C. Estimating Biomass of Individual Pine Trees Using Airborne Lidar. Biomass Bioenergy 2007, 31, 646–655. [Google Scholar] [CrossRef]
- Jenks, G.F. The Data Model Concept in Statistical Mapping. Int. Yearb. Cartogr. 1967, 7, 186–190. [Google Scholar]
- Bezdek, J.C.; Ehrlich, R.; Full, W. FCM: The Fuzzy c-Means Clustering Algorithm. Comput. Geosci. 1984, 10, 191–203. [Google Scholar] [CrossRef]
- Roussel, J.-R.; Auty, D.; Coops, N.C.; Tompalski, P.; Goodbody, T.R.; Meador, A.S.; Bourdon, J.-F.; De Boissieu, F.; Achim, A. lidR: An R Package for Analysis of Airborne Laser Scanning (ALS) Data. Remote Sens. Environ. 2020, 251, 112061. [Google Scholar] [CrossRef]
- Bechtold, S.; Höfle, B. Helios: A Multi-Purpose Lidar Simulation Framework for Research, Planning and Training of Laser Scanning Operations with Airborne, Ground-Based Mobile and Stationary Platforms. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 3, 161–168. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; Latifi, H.; Hartig, F. Using Synthetic Data to Evaluate the Benefits of Large Field Plots for Forest Biomass Estimation with LiDAR. Remote Sens. Environ. 2018, 213, 115–128. [Google Scholar] [CrossRef]
- Winiwarter, L.; Pena, A.M.E.; Weiser, H.; Anders, K.; Sánchez, J.M.; Searle, M.; Höfle, B. Virtual Laser Scanning with HELIOS++: A Novel Take on Ray Tracing-Based Simulation of Topographic Full-Waveform 3D Laser Scanning. Remote Sens. Environ. 2022, 269, 112772. [Google Scholar] [CrossRef]
- Khosravipour, A.; Skidmore, A.K.; Wang, T.; Isenburg, M.; Khoshelham, K. Effect of Slope on Treetop Detection Using a LiDAR Canopy Height Model. ISPRS J. Photogramm. Remote Sens. 2015, 104, 44–52. [Google Scholar] [CrossRef]
- Nie, S.; Wang, C.; Xi, X.; Luo, S.; Zhu, X.; Li, G.; Liu, H.; Tian, J.; Zhang, S. Assessing the Impacts of Various Factors on Treetop Detection Using LiDAR-Derived Canopy Height Models. IEEE Trans. Geosci. Remote Sens. 2019, 57, 10099–10115. [Google Scholar] [CrossRef]






| Type | Number of Plots | Stand Density (stems/ha) | Tree Height (m) | Crown Area (m2) | |||
|---|---|---|---|---|---|---|---|
| Range | Mean | Range | Mean | Range | Mean | ||
| Coniferous plot | 9 | 233–811 | 510 | 3.34–46.81 | 26.71 | 3.40–112.45 | 38.93 |
| Broadleaved plot | 9 | 211–677 | 382 | 8.27–31.23 | 21.86 | 7.07–136.53 | 45.22 |
| Mixed plot | 3 | 233–288 | 262 | 3.69–39.23 | 22.60 | 4.43–337.53 | 54.29 |
| Method | Recall (r) | Precision (p) | Overall Accuracy (f) |
|---|---|---|---|
| Multiscale adaptive LM | 86.31% | 88.27% | 87.28% |
| LM with larger window | 75.45% | 92.35% | 83.05% |
| LM with smaller window | 90.46% | 70.39% | 79.17% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, Y.; Niu, Y.; Wang, L.; Li, W. Individual-Tree Segmentation from UAV–LiDAR Data Using a Region-Growing Segmentation and Supervoxel-Weighted Fuzzy Clustering Approach. Remote Sens. 2024, 16, 608. https://doi.org/10.3390/rs16040608
Fu Y, Niu Y, Wang L, Li W. Individual-Tree Segmentation from UAV–LiDAR Data Using a Region-Growing Segmentation and Supervoxel-Weighted Fuzzy Clustering Approach. Remote Sensing. 2024; 16(4):608. https://doi.org/10.3390/rs16040608
Chicago/Turabian StyleFu, Yuwen, Yifang Niu, Li Wang, and Wang Li. 2024. "Individual-Tree Segmentation from UAV–LiDAR Data Using a Region-Growing Segmentation and Supervoxel-Weighted Fuzzy Clustering Approach" Remote Sensing 16, no. 4: 608. https://doi.org/10.3390/rs16040608
APA StyleFu, Y., Niu, Y., Wang, L., & Li, W. (2024). Individual-Tree Segmentation from UAV–LiDAR Data Using a Region-Growing Segmentation and Supervoxel-Weighted Fuzzy Clustering Approach. Remote Sensing, 16(4), 608. https://doi.org/10.3390/rs16040608








