Correction of Ionospheric Phase in SAR Interferometry Considering Wavenumber Shift
Abstract
1. Introduction
2. Materials and Methods
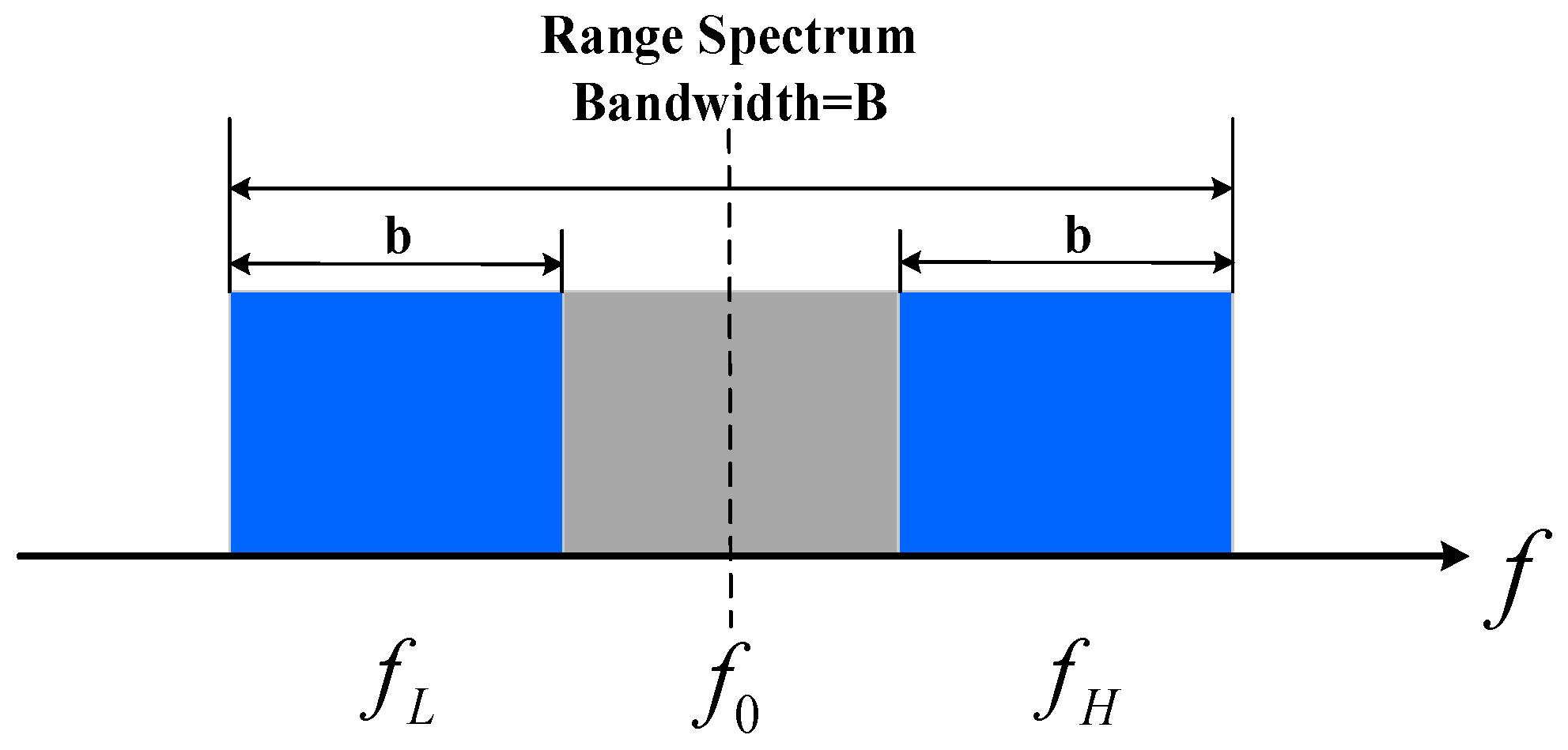
2.1. Influence of Wavenumber Shift on RSS method without CBF
2.2. Influence of Wavenumber Shift on RSS Method with CBF
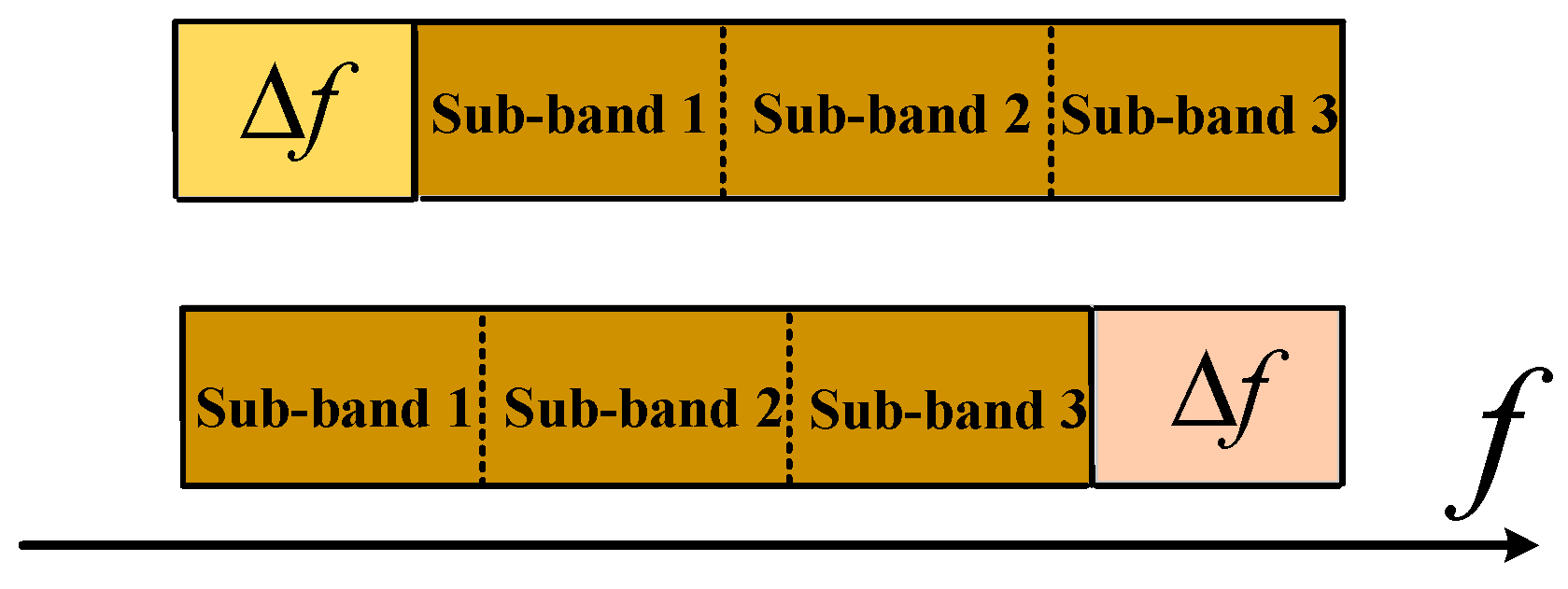
2.3. The MTSVD-Based Multi-Sub-Band RSS Method Considering Wavenumber Shift
2.3.1. Multi-Sub-Band RSS Method Based on MTSVD
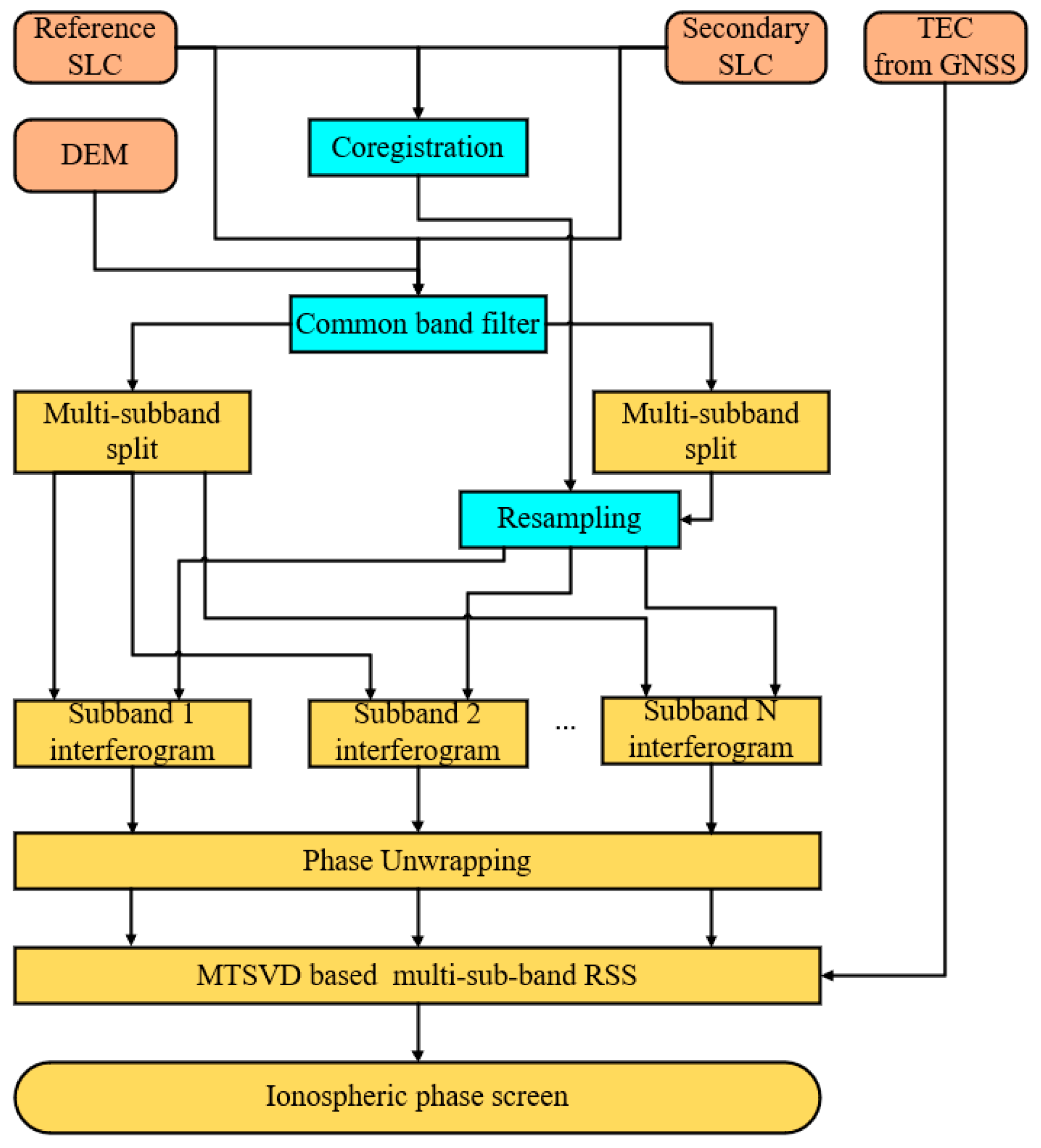
2.3.2. Processing Workflow
- Terrain-adaptive common band filtering
- 2.
- Multi-sub-band split and interferograms generation
- 3.
- Phase unwrapping
- 4.
- Ionospheric phase screen (IPS) estimation
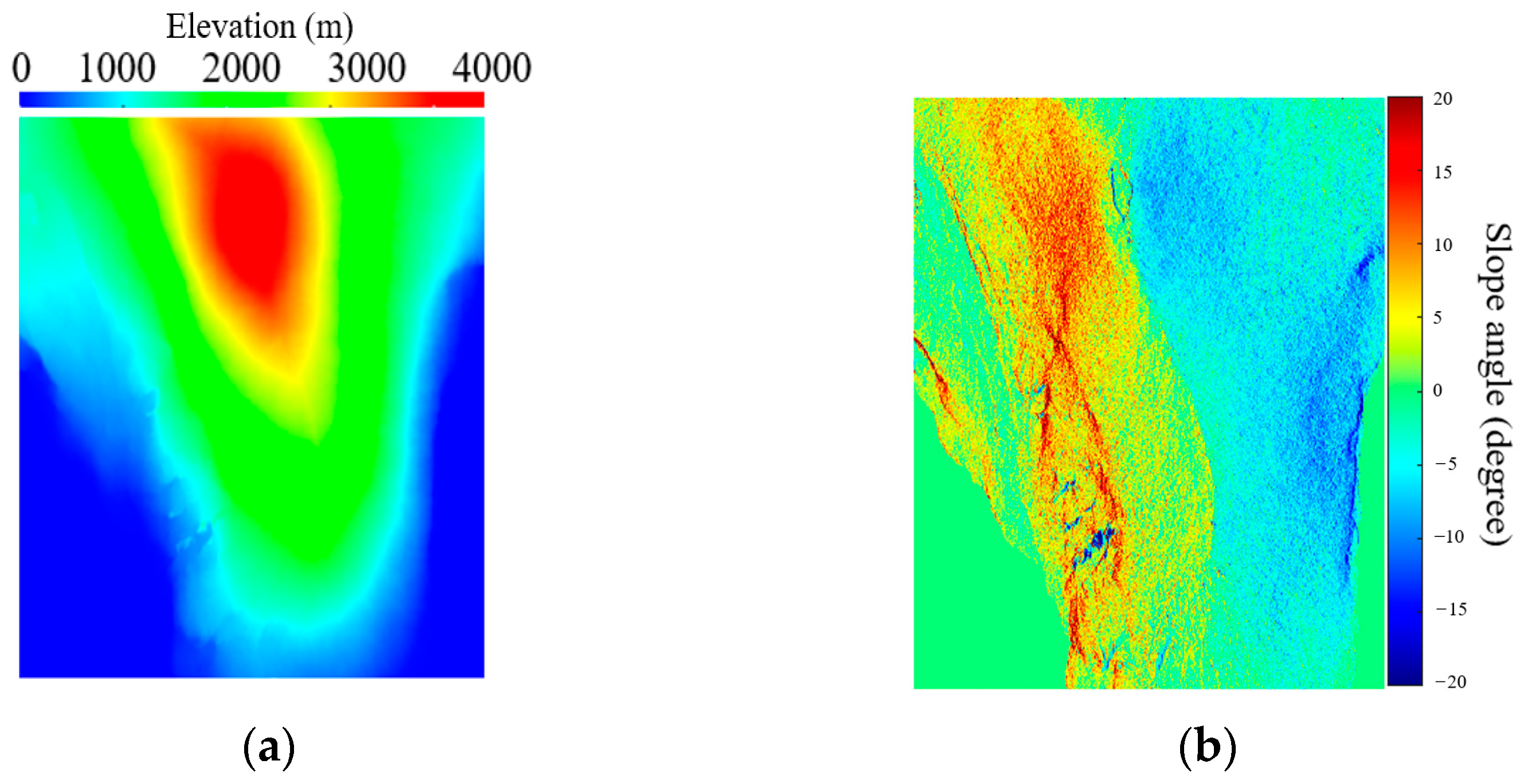
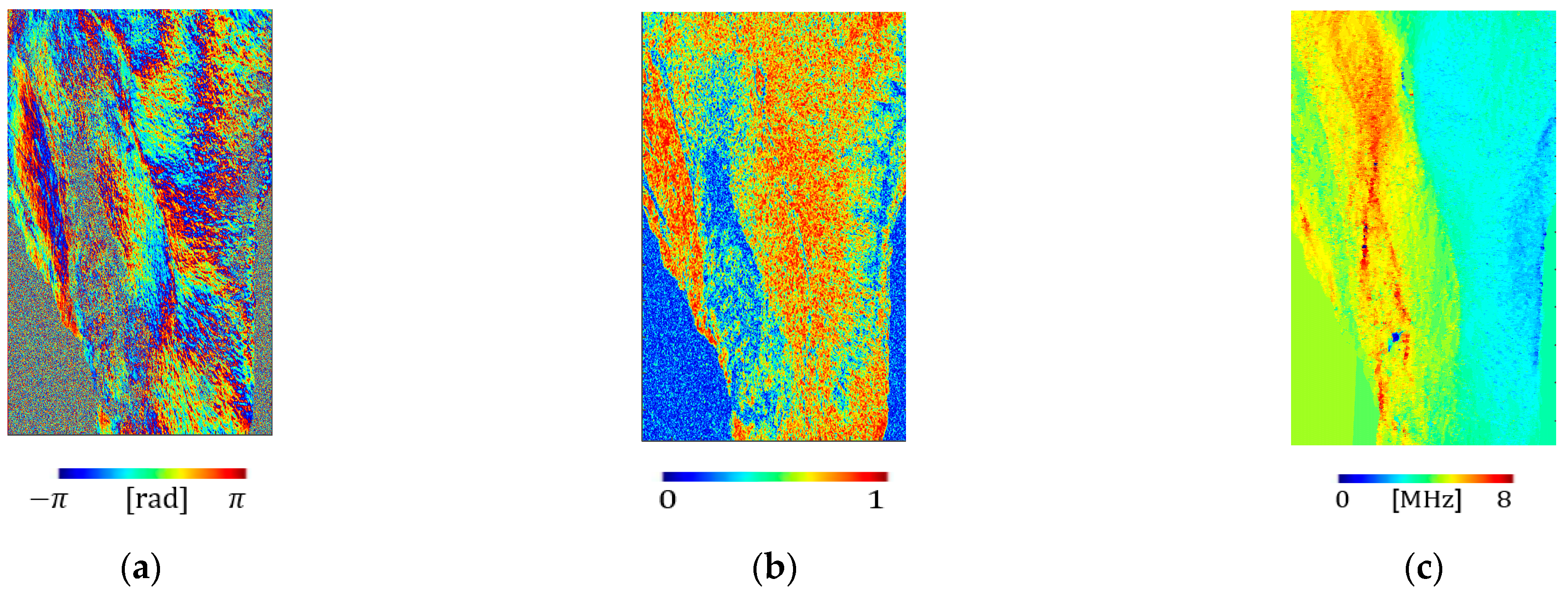
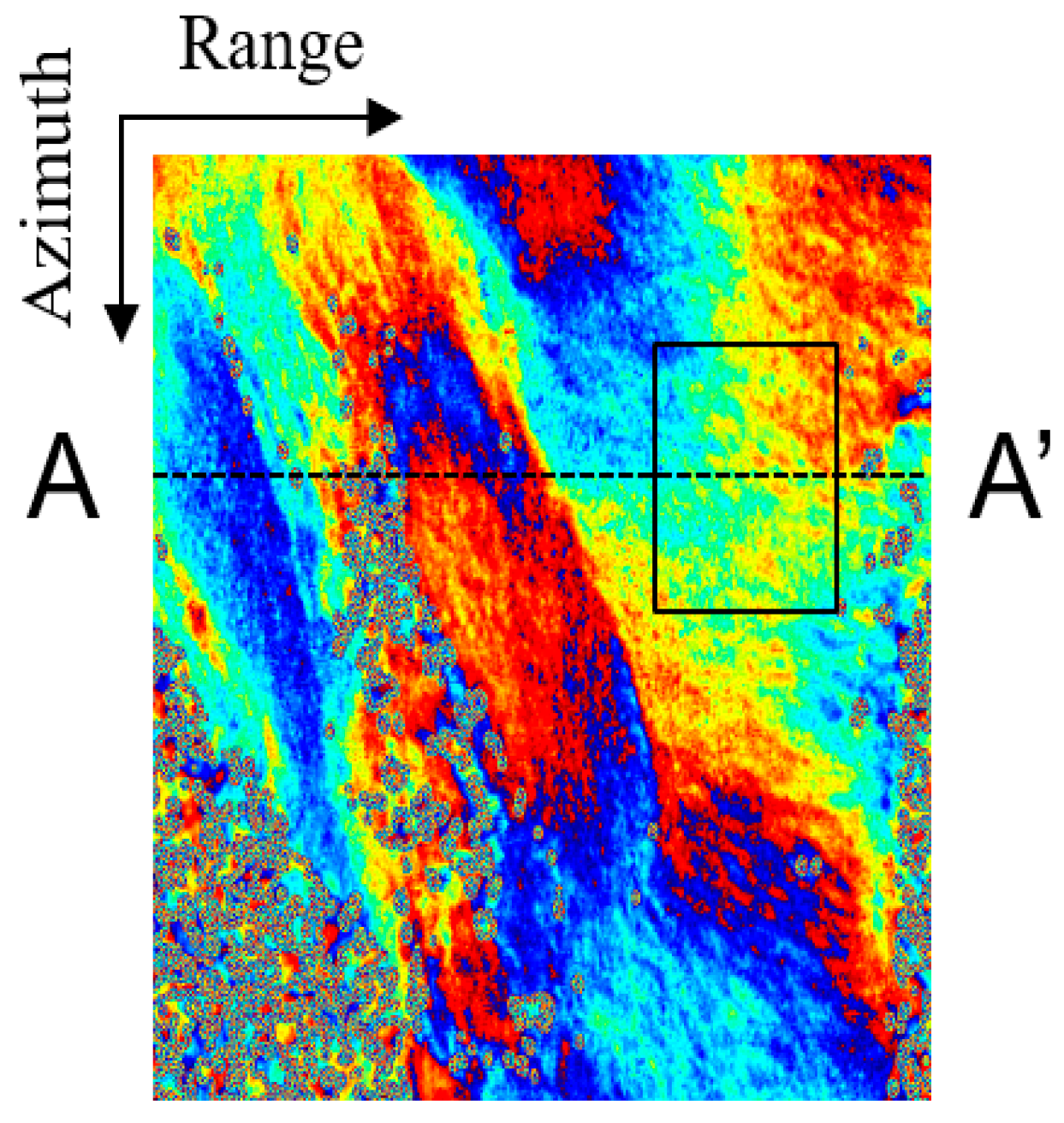
3. Experimental Results
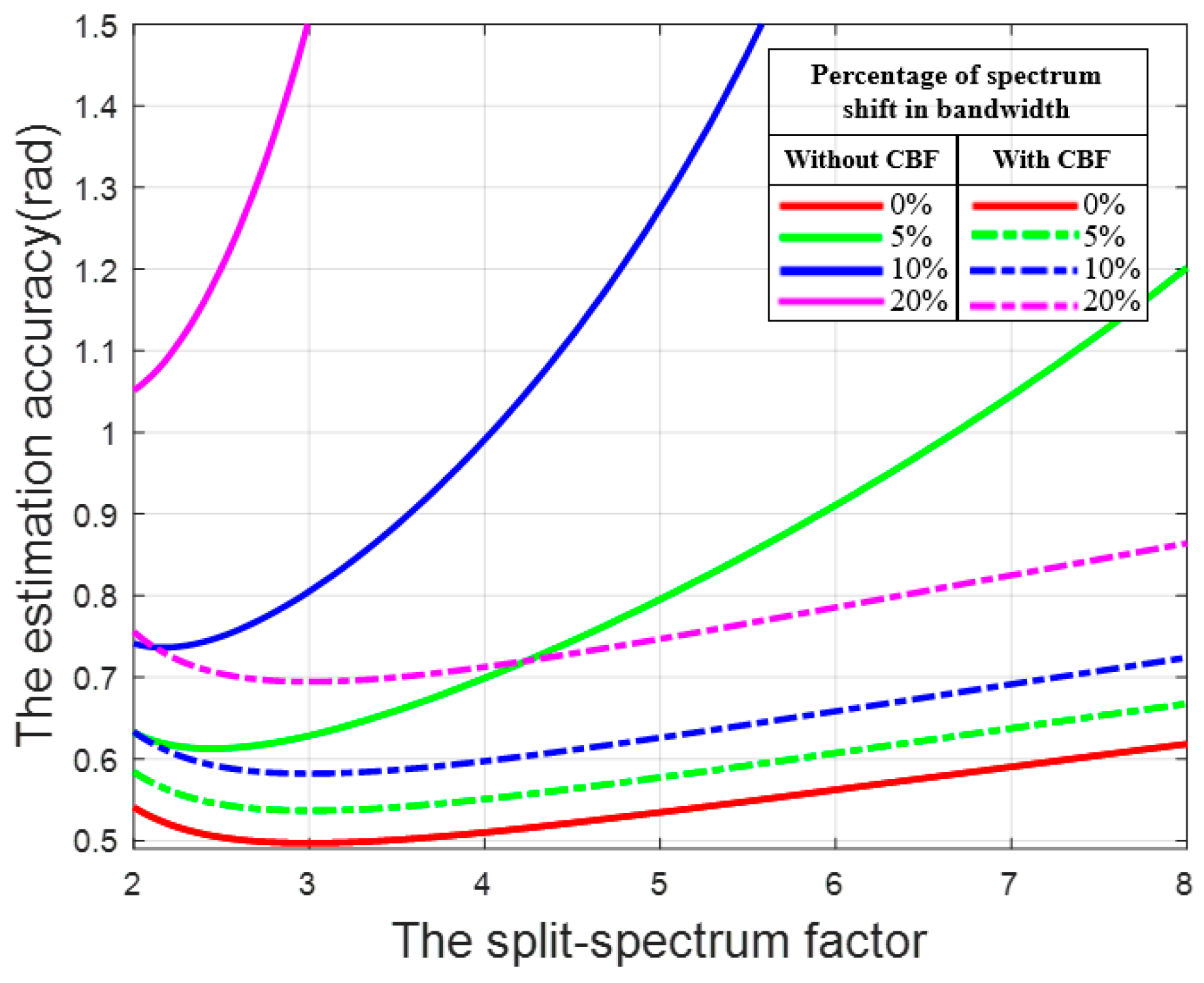
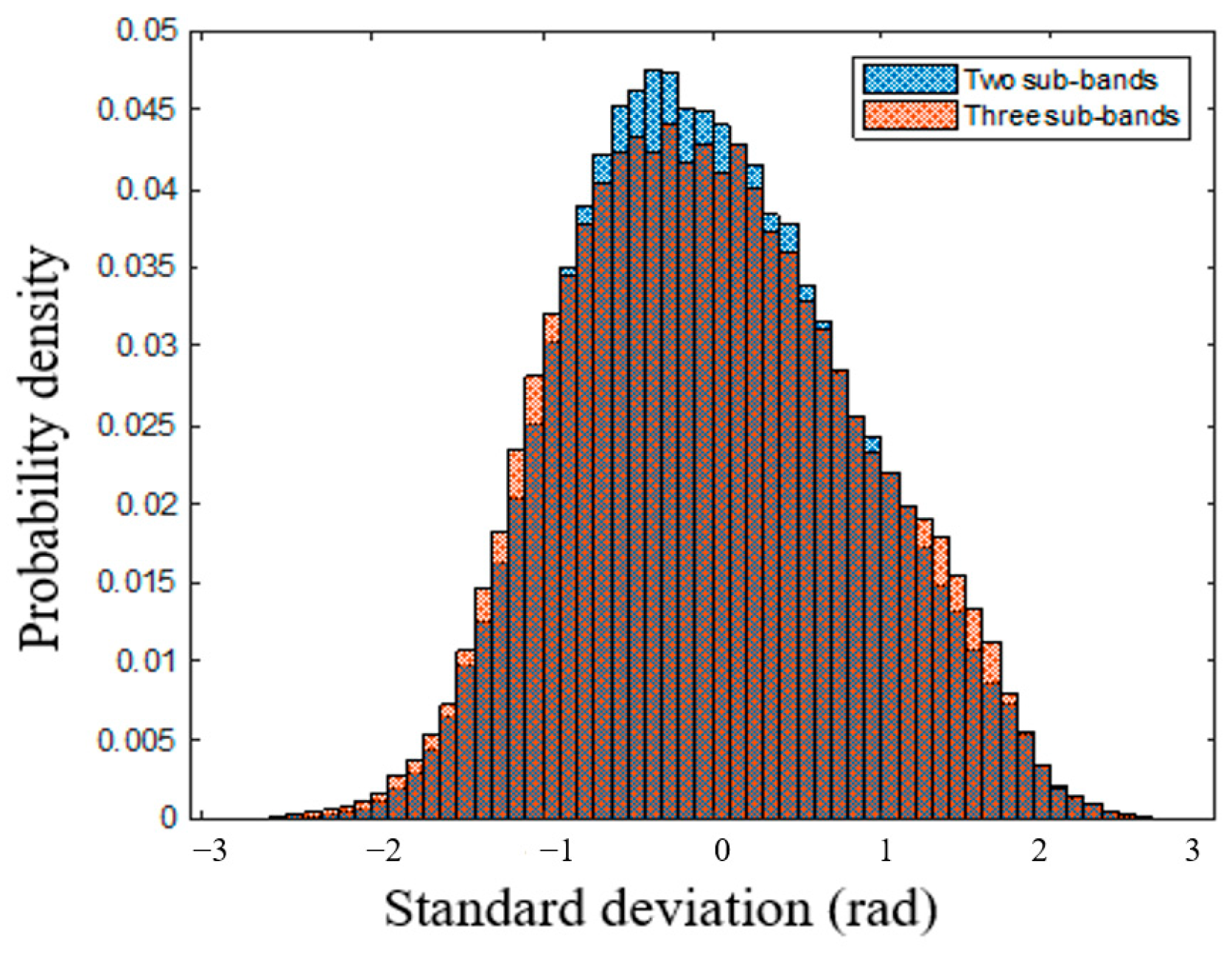
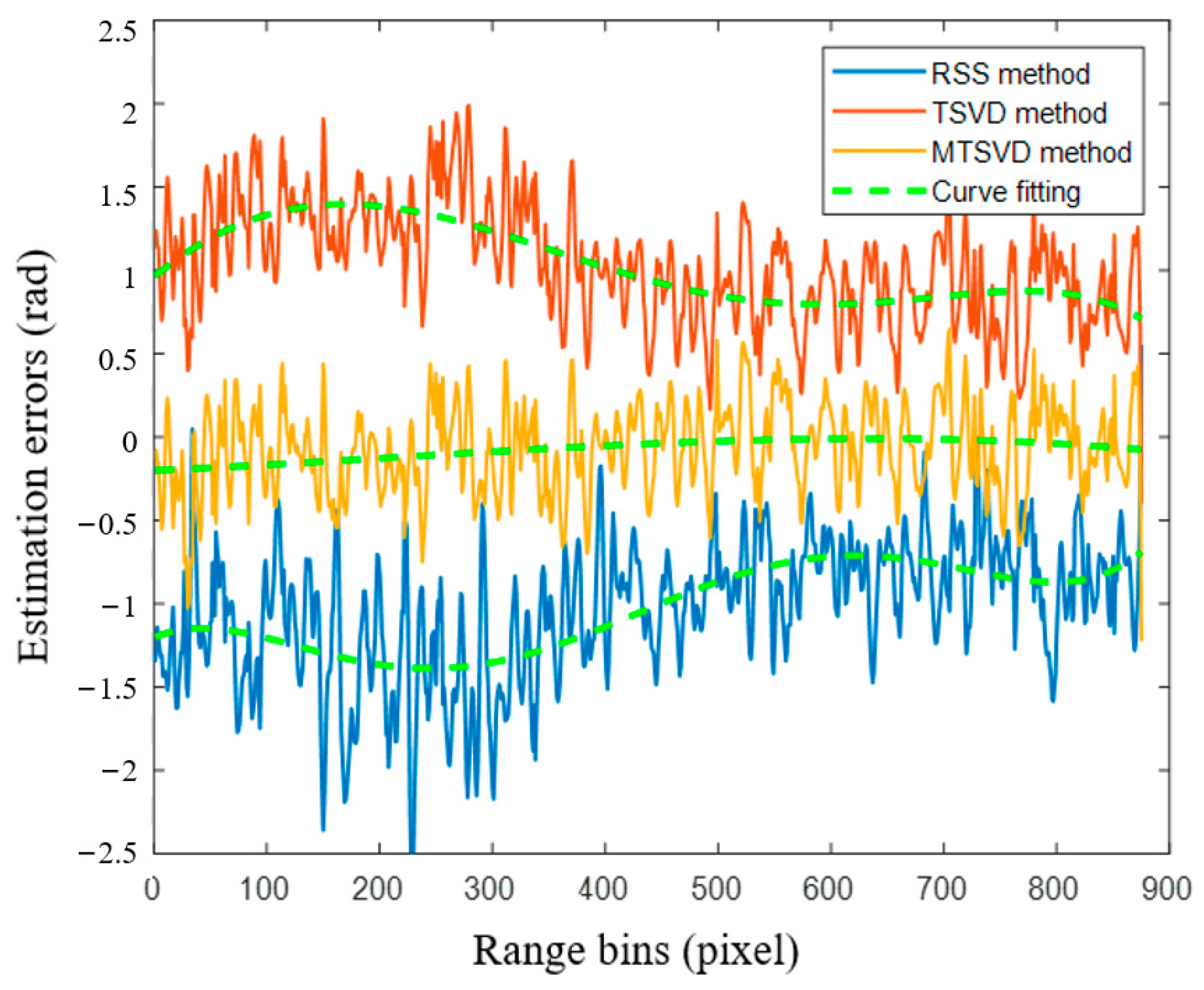
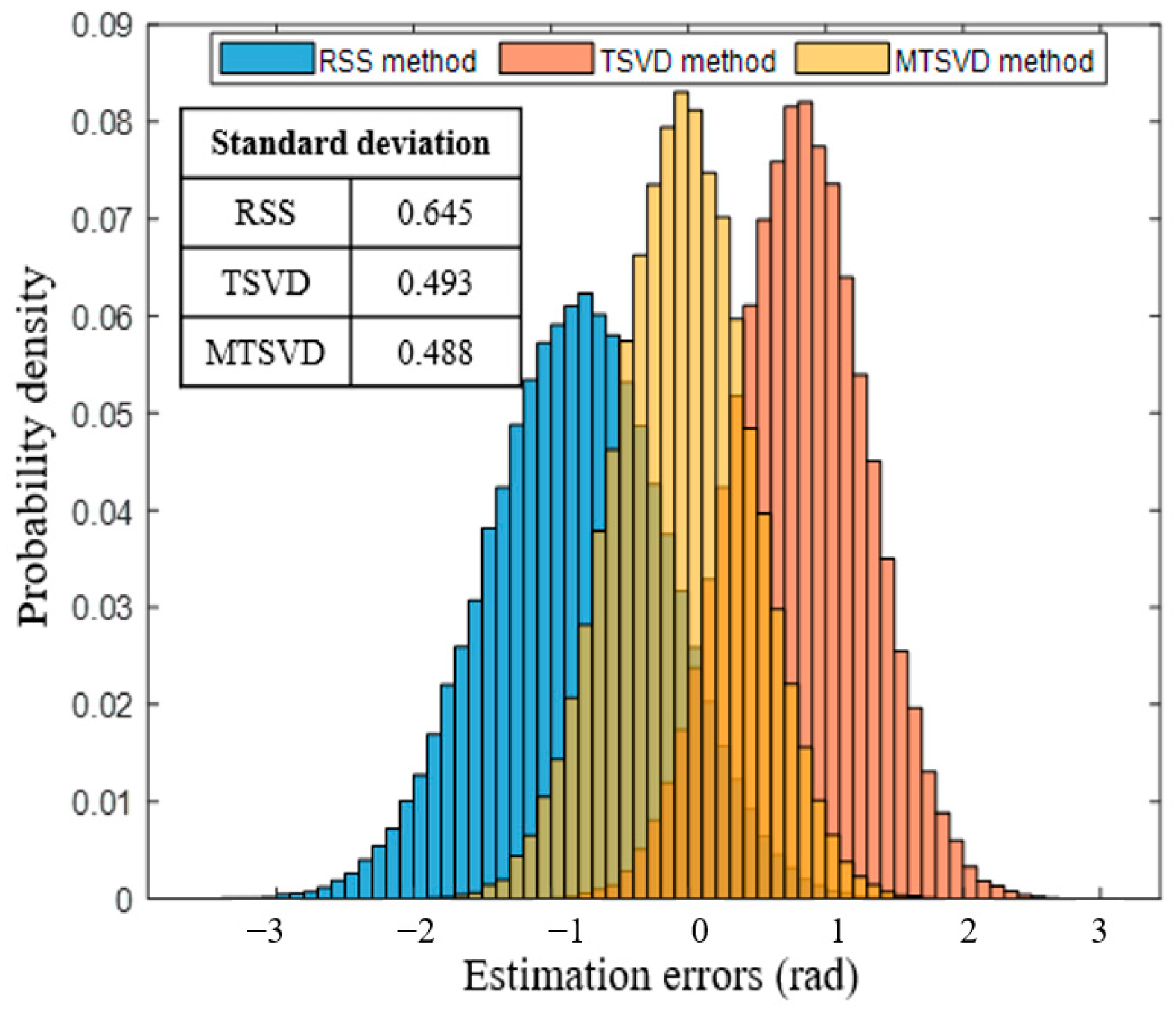
3.1. The RSS Method without CBF
3.2. The RSS Method with CBF
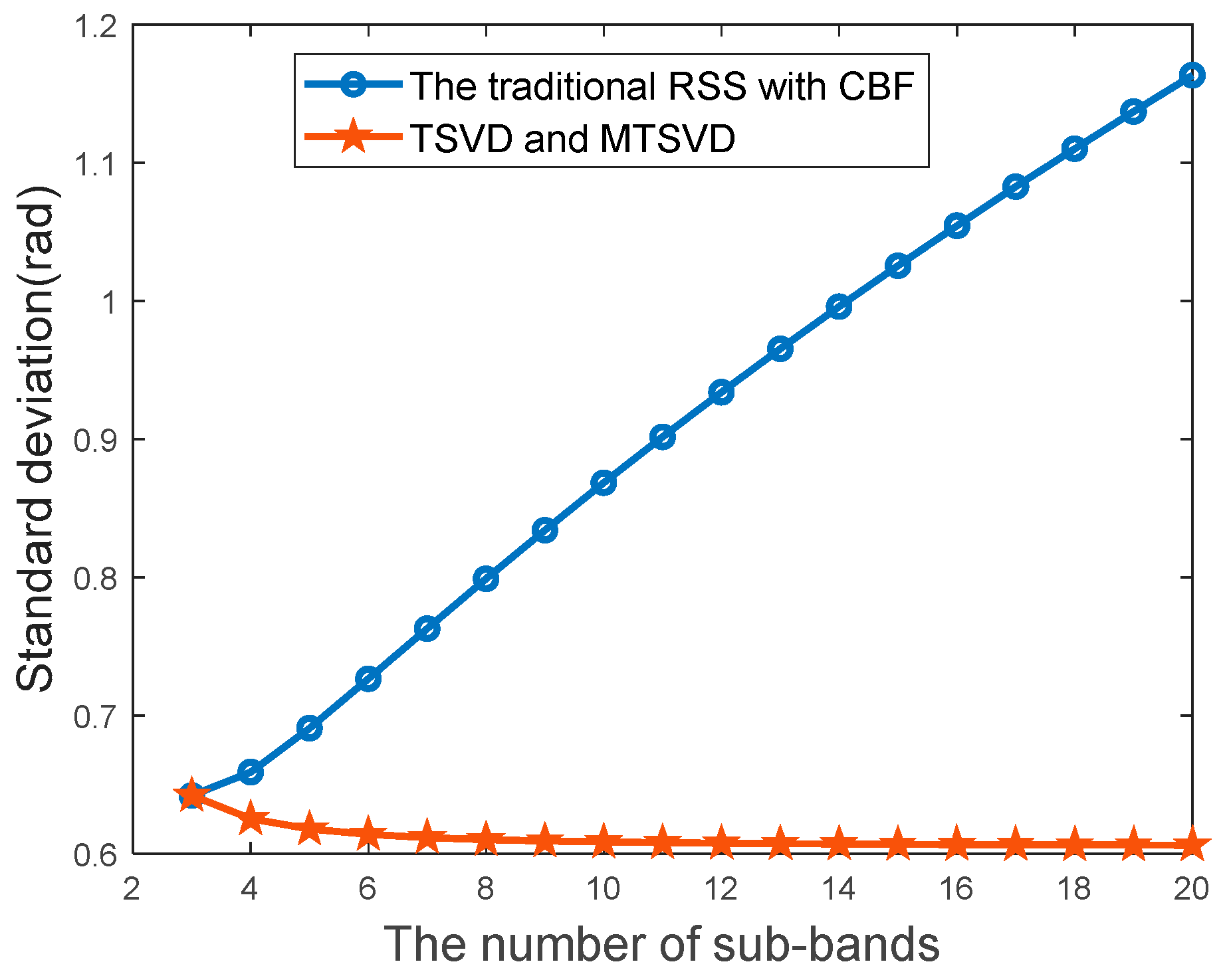
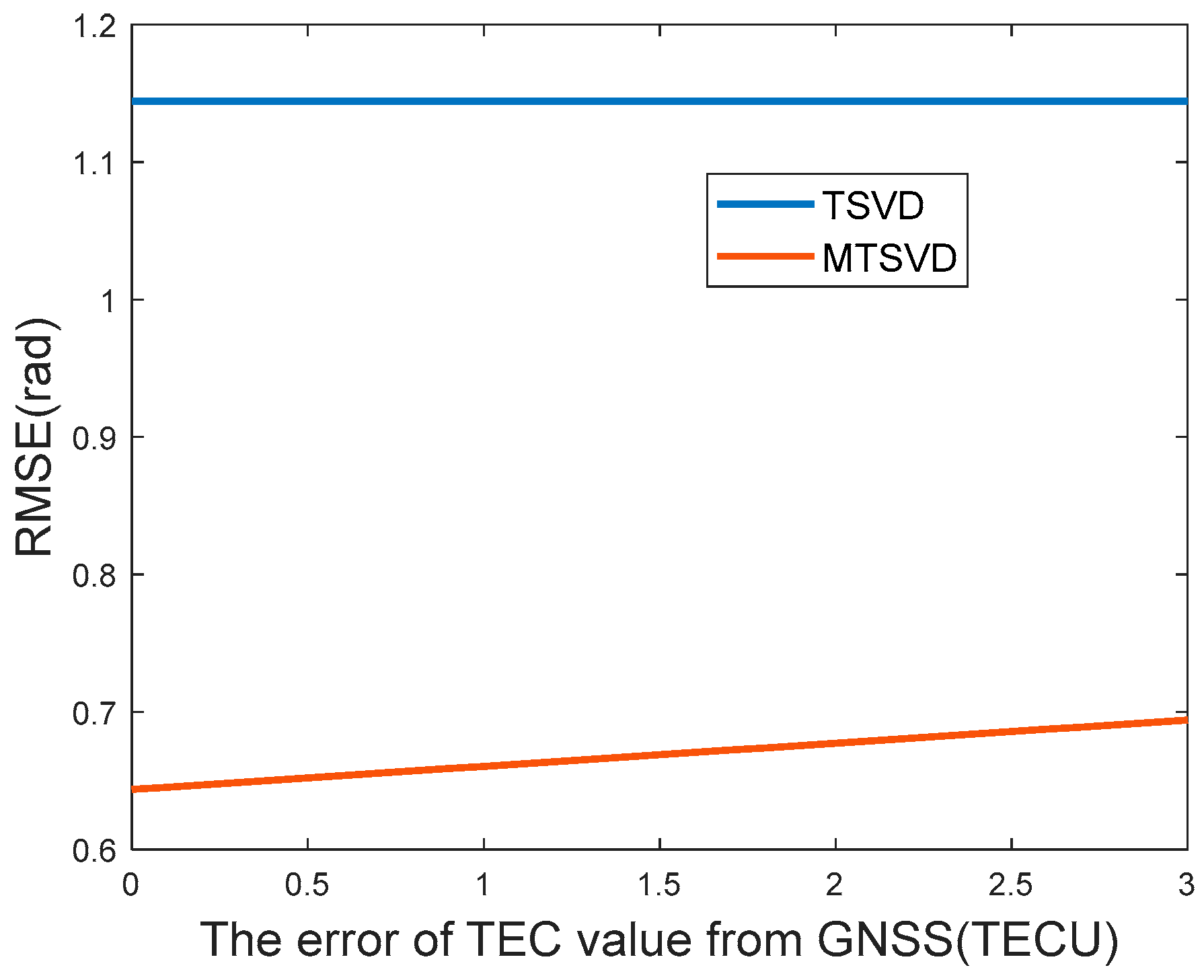
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rosen, P.A.; Hensley, S.; Joughin, I.R.; Li, F.K.; Madsen, S.N.; Rodriguez, E.; Goldstein, R.M. Synthetic Aperture Radar interferometry. Proc. IEEE 2000, 88, 333–382. [Google Scholar] [CrossRef]
- Bamler, R.; Hartl, P. Synthetic Aperture Radar interferometry. Inverse Probl. 1998, 14, R1. [Google Scholar] [CrossRef]
- Liao, Q.; Sheng, Z.; Zhou, S.; Guo, P.; Long, Z.; He, M.; Guan, J. A preliminary study on the inversion method for the refraction structure parameter from vortex electromagnetic waves. Remote Sens. 2023, 15, 3140. [Google Scholar] [CrossRef]
- He, Y.; Zhu, X.; Sheng, Z.; He, M. Identification of stratospheric disturbance information in China based on the round-trip intelligent sounding system. Atmos. Chem. Phys. 2024, 24, 3839–3856. [Google Scholar] [CrossRef]
- Zebker, H.A.; Rosen, P.A.; Hensley, S. Atmospheric effects in interferometric synthetic aperture radar surface deformation and topographic maps. J. Geophys. Res. Solid Earth 1997, 102, 7547–7563. [Google Scholar] [CrossRef]
- Meyer, F.J.; Nicoll, J. The impact of the ionosphere on interferometric SAR processing. In Proceedings of the IGARSS 2008—2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 6–11 July 2008. [Google Scholar]
- Wegmuller, U.; Werner, C.; Strozzi, T.; Wiesmann, A. Ionospheric electron concentration effects on SAR and insar. In Proceedings of the 2006 IEEE International Symposium on Geoscience and Remote Sensing, Denver, CO, USA, 31 July–4 August 2006. [Google Scholar]
- Meyer, F.J. Performance requirements for ionospheric correction of low-frequency SAR Data. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3694–3702. [Google Scholar] [CrossRef]
- Yunjun, Z.; Fattahi, H.; Pi, X.; Rosen, P.; Simons, M.; Agram, P.; Aoki, Y. Range geolocation accuracy of C-/L-band SAR and its implications for operational stack coregistration. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–19. [Google Scholar] [CrossRef]
- Jin, S.; Park, J.U.; Wang, J.L.; Choi, B.K.; Park, P.H. Electron density profiles derived from ground-based GPS observations. J. Navig. 2006, 59, 395–401. [Google Scholar] [CrossRef]
- Liao, W.-T.; Tseng, K.-H.; Lee, I.-T.; Liibusk, A.; Lee, J.-C.; Liu, J.-Y.; Chang, C.-P.; Lin, Y.-C. Sentinel-1 interferometry with ionospheric correction from global and local TEC maps for land displacement detection in Taiwan. Adv. Space Res. 2020, 65, 1447–1465. [Google Scholar] [CrossRef]
- Gomba, G.; De Zan, F. Bayesian data combination for the estimation of ionospheric effects in sar interferograms. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6582–6593. [Google Scholar] [CrossRef]
- Freeman, A. Calibration of linearly polarized polarimetric SAR data subject to Faraday rotation. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1617–1624. [Google Scholar] [CrossRef]
- Rosen, P.; Lavalle, M.; Pi, X.; Buckley, S.; Szeliga, W.; Zebker, H.; Gurrola, E. Techniques and tools for estimating ionospheric effects in interferometric and polarimetric SAR data. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011. [Google Scholar]
- Jung, H.-S.; Lee, D.-T.; Lu, Z.; Won, J.-S. Ionospheric correction of Sar Interferograms by multiple-aperture interferometry. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3191–3199. [Google Scholar] [CrossRef]
- Chen, A.C.; Zebker, H.A. Reducing ionospheric effects in Insar data using accurate coregistration. IEEE Trans. Geosci. Remote Sens. 2014, 52, 60–70. [Google Scholar] [CrossRef]
- Gomba, G.; Parizzi, A.; De Zan, F.; Eineder, M.; Bamler, R. Toward operational compensation of ionospheric effects in sar interferograms: The split-spectrum method. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1446–1461. [Google Scholar] [CrossRef]
- Fattahi, H.; Simons, M.; Agram, P. Insar Time-series estimation of the Ionospheric Phase Delay: An extension of the split range-spectrum technique. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5984–5996. [Google Scholar] [CrossRef]
- Gomba, G.; De Zan, F.; Parizzi, A. Ionospheric phase screen and ionospheric azimuth shift estimation combining the split-spectrum and multi-squint methods. In Proceedings of the EUSAR 2016: 11th European Conference on Synthetic Aperture Radar, Hamburg, Germany, 6–9 June 2016; VDE: Berlin, Germany, 2016. [Google Scholar]
- Zhang, B.; Wang, C.; Ding, X.; Zhu, W.; Wu, S. Correction of ionospheric artifacts in sar data: Application to fault slip inversion of 2009 southern sumatra earthquake. IEEE Geosci. Remote Sens. Lett. 2017, 15, 1327–1331. [Google Scholar] [CrossRef]
- Zhang, B.; Ding, X.; Zhu, W.; Wang, C.; Zhang, L.; Liu, Z. Mitigating ionospheric artifacts in COSEISMIC interferogram based on offset field derived from Alos-Palsar Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3050–3059. [Google Scholar] [CrossRef]
- Rosen, P.A.; Hensley, S.; Chen, C. Measurement and mitigation of the ionosphere in L-band interferometric SAR Data. In Proceedings of the 2010 IEEE Radar Conference, Arlington, VA, USA, 10–14 May 2010. [Google Scholar]
- Brcic, R.; Parizzi, A.; Eineder, M.; Bamler, R.; Meyer, F. Estimation and compensation of ionospheric delay for sar interferometry. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010. [Google Scholar]
- Gatelli, F.; Guamieri, A.M.; Parizzi, F.; Pasquali, P.; Prati, C.; Rocca, F. The wavenumber shift in sar interferometry. IEEE Trans. Geosci. Remote Sens. 2010, 32, 855–865. [Google Scholar] [CrossRef]
- Bamler, R.; Eineder, M. Accuracy of differential shift estimation by correlation and split-bandwidth interferometry for wideband and delta-k SAR systems. IEEE Geosci. Remote Sens. Lett. 2005, 2, 151–155. [Google Scholar] [CrossRef]
- Hansen, P.C.; Sekii, T.; Shibahashi, H. The modified truncated SVD method for regularization in general form. SIAM J. Sci. Stat. Comput. 1992, 13, 1142–1150. [Google Scholar] [CrossRef]
- Hansen, P.C. Regularization tools: A MATLAB package for analysis and solution of discrete ill-posed problems. Numer. Algorithms 1994, 6, 1–35. [Google Scholar] [CrossRef]
- Noschese, S.; Reichel, L. A modified truncated singular value decomposition method for discrete ill-posed problems. Numer. Linear Algebra Appl. 2014, 21, 813–822. [Google Scholar] [CrossRef]
- Li, Z.; Yuan, Y.; Wang, N.; Hernandez-Pajares, M.; Huo, X. Shpts: Towards a new method for generating precise global ionospheric TEC map based on spherical harmonic and generalized trigonometric series functions. J. Geod. 2014, 89, 331–345. [Google Scholar] [CrossRef]
- Fletcher, K. Insar Principles: Guidelines for SAR Interferometry Processing and Interpretation; ESA: Noordwijk, The, Netherlands, 2007. [Google Scholar]
- Fornaro, G.; Guarnieri, A.M. Minimum mean square error space-varying filtering of interferometric SAR data. IEEE Trans. Geosci. Remote Sens. 2002, 40, 11–21. [Google Scholar] [CrossRef][Green Version]
- Wegmüller, U.; Werner, C.; Frey, O.; Magnard, C.; Strozzi, T. Reformulating the split-spectrum method to facilitate the estimation and compensation of the ionospheric phase in sar interferograms. Procedia Comput. Sci. 2018, 138, 318–325. [Google Scholar] [CrossRef]
- Chen, C.W.; Zebker, H.A. Phase unwrapping for large SAR interferograms: Statistical segmentation and Generalized Network Models. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1709–1719. [Google Scholar] [CrossRef]
- Chen, P.; Yao, Y.; Yao, W. Global ionosphere maps based on GNSS, satellite altimetry, radio occultation and Doris. GPS Solut. 2016, 21, 639–650. [Google Scholar] [CrossRef]
- Reuveni, Y.; Bock, Y.; Tong, X.; Moore, A.W. Calibrating interferometric synthetic aperture radar (INSAR) images with regional GPS network atmosphere models. Geophys. J. Int. 2015, 202, 2106–2119. [Google Scholar] [CrossRef]
- Du, S.; Yu, A.; Zhang, Y.; Zhang, Q.; Wu, P.; Wang, Q. Research on ionospheric effects and error calibration for L-band spaceborne D-InSAR. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 5943–5946. [Google Scholar]
- Yang, J.; Huang, W.; Xia, G.; Zhou, C.; Chen, Y. Operational forecasting of Global Ionospheric TEC maps 1-, 2-, and 3-day in advance by CONVLSTM model. Remote Sens. 2024, 16, 1700. [Google Scholar] [CrossRef]
- Cooper, C.; Mitchell, C.N.; Wright, C.J.; Jackson, D.R.; Witvliet, B.A. Measurement of ionospheric total electron content using single-frequency geostationary satellite observations. Radio Sci. 2019, 54, 10–19. [Google Scholar] [CrossRef]
- Pinheiro, M.; Reigber, A.; Moreira, A. Large-baseline insar for precise topographic mapping: A framework for tandem-X large-baseline data. Adv. Radio Sci. 2017, 15, 231–241. [Google Scholar] [CrossRef]
- Krieger, G.; Hajnsek, I.; Papathanassiou, K.P.; Younis, M.; Moreira, A. Interferometric synthetic aperture radar (SAR) missions employing formation flying. Proc. IEEE 2010, 98, 816–843. [Google Scholar] [CrossRef]
- Wegmuller, U.; Santoro, M.; Werner, C.; Strozzi, T.; Wiesmann, A. ERS-Envisat Tandem Cross—Interferometry coherence estimation. In Proceedings of the 2009 IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 12–17 July 2009. [Google Scholar]
- Jiang, H.; Dong, J.; Jiang, L.; Li, D. Moon-based SAR for Earth observation and its spatial baseline decorrelation in repeat-pass interferometry. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019. [Google Scholar]
- Li, G.; Ding, Z.; Li, M.; Zhang, T.; Zeng, T.; Long, T. Earth-based repeat-pass SAR interferometry of the moon: Spatial–temporal baseline analysis. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Meyer, F.J.; Sandwell, D.T. SAR interferometry at Venus for topography and change detection. Planet. Space Sci. 2012, 73, 130–144. [Google Scholar] [CrossRef]



| Parameters | Value | Unit | |
|---|---|---|---|
| Radar frequency | 1.27 | GHz | |
| Incident angle | 34.3 | degrees | |
| Inclination | Descending | / | |
| Reference SLC | Date | 4 May 2008 | |
| Time | 20:42 (UTC) | ||
| Mode | FBD | ||
| Secondary SLC | Date | 19 June 2008 | / |
| Time | 20:41 (UTC) | ||
| Mode | FBD | ||
| Azimuth | Resolution | 3.2 | m |
| Width | 60 | km | |
| Ground range | Resolution | 16.6 | m |
| Width | 70 | km | |
| Perpendicular baseline | 2400 | m | |
| Temporal baseline | 46 | day | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Hu, Z.; Wang, Y.; Dong, Z.; Li, H. Correction of Ionospheric Phase in SAR Interferometry Considering Wavenumber Shift. Remote Sens. 2024, 16, 2555. https://doi.org/10.3390/rs16142555
Li G, Hu Z, Wang Y, Dong Z, Li H. Correction of Ionospheric Phase in SAR Interferometry Considering Wavenumber Shift. Remote Sensing. 2024; 16(14):2555. https://doi.org/10.3390/rs16142555
Chicago/Turabian StyleLi, Gen, Zihan Hu, Yifan Wang, Zehua Dong, and Han Li. 2024. "Correction of Ionospheric Phase in SAR Interferometry Considering Wavenumber Shift" Remote Sensing 16, no. 14: 2555. https://doi.org/10.3390/rs16142555
APA StyleLi, G., Hu, Z., Wang, Y., Dong, Z., & Li, H. (2024). Correction of Ionospheric Phase in SAR Interferometry Considering Wavenumber Shift. Remote Sensing, 16(14), 2555. https://doi.org/10.3390/rs16142555





