Abstract
The Intermittent Small Baseline Subset approach to Interferometric Synthetic Aperture Radar data was originally devised as a way to recover information from regions with intermittent coherence, making it particularly useful in agricultural regions or those featuring significant vegetation. However, as modern data products grow in size, the increased computational complexity that this methodology demands makes processing more daunting. Here, we present a solution: leveraging the Bifrost data processing framework and GPUs, we analyze Sentinel-1 data covering a large region of northern California and are able to achieve dramatic speed-ups on the order of 300–400 times faster than CPU-bound implementations of ISBAS, processing the entire dataset in only 5 h.
1. Introduction
Interferometric Synthetic Aperture Radar (InSAR) techniques typically make use of repeated observations of a particular location on the Earth’s surface by a ground-sensing satellite. Measurements made on different dates can then be interfered, producing interferograms containing information about changes in phase (related to changes in ground height), as well as coherence, which is a measure of the reliability of said phase information.
The Small Baseline Subset (SBAS; ref. [1]) approach was developed as an effective way to process these data into meaningful measures of ground deformation. Instead of generating all possible interferograms (), one can instead sequentially generate interferograms for nearby pairs of dates (the “small baselines”). Provided that this set of date pairs sufficiently connects all observation dates, the required number of interferograms can be significantly lower without a significant loss of information. While this particular approach gained significant popularity due to its computational advantages, it can suffer when coherence is intermittent, as the typical approach only utilizes pixels that maintain high coherence over all interferograms. This means that information from regions with such intermittent coherence (such as regions of vegetation, which will vary on seasonal timescales) can be completely lost unless other methods are invoked.
One such method is Intermittent SBAS (ISBAS). Created with the intention of recovering this information, the algorithm described in Sowter et al. [2] attempts to solve each pixel with a sufficient number of high-coherence interferograms. More details on the exact process behind this solution can be found in the original paper as well as through the original code (https://github.com/ericlindsey/isbas, accessed on 5 July 2024) of the implementation of this algorithm, on which this work is based. Summarizing somewhat, this technique has the advantage that it can recover information from these intermittent areas, given more access to vegetated or agricultural regions, but it suffers from increased computational complexity, leading to processing times which make dealing with larger or more modern data untenable.
This paper aims to illustrate the effectiveness of Bifrost, which itself arose from a similar computational demand in a somewhat different field: radio astronomy. Modern radio astronomy frequently deals with a large number of sensors, producing significant data streams and thus requiring significant computation. The Bifrost framework [3] was created to handle just such streams originally from the Long Wavelength Array [4], which is a set of low-frequency radio telescopes operating in New Mexico. The advantage comes in that Bifrost makes it easy to establish processing streams (or offline pipelines) that can pass data along to Graphics Processing Units (GPUs) for much more rapid processing where it is allowed. While other stages in the general InSAR workflow have been bolstered by GPU processing (see Dong et al. [5], Chang et al. [6] for examples), to our knowledge, this work represents the first such GPU implementation for this particular algorithm of time-series inversion, and it is certainly the first implemented via the use of Bifrost.
GPU support is primarily provided through NVidia’s Compute Unified Device Architecture (CUDA) (Support for AMD via ROCm is currently under development) and is accessed through internal Bifrost routines or through CuPy [7] through a compatibility layer. Many operations for data manipulation/transformation are provided with Bifrost, and more complex or specific processing can be handled using custom ‘blocks’, which often require little more work than changing NumPy function calls to CuPy.
In the sections to follow, we will outline the testing performed and the large calculation speed-ups gained from the use of Bifrost to process InSAR ISBAS datasets. Section 2 discusses the choice of data and the basic process behind the pipeline as well as the various benchmarks performed to measure these speed-ups. Finally, Section 3 and Section 4 discuss our results and their broader implications for this particular application of Bifrost.
2. Materials and Methods
2.1. Data
The dataset that we chose to use for this work covers a portion of northern California in the United States observed by the Sentinel-1 satellite [8]. This includes 225 observations at C-band (5.5 cm) on descending passes between June 2015 and September 2023. This region was chosen specifically for the likely presence of areas with intermittent coherence, which is the core use case for which the original code was developed, and also features of geological interest. Our objective then was to benchmark these data and see what kinds of improvement have been made on various scales. We began from a large number of interferograms (2195 in total), each 7077 by 7603 pixels. This allows us to easily extract smaller subsets for specific testing while also opening up the capability to process the full dataset in a reasonable amount of time.
2.2. Pipeline
The Bifrost ISBAS pipeline (BISBAS; https://github.com/ProfundityOfScope/BISBAS, accessed on 5 July 2024)) developed for this work takes as input the unwrapped interferograms and runs through the steps defined in the ISBAS analysis.
- Masking of the interferograms based on a minimum coherence or presence of water;
- Referencing interferograms to a provided reference point;
- Time-series inversion, where the time series is solved for from the interferograms;
- Removal of residual “ramps” present in the individual date images;
- Estimation of ground velocities from the time series.
The pipeline is assembled from a series of Bifrost ‘blocks’ which perform one or some combination of the above steps. These blocks are a central component of creating a Bifrost pipeline, with a given block typically receiving data from one or more ring buffers, performing some sort of transformation, and outputting the result to another ring buffer. Figure 1 shows an illustration of how the blocks are connected with basically all mathematical operations happening on the GPU side. Data flow through the pipeline in ‘gulps’, which represent all interferogram information for a given set of pixels. The number of pixels, and thus the size of the gulp, can be set manually or automatically determined from the available memory on the GPU. Phase data are read alongside the corresponding coherence and water mask, which are then used to apply a mask where coherence is less than 0.3 or water is present in the NASA SWBD dataset [9].
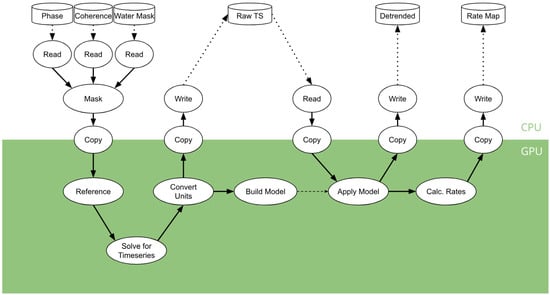
Figure 1.
A graph diagram showing how various elements in the BISBAS processing pipeline are connected together. Each round node represents a Bifrost block, which lives on either the CPU or GPU (or spans the gap, in the case of Copy), and solid arrows can be thought of as the ring buffers which Bifrost leverages. Cylindrical icons denote data saved to disk. Here, you can see the division into two individual pipeline components: the first to perform the time-series inversion, the second to apply a detrending and calculate rates.
These masked data are then passed to the GPU, where more math-intensive steps can be performed. The first of these involves referencing the interferograms, effectively subtracting a value from each interferogram pixel such that the phase data near the reference point will be zero in all interferograms. The bulk of computation time during this data reduction is used during the step of time-series inversion, where we solve for the model rates which are used to generate the time-series data from the base interferograms. This typically takes the form of the equation
where the matrix represents the difference in dates between the measurements used to generate the interferogram, x is the model rates and is the interferogram data. Typically, solving for x would be straightforward, since the problem is over-determined, so a least-squares approach would suffice. Complications arise when we introduce masking into the data such that NaN values appear. A typical solution for this would be to remove the offending NaN values from and their corresponding rows from and then proceed with your solution method of choice (assuming that the resulting matrix is still full rank; otherwise, the pixel is skipped).
As this solve must be performed for every single pixel in a given dataset, the added time required for these on-the-fly modifications becomes significant. Beyond the time requirement, the size of the problem changing during each step is problematic if the goal is GPU processing, which would generally require problems to remain consistent in the usage of memory. With this in mind, we modify the problem somewhat to avoid this issue and also optimize toward the types of operations GPUs are well suited for.
To handle the NaN values, we introduce a masking matrix, , which is a diagonal matrix generated from . If a value is present in the data, then the corresponding element , while if the value is missing (NaN), then . If we wish to insert this masking matrix, then our modified problem takes the form
The resultant problem features a new left-hand matrix, which we may call , and a new data vector . The size of these new matrices and vectors will remain constant in memory for every pixel, allowing the problem to be moved more easily to the GPU. Once the relevant broadcasting and matrix multiplications are performed, we are left with a few relatively small matrices ( is , with being the number of observation dates), and so it is possible to perform this solve for all pixels in a gulp simultaneously, effectively as a tensor problem, via the linalg.solve function in cupy.
The matrix is also functionally equivalent to the Gram matrix of . We can leverage this in checking if the resulting problem is still full rank. This check in the original code is made via a singular value decomposition, which checks the rank of the truncated for each pixel. Instead, we can check whether the Gramian (the determinant of the Gram matrix) is non-zero. The mostly diagonal composition of in most time-series inversion problems means that the determinant will be significantly faster than a typical rank check, even if the said rank check could be performed on the GPU. As the condition of the Gram matrix is the square of the original matrix, we opt to use a slogdet function for this, which is better in cases of potential numerical instability, as it calculates the logarithm of the determinant, which is less prone to under- or overflow. For singular pixels, the resultant model is simply set to all-NaN.
As a final measure toward catching these numerical uncertainties, we check the new time-series solutions against a threshold which can either be supplied from the user or precomputed from a random set of pixels throughout the entire image. Pixels containing time-series values larger than this threshold (typically 10 times the standard deviation) are discarded, as they likely suffered from these numerical instability effects. We note that this affects only a small percentage of pixels, fewer than 1 in 10,000 in this dataset using this hardware (see Section 2.3).
Here, it is worth taking a brief aside to discuss the complexity and how it scales with the number of interferograms and the number of dates that those interferograms were calculated from. The steps described above, specifically the time-series inversion and the relevant checks involved, dominant the time complexity of the entire process for both methodologies. The original CPU-bound code’s time complexity is largely dictated by singular value decomposition, an operation for each pixel, performed in both the matrix rank check and (if the matrix is full rank) the calculation of the pseudo-inverse. For each pixel in the new implementation, we expect the construction of the matrices to scale as and the solves to scale as , but as for nearly all conceivable cases, we can say that both implementations scale as for each pixel. The relative difference in speed comes from being able to dramatically parallelize these operations on the GPU. In both cases, having more masked data will mean faster processing times, as the old implementation skips solves and the new one trivializes them, with the overall speed-up factor decreasing slightly as more masked pixels are present.
After converting the time series into the appropriate units (typically millimeters), the data split: one copy being taken off the GPU to be written to disk, and the other sent to a block which accumulates the solution to the detrending step. This removal of residual linear or quadratic trends across the image is typically performed sequentially over each image, raveling the data, and removing any NaN values on the fly. We instead opt to accumulate the matrices which can be solved for these trend parameters on the fly during our pipeline, as the math involved is similar to that described above and also benefits in speed from GPU processing. After the entire dataset has been processed, we can then quickly perform the detrending solve (this typically involves a few hundred matrices no larger than 6 × 6), then read the data back in, copying it to the GPU, and subtracting the model to remove these residual trends. The detrended data are split, one copy again being sent to be written to disk, and the other copy used to calculate rates for each pixel, which is another solve that benefits dramatically from the GPU acceleration. Finally, the rates are copied out to be written to disk.
2.3. Benchmarking
To measure the increase in processing speed, we ran our pipeline, as well as the original ISBAS code, on three subsets of the dataset. For benchmark purposes, we report only the time to complete the time-series inversion, as the other steps typically do not impact the overall processing time significantly, and we are generally more interested in the time-series inversion. The minimum coherence used for masking in all benchmarks is set to 0.3. All benchmarks and tests were performed on a local compute node running Ubuntu 20.04.6 LTS and CUDA version 12.4, equipped with a dual AMD EPYC 7313 16-core processor, 512 GiB of memory, and an NVIDIA RTX A4000 series GPU. Summary information on our benchmarks for these subsets can be found in Table 1.

Table 1.
Runtimes for various datasets processed by the two different codes. The values listed for the Small Images subset represent the median values for the various timing trials over randomized locations. For the Full Data, the ISBAS code was stopped after about an hour of processing, and the total processing time was estimated from the time to process the few rows it had so far completed.
The first of these subsets (denoted as “Small Images” in Table 1) used all 2195 interferograms of a small region (200 × 200 pixels) around a trial point in the full data. This subset was most commonly used for testing, as the total processing time for both codes was manageable and allowed for quick iteration or debugging. Choosing reference points randomly such that at least 95% of the data was land in the water mask, we generated 50 such datasets to evaluate the consistency of both implementations. The original CPU-bound code had a range of times from 2770 to 4362 s with a median of 3806 s. For the Bifrost implementation, this range of times was from 9.173 to 9.541 s with a median of 9.459 s.
One such Small Image dataset was used to generate Figure 2, which illustrates the strong agreement between the two methods. We use the maximum mean change to quantify this agreement, as it generally works well when comparing floating point numbers and can be thought of as somewhat analogous to a percent error. The median value for the maximum mean change in this region is 0.0042 with an inner quartile range of 0.0023 to 0.0097. These quite small errors probably originate from small numerical differences between Numpy and Cupy implementations of the same algorithm, combined with the 32-bit precision used to match the original implementation, and typically only arise when there are a larger number of missing interferograms; thus, the resulting problem is less well constrained. Some degree of this effect could be mitigated by moving to 64-bit numbers at the cost of some performance.
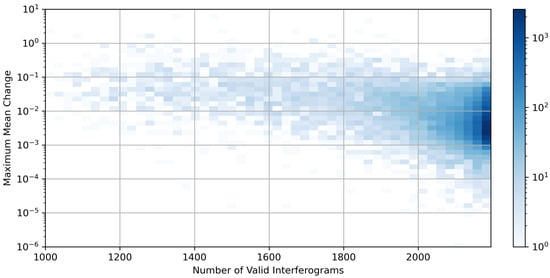
Figure 2.
A 2D histogram of pixels in a “Small Images” dataset (as described in Section 2.3 and Table 1). For each pixel in the subset, we find the number of non-NaN interferograms that were used and then calculate the maximum mean change between the ISBAS and BISBAS implementations for a particular date (here, the 30th time-series data, having been chosen at random) in the final data. The overwhelming majority of data in the subset agree at very high levels, and larger disagreements appear to come from increased numerical uncertainty when fewer interferograms are used.
The second subset was chosen to be somewhat more representative of real-world use cases for the original code, which was intended to operate on data taken by satellites such as ERS or ENVISAT. While the data from these could feature a similar number of pixels in each interferogram, a given dataset would more typically include only a few tens of dates, producing a somewhat smaller number of interferograms. As such, our “Fewer Dates” subset used only interferograms from the first 25 dates in the dataset, producing a new dataset that had 195 full-sized interferograms. From this dataset, we can see a more typical timescale on which the ISBAS code was expected to run, here 14 h, as well as our accelerated processing time of less than 3 min. The original processing time becomes cumbersome if any sort of iteration is required in the processing of the data, and it becomes even more problematic as the field moves toward longer timescales with more observation dates.
Finally, we test our pipeline against the entirety of the dataset. This “Full Data” subset represents a modern stress test that is meant to demonstrate the capabilities afforded by GPU acceleration via Bifrost. The utility of the ISBAS schema is that it allows one to process a given pixel even with some number of dates missing, but on modern datasets where the number of dates is fairly large, the time cost of such an algorithm can be extremely prohibitive. Based on the time it took to complete each pixel, we estimated that it would take the original ISBAS approximately 51 days to fully process this full dataset; meanwhile, it can be processed using our Bifrost accelerated version in around 5 h.
From these tests, we can see a marked performance gain. The computation time in both cases scales strongly with the number of interferograms and to a lesser extent with the number of pixels. Larger amounts of data require more transfers to and from the GPU, but the overall speed-up is significant enough that these effects are fairly small and could be remedied via hardware upgrades or more thorough optimization of the data transfer and, particularly, the gulp size.
3. Results
In Section 2.3, we observed a dramatic increase in processing speed, which was significant enough that we should expect it to allow new methodologies to be explored in the usage of the ISBAS method. The utility of the intermittent approach that ISBAS takes is that you can still extract information, even if the chain of interferograms is not completely perfect from start to finish, which is particularly advantageous in regions with variable coherence. The information is not necessarily difficult to find for a single pixel, but solving across the entire image quickly grew to be prohibitive as modern satellites produced more and larger datasets.
Using a framework like Bifrost, however, we offer a speed-up that is more than sufficient to keep pace. Given the typical observation cadence of these instruments, it is likely that this allows ISBAS processing to occur effectively in real time as data come down from orbit, as it would take significantly more data volume to slow the new pipeline down enough to lag behind. Furthermore, such short processing times make it fairly trivial to tweak the parameters and observe changes in the results. A simple example of this is the minimum coherence, which we commonly changed to see the effects on the images during testing. This is especially apparent in smaller selected regions, where one might wish to quickly change the parameters to seek out some sort of signal in a region of interest. Several such potential regions are shown in Figure 3.
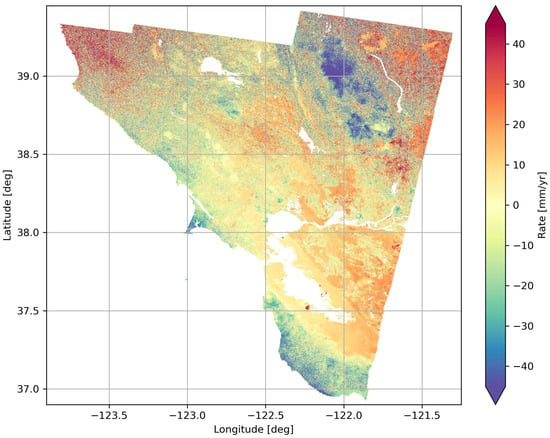
Figure 3.
The rate map produced from the full dataset, showing a region of northern California. Two of the more apparent features here will be the San Andreas fault, a sharp line of discontinuity to the west of the San Francisco Bay, and the Bair Island wetlands, a region of large positive velocities on the southern side of the Bay. The latter is likely the result of the restoration of the wetlands that has been occurring in that region.
We also discussed in Section 2.3 that we had directly compared data from ISBAS and BISBAS to look at the relative errors that could be imparted from changes in numerical methods. Typical errors seem to be less than 1% with higher errors occurring mainly in regions with lower coherence and/or more points below the coherence cut-off. In both cases, the actual math going into finding the time-series solutions will tend to feature more numerical instability and can cause mild divergences between the two implementations. This can be mitigated to some extent using a higher coherence threshold, which would in any case be typical when searching out strong signals in the data. Overall, we find the numerical agreement to be more than sufficient for use and analysis.
4. Discussion and Conclusions
The implementation of GPU acceleration via the Bifrost framework has allowed us to achieve massive increases in computation speed toward the application of this Intermittent SBAS approach on modern data products. Being able to solve for time-series solutions and the rates of ground regions with intermittent coherence is a massive boon in recovering pieces of the time series, but modern datasets have begun to make processing time prohibitive. With the advent of a framework such as described here, this approach should be much more capable of keeping pace with increasing data volumes and opens the door to further iteration and development. Extensions of the Bifrost implementation to earlier stages in the data reduction process, such as phase unwrapping or applying atmospheric corrections, could continue to accelerate processing, potentially showing even larger speed-ups. Dramatically reduced processing times also allow for new steps in the process to be developed, such as more rigorous estimation of errors, or others that we can only speculate on. In this regard, Bifrost has proven to have significant utility outside its original astronomical use-case.
Author Contributions
Conceptualization, J.D., G.B.T. and E.O.L.; methodology, S.B. and J.D.; software, S.B. and J.D.; validation, S.B. and J.D.; formal analysis, S.B.; investigation, S.B.; resources, G.B.T. and J.D.; data curation, E.O.L.; writing—original draft preparation, S.B.; writing—review and editing, G.B.T., J.D. and E.O.L.; visualization, S.B.; supervision, G.B.T. and J.D.; project administration, G.B.T.; funding acquisition, G.B.T. and J.D. All authors have read and agreed to the published version of the manuscript.
Funding
Initial Bifrost development was supported by NSF Grants OCI/1060067, OIA/1125087, AST/1139974 and AST-1106059. Continued development of Bifrost is supported by NSF award OAC/2103707. Bifrost was originally developed for use with the LWA-SV station, the construction of which has been supported by the Office of Naval Research under contract N00014-07-C-0147 and by the Air Force Office of Scientific Research.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
This research has made use of the following software libraries: Bifrost 0.10.0 [3], CuPy 12.0.0 [7], matplotlib 3.6.1 [10], numpy 1.23.1 [11], scipy 1.9.3 [12].
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SAR | Synthetic Aperture Radar |
| InSAR | Interferometric SAR |
| ISBAS | Intermittent Small Baseline Subset |
| GPU | Graphics Processing Unit |
References
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Sowter, A.; Bateson, L.; Strange, P.; Ambrose, K.; Syafiudin, M.F. DInSAR estimation of land motion using intermittent coherence with application to the South Derbyshire and Leicestershire coalfields. Remote Sens. Lett. 2013, 4, 979–987. [Google Scholar] [CrossRef]
- Cranmer, M.D.; Barsdell, B.R.; Price, D.C.; Dowell, J.; Garsden, H.; Dike, V.; Eftekhari, T.; Hegedus, A.M.; Malins, J.; Obenberger, K.S.; et al. Bifrost: A Python/C++ Framework for High-Throughput Stream Processing in Astronomy. J. Astron. Instrum. 2017, 6, 1750007. [Google Scholar] [CrossRef]
- Taylor, G.B.; Ellingson, S.W.; Kassim, N.E.; Craig, J.; Dowell, J.; Wolfe, C.N.; Hartman, J.; Bernardi, G.; Clarke, T.; Cohen, A.; et al. First Light for the First Station of the Long Wavelength Array. J. Astron. Instrum. 2012, 1, 1250004. [Google Scholar] [CrossRef]
- Dong, L.; Zhang, T.; Liu, F.; Liu, R.; You, H. GPU Acceleration for SAR Satellite Image Ortho-Rectification. Remote Sens. 2024, 16, 1301. [Google Scholar] [CrossRef]
- Chang, S.; Deng, Y.; Zhang, Y.; Zhao, Q.; Wang, R.; Zhang, K. An Advanced Scheme for Range Ambiguity Suppression of Spaceborne SAR Based on Blind Source Separation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–12. [Google Scholar] [CrossRef]
- Okuta, R.; Unno, Y.; Nishino, D.; Hido, S.; Loomis, C. CuPy: A NumPy-Compatible Library for NVIDIA GPU Calculations. In Proceedings of the Workshop on Machine Learning Systems (LearningSys) in The Thirty-first Annual Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Torres, R.; Snoeij, P.; Geudtner, D.; Bibby, D.; Davidson, M.; Attema, E.; Potin, P.; Rommen, B.; Floury, N.; Brown, M.; et al. GMES Sentinel-1 mission. Remote Sens. Environ. 2012, 120, 9–24. [Google Scholar] [CrossRef]
- NASA JPL. NASA Shuttle Radar Topography Mission Water Body Data Shapefiles & Raster Files; NASA EOSDIS Land Processes Distributed Active Archive Center: Sioux Falls, SD, USA, 2013. [CrossRef]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef] [PubMed]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).