Enhancing GNSS Deformation Monitoring Forecasting with a Combined VMD-CNN-LSTM Deep Learning Model
Abstract
1. Introduction
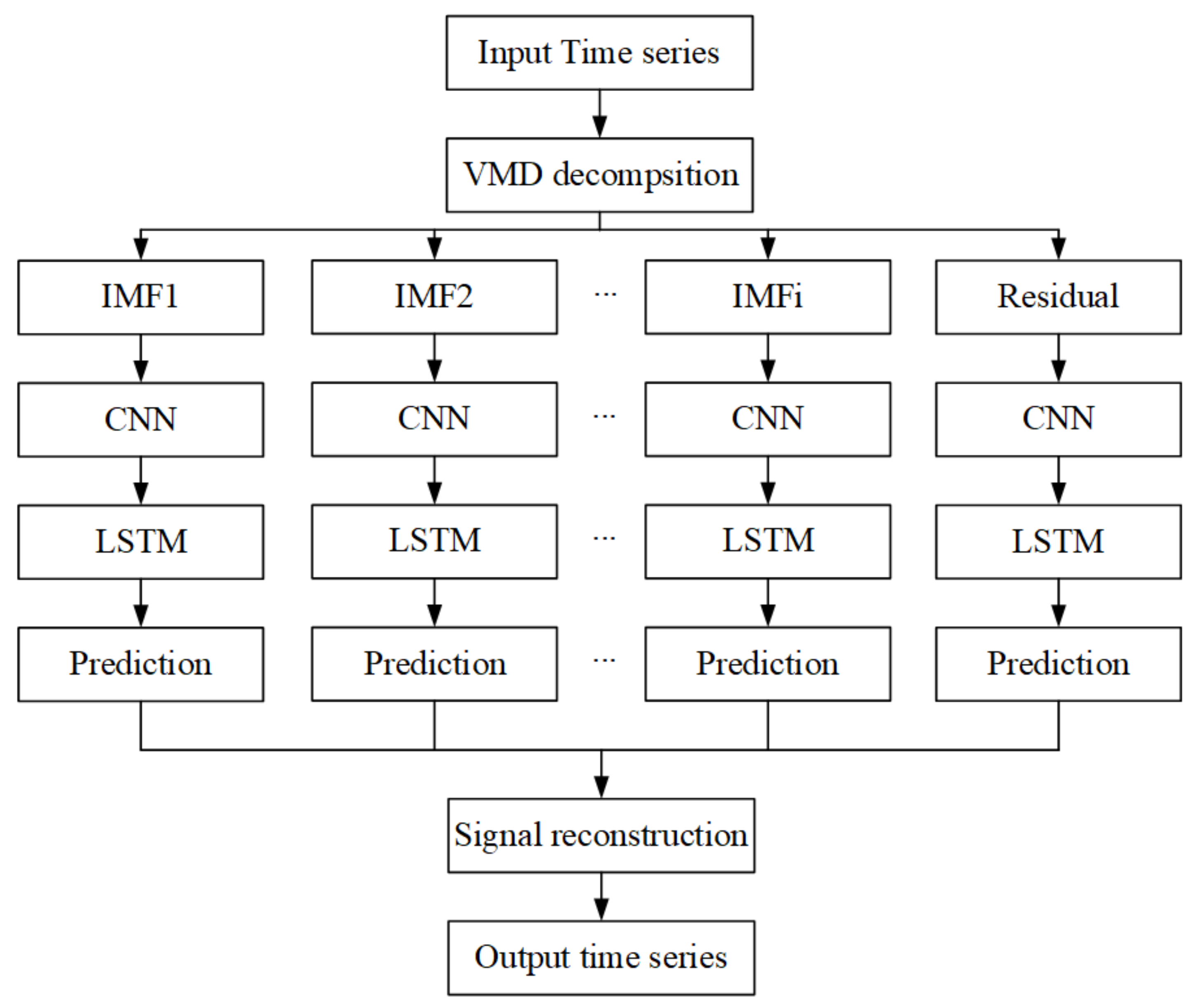
2. Methods
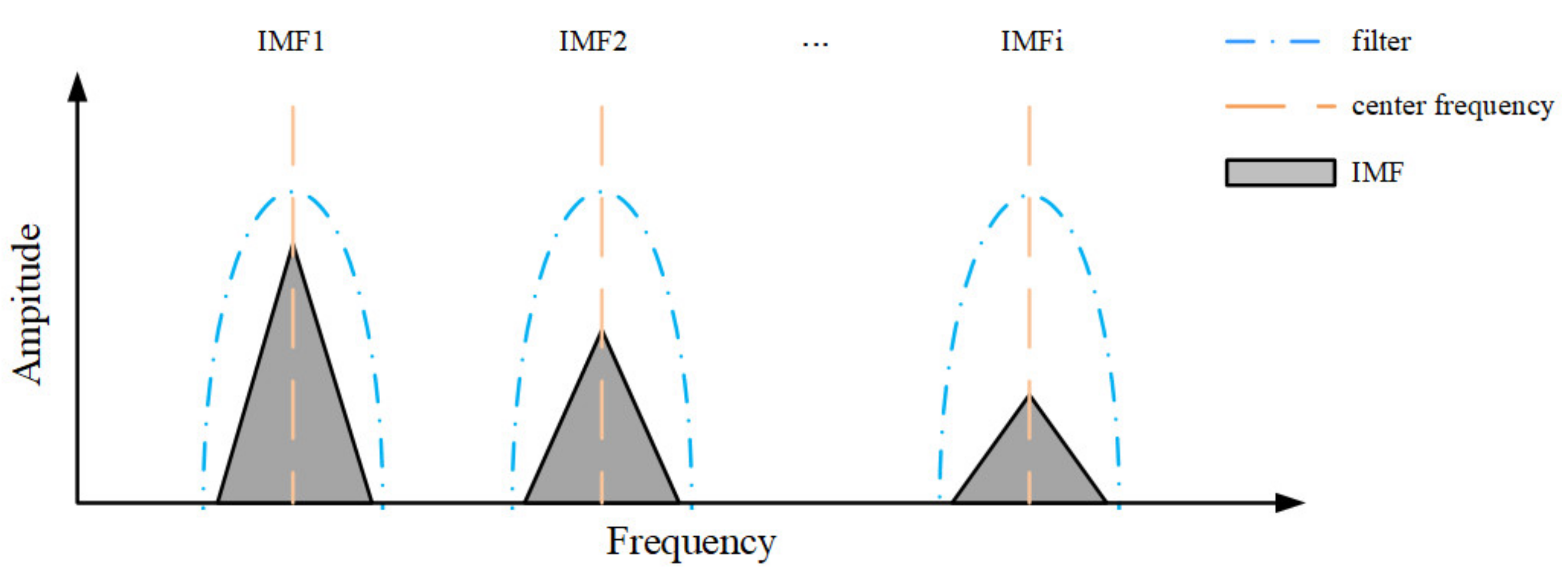
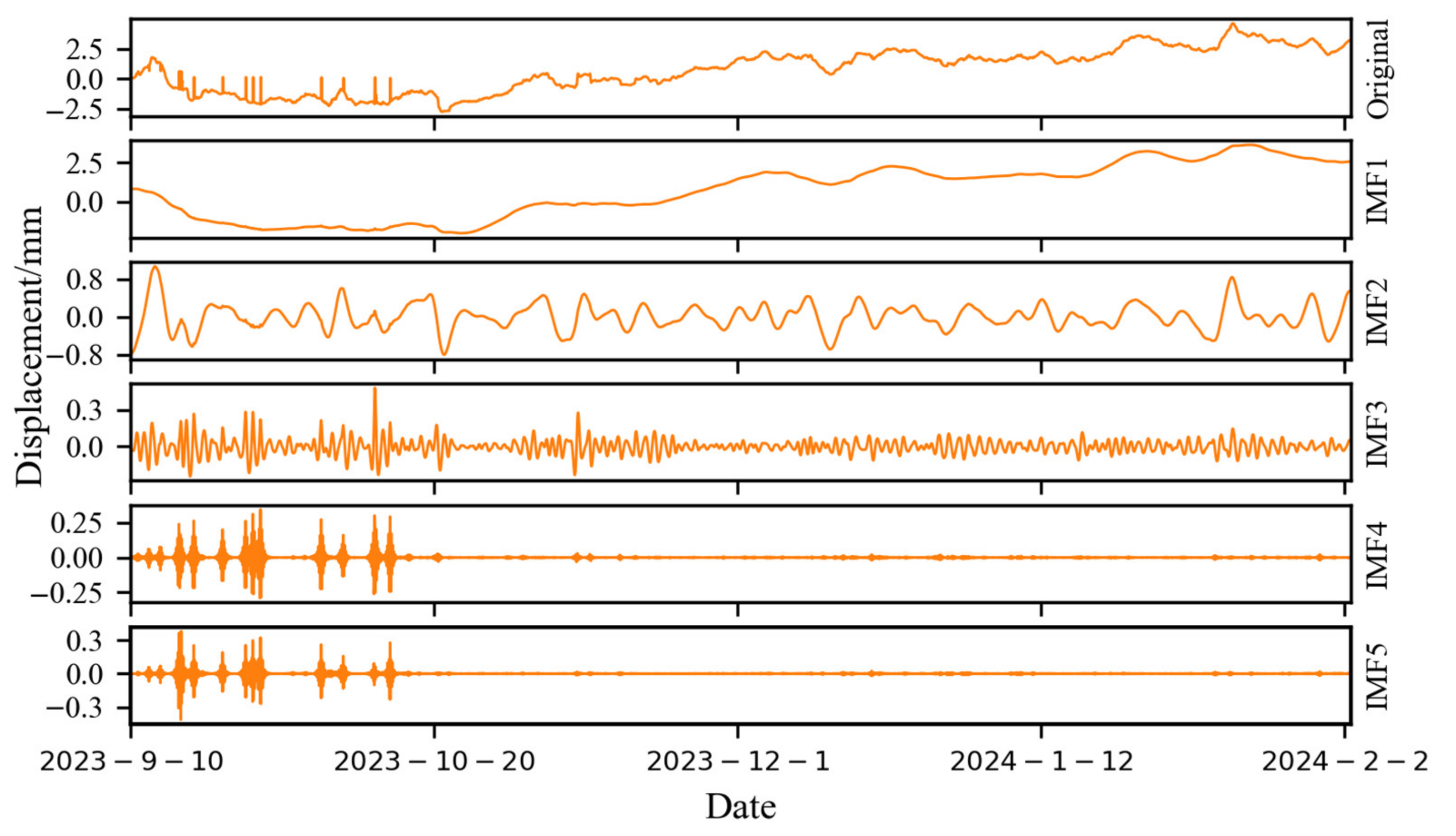
2.1. VMD
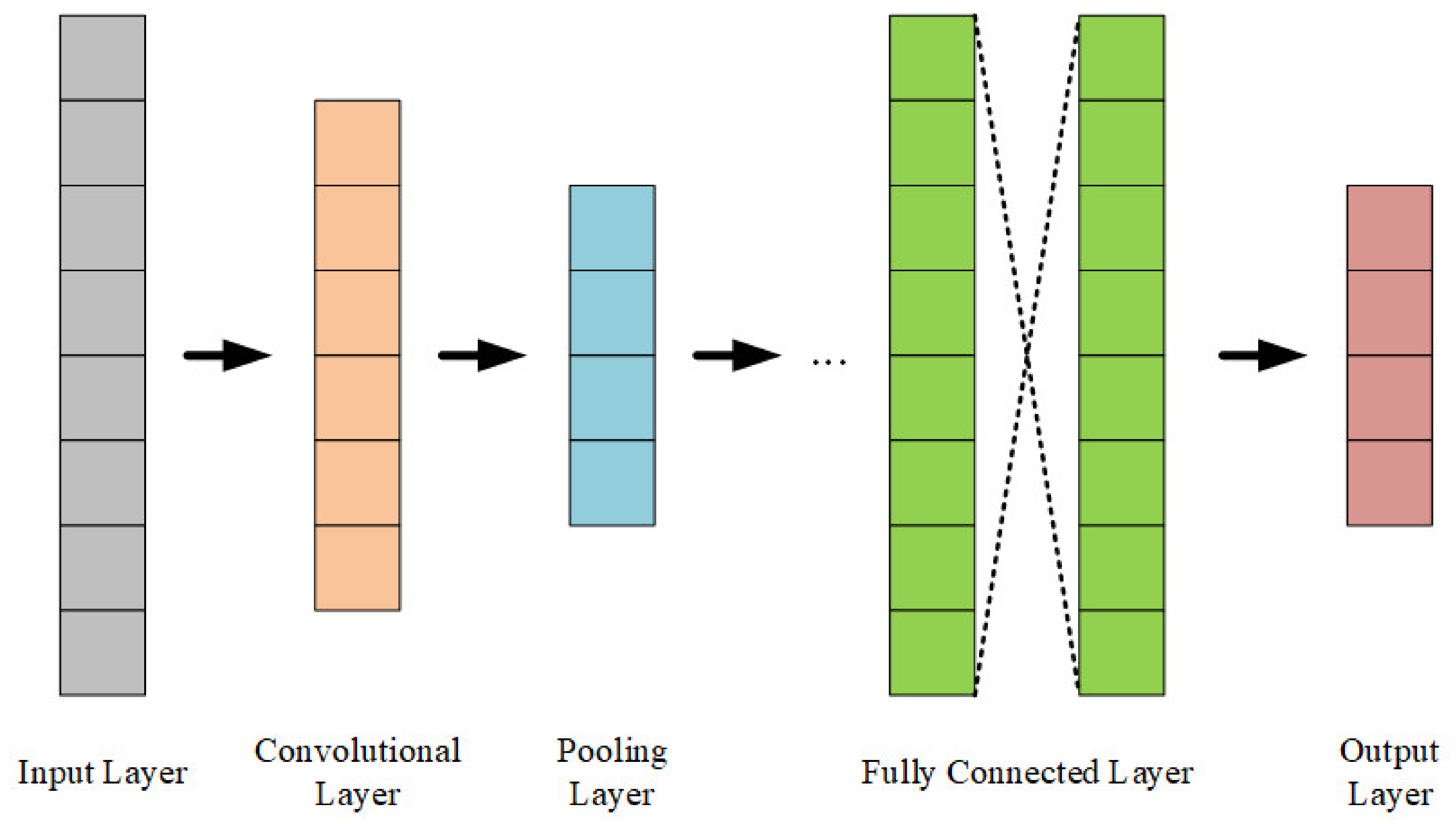
2.2. CNN
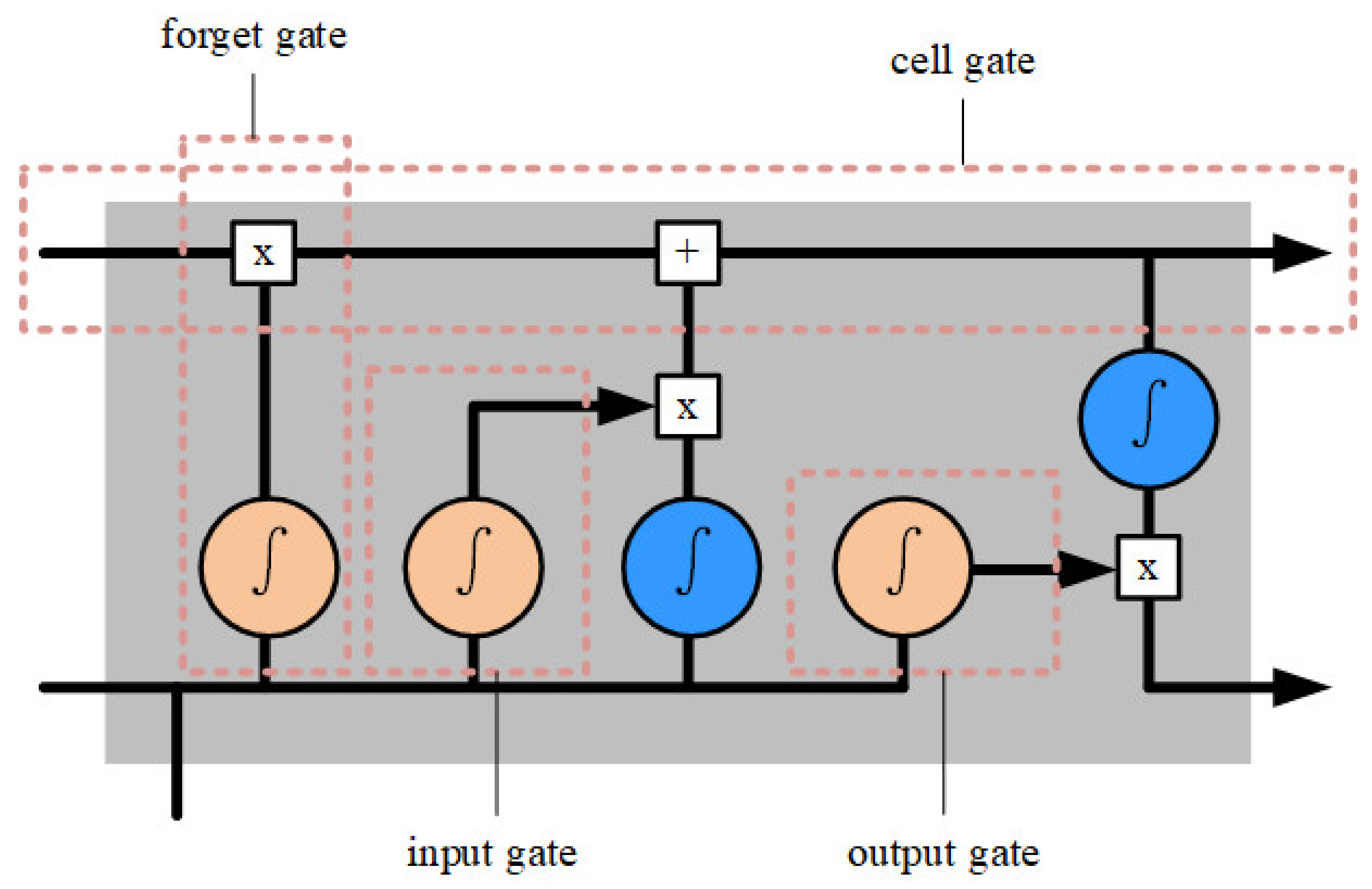
2.3. LSTM
3. Experiment
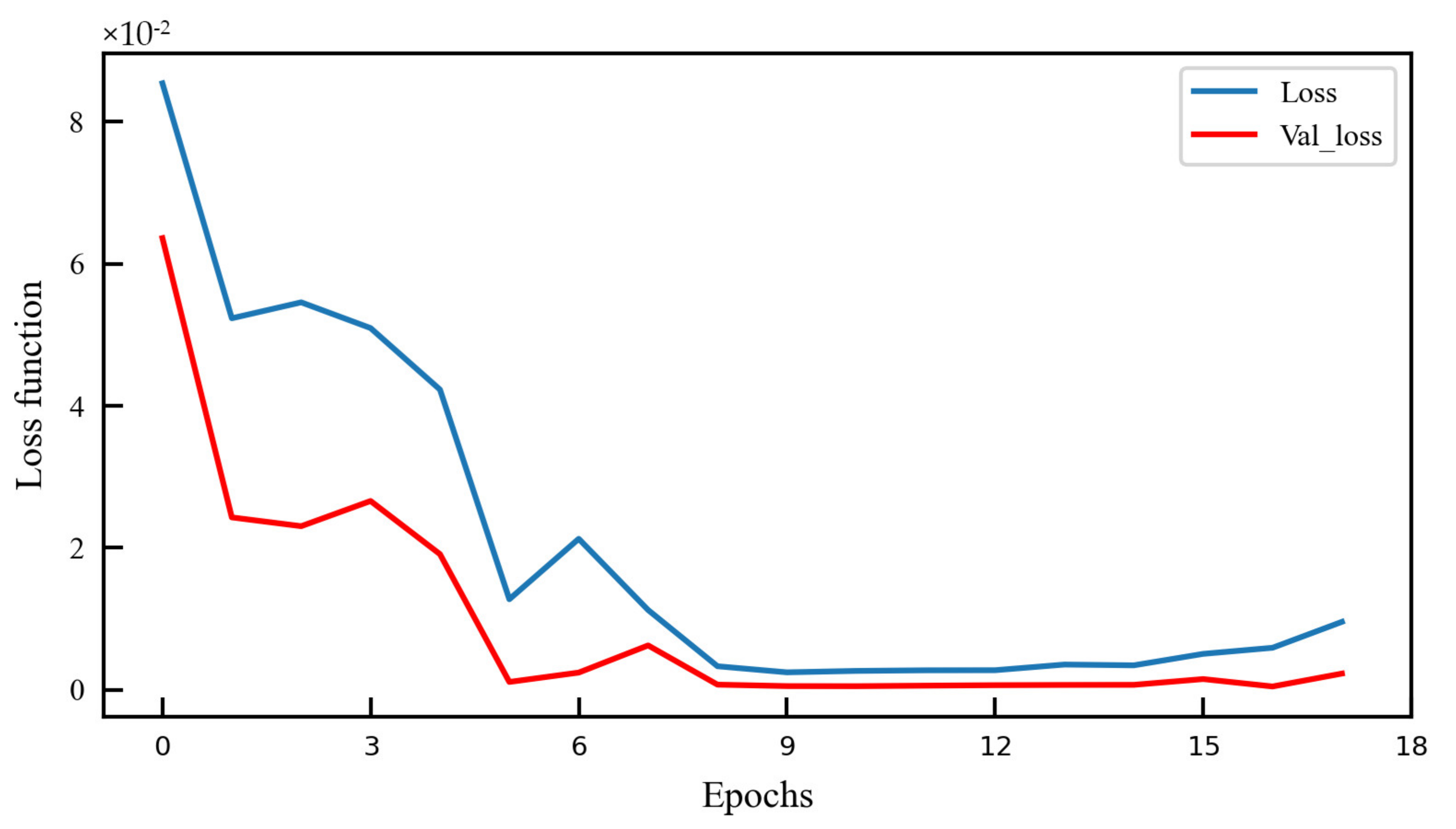
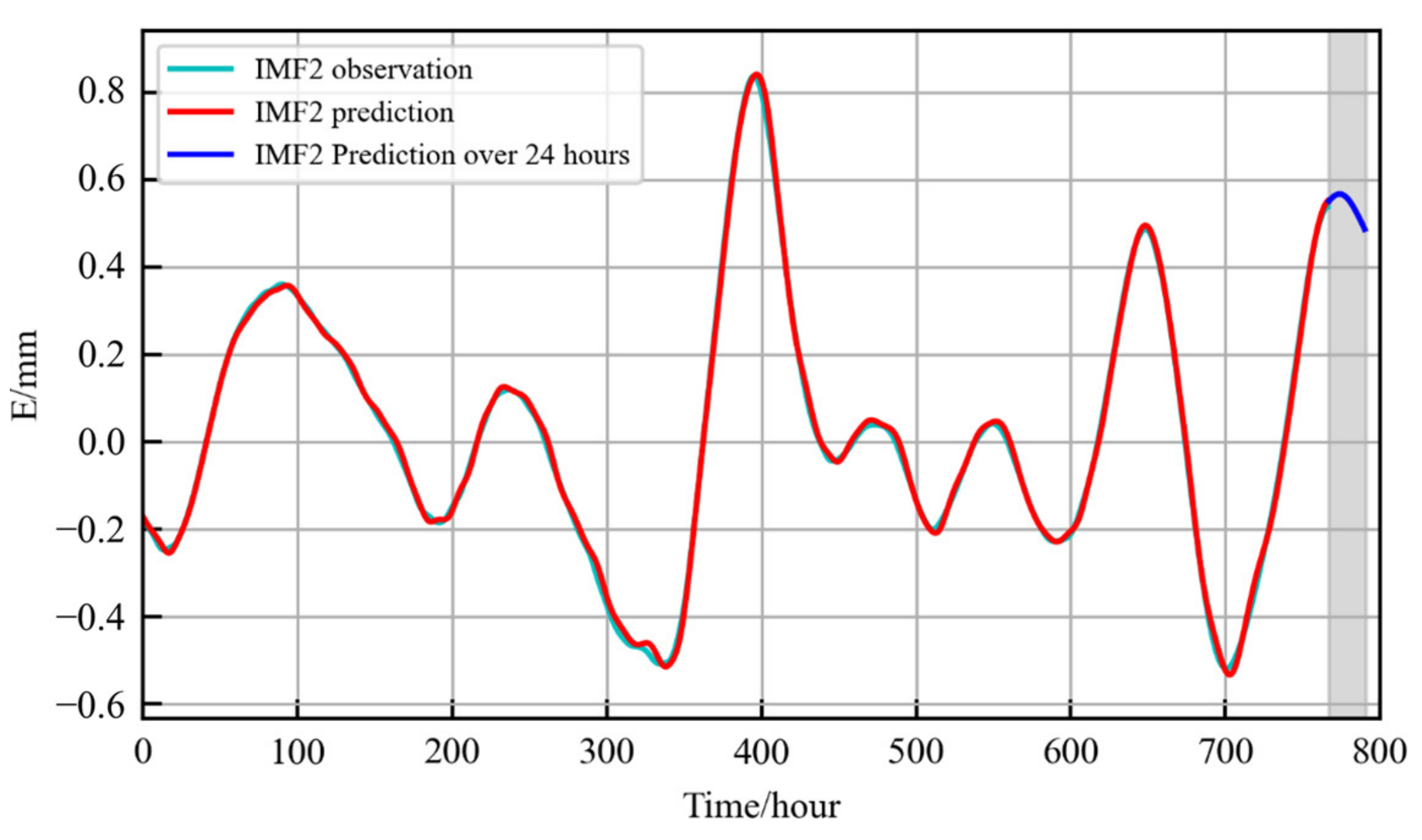
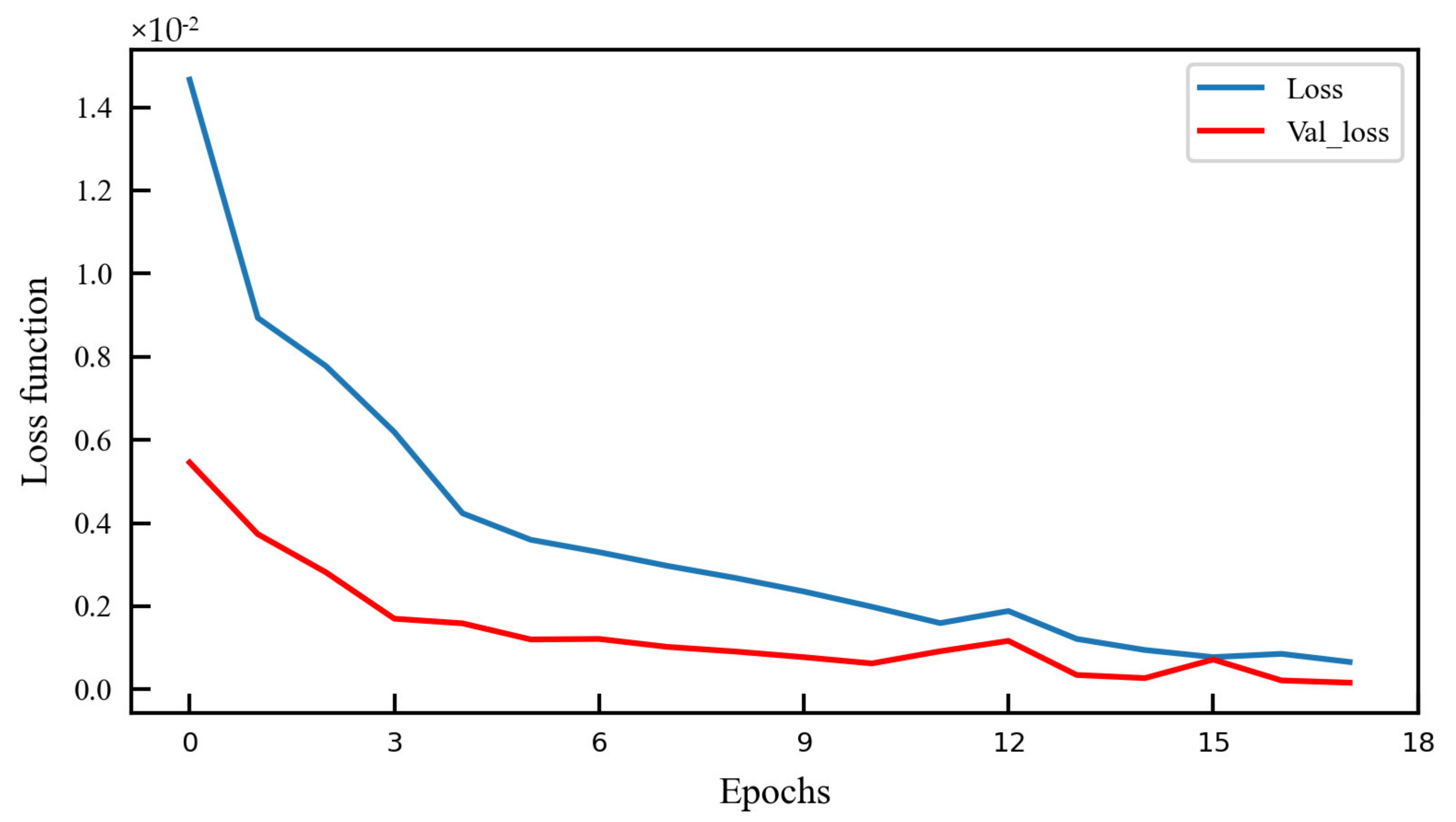
3.1. The Feasibility Experiment
3.2. The Comparative Experiment
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Strygina, M.A.; Gritsuk, I.I. Hydrological safety and risk assessment of hydraulic structures. RUDN J. Eng. Res. 2018, 19, 317–324. [Google Scholar] [CrossRef]
- Tian, D.; Liu, H.; Chen, S.; Li, M.; Liu, C. Human error analysis for hydraulic engineering: Comprehensive system to reveal accident evolution process with text knowledge. J. Constr. Eng. Manag. 2022, 148, 04022093. [Google Scholar] [CrossRef]
- Hudnut, K.W.; Behr, J.A. Continuous GPS Monitoring of Structural Deformation at Pacoima Dam, California. Seismol. Res. Lett. 1998, 69, 299–308. [Google Scholar] [CrossRef]
- Rossi, G.; Zuliani, D.; Fabris, P. Long-term GNSS measurements from the northern Adria microplate reveal fault-induced fluid mobilization. Tectonophysics 2016, 690, 142–159. [Google Scholar] [CrossRef]
- Dardanelli, G.; Pipitone, C. Hydraulic models and finite elements for monitoring of an earth dam, by using GNSS techniques. Period. Polytech. Civ. Eng. 2017, 61, 421–433. [Google Scholar] [CrossRef]
- Barzaghi, R.; Cazzaniga, N.E.; De Gaetani, C.I.; Pinto, L.; Tornatore, V. Estimating and comparing dam deformation using classical and GNSS techniques. Sensors 2018, 18, 756. [Google Scholar] [CrossRef] [PubMed]
- Riguzzi, F.; Devoti, R.; Pietrantonio, G. GNSS data provide unexpected insights in hydrogeologic processes. Bull. Geophys. Oceanogr. 2021, 62, 637–646. [Google Scholar] [CrossRef]
- Jiang, W.; Liang, Y.; Yu, Z.; Xiao, Y.; Chen, Y.; Chen, Q. Progress and thoughts on application of satellite positioning technology in deformation monitoring of water conservancy projects. Geomat. Inf. Sci. Wuhan Univ. 2022, 47, 1625–1634. [Google Scholar]
- Harvey, A.C. Forecasting, Structural Time Series Models and the Kalman Filter; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- De Lannoy, G.J.; Reichle, R.H.; Houser, P.R.; Pauwels, V.R.; Verhoest, N.E. Correcting for forecast bias in soil moisture assimilation with the ensemble Kalman filter. Water Resour. Res. 2007, 43, 9. [Google Scholar] [CrossRef]
- Cassola, F.; Burlando, M. Wind speed and wind energy forecast through Kalman filtering of Numerical Weather Prediction model output. Appl. Energy 2012, 99, 154–166. [Google Scholar] [CrossRef]
- Kalnay, E.; Ota, Y.; Miyoshi, T.; Liu, J. A simpler formulation of forecast sensitivity to observations: Application to ensemble Kalman filters. Tellus A Dyn. Meteorol. Oceanogr. 2012, 64, 18462. [Google Scholar] [CrossRef]
- Lu, F.; Zeng, H. Application of Kalman filter model in the landslide deformation forecast. Sci. Rep. 2020, 10, 1028. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.-H.; Lee, P.-C. Novel high-precision grey forecasting model. Autom. Constr. 2007, 16, 771–777. [Google Scholar] [CrossRef]
- Ho, P.H. Forecasting construction manpower demand by gray model. J. Constr. Eng. Manag. 2010, 136, 1299–1305. [Google Scholar] [CrossRef]
- Chang, C.-J.; Li, D.-C.; Huang, Y.-H.; Chen, C.-C. A novel gray forecasting model based on the box plot for small manufacturing data sets. Appl. Math. Comput. 2015, 265, 400–408. [Google Scholar] [CrossRef]
- Yang, F.; Tang, X.; Gan, Y.; Zhang, X.; Li, J.; Han, X. Forecast of freight volume in Xi’an based on gray GM (1, 1) model and Markov forecasting model. J. Math. 2021, 2021, 6686786. [Google Scholar] [CrossRef]
- Wang, Z.-X.; He, L.-Y.; Zhao, Y.-F. Forecasting the seasonal natural gas consumption in the US using a gray model with dummy variables. Appl. Soft Comput. 2021, 113, 108002. [Google Scholar] [CrossRef]
- Newbold, P. ARIMA model building and the time series analysis approach to forecasting. J. Forecast. 1983, 2, 23–35. [Google Scholar] [CrossRef]
- Van Der Voort, M.; Dougherty, M.; Watson, S. Combining Kohonen maps with ARIMA time series models to forecast traffic flow. Transp. Res. Part C Emerg. Technol. 1996, 4, 307–318. [Google Scholar] [CrossRef]
- Meyler, A.; Kenny, G.; Quinn, T. Forecasting Irish Inflation Using ARIMA Models. Cent. Bank Financ. Serv. Auth. Irel. Tech. 1998, 3, 1–48. [Google Scholar]
- Siami-Namini, S.; Tavakoli, N.; Namin, A.S. A comparison of ARIMA and LSTM in forecasting time series. In Proceedings of the 2018 17th IEEE International Conference on Machine Learning and Applications (ICMLA), Orlando, FL, USA, 17–20 December 2018; pp. 1394–1401. [Google Scholar] [CrossRef]
- Duan, C.; Hu, M.; Zhang, H. Comparison of ARIMA and LSTM in Predicting Structural Deformation of Tunnels during Operation Period. Data 2023, 8, 104. [Google Scholar] [CrossRef]
- Huang, S.-C. Analysis of a model to forecast thermal deformation of ball screw feed drive systems. Int. J. Mach. Tools Manuf. 1995, 35, 1099–1104. [Google Scholar] [CrossRef]
- Bruni, C.; Forcellese, A.; Gabrielli, F.; Simoncini, M. Modelling of the rheological behaviour of aluminium alloys in multistep hot deformation using the multiple regression analysis and artificial neural network techniques. J. Mater. Process. Technol. 2006, 177, 323–326. [Google Scholar] [CrossRef]
- Du, S.; Li, Y. A novel deformation forecasting method utilizing comprehensive observation data. Adv. Mech. Eng. 2018, 10, 1687814018796330. [Google Scholar] [CrossRef]
- Lin, C.; Li, T.; Chen, S.; Liu, X.; Lin, C.; Liang, S. Gaussian process regression-based forecasting model of dam deformation. Neural Comput. Appl. 2019, 31, 8503–8518. [Google Scholar] [CrossRef]
- Zhang, B.; Qiu, L.; Zhou, Z. Prediction Analysis for Building Deformation Based on Multiple Linear Regression Model. Proc. IOP Conf. Ser. Earth Environ. Sci. 2020, 455, 012047. [Google Scholar] [CrossRef]
- Gao, N.; Gao, C.-Y. Deformation forecasting with a novel high precision grey forecasting model based on genetic algorithm. Comput. Model. New Technol. 2014, 18, 212–217. [Google Scholar]
- Du, S.; Zhang, J.; Deng, Z.; Li, J. A new approach of geological disasters forecasting using meteorological factors based on genetic algorithm optimized BP neural network. Elektron. Ir Elektrotechnika 2014, 20, 57–62. [Google Scholar] [CrossRef][Green Version]
- Wang, X.; Yang, K.; Shen, C. Study on MPGA-BP of gravity dam deformation prediction. Math. Probl. Eng. 2017, 2017, 2586107. [Google Scholar] [CrossRef]
- Luo, J.; Ren, R.; Guo, K. The deformation monitoring of foundation pit by back propagation neural network and genetic algorithm and its application in geotechnical engineering. PLoS ONE 2020, 15, e0233398. [Google Scholar] [CrossRef]
- Liao, K.; Zhang, W.; Zhu, H.-H.; Zhang, Q.; Shi, B.; Wang, J.-T.; Xu, W.-T. Forecasting reservoir-induced landslide deformation using genetic algorithm enhanced multivariate Taylor series Kalman filter. Bull. Eng. Geol. Environ. 2022, 81, 104. [Google Scholar] [CrossRef]
- Benabou, L. Development of LSTM networks for predicting viscoplasticity with effects of deformation, strain rate, and temperature history. J. Appl. Mech. 2021, 88, 071008. [Google Scholar] [CrossRef]
- Wang, S.; Yang, B.; Chen, H.; Fang, W.; Yu, T. LSTM-based deformation prediction model of the embankment dam of the danjiangkou hydropower station. Water 2022, 14, 2464. [Google Scholar] [CrossRef]
- Bui, K.T.T.; Torres, J.F.; Gutiérrez-Avilés, D.; Nhu, V.H.; Bui, D.T.; Martínez-Álvarez, F. Deformation forecasting of a hydropower dam by hybridizing a long short-term memory deep learning network with the coronavirus optimization algorithm. Comput. Aided Civ. Infrastruct. Eng. 2022, 37, 1368–1386. [Google Scholar] [CrossRef]
- Zhao, Z.; Li, Y.; Liu, C.; Gao, J. On-line part deformation prediction based on deep learning. J. Intell. Manuf. 2020, 31, 561–574. [Google Scholar] [CrossRef]
- Pan, J.; Liu, W.; Liu, C.; Wang, J. Convolutional neural network-based spatiotemporal prediction for deformation behavior of arch dams. Expert Syst. Appl. 2023, 232, 120835. [Google Scholar] [CrossRef]
- Luo, S.; Wei, B.; Chen, L. Multi-point deformation monitoring model of concrete arch dam based on MVMD and 3D-CNN. Appl. Math. Model. 2024, 125, 812–826. [Google Scholar] [CrossRef]
- Ran, Y.F.; Xiong, G.C.; Li, S.S.; Ye, L.Y. Study on deformation prediction of landslide based on genetic algorithm and improved BP neural network. Kybernetes 2010, 39, 1245–1254. [Google Scholar] [CrossRef]
- Gao, C.; Cui, X. Nonlinear time series of deformation forecasting using improved BP neural networks. Comput. Model. New Technol. 2014, 18, 249–253. [Google Scholar]
- Cui, D.; Zhu, C.; Li, Q.; Huang, Q.; Luo, Q. Research on deformation prediction of foundation pit based on PSO-GM-BP model. Adv. Civ. Eng. 2021, 2021, 8822929. [Google Scholar] [CrossRef]
- González-Cavieres, L.; Pérez-Won, M.; Tabilo-Munizaga, G.; Jara-Quijada, E.; Díaz-Álvarez, R.; Lemus-Mondaca, R. Advances in vacuum microwave drying (VMD) systems for food products. Trends Food Sci. Technol. 2021, 116, 626–638. [Google Scholar] [CrossRef]
- Mahjoub, S.; Chrifi-Alaoui, L.; Marhic, B.; Delahoche, L. Predicting energy consumption using LSTM, multi-layer GRU and drop-GRU neural networks. Sensors 2022, 22, 4062. [Google Scholar] [CrossRef] [PubMed]






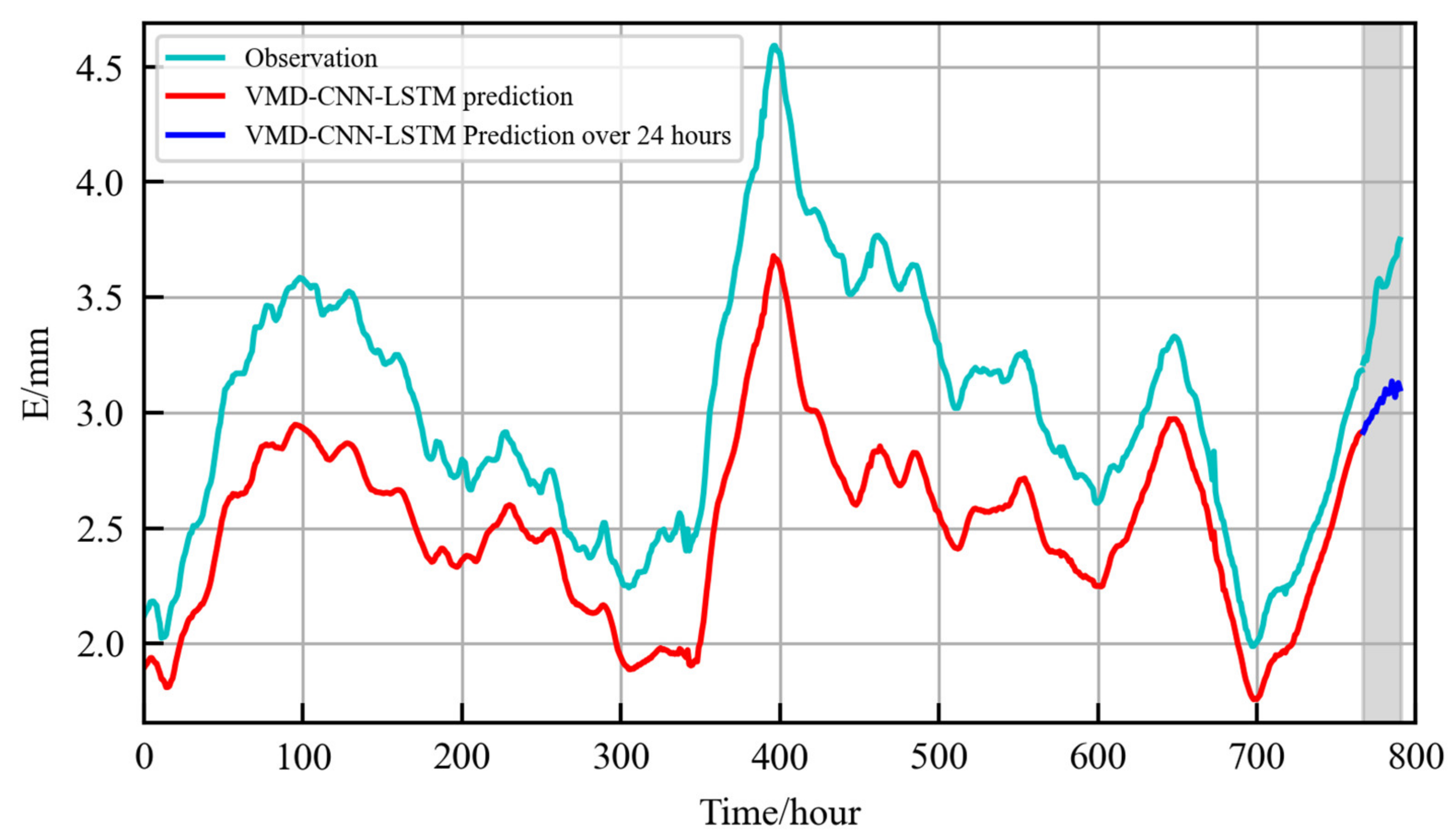


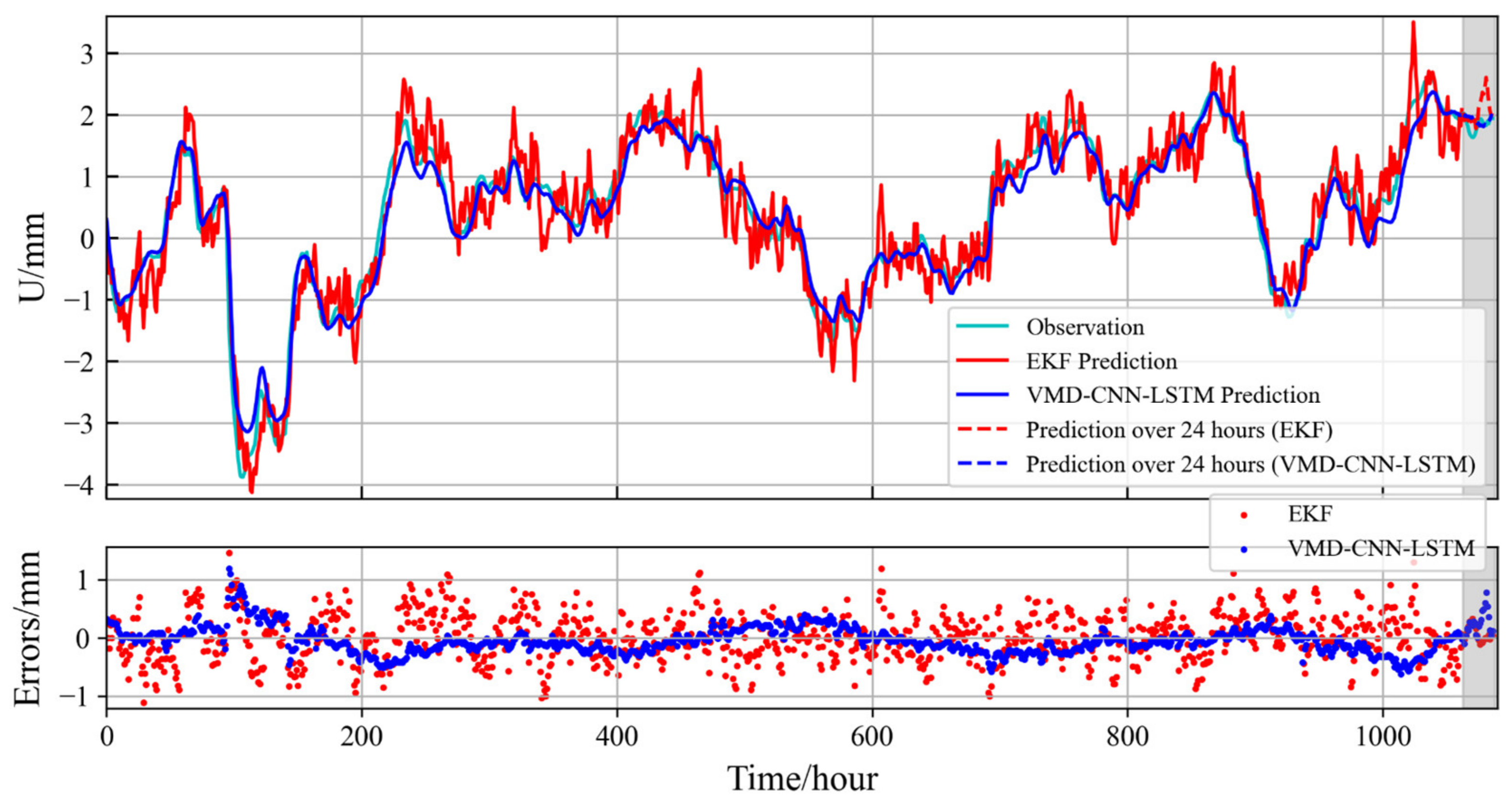
| Configuration | Parameter |
|---|---|
| The experiment period | 10 September 2023–21 February 2024 |
| GNSS systems | BDS(B1I, B2I), Galileo(E1B/C, E5b), GPS(L1C/A, L2C) |
| Sampling frequency | 1 Hz |
| Ambiguity resolution method | MLAMBDA |
| Multipath error model | Stellar day filter in observational domain |
| Troposphere method | Saastamoinen model + random walk |
| Ionosphere method | Broadcast model |
| Intervals of outputs | 1 h |
| Smoothing filter method | Rauch–Tung–Striebel smoother filtering method |
| MSE (mm) | RMSE (mm) | MAE (mm) | R2 | |
|---|---|---|---|---|
| IMF1 | 0.0065 | 0.0809 | 0.0724 | −0.6943 |
| IMF2 | 2.852 × 10−5 | 0.0053 | 0.0042 | 0.9988 |
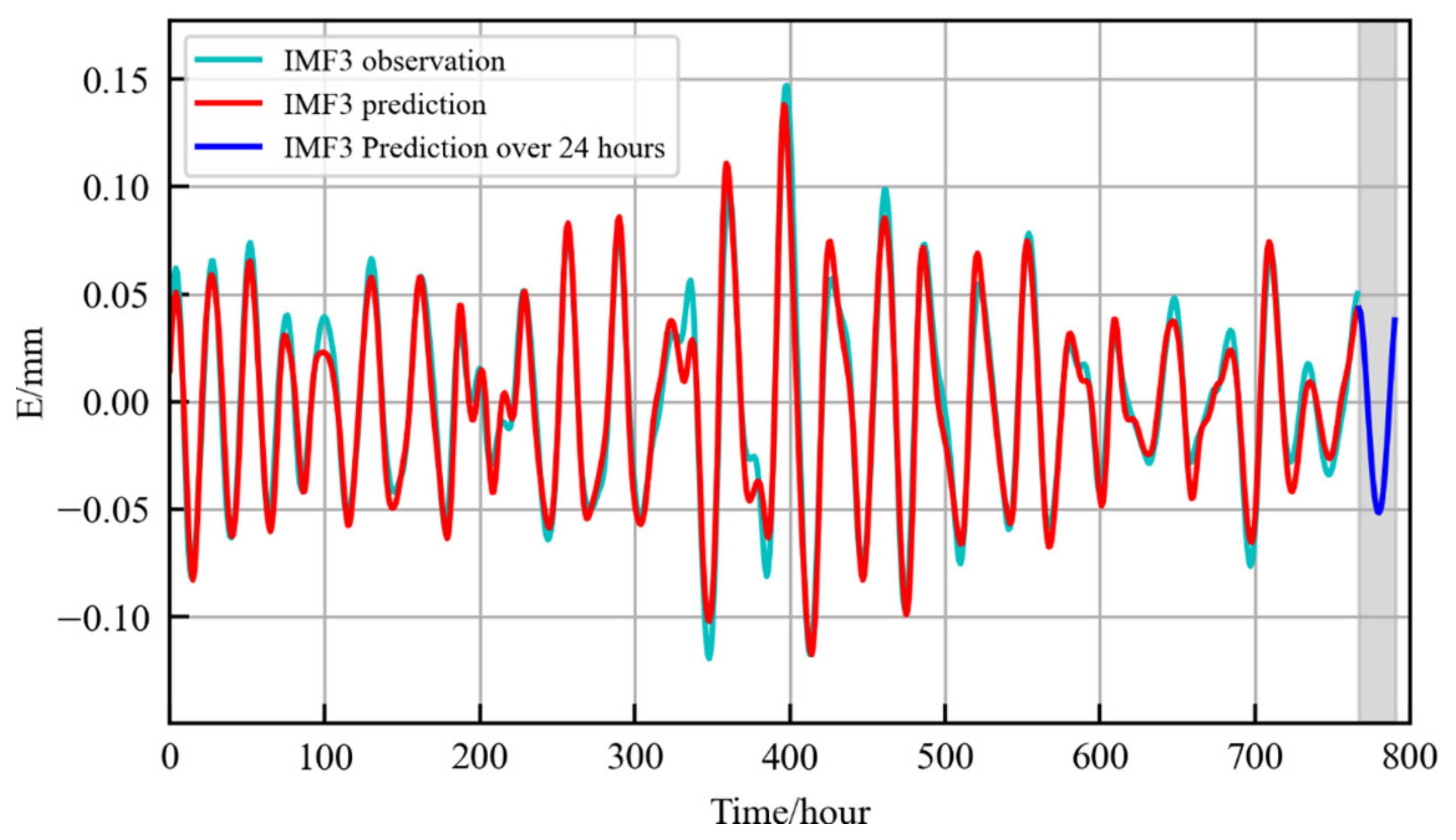
| IMF3 | 0.0002 | 0.0134 | 0.0107 | 0.9530 |
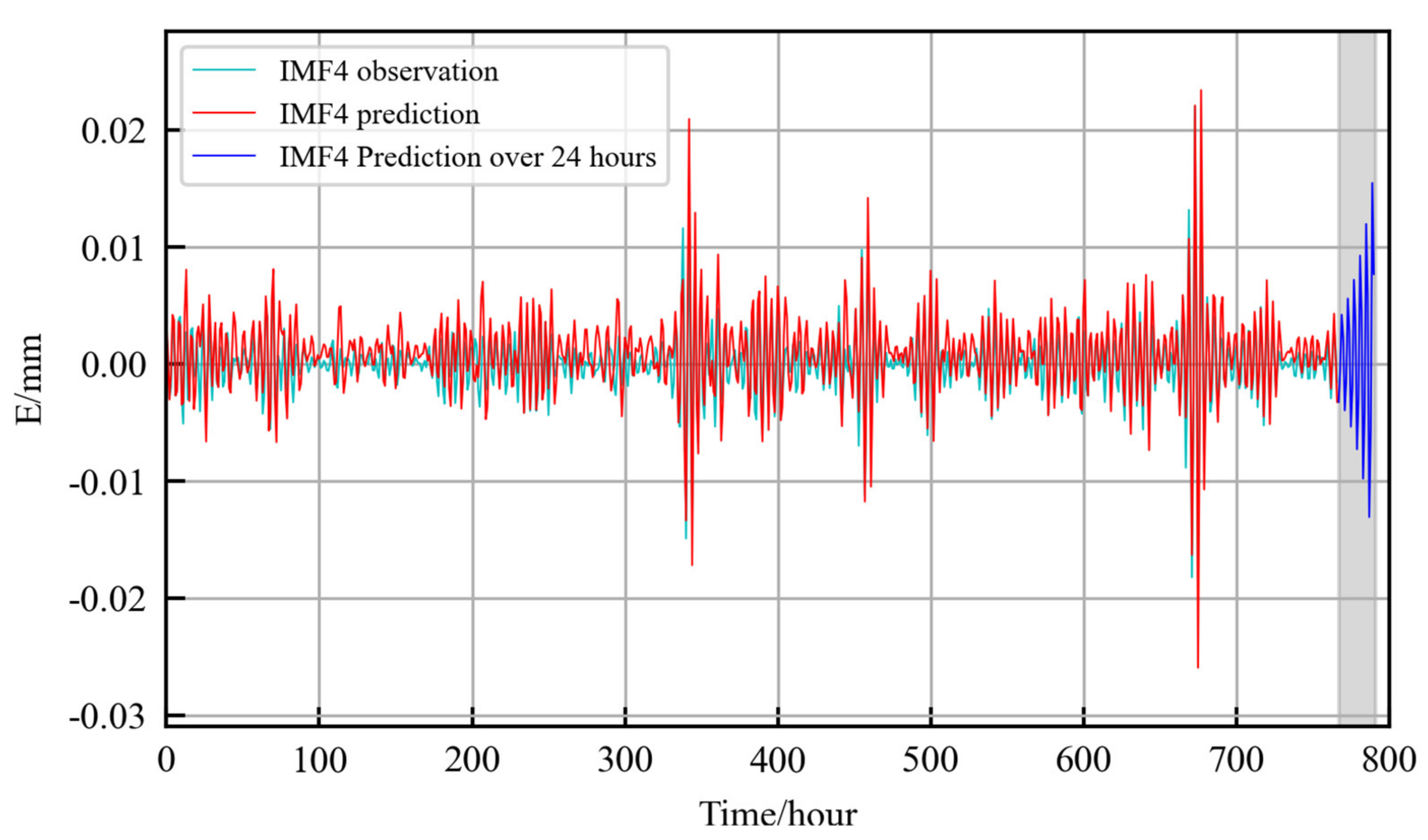
| IMF4 | 6.9622 × 10−6 | 0.0026 | 0.0020 | 0.6527 |
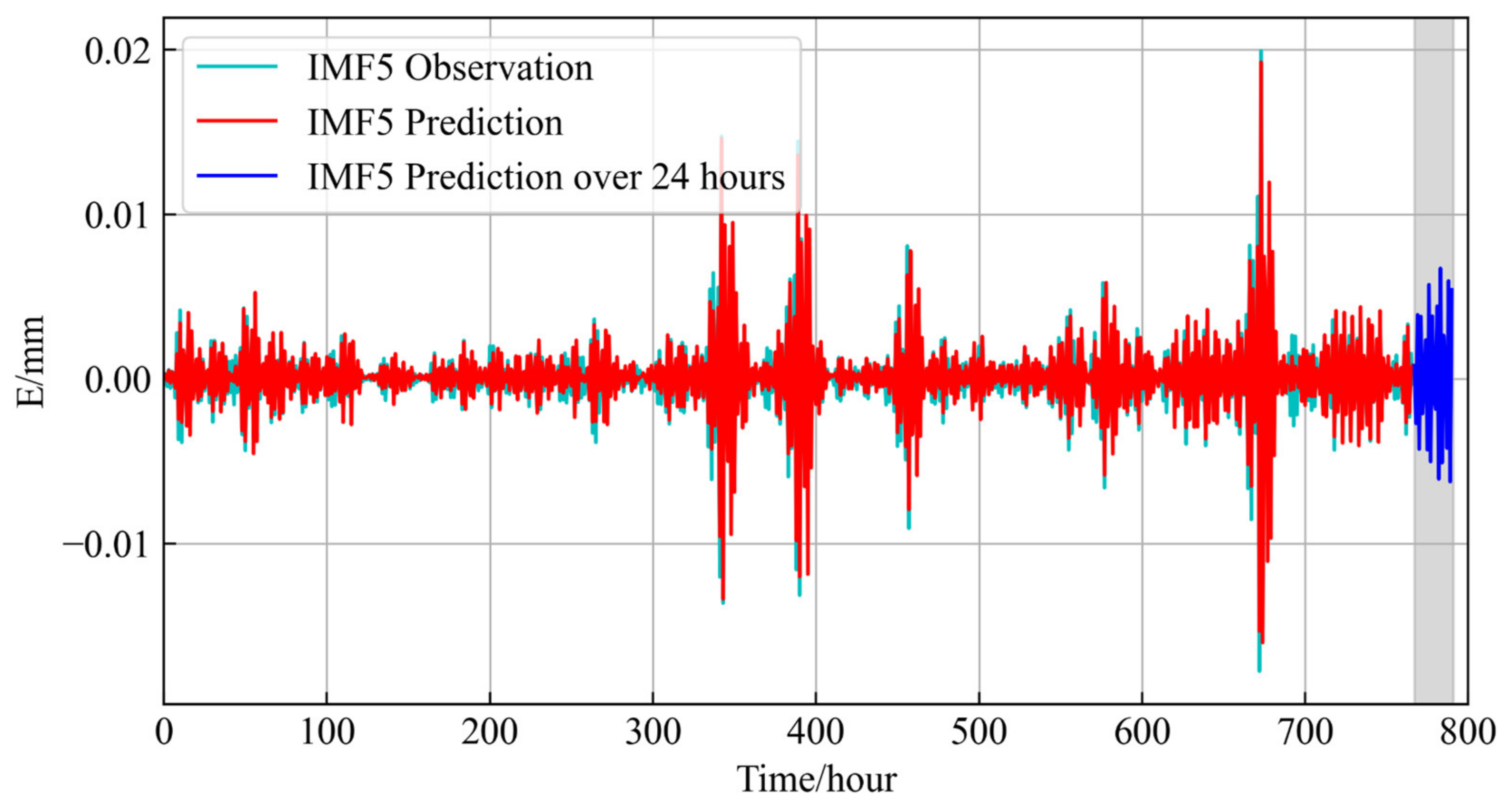
| IMF5 | 4.3939 × 10−6 | 0.0021 | 0.0017 | 0.6078 |
| MSE (mm) | RMSE (mm) | MAE (mm) | R2 | |
|---|---|---|---|---|
| EKF | 0.1646 | 0.4057 | 0.3236 | 0.9037 |
| VMD-CNN-LSTM | 0.0541 | 0.2326 | 0.1833 | 0.9654 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Y.; Meng, X.; Wang, J.; Li, H.; Lu, X.; Ding, J.; Jia, Y.; Yang, Y. Enhancing GNSS Deformation Monitoring Forecasting with a Combined VMD-CNN-LSTM Deep Learning Model. Remote Sens. 2024, 16, 1767. https://doi.org/10.3390/rs16101767
Xie Y, Meng X, Wang J, Li H, Lu X, Ding J, Jia Y, Yang Y. Enhancing GNSS Deformation Monitoring Forecasting with a Combined VMD-CNN-LSTM Deep Learning Model. Remote Sensing. 2024; 16(10):1767. https://doi.org/10.3390/rs16101767
Chicago/Turabian StyleXie, Yilin, Xiaolin Meng, Jun Wang, Haiyang Li, Xun Lu, Jinfeng Ding, Yushan Jia, and Yin Yang. 2024. "Enhancing GNSS Deformation Monitoring Forecasting with a Combined VMD-CNN-LSTM Deep Learning Model" Remote Sensing 16, no. 10: 1767. https://doi.org/10.3390/rs16101767
APA StyleXie, Y., Meng, X., Wang, J., Li, H., Lu, X., Ding, J., Jia, Y., & Yang, Y. (2024). Enhancing GNSS Deformation Monitoring Forecasting with a Combined VMD-CNN-LSTM Deep Learning Model. Remote Sensing, 16(10), 1767. https://doi.org/10.3390/rs16101767







