Abstract
Sea surface salinity (SSS) variability at mesoscales has become an important research topic in recent decades, thanks to satellite missions enabling observations of SSS with global capacity and mesoscale resolution. Here, we analyze the near-global data of the Aquarius/SAC-D along-track SSS, focusing on the slopes of SSS variance spectra in the mesoscale range from 180 to 430 km. In the vast extratropics, the spectral slope is close to −2, indicating a dynamical regime for the inverse cascade of depth-integrated energy identified by the surface quasi-geostrophic theory. However, the spectral slopes in regions near the mouths of the largest rivers are steeper than −2, reaching −3, possibly due to the large river freshwater flux. In addition, data from high-resolution thermosalinograph are used to validate satellite measurements and show good consistency in terms of SSS variance spectral slopes.
1. Introduction
Ocean salinity plays an essential role in the global hydrological cycle, density-driven circulation, and the Earth’s climate system [1,2]. The cycling of fresh water between the atmosphere and the ocean leaves a strong imprint on ocean salinity [3,4]. To some extent, sea surface salinity (SSS) variability serves as an indicator of changes in the global water cycle, such as the intensification of the hydrological cycle in response to climate change [5,6,7,8,9,10]. By altering ocean density, advection, mixing, and stratification, the variation in ocean salinity also has profound impacts on ocean circulation [11,12], which in turn regulates the Earth’s climate. Thus, as an important part of the ocean salinity, knowledge of SSS variability and the physical processes governing the distribution of SSS has become an important research topic in recent decades.
The distribution of SSS is driven by various physical processes, spanning over a broad range of scales in space and time. Among these physical processes, mesoscale variability is the essential component of ocean dynamics. Mesoscale eddies, which have typical horizontal scales of O (100) km and timescales on the order of a month, play an important role in shaping the distribution of ocean salinity and dominate the kinetic energy in the upper ocean [13,14]. For these reasons, studies on mesoscale SSS variability have persisted with many approaches, most of which rely on high-resolution in situ observations or outputs from ocean models (e.g., [15,16]). However, previous studies have been constrained by small-area measurements, insufficient record length, or uncertainty in the forcing fields and the model parameterization. In this regard, a more reliable global map depicting the response of SSS variability to mesoscale dynamics is desirable.
The launch of three satellite missions—Aquarius/SAC-D (Aquarius), Soil Moisture and Ocean Salinity (SMOS), and Soil Moisture Active Passive (SMAP)—has initiated a new era in the study of salinity variability [17,18]. For over a decade, satellite observation has provided continuous global sampling of the SSS, enabling statistical and dynamic investigations of SSS variability from a global perspective. Several studies have demonstrated the capability of satellite SSS measurements to reveal oceanic processes at mesoscales [19,20,21,22,23,24]. For example, the eddy-induced SSS signature has been identified and used to assess the ocean transport of salinity in the North Atlantic subtropical gyre [21]. However, satellite-based observations are prone to large errors, including instrument noise (assumed to be random) and sampling errors [25]. These errors are typically about 0.15–0.25 PSU in the low and mid-latitudes [26,27], comparable to the eddy-induced SSS anomaly on the order of 0.1–0.3 PSU [19,23]. If not well accounted for, these errors can significantly affect the salinity measurement and lower the signal-to-noise ratio for mesoscale signals.
In this study, we take advantage of the unique Aquarius measurement geometry and analyze the spatial wavenumber spectra of the original Level 2 (L2) along-track SSS data. The benefit of using L2 along-track Aquarius data lies in their high accuracy level of 0.2 PSU compared to other satellite swath data [1]. Given their footprint resolution (~100 km) and the applied bin range, Aquarius data are expected to efficiently resolve large mesoscale structures [21]. The wavenumber spectrum is an efficient approach to analyze the spatial variability of SSS in the frequency domain and has been widely used in previous studies. As observed in earlier studies on the along-track sea surface height (SSH) or SSS spectra, one advantage of using the along-track spectra is the clear identification of random noise, or the so-called noise level, at short wavelengths, which can be subtracted out [28,29,30,31]. By focusing on wavelengths ranging from 180 to 430 km, our study aims to illustrate mesoscale SSS dynamics with minimal influence from instrument noise and/or sampling error. By removing instrument noise and/or sampling error, we calculate the SSS variance spectrum within the 180–430 km range. The rationale behind this length-range selection is explained in the Methods section.
The tracer variance spectrum can be related to the kinetic energy spectrum. In the inertial range, the spectral slopes of the kinetic energy spectrum and tracer variance spectrum are nearly constant and obey the power-law form of ~k−p [32,33,34]. If the kinetic energy spectrum scales with k−p for p < 3, the associated tracer variance spectrum is ~k(p−5)/2; and for p ≥ 3, the associated tracer variance spectrum becomes ~k−1 [34]. For example, in the inverse energy-cascade range of quasi-geostrophic (QG) turbulence [35], the kinetic energy spectrum has p = 5/3, and the associated tracer variance spectrum is then ~k−5/3; in the enstrophy cascade range, the kinetic energy spectrum has p = 3, and the associated tracer variance spectrum is then ~k−1 [34]. Furthermore, in the inverse cascade of depth-integrated energy for surface quasi-geostrophic (SQG) turbulence, the kinetic energy spectrum has p = 1, and the associated tracer variance spectrum becomes ~k−2 [36].
Previous estimates of the spectral slopes of SSS variability have mostly relied on sparse in situ observations or remote sensing from limited regions. Typically, for the wavelength band longer than 100 km, the slope values have been estimated to range between −5/3 and −3. For example, with the combination of in situ data and numerical output, Droghei et al. [15] estimated the salinity variance spectra in the Salinity Processes in the Upper-Ocean Regional Study (SPURS-1) experiment in the subtropical North Atlantic. They found that the slope of SSS variance spectra is −5/3 in the large-scale range (about >200 km) and gradually steepens to −3 around 125 km. Using satellite SMOS data and in situ observations, Buongiorno Nardelli et al. [37] found that the slopes of SSS variance spectra range between −2 and −3 in the mesoscale range (about <325 km) in the wide zonal band of the Southern Hemisphere (10°S–65°S). However, these studies do not provide a global picture of SSS variance spectral slopes, and it is unclear to what extent the satellite-based global SSS variance spectra can be explained by the geostrophic turbulence energy spectrum.
The aim of this work is twofold. First, we calculate, for the first time, the spectral slopes of SSS variance at mesoscales in the near-global ocean and link the spectral slopes with the geostrophic turbulence energy spectrum. Second, we compare satellite results with the high-resolution in situ measurements in terms of SSS spectral slopes. This comparison serves as a metric to validate and quantify the fidelity of satellite SSS measurements.
The rest of the paper is organized as follows. In Section 2, we present the methodology and datasets. In Section 3, we describe the global distribution of SSS variability inferred from Aquarius satellite data and validate the satellite estimates of spatial slope using high-resolution thermosalinograph (TSG) data. The results are summarized and discussed in Section 4.
2. Materials and Methods
2.1. Data
2.1.1. Satellite Sea Surface Salinity
The Aquarius satellite mission, operational from August 2011 to June 2015, contributed to our understanding of SSS dynamics. Equipped with three microwave radiometers, the generated three beams were directed at different angles relative to the sea surface. Each beam produced elliptical footprints on the sea surface, covering an approximate radius of 100 km, with a sampling interval along the track of about 10 km. The equatorial crossings of Aquarius’s orbits were at 6 PM (ascending) and 6 AM (descending) local time, with a repeat cycle of 7 days. These allowed for comprehensive spatiotemporal coverage of SSS measurements across the global ocean. In this study, we use the Aquarius Level-2 (L2) version 5.0 (V5) dataset, which is distributed by the Physical Oceanography Distributed Active Archive Center (PO.DAAC) of the Jet Propulsion Laboratory (JPL). To ensure data quality, the quality status of the Level-2 SSS data is checked following the method proposed by Melnichenko et al. [30]. We exclude from the analysis data points, which are contaminated by land (land fraction > 0.01) and sea ice (ice fraction > 0.01), are flagged as severely contaminated by radio frequency interference, and are acquired in high winds (wind speed > 20 m s−1). Additionally, we use the Aquarius Level-3 (L3) V5 to obtain a time-mean map spanning from January 2012 to December 2014.
2.1.2. Thermosalinograph Sea Surface Salinity
For comparison with the satellite data, we use ship-based TSG salinity data collected by research vessels and Volunteer Observing Ships (VOSs) [38]. Here, the delayed-mode data provided by the French Sea Surface Salinity Observation Service [39] are used. These data undergo rigorous quality-control procedures, including adjustments for systematic biases in the ship tracks. Covering the period from 1993 to 2019, the TSG SSS measurements have a spatial resolution of about 1–3 km along tracks. To maintain consistency, the TSG SSS measurements are interpolated into 2.5 km intervals. Only SSS measurements classified as “good” are selected for the analysis.
2.2. Methods
2.2.1. Wavenumber Spectra Estimation Using Aquarius Data
Following the techniques proposed by Xu and Fu [31], the along-track SSS wavenumber spectrum is computed in 10° × 10° spatial bins. These bins are systematically moved in 3° steps in both zonal and meridional directions across the global ocean (Figure 1). To prepare for spectral slope calculations, the time average is first removed at each footprint to obtain SSS anomalies. Within each 10° spatial bin, samples along the track are detrended to reduce energy at scales larger than half the bin size. For each spatial bin, the mean spectrum is preserved by averaging all individual spectra of each Aquarius beam (Figure 1a,b). Furthermore, the noise level is estimated by horizontally fitting the spectrum in the wavelength band of 20–25 km (Figure 1b, dashed line). This wavelength band is approximately the smallest-length scale resolved by the Aquarius. Here, the noise (e.g., Figure 1b, dashed line) is primarily instrumental white noise. The signal-to-noise ratio is defined as the ratio of the low-wavenumber signal variance to the noise variance at 20–25 km. The global-ocean noise level and the signal-to-noise ratio are shown in Figure 2. Particularly, the signal-to-noise ratio ranges from 1 to 10 at a 180 km wavelength; because of this high ratio, the subtraction of noise from the mean spectrum (Figure 1b, yellow curve) makes the SSS variance spectrum largely unaffected at low wavenumbers (Figure 1b, black curve).
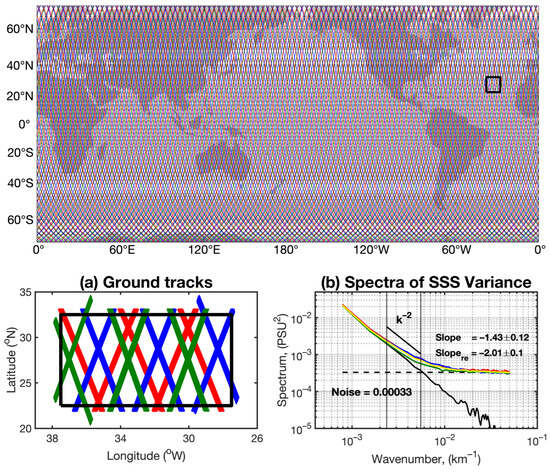
Figure 1.
Top panel: Example pattern of Aquarius ground tracks over a 7-day period. Three radiometer beams are shown in different colors. A zoom over the area in the subtropical North Atlantic (black rectangle) is provided in panel (a). Multiple SSS ground tracks from 2011 to 2015 are collected and plotted in different colors. An example of their long-time mean SSS variance spectra is shown in panel (b). The yellow curves show the ensemble mean of the SSS variance spectrum for all beams (red, green, and blue colors), and the black curve is obtained after removing their noise, which is shown as the dashed line.
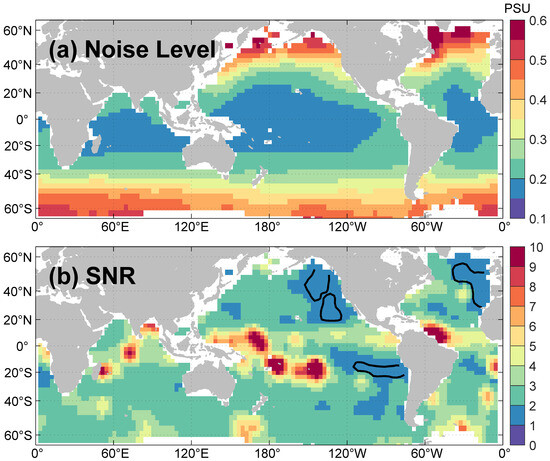
Figure 2.
(a) Global pattern of the noise level (unit is PSU) estimated at 20–25 km. (b) Signal-to-noise ratio (SNR) at 180 km.
The SSS variance spectrum is then unbiased by removing a constant noise level estimated in the wavelength band of 20–25 km, before performing a linear slope estimate. Subsequently, we calculate the spectral slope by a least-squares regression applied to the spectra within a fixed wavelength band ranging from 180 to 430 km. The choice of the lower limit (180 km) aims to ensure robust slope estimation since the shape of the spectrum shows considerably more variability below this threshold. Following noise removal, the spectral slopes have generally become steeper than previous estimates (Figure 1b, black line).
A noise-level sensitivity is tested by increasing/decreasing the noise level by 10%. The results are shown in Supplementary Materials Figure S1. Remarkably, the influence of ±10% of noise level on the spectral slope estimate is negligible, indicating that the results derived from the selected 180–430 km wavenumber band are robust and independent of the choice of noise estimate. Additionally, we use 20° × 20° spatial bins to examine our spectral slope estimate, revealing a very similar result as depicted in Figure S2. The bias of the spectrum slope in the wavelength band is evaluated using a 95% confidence interval on the slope regression coefficient, following the approach proposed by Xu and Fu [40], as demonstrated in Supporting Information Figure S3.
2.2.2. Wavenumber Spectra Estimation Using TSG Data
High-resolution TSG data are used to estimate the wavenumber spectra of SSS variability in a few selected areas. The choice of the areas is dictated by the availability of data. Specifically, we analyze the TSG data in four designated boxes (Boxes A–D in Figure 3). To ensure robust analysis, relatively straight segments of ship tracks are analyzed, comprising a minimum of 20 segments in each box, with each segment spanning 1200 km or longer (Figure 3a). The approach employed to estimate the wavenumber spectra from the TSG data follows the approach used to analyze the Aquarius ground-track data (see Figure 1b and Figure 3b, black curves). This consistent approach allows for a comparative analysis of SSS variability across different datasets, enabling insights into regional and global patterns of SSS dynamics.
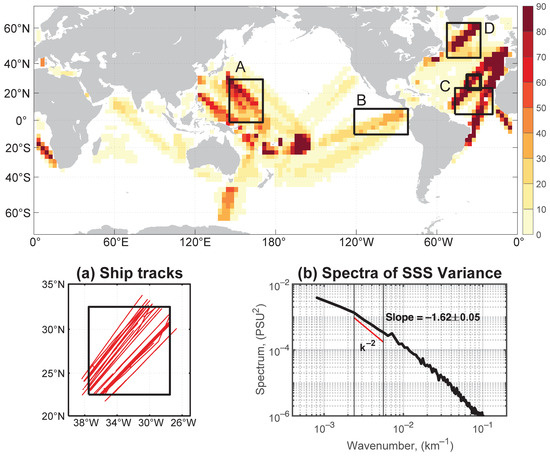
Figure 3.
Number of Volunteer Observing Ship (VOS) lines per 10° × 10° bin from 1993 to 2019. Black rectangles indicate the areas selected for the box-averaged analysis in Figure 5. VOS tracks within the same box as shown in Figure 1 (bold black rectangle) are displayed in panel (a) (red lines). As a comparison, panel (b) shows the long-time mean SSS variance spectra depicted by the black curve.
3. Results
3.1. Global Wavenumber Spectra of SSS Variance of Aquarius Data
The global distribution of the SSS spectral slope is shown in Figure 4. The slope differences between with (Figure 4a) and without noise (Figure 4b) are relatively large (>5/6) in the Eastern North Pacific, the Southeastern Tropical Pacific, and the Northern Subpolar Atlantic (Figure 4c). In the vast extratropical oceans (poleward from the 20° latitudes), after the removal of noise, the spectral slope hovers about −2, (Figure 4b, light green), with a slope bias of approximately ±1/6 (Supplementary Materials Figure S3). This −2 slope agrees with the tracer variance spectral slope predicted by the SQG turbulence theory in the inverse cascade range of depth-integrated energy [36]. Nonetheless, notable deviations are observed, particularly over the Northern Pacific and Northern Atlantic Oceans, where a steeper slope of −7/3 prevails. In these regions, the signal-to-noise ratio (Figure 2b, blue) is very low (less than 2) at wavelengths below 180 km; then, due to the removal of noise, less variance is accounted for at smaller wavelengths in calculating the spectrum, thus causing a steeper slope.
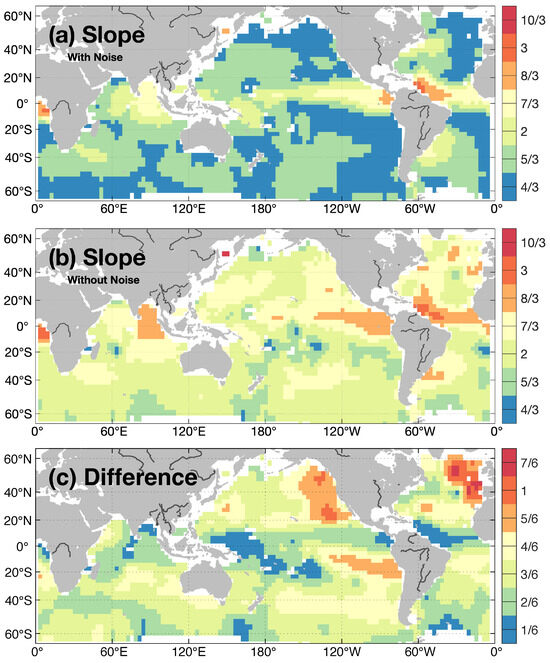
Figure 4.
Global pattern of the spectral slopes (−1) estimated from mean SSS variance spectra (a) with noise and (b) without noise. (c) Spectral slopes’ difference between with and without noise (b minus a). Unit is log(PSU2)/log(km−1). The gray lines on lands indicate the global largest 20 rivers according to [41].
In most areas of the tropics, the slopes of the SSS variance spectrum are steeper than −2 and disagree with the SQG theoretical prediction. Notably, regions with large spectral slopes (Figure 4b, orange-red) are located around the river plumes formed by the world largest rivers (Figure 4b, gray lines). It is evident near the plumes of the Amazon–Orinoco, and Congo in the Equatorial Atlantic, La Plata–Parana in the Southern Atlantic, St. Lawrence in the Northern Atlantic, Ganges–Brahmaputra–Irrawaddy in the Bay of Bengal, and Amur in the Sea of Sea of Okhotsk. These large rivers discharge great volumes of fresh water into the ocean; this could increase the SSS variance at larger scales and thereby steepen spectral slopes.
Moreover, another obvious area with a large spectral slope is in the Eastern Equatorial Pacific, where the surface waters are further adjusted by localized oceanic dynamics, such as the Tropical Instability Waves-induced SSS anomalies in the Eastern Pacific Fresh Pool [20] and the migration of the eastern edge of western warm pool related to the El Niño–Southern Oscillation (ENSO) [42,43]; accordingly, the spectral slope of SSS variance could be steepened due to the elevated variance at larger scales and display east–west and inter-hemispheric asymmetries, particularly in the Pacific Ocean. Similarly, the large spectral slopes in the Eastern Equatorial Indian Ocean and Eastern Equatorial Atlantic might also be related to ENSO-caused SSS anomalies. In addition, in the North Atlantic, large spectral slopes are also observed, and this may be caused by the strong surface cooling-induced SSS anomalies.
In addition, the first deformation radius in the tropics can exceed 250 km [31,34]; therefore, the wavelength band of 180–430 km for the spectrum calculation contains variance at scales below the tropical mesoscales. The relatively low variance at these smaller scales may also steepen the spectral slope.
3.2. Global Wavenumber Spectra of SSS Variance of TSG Observations
To compare the above spectra computed from satellite data, here we use historic TSG data to compute SSS variance spectra. Examples of the selected regions where the spectral slopes were derived can be seen in Figure 5. To ensure the dynamical consistency of spectral slope estimates across regions, average spectral slopes are shown in bold. Computed over the period from 1993 to 2019 for the TSG data, the spectral slopes over the 180–430 km band of the four boxes are −1.82, −2.46, −2.05, and −1.56, respectively, as shown in Figure 5a–d. These spectral slopes overall agree with the slopes computed from satellite data, although systematically steeper slopes are observed in all boxes for Aquarius (Figure 5e–h). This discrepancy is likely related to differences in sampling strategies between the different observational platforms. Because of the smooth effect within the Aquarius footprint, signal variance is reduced at high wavenumbers close to the footprint resolution, resulting in a steepening of the spectral slope.
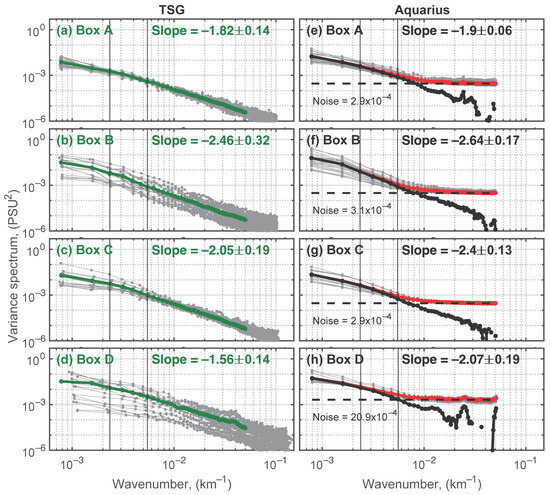
Figure 5.
Wavenumber spectrum of SSS calculated from (a–d) TSG data and (e–h) Aquarius SSS datasets. For TSG data, the gray curves show individual wavenumber spectrum, and the green curves show their regional averages. For Aquarius data, the red curves show the regional averages, and the black curves show the spectrum without noise. The locations of the boxes are shown in Figure 3 by the black rectangles.
4. Discussion and Conclusions
Using Aquarius along-track SSS data, we computed a near-global map of spectral slopes for SSS variance at mesoscales (180–430 km). Also, we conducted a comparative analysis of spectral slopes calculated from satellite measurements and in situ TSG data for the purpose of validating satellite measurements.
We show that, across the vast extratropical oceans, the spectral slope of SSS variance is close to −2 (Figure 4b) at mesoscales. This −2 slope implies a dynamical regime for an inverse cascade of depth-integrated energy, as identified by SQG theory [36]. In fact, similar −2 slopes have been found in the variance spectra of other oceanic variables, such as spice and temperature, based on data collected from the Subtropical North Pacific [32,44]. These studies also indicate that the −2 slope remains at different depths from the surface down to 1000 m.
By contrast, near the large river plumes, the spectral slopes are steeper than −2 (e.g., −3 and −8/3). The intense river discharge could elevate SSS variance at larger scales, steepening the spectral slope. Additionally, the large spectral slopes in the Eastern Equatorial Pacific, eastern Equatorial Indian Ocean, and Eastern Equatorial Atlantic may be due to the tropical instability waves and ENSO-induced SSS anomalies. Briefly, the large river discharge and strong large-scale air–sea interaction can induce SSS variability at oceanic mesoscales; these factors may cause discrepancies in SSS variance spectral slopes between satellite observations and the predictions by geostrophic turbulence theory, which primarily accounts for the ocean currents effects on the tracer variance spectra. Further studies are needed to better understand what ocean dynamical processes control the SSS variance spectra.
Regional-scale differences in the estimates derived from different SSS products may cause variations in spatial resolution and/or different levels of noise. These include various types of biases that may be present in satellite SSS data [27]. We use high-resolution TSG data to validate spectral slope estimates and find that the differences between the satellite and in situ observations vary regionally. The TSG data show flatter slopes (approximately 4–15% systematically) in comparison to those of Aquarius, particularly pronounced in the Northern Polar Atlantic (up to about 25%). Overall, the agreement between the satellite and in situ data is sufficiently robust to support our analysis and conclusions.
Although the global distribution of the SSS spectral slope over the 2-year generally aligns with the long-term mean value obtained by the in situ data, systematic differences arise from data sampling and in the study period. Moreover, after the strict quality control of the Aquarius along-track data, the spectral slope in the enclosed seas is actually severely affected by the surrounding land and radio frequency interference, so there may be visible data missing on the global pattern. In fact, the duration of the time series or the seasonality of the SSS spectral slope can also influence slope estimation. The seasonality of the mesoscale SSS variability intensifies during the boreal spring and autumn seasons (Supplementary Materials Figure S4), warranting further exploration.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/rs16101753/s1, Figure S1. Results of the noise level sensitivity test by (a) decreasing and (b) increasing the noise level by 10%. Global pattern of the spectral slope (−1) estimated from mean SSS wavenumber spectrum after noise level removal (e.g., Figure 1b, black curve). Unit is log(PSU2)/log(km−1). Figure S2. Same as Figure 4b, but for the 20° by 20° bin box. Figure S3. The bias of the spectral slope at 95% confidence levels. Figure S4. Seasonal anomaly pattern of spectral slope (−1) estimated from mean SSS variance spectrum after noise level removal during boreal: (a) December to February (DJF); (b) March to May (MAM); (c) June to August (JJA); and (d) September to November (SON). Unit is log(PSU2)/log(km−1).
Author Contributions
Conceptualization, D.L.Y. and P.W.; Methodology, D.L.Y.; Analysis, D.L.Y. and P.W.; Writing—Original Draft Preparation, D.L.Y.; Writing—Review and Editing, D.L.Y. and P.W.; Funding Acquisition, D.L.Y. and P.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key Research and Development Program of China (Grant No. 2023YFC3008200), the National Natural Science Foundation of China (NSFC) (Grant Nos. 42306011, 42206017, 42227901 and 42230603), the Natural Science Foundation of Guangdong Province (No. 2022A1515110914), and Southern Marine Science and Engineering Guangdong Laboratory (Zhuhai) (Nos. SML2023SP238 and SML2023SP240).
Data Availability Statement
The Aquarius L2 V5.0 SSS dataset distributed by the PO.DAAC JPL is freely distributed at https://podaac-www.jpl.nasa.gov/dataset/AQUARIUS_L2_SSS_V5#. The Aquarius L3 SSS used for removing the long-time mean is available for public access at https://podaac.jpl.nasa.gov/dataset/AQUARIUS_L3_SSS_SMI_7DAY-RUNNINGMEAN_V5. The TSG delayed-mode SSS data provided by the LEGOS are freely distributed at https://sss.sedoo.fr/sss-search/. River geographic data are freely accessed at https://rda.ucar.edu/datasets/ds551-0/. All data were accessed on 19 April 2024.
Acknowledgments
We greatly appreciate the guidance given by Oleg Melnichenko for data processing. This work was initiated by Oleg Melnichenko and Daling Li Yi. We also would like to thank three anonymous reviewers for their helpful and constructive comments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Reul, N.; Grodsky, S.A.; Arias, M.; Boutin, J.; Catany, R.; Chapron, B.; D’Amico, F.; Dinnat, E.; Donlon, C.; Fore, A.; et al. Sea Surface Salinity Estimates from Spaceborne L-Band Radiometers: An Overview of the First Decade of Observation (2010–2019). Remote Sens. Environ. 2020, 242, 111769. [Google Scholar] [CrossRef]
- Vinogradova, N.; Lee, T.; Boutin, J.; Drushka, K.; Fournier, S.; Sabia, R.; Stammer, D.; Bayler, E.; Reul, N.; Gordon, A.; et al. Satellite Salinity Observing System: Recent Discoveries and the Way Forward. Front. Mar. Sci. 2019, 6, 1–23. [Google Scholar] [CrossRef]
- Durack, P.J. Ocean Salinity and the Global Water Cycle. Oceanography 2015, 28, 20–31. [Google Scholar] [CrossRef]
- Schmitt, R.W. Salinity and the Global Water Cycle. Oceanography 2008, 21, 12–19. [Google Scholar] [CrossRef]
- Durack, P.J.; Wijffels, S.E. Fifty-Year Trends in Global Ocean Salinities and Their Relationship to Broad-Scale Warming. J. Clim. 2010, 23, 4342–4362. [Google Scholar] [CrossRef]
- Vinogradova, N.; Ponte, R. In Search of Fingerprints of the Recent Intensification of the Ocean Water Cycle. J. Clim. 2017, 30, 5513–5528. [Google Scholar] [CrossRef]
- Yu, L.; Josey, S.A.; Bingham, F.M.; Lee, T. Intensification of the Global Water Cycle and Evidence from Ocean Salinity: A Synthesis Review. Ann. N. Y. Acad. Sci. 2020, 1472, 76–94. [Google Scholar] [CrossRef] [PubMed]
- Nichols, R.E.; Subrahmanyam, B. Estimation of Surface Freshwater Fluxes in the Arctic Ocean Using Satellite-Derived Salinity. Remote Sens. Earth Syst. Sci. 2019, 2, 247–259. [Google Scholar] [CrossRef]
- Dong, J.; Jin, M.; Liu, Y.; Dong, C. Interannual Variability of Surface Salinity and Ekman Pumping in the Canada Basin during Summertime of 2003–2017. J. Geophys. Res. Oceans 2021, 126, e2021JC017176. [Google Scholar] [CrossRef]
- Fournier, S.; Lee, T.; Wang, X.; Armitage, T.W.K.; Wang, O.; Fukumori, I.; Kwok, R. Sea Surface Salinity as a Proxy for Arctic Ocean Freshwater Changes. J. Geophys. Res. Oceans 2020, 125, e2020JC016110. [Google Scholar] [CrossRef]
- Lukas, R.; Lindstrom, E. The Mixed Layer of the Western Equatorial Pacific Ocean. J. Geophys. Res. 1991, 96, 3343–3357. [Google Scholar] [CrossRef]
- Yang, Q.; Dixon, T.H.; Myers, P.G.; Bonin, J.; Chambers, D.; Van Den Broeke, M.R. Recent Increases in Arctic Freshwater Flux Affects Labrador Sea Convection and Atlantic Overturning Circulation. Nat. Commun. 2016, 7, 10525. [Google Scholar] [CrossRef] [PubMed]
- Chelton, D.B.; Schlax, M.G.; Samelson, R.M. Global Observations of Nonlinear Mesoscale Eddies. Prog. Oceanogr. 2011, 91, 167–216. [Google Scholar] [CrossRef]
- Ferrari, R.; Wunsch, C. The Distribution of Eddy Kinetic and Potential Energies in the Global Ocean. Tellus Ser. Dyn. Meteorol. Oceanogr. 2010, 62, 92–108. [Google Scholar] [CrossRef]
- Droghei, R.; Buongiorno Nardelli, B.; Santoleri, R. Combining in Situ and Satellite Observations to Retrieve Salinity and Density at the Ocean Surface. J. Atmos. Ocean. Technol. 2016, 33, 1211–1223. [Google Scholar] [CrossRef]
- Kolodziejczyk, N.; Hernandez, O.; Boutin, J.; Reverdin, G. SMOS Salinity in the Subtropical North Atlantic Salinity Maximum: 2. Two-Dimensional Horizontal Thermohaline Variability. J. Geophys. Res. Oceans 2015, 120, 972–987. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.P.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.J.; Font, J.; Reul, N.; Gruhier, C.; et al. The SMOS L: New Tool for Monitoring Key Elements Ofthe Global Water Cycle. Proc. IEEE 2010, 98, 666–687. [Google Scholar] [CrossRef]
- Lagerloef, G.; Boutin, J.; Chao, Y.; Delcroix, T.; Font, J.; Niiler, P.; Reul, N.; Riser, S.; Schmitt, R.; Stammer, D.; et al. Resolving the Global Surface Salinity Field and Variations by Blending Satellite and In Situ Observations; ESA Publisher WPP: Venice, Italy, 2010; Volume 2, p. 306. [Google Scholar]
- Delcroix, T.; Chaigneau, A.; Soviadan, D.; Boutin, J.; Pegliasco, C. Eddy-Induced Salinity Changes in the Tropical Pacific. J. Geophys. Res. Oceans 2019, 124, 374–389. [Google Scholar] [CrossRef]
- Lee, T.; Lagerloef, G.; Gierach, M.M.; Kao, H.-Y.; Yueh, S.; Dohan, K. Aquarius Reveals Salinity Structure of Tropical Instability Waves. Geophys. Res. Lett. 2012, 39, L12610. [Google Scholar] [CrossRef]
- Melnichenko, O.; Amores, A.; Maximenko, N.; Hacker, P.; Potemra, J. Signature of Mesoscale Eddies in Satellite Sea Surface Salinity Data. J. Geophys. Res. Oceans 2017, 122, 1416–1424. [Google Scholar] [CrossRef]
- Lin, X.; Qiu, Y.; Sun, D. Thermohaline Structures and Heat/Freshwater Transports of Mesoscale Eddies in the Bay of Bengal Observed by Argo and Satellite Data. Remote Sens. 2019, 11, 2989. [Google Scholar] [CrossRef]
- Melnichenko, O.; Hacker, P.; Müller, V. Observations of Mesoscale Eddies in Satellite Sss and Inferred Eddy Salt Transport. Remote Sens. 2021, 13, 315. [Google Scholar] [CrossRef]
- Yang, Y.; Guo, Y.; Zeng, L.; Wang, Q. Eddy-Induced Sea Surface Salinity Changes in the South China Sea. Front. Mar. Sci. 2023, 10, 1113752. [Google Scholar] [CrossRef]
- Vinogradova, N.T.; Ponte, R.M. Assessing Temporal Aliasing in Satellite-Based Surface Salinity Measurements. J. Atmos. Ocean. Technol. 2012, 29, 1391–1400. [Google Scholar] [CrossRef]
- Boutin, J.; Vergely, J.L.; Marchand, S.; D’Amico, F.; Hasson, A.; Kolodziejczyk, N.; Reul, N.; Reverdin, G.; Vialard, J. New SMOS Sea Surface Salinity with Reduced Systematic Errors and Improved Variability. Remote Sens. Environ. 2018, 214, 115–134. [Google Scholar] [CrossRef]
- Kao, H.Y.; Lagerloef, G.S.E.E.; Lee, T.; Melnichenko, O.; Meissner, T.; Hacker, P. Assessment of Aquarius Sea Surface Salinity. Remote Sens. 2018, 10, 1341. [Google Scholar] [CrossRef]
- Chen, S.; Qiu, B. Sea Surface Height Variability in the 30–120 Km Wavelength Band From Altimetry Along-Track Observations. J. Geophys. Res. Oceans 2021, 126, e2021JC017284. [Google Scholar] [CrossRef]
- Dufau, C.; Orsztynowicz, M.; Dibarboure, G.; Morrow, R.; Le Traon, P. Mesoscale Resolution Capability of Altimetry: Present and Future. J. Geophys. Res. Oceans 2016, 121, 4910–4927. [Google Scholar] [CrossRef]
- Melnichenko, O.; Hacker, P.; Maximenko, N.; Lagerloef, G.; Potemra, J. Spatial Optimal Interpolation of Aquarius Sea Surface Salinity: Algorithms and Implementation in the North Atlantic. J. Atmos. Ocean. Technol. 2014, 31, 1583–1600. [Google Scholar] [CrossRef]
- Xu, Y.; Fu, L.L. The Effects of Altimeter Instrument Noise on the Estimation of the Wavenumber Spectrum of Sea Surface Height. J. Phys. Oceanogr. 2012, 42, 2229–2233. [Google Scholar] [CrossRef]
- Callies, J.J.J.; Ferrari, R. Interpreting Energy and Tracer Spectra of Upper-Ocean Turbulence in the Submesoscale Range (1–200Km). J. Phys. Oceanogr. 2013, 43, 2456–2474. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Sov. Phys. Usp. 1968, 10, 734–746. [Google Scholar] [CrossRef]
- Vallis, G.K. Atmospheric and Oceanic Fluid Dynamics; Cambridge University Press: Cambridge, MA, USA, 2006; pp. 337–370. [Google Scholar]
- Charney, J.G. Geostrophic Turbulence. J. Atmos. Sci. 1971, 28, 1087–1095. [Google Scholar] [CrossRef]
- Blumen, W. Uniform Potential Vorticity Flow: Part I. Theory of Wave Interactions and Two-Dimensional Turbulence. J. Atmos. Sci. 1978, 35, 774–783. [Google Scholar] [CrossRef]
- Buongiorno Nardelli, B.; Droghei, R.; Santoleri, R. Multi-Dimensional Interpolation of SMOS Sea Surface Salinity with Surface Temperature and in Situ Salinity Data. Remote Sens. Environ. 2016, 180, 392–402. [Google Scholar] [CrossRef]
- Delcroix, T.; Alory, G.; Téchiné, P.; Diverrès, D.; Varillon, D.; Cravatte, S.; Gouriou, Y.; Grelet, J.; Jacquin, S.; Kestenare, E.; et al. Sea Surface Salinity data from Voluntary Observing Ships Network. 2002. Available online: https://www.pigma.org/geonetwork/5a8srv/api/records/acbe0443-19c1-5fa6-e309-50e6fdf732f3 (accessed on 19 April 2024).
- Alory, G.; Delcroix, T.; Téchiné, P.; Diverrès, D.; Varillon, D.; Cravatte, S.; Gouriou, Y.; Grelet, J.; Jacquin, S.; Kestenare, E.; et al. The French Contribution to the Voluntary Observing Ships Network of Sea Surface Salinity. Deep Sea Res. Part Oceanogr. Res. Pap. 2015, 105, 1–18. [Google Scholar] [CrossRef]
- Xu, Y.; Fu, L.L. Global Variability of the Wavenumber Spectrum of Oceanic Mesoscale Turbulence. J. Phys. Oceanogr. 2011, 41, 802–809. [Google Scholar] [CrossRef]
- Dai, A.; Trenberth, K. Estimates of Freshwater Discharge from Continents: Latitudinal and Seasonal Variations. J. Hydrometeorol. 2002, 3, 660–687. [Google Scholar] [CrossRef]
- Qu, T.; Yu, J.Y. ENSO Indices from Sea Surface Salinity Observed by Aquarius and Argo. J. Oceanogr. 2014, 70, 367–375. [Google Scholar] [CrossRef]
- Qi, J.; Zhang, L.; Qu, T.; Yin, B.; Xu, Z.; Yang, D.; Li, D.; Qin, Y. Salinity Variability in the Tropical Pacific during the Central-Pacific and Eastern-Pacific El Niño Events. J. Mar. Syst. 2019, 199, 103225. [Google Scholar] [CrossRef]
- Cole, S.T.; Rudnick, D.L. The Spatial Distribution and Annual Cycle of Upper Ocean Thermohaline Structure. J. Geophys. Res. Oceans 2012, 117, C02027. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).