LASSO (L1) Regularization for Development of Sparse Remote-Sensing Models with Applications in Optically Complex Waters Using GEE Tools
Abstract
1. Introduction
1.1. Remote Sensing of Water Quality
1.2. Water Quality Models for Optically Complex Waters
1.3. Approach
1.4. Study Area
2. Data and Methods
2.1. Overview
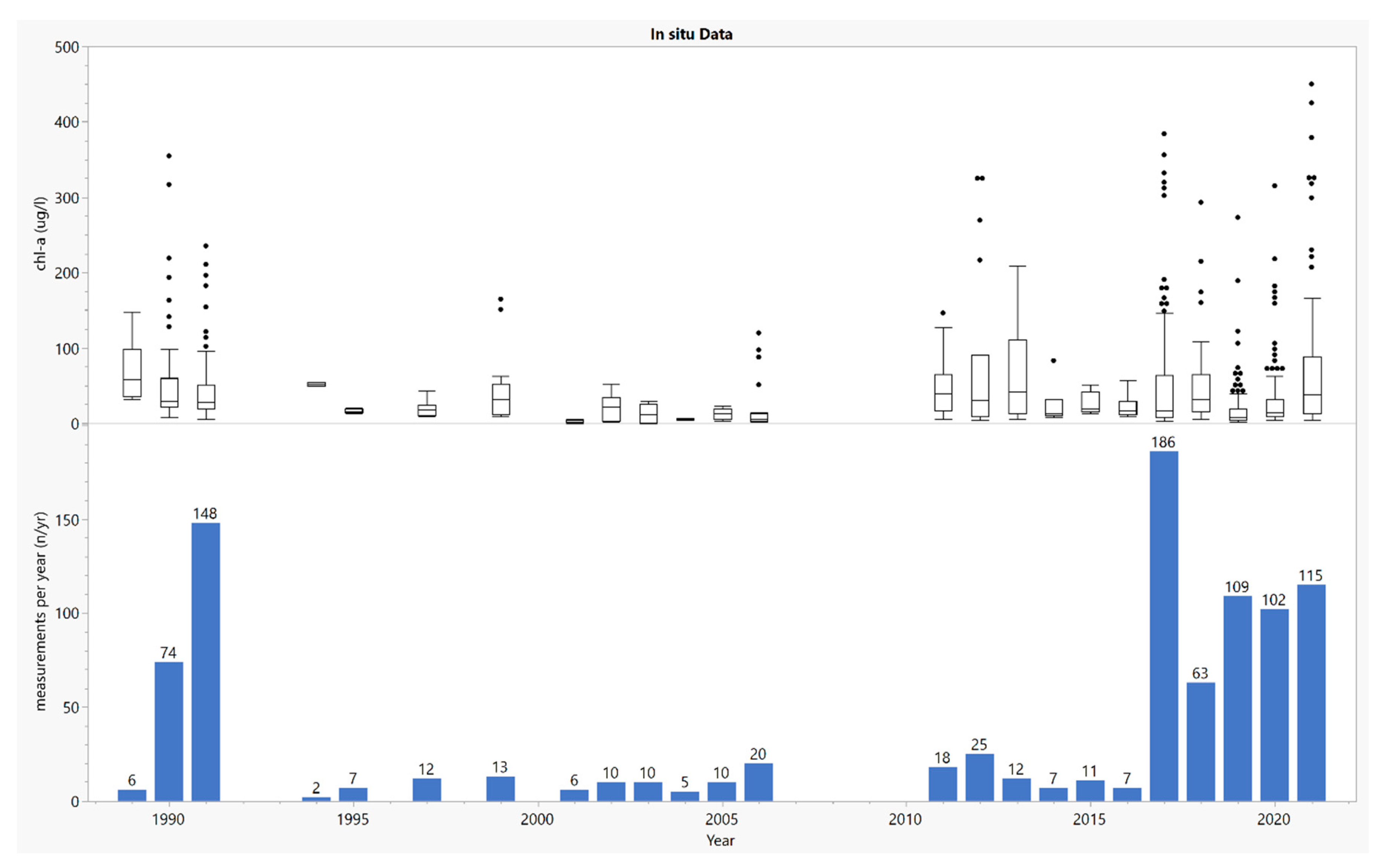
2.2. Study Data
2.3. Model Parameters
2.4. Negative and Small Reflectance Values
2.5. Alpha
2.6. Model Training, Error Estimation, and Evaluation
2.7. Code and Notebooks
3. Case Study and Results
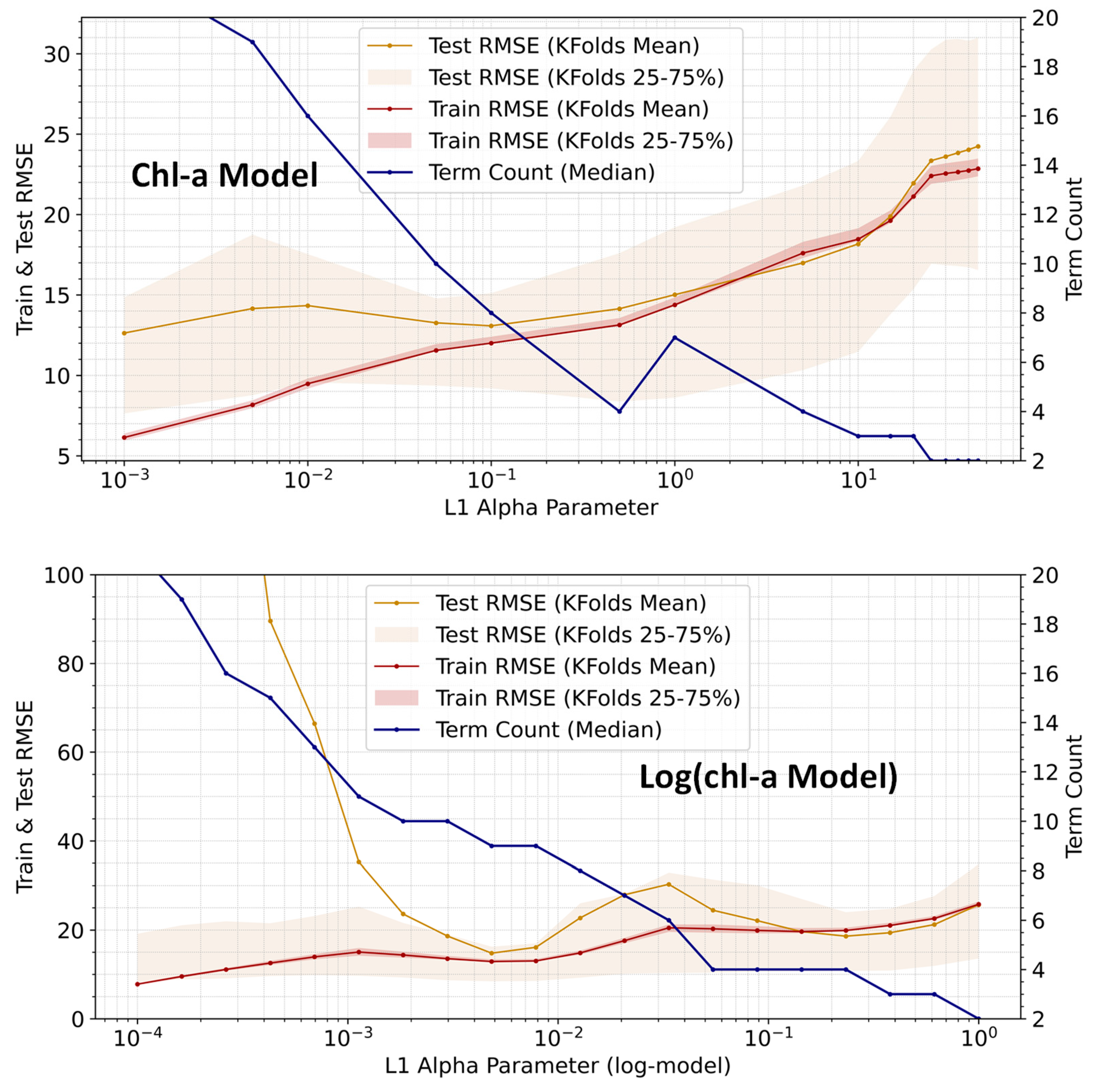
3.1. Impact of Alpha Selection
3.2. Model Terms and Stability
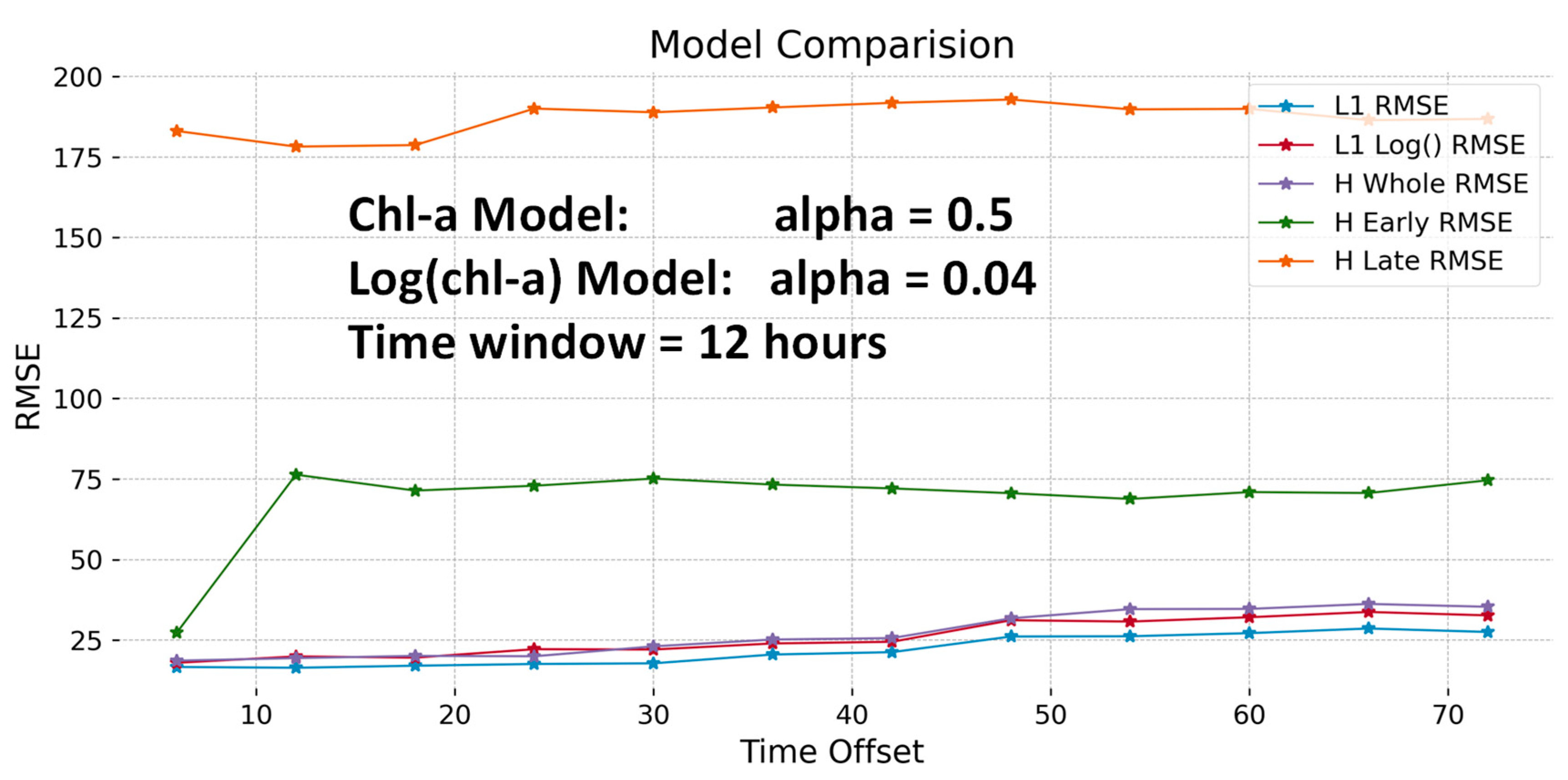
3.3. Impact of Time Coincidence
3.4. Pixel Resolution
3.5. Model Comparisons
3.6. Optically Complex Water and SWIR1
4. Discussion
4.1. L1 Regularization
4.2. Significance of Temporal Coincidence and Spatial Resolution
4.3. Data Engineering and Feature Selection
4.4. Model Creation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sellner, K.G.; Doucette, G.J.; Kirkpatrick, G.J. Harmful algal blooms: Causes, impacts and detection. J. Ind. Microbiol. Biotechnol. 2003, 30, 383–406. [Google Scholar] [CrossRef]
- Kloiber, S.M.; Brezonik, P.L.; Olmanson, L.G.; Bauer, M.E. A procedure for regional lake water clarity assessment using Landsat multispectral data. Remote Sens. Environ. 2002, 82, 38–47. [Google Scholar] [CrossRef]
- Fuller, L.M.; Aichele, S.S.; Minnerick, R.J. Predicting Water Quality by Relating Secchi-Disk Transparency and CHLORophyll a Measurements to Satellite Imagery for Michigan Inland Lakes, August 2002; U.S. Geological Survey: Reston, VA, USA, 2004; pp. 2004–5086. [Google Scholar]
- Olmanson, L.G.; Bauer, M.E.; Brezonik, P.L. A 20-year Landsat water clarity census of Minnesota’s 10,000 lakes. Remote Sens. Environ. 2008, 112, 4086–4097. [Google Scholar] [CrossRef]
- Allan, M.G.; Hamilton, D.P.; Hicks, B.; Brabyn, L. Empirical and semi-analytical chlorophyll a algorithms for multi-temporal monitoring of New Zealand lakes using Landsat. Environ. Monit. Assess. 2015, 187, 1–24. [Google Scholar] [CrossRef]
- Brezonik, P.; Menken, K.D.; Bauer, M. Landsat-Based Remote Sensing of Lake Water Quality Characteristics, Including Chlorophyll and Colored Dissolved Organic Matter (CDOM). Lake Reserv. Manag. 2005, 21, 373–382. [Google Scholar] [CrossRef]
- Brivio, P.A.; Giardino, C.; Zilioli, E. Determination of chlorophyll concentration changes in Lake Garda using an image-based radiative transfer code for Landsat TM images. Int. J. Remote Sens. 2001, 22, 487–502. [Google Scholar] [CrossRef]
- Kutser, T. Quantitative detection of chlorophyll in cyanobacterial blooms by satellite remote sensing. Limnol. Oceanogr. 2004, 49, 2179–2189. [Google Scholar] [CrossRef]
- Mayo, M.; Gitelson, A.; Yacobi, Y.; Ben-Avraham, Z. Chlorophyll distribution in lake Kinneret determined from Landsat Thematic Mapper data. Remote Sens. 1995, 16, 175–182. [Google Scholar] [CrossRef]
- Yip, H.; Johansson, J.; Hudson, J. A 29-year assessment of the water clarity and chlorophyll-a concentration of a large reservoir: Investigating spatial and temporal changes using Landsat imagery. J. Great Lakes Res. 2015, 41, 34–44. [Google Scholar] [CrossRef]
- NASA. Landsat—Earth Observation Satellites; 2015–3081; National Aeronautics and Space Administration: Reston, VA, USA, 2016; p. 4. [Google Scholar]
- Potes, M.; Rodrigues, G.; Penha, A.M.; Novais, M.H.; Costa, M.J.; Salgado, R.; Morais, M.M. Use of Sentinel 2–MSI for water quality monitoring at Alqueva reservoir, Portugal. Proc. IAHS 2018, 380, 73–79. [Google Scholar] [CrossRef]
- Vargas-Lopez, I.A.; Rivera-Monroy, V.H.; Day, J.W.; Whitbeck, J.; Maiti, K.; Madden, C.J.; Trasviña-Castro, A. Assessing chlorophyll a spatiotemporal patterns combining in situ continuous fluorometry measurements and Landsat 8/OLI data across the Barataria Basin (Louisiana, USA). Water 2021, 13, 512. [Google Scholar] [CrossRef]
- Hansen, C.H.; Burian, S.J.; Dennison, P.E.; Williams, G.P. Spatiotemporal variability of lake water quality in the context of remote sensing models. Remote Sens. 2017, 9, 409. [Google Scholar] [CrossRef]
- Hansen, C.H.; Williams, G.P. Evaluating remote sensing model specification methods for estimating water quality in optically diverse lakes throughout the growing season. Hydrology 2018, 5, 62. [Google Scholar] [CrossRef]
- Carder, K.L.; Chen, F.; Lee, Z.; Hawes, S.; Kamykowski, D. Semianalytic Moderate-Resolution Imaging Spectrometer algorithms for chlorophyll a and absorption with bio-optical domains based on nitrate-depletion temperatures. J. Geophys. Res. Ocean. 1999, 104, 5403–5421. [Google Scholar] [CrossRef]
- Garver, S.A.; Siegel, D.A. Inherent optical property inversion of ocean color spectra and its biogeochemical interpretation: 1. Time series from the Sargasso Sea. J. Geophys. Res. Ocean. 1997, 102, 18607–18625. [Google Scholar] [CrossRef]
- Peterson, K.T.; Sagan, V.; Sloan, J.J. Deep learning-based water quality estimation and anomaly detection using Landsat-8/Sentinel-2 virtual constellation and cloud computing. GIScience Remote Sens. 2020, 57, 510–525. [Google Scholar] [CrossRef]
- Sagan, V.; Peterson, K.T.; Maimaitijiang, M.; Sidike, P.; Sloan, J.; Greeling, B.A.; Maalouf, S.; Adams, C. Monitoring inland water quality using remote sensing: Potential and limitations of spectral indices, bio-optical simulations, machine learning, and cloud computing. Earth-Sci. Rev. 2020, 205, 103187. [Google Scholar] [CrossRef]
- Hafeez, S.; Wong, M.S.; Ho, H.C.; Nazeer, M.; Nichol, J.; Abbas, S.; Tang, D.; Lee, K.H.; Pun, L. Comparison of machine learning algorithms for retrieval of water quality indicators in case-II waters: A case study of Hong Kong. Remote Sens. 2019, 11, 617. [Google Scholar] [CrossRef]
- Cao, Z.; Ma, R.; Duan, H.; Pahlevan, N.; Melack, J.; Shen, M.; Xue, K. A machine learning approach to estimate chlorophyll-a from Landsat-8 measurements in inland lakes. Remote Sens. Environ. 2020, 248, 111974. [Google Scholar] [CrossRef]
- Hansen, C.H.; Burian, S.J.; Dennison, P.E.; Williams, G.P. Evaluating historical trends and influences of meteorological and seasonal climate conditions on lake chlorophyll a using remote sensing. Lake Reserv. Manag. 2019, 36, 45–63. [Google Scholar] [CrossRef]
- Hansen, C.H.; Williams, G.P.; Adjei, Z.; Barlow, A.; Nelson, E.J.; Miller, A.W. Reservoir water quality monitoring using remote sensing with seasonal models: Case study of five central-Utah reservoirs. Lake Reserv. Manag. 2015, 31, 225–240. [Google Scholar] [CrossRef]
- Efron, B.; Hastie, T.; Johnstone, I.; Tibshirani, R. Least angle regression. Ann. Stat. 2004, 32, 407–499. [Google Scholar] [CrossRef]
- Le, C.; Li, Y.; Zha, Y.; Wang, Q.; Zhang, H.; Yin, B. Remote sensing of phycocyanin pigment in highly turbid inland waters in Lake Taihu, China. Int. J. Remote Sens. 2011, 32, 8253–8269. [Google Scholar] [CrossRef]
- Gons, H.J. Optical Teledetection of Chlorophyllain Turbid Inland Waters. Environ. Sci. Technol. 1999, 33, 1127–1132. [Google Scholar] [CrossRef]
- Hansen, C.H.; Williams, G.P.; Adjei, Z. Long-Term Application of Remote Sensing Chlorophyll Detection Models: Jordanelle Reservoir Case Study. Nat. Resour. 2015, 06, 123–129. [Google Scholar] [CrossRef]
- Tanner, K.B.; Cardall, A.C.; Williams, G.P. A Spatial Long-Term Trend Analysis of Estimated Chlorophyll-a Concentrations in Utah Lake Using Earth Observation Data. Remote Sens. 2022, 14, 3664. [Google Scholar] [CrossRef]
- Bertani, I.; Steger, C.E.; Obenour, D.R.; Fahnenstiel, G.L.; Bridgeman, T.B.; Johengen, T.H.; Sayers, M.J.; Shuchman, R.A.; Scavia, D. Tracking cyanobacteria blooms: Do different monitoring approaches tell the same story? Sci. Total Environ. 2017, 575, 294–308. [Google Scholar] [CrossRef]
- Tate, R.S. Landsat Collections Reveal Long-Term Algal Bloom Hot Spots of Utah Lake. Master’s Thesis, Brigham Young University, Provo, UT, USA, 2019. [Google Scholar]
- Pettersson, L.H.; Pozdnyakov, D. Potential of remote sensing for identification, delineation, and monitoring of harmful algal blooms. In Monitoring of Harmful Algal Blooms; Springer: New York, NY, USA, 2013; pp. 49–111. [Google Scholar]
- Buitinck, L.; Louppe, G.; Blondel, M.; Pedregosa, F.; Mueller, A.; Grisel, O.; Niculae, V.; Prettenhofer, P.; Gramfort, A.; Grobler, J. API design for machine learning software: Experiences from the scikit-learn project. arXiv 2013, arXiv:1309.0238. [Google Scholar]
- Meinshausen, N.; Bühlmann, P. Stability selection. J. R. Stat. Soc. Ser. B Stat. Methodol. 2010, 72, 417–473. [Google Scholar] [CrossRef]
- Bühlmann, P.; Van De Geer, S. Statistics for High-Dimensional Data: Methods, Theory and Applications; Springer Science & Business Media: New York, NY, USA, 2011. [Google Scholar]
- Nelson, S.A.C.; Soranno, P.A.; Cheruvelil, K.S.; Batzli, S.A.; Skole, D.L. Regional assessment of lake water clarity using satellite remote sensing. J. Limnol. 2003, 62, 27. [Google Scholar] [CrossRef]
- Merritt, L.B.; Miller, A.W. Interim Report on Nutrient Loadings to Utah Lake: 2016; Jordan River, Farmington Bay & Utah Lake Water Quality Council: Provo, UT, USA, 2016. [Google Scholar]
- Cardall, A.; Tanner, K.B.; Williams, G.P. Google Earth Engine Tools for Long-Term Spatiotemporal Monitoring of Chlorophyll-a Concentrations. Open Water J. 2021, 7, 4. [Google Scholar]
- Masek, J.G.; Vermote, E.F.; Saleous, N.E.; Wolfe, R.; Hall, F.G.; Huemmrich, K.F.; Feng, G.; Kutler, J.; Teng-Kui, L. A Landsat surface reflectance dataset for North America, 1990–2000. IEEE Geosci. Remote Sens. Lett. 2006, 3, 68–72. [Google Scholar] [CrossRef]
- Vermote, E.; Justice, C.; Claverie, M.; Franch, B. Preliminary analysis of the performance of the Landsat 8/OLI land surface reflectance product. Remote Sens. Environ. 2016, 185, 46–56. [Google Scholar] [CrossRef] [PubMed]
- Kou, L.; Labrie, D.; Chylek, P. Refractive indices of water and ice in the 0.65-to 2.5-μm spectral range. Appl. Opt. 1993, 32, 3531–3540. [Google Scholar] [CrossRef] [PubMed]
- Smith, B.; Pahlevan, N.; Schalles, J.; Ruberg, S.; Errera, R.; Ma, R.; Giardino, C.; Bresciani, M.; Barbosa, C.; Moore, T.; et al. A Chlorophyll-a Algorithm for Landsat-8 Based on Mixture Density Networks. Front. Remote Sens. 2021, 1, 623678. [Google Scholar] [CrossRef]
- Matthews, M.W. A current review of empirical procedures of remote sensing in inland and near-coastal transitional waters. Int. J. Remote Sens. 2011, 32, 6855–6899. [Google Scholar] [CrossRef]
- Hansen, C.; Swain, N.; Munson, K.; Adjei, Z.; Williams, G.P.; Miller, W. Development of sub-seasonal remote sensing chlorophyll-a detection models. Am. J. Plant Sci. 2013, 4, 21–26. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Wainwright, M. Statistical Learning with Sparsity; CRC Press; Taylor and Francis Group: Boca Raton, FL, USA, 2015; Volume 143. [Google Scholar]






| Characteristic Name | N | Mean | Median | Max. | Min. | Std. Dev | Skew | Kurt. |
|---|---|---|---|---|---|---|---|---|
| Depth, Secchi disk (m) | 3083 | 0.27 | 0.25 | 7.00 | 0.00 | 0.21 | 15.29 | 402.48 |
| Turbidity (NTU) | 683 | 62.30 | 41.60 | 790.00 | 0.10 | 89.12 | 5.31 | 33.68 |
| Total suspended solids (mg/L) | 1281 | 63.26 | 45.00 | 900.00 | 1.00 | 75.46 | 5.20 | 38.85 |
| Total dissolved solids (mg/L) | 1061 | 1016.94 | 1000.00 | 2340.00 | 106.00 | 281.45 | 0.26 | 0.78 |
| Total volatile solids (mg/L) | 716 | 12.30 | 9.00 | 110.00 | 2.00 | 11.09 | 3.40 | 18.40 |
| Specific conductance (µmho/cm) | 6614 | 1758.35 | 1772.15 | 20,980.0 | 0.00 | 501.40 | 14.41 | 539.50 |
| Calcium (mg/L) | 1058 | 62.59 | 59.00 | 213.00 | 24.50 | 21.93 | 3.35 | 13.98 |
| Hardness, Ca, Mg (mg/L) | 715 | 413.27 | 406.40 | 898.50 | 137.20 | 94.67 | 1.70 | 5.04 |
| Carbonate (mg/L) | 690 | 2.89 | N/A | 123.00 | 0.00 | 6.26 | 10.70 | 195.91 |
| Chlorophyll a, (µg/L) | 821 | 40.51 | 21.30 | 597.50 | 0.20 | 58.84 | 3.92 | 21.76 |
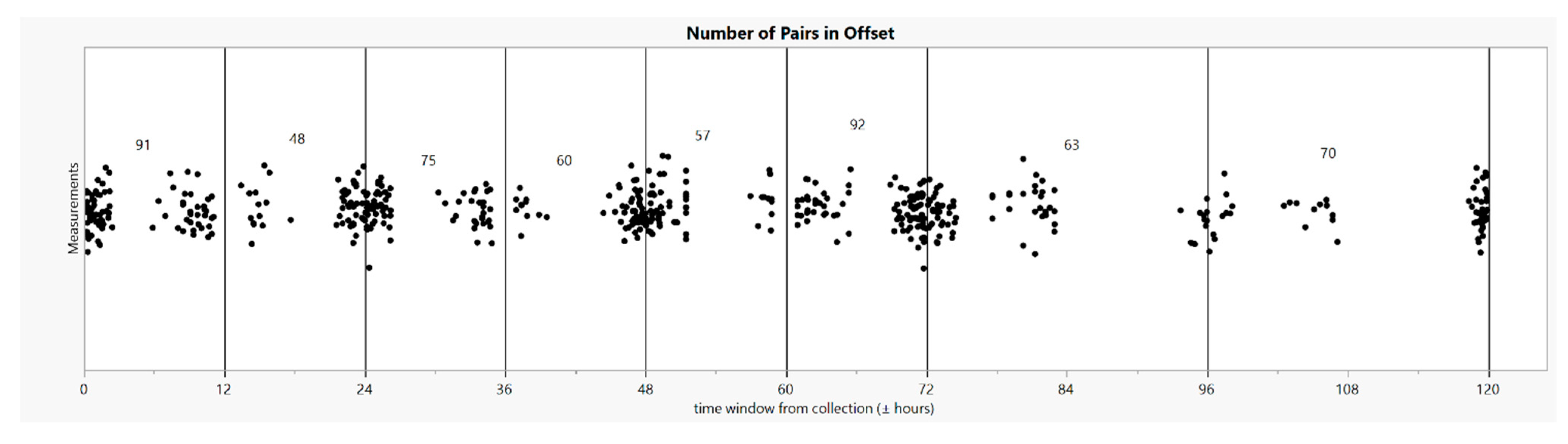
| Offset (Hours) | N | Mean | Median | Std Dev | Cumulative N | Cum. Mean | Cum. Std Dev |
|---|---|---|---|---|---|---|---|
| 0–12 | 91 | 32.84 | 16.6 | 60.37 | 91 | 32.84 | 60.37 |
| 12–24 | 48 | 31.06 | 11.35 | 73.12 | 139 | 32.23 | 65.03 |
| 24–36 | 75 | 32.94 | 15.16 | 46.42 | 214 | 32.48 | 59.17 |
| 36–48 | 60 | 44.24 | 31.75 | 48.33 | 274 | 35.05 | 56.98 |
| 48–60 | 57 | 28.87 | 11.5 | 37.21 | 331 | 33.99 | 54.10 |
| 60–72 | 92 | 33.62 | 23.35 | 35.28 | 423 | 33.91 | 50.59 |
| 72–96 | 63 | 44.74 | 21.30 | 57.57 | 486 | 35.31 | 51.55 |
| 96–120 | 70 | 48.00 | 21.62 | 69.72 | 556 | 36.91 | 54.17 |
| All | 556 | 36.91 | 17.75 | 54.25 | N/A | 36.91 | 54.25 |
| Band Name | Satellite Bands | ||
|---|---|---|---|
| Landsat 8 | Landsat 7 | Landsat 5 | |
| Blue | SR_B2 | SR_B1 | SR_B1 |
| green | SR_B3 | SR_B2 | SR_B2 |
| red | SR_B4 | SR_B3 | SR_B3 |
| NIR 1 | SR_B5 | SR_B4 | SR_B4 |
| SWIR1 2 | SR_B6 | SR_B5 | SR_B5 |
| SWIR2 2 | SR_B7 | SR_B7 | SR_B7 |
| SurfTempK 3 | ST_B10 | ST_B6 | ST_B6 |
| Chl-a Model | Chl-a Model | Chl-a Model | Log(chl-a) Model | Log(chl-a) Model | Log(chl-a) Model |
|---|---|---|---|---|---|
| Alpha (α) | Number of Terms | RMSE | Alpha (α) | Number of Terms | RMSE |
| 0.005 | 22 | 25.46 | 0.0001 | 23 | 36.89 |
| 0.01 | 20 | 25.82 | 0.0002 | 20 | 36.35 |
| 0.05 | 16 | 26.69 | 0.0005 | 19 | 35.69 |
| 0.1 | 12 | 27.24 | 0.0010 | 14 | 35.96 |
| 0.5 | 8 | 27.52 | 0.0022 | 11 | 35.81 |
| 1 | 8 | 27.89 | 0.0046 | 10 | 35.73 |
| 5 | 4 | 31.10 | 0.0100 | 10 | 37.31 |
| 10 | 3 | 31.32 | 0.0215 | 9 | 42.32 |
| 25 | 3 | 31.94 | 0.0464 | 8 | 53.91 |
| 50 | 2 | 32.61 | 0.1000 | 7 | 64.34 |
| Window Size (Hours) | # of Data Pairs | RMSE (chla) | RMSE (log(chla)) |
|---|---|---|---|
| 6 | 55 | 11.67 | 11.09 |
| 12 | 85 | 10.78 | 16.99 |
| 18 | 99 | 12.12 | 16.52 |
| 24 | 123 | 15.80 | 20.54 |
| 30 | 168 | 17.44 | 23.12 |
| 36 | 193 | 19.55 | 22.98 |
| 42 | 202 | 20.98 | 25.24 |
| 48 | 249 | 26.04 | 33.53 |
| 54 | 290 | 26.07 | 33.37 |
| 60 | 300 | 26.22 | 33.63 |
| 66 | 328 | 28.38 | 35.87 |
| 72 | 388 | 27.40 | 34.45 |
| Window Size (Hours) | 30 m # Data Pairs | 30 m Test RMSE | 90 m # Data Pairs | 90 m Test RMSE |
|---|---|---|---|---|
| 6 | 55 | 11.67 | 55 | 12.45 |
| 12 | 85 | 10.78 | 86 | 15.82 |
| 18 | 99 | 12.12 | 99 | 15.76 |
| 24 | 123 | 15.80 | 126 | 20.23 |
| 30 | 168 | 17.44 | 173 | 25.46 |
| 36 | 193 | 19.55 | 198 | 21.94 |
| 42 | 202 | 20.98 | 209 | 24.23 |
| 48 | 249 | 26.04 | 258 | 32.71 |
| 54 | 290 | 26.07 | 304 | 32.58 |
| 60 | 300 | 26.22 | 318 | 33.33 |
| 66 | 328 | 28.38 | 349 | 36.56 |
| 72 | 388 | 27.40 | 411 | 35.14 |
| Alpha | 30 m Chl-a | 30 m Chl-a | 90 m Chl-a | 90 m Chl-a |
|---|---|---|---|---|
| Values (α) | Number of Terms | RMSE | Number of Terms | RMSE |
| 0.005 | 20 | 8.45 | 17 | 9.44 |
| 0.01 | 18 | 9.73 | 15 | 10.90 |
| 0.05 | 11 | 11.72 | 10 | 12.25 |
| 0.1 | 8 | 12.15 | 8 | 12.53 |
| 0.5 | 4 | 13.15 | 6 | 13.54 |
| 1 | 7 | 14.61 | 5 | 13.74 |
| 5 | 4 | 17.68 | 4 | 15.21 |
| 10 | 3 | 18.50 | 3 | 16.44 |
| 25 | 2 | 22.54 | 3 | 21.39 |
| 50 | 2 | 23.01 | 2 | 22.74 |
| Alpha (α) | 30 m Log(chl-a) | 30 m Log(chl-a) | 90 m Log(chl-a) | 90 m Log(chl-a) |
|---|---|---|---|---|
| Values | Number of Terms | RMSE | Number of Terms | RMSE |
| 0.0001 | 22 | 55.76 | 20 | 53.47 |
| 0.0002 | 18 | 54.96 | 18 | 52.83 |
| 0.0005 | 15 | 54.39 | 14 | 51.88 |
| 0.0010 | 10 | 54.52 | 11 | 51.17 |
| 0.0022 | 10 | 54.48 | 7 | 50.87 |
| 0.0046 | 10 | 54.73 | 8 | 51.58 |
| 0.0100 | 9 | 56.04 | 7 | 52.86 |
| 0.0215 | 7 | 59.74 | 5 | 55.55 |
| 0.0464 | 4 | 59.87 | 4 | 60.24 |
| 0.1000 | 4 | 57.41 | 4 | 56.61 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cardall, A.C.; Hales, R.C.; Tanner, K.B.; Williams, G.P.; Markert, K.N. LASSO (L1) Regularization for Development of Sparse Remote-Sensing Models with Applications in Optically Complex Waters Using GEE Tools. Remote Sens. 2023, 15, 1670. https://doi.org/10.3390/rs15061670
Cardall AC, Hales RC, Tanner KB, Williams GP, Markert KN. LASSO (L1) Regularization for Development of Sparse Remote-Sensing Models with Applications in Optically Complex Waters Using GEE Tools. Remote Sensing. 2023; 15(6):1670. https://doi.org/10.3390/rs15061670
Chicago/Turabian StyleCardall, Anna Catherine, Riley Chad Hales, Kaylee Brooke Tanner, Gustavious Paul Williams, and Kel N. Markert. 2023. "LASSO (L1) Regularization for Development of Sparse Remote-Sensing Models with Applications in Optically Complex Waters Using GEE Tools" Remote Sensing 15, no. 6: 1670. https://doi.org/10.3390/rs15061670
APA StyleCardall, A. C., Hales, R. C., Tanner, K. B., Williams, G. P., & Markert, K. N. (2023). LASSO (L1) Regularization for Development of Sparse Remote-Sensing Models with Applications in Optically Complex Waters Using GEE Tools. Remote Sensing, 15(6), 1670. https://doi.org/10.3390/rs15061670








