Global Water Quality of Inland Waters with Harmonized Landsat-8 and Sentinel-2 Using Cloud-Computed Machine Learning
Abstract
1. Introduction
2. Materials and Methods
2.1. Sources of Global Water Quality Dataset
2.2. Field Dataset Compliance by Lake Selection, Satellite Coincidence and Data Curation
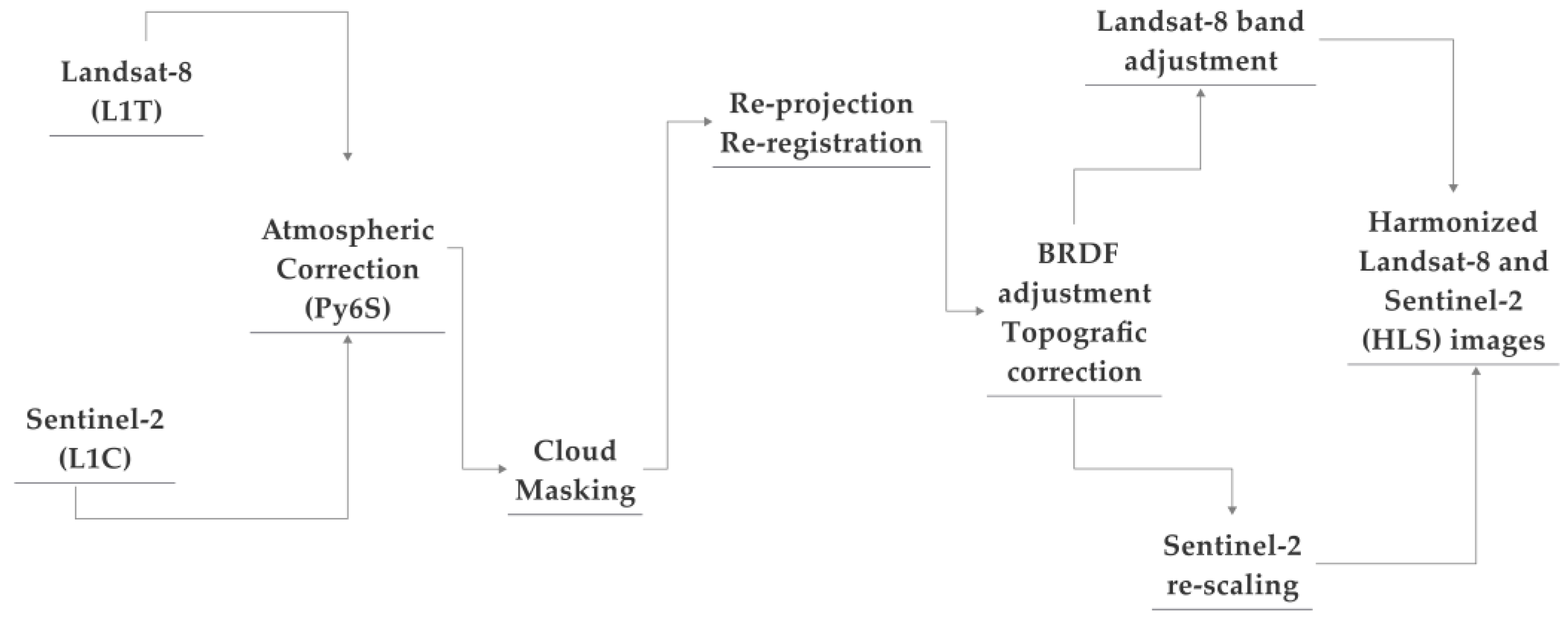
2.3. Harmonization of Landsat-8 and Sentinel-2 Data
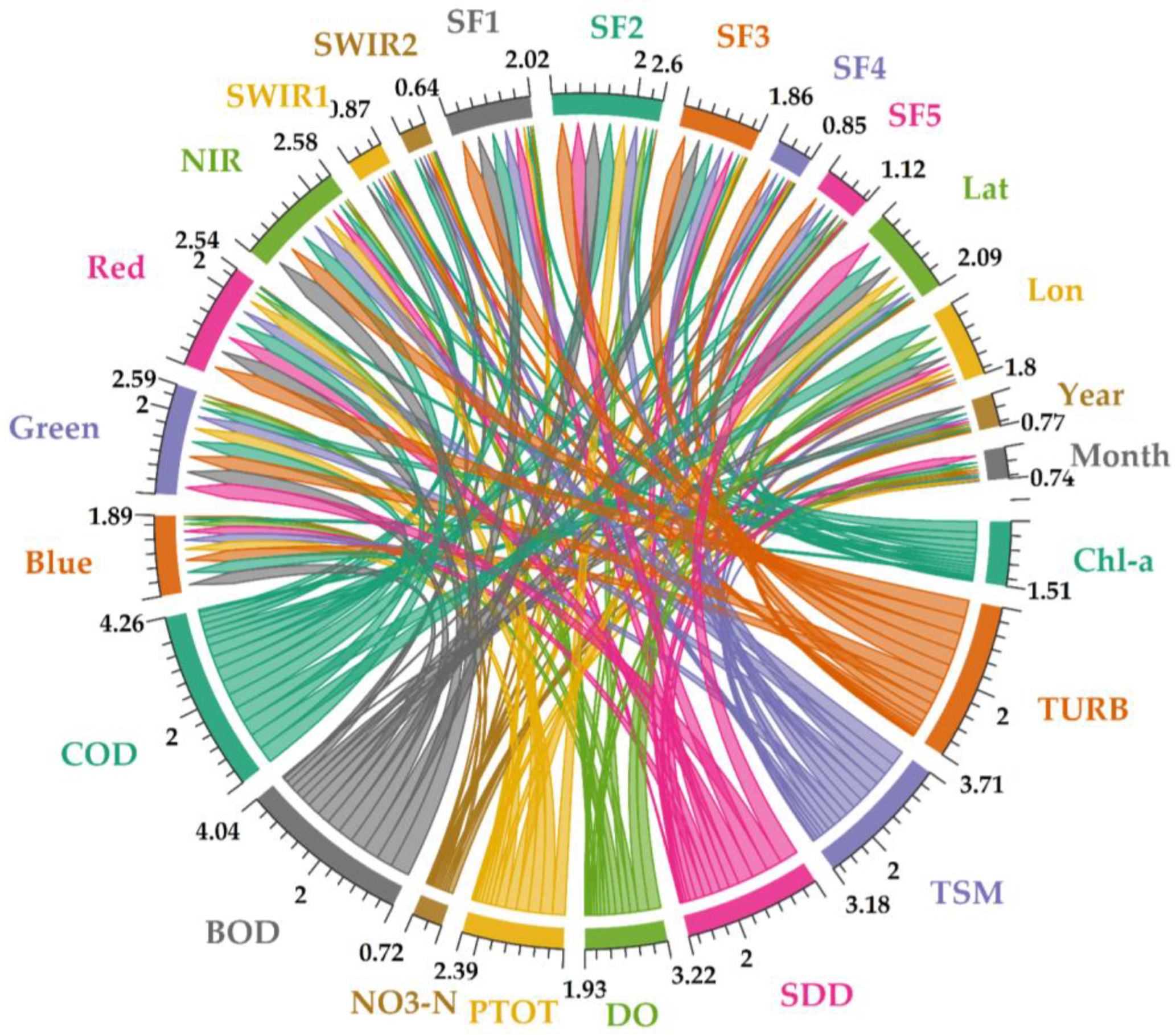
2.4. Feature Engineering and Dataset Arrangement
2.5. Machine Learning Algorithms
2.6. Model Evaluation
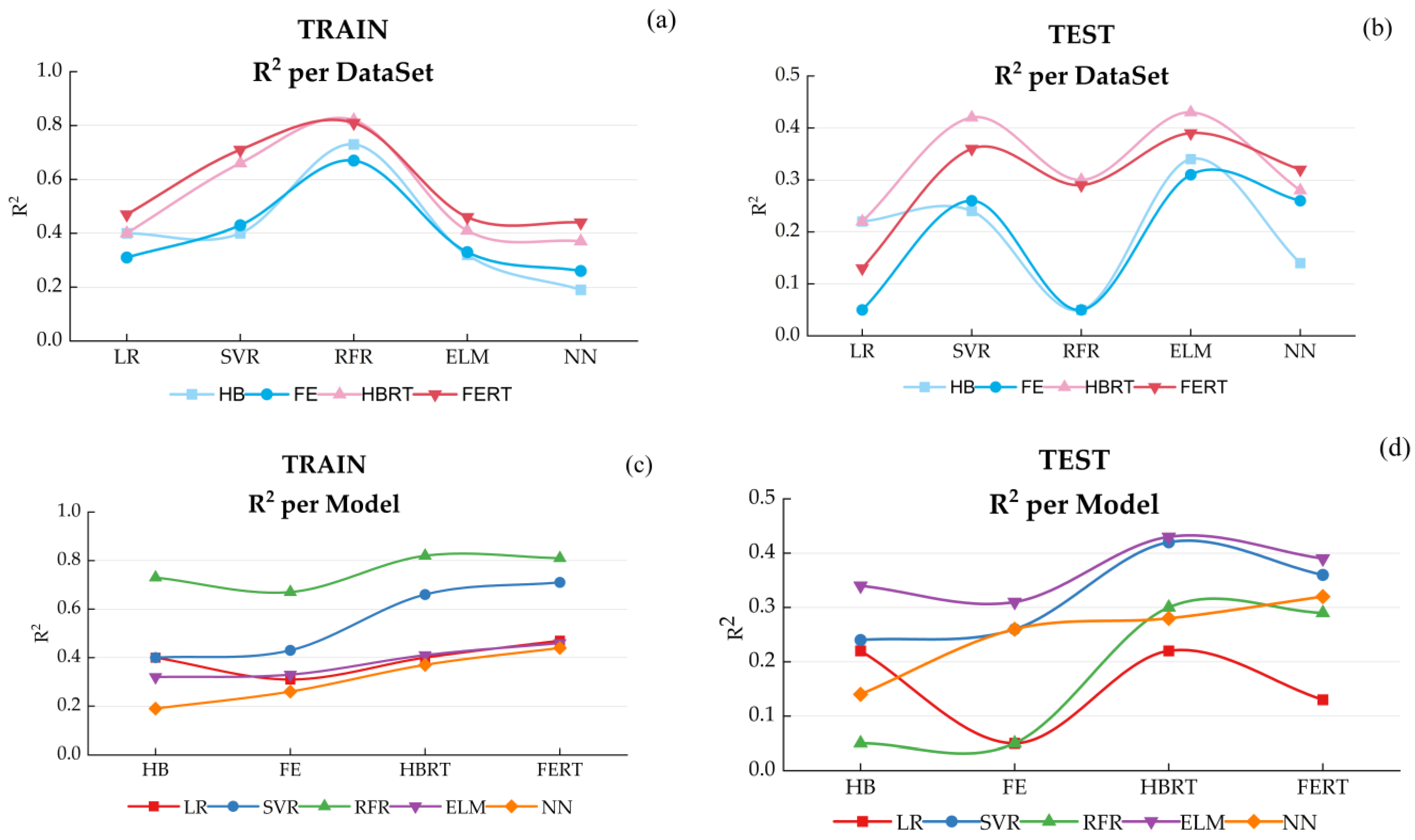
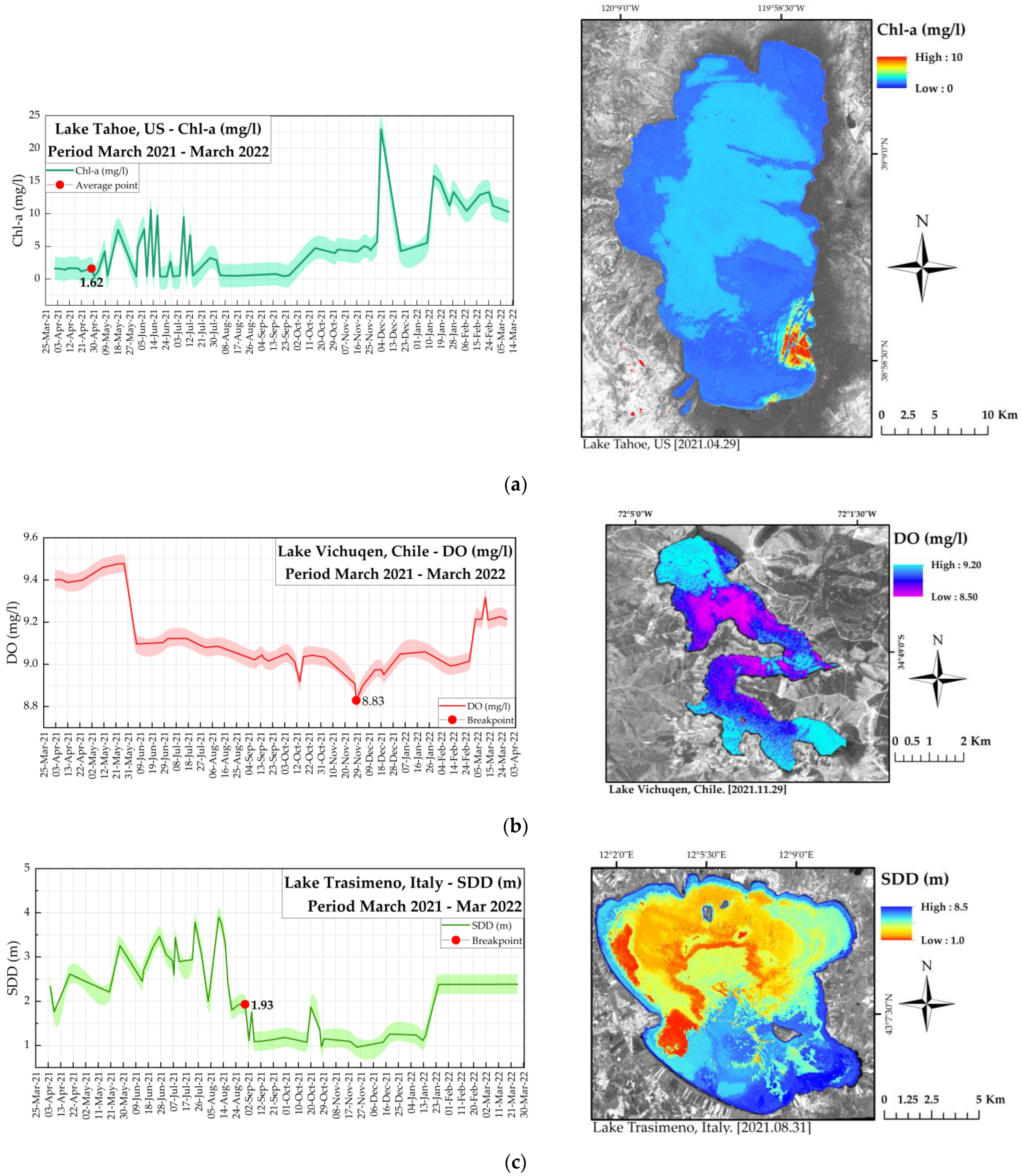
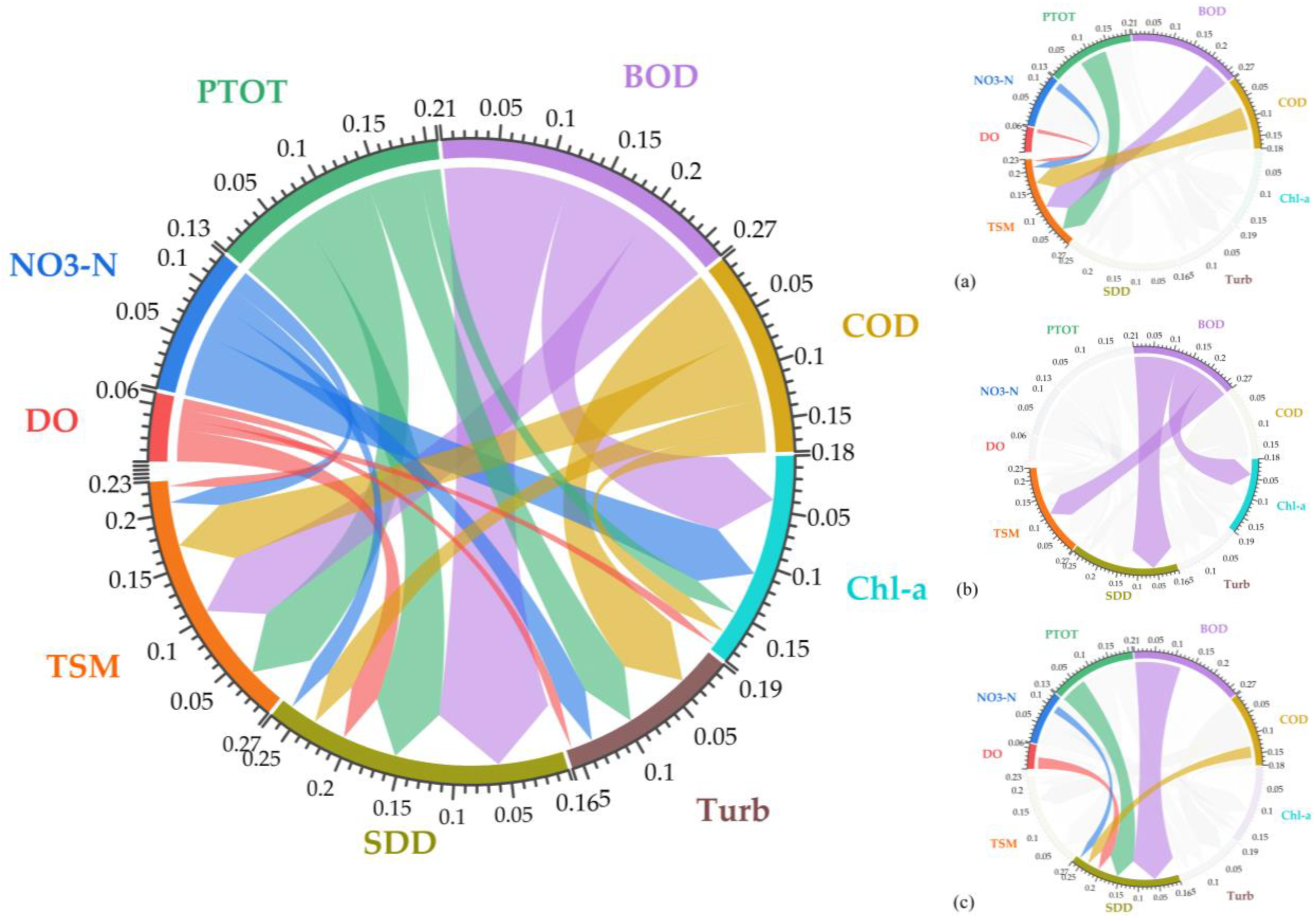
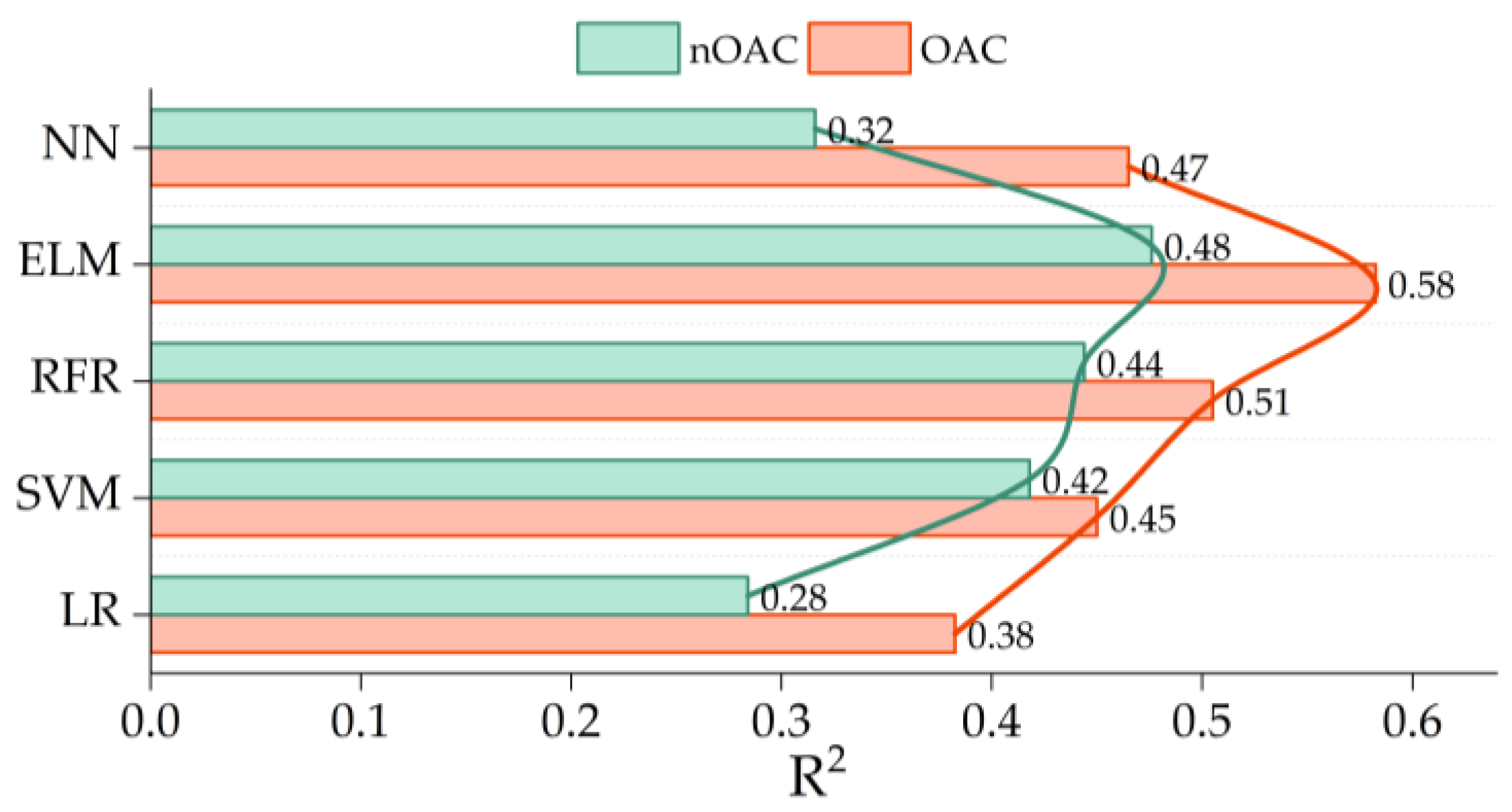
3. Results
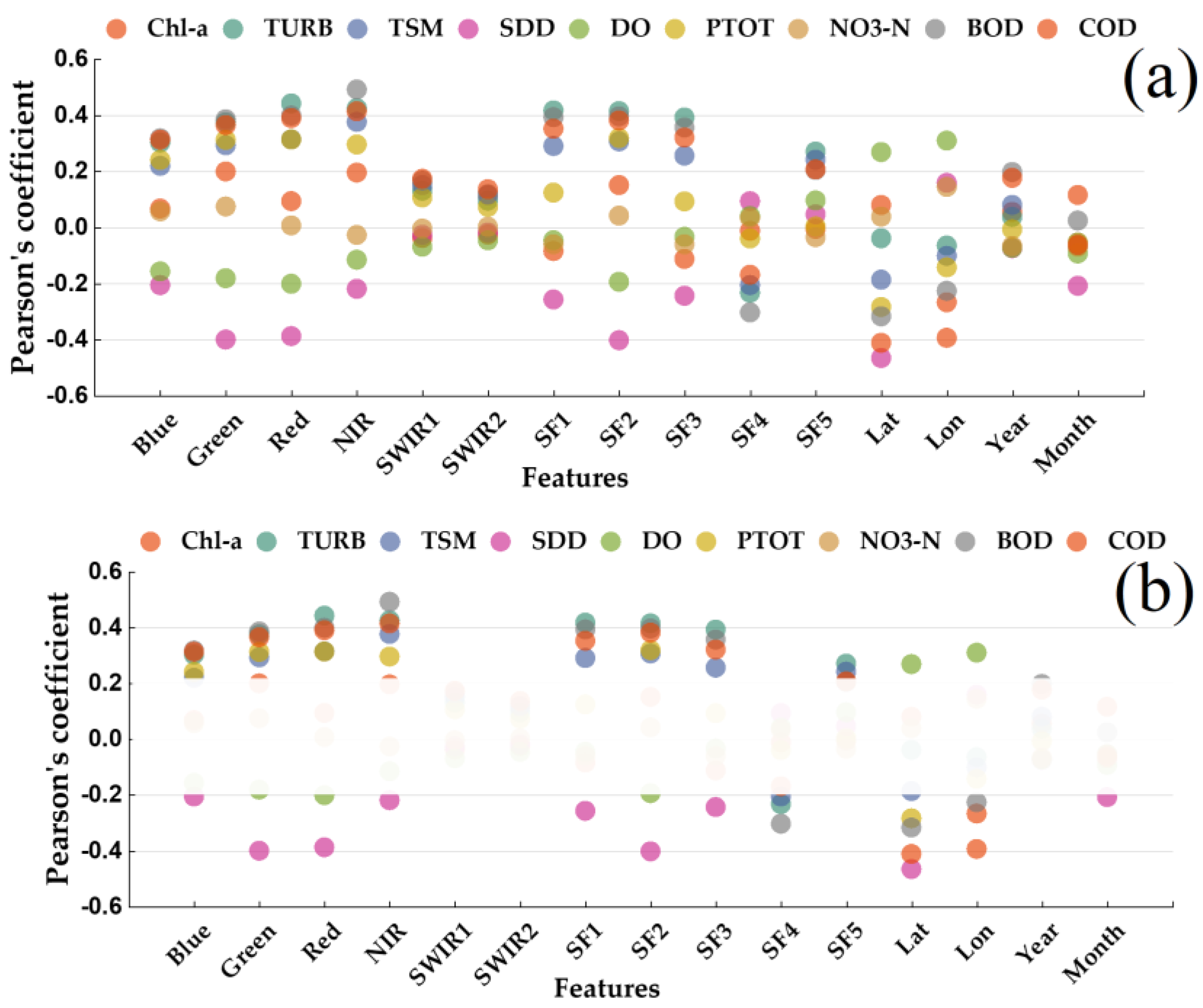
3.1. Correlation of Water Parameters and Derived Predictors
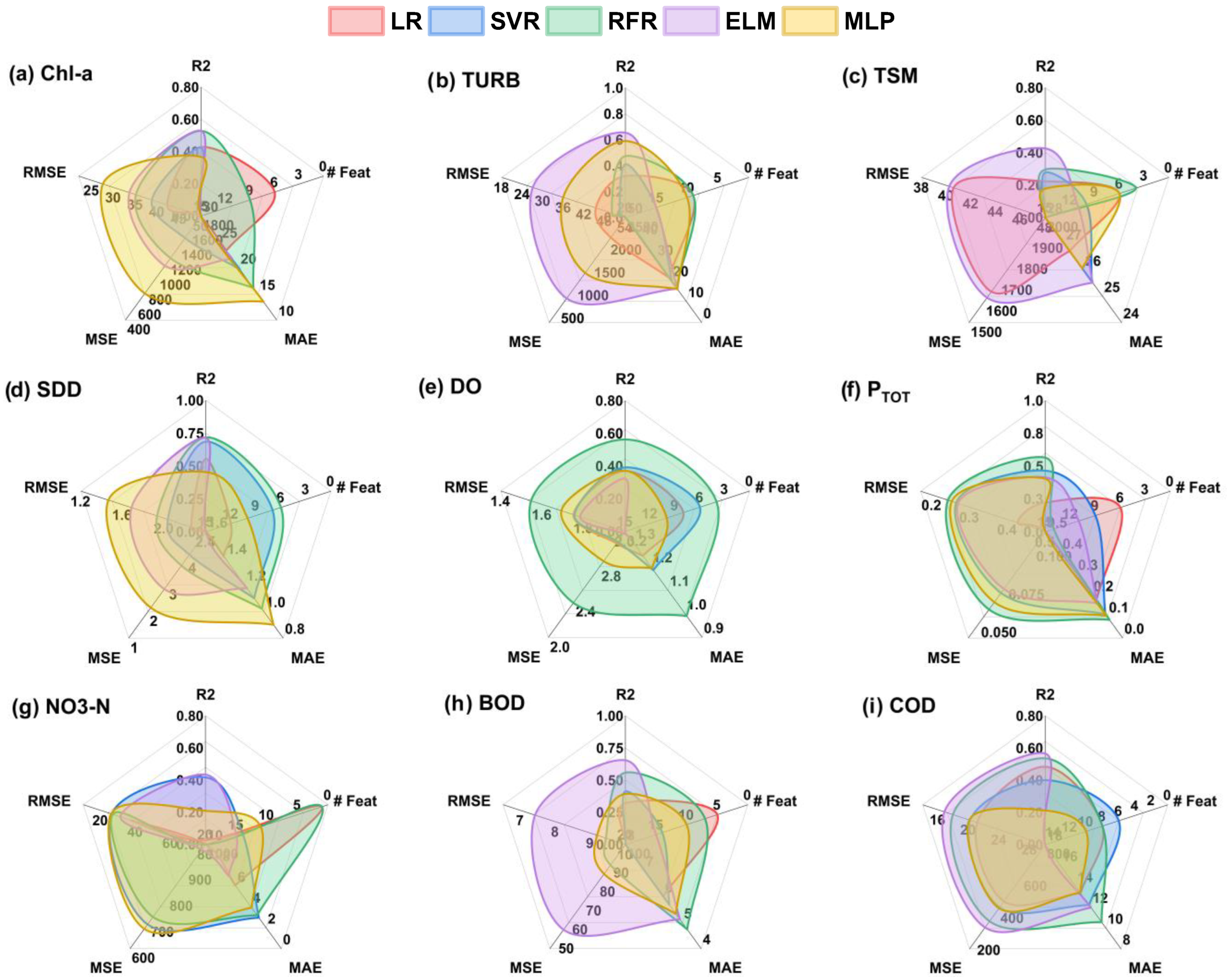
3.2. Model and Dataset Evaluation
3.3. Model Capabilities
3.4. Correlation between OAC and nOAC
4. Discussion
4.1. Global Water Quality Data Availability
4.2. Harmonized Remote Sensing Data for Water Quality Estimation
4.3. Machine Learning Models and Cloud Computing
4.4. Estimation of OAC and nOAC
4.5. Inherent Lakes’ Characteristics as Model Improvers
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- UNEP. A Snapshot of the World’s Water Quality: Towards a Global Assessment; United Nations Environment Programme: Nairobi, Kenya, 2016; p. 162. [Google Scholar]
- UNEP. GEMStat 2020. Website Data Portal. Available online: https://gemstat.bafg.de/applications/public.html?publicuser=PublicUser#gemstat/Stations (accessed on 15 February 2021).
- Anon. An Integrated Water-Monitoring Network for Wisconsin; G.S.U. Water Resources Center, Ed.; University of Wisconsin: Madison, WI, USA, 1998. [Google Scholar]
- EPA. Elements of a State Water Monitoring and Assessment Program; Environmental Protection Agency, Assessment and Watershed Protection Division, Office of Wetlands, Oceans and Watershed: Washington, DC, USA, 2001.
- Gholizadeh, M.H.; Melesse, A.M.; Reddi, L. A Comprehensive Review on Water Quality Parameters Estimation Using Remote Sensing Techniques. Sensors 2016, 16, 1298. [Google Scholar] [CrossRef]
- Matthews, M.W. A current review of empirical procedures of remote sensing in inland and near-coastal transitional waters. Int. J. Remote Sens. 2011, 32, 6855–6899. [Google Scholar] [CrossRef]
- Giardino, C.; Brando, V.E.; Gege, P.; Pinnel, N.; Hochberg, E.; Knaeps, E.; Reusen, I.; Doerffer, R.; Bresciani, M.; Braga, F.; et al. Imaging Spectrometry of Inland and Coastal Waters: State of the Art, Achievements and Perspectives. Surv. Geophys. 2019, 40, 401–429. [Google Scholar] [CrossRef]
- Doxaran, D.; Froidefond, J.M.; Lavender, S.; Castaing, P. Spectral signature of highly turbid waters: Application with SPOT data to quantify suspended particulate matter concentrations. Remote Sens. Environ. 2002, 81, 149–161. [Google Scholar] [CrossRef]
- IOCCG. Remote Sensing of Ocean Colour in Coastal, and Other Optically-Complex. In Waters; Sathyendranath, S., Ed.; IOCCG: Dartmouth, NS, Canada, 2000. [Google Scholar]
- Claverie, M.; Ju, J.; Masek, J.G.; Dungan, J.L.; Vermote, E.F.; Roger, J.-C.; Skakun, S.V.; Justice, C. The Harmonized Landsat and Sentinel-2 surface reflectance data set. Remote Sens. Environ. 2018, 219, 145–161. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, R.; Duan, H.; Loiselle, S.; Xu, J. A Spectral Decomposition Algorithm for Estimating Chlorophyll-a Concentrations in Lake Taihu, China. Remote Sens. 2014, 6, 5090–5106. [Google Scholar] [CrossRef]
- Bonansea, M.; Rodriguez, M.C.; Pinotti, L.; Ferrero, S. Using multi-temporal Landsat imagery and linear mixed models for assessing water quality parameters in Río Tercero reservoir (Argentina). Remote Sens. Environ. 2015, 158, 28–41. [Google Scholar] [CrossRef]
- Peterson, K.T.; Sagan, V.; Sidike, P.; Cox, A.L.; Martinez, M. Suspended Sediment Concentration Estimation from Landsat Imagery along the Lower Missouri and Middle Mississippi Rivers Using an Extreme Learning Machine. Remote Sens. 2018, 10, 1503. [Google Scholar] [CrossRef]
- Peterson, K.T.; Sagan, V.; Sloan, J.J. Deep learning-based water quality estimation and anomaly detection using Landsat-8/Sentinel-2 virtual constellation and cloud computing. GISci. Remote Sens. 2020, 57, 510–525. [Google Scholar] [CrossRef]
- Pyo, J.; Cho, K.H.; Kim, K.; Baek, S.-S.; Nam, G.; Park, S. Cyanobacteria cell prediction using interpretable deep learning model with observed, numerical, and sensing data assemblage. Water Res. 2021, 203, 117483. [Google Scholar] [CrossRef]
- He, J.; Chen, Y.; Wu, J.; Stow, D.A.; Christakos, G. Space-time chlorophyll-a retrieval in optically complex waters that accounts for remote sensing and modeling uncertainties and improves remote estimation accuracy. Water Res. 2020, 171, 115403. [Google Scholar] [CrossRef]
- Chen, K.; Chen, H.; Zhou, C.; Huang, Y.; Qi, X.; Shen, R.; Liu, F.; Zuo, M.; Zou, X.; Wang, J.; et al. Comparative analysis of surface water quality prediction performance and identification of key water parameters using different machine learning models based on big data. Water Res. 2020, 171, 115454. [Google Scholar] [CrossRef]
- Chen, Y.; Arnold, W.A.; Griffin, C.G.; Olmanson, L.G.; Brezonik, P.L.; Hozalski, R.M. Assessment of the chlorine demand and disinfection byproduct formation potential of surface waters via satellite remote sensing. Water Res. 2019, 165, 115001. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Wang, X.; Zhao, Z.; Han, S.; Liu, Z. Lagoon water quality monitoring based on digital image analysis and machine learning estimators. Water Res. 2020, 172, 115471. [Google Scholar] [CrossRef] [PubMed]
- Xu, T.; Coco, G.; Neale, M. A predictive model of recreational water quality based on adaptive synthetic sampling algorithms and machine learning. Water Res. 2020, 177, 115788. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, L.; Deng, L.; Ouyang, B. Retrieval of water quality parameters from hyperspectral images using a hybrid feedback deep factorization machine model. Water Res. 2021, 204, 117618. [Google Scholar] [CrossRef] [PubMed]
- Arias-Rodriguez, L.F.; Duan, Z.; Sepúlveda, R.; Martinez-Martinez, S.I.; Disse, M. Monitoring Water Quality of Valle de Bravo Reservoir, Mexico, Using Entire Lifespan of MERIS Data and Machine Learning Approaches. Remote Sens. 2020, 12, 1586. [Google Scholar] [CrossRef]
- Hartling, S.; Sagan, V.; Sidike, P.; Maimaitijiang, M.; Carron, J. Urban tree species classification using a WorldView-2/3 and LiDAR data fusion approach and deep learning. Sensors 2019, 19, 1284. [Google Scholar] [CrossRef] [PubMed]
- Sidike, P.; Sagan, V.; Maimaitijiang, M.; Maimaitiyiming, M.; Shakoor, N.; Burken, J.; Mockler, T.; Fritschi, F.B. dPEN: Deep Progressively Expanded Network for mapping heterogeneous agricultural landscape using WorldView-3 satellite imagery. Remote Sens. Environ. 2019, 221, 756–772. [Google Scholar] [CrossRef]
- Maimaitijiang, M.; Sagan, V.; Sidike, P.; Hartling, S.; Esposito, F.; Fritschi, F.B. Soybean yield prediction from UAV using multimodal data fusion and deep learning. Remote Sens. Environ. 2020, 237, 111599. [Google Scholar] [CrossRef]
- Pahlevan, N.; Smith, B.; Schalles, J.; Binding, C.; Cao, Z.; Ma, R.; Alikas, K.; Kangro, K.; Gurlin, D.; Nguyen, H.; et al. Seamless retrievals of chlorophyll-a from Sentinel-2 (MSI) and Sentinel-3 (OLCI) in inland and coastal waters: A machine-learning approach. Remote Sens. Environ. 2020, 240, 111604. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Du, B. Deep learning for remote sensing data: A technical tutorial on the state of the art. IEEE Geosci. Remote Sens. Mag. 2016, 4, 22–40. [Google Scholar] [CrossRef]
- Ball, J.E.; Anderson, D.T.; Chan Sr, C.S. Comprehensive survey of deep learning in remote sensing: Theories, tools, and challenges for the community. J. Appl. Remote Sens. 2017, 11, 042609. [Google Scholar] [CrossRef]
- Alom, M.Z.; Taha, T.M.; Yakopcic, C.; Westberg, S.; Sidike, P.; Nasrin, M.S.; Hasan, M.; Van Essen, B.C.; Awwal, A.A.S.; Asari, V.K. A State-of-the-Art Survey on Deep Learning Theory and Architectures. Electronics 2019, 8, 292. [Google Scholar] [CrossRef]
- Ma, L.; Liu, Y.; Zhang, X.; Ye, Y.; Yin, G.; Johnson, B.A. Deep learning in remote sensing applications: A meta-analysis and review. ISPRS J. Photogramm. Remote Sens. 2019, 152, 166–177. [Google Scholar] [CrossRef]
- Arias-Rodriguez, L.F.; Duan, Z.; de Jesús Díaz-Torres, J.; Basilio Hazas, M.; Huang, J.; Kumar, B.U.; Tuo, Y.; Disse, M. Integration of Remote Sensing and Mexican Water Quality Monitoring System Using an Extreme Learning Machine. Sensors 2021, 21, 4118. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Sagan, V.; Peterson, K.T.; Maimaitijiang, M.; Sidike, P.; Sloan, J.; Greeling, B.A.; Maalouf, S.; Adams, C. Monitoring inland water quality using remote sensing: Potential and limitations of spectral indices, bio-optical simulations, machine learning, and cloud computing. Earth-Sci. Rev. 2020, 205, 103187. [Google Scholar] [CrossRef]
- Nguyen, M.; Baez-Villanueva, O.; Bui, D.; Nguyen, P.; Ribbe, L. Harmonization of Landsat and Sentinel 2 for Crop Monitoring in Drought Prone Areas: Case Studies of Ninh Thuan (Vietnam) and Bekaa (Lebanon). Remote Sens. 2020, 12, 281. [Google Scholar] [CrossRef]
- Thorslund, J.; van Vliet, M.T. A global dataset of surface water and groundwater salinity measurements from 1980–2019. Sci. Data 2020, 7, 1–11. [Google Scholar] [CrossRef] [PubMed]
- WQP. Water Quality Portal. 2021. Available online: https://www.waterqualitydata.us/wqp_description/ (accessed on 15 January 2022).
- GobMX. Calidad del agua en México. 2021. Available online: https://www.gob.mx/conagua/articulos/calidad-del-agua (accessed on 15 January 2022).
- GobCa. Open Government Portal. 2021. Available online: https://search.open.canada.ca/en/od/ (accessed on 15 January 2022).
- GobChl. Ministerio de Obras Públicas, MOP—Morandé 59, Santiago de Chile. Direccion General de Aguas. Available online: https://dga.mop.gob.cl/servicioshidrometeorologicos/Paginas/default.aspx (accessed on 15 January 2022).
- Bulgarelli, B.; Kiselev, V.; Zibordi, G. Adjacency effects in satellite radiometric products from coastal waters: A theoretical analysis for the northern Adriatic Sea. Appl. Opt. 2017, 53, 1523–1545. [Google Scholar] [CrossRef] [PubMed]
- Lehner, B.; Döll, P. Development and validation of a global database of lakes, reservoirs and wetlands. J. Hydrol. 2004, 296, 1–22. [Google Scholar] [CrossRef]
- Storey, J.; Roy, D.P.; Masek, J.; Gascon, F.; Dwyer, J.; Choate, M. A note on the temporary misregistration of Landsat-8 Operational Land Imager (OLI) and Sentinel-2 Multi Spectral Instrument (MSI) imagery. Remote Sens. Environ. 2016, 186, 121–122. [Google Scholar] [CrossRef]
- Vermote, E.F.; Tanré, D.; Deuze, J.L.; Herman, M.; Morcette, J.-J. Second Simulation of the Satellite Signal in the Solar Spectrum, 6S: An overview. IEEE Trans. Geosci. Remote Sens. 1997, 35, 675–686. [Google Scholar] [CrossRef]
- Wilson, R. Py6S: A Python interface to the 6S radiative transfer model. Comput. Geosci. 2012, 51, 166–171. Available online: http://rtwilson.com/academic/Wilson_2012_Py6S_Paper.pdf (accessed on 15 January 2022). [CrossRef]
- Murphy, S. Atmospheric Correction of Sentinel 2 Imagery in Google Earth Engine Using Py6S. 2018. Available online: https://github.com/samsammurphy/gee-atmcorr-S2 (accessed on 7 August 2021).
- Zupanc, A. Improving Cloud Detection with Machine Learning. 2017. Available online: https://medium.com/sentinel-hub/improving-cloud-detection-with-machine-learning-c09dc5d7cf13 (accessed on 18 August 2021).
- Poortinga, A.; Tenneson, K.; Shapiro, A.; Nquyen, Q.; San Aung, K.; Chishtie, F.; Saah, D. Mapping Plantations in Myanmar by Fusing Landsat-8, Sentinel-2 and Sentinel-1 Data along with Systematic Error Quantification. Remote Sens. 2019, 11, 831. [Google Scholar] [CrossRef]
- Housman, I.W.; Chastain, R.A.; Finco, M.V. An Evaluation of Forest Health Insect and Disease Survey Data and Satellite-Based Remote Sensing Forest Change Detection Methods: Case Studies in the United States. Remote Sens. 2018, 10, 1184. [Google Scholar] [CrossRef]
- Hollstein, A.; Segl, K.; Guanter, L.; Brell, M.; Enesco, M. Ready-to-Use Methods for the Detection of Clouds, Cirrus, Snow, Shadow, Water and Clear Sky Pixels in Sentinel-2 MSI Images. Remote Sens. 2016, 8, 666. [Google Scholar] [CrossRef]
- GEE. Registering Images. 2021. Available online: https://developers.google.com/earth-engine/guides/register (accessed on 24 August 2021).
- Masek, J.; Gao, F.; Wolfe, R. Automated registration and orthorectification package for Landsat and Landsat-like data processing. J. Appl. Remote Sens. 2009, 3, 033515. [Google Scholar] [CrossRef]
- Keys, R. Cubic convolution interpolation for digital image processing. IEEE Trans. Acoust. Speech Signal Process. 1981, 29, 1153–1160. [Google Scholar] [CrossRef]
- GEE. Projections. 2021. Available online: https://developers.google.com/earthengine/guides/projections (accessed on 24 August 2021).
- Roy, D.P.; Zhang, H.K.; Ju, J.; Gomez-Dans, J.L.; Lewis, P.E.; Schaaf, C.B.; Sun, Q.; Li, J.; Huang, H.; Kovalskyy, V. A general method to normalize Landsat reflectance data to nadir BRDF adjusted reflectance. Remote Sens. Environ. 2016, 176, 255–271. [Google Scholar] [CrossRef]
- Roy, D.P.; Li, J.; Zhang, H.K.; Yan, L.; Huang, H.; Li, Z. Examination of Sentinel-2A multi-spectral instrument (MSI) reflectance anisotropy and the suitability of a general method to normalize MSI reflectance to nadir BRDF adjusted reflectance. Remot. Sens. Environ. 2017, 199, 25–38. [Google Scholar] [CrossRef]
- Soenen, S.A.; Peddle, D.R.; Coburn, C.A. SCS+C: A modified Sun-canopy-sensor topographic correction in forested terrain. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2148–2159. [Google Scholar] [CrossRef]
- Chastain, R.; Housman, I.; Goldstein, J.; Finco, M.; Tenneson, K. Empirical cross sensor comparison of Sentinel-2A and 2B MSI, Landsat-8 OLI, and Landsat-7 ETM+ top of atmosphere spectral characteristics over the conterminous United States. Remote Sens. Environ. 2019, 2019, 274–285. [Google Scholar] [CrossRef]
- Dekker, A.; Malthus, T.; Seyhan, E. Quantitative modeling of inland water quality for high-resolution MSS systems. IEEE Trans. Geosci. Remote Sens. 1991, 29, 89–95. [Google Scholar] [CrossRef]
- Doxaran, D.; Froidefond, J.-M.; Castaing, P. Remote-sensing reflectance of turbid sediment-dominated waters. Reduction of sediment type variations and changing illumination conditions effects by use of reflectance ratios. Appl. Opt. 2003, 42, 2623–2634. [Google Scholar] [CrossRef] [PubMed]
- Lathrop, R.G.; Lillesand, T.M. Monitoring water quality and river plume transport in Green Bay, Lake Michigan with SPOT-1 imagery. Photogramm. Eng. Remote Sens. 1989, 55, 349–354. [Google Scholar]
- Odermatt, D.; Gitelson, A.; Brando, V.E.; Schaepman, M. Review of constituent retrieval in optically deep and complex waters from satellite imagery. Remot. Sens. Environ. 2012, 118, 116–126. [Google Scholar] [CrossRef]
- Ritchie, J.C.; Zimba, P.V.; Everitt, J.H. Remote Sensing Techniques to Assess Water Quality. Photogramm. Eng. Remote Sens. 2003, 69, 695–704. [Google Scholar] [CrossRef]
- Sudheer, K.; Chaubey, I.; Garg, V. Lake water quality assessment from landsat thematic mapper data using neural network: An approach to optimal band combination selection. JAWRA J. Am. Water Resour. Assoc. 2006, 42, 1683–1695. [Google Scholar] [CrossRef]
- Svab, E.; Tyler, A.N.; Preston, T.; Présing, M.; Balogh, K.V. Characterizing the spectral reflectance of algae in lake waters with high suspended sediment concentrations. Int. J. Remote Sens. 2005, 26, 919–928. [Google Scholar] [CrossRef]
- Dörnhöfer, K.; Oppelt, N. Remote sensing for lake research and monitoring–Recent advances. Ecol. Indic. 2016, 64, 105–122. [Google Scholar] [CrossRef]
- Bonansea, M.; Ledesma, M.; Rodriguez, M.C.; Pinotti, L. Using new remote sensing satellites for assessing water quality in a reservoir. Hydrol. Sci. J. 2019, 64, 34–44. [Google Scholar] [CrossRef]
- Hicks, B.J.; Stichbury, G.A.; Brabyn, L.K.; Allan, M.G.; Ashraf, S. Hindcasting water clarity from Landsat satellite images of unmonitored shallow lakes in the Waikato region, New Zealand. Environ. Monit. Assess. 2013, 185, 7245–7261. [Google Scholar] [CrossRef] [PubMed]
- Duan, H.; Ma, R.; Zhang, Y.; Zhang, B. Remote-sensing assessment of regional inland lake water clarity in northeast China. Limnology 2009, 10, 135–141. [Google Scholar] [CrossRef]
- Cheng, K.S.; Lei, T.C. Reservoir trophic state evaluation using lanisat tm images 1. JAWRA J. Am. Water Resour. Assoc. 2001, 37, 1321–1334. [Google Scholar] [CrossRef]
- Vapnik, V.; Golowich, S.E.; Smola, A. Support Vector Method for Function Approximation, Regression Estimation and Signal Processing; MIT Press: Cambridge, MA, USA, 1997; pp. 281–287. [Google Scholar]
- Azamathulla, H.; Wu, F.-C. Support vector machine approach for longitudinal dispersion coefficients in natural streams. Appl. Soft Comput. 2011, 11, 2902–2905. [Google Scholar] [CrossRef]
- Samui, P. Support vector machine applied to settlement of shallow foundations on cohesionless soils. Comput. Geotech. 2008, 35, 419–427. [Google Scholar] [CrossRef]
- Wang, X.; Ma, L.; Wang, X. Apply semi-supervised support vector regression for remote sensing water quality retrieving. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 2757–2760. [Google Scholar]
- Maier, P.M.; Keller, S. Machine learning regression on hyperspectral data to estimate multiple water parameters. In Proceedings of the 9th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Amsterdam, The Netherlands, 23–26 September 2018; pp. 1–5. [Google Scholar]
- Ruescas, A.B.; Hieronymi, M.; Mateo-Garcia, G.; Koponen, S.; Kallio, K.; Camps-Valls, G. Machine Learning Regression Approaches for Colored Dissolved Organic Matter (CDOM) Retrieval with S2-MSI and S3-OLCI Simulated Data. Remote Sens. 2018, 10, 786. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Hastie, T.T. The Elements of Statistical Learning; Mathematical Intelligencer, Ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Keiner, L.E. Estimating oceanic chlorophyll concentrations with neural networks. Int. J. Remote Sens. 1999, 20, 189–194. [Google Scholar] [CrossRef]
- Giardino, C.; Bresciani, M.; Cazzaniga, I.; Di Nicolantonio, W.; Cacciari, A.; Matta, E.; Rampini, A.; Gianinetto, M.; Ober, G. Combining In Situ and Multi-Sensor Satellite Data to Assess the Impact of Atmospheric Deposition in Lake Garda. In Proceedings of the 2013 European Space Agency Living Planet Symposium, Edinburgh, UK, 9–13 September 2013; pp. 1–5. [Google Scholar]
- Panda, S.S.; Garg, V.; Chaubey, I. Artificial neural networks application in lake water quality estimation using satellite imagery. J. Environ. Inform. 2004, 4, 65–74. [Google Scholar] [CrossRef]
- Blix, K.; Pálffy, K.; Tóth, V.R.; Eltoft, T. Remote Sensing of Water Quality Parameters over Lake Balaton by Using Sentinel-3 OLCI. Water 2018, 10, 1428. [Google Scholar] [CrossRef]
- Delgado, A.L.; Pratolongo, P.D.; Gossn, J.I.; Dogliotti, A.I.; Arena, M.; Villagran, D.; Severini, M.F. Evaluation of derived total suspended matter products from ocean and land colour instrument imagery (OLCI) in the inner and mid-shelf of Buenos Aires Province (Argentina). In Proceedings of the Extended Abstract Submitted to the XXIV Ocean Optics Conference, Dubrovnik, Croatia, 16 October 2018. [Google Scholar]
- NASA. A Harmonized Surface Reflectance Product. 2022. Available online: https://hls.gsfc.nasa.gov/ (accessed on 12 September 2022).
- Kwong, I.H.Y.; Wong, F.K.K.; Fung, T. Automatic Mapping and Monitoring of Marine Water Quality Parameters in Hong Kong Using Sentinel-2 Image Time-Series and Google Earth Engine Cloud Computing. Front. Mar. Sci. 2022, 609, 871470. [Google Scholar] [CrossRef]
- Castrillo, M.; García, L. Estimation of high frequency nutrient concentrations from water quality surrogates using machine learning methods. Water Res. 2020, 172, 115490. [Google Scholar] [CrossRef] [PubMed]
- Niroumand-Jadidi, M.; Bovolo, F.; Bruzzone, L. Water Quality Retrieval from PRISMA Hyperspectral Images: First Experience in a Turbid Lake and Comparison with Sentinel-2. Remote Sens. 2020, 12, 3984. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, L.; Ren, H.; Deng, L.; Zhang, P. Retrieval of Water Quality Parameters from Hyperspectral Images Using Hybrid Bayesian Probabilistic Neural Network. Remote Sens. 2020, 12, 1567. [Google Scholar] [CrossRef]
- Topp, S.N.; Pavelsky, T.M.; Jensen, D.; Simard, M.; Ross, M.R.V. Research Trends in the Use of Remote Sensing for Inland Water Quality Science: Moving Towards Multidisciplinary Applications. Water 2020, 12, 169. [Google Scholar] [CrossRef]
- Kravitz, J.; Matthews, M.; Lain, L.; Fawcett, S.; Bernard, S. Potential for High Fidelity Global Mapping of Common Inland Water Quality Products at High Spatial and Temporal Resolutions Based on a Synthetic Data and Machine Learning Approach. Front. Environ. Sci. 2021, 9, 19. [Google Scholar] [CrossRef]
- El-Din, M.S.; Gaber, A.; Koch, M.; Ahmed, R.S.; Bahgat, I. Remote sensing application for water quality assessment in lake timsah, suez canal, egypt. J. Remote Sens. Technol. 2013, 1, 61–74. [Google Scholar] [CrossRef]
- Gómez, J.A.D.; Alonso, C.A.; García, A.A. Remote sensing as a tool for monitoring water quality parameters for Mediterranean Lakes of European Union water framework directive (WFD) and as a system of surveillance of cyanobacterial harmful algae blooms (SCyanoHABs). Environ. Monit. Assess. 2011, 181, 317–334. [Google Scholar] [CrossRef] [PubMed]
- Odermatt, D.; Heege, T.; Nieke, J.; Kneubuhler, M.; Itten, K. Water Quality Monitoring for Lake Constance with a Physically Based Algorithm for MERIS Data. Sensors 2008, 8, 4582–4599. [Google Scholar] [CrossRef]
- Wang, F.; Han, L.; Kung, H.-T.; Van Arsdale, R.B. Applications of Landsat-5 TM imagery in assessing and mapping water quality in Reelfoot Lake, Tennessee. Int. J. Remote Sens. 2006, 27, 5269–5283. [Google Scholar] [CrossRef]
- Brezonik, P.; Menken, K.D.; Bauer, M. Landsat-based Remote Sensing of Lake Water Quality Characteristics, Including Chlorophyll and Colored Dissolved Organic Matter (CDOM). Lake Reserv. Manag. 2005, 21, 373–382. [Google Scholar] [CrossRef]
- Kallio, K.; Kutser, T.; Hannonen, T.; Koponen, S.; Pulliainen, J.; Vepsäläinen, J.; Pyhälahti, T. Retrieval of water quality from airborne imaging spectrometry of various lake types in different seasons. Sci. Total. Environ. 2001, 268, 59–77. [Google Scholar] [CrossRef]
- Zilioli, E.; Brivio, P. The satellite derived optical information for the comparative assessment of lacustrine water quality. Sci. Total. Environ. 1997, 196, 229–245. [Google Scholar] [CrossRef]
- Pattiaratchi, C.; Lavery, P.; Wyllie, A.; Hick, P. Estimates of water quality in coastal waters using multi-date Landsat Thematic Mapper data. Int. J. Remote Sens. 1994, 15, 1571–1584. [Google Scholar] [CrossRef]
- Chacon-Torres, A.; Ross, L.G.; Beveridge, M.; Watson, A.I. The application of SPOT multispectral imagery for the assessment of water quality in Lake Pátzcuaro, Mexico. Int. J. Remote Sens. 1992, 13, 587–603. [Google Scholar] [CrossRef]
- Buma, W.; Lee, S.-I. Evaluation of Sentinel-2 and Landsat 8 Images for Estimating Chlorophyll-a Concentrations in Lake Chad, Africa. Remote Sens. 2020, 12, 2437. [Google Scholar] [CrossRef]
- Palmer, S.C.J.; Hunter, P.D.; Lankester, T.; Hubbard, S.; Spyrakos, E.; Tyler, A.N.; Présing, M.; Horváth, H.; Lamb, A.; Balzter, H.; et al. Validation of Envisat MERIS algorithms for chlorophyll retrieval in a large, turbid and optically-complex shallow lake. Remote Sens. Environ. 2015, 157, 158–169. [Google Scholar] [CrossRef]
- Turner, D. Remote Sensing of Chlorophyll a Concentrations to Support the Deschutes Basin Lake and Reservoirs TMDLs. 2010. Available online: https://www.oregon.gov/deq/FilterDocs/RemoteSensingChlorophylla.pdf (accessed on 12 September 2022).
- Alikas, K.; Kangro, K.; Reinart, A. Detecting cyanobacterial blooms in large North European lakes using the Maximum Chlorophyll Index. Oceanologia 2010, 52, 237–257. [Google Scholar] [CrossRef]
- Han, L.; Jordan, K.J. Estimating and mapping chlorophyll-a concentration in Pensacola Bay, Florida using Landsat ETM+ data. Int. J. Remote Sens. 2005, 26, 5245–5254. [Google Scholar] [CrossRef]
- Kallio, K.; Koponen, S.; Pulliainen, J. Feasibility of airborne imaging spectrometry for lake monitoring—A case study of spatial chlorophyll a distribution in two meso-eutrophic lakes. Int. J. Remote Sens. 2003, 24, 3771–3790. [Google Scholar] [CrossRef]
- Allee, R.J.; Johnson, J.E. Use of satellite imagery to estimate surface chlorophyll a and Secchi disc depth of Bull Shoals Reservoir, Arkansas, USA. Int. J. Remote Sens. 1999, 20, 1057–1072. [Google Scholar] [CrossRef]
- Gower, J.F.R. Observations of in situ fluorescence of chlorophyll-a in Saanich Inlet. Bound. Layer Meteorol. 1980, 18, 235–245. [Google Scholar] [CrossRef]
- Bi, S.; Li, Y.; Wang, Q.; Lyu, H.; Liu, G.; Zheng, Z.; Du, C.; Mu, M.; Xu, J.; Lei, S.; et al. Inland Water Atmospheric Correction Based on Turbidity Classification Using OLCI and SLSTR Synergistic Observations. Remote Sens. 2018, 10, 1002. [Google Scholar] [CrossRef]
- Pereira, L.S.; Andes, L.C.; Cox, A.L.; Ghulam, A. Measuring Suspended-Sediment Concentration and Turbidity in the Middle Mississippi and Lower Missouri Rivers using Landsat Data. JAWRA J. Am. Water Resour. Assoc. 2017, 54, 440–450. [Google Scholar] [CrossRef]
- Papoutsa, C.R.; Retalis, A.; Toulios, L.; Hadjimitsis, D.G. Defining the Landsat TM/ETM+ and CHRIS/PROBA spectral regions in which turbidity can be retrieved in inland waterbodies using field spectroscopy. Int. J. Remote Sens. 2014, 35, 1674–1692. [Google Scholar] [CrossRef]
- Guo, H.; Huang, J.J.; Zhu, X.; Wang, B.; Tian, S.; Xu, W.; Mai, Y. A generalized machine learning approach for dissolved oxygen estimation at multiple spatiotemporal scales using remote sensing. Environ. Pollut. 2021, 288, 117734. [Google Scholar] [CrossRef]
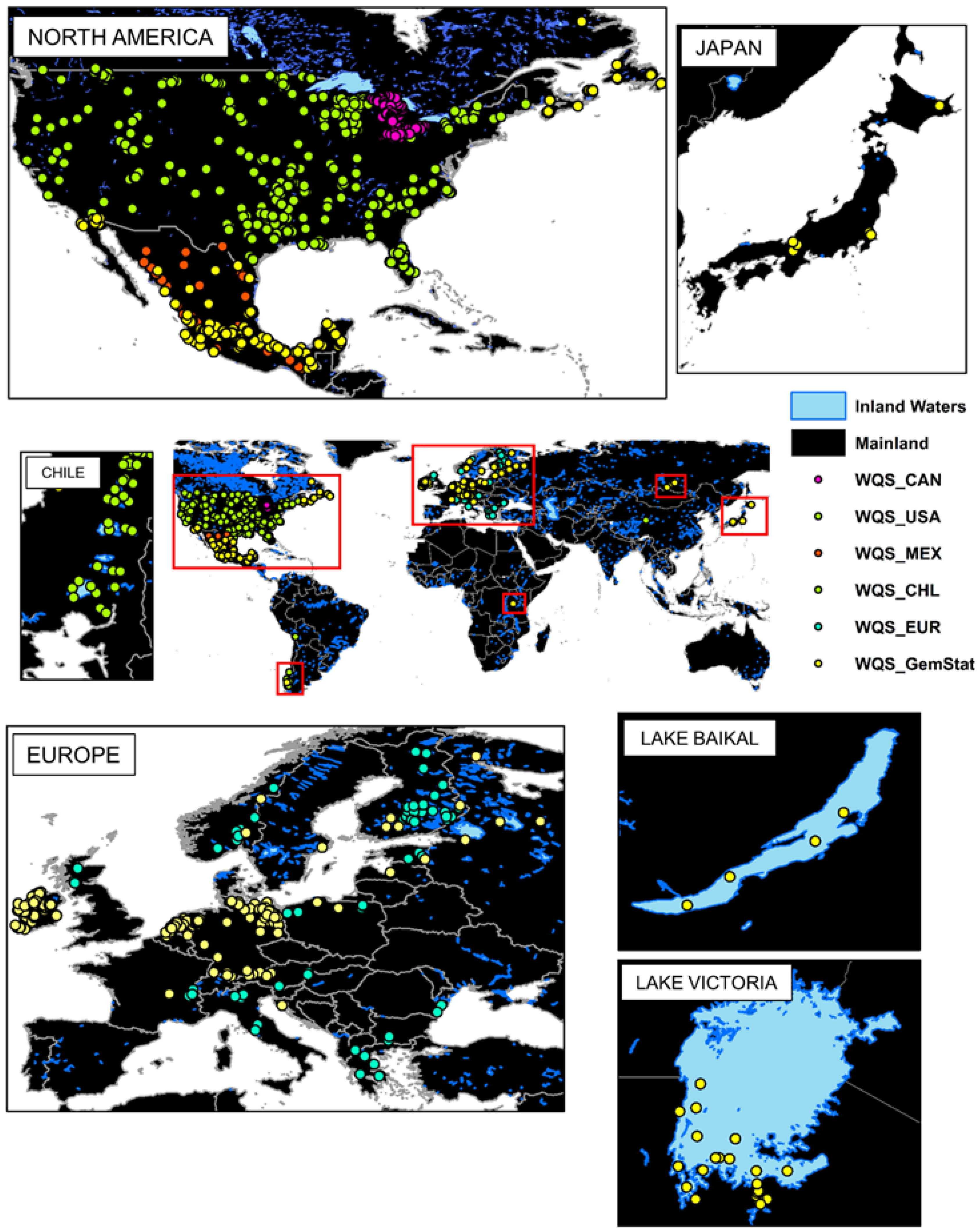


| Source | Data Location | Region |
|---|---|---|
| Water Quality Portal (WQP) | waterqualitydata.us (accessed on 15 January 2022) | United States |
| European Environment Agency (EEA) Waterbase | eea.europa.eu/data-and-maps/data/waterbase (accessed on 13 January 2022) | Europe |
| Mexican National Water Monitoring Network | gob.mx/conagua/articulos/calidad-del-agua (accessed on 1 September 2021) | Mexico |
| Open Government Portal of Canada | open.canada.ca/en/od (accessed on 15 January 2022) | Canada |
| General Chilean Water Directorade | dga.mop.gob.cl/servicioshidrometeorologicos (accessed on 15 January 2022) | Chile |
| Global Freshwater Quality Database (GEMStat) | gemstat.org/data (accessed on 7 January 2022) | Global |
| Region | n | Lakes |
|---|---|---|
| United States | 263,699 | 43 |
| Europe | 17,681 | 64 |
| Mexico | 9086 | 32 |
| Canada | 5412 | 2 |
| Japan | 1292 | 3 |
| Chile | 897 | 16 |
| Russia | 32 | 1 |
| Region | n | Lakes |
|---|---|---|
| United States | 2032 | 33 |
| Europe | 1540 | 54 |
| Mexico | 2875 | 32 |
| Canada | 16 | 2 |
| Japan | 202 | 3 |
| Chile | 206 | 14 |
| Russia | 13 | 1 |
| Parameter | n | Type |
|---|---|---|
| Chlorophyll-a (Chl-a: mg/L) | 1080 | OAC |
| Turbidity (TURB: NTU) | 554 | OAC |
| Total suspended matter (TSM (mg/L) | 291 | OAC |
| Secchi disk depth (SDD: m) | 694 | OAC |
| Dissolved oxygen (DO: mg/L) | 1872 | nOAC |
| Total phosphorus (PTOT: mg/L) | 987 | nOAC |
| Nitrate (NO3-N: mg/L) | 711 | nOAC |
| Biochemical oxygen demand (BOD: mg/L) | 214 | nOAC |
| Chemical oxygen demand (COD: mg/L) | 481 | nOAC |
| Parameter | Chl-a | TURB | TSM | SDD | DO | PTOT | NO3-N | BOD | COD |
|---|---|---|---|---|---|---|---|---|---|
| Count | 1080 | 711 | 1872 | 987 | 694 | 291 | 554 | 214 | 481 |
| Mean | 26.87 | 2.89 | 8.80 | 0.20 | 2.73 | 40.65 | 24.48 | 11.25 | 30.39 |
| St. Dev. | 52.53 | 23.98 | 2.24 | 0.39 | 3.31 | 54.71 | 55.11 | 12.65 | 27.98 |
| Min | 0.00 | 0.00 | 1.30 | 0.00 | 0.00 | 1.00 | 0.10 | 0.50 | 2.10 |
| 25% Perc. | 1.90 | 0.04 | 7.60 | 0.03 | 0.67 | 12.00 | 2.30 | 3.42 | 13.00 |
| Median | 6.80 | 0.18 | 8.90 | 0.07 | 1.20 | 20.00 | 5.30 | 5.99 | 22.00 |
| 75% Perc. | 22.90 | 1.41 | 10.00 | 0.18 | 3.20 | 43.72 | 18.00 | 17.00 | 39.00 |
| Max | 561.07 | 443.00 | 27.00 | 5.73 | 18.00 | 520.00 | 578.70 | 94.00 | 270.00 |
| Feature | Formula | Naming |
|---|---|---|
| Ratio of red and green plus near infrared | Red/Green + NIR | SF1 |
| Average of green plus red | (Green + Red)/2 | SF2 |
| Ration of green and red | Green/Red | SF3 |
| Ratio of red and green | Red/Green | SF4 |
| Radio of near infrared and green | NIR/Green | SF5 |
| Latitude | - | Lat |
| Longitude | - | Lon |
| Month | - | Month |
| Year | - | Year |
| Dataset | Features | Description |
|---|---|---|
| HB (harmonized bands) | HLS bands | Original harmonized Landsat–Sentinel bands |
| FE (feature engineering) | H-bands, red/green + NIR, (green + red)/2, green/red, red/green, NIR/green | HLS bands and the radiometric band ratios |
| HBRT (HLS bands and region and time) | HB, latitude, longitude, year and month | HB dataset, region and time |
| FERT (engineering and region and time) | FE, latitude, longitude, year and month | FE dataset, region and time |
| TRAIN | TEST | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model | Dataset | R2 | RMSE | MSE | MAE | # Feat | Dataset | R2 | RMSE | MSE | MAE | # Feat | |
| Chl-a | |||||||||||||
| LR | HBRT | 0.48 | 38.42 | 1475.96 | 20.58 | 9 | HB | 0.43 | 42.25 | 1784.68 | 23.34 | 6 | |
| SVR | FERT | 0.63 | 33.66 | 1132.83 | 13.87 | 15 | FERT | 0.42 | 38.76 | 1502.37 | 19.74 | 15 | |
| RFR | FERT | 0.81 | 23.92 | 572.21 | 9.60 | 10 | HBRT | 0.53 | 35.11 | 1232.70 | 16.18 | 9 | |
| ELM | FERT | 0.53 | 36.20 | 1310.31 | 19.08 | 15 | FERT | 0.53 | 33.61 | 1129.74 | 21.77 | 15 | |
| MLP | FERT | 0.62 | 60.43 | 3652.16 | 25.86 | 15 | FERT | 0.37 | 27.53 | 758.13 | 13.53 | 15 | |
| TURB | |||||||||||||
| LR | HBRT | 0.70 | 27.53 | 757.80 | 13.29 | 9 | HBRT | 0.32 | 45.40 | 2060.82 | 21.37 | 9 | |
| SVR | FERT | 0.97 | 9.21 | 84.77 | 1.60 | 15 | FERT | 0.41 | 52.32 | 2737.40 | 19.22 | 15 | |
| RFR | HBRT | 0.82 | 22.01 | 484.41 | 7.59 | 9 | HBRT | 0.47 | 50.05 | 2504.73 | 16.50 | 9 | |
| ELM | HBRT | 0.43 | 44.33 | 1964.97 | 20.43 | 10 | FERT | 0.65 | 26.97 | 727.41 | 16.06 | 15 | |
| MLP | HBRT | 0.60 | 30.11 | 906.71 | 13.46 | 15 | HBRT | 0.61 | 40.44 | 1635.66 | 17.40 | 10 | |
| TSM | |||||||||||||
| LR | HB | 0.51 | 32.96 | 1086.33 | 22.13 | 6 | HB | 0.22 | 40.58 | 1646.95 | 26.72 | 6 | |
| SVR | FERT | 0.89 | 16.02 | 256.70 | 4.07 | 15 | HBRT | 0.28 | 54.79 | 3001.95 | 25.55 | 10 | |
| RFR | FERT | 0.79 | 24.18 | 584.45 | 15.11 | 4 | HBRT | 0.30 | 52.04 | 2708.02 | 28.09 | 4 | |
| ELM | FERT | 0.30 | 48.57 | 2358.74 | 28.39 | 15 | FE | 0.43 | 40.23 | 1618.31 | 25.52 | 11 | |
| MLP | HB | 0.28 | 36.27 | 1315.51 | 22.28 | 6 | HB | 0.30 | 48.39 | 2341.57 | 26.06 | 6 | |
| SDD | |||||||||||||
| LR | HBRT | 0.70 | 1.81 | 3.28 | 1.18 | 9 | FERT | 0.56 | 2.26 | 5.10 | 1.42 | 12 | |
| SVR | FERT | 0.82 | 1.39 | 1.92 | 0.49 | 15 | HBRT | 0.69 | 2.03 | 4.14 | 1.10 | 7 | |
| RFR | FERT | 0.88 | 1.18 | 1.40 | 0.58 | 14 | HBRT | 0.72 | 1.93 | 3.73 | 1.02 | 6 | |
| ELM | FERT | 0.70 | 1.84 | 3.39 | 1.20 | 15 | FERT | 0.72 | 1.69 | 2.84 | 1.17 | 15 | |
| MLP | FERT | 0.80 | 2.62 | 6.87 | 1.54 | 15 | FERT | 0.58 | 1.65 | 2.73 | 0.94 | 15 | |
| DO | |||||||||||||
| LR | HBRT | 0.40 | 1.69 | 2.84 | 1.17 | 8 | HBRT | 0.37 | 1.75 | 3.07 | 1.25 | 8 | |
| SVR | HBRT | 0.44 | 1.64 | 2.68 | 1.06 | 6 | HBRT | 0.39 | 1.76 | 3.08 | 1.19 | 6 | |
| RFR | HBRT | 0.83 | 0.94 | 0.88 | 0.58 | 4 | HBRT | 0.56 | 1.55 | 2.39 | 0.99 | 4 | |
| ELM | FERT | 0.40 | 1.72 | 2.96 | 1.24 | 15 | FERT | 0.32 | 1.78 | 3.18 | 1.32 | 15 | |
| MLP | HBRT | 0.53 | 1.88 | 3.53 | 1.33 | 10 | FERT | 0.37 | 1.69 | 2.86 | 1.19 | 10 | |
| PTOT | |||||||||||||
| LR | HBRT | 0.52 | 0.25 | 0.06 | 0.14 | 9 | HB | 0.22 | 0.43 | 0.18 | 0.17 | 6 | |
| SVR | HBRT | 0.79 | 0.17 | 0.03 | 0.05 | 9 | HBRT | 0.47 | 0.26 | 0.07 | 0.11 | 9 | |
| RFR | FERT | 0.84 | 0.15 | 0.02 | 0.05 | 14 | FERT | 0.56 | 0.24 | 0.06 | 0.09 | 14 | |
| ELM | FERT | 0.57 | 0.22 | 0.05 | 0.13 | 15 | FE | 0.41 | 0.27 | 0.07 | 0.16 | 11 | |
| MLP | FERT | 0.58 | 0.31 | 0.09 | 0.14 | 15 | FERT | 0.40 | 0.25 | 0.06 | 0.10 | 15 | |
| NO3-N | |||||||||||||
| LR | HBRT | 0.30 | 4.66 | 21.71 | 0.30 | 2 | FERT | 0.03 | 37.25 | 1387.90 | 6.07 | 1 | |
| SVR | HBRT | 0.82 | 2.48 | 6.17 | 0.94 | 9 | FERT | 0.42 | 26.32 | 692.88 | 2.96 | 14 | |
| RFR | HBRT | 0.78 | 2.64 | 6.98 | 0.77 | 2 | FERT | -1.52 | 26.86 | 721.55 | 3.19 | 1 | |
| ELM | FERT | 0.42 | 14.57 | 212.43 | 6.58 | 15 | HBRT | 0.43 | 31.31 | 980.11 | 6.96 | 15 | |
| MLP | FE | 0.05 | 4.94 | 24.40 | 2.61 | 11 | FE | 0.21 | 25.99 | 675.47 | 3.93 | 11 | |
| BOD | |||||||||||||
| LR | HB | 0.56 | 7.33 | 53.80 | 4.96 | 5 | HB | 0.32 | 10.08 | 101.54 | 6.00 | 5 | |
| SVR | HBRT | 0.71 | 6.01 | 36.15 | 2.58 | 9 | FERT | 0.41 | 10.55 | 111.33 | 5.68 | 14 | |
| RFR | HBRT | 0.87 | 4.21 | 17.72 | 2.17 | 7 | HBRT | 0.56 | 9.44 | 89.12 | 4.74 | 7 | |
| ELM | FERT | 0.42 | 9.95 | 98.96 | 6.16 | 15 | FERT | 0.65 | 7.41 | 54.96 | 5.12 | 15 | |
| MLP | HB | 0.57 | 9.67 | 93.51 | 7.09 | 6 | HBRT | 0.39 | 9.19 | 84.44 | 5.33 | 10 | |
| COD | |||||||||||||
| LR | HBRT | 0.52 | 19.21 | 368.94 | 12.45 | 8 | HBRT | 0.48 | 21.11 | 445.72 | 13.34 | 8 | |
| SVR | FERT | 0.64 | 17.86 | 319.10 | 8.47 | 15 | HBRT | 0.40 | 20.21 | 408.63 | 12.20 | 6 | |
| RFR | HBRT | 0.83 | 11.75 | 138.15 | 6.07 | 8 | HBRT | 0.54 | 17.94 | 321.67 | 10.56 | 8 | |
| ELM | FERT | 0.38 | 22.15 | 490.49 | 13.92 | 15 | FERT | 0.57 | 16.83 | 283.16 | 11.95 | 15 | |
| MLP | HBRT | 0.39 | 31.23 | 975.36 | 15.72 | 10 | HBRT | 0.21 | 20.09 | 403.41 | 13.39 | 10 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arias-Rodriguez, L.F.; Tüzün, U.F.; Duan, Z.; Huang, J.; Tuo, Y.; Disse, M. Global Water Quality of Inland Waters with Harmonized Landsat-8 and Sentinel-2 Using Cloud-Computed Machine Learning. Remote Sens. 2023, 15, 1390. https://doi.org/10.3390/rs15051390
Arias-Rodriguez LF, Tüzün UF, Duan Z, Huang J, Tuo Y, Disse M. Global Water Quality of Inland Waters with Harmonized Landsat-8 and Sentinel-2 Using Cloud-Computed Machine Learning. Remote Sensing. 2023; 15(5):1390. https://doi.org/10.3390/rs15051390
Chicago/Turabian StyleArias-Rodriguez, Leonardo F., Ulaş Firat Tüzün, Zheng Duan, Jingshui Huang, Ye Tuo, and Markus Disse. 2023. "Global Water Quality of Inland Waters with Harmonized Landsat-8 and Sentinel-2 Using Cloud-Computed Machine Learning" Remote Sensing 15, no. 5: 1390. https://doi.org/10.3390/rs15051390
APA StyleArias-Rodriguez, L. F., Tüzün, U. F., Duan, Z., Huang, J., Tuo, Y., & Disse, M. (2023). Global Water Quality of Inland Waters with Harmonized Landsat-8 and Sentinel-2 Using Cloud-Computed Machine Learning. Remote Sensing, 15(5), 1390. https://doi.org/10.3390/rs15051390










