Some Key Issues on Pseudorange-Based Point Positioning with GPS, BDS-3, and Galileo Observations
Abstract
1. Introduction
2. Methodology of SPP
2.1. Pseudorange Observation Equations
2.2. Single-Frequency SPP
2.3. Dual-Frequency SPP
2.4. The Handling of Receiver Clock Offsets in Multi-GNSS SPP
3. Data Sets and Processing Strategies
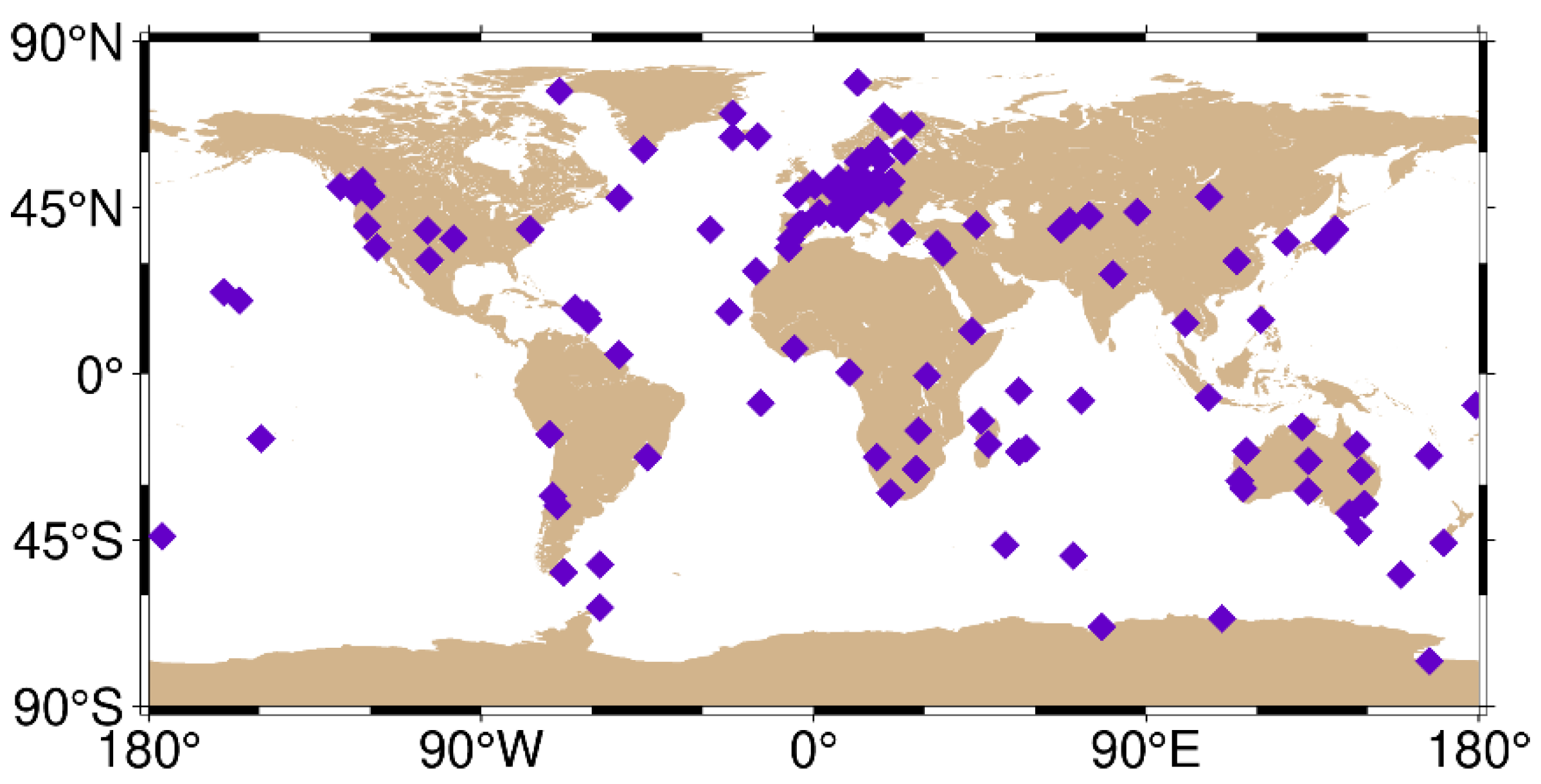
3.1. Data
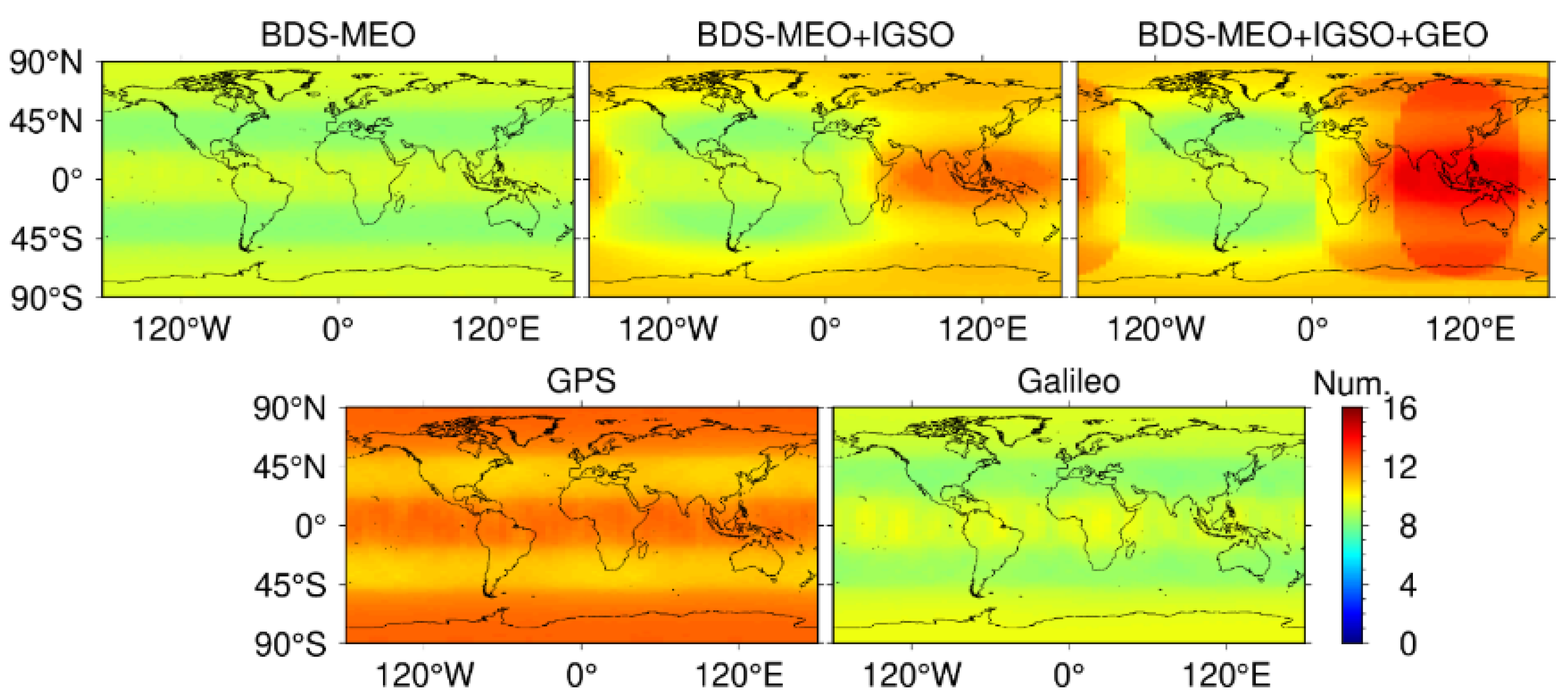
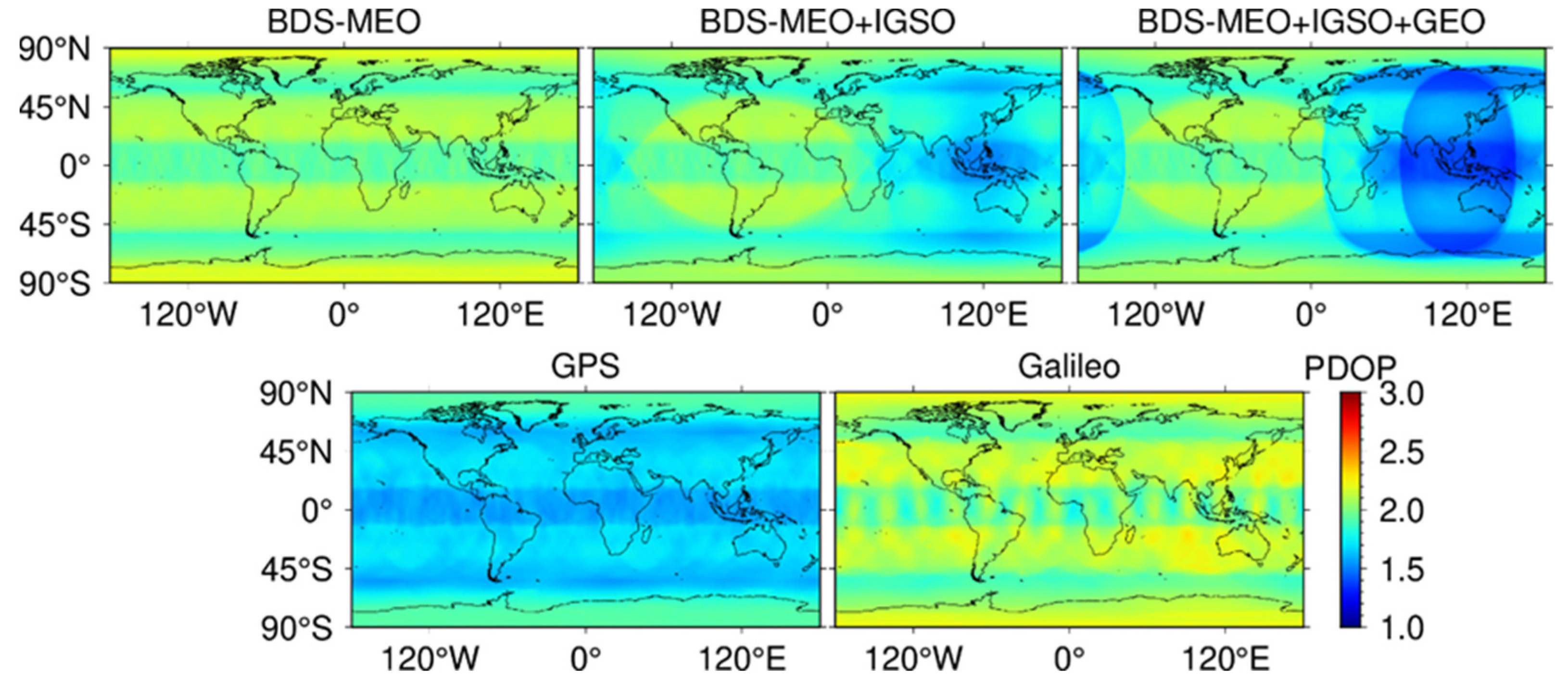
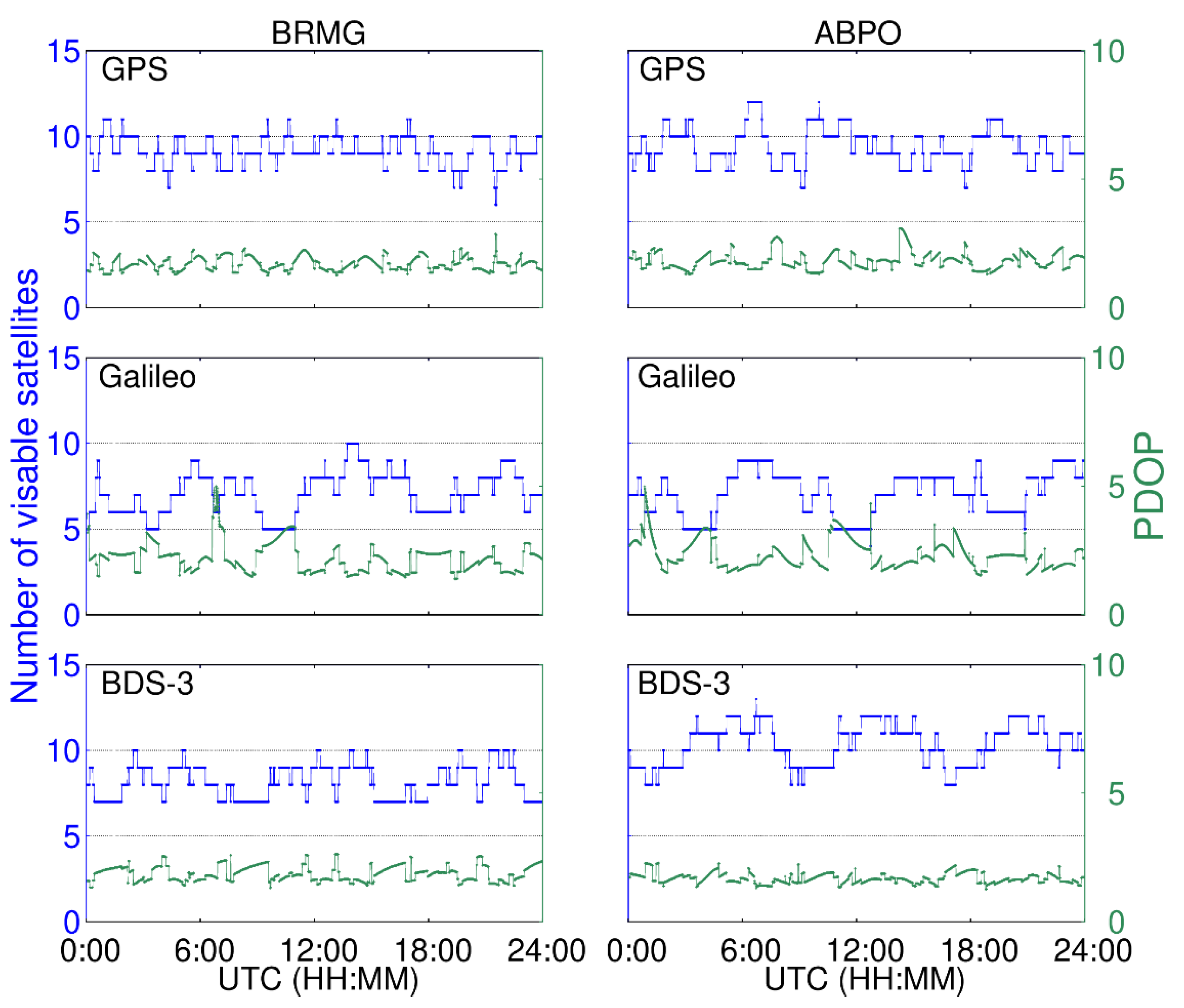
3.2. Availability Analysis of GNSS Constellations
4. Results Validation and Discussion
4.1. The Impact of Adding MEO, IGSO, and GEO Satellites for BDS-3 SPP
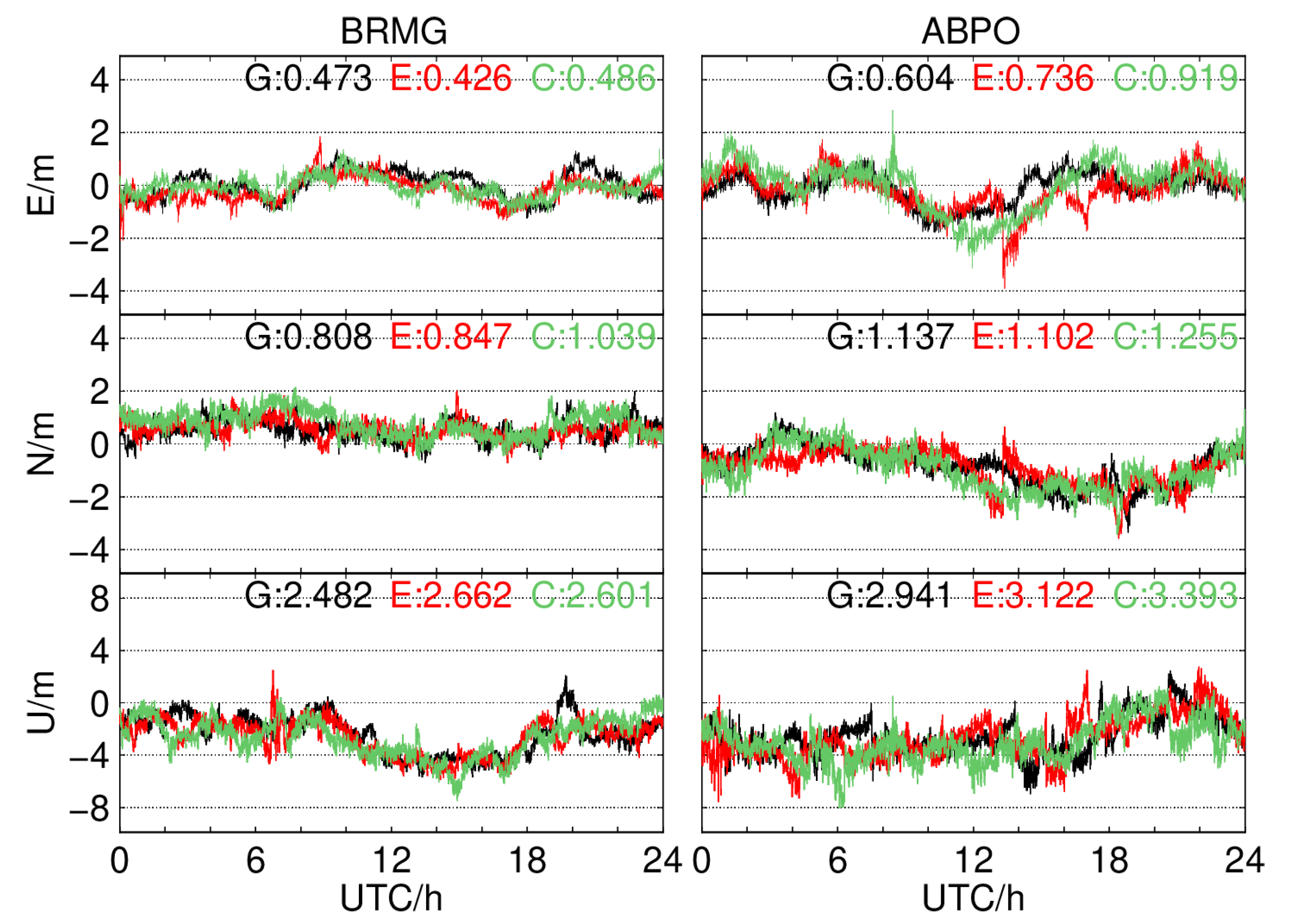
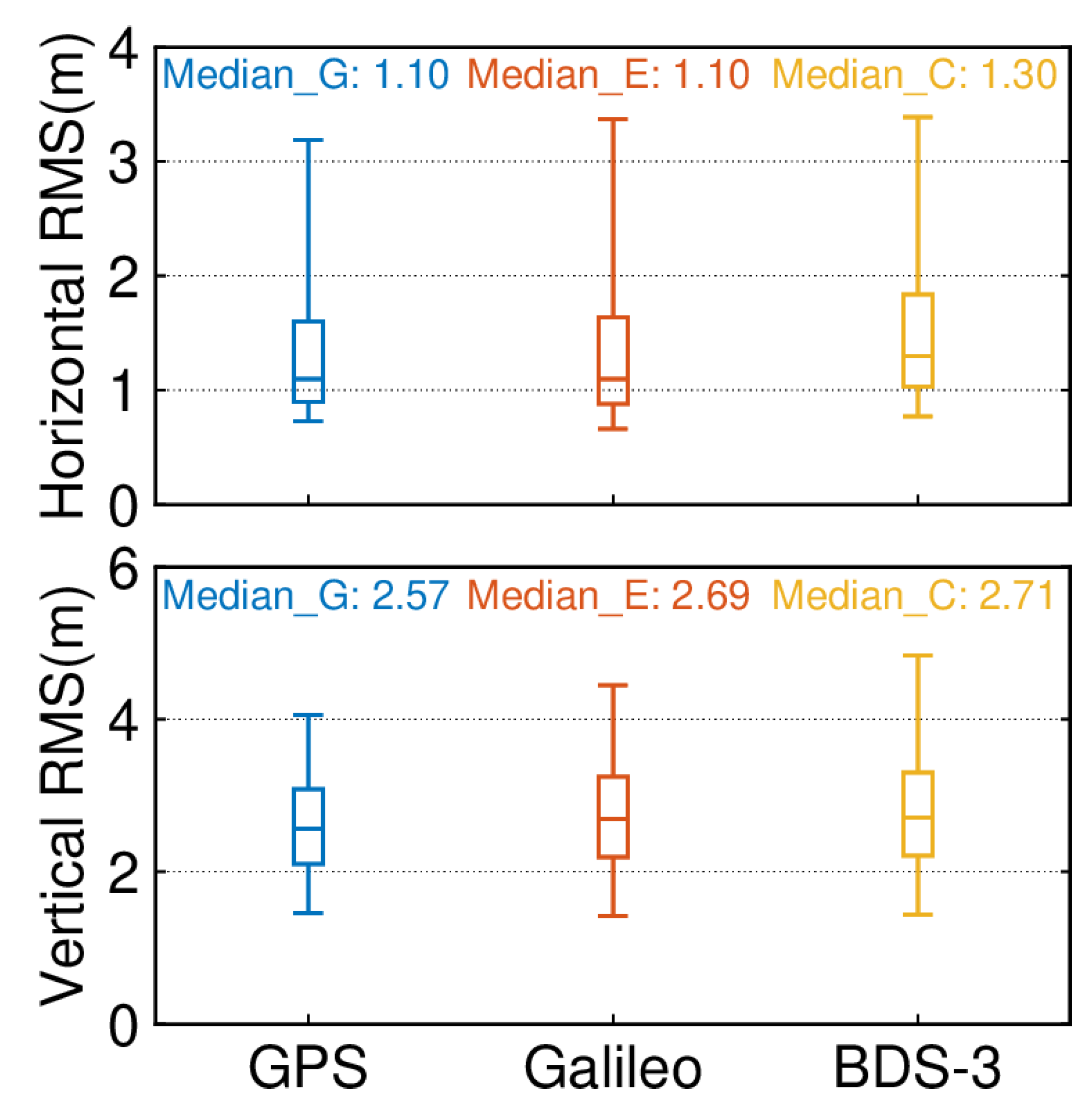
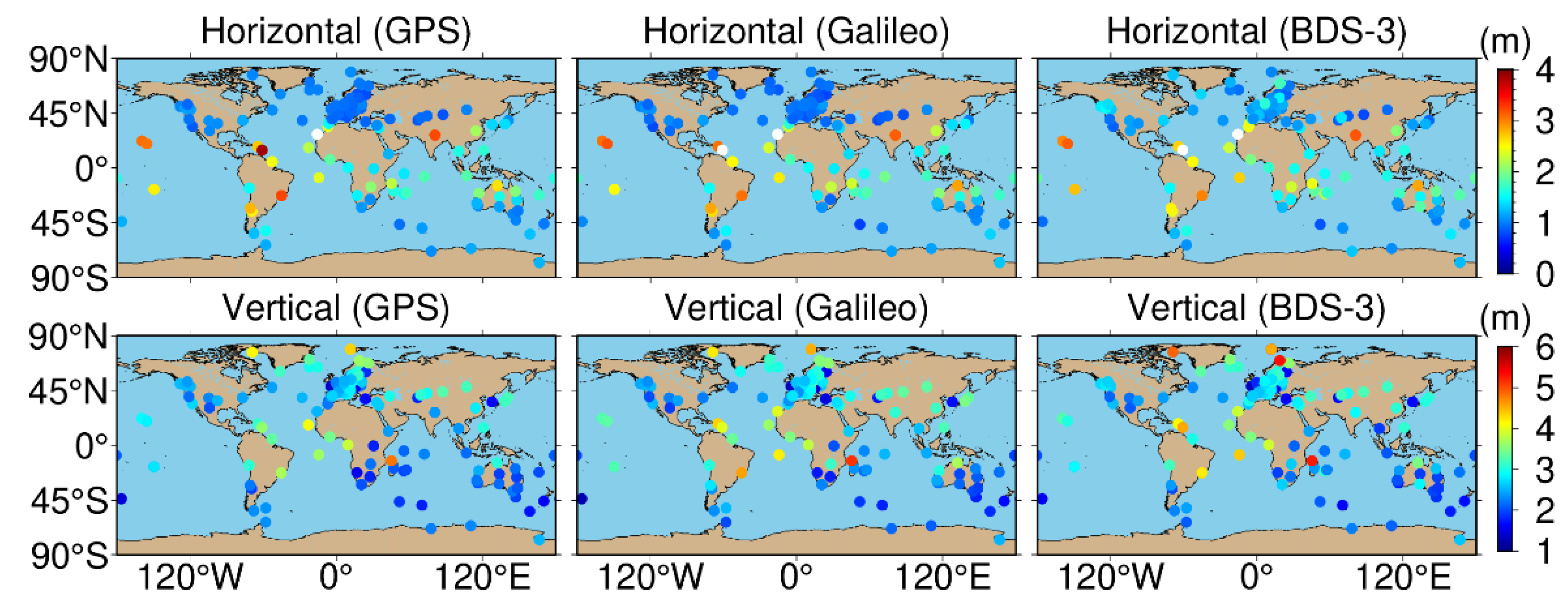
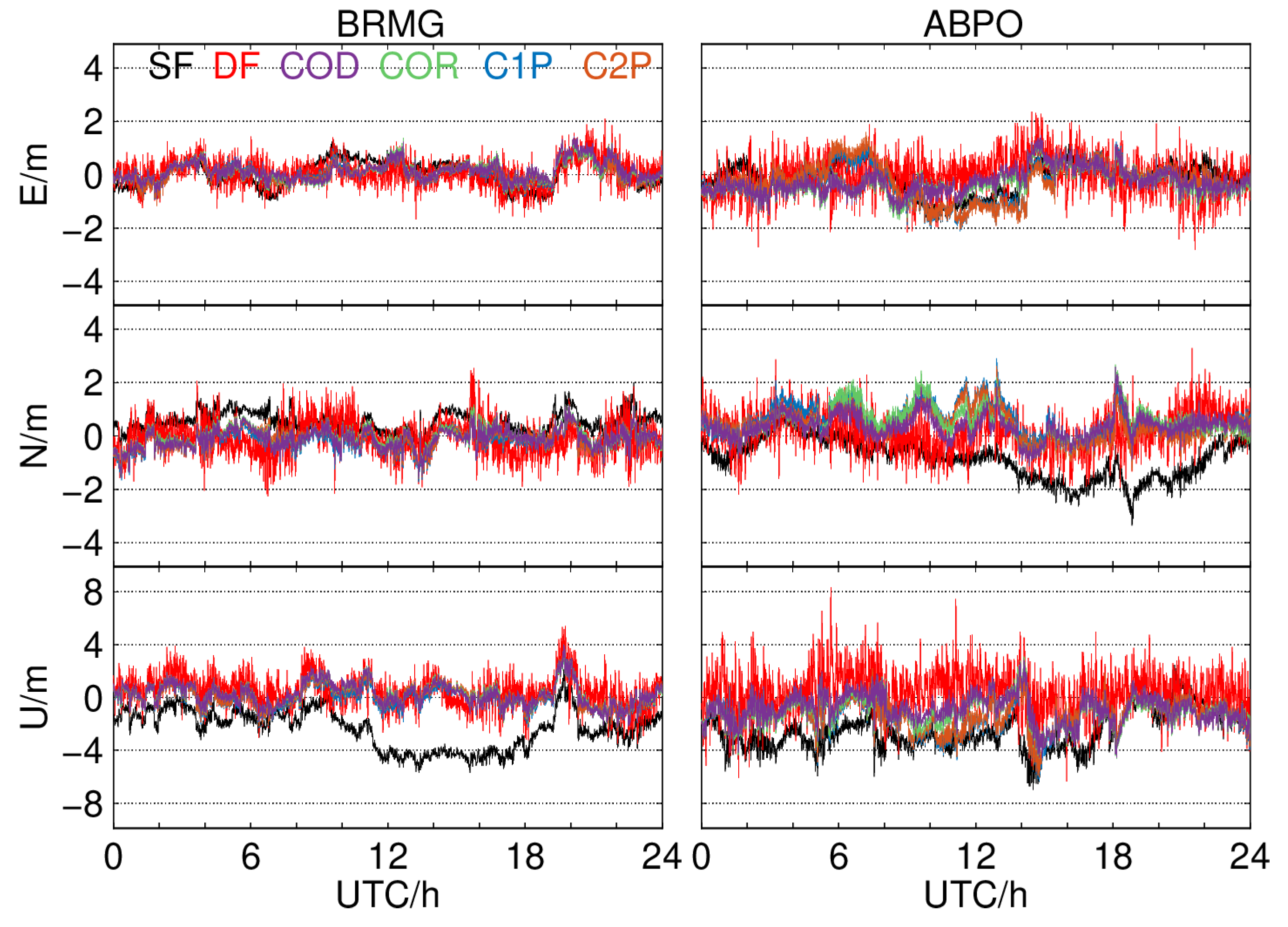
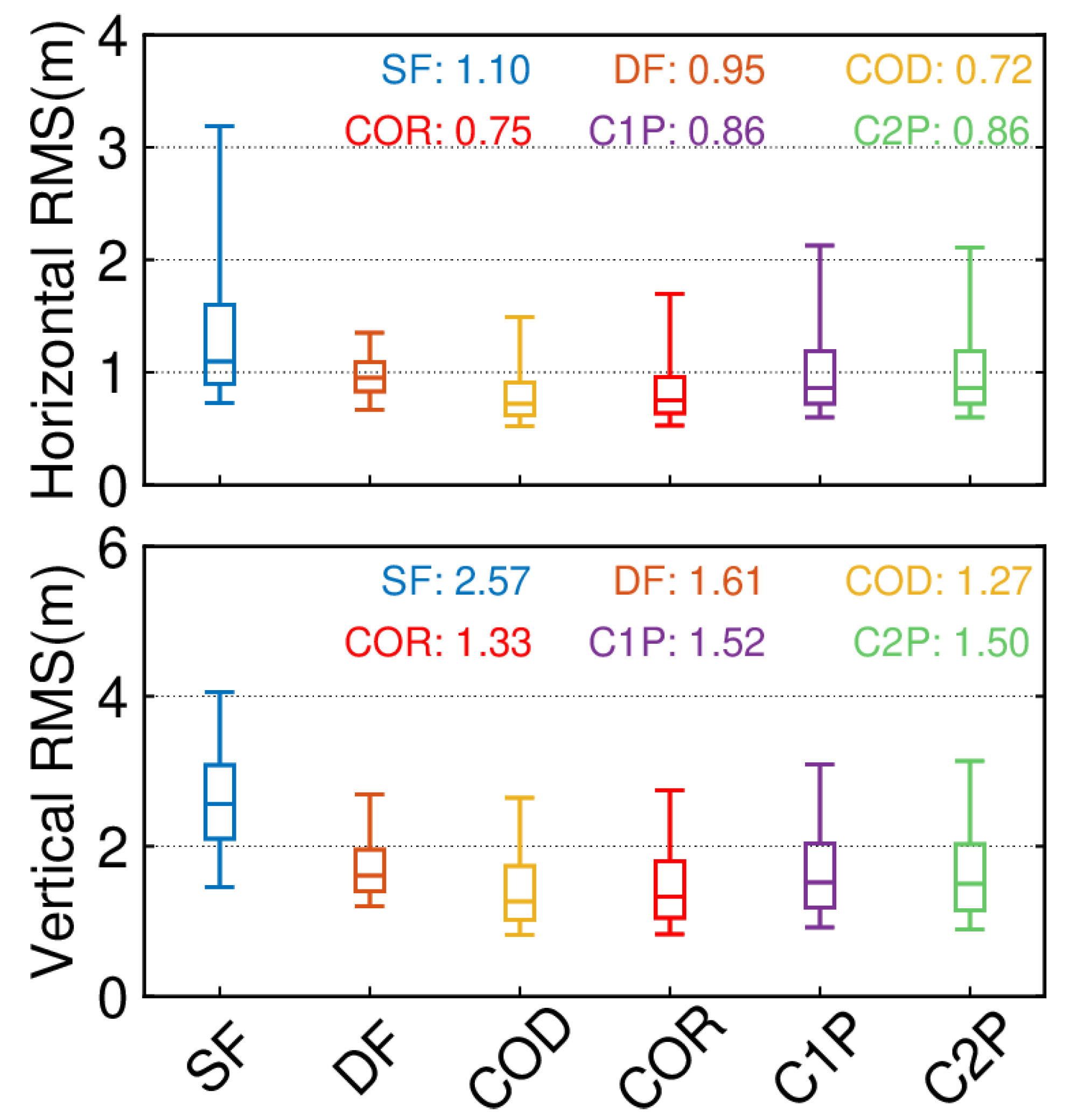
4.2. Single-System and Single-Frequency SPP (G, C, E)
4.3. Single-System and Dual-Frequency SPP (G, C, E)
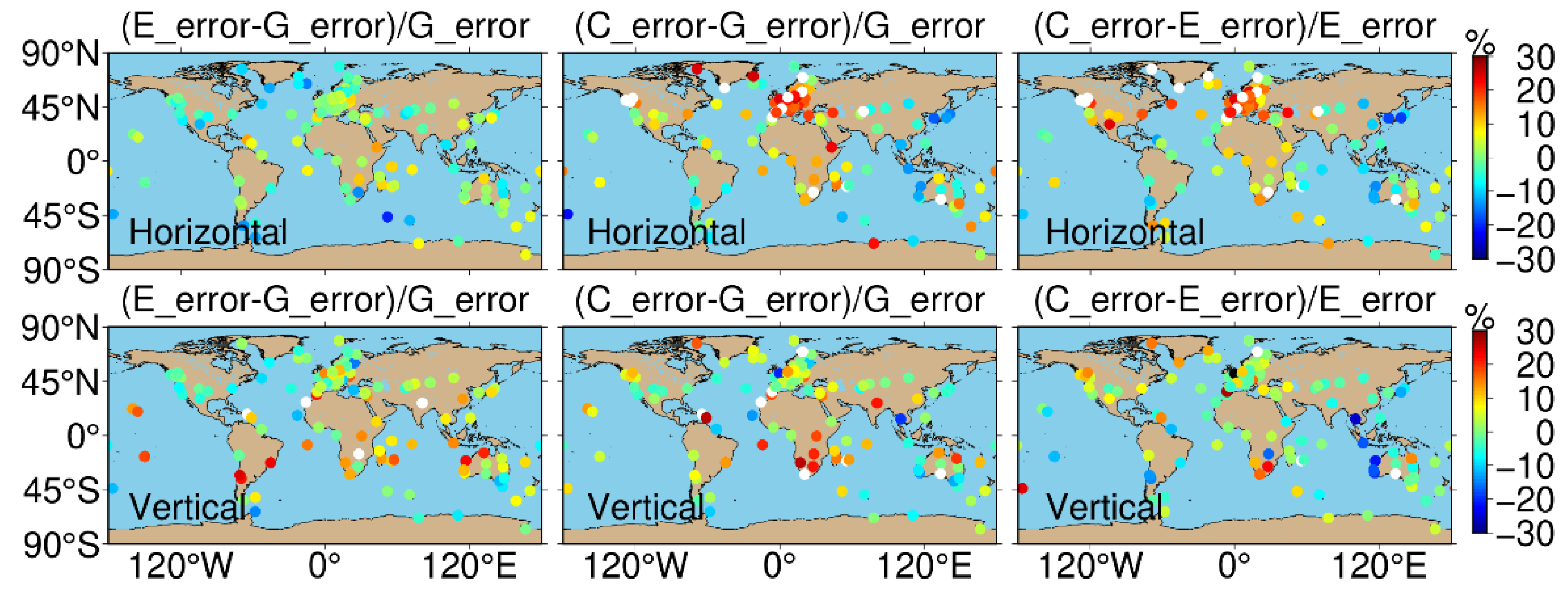
4.4. Dual-System and Single-Frequency SPP (GE, GC, CE)
4.5. SPP with GIM Products
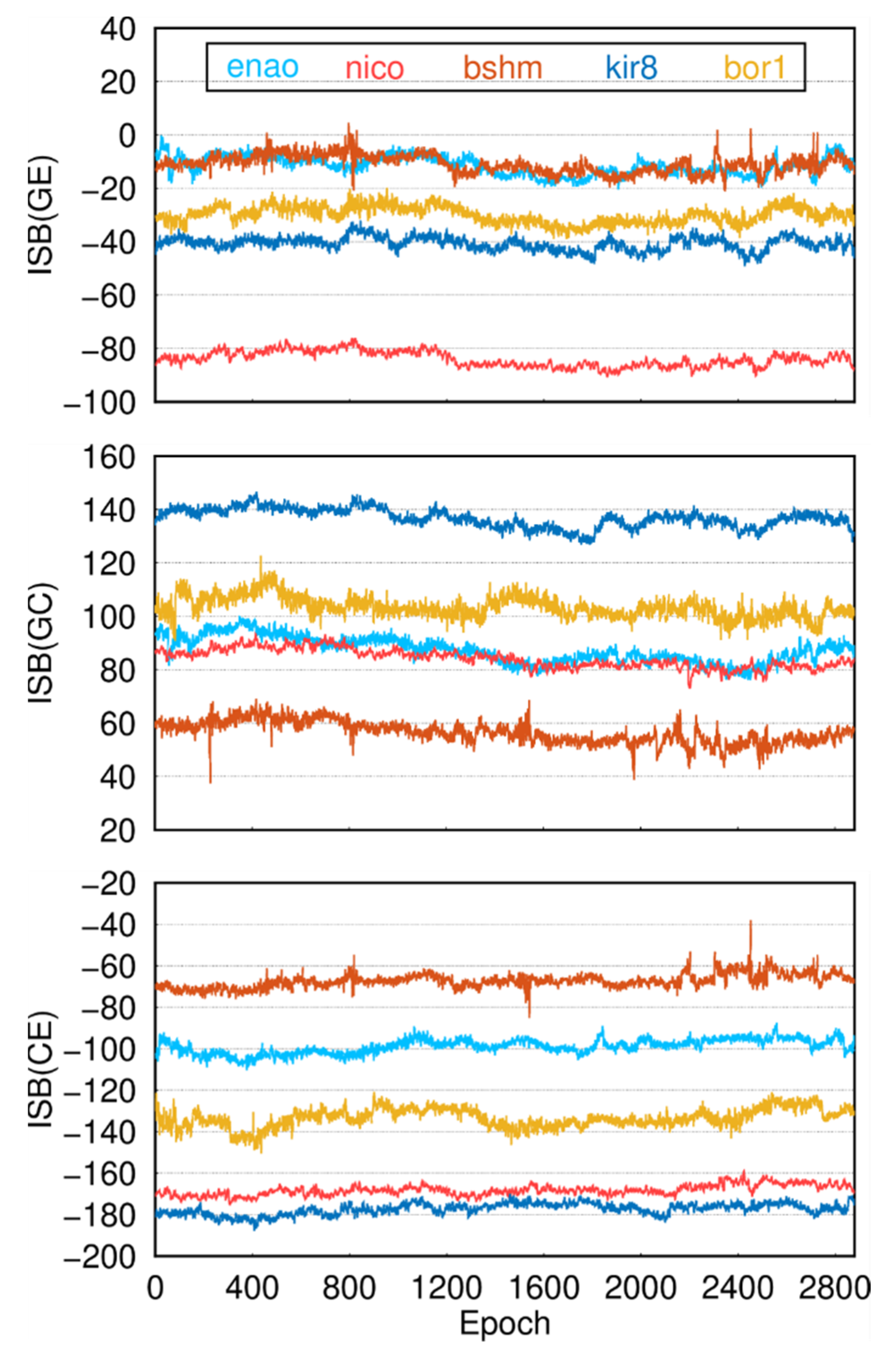
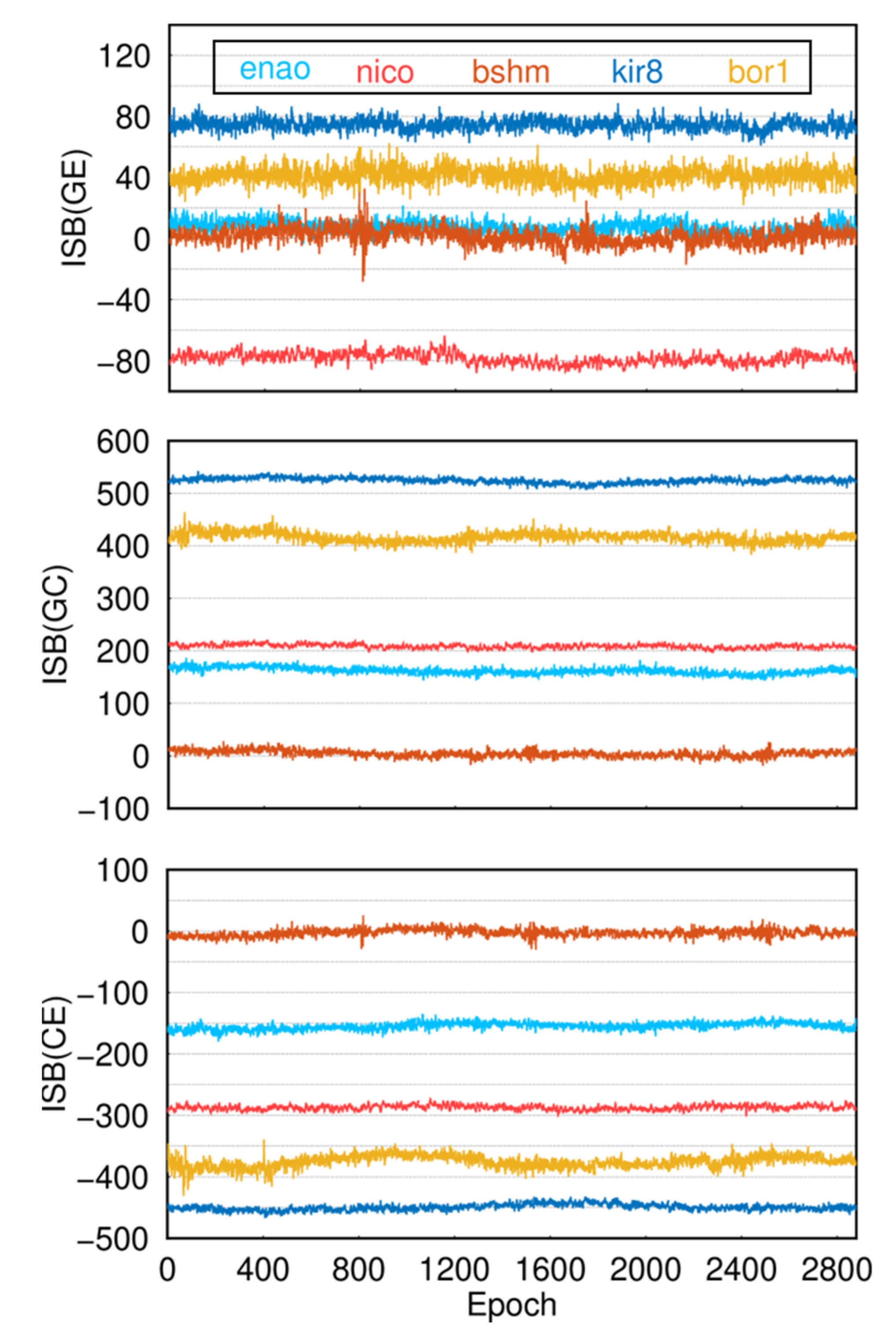
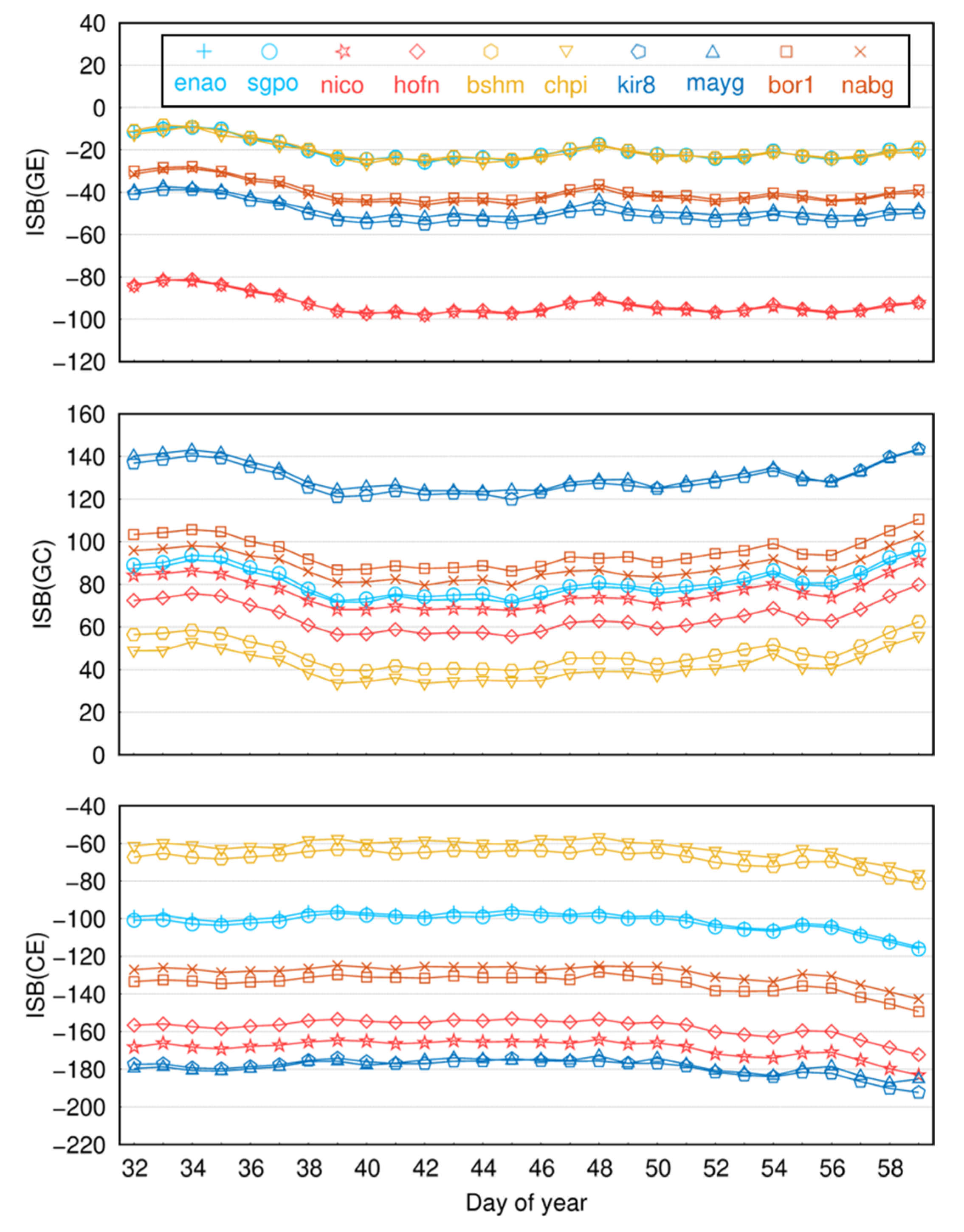
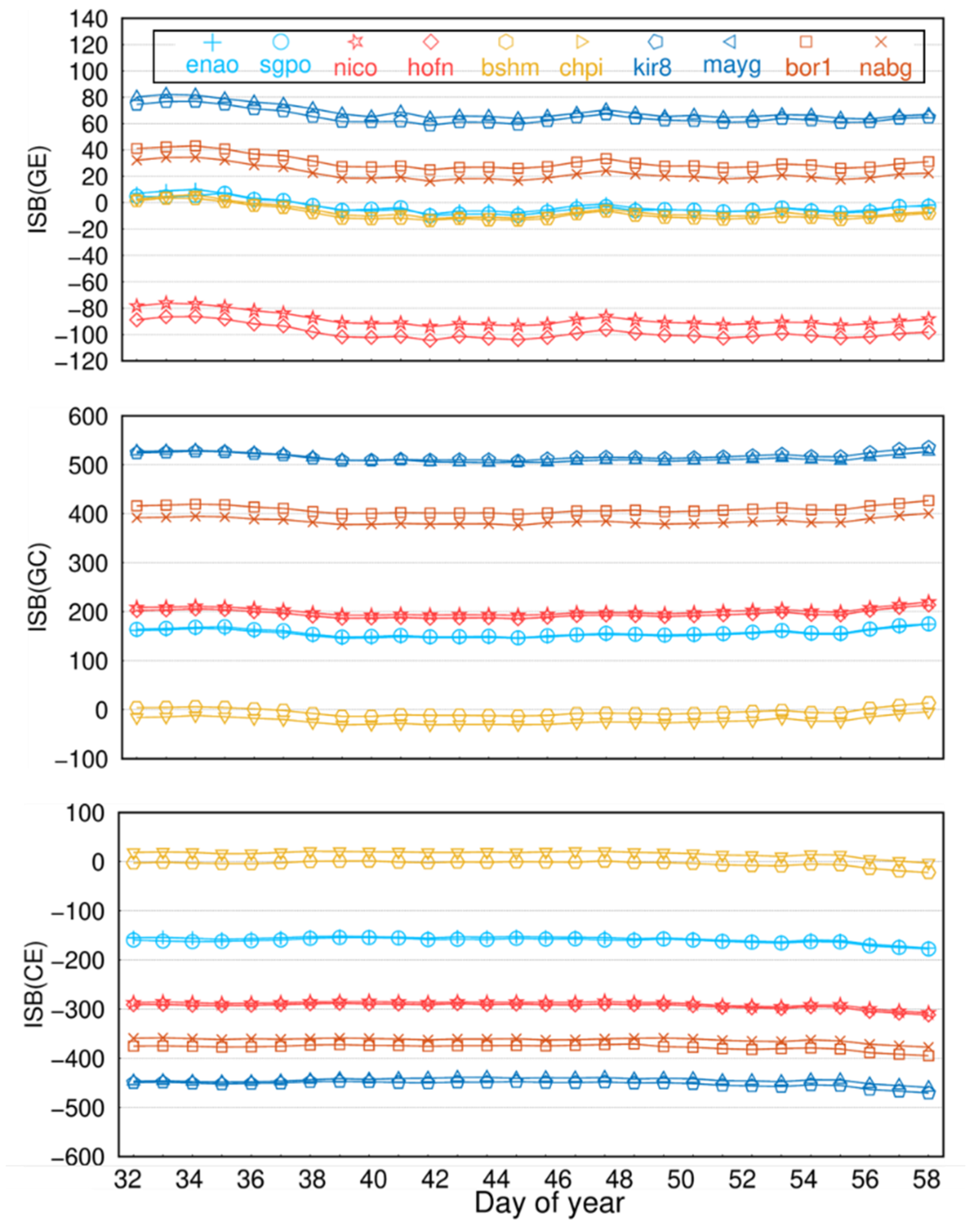
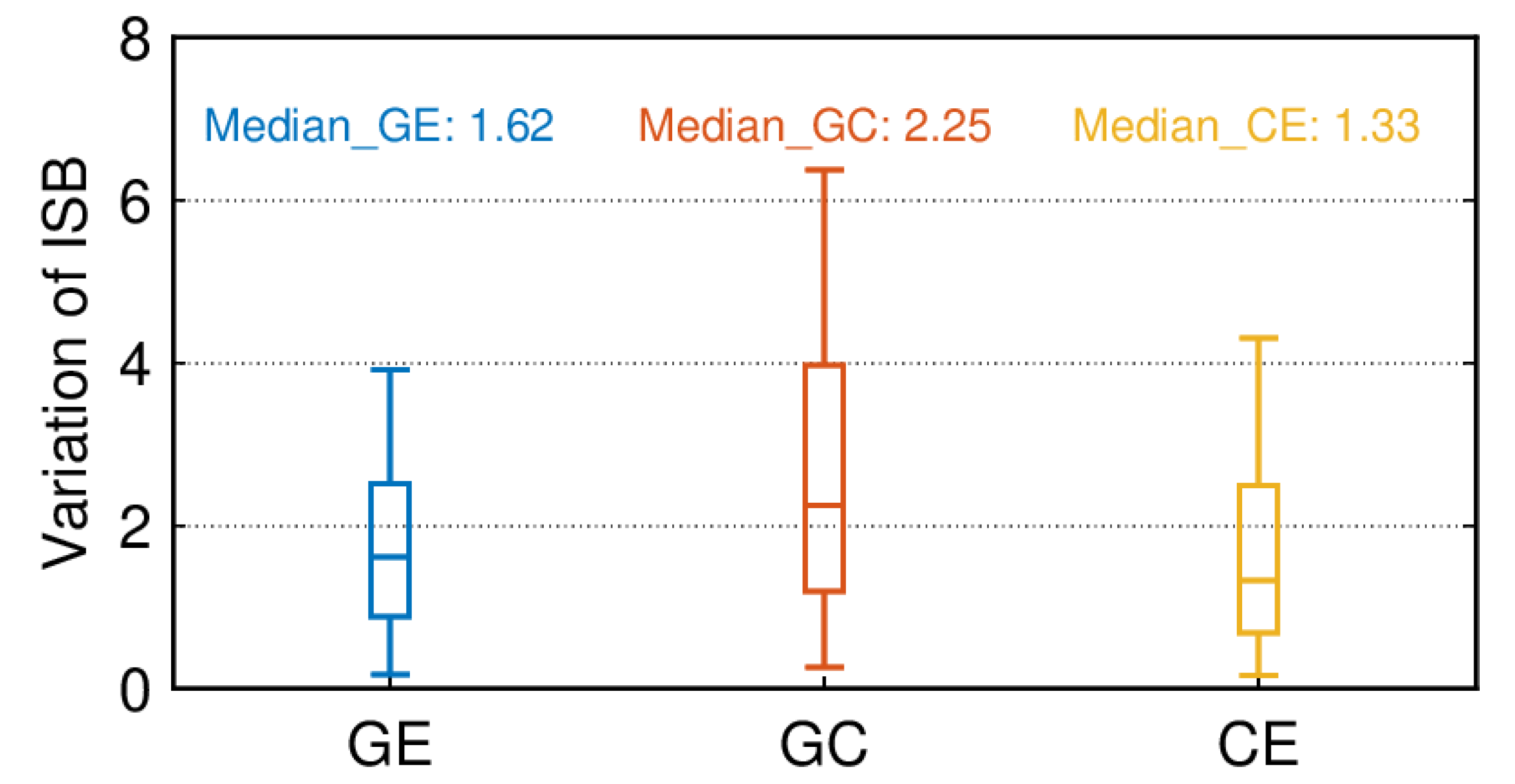
4.6. ISB
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zheng, F.; Gu, S.; Gong, X.; Lou, Y.; Fan, L.; Shi, C. Real-time single-frequency pseudorange positioning in China based on regional satellite clock and ionospheric models. GPS Solut. 2020, 24, 6. [Google Scholar] [CrossRef]
- Hu, J.; Li, P.; Zhang, X.; Bisnath, S.; Pan, L. Precise point positioning with BDS-2 and BDS-3 constellations: Ambiguity resolution and positioning comparison. Adv. Space Res. 2022, 70, 1830–1846. [Google Scholar] [CrossRef]
- Zhou, F.; Li, X.; Li, W.; Chen, W.; Dong, D.; Wickert, J.; Schuh, H. The Impact of Estimating High-Resolution Tropospheric Gradients on Multi-GNSS Precise Positioning. Sensors 2017, 17, 756. [Google Scholar] [CrossRef]
- Ma, H.; Psychas, D.; Xing, X.; Zhao, Q.; Verhagen, S.; Liu, X. Influence of the inhomogeneous troposphere on GNSS positioning and integer ambiguity resolution. Adv. Space Res. 2021, 67, 1914–1928. [Google Scholar] [CrossRef]
- Paziewski, J.; Wielgosz, P. Assessment of GPS + Galileo and multi-frequency Galileo single-epoch precise positioning with network corrections. GPS Solut. 2014, 18, 571–579. [Google Scholar] [CrossRef]
- Liu, J.; Cao, C. Development status and trend of global navigation satellite system. J. Navig. Position. 2020, 8, 1–8. [Google Scholar] [CrossRef]
- Yang, Z.; Xue, B. The developed procedures and developing trends of the American navigation satellites. J. Navig. Position. 2021, 9, 1–12. [Google Scholar] [CrossRef]
- Montenbruck, O.; Steigenberger, P.; Hauschild, A. Broadcast versus precise ephemerides: A multi-GNSS perspective. GPS Solut. 2015, 19, 321–333. [Google Scholar] [CrossRef]
- Xu, Y.; Ji, S. Data quality assessment and the positioning performance analysis of BeiDou in Hong Kong. Surv. Rev. 2015, 47, 446–457. [Google Scholar] [CrossRef]
- Robustelli, U.; Pugliano, G. Galileo Single Point Positioning Assessment Including FOC Satellites in Eccentric Orbits. Remote Sens. 2019, 11, 1555. [Google Scholar] [CrossRef]
- CSNO. The Current Constellation of the BDS System. China Satellite Navigation Office. 2021. Available online: http://www.csno-tarc.cn/system/constellation (accessed on 2 June 2022).
- Yang, Z.; Xue, B. The developed procedures and developing trends of BeiDou satellite navigation system. J. Navig. Position. 2022, 10, 1–14. [Google Scholar] [CrossRef]
- Yang, Y.; Li, J.; Wang, A.; Xu, J.; He, H.; Guo, H.; Shen, J.; Dai, X. Preliminary assessment of the navigation and positioning performance of BeiDou regional navigation satellite system. Sci. China Earth Sci. 2014, 57, 144–152. [Google Scholar] [CrossRef]
- Guo, F.; Zhang, X.; Wang, J. Timing group delay and differential code bias corrections for BeiDou positioning. J. Geod. 2015, 89, 427–445. [Google Scholar] [CrossRef]
- Padokhin, A.M.; Mylnikova, A.A.; Yasyukevich, Y.V.; Morozov, Y.V.; Kurbatov, G.A.; Vesnin, A.M. Galileo E5 AltBOC Signals: Application for Single-Frequency Total Electron Content Estimations. Remote. Sens. 2021, 13, 3973. [Google Scholar] [CrossRef]
- Luo, X.; Lou, Y.; Gong, X.; Gu, S.; Chen, B. Benefit of Sparse Reference Network in BDS Single Point Positioning with Single-Frequency Measurements. J. Navig. 2018, 71, 403–418. [Google Scholar] [CrossRef]
- Zhang, Z.; Pan, L. Current performance of open position service with almost fully deployed multi-GNSS constellations: GPS, GLONASS, Galileo, BDS-2, and BDS-3. Adv. Space Res. 2022, 69, 1994–2019. [Google Scholar] [CrossRef]
- Blanco-Delgado, N.; Nunes, F.D. Satellite selection based on WDOP concept and convex geometry. In Proceedings of the 2010 5th ESA Workshop on Satellite Navigation Technologies and European Workshop on GNSS Signals and Signal Processing (NAVITEC), Noordwijk, The Netherlands, 8–10 December 2010; pp. 1–8. [Google Scholar] [CrossRef]
- Klobuchar, J.A. Ionospheric Time-Delay Algorithm for Single-Frequency GPS Users. IEEE Trans. Aerosp. Electron. Syst. 1987, 3, 325–331. [Google Scholar] [CrossRef]
- Wu, X.; Hu, X.; Wang, G.; Zhong, H.; Tang, C. Evaluation of COMPASS ionospheric model in GNSS positioning. Adv. Space Res. 2013, 51, 959–968. [Google Scholar] [CrossRef]
- Yang, C.; Guo, J.; Geng, T.; Zhao, Q.; Jiang, K.; Xie, X.; Lv, Y. Assessment and Comparison of Broadcast Ionospheric Models: NTCM-BC, BDGIM, and Klobuchar. Remote Sens. 2020, 12, 1215. [Google Scholar] [CrossRef]
- Li, Q.; Su, X.; Xu, Y.; Ma, H.; Liu, Z.; Cui, J.; Geng, T. Performance Analysis of GPS/BDS Broadcast Ionospheric Models in Standard Point Positioning during 2021 Strong Geomagnetic Storms. Remote Sens. 2022, 14, 4424. [Google Scholar] [CrossRef]
- Li, M.; Yuan, Y.; Wang, N.; Li, Z.; Huo, X. Performance of various predicted GNSS global ionospheric maps relative to GPS and JASON TEC data. GPS Solut. 2018, 22, 55. [Google Scholar] [CrossRef]
- Pan, L.; Cai, C.; Santerre, R.; Zhang, X. Performance evaluation of single-frequency point positioning with GPS, GLONASS, BeiDou and Galileo. Surv. Rev. 2017, 49, 197–205. [Google Scholar] [CrossRef]
- Ryan, S.; Petovello, M.; Lachapelle, G. Augmentation of GPS for Ship Navigation in Constricted Water Ways. In Proceedings of the 1998 National Technical Meeting of The Institute of Navigation, Long Beach, CA, USA, 21–23 January 1998; pp. 459–467. [Google Scholar]
- Cai, C.; Gao, Y.; Pan, L.; Dai, W. An analysis on combined GPS/COMPASS data quality and its effect on single point positioning accuracy under different observing conditions. Adv. Space Res. 2014, 54, 818–829. [Google Scholar] [CrossRef]
- Cai, C.; Luo, X.; Liu, Z.; Xiao, Q. Galileo Signal and Positioning Performance Analysis Based on Four IOV Satellites. J. Navig. 2014, 67, 810–824. [Google Scholar] [CrossRef]
- Odolinski, R.; Teunissen, P.J.G.; Odijk, D. First combined COMPASS/BeiDou-2 and GPS positioning results in Australia. Part I: Single-receiver and relative code-only positioning. J. Spat. Sci. 2014, 59, 3–24. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, J. GNSS receiver autonomous integrity monitoring (RAIM) algorithm based on robust estimation. Geod. Geodyn. 2016, 7, 117–123. [Google Scholar] [CrossRef]
- Wang, J.; Knight, N.L.; Lu, X. Impact of the GNSS Time Offsets on Positioning Reliability. J. Glob. Position. Syst. 2011, 10, 165–172. [Google Scholar] [CrossRef]
- Teng, Y.; Wang, J. New Characteristics of Geometric Dilution of Precision (GDOP) for Multi-GNSS Constellations. J. Navig. 2014, 67, 1018–1028. [Google Scholar] [CrossRef]
- Montenbruck, O.; Hauschild, A.; Hessels, U. Characterization of GPS/GIOVE sensor stations in the CONGO network. GPS Solut. 2011, 15, 193–205. [Google Scholar] [CrossRef]
- Zeng, A.; Yang, Y.; Ming, F.; Jing, Y. BDS–GPS inter-system bias of code observation and its preliminary analysis. GPS Solut. 2017, 21, 1573–1581. [Google Scholar] [CrossRef]
- Zhou, F.; Dong, D.; Li, W.; Jiang, X.; Wickert, J.; Schuh, H. GAMP: An open-source software of multi-GNSS precise point positioning using undifferenced and uncombined observations. GPS Solut. 2018, 22, 33. [Google Scholar] [CrossRef]
- Yang, Y.; Li, J.; Xu, J.; Tang, J.; Guo, H.; He, H. Contribution of the Compass satellite navigation system to global PNT users. Chin. Sci. Bull. 2011, 56, 2813–2819. [Google Scholar] [CrossRef]
- Geng, J.; Meng, X.; Dodson, A.H.; Teferle, F.N. Integer ambiguity resolution in precise point positioning: Method comparison. J. Geod. 2010, 84, 569–581. [Google Scholar] [CrossRef]

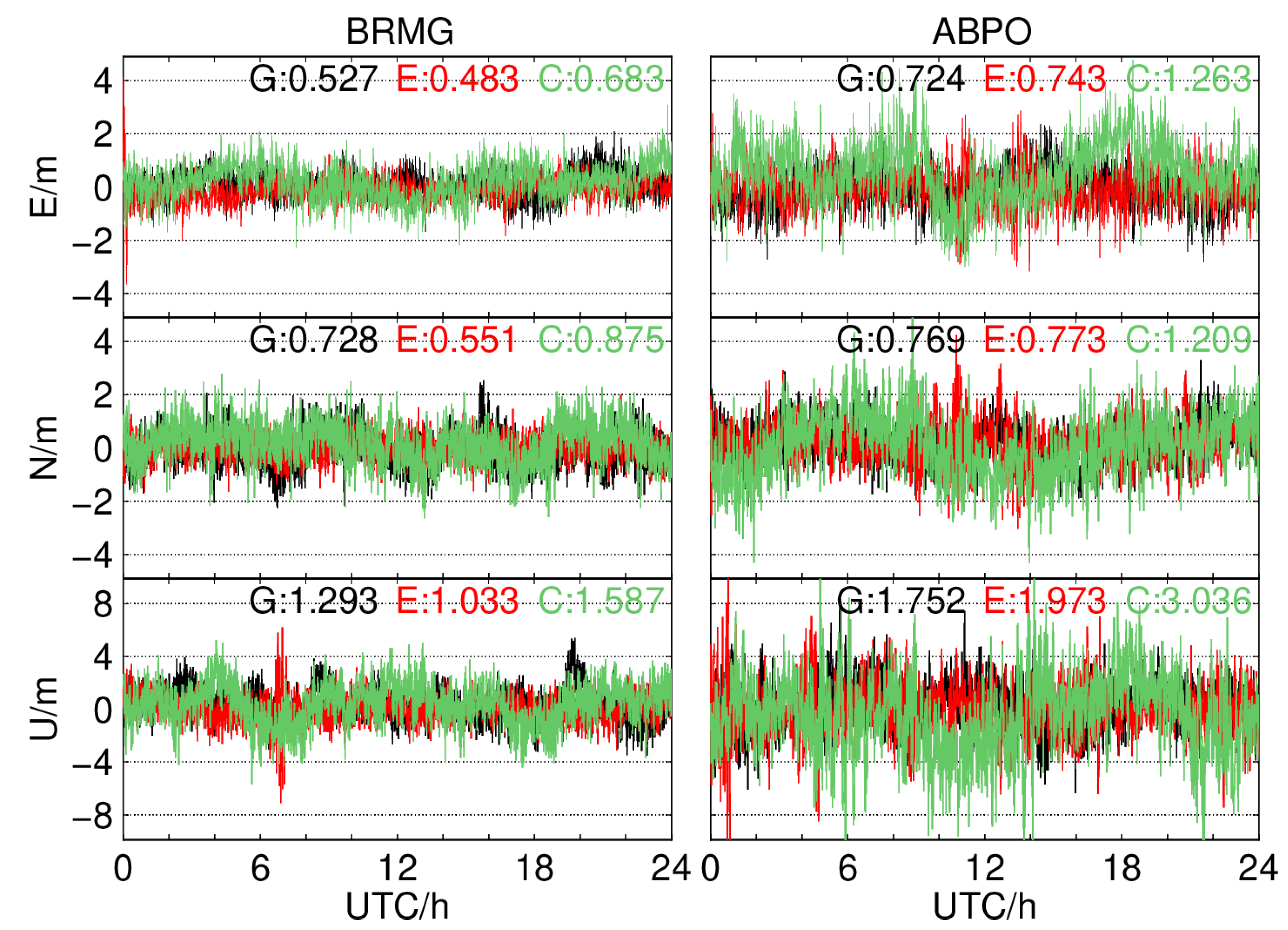
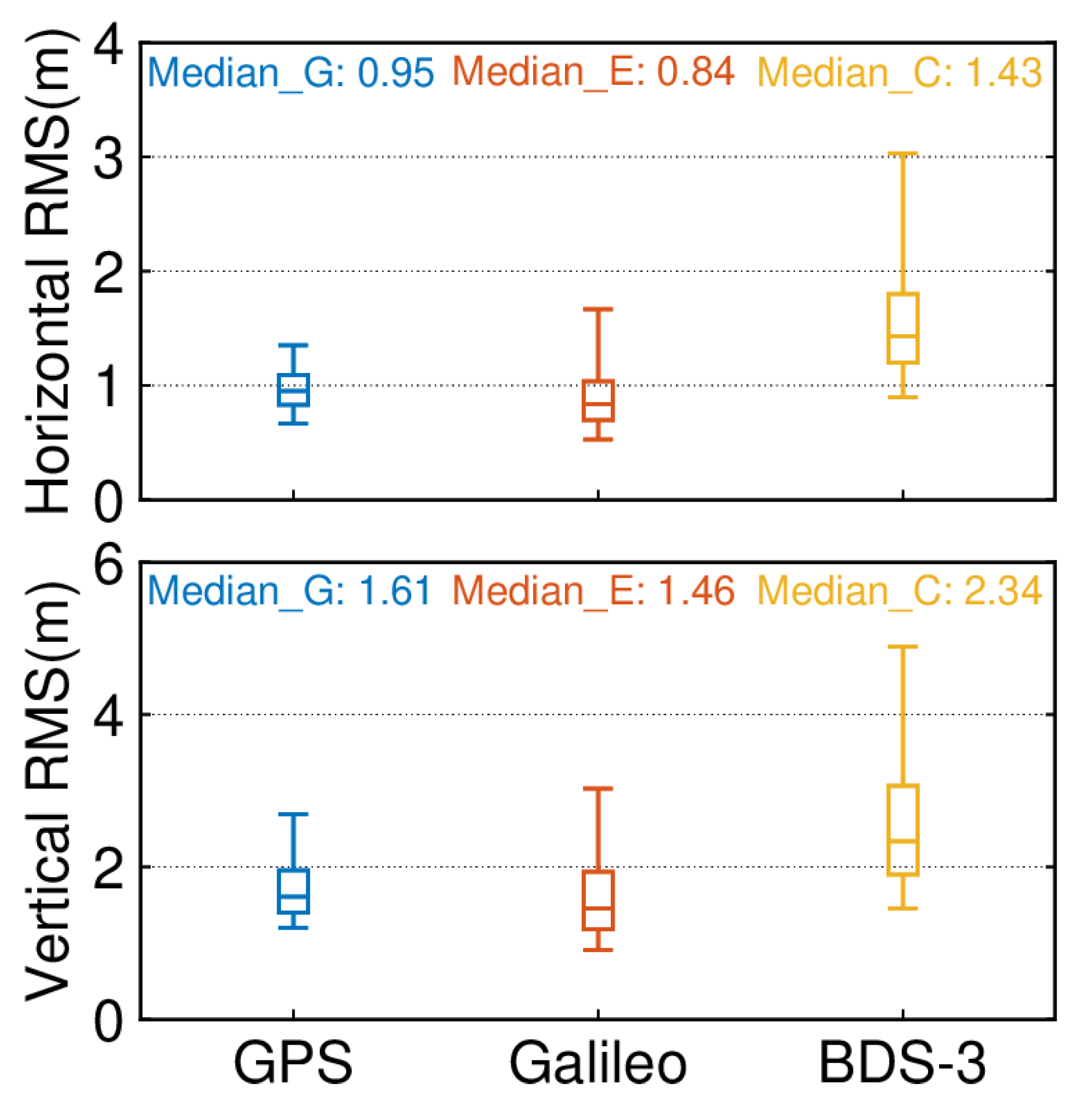
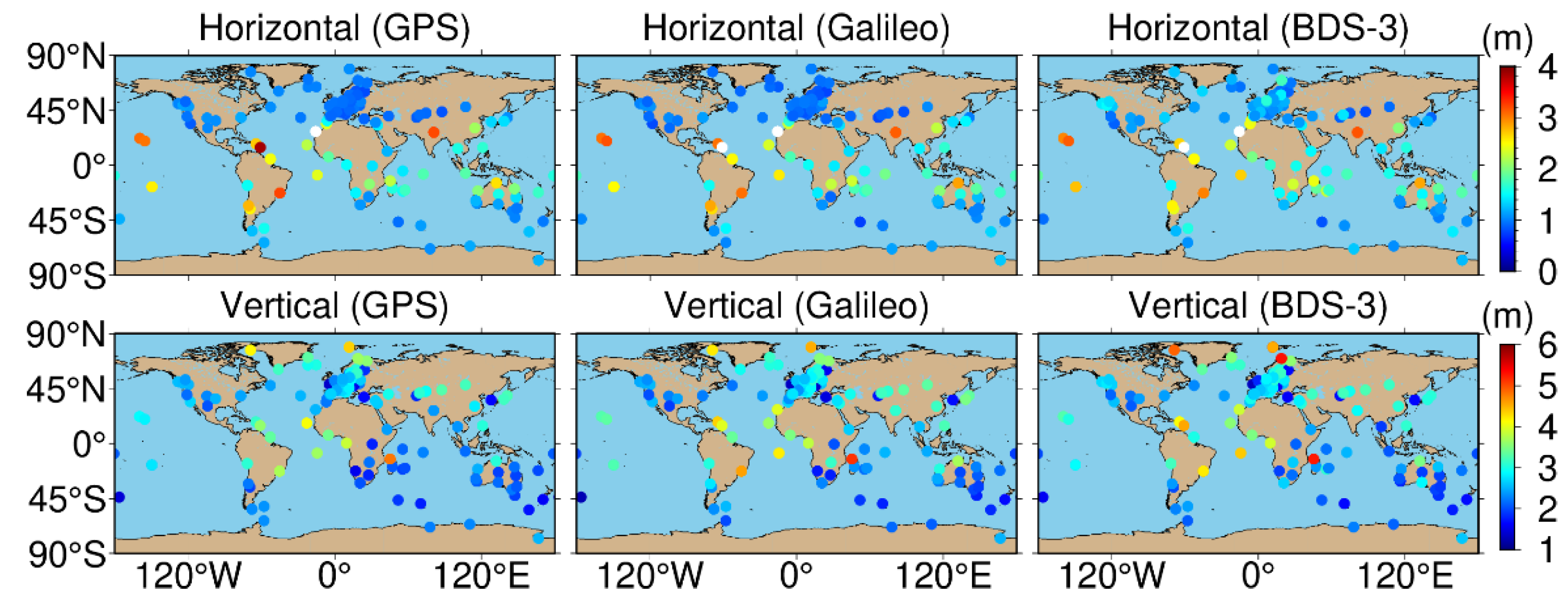

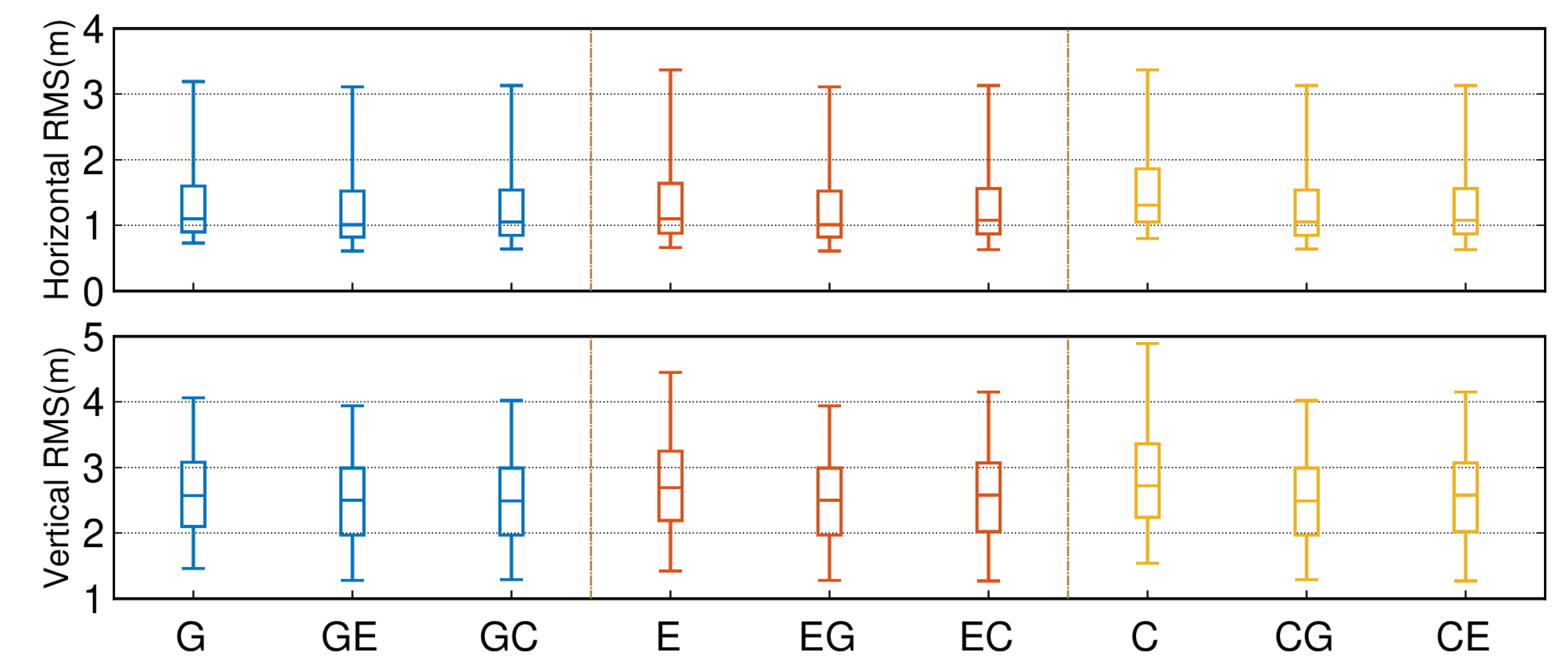
| Items | Strategies |
|---|---|
| Number of tracking stations | 145 |
| Number of satellites | GPS(32), BDS-3(30), Galileo(30) |
| Signal selection | GPS(L1, L2), BDS-3(B1, B3), Galileo(E1, E5a) |
| Sampling rate | 30 s |
| Satellite elevation cut-off | 7° |
| Weight of observation value | Prior standard deviation of measurement error |
| Tropospheric delay | Saastamoinen delay model |
| Ionospheric delay | Single frequency and IF combination |
| Satellite Type Added | Number Of Stations with Gain | Number of Stations with Reduced |
|---|---|---|
| MEO+IGSO | 50 | 53 |
| MEO+IGSO+GEO | 40 | 30 |
| Component | Sys | Negative Gain | Median | Positive Gain | Median |
|---|---|---|---|---|---|
| Horizontal | GE | 13 | −3.2% | 132 | 7.4% |
| GC | 14 | −3.6% | 131 | 14.2% | |
| EG | 2 | −2.0% | 143 | 7.2% | |
| EC | 17 | −1.2% | 128 | 12.2% | |
| CG | 20 | −1.6% | 125 | 5.5% | |
| CE | 51 | −3.0% | 94 | 5.4% | |
| Vertical | GE | 24 | −2.2% | 121 | 6.9% |
| GC | 20 | −2.9% | 125 | 8.4% | |
| EG | 28 | −1.0% | 117 | 5.2% | |
| EC | 24 | −4.2% | 121 | 7.3% | |
| CG | 28 | −1.7% | 117 | 4.6% | |
| CE | 30 | −1.9% | 115 | 5.2% |
| Receiver | Model | Number |
|---|---|---|
| JAVAD | TRE_3 | 7 |
| TRE_3 DELTA | 17 | |
| LEICA | LEICA GR50 | 8 |
| SEPT | ASTERX4 | 4 |
| POLARX5 | 61 | |
| POLARX5TR | 19 | |
| TRIMBLE | ALLOY | 23 |
| TRIMBLE | NETR9 | 4 |
| Station | Receiver | G-E | G-C | C-E | |||
|---|---|---|---|---|---|---|---|
| Mean | STD | Mean | STD | Mean | STD | ||
| enao | JAVAD TRE_3 | −20.51 | ±4.90 | 80.24 | ±6.83 | −100.68 | ±4.68 |
| sgpo | JAVAD TRE_3 | −20.49 | ±4.81 | 81.43 | ±6.90 | −102.14 | ±4.51 |
| nico | LEICA GR50 | −93.23 | ±4.89 | 75.64 | ±6.66 | −169.13 | ±4.61 |
| yebe | LEICA GR50 | −93.44 | ±4.87 | 73.9 | ±6.85 | −167.84 | ±4.76 |
| bshm | SEPT POLARX5 | −20.16 | ±4.89 | 47.53 | ±6.69 | −67.61 | ±4.44 |
| chpi | SEPT POLARX5 | −20.77 | ±4.64 | 41.93 | ±6.42 | −62.12 | ±4.53 |
| kir8 | TRIMBLE ALLOY | −50.15 | ±4.91 | 129.33 | ±6.66 | −179.35 | ±4.62 |
| mayg | TRIMBLE ALLOY | −47.44 | ±4.41 | 131.27 | ±6.46 | −178.75 | ±4.14 |
| bor1 | TRIMBLE NETR9 | −39.5 | ±4.96 | 95.19 | ±6.75 | −134.78 | ±4.76 |
| nabg | TRIMBLE NETR9 | −40.69 | ±5.02 | 88.29 | ±6.39 | −128.8 | ±4.28 |
| Station | Receiver | G-E | G-C | C-E | |||
|---|---|---|---|---|---|---|---|
| Mean | STD | Mean | STD | Mean | STD | ||
| enao | JAVAD TRE_3 | −2.58 | ±4.13 | 155.14 | ±5.78 | −157.67 | ±5.76 |
| sgpo | JAVAD TRE_3 | −3.61 | ±3.95 | 157.55 | ±5.50 | −161.17 | ±5.34 |
| nico | LEICA GR50 | −88.49 | ±3.49 | 201.12 | ±4.03 | −289.62 | ±4.32 |
| yebe | LEICA GR50 | −98.42 | ±4.03 | 195.31 | ±5.09 | −293.75 | ±5.10 |
| bshm | SEPT POLARX5 | −8.41 | ±5.01 | −4.26 | ±6.60 | −4.16 | ±6.64 |
| chpi | SEPT POLARX5 | −6.61 | ±4.02 | −22.36 | ±5.50 | −15.86 | ±5.67 |
| kir8 | TRIMBLE ALLOY | −64.94 | ±4.11 | 517.59 | ±5.10 | −452.53 | ±5.01 |
| mayg | TRIMBLE ALLOY | −69.06 | ±5.16 | 514.02 | ±6.33 | −444.76 | ±6.49 |
| bor1 | TRIMBLE NETR9 | −30.79 | ±5.57 | 408.88 | ±9.74 | −377.68 | ±12.74 |
| nabg | TRIMBLE NETR9 | −22.25 | ±3.82 | 385.06 | ±8.44 | −386.85 | ±8.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, F.; Wang, X. Some Key Issues on Pseudorange-Based Point Positioning with GPS, BDS-3, and Galileo Observations. Remote Sens. 2023, 15, 797. https://doi.org/10.3390/rs15030797
Zhou F, Wang X. Some Key Issues on Pseudorange-Based Point Positioning with GPS, BDS-3, and Galileo Observations. Remote Sensing. 2023; 15(3):797. https://doi.org/10.3390/rs15030797
Chicago/Turabian StyleZhou, Feng, and Xiaoyang Wang. 2023. "Some Key Issues on Pseudorange-Based Point Positioning with GPS, BDS-3, and Galileo Observations" Remote Sensing 15, no. 3: 797. https://doi.org/10.3390/rs15030797
APA StyleZhou, F., & Wang, X. (2023). Some Key Issues on Pseudorange-Based Point Positioning with GPS, BDS-3, and Galileo Observations. Remote Sensing, 15(3), 797. https://doi.org/10.3390/rs15030797






