A High-Precision Baseline Calibration Method Based on Estimation of Azimuth Fringe Frequency with THz Interferometry SAR
Abstract
:1. Introduction
2. Theory of High-Precision THz InSAR Model
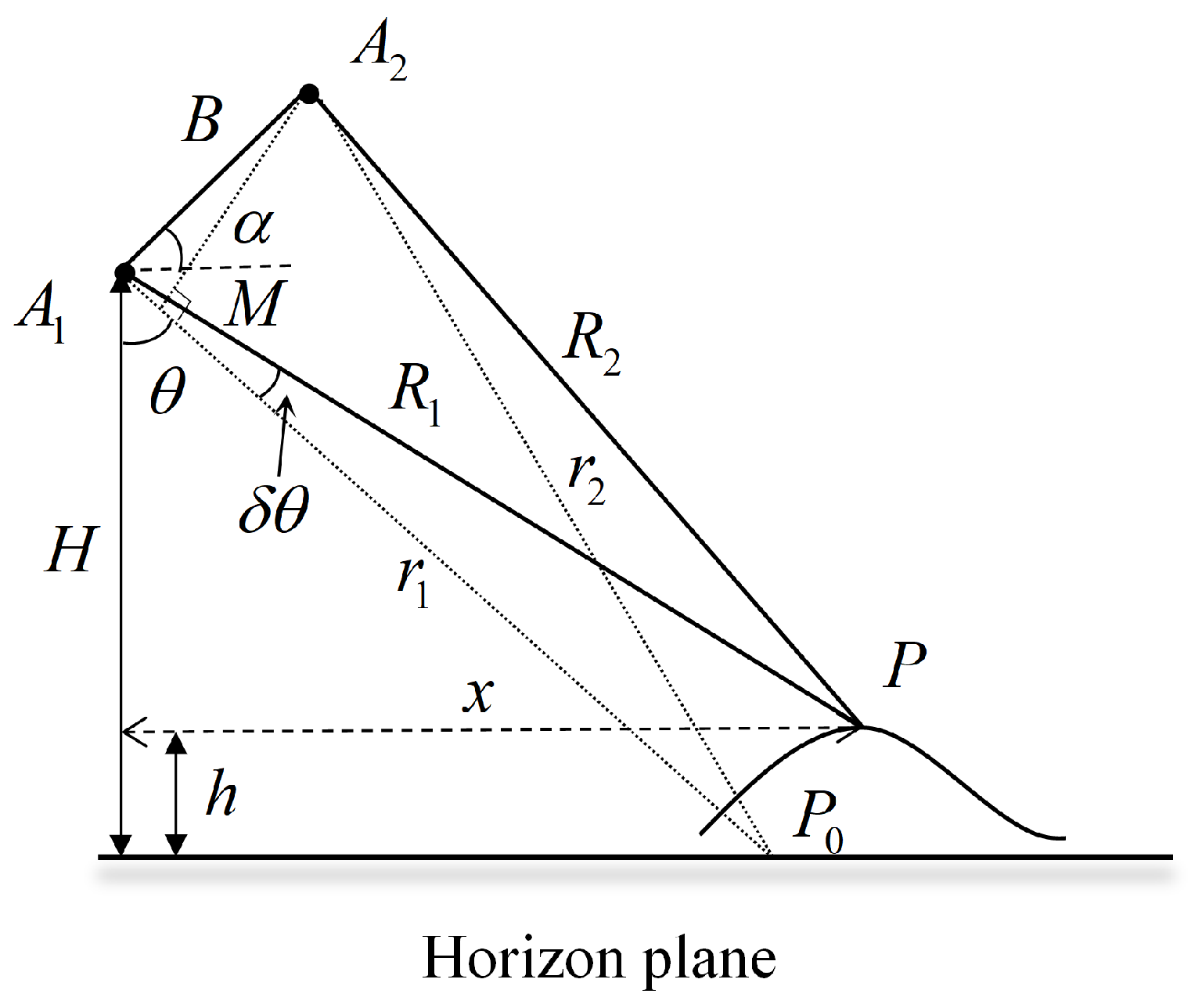
2.1. The Principle of SAR Interferometry
2.2. The Analysis of Height Errors Based on InSAR Parameter Errors
2.3. The Coherence of InSAR System
3. Processing of the EAFF Calibration Method
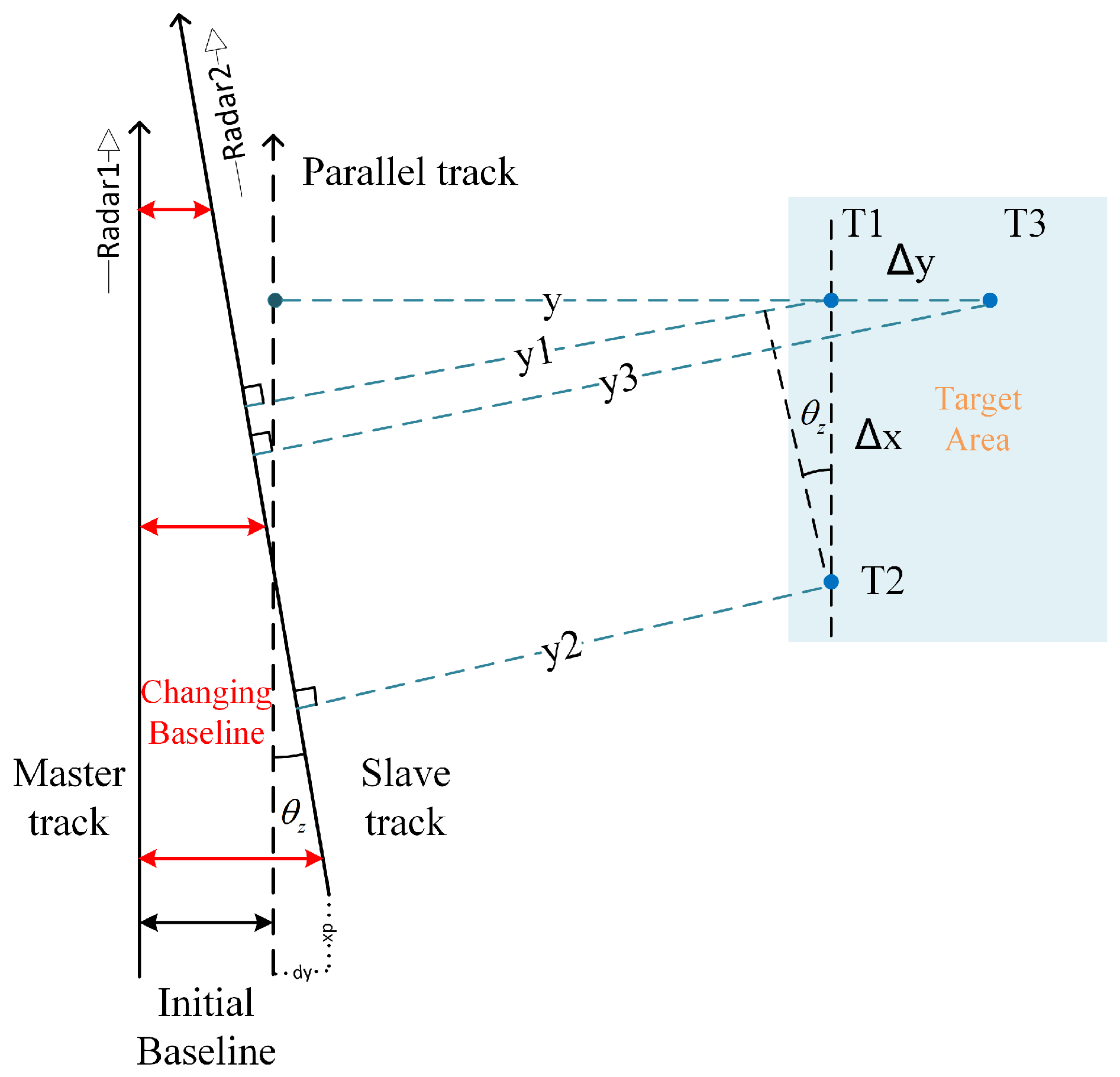
3.1. The Establishment of Models and Theoretical Framework
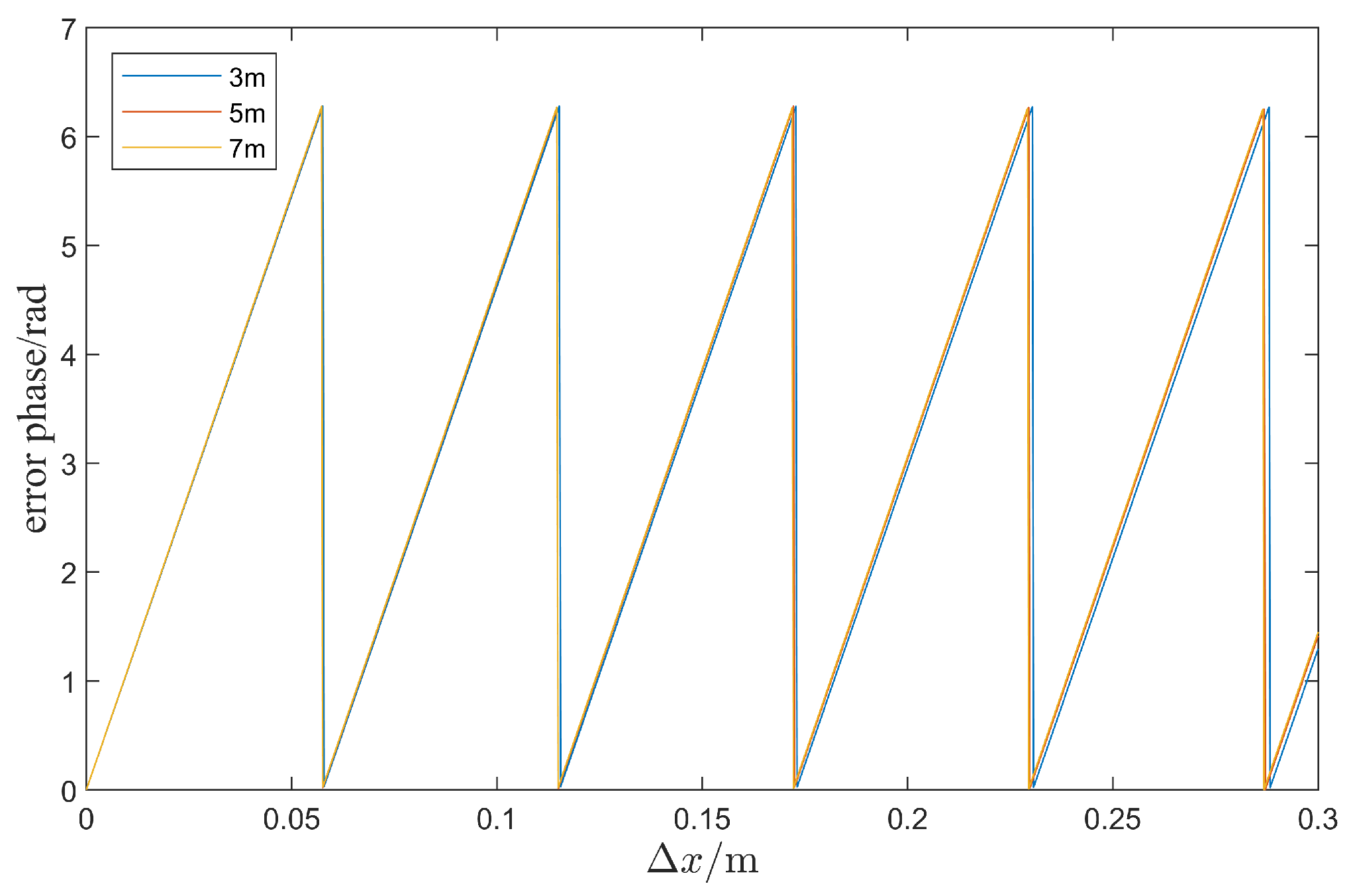
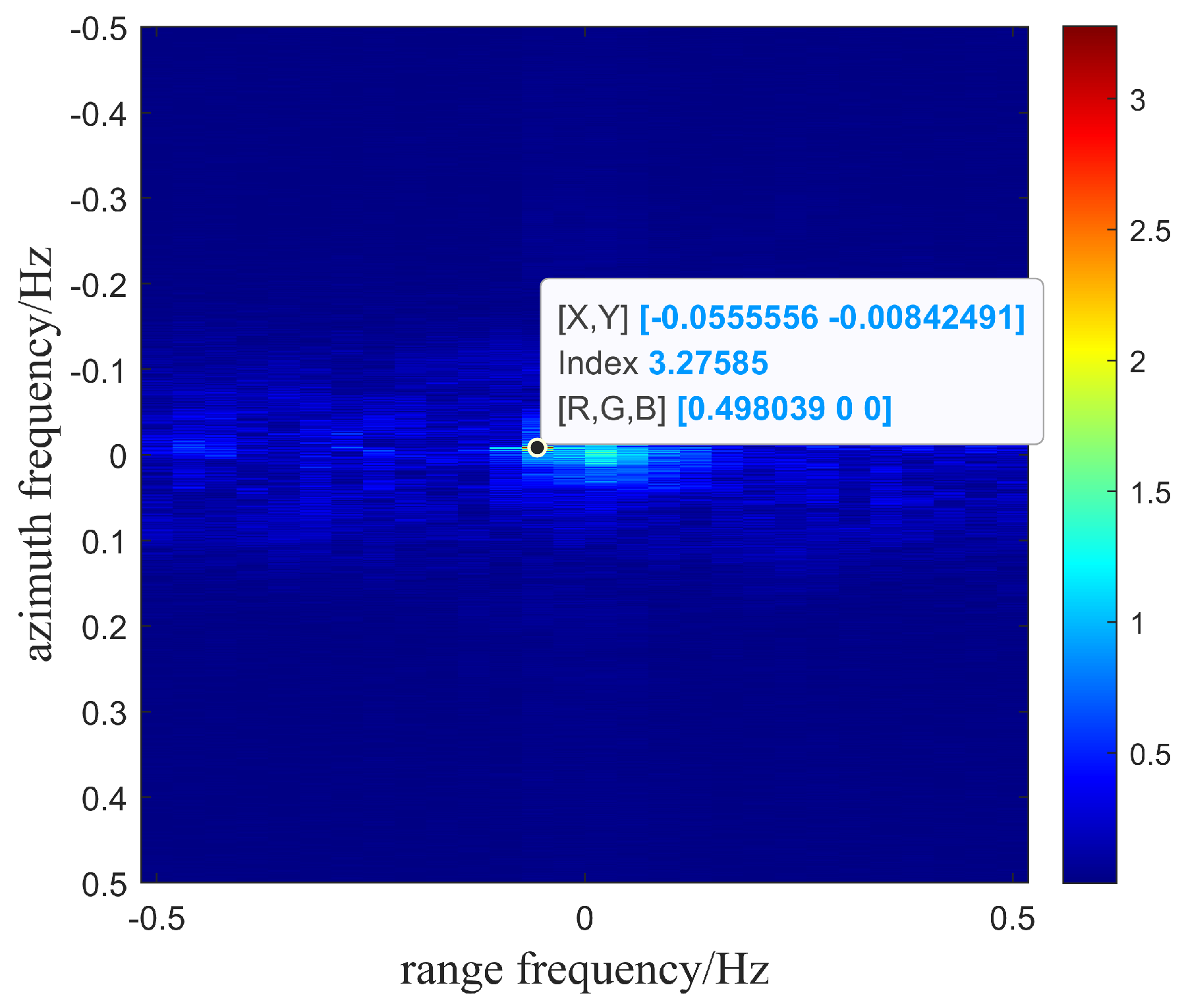
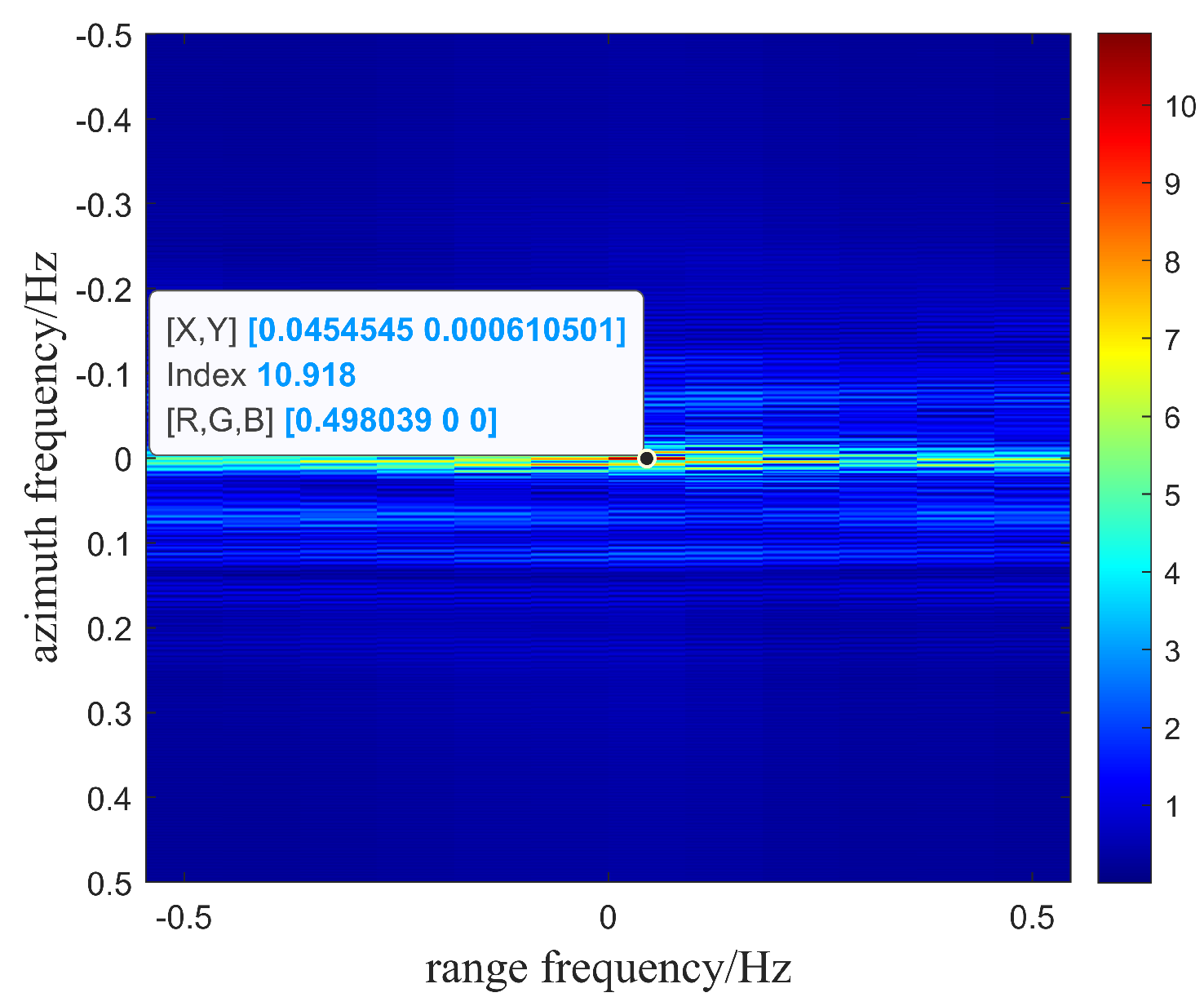
3.2. The Processing and Resolution Analysis of the EAFF Method
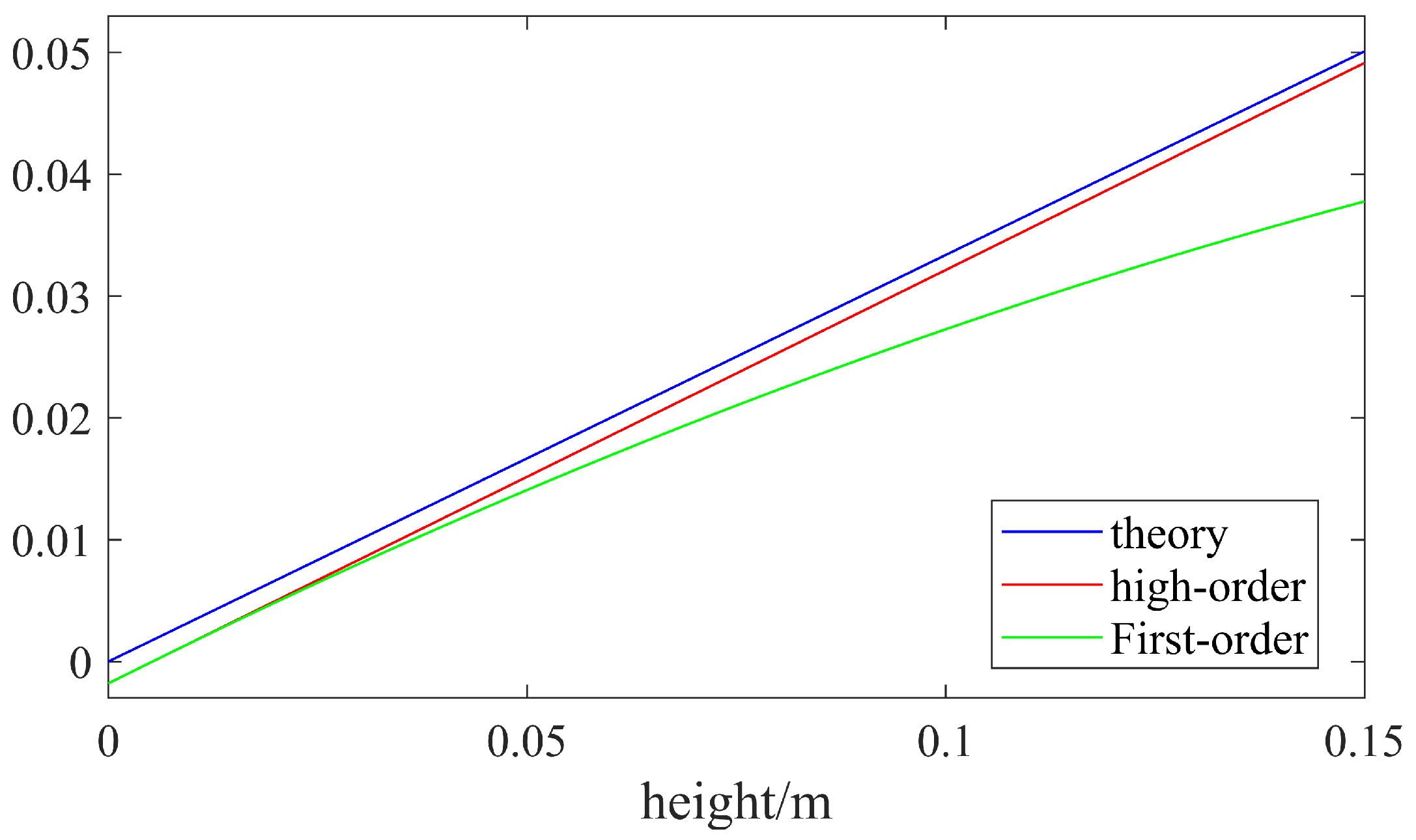
4. The Simulation for EAFF Baseline Calibration Accuracy
5. The Experimental Results for Repeat-Pass THz InSAR
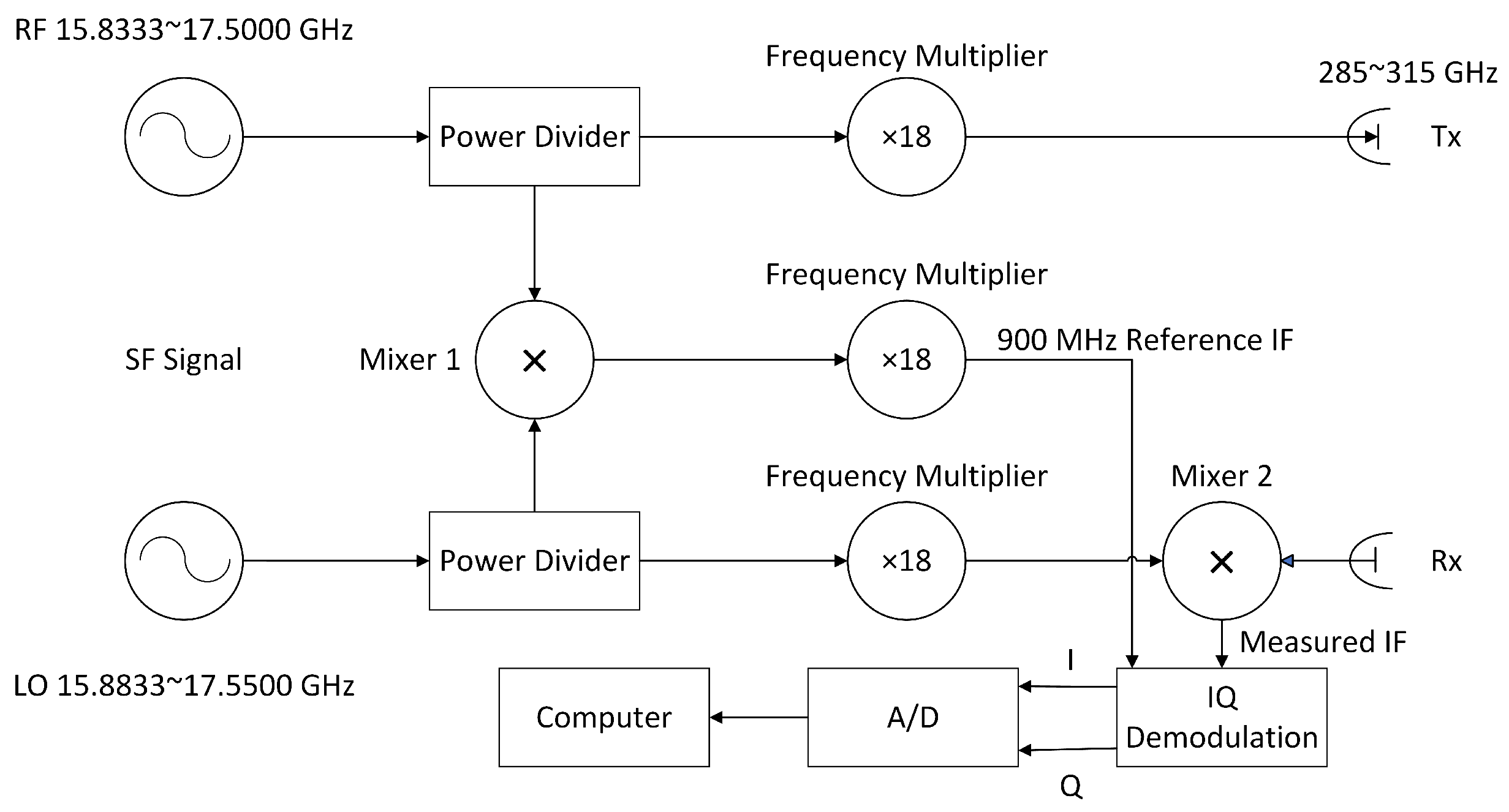
5.1. The Introduction of THz-SAR System
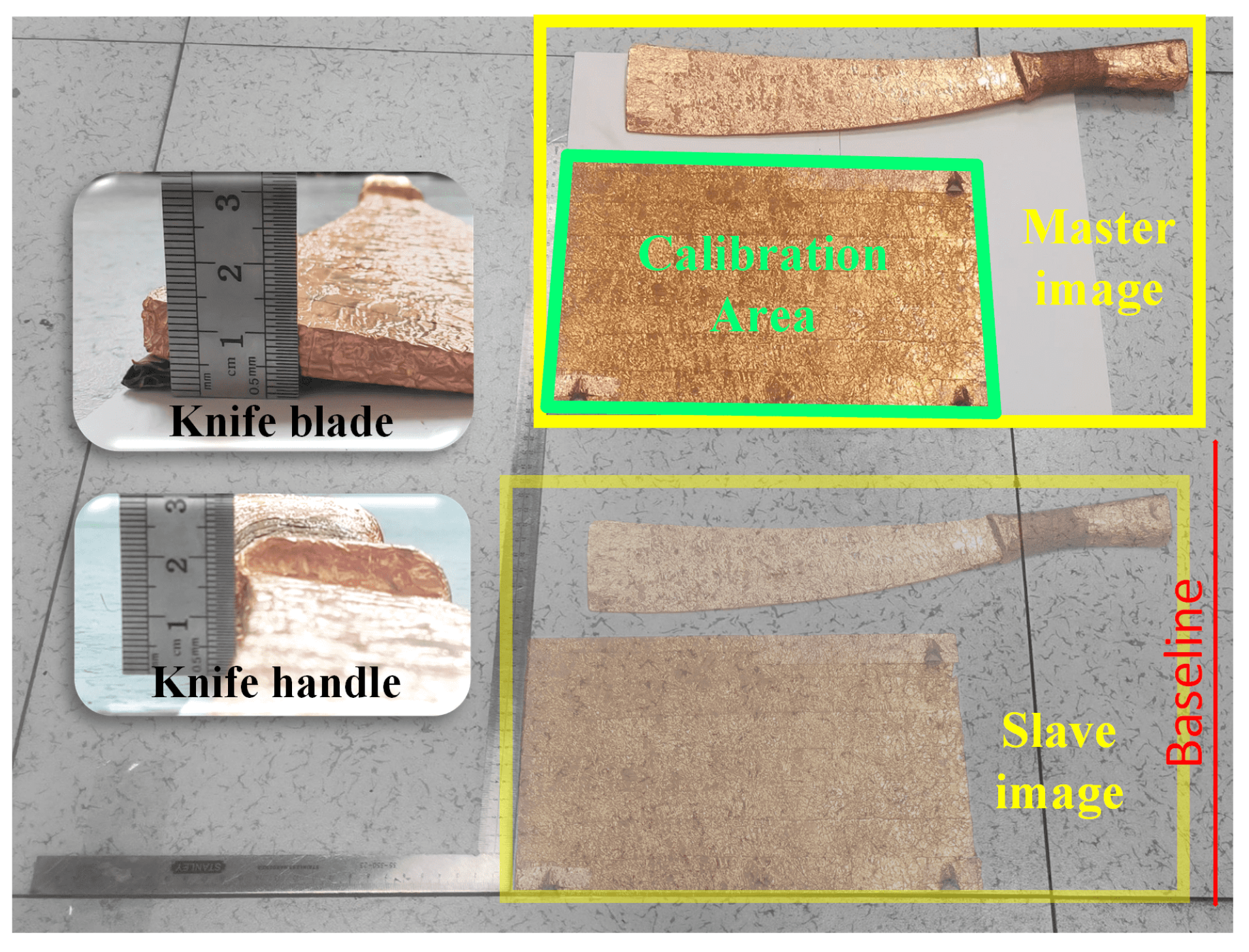
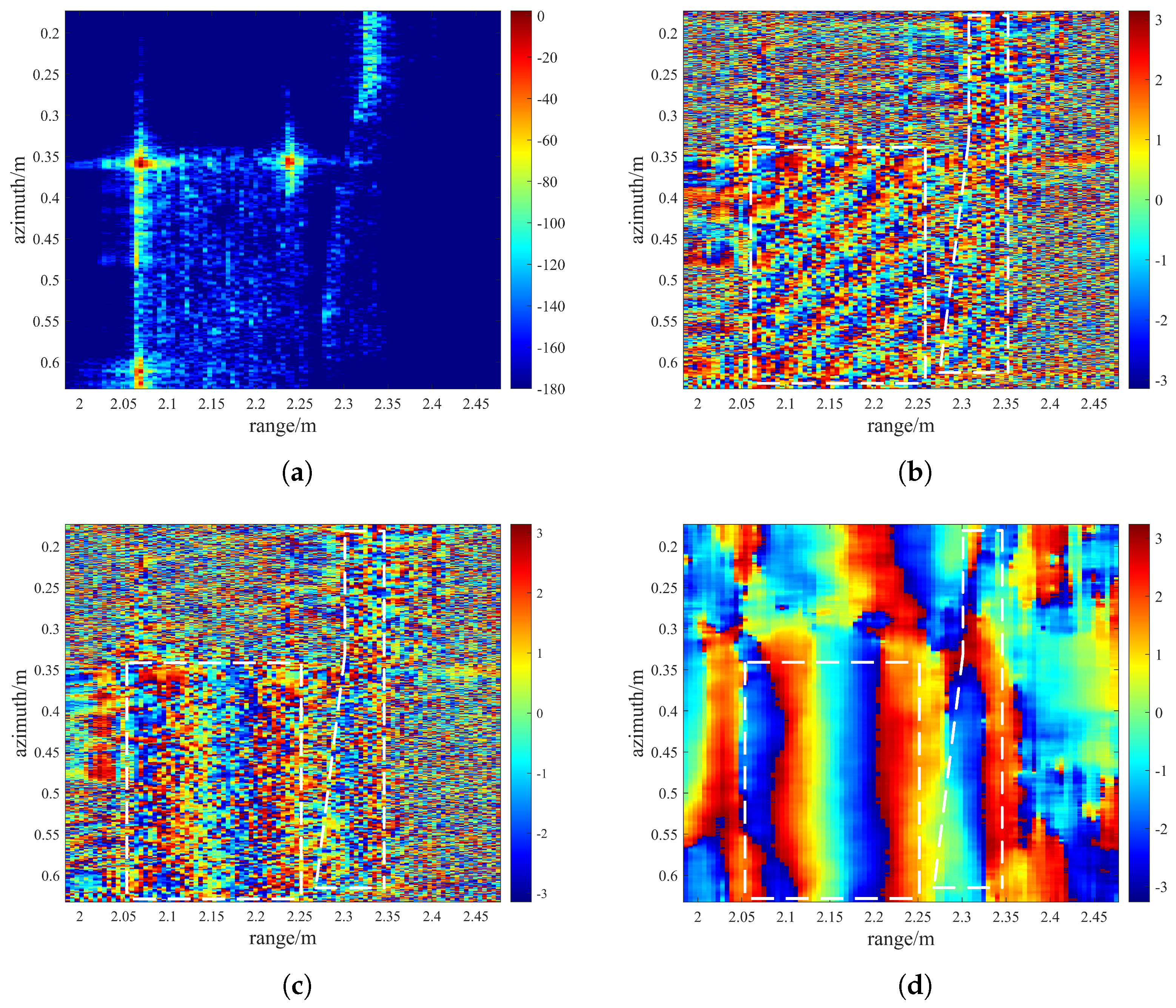
5.2. The Experiment of the Knife Model
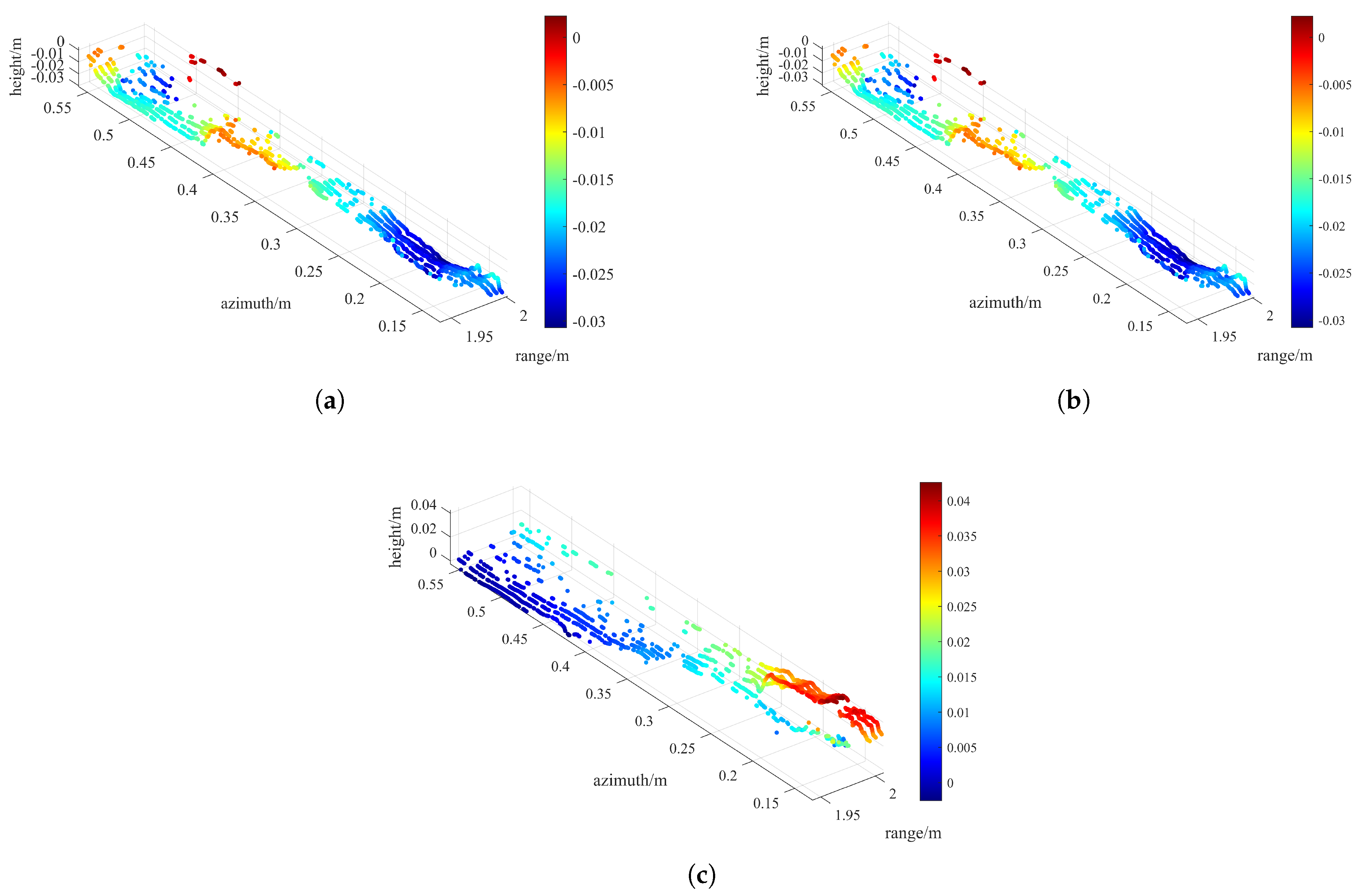
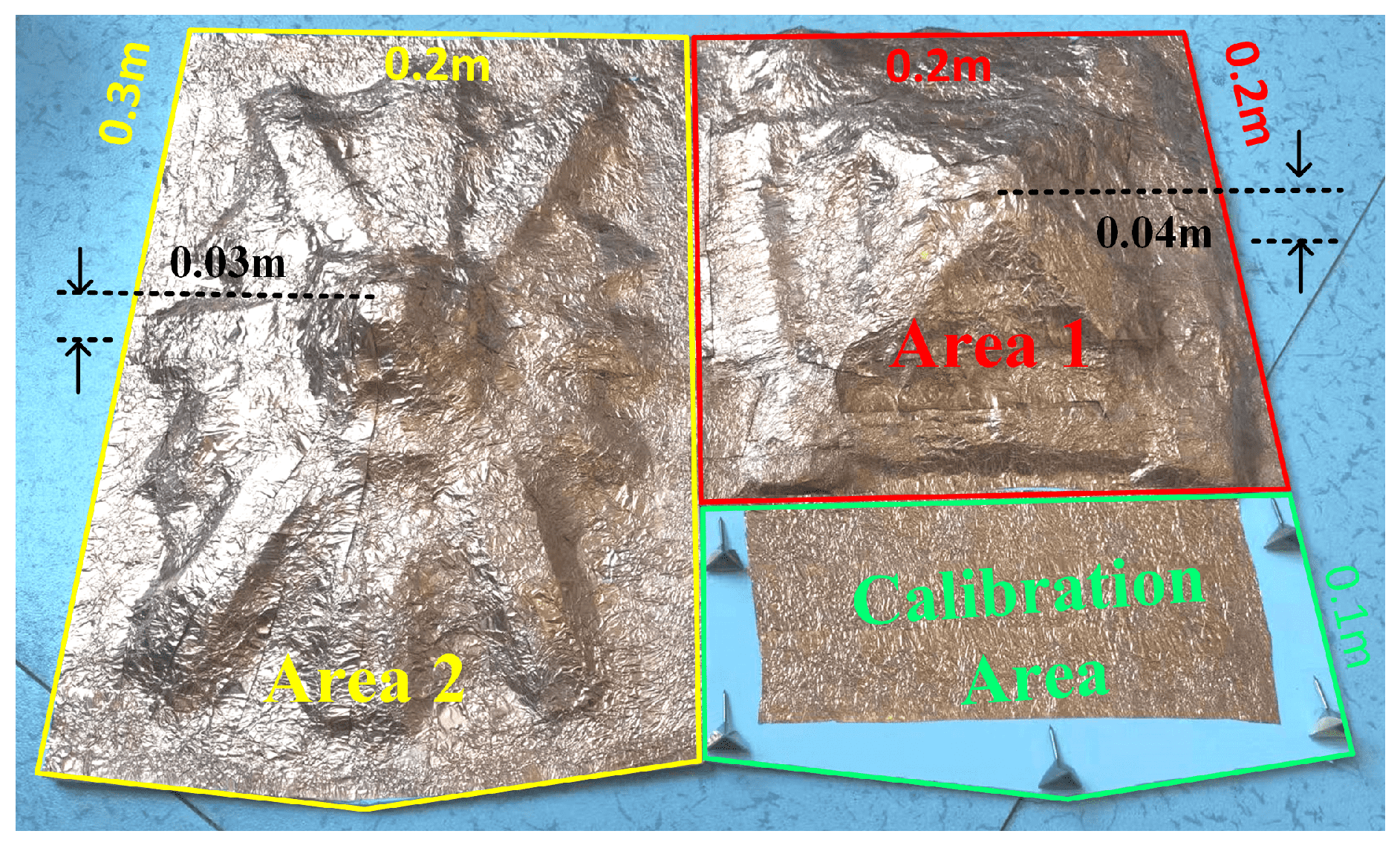
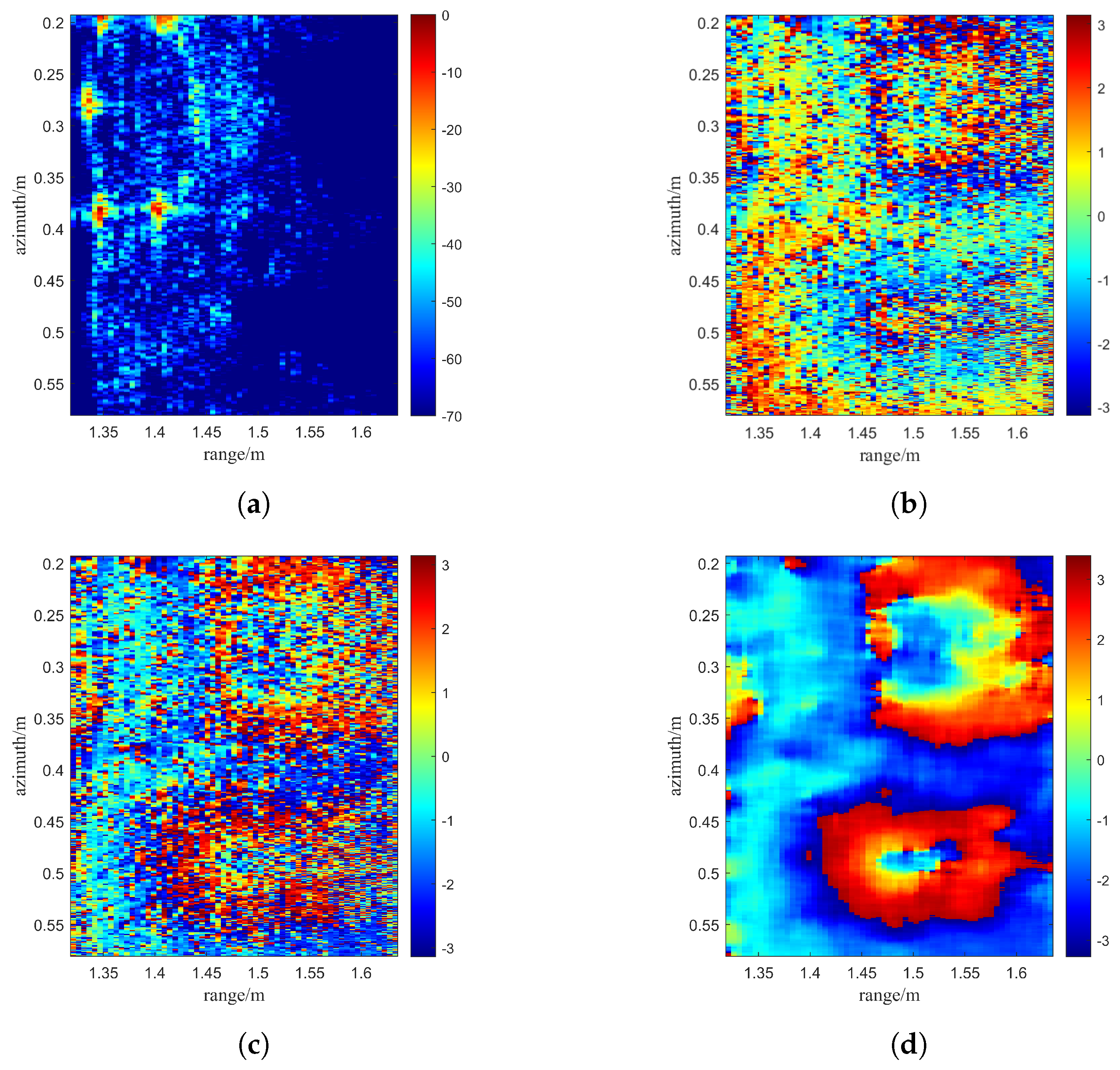
5.3. The Experiment of the Terrain Model
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Sheen, D.; McMakin, D.; Hall, T. Three-dimensional millimeter-wave imaging for concealed weapon detection. IEEE Trans. Microw. Theory Tech. 2001, 49, 1581–1592. [Google Scholar] [CrossRef]
- Gu, S.; Li, C.; Gao, X.; Sun, Z.; Fang, G. Three-Dimensional Image Reconstruction of Targets Under the Illumination of Terahertz Gaussian Beam—Theory and Experiment. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2241–2249. [Google Scholar] [CrossRef]
- Cooper, K.B.; Dengler, R.J.; Llombart, N.; Thomas, B.; Chattopadhyay, G.; Siegel, P.H. THz Imaging Radar for Standoff Personnel Screening. IEEE Trans. Terahertz Sci. Technol. 2011, 1, 169–182. [Google Scholar] [CrossRef]
- Palm, S.; Sommer, R.; Tessmann, A.; Stilla, U. Ultra-high resolution imaging of facades and vertical infrastructure by carborne sar and airborne csar. ISPRS Ann. Photogramm. Remote. Sens. Spat. Inf. Sci. 2019, IV-2/W7, 129–136. [Google Scholar] [CrossRef]
- Shi, S.; Li, C.; Hu, J.; Zhang, X.; Fang, G. Study of Phase Error Reconstruction and Motion Compensation for Terahertz SAR With Sparsity-Promoting Parameter Estimation. IEEE Trans. Terahertz Sci. Technol. 2021, 11, 122–134. [Google Scholar] [CrossRef]
- Fan, L.; Wang, H.; Yang, Q.; Wang, Y.; Deng, B.; Xiao, H. High Frame-Rate and Low-Latency Video SAR Based on Robust Doppler Parameters Estimation in the Terahertz Regime. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5207016. [Google Scholar] [CrossRef]
- Li, Z.; Mei, J.; Bai, J.; Xiao, Y.; Wang, Y.; Zhang, J. A terahertz synthetic aperture radar with centimeter-level resolution. In Proceedings of the 2021 46th International Conference on Infrared, Millimeter and Terahertz Waves (IRMMW-THz), Chengdu, China, 29 August–3 September 2021; pp. 1–2. [Google Scholar] [CrossRef]
- Mei-Yan, L.; Zhu-Yun, R.; Guang-Hui, L.; Cun-Lin, Z.; Fathy, A.E. THz ISAR imaging using GPU-accelerated phase compensated back projection algorithm. J. Infrared Millim. Waves 2022, 41, 448–456. [Google Scholar] [CrossRef]
- Rosen, P.; Hensley, S.; Joughin, I.; Li, F.; Madsen, S.; Rodriguez, E.; Goldstein, R. Synthetic aperture radar interferometry. Proc. IEEE 2000, 88, 333–382. [Google Scholar] [CrossRef]
- Zhang, G.; Li, C.; Wang, Z.; Hu, J.; Zheng, S.; Liu, X.; Fang, G. An Efficient Spectrum Reconstruction Algorithm for Non-Uniformly Sampled Signals and Its Application in Terahertz SAR. Remote Sens. 2023, 15, 4427. [Google Scholar] [CrossRef]
- Pohl, N.; Stanko, S.; Caris, M.; Tessmann, A.; Schlechtweg, M. An ultra-high resolution radar-system operating at 300 GHz. In Proceedings of the 2015 IEEE Topical Conference on Wireless Sensors and Sensor Networks (WiSNet), San Diego, CA, USA, 25–28 January 2015; pp. 62–64. [Google Scholar] [CrossRef]
- Cui, S.S.; Li, Q.; Chen, G.H. Terahertz digital holography image denoising using stationary wavelet transform. In Proceedings of the Selected Papers from Conferences of the Photoelectronic Technology Committee of the Chinese Society of Astronautics, Suzhou, China, 19–24 October 2014; Du, X., Fan, D., Le, J., Lv, Y., Yao, J., Bao, W., Wang, L., Eds.; PT II; Proceedings of SPIE 9522. SPIE: Bellingham, WA, USA, 2015. [Google Scholar]
- Small, D.; Werner, C.; Nuesch, D. Baseline modelling for ERS-1 SAR interferometry. In Proceedings of the IGARSS ’93—IEEE International Geoscience and Remote Sensing Symposium, Tokyo, Japan, 18–21 August 1993; Volume 3, pp. 1204–1206. [Google Scholar] [CrossRef]
- Joughin, I.; Winebrenner, D.; Fahnestock, M.; Kwok, R.; Krabill, W. Measurement of ice-sheet topography using satellite-radar interferometry. J. Glaciol. 1996, 42, 10–22. [Google Scholar] [CrossRef]
- Mou, J.; Wang, Y.; Hong, J.; Wang, Y.; Wang, A. Baseline Calibration of L-Band Spaceborne Bistatic SAR TwinSAR-L for DEM Generation. Remote Sens. 2023, 15, 3024. [Google Scholar] [CrossRef]
- Qi, Y.; Wang, Y.; Hong, J.; Du, S. Additional Reference Height Error Analysis for Baseline Calibration Based on a Distributed Target DEM in TwinSAR-L. Remote Sens. 2021, 13, 2750. [Google Scholar] [CrossRef]
- Gatelli, F.; Monti Guamieri, A.; Parizzi, F.; Pasquali, P.; Prati, C.; Rocca, F. The wavenumber shift in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 1994, 32, 855–865. [Google Scholar] [CrossRef]
- Xu, B.; Li, Z.; Zhu, Y.; Shi, J.; Feng, G. SAR Interferometric Baseline Refinement Based on Flat-Earth Phase without a Ground Control Point. Remote Sens. 2020, 12, 233. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, H.; Li, S.; Zeng, G. An Improved InSAR Baseline Estimation Based on Interferometric Fringe Frequency. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 4296–4299. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, Y.; Fu, H.; Zhu, J.; Yu, Y.; Li, R.; Zhang, S.; Qu, Z.; Hu, S. Parameterized Modeling and Calibration for Orbital Error in TanDEM-X Bistatic SAR Interferometry over Complex Terrain Areas. Remote Sens. 2021, 13, 5124. [Google Scholar] [CrossRef]
- Rodríguez, E.; Martín, J.M. Theory and Design of Interferometric Synthetic Aperture Radars; IET Digital Library. 1992. Available online: https://digital-library.theiet.org/content/journals/10.1049/ip-f-2.1992.0018 (accessed on 27 October 2023).
- Cumming, I.G.; Wong, F.H. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation. Artech House 2005, 1, 108–110. [Google Scholar]
- Just, D.; Bamler, R. Phase statistics of interferograms with applications to synthetic-aperture radar. Appl. Opt. 1994, 33, 4361–4368. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.S.; Hoppel, K.; Mango, S.; Miller, A. Intensity and phase statistics of multilook polarimetric and interferometric SAR imagery. IEEE Trans. Geosci. Remote Sens. 1994, 32, 1017–1028. [Google Scholar] [CrossRef]
- Chen, C.W. A Spectral Model for Multilook InSAR Phase Noise Due to Geometric Decorrelation. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5207611. [Google Scholar] [CrossRef]
- Lohman, R.; Simons, M. Some thoughts on the use of InSAR data to constrain models of surface deformation: Noise structure and data downsampling. Geochem. Geophys. Geosystems 2005, 6. [Google Scholar] [CrossRef]
- Simons, M.; Fialko, Y.; Rivera, L. Coseismic deformation from the 1999 Mw 7.1 Hector Mine, California, Earthq. Inferred InSAR GPS Obs. Bull. Seismol. Soc. Am. 2002, 92, 1390–1402. [Google Scholar] [CrossRef]
- Spagnolini, U. 2-D phase unwrapping and instantaneous frequency estimation. IEEE Trans. Geosci. Remote Sens. 1995, 33, 579–589. [Google Scholar] [CrossRef]
- Eichel, P.H.; Ghiglia, D.C.; Jakowatz, C.V., Jr. Spotlight SAR Interferometry for Terrain Elevation Mapping and Interferometric Change Detection; USDOE: Washington, DC, USA, 1996. [Google Scholar] [CrossRef]

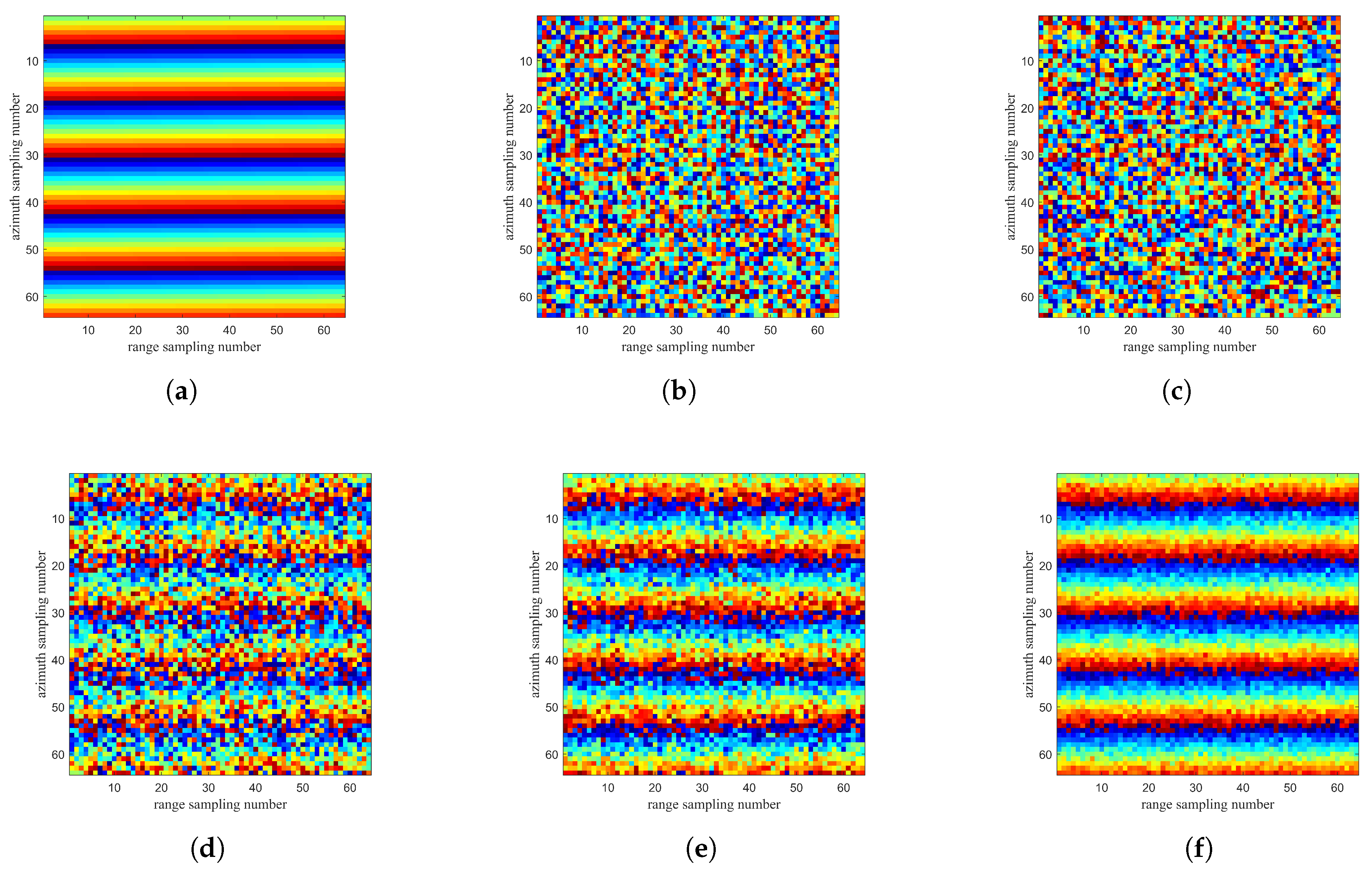
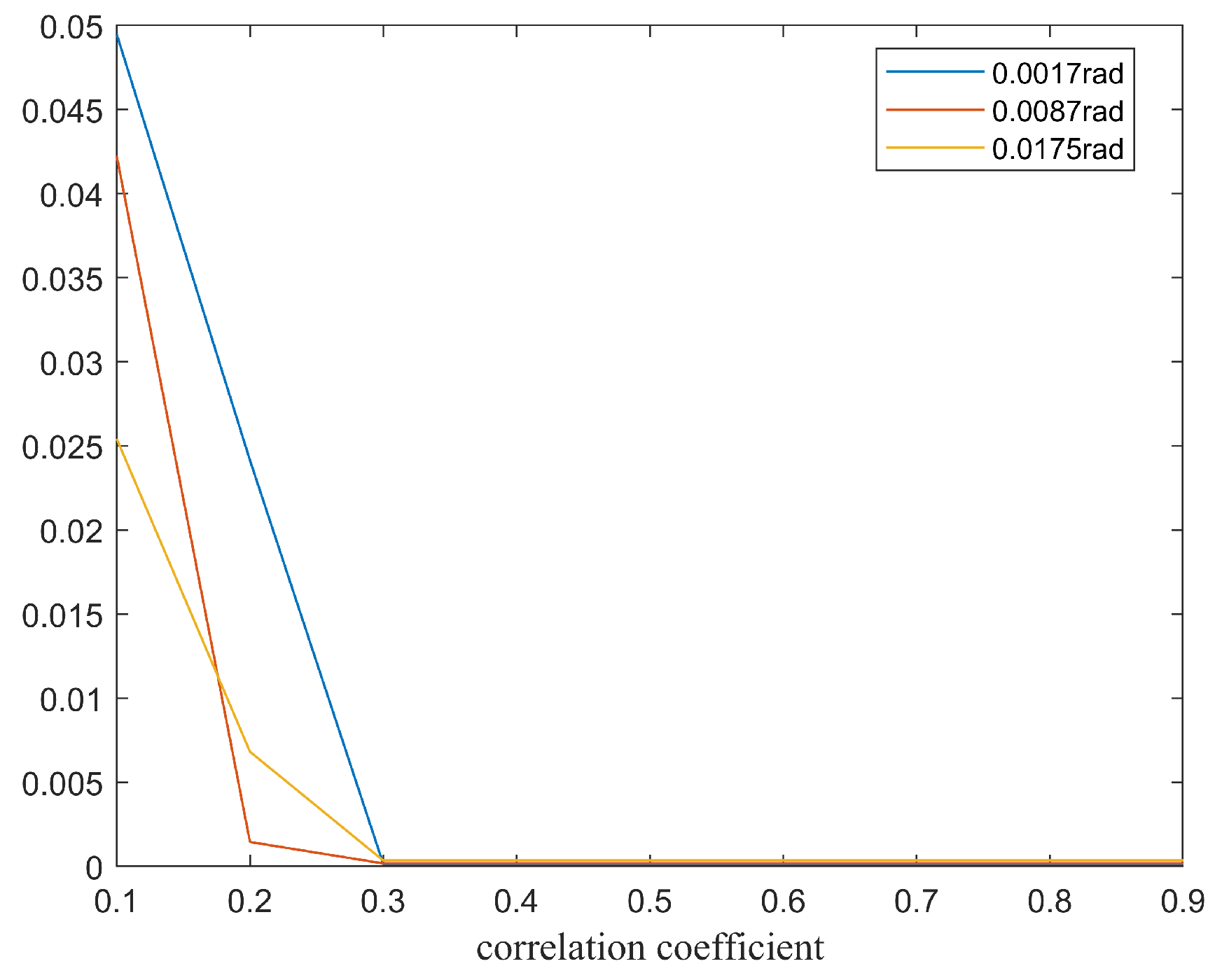
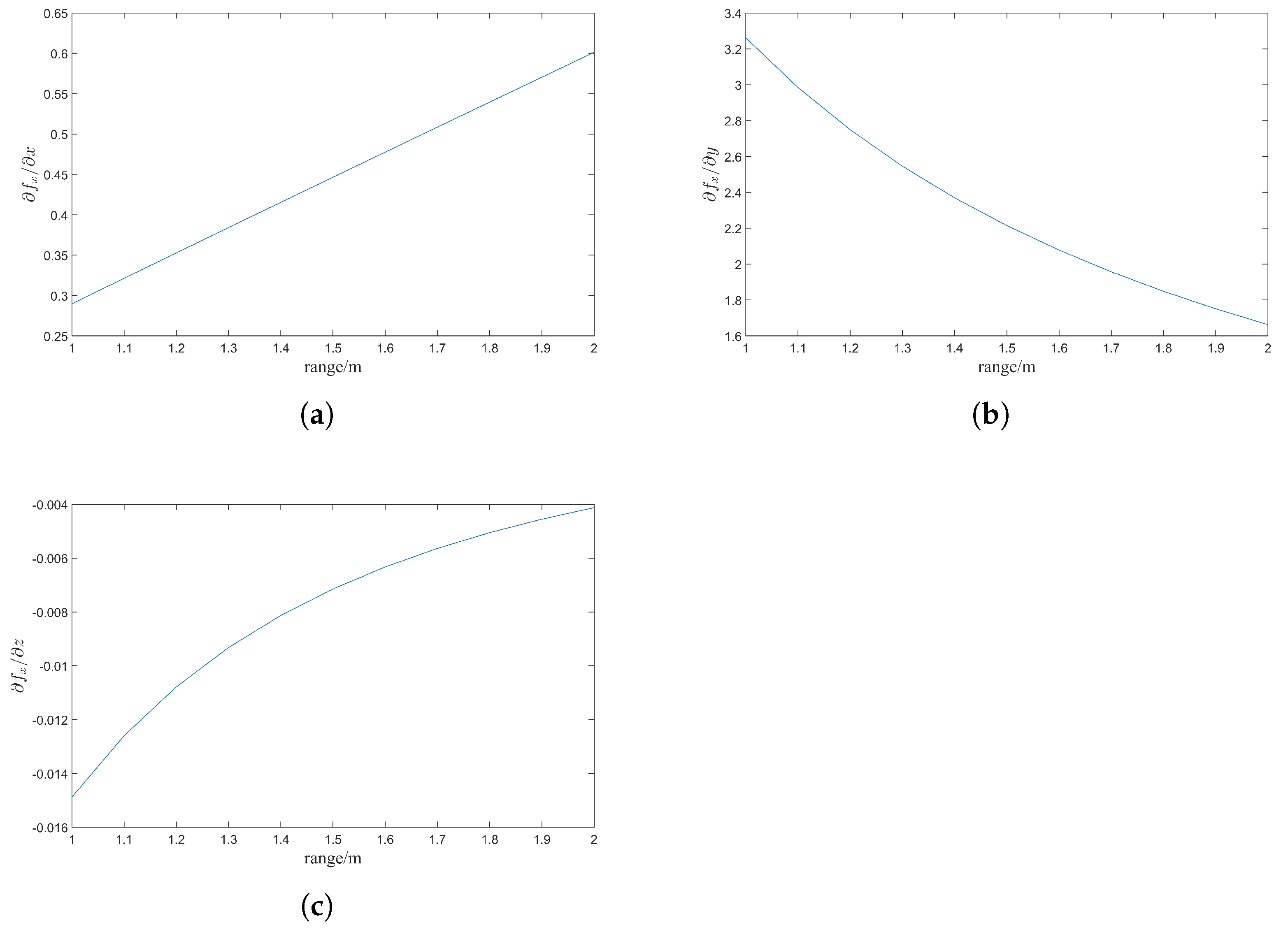
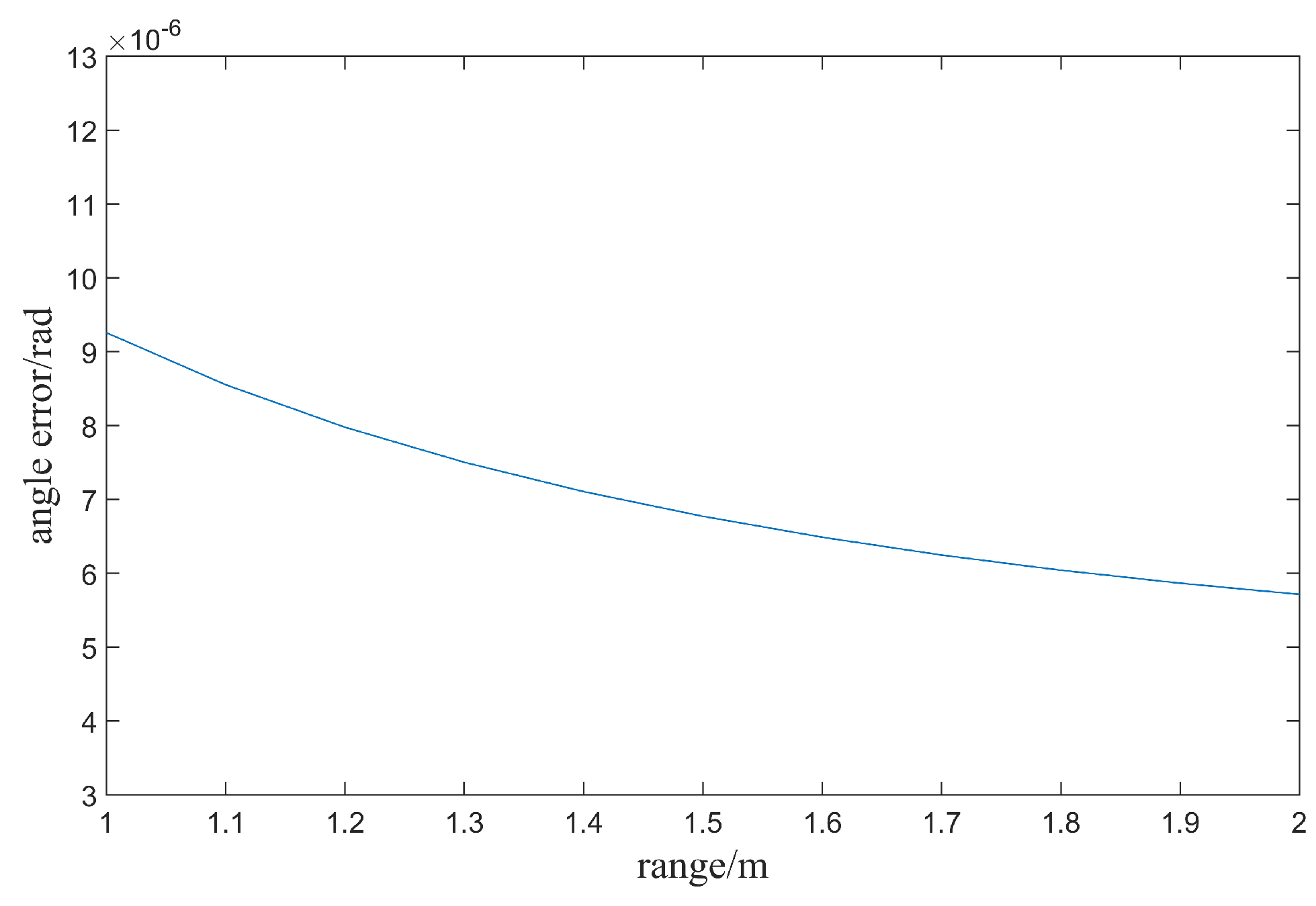


| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Range sampling number | 64 | - | |
| Azimuth sampling number | 64 | - | |
| Range resolution | 0.005 | m | |
| Azimuth resolution | 0.005 | m | |
| Wavelength | 0.001 | m | |
| Radar look angle | 75 | ° | |
| Radar height | H | 0.33 | m |
| Baseline length | B | 0.1 | m |
| Baseline tilted angle | 0 | ° | |
| Height ambiguous | 0.0238 | m | |
| Rotation angle accuracy | 0.001 | rad | |
| Frequency accuracy | 1.93 | Hz | |
| Up-sampling number | 128 | - |
| Parameters | Value | Unit |
|---|---|---|
| Center frequency | 300 | GHz |
| Bandwidth | 28.8 | GHz |
| range solution | 5.2 | mm |
| Number of frequency steps | 1601 | |
| Frequency step | 18 | MHz |
| Azimuth beam width | 6.5 | (°) |
| Azimuth sampling rate | 412.8 | Hz |
| Transmitting power | 0.5 | mW |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Li, C.; Zhang, G.; Zheng, S.; Liu, X.; Fang, G. A High-Precision Baseline Calibration Method Based on Estimation of Azimuth Fringe Frequency with THz Interferometry SAR. Remote Sens. 2023, 15, 5755. https://doi.org/10.3390/rs15245755
Wang Z, Li C, Zhang G, Zheng S, Liu X, Fang G. A High-Precision Baseline Calibration Method Based on Estimation of Azimuth Fringe Frequency with THz Interferometry SAR. Remote Sensing. 2023; 15(24):5755. https://doi.org/10.3390/rs15245755
Chicago/Turabian StyleWang, Zeyu, Chao Li, Guohua Zhang, Shen Zheng, Xiaojun Liu, and Guangyou Fang. 2023. "A High-Precision Baseline Calibration Method Based on Estimation of Azimuth Fringe Frequency with THz Interferometry SAR" Remote Sensing 15, no. 24: 5755. https://doi.org/10.3390/rs15245755
APA StyleWang, Z., Li, C., Zhang, G., Zheng, S., Liu, X., & Fang, G. (2023). A High-Precision Baseline Calibration Method Based on Estimation of Azimuth Fringe Frequency with THz Interferometry SAR. Remote Sensing, 15(24), 5755. https://doi.org/10.3390/rs15245755








