Physically Based Thermal Infrared Snow/Ice Surface Emissivity for Fast Radiative Transfer Models

Abstract

Accurate thermal infrared (TIR) fast-forward models are critical for weather forecasting via numerical weather prediction (NWP) satellite radiance assimilation and operational environmental data record (EDR) retrieval algorithms. The thermodynamic and compositional data about the surface and lower troposphere are derived from semi-transparent TIR window bands (i.e., surface-sensitive channels) that can span into the far-infrared (FIR) region under dry polar conditions. To model the satellite observed radiance within these bands, an accurate a priori emissivity is necessary for the surface in question, usually provided in the form of a physical or empirical model. To address the needs of hyperspectral TIR satellite radiance assimilation, this paper discusses the research, development, and preliminary validation of a physically based snow/ice emissivity model designed for practical implementation within operational fast-forward models such as the U.S. National Oceanic and Atmospheric Administration (NOAA) Community Radiative Transfer Model (CRTM). To accommodate the range of snow grain sizes, a hybrid modeling approach is adopted, combining a layer scattering model based on the Mie theory (viz., the Wiscombe–Warren 1980 snow albedo model, its complete derivation provided in the Appendices) with a specular facet model. The Mie-scattering model is valid for the smallest snow grain sizes typical of fresh snow and frost, whereas the specular facet model is better suited for the larger sizes and welded snow surfaces typical of aged snow. Comparisons of the model against the previously published spectral emissivity measurements show reasonable agreement across zenith observing angles and snow grain sizes, and preliminary observing system experiments (OSEs) have revealed notable improvements in snow/ice surface window channel calculations versus hyperspectral TIR satellite observations within the NOAA NWP radiance assimilation system.

1. Introduction

Accurate forward radiative transfer (RT) calculations are fundamental to satellite thermal infrared (TIR) radiance data assimilation for numerical weather prediction (NWP) models and within environmental data record (EDR) inversion (retrieval) algorithms [1,2]. Within operational contexts where minimal latency is essential, fast RT-models (RTM), or “fast-models” for short, are important for providing the timely, accurate forward calculations (calc) needed for global NWP assimilation and geophysical parameter retrievals [3]. Information about the lower troposphere and surface are derived from semi-transparent TIR spectral window channels (e.g., the 800–1200 cm${}^{-1}$ and 2400–3000 cm${}^{-1}$ spectral window bands), which require a priori information about both the surface emissivity and bidirectional reflectance distribution function (BRDF) within the forward radiance calculations performed by the RTM. Notable examples of fast-models include the U.S Joint Center for Satellite Data Assimilation (JCSDA) community radiative transfer model (CRTM) [2,4], used by the U.S. National Oceanic and Atmospheric Administration (NOAA) FV3GFS model, NASA/GMAO, and Naval Research Laboratory (NRL); the radiative transfer for TOVS (RTTOV) model [5], used by the European Centre for Medium-Range Weather Forecasts (ECMWF); NASA Langley Research Center (LaRC)’s principal component RTM (PCRTM) [6], used within their experimental all-sky (cloudy) retrieval algorithm; and University of Maryland Baltimore County (UMBC)’s stand-alone radiative transfer algorithm (SARTA) [7], used within the NOAA unique combined atmospheric processing system (NUCAPS) retrieval algorithm [8].

Today’s satellite passive TIR sounding systems used for assimilation and retrieval algorithms are based on high-resolution spectrometers, which provide atmospheric profile information within thousands of spectral channels (i.e., hyperspectral). Notable among those in low Earth orbit (LEO) are the Suomi National Polar-orbiting Partnership (SNPP) and joint polar satellite system (JPSS) cross-track infrared sounders (CrIS) [9], the Metop-series infrared atmospheric sounding interferometers (IASI) [10], and the NASA aqua atmospheric infrared sounder (AIRS) [11]. Both CrIS and IASI are Fourier transform spectrometers (FTS), whereas AIRS is a grating spectrometer. Information about the lower troposphere and surface is derived from these instruments within hundreds of microwindow channels, that is, narrow regions with relatively high transmittance located in between absorption lines. To forward-model accurately the observed radiance within these bands, the spectral emissivity of the surface must be specified with a similar degree of accuracy, given that the emissivity factors directly into the surface-leaving radiance.

Knowledge of the TIR surface emissivity over snow and ice surfaces is known to be important within the context of climate change, where the impact of greenhouse gas absorption has been observed to have a greater impact on the surface temperatures over polar regions, particularly the northern hemisphere (NH) Arctic [12]. The greater warming trend over polar regions is expected to continue for various reasons, one of which is feedback mechanisms. Recent studies have also brought attention to the importance of modeling snow/ice surface emissivity in the far IR (FIR) spectrum ($\nu <670$ cm${}^{-1}$), given that it factors prominently within the total outgoing longwave radiation (OLR) budget [13], and extremely dry atmospheres characteristic of polar region conditions (sometimes with high surface elevations, e.g., Greenland, Antarctic, etc.) reduce FIR absorption to the point of becoming semi-transparent under these conditions [14].

1.1. Satellite Observing System Experiments over Snow-Covered Regions

The analysis and forecast errors in the polar regions are typically larger than other regions around the globe. The sources of these large errors include the lack of conventional in situ observations, errors in the inversion process, and lack of knowledge of the physics and dynamics of the cryosphere. Reducing the errors within the radiance data assimilation process will result in better use of the existing data, improve the analysis, improve our knowledge of weather over the cryosphere, and potentially increase forecast skill. It is noted that radiance assimilation is essentially a “retrieval” within a NWP model and is, thus, an ill-posed estimation problem with no unique solution. The importance of accurate surface/skin temperatures has long been recognized in this respect [15], and surface emissivity is key to this. While obtaining estimates of TIR-FIR surface emissivity for snow and ice is not trivial, these have the potential to be significantly more accurate than those for passive microwave (MW) channels.

At NOAA/NCEP, the previous FV3GFS data assimilation studies [16] revealed discrepancies in clear-sky CRTM calculations (calc) versus CrIS/IASI observations (obs). Latitudinally varying discrepancies on the order of ≈0.5 K biases were observed over oceans, but much larger discrepancies (>5 K biases) have since been observed over snow/ice regions. The TIR emissivity a priori for snow/ice surfaces within the CRTM date back to the original CRTM Version 1 [4] and are shown in Figure 1. Notably, these spectra do not include observing angle dependence and are coarse spectral resolution. These are no longer adequate as constraints for retrieving lower tropospheric profile information from today’s operational hyperspectral TIR sounder instruments.

Figure 2 shows the results of an observing system experiment (OSE) of global “obs − calc” (sometimes also referred to as “obs minus background”, or “$O-B$” for short, within data assimilation studies) for CrIS and IASI microwindow channels centered at 962.5 cm${}^{-1}$ (channels #501 and #1271, respectively) over snow surfaces within the FV3GFS gridpoint statistical interpolation (GSI) [17]. NOAA/NCEP uses the 962.5 cm${}^{-1}$ channel for obs − calc comparisons given that it is the cleanest longwave TIR microwindow channel. Other longwave microwindow channels can contain water vapor and/or other trace gas absorption lines (e.g., chlorofluorocarbons and nitric acid) that are not spectrally resolvable with the current data assimilation system. More discussion on the OSE is found in Section 3.1. The obs − calc spread over snow surfaces is more than a factor of 5 greater than the comparable results obtained over oceans, spanning $\pm 10$ K. Both results are skewed negative, with the CrIS more visibly so, in addition to the noticeable kurtosis. The negative skewness suggests that there are likely issues with residual cloud contamination and, thus, not all of the $\pm 10$ K is attributable to emissivity errors. However, by itself, cloud contamination would only contribute to negative obs − calc bias in transparent microwindows [18], so emissivity error is a contributor to the total error in the overall forward model calc. For reference, a systematic error of $\approx |$0.2–0.6| K was estimated for surface temperatures from a mere 1% uncertainty in emissivity over oceans [19].

Therefore, there is a need for improved snow/ice hyperspectral TIR-FIR surface emissivity model(s) for operational fast-models (viz., CRTM) as discussed more below. Discrepancies of this type are also evident within physical 1DVAR inversion (retrieval) algorithms; for example, operational temperature profile EDRs derived from NUCAPS. NUCAPS have heretofore used a regression algorithm based on cloud-cleared radiances [20] to provide a first-guess for emissivity over land/snow/ice surfaces (in addition to the T/H${}_2$O first guess), but more recently have implemented the combined ASTER MODIS emissivity over land (CAMEL) [21,22] as an option.

1.2. Surface Emissivity Considerations and Modeling Approaches

The directional emissivity of a terrestrial surface in thermodynamic equilibrium is defined as [23,24,25]

$${ϵ}_{\nu }\left({\theta }_o\right)\equiv \frac{I_{\nu s}\left({\theta }_o\right)}{B_{\nu }\left(T_s\right)},$$

(1)

where ${\theta }_o$ is the zenith observing angle, $B_{\nu }$ is the Planck spectral blackbody radiance at surface skin temperature $T_s$ (K) and wavenumber $\nu$ (cm${}^{-1}$), and $I_{\nu s}\left({\theta }_o\right)\equiv {ϵ}_{\nu }\left({\theta }_o\right)B_{\nu }\left(T_s\right)$ is the surface-emitted radiance, typically in units of mWm${}^{-2}$sr${}^{-1}$cm. In practice, $I_{\nu s}$ is separated from the surface-leaving radiance measured by an observer (e.g., a downlooking detector) at the surface, $R_{\nu s}$, by subtracting the surface-reflected radiance, which, assuming azimuthal symmetry, is given by

$$I_{\nu s}\left({\theta }_o\right)=R_{\nu s}\left({\theta }_o\right)-2{\int }_0^{\pi /2}{r}_{\nu }(\theta ,{\theta }_o)I_{\nu }^{\downarrow }\left(\theta \right)cos\left(\theta \right)sin\left(\theta \right)d\theta ,$$

(2)

where $r_{\nu }(\theta ,{\theta }_o)$ is the bidirectional reflectance distribution function (BRDF) (sr${}^{-1}$) [26], and $I_{\nu }^{\downarrow }$ is the downwelling atmospheric radiance at zenith angle $\theta$. From Equations (1) and (2), one can see that what we call “emissivity” in practice involves the necessity of correctly specifying the surface reflectance, because it is convolved with the direct emission. In the case of a Lambertian (or perfectly diffuse) surface, the reflectance does not vary over the hemisphere ($\theta =[0,\pi ])$; that is, $r_{\nu }(\theta ,{\theta }_o)=r_{\nu }(\pi ,{\theta }_o)$, and Equation (2) becomes

$$I_{\nu s}\left({\theta }_o\right)=R_{\nu s}\left({\theta }_o\right)-{\alpha }_{\nu }\left(\pi ,{\theta }_o\right)F_{\nu }^{\downarrow },$$

(3)

where $F_{\nu }^{\downarrow }\equiv 2\int I_{\nu }^{\downarrow }\left(\theta \right)cos\theta sin\theta d\theta$ is the downwelling spectral irradiance (flux), and ${\alpha }_{\nu }(\pi ,{\theta }_o)\equiv r_{\nu }(\pi ,{\theta }_o)$ is defined as the hemispherical-directional reflectance or albedo (sr${}^{-1}$). Equations (1)–(3) provide the basis for both modeling and measuring spectral TIR surface emissivity, as discussed more in this paper.

There are generally two approaches taken for modeling the TIR emissivity of terrestrial surfaces, these being physical models and empirical models, with “hybrid” models involving a combination of the two. Physical models are based upon first-principles and simplifying assumptions for spectral regimes (e.g., the geometrical optics limit, etc.). Generally speaking, ocean surfaces are the simplest to model in the TIR-FIR spectral region, given that they are spatially uniform, with individual surface roughness elements, being large relative to the wavelength of radiation and their ensemble inclinations being known as a function of surface wind speed [27]. These unique features of ocean surfaces have allowed the development and use of physical models for over a decade [28]. Conversely, land surfaces are extremely inhomogeneous in terms of spatiotemporal uniformity, roughness, and optical properties, and thus, over land, empirically-derived merged atlases, for example CAMEL [21,22] have been implemented, and these include snow and ice surfaces. CAMEL ice and snow emissivity are based on principal component (PC)-based regression between the combined MODIS and ASTER emissivity retrievals and four laboratory measurements from the Ecosystem Spaceborne Thermal Radiometer Experiment on Space Station (ECOSTRESS) spectral library, (formerly known as the Advanced Spaceborne Thermal Emission Reflection Radiometer, ASTER spectral library) [29].

However, as with oceans, the RT associated with snow and ice surfaces in principle may be modeled physically assuming idealized conditions (e.g., uniform, level, pure snow/ice surfaces). Notable examples of these have included models developed by Berger [30], which exclusively relied on geometrical optics; Wiscombe and Warren [31], which was based on Mie-scattering and delta-Eddington approximation; and Wald [32], which was based on a “diffraction-substraction” method to account for the close packing of snow particles. This paper outlines the work undertaken toward selecting, deriving, implementing, and testing a hybrid physical model for calculating a priori snow/ice surface emissivity for convenient implementation within CRTM and other fast-models, as well as global empirical atlases such as CAMEL.

2. Methodology

After conducting a thorough literature review of the previous research on the topic [33,34], we chose to implement the Wiscombe and Warren (1980) [31] snow albedo model (hereafter, “WW80”) in the initial step toward a CRTM forward model upgrade. We found the WW80 model to be ideal in terms of both theoretical basis (applying the Mie-scattering theory for single scattering by randomly oriented snow particles [24] modeled as spheres, discussed more below) and practical application (encapsulated within a relatively simple formula providing albedo as a function of observing angle). Early follow-up studies indicated some success in applying the WW80 model to TIR emissivity [35], and it also currently forms the basis for solar spectrum reflectances in the snow, ice, and aerosol radiative model with adding–doubling, Version 3 (SNICAR-ADv3) community model [36].

In terms of its TIR application, Warren [33] acknowledged that the WW80 model “assumes that the scattering properties of a snow grain are not affected by the proximity of neighboring grains” (i.e., it assumes the far-field limit in the application of the Mie-scattering theory [31]), which is legitimate for solar wavelengths. Dozier and Warren investigated various physical dependencies (e.g., snow density, non-sphericity), and they concluded under the subsection “Density” that “near-field effects are unlikely to be important for $\lambda <50$$\mathsf{\mu }$m”. They based this on calculations simulating near-field effects by making an adjustment to the real part of the refractive index, $n_{\nu }$, but their model was otherwise based on WW80, as is encapsulated in their Figure 1b. Wald [32] pointed out that the far-field assumption is valid only for particles “separated by three particle radii” ($3r$), which breaks down for larger sizes when snow grains become opaque, densely packed, and welded together. To model emissivity for a particle radii $r>50$ $\mathsf{\mu }$m, Wald proposed a “diffraction subtraction” methodology but acknowledged that WW80 is otherwise legitimate for small particle sizes $r<20$ $\mathsf{\mu }$m in the TIR [32]; unfortunately, a straightforward expression or derivation for emissivity was not provided in the paper.

2.1. Wiscombe–Warren (WW80) Model

In solar spectrum convention (e.g., the WW80 model), the spectral surface albedo is typically defined as directional-hemispherical $({\theta }_o,\pi )$ reflectance, given by [26,35,37,38,39,40]

$${\alpha }_{\nu }({\theta }_o,\pi )\equiv \frac{F_{\nu }^{\uparrow }}{F_{\nu }^{\downarrow }(\Delta {\theta }_o)}=\frac{F_{\nu }^{\uparrow }}{{\mu }_o\pi I_{\nu }\left({\theta }_o\right)},$$

(4)

where $\nu$ is the spectral wavenumber (cm${}^{-1}$); ${\theta }_o$ is the local zenith angle of the origin (or, reciprocally, the observer); ${\mu }_o\equiv cos{\theta }_o$, $F_{\nu }^{\uparrow }$ and $F_{\nu }^{\downarrow }(\Delta {\theta }_o)$ are the hemispherical upwelling (surface-leaving) and conical downwelling (surface-incident) fluxes, respectively; and $I_{\nu }\left({\theta }_o\right)$ is the radiant intensity defined by $F_{\nu }^{\downarrow }/\pi$ [41]. Note that lower-case letter o subscripts have been chosen to signify either the “origin” or “observer” angle to distinguish it from naught (0) subscripts, which are reserved in this paper to designate zeroth order polynomial expansions or zeroth moments. As written, the denominator term, ${\mu }_o\pi I_{\nu }$, is the surface-incident conical flux, which is typically taken to be the solar irradiance (a source term) in visible-spectrum applications (usually denoted $\pi F_{\odot }$). However, in the current application (TIR-FIR emission), by reciprocity, the albedo given by Equation (4) is also equivalent to the hemispherical-directional $(\pi ,{\theta }_o)$ reflectance [35,42] referred to in Equation (3); that is, ${\alpha }_{\nu }={\alpha }_{\nu }(\pi ,{\theta }_o)$, and thus, ${\theta }_o$ may instead be interpreted as the observer angle.

From Equations (1), (3), and Kirchhoff’s law, the hemispherical-directional snow/ice emissivity may then be obtained from [24,31,35]:

$${ϵ}_{\nu s}\left({\theta }_o\right)=1-{\alpha }_{\nu }(\pi ,{\theta }_o).$$

(5)

To derive the albedo (and thus, emissivity) analytically, expressions must, thus, be found for $F_{\nu }^{\uparrow }$ and $F_{\nu }^{\downarrow }$, the derivations of which are detailed in Appendix A, Appendix B, Appendix C and Appendix D.

The Mie theory provides fundamental values for the Mie efficiencies pertaining to single-particle extinction ($Q_e$), scattering ($Q_s$), absorption ($Q_a$), and backscattering ($Q_b$), from which other parameters such as the single-scattering albedo ($\varpi$) and asymmetry parameter (g) can be derived as a function of the complex refractive index, $N_{\nu }$ [43,44], and snow grain size (particle radius), r. In reality, snow grains are not spherical, and for any given snowpack, there are a range of particle sizes. Typically, these complications are accounted for by introducing a “radiatively effective radius” for a size distribution of spheres defined as $r_e\equiv 3\beta /{\rho }_i$, where $\beta$ is the specific surface area, and ${\rho }_i$ is the density of ice [45]. Because this paper assumes Mie scattering, the terms “particle size”, “particle radius”, and “snow grain size” are used interchangeably to refer to a mean effective particle size of a given snowpack.

The authors adapted and utilized MATLAB research-code for performing Mie calculations (after Ref. [46]); MATLAB is extremely well-suited for this purpose, possessing built-in Bessel functions while efficiently using matrix syntax that optimally retains direct correspondence with the theoretical formulations. However, given that the single-scattering of individual snow grains tends to have a strong forward peak, the WW80 model applies the delta-Eddington approximation (D–E) for radiative transfer, discussed more in Appendix B, to account for multiple scattering within the RT equation (RTE). The D-E approximation begins with a truncated two-term Henyey–Greenstein (H-G) phase function but accounts for the strong forward scattering peak of snow by including a Dirac delta function term. The D-E phase function is, thus, approximated as

$$P_{\nu }^{*}(cos\Theta )\equiv 2f_{\nu }\delta (1-cos\Theta )+(1-f_{\nu })(1+3g_{\nu }^{*}cos\Theta ),$$

(6)

where asterisks denote D-E approximation quantities, $f_{\nu }$ is the forward scattered fraction, and $g_{\nu }^{*}\equiv \frac{g_{\nu }}{1+g_{\nu }}$ is the asymmetry parameter of the truncated Eddington phase function. The original Eddington approximation is then applied to the D-E scaled RTE (using the simplified phase function), thus, allowing the RTE to be significantly simplified into an analytically solvable set of coupled ordinary differential equations (ODEs) (cf. Appendix B.2 and Appendix B.3).

From these assumptions and after considerable derivation (see Appendix A, Appendix B, Appendix C and Appendix D), solving for the upward and downward fluxes, $F_{\nu }^{\uparrow }$ and $F_{\nu }^{\downarrow }$, it can be shown that the albedo (i.e., the hemispherical-directional BRDF) for a flat, uniform snowpack surface, assuming quasi-infinite optical depth (${\tau }_{\nu }\to \infty$), is given by [31]

$${\alpha }_{\nu }\left({\theta }_o\right)={\varpi }_{\nu }^{*}·\left(\frac{1}{1+{\phi }_{\nu }}\right)\left(\frac{1-b_{\nu }{\xi }_{\nu }cos{\theta }_o}{1+{\xi }_{\nu }cos{\theta }_o}\right),$$

(7)

where ${\xi }_{\nu }$, $b_{\nu }$, and ${\phi }_{\nu }$, denote intermediate variables, defined as

$$\begin{array}{cc}\hfill & {\xi }_{\nu }\equiv \sqrt{3(1-{\varpi }_{\nu }^{*}{g}_{\nu }^{*})(1-{\varpi }_{\nu }^{*})},\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill & b_{\nu }\equiv \frac{g_{\nu }^{*}}{1-{\varpi }_{\nu }^{*}{g}_{\nu }^{*}},\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill & {\phi }_{\nu }\equiv \frac{2{\xi }_{\nu }}{3(1-{\varpi }_{\nu }^{*}{g}_{\nu }^{*})},\hfill \end{array}$$

(10)

${\varpi }_{\nu }^{*}\equiv \frac{(1-f){\varpi }_{\nu }}{1-f{\varpi }_{\nu }}$ being the D-E scaled Mie single-scattering albedo.

Note that in previous publications [31,47,48,49], the intermediate variable represented by ${\phi }_{\nu }$ in Equation (A66) was denoted with an upper case P. In the original WW80 paper, no explanation was given as to what the significance was behind that specific symbol, which led to unnecessary confusion, especially given that P is also the standard symbol for the phase function, $P_{\nu }$, not to mention the Legendre polynomials used in the derivation (cf. Appendix A), these being directly relevant to the physical model. It was subsequently learned during the course of this research that P was a purely mathematical construct that originated during the solution of the ODEs (cf. Appendix C) but otherwise carries no physically relevant meaning within the symbol itself for albedo. Given that TIR-FIR albedo and emissivity are physical variables, we have, thus, chosen to break from this usage, rendering it instead using an analogous Greek letter ${\phi }_{\nu }$ to avoid further confusion with the variables mentioned.

Although the assumption of quasi-infinite optical depth is justified in the longwave TIR-FIR spectrum, we nevertheless implemented the full-scattering version of the WW80 model [Equation (3), op. cit.; cf. Appendix D], where the range of validity extends to solar-reflectance (visible) wavelengths. Implicit in the Mie-scattering calculations are functional dependencies on snow grain size (effective radii), r ($\mathsf{\mu }$m), and complex refractive index, $N_{\nu }$. For both the Mie calculations and the Fresnel reflectance calculations discussed in Section 2.2 below, we use the temperature-dependent, TIR-FIR optical constants of ice ($N_{\nu }$) published by Iwabuchi and Yang [44]. It should be noted that snow grain size is known to grow as a snow pack ages [50], and thus, this parameter accounts for the age of the snow pack. Thus, the snow surface emissivity computed from Equation (5) is a function of ${\theta }_o$, r, and $N_{\nu }\left(T\right)$.

As a “sanity-check”, the output from our research code implementation of the WW80 model was tested against those published previously by Dozier and Warren [35] to confirm that the model was implemented properly. Figure 3 shows results from our implementation of Equations (5) and (7) in a manner that visually duplicates the results published by Ref. [35]. The subtle differences between our implementation and Ref. [35] may be attributed to the difference in the optical constants used in the Mie calculations; in our case, we used the most recent temperature-dependent data available [44], which are expected to be more accurate than those that were available to Ref. [35] in 1982.

The model calculations were then tested against the earlier published laboratory and field measurements, namely, the ECOSTRESS (ASTER) library [29,51] and those of Ref. [52], the latter including multi-angle field observations. The model calculations were found to agree reasonably well for smaller particle sizes ($r<30$ $\mathsf{\mu }$m) but did not capture the size dependence for larger sizes. It was subsequently learned that this is a known problem with the WW80 model, but the model was nevertheless implemented within an offline version of the CRTM, given that the particle size dependence was a lesser concern compared to the spectral and angular dependencies. Results from the initial CRTM implementation of the WW80 model are presented in Section 3.1.

2.2. Hybrid Physical Model

The additional research into the large particle size problem led to the observation that the albedo of snow surfaces gradually becomes more specular as it becomes coarser grained. We directly noticed this ourselves when studying the field and laboratory data, but we subsequently learned that others had also noticed this previously [32,53]. As snow ages, the snow grains not only grow larger via sublimation metamorphosis [50] but they also “weld” together [32] into an ice surface as opposed to a scattering layer. Because of the relationship between snow grain size and snowpack age, the particle radius parameter is necessary to account for the age of the snow pack.

Table 1. Measured Mean Sizes of Snow Grains ($\mathsf{\mu }$m) During Metamorphosis (From Yosida, 1962 [50]).

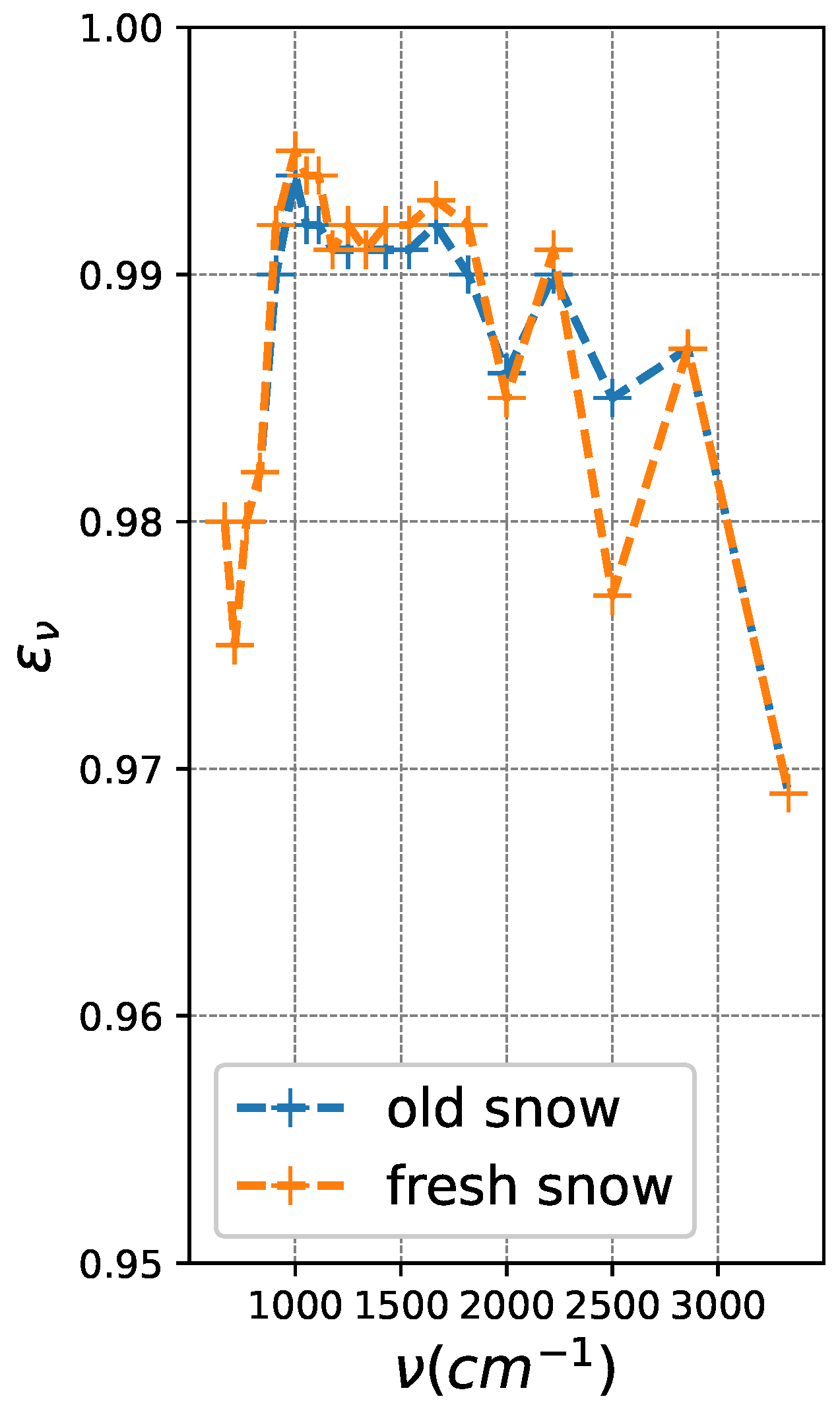
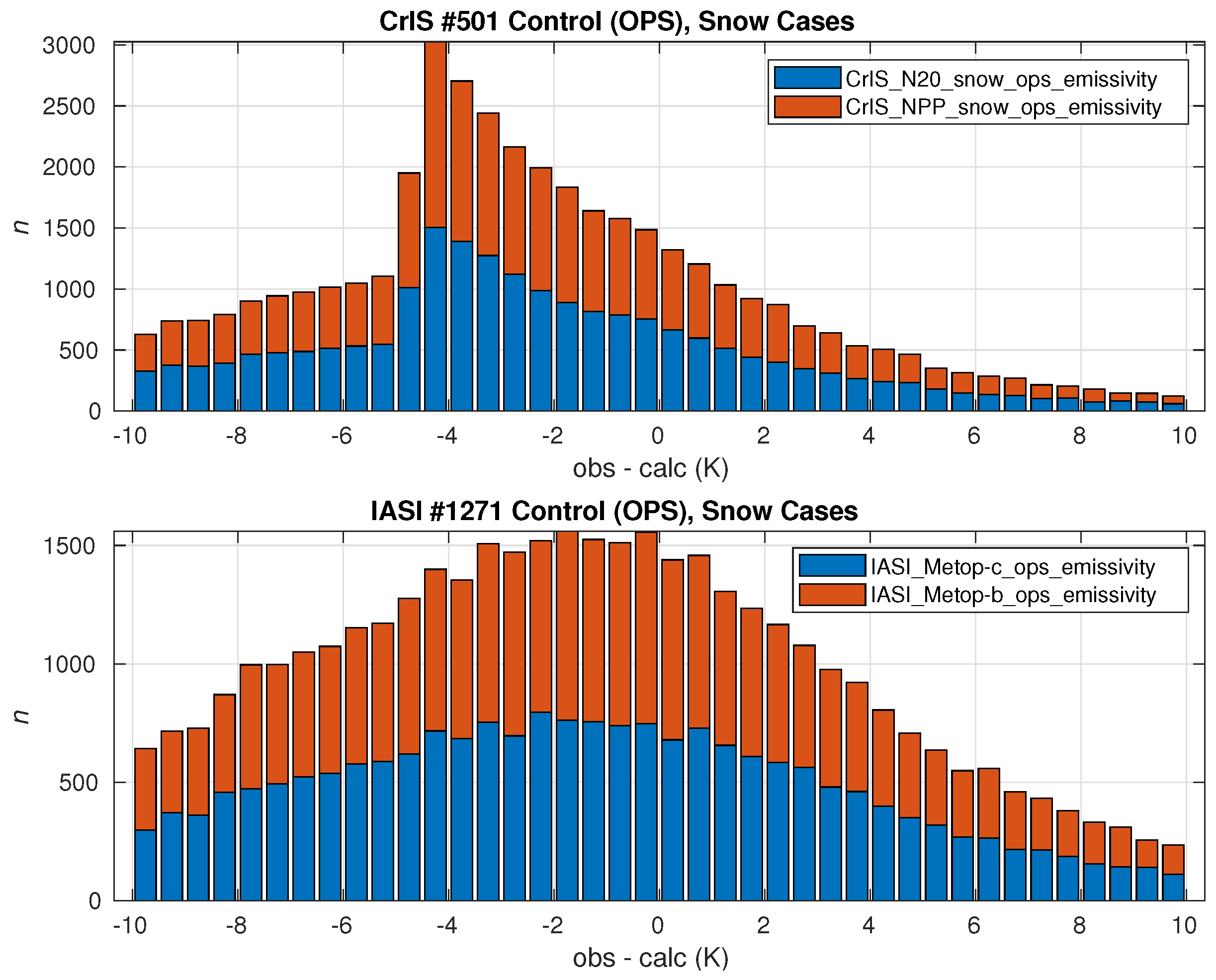
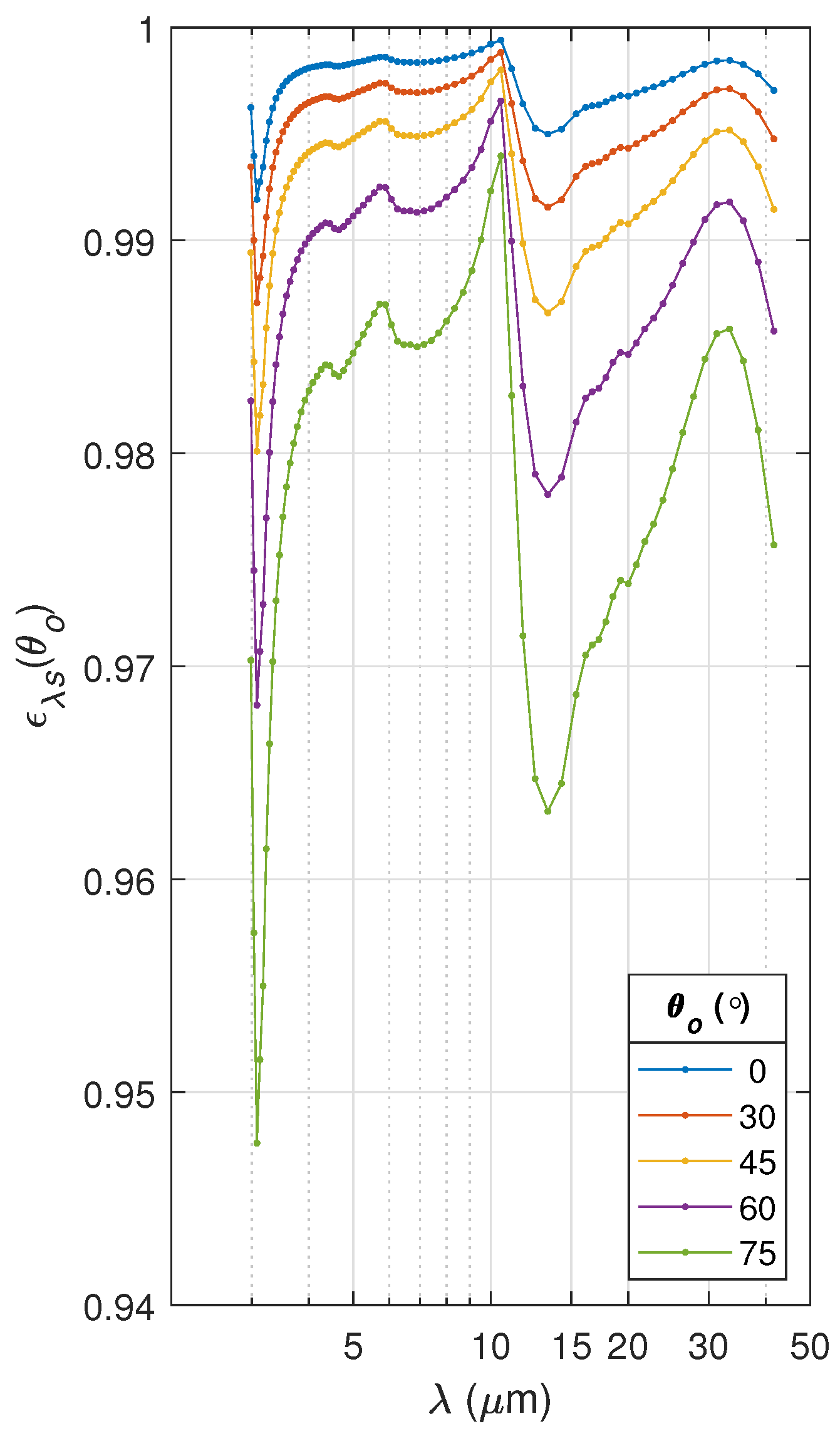
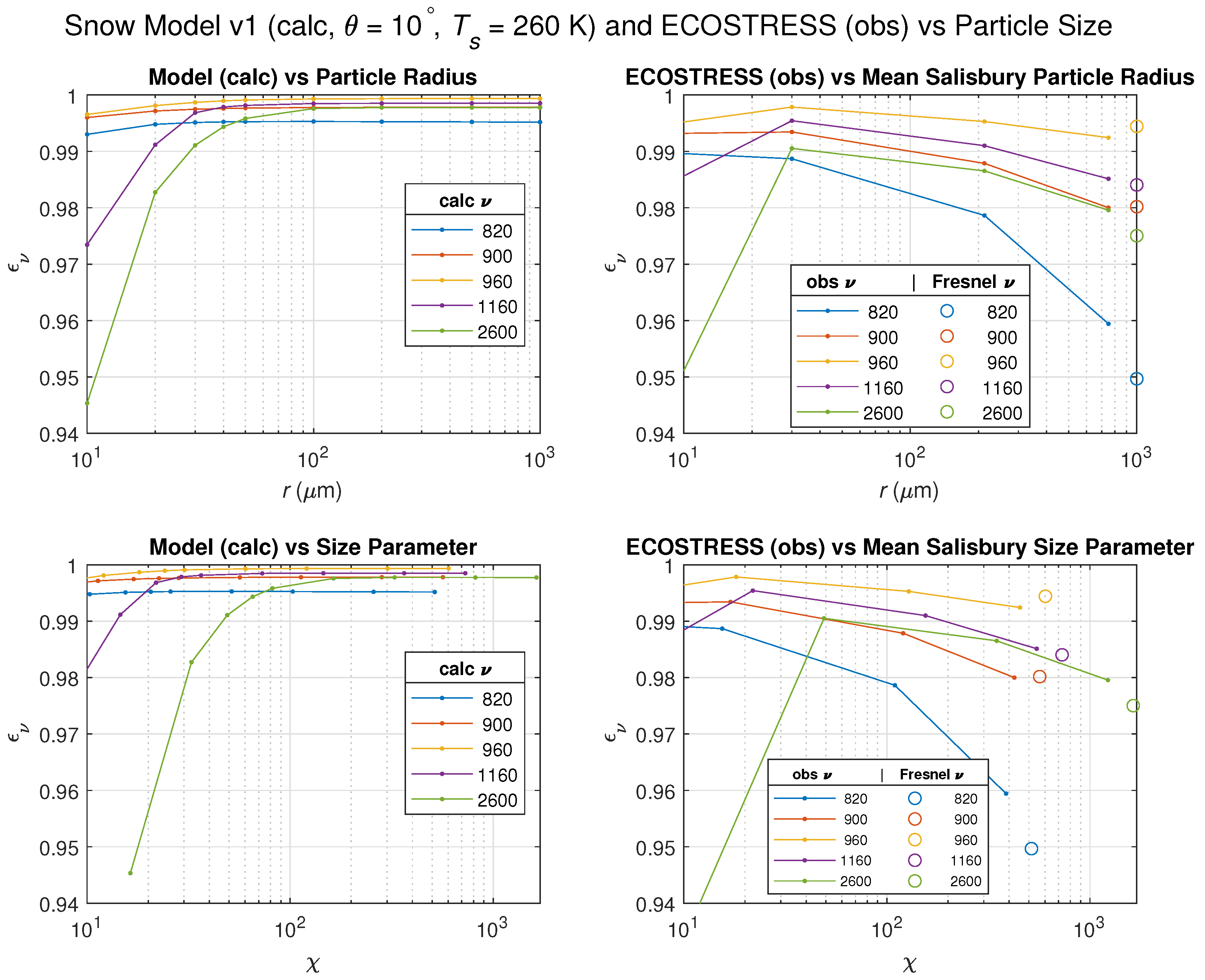
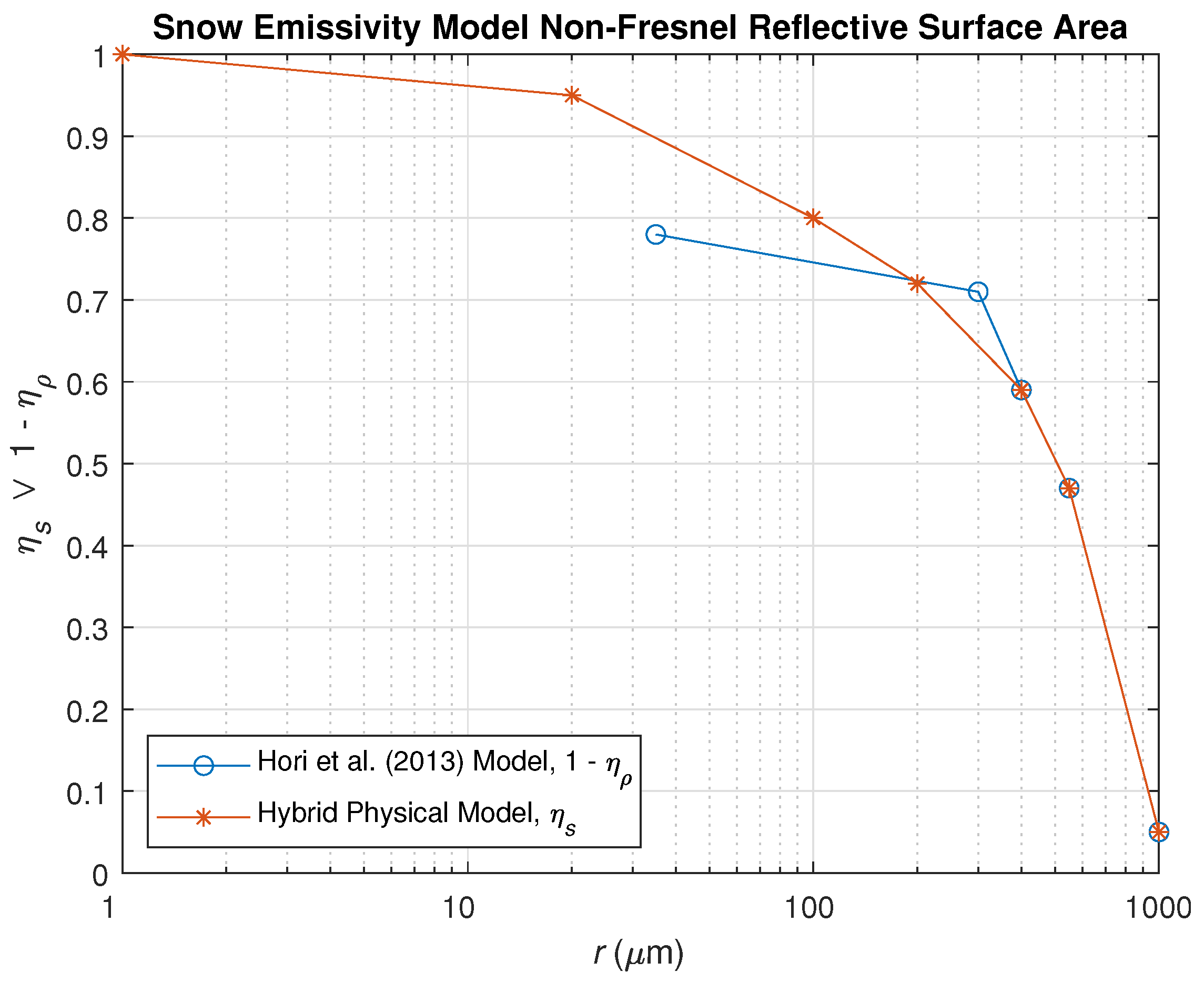
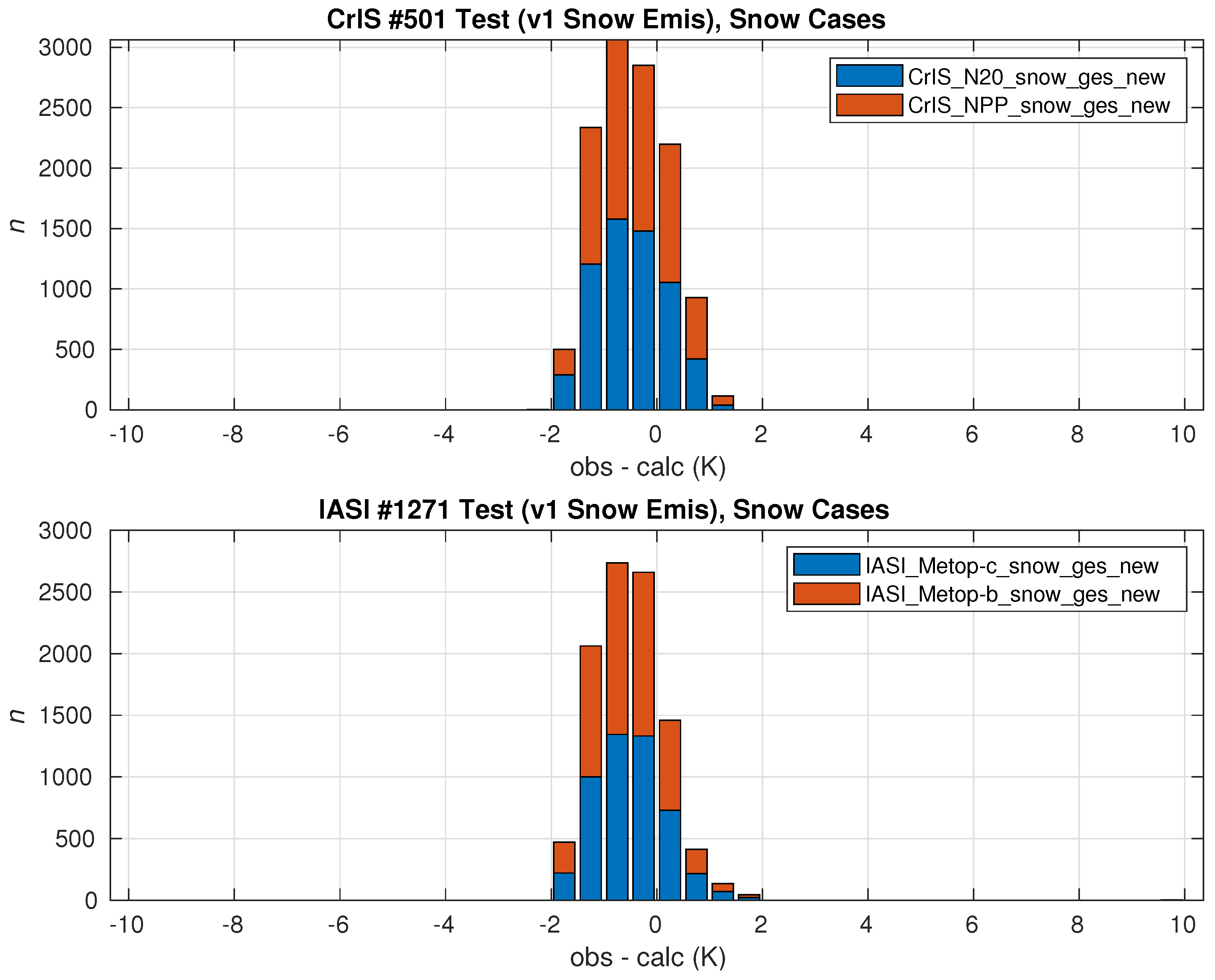
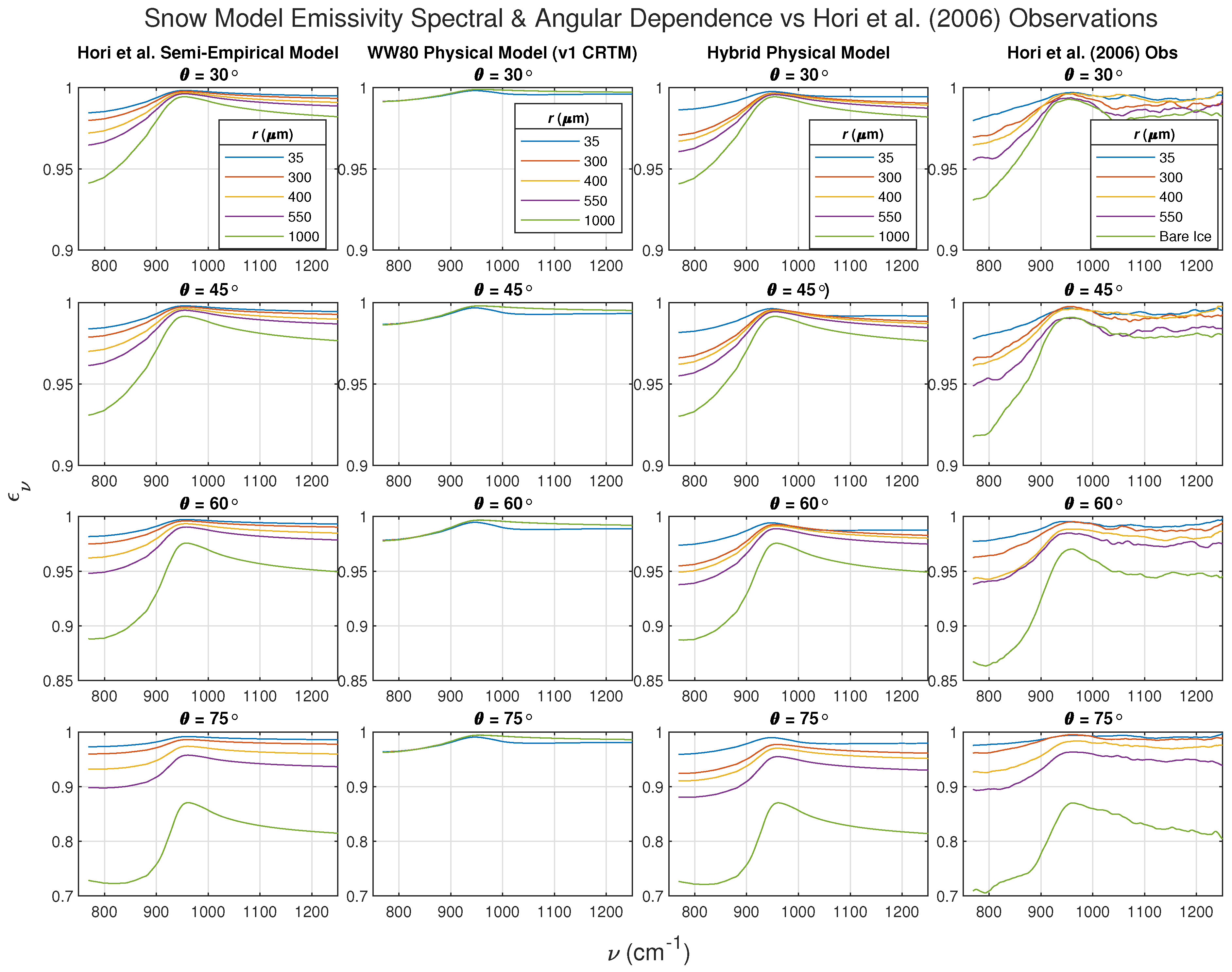
# of Days after Snow Deposition	Mean Length $\overline{\mathit{\ell }}$ ($\mathbf{\mu }$m)	Mean Radius $\overline{\mathit{r}}$ ($\mathbf{\mu }$m)	Mean Constriction $\overline{\mathit{w}}$ ($\mathbf{\mu }$m)
1	200	45	50
5	190	45	50
9	260	60	80
15	430	80	100
24	600	110	140
31	570	130	160

Lengths (ℓ) were defined to be the lengths between the extremities of ice crystals; radii (r) were defined as the thickness of the snow grains at their thickest portions; and constriction widths (w) were defined as the thickness at the narrowest portion [50].

reproduces the snow grain size measurements (mean length, diameter, and constriction width, in micrometers) observed by Yosida [50] as a function of age, which provide here an indication of the relationship between the snowpack grain size and age.

A subsequent examination of the particle size dependence seemed to reveal a linear transition from the scattering-layer regime (i.e., the WW80 model) to a Fresnel surface reflectance regime, as illustrated in Figure 4. In this figure, dependencies on particle size are shown as a function of particle radius (r) and size parameter ($\chi \equiv 2\pi r/\lambda$) in the top and bottom row plots, respectively. The left and right columns show the WW80 model calculations and ECOSTRESS measurements [29,51], respectively. Here, it can be seen in the left hand plots that the WW80 model asymptotes to constant values of emissivity above a certain particle size, these varying with the spectral channel, with the higher wavenumber (shorter wavelength) channels (e.g., 1160 and 2600 cm${}^{-1}$), being the last to flatten out as would be expected. In the right hand plots, however, the laboratory measurements show a decrease in emissivity where the WW80 flattened out. It was then noticed that, roughly speaking, these emissivities could be linearly extrapolated to the Fresnel values at a nominal large particle size (i.e., 1000 $\mathsf{\mu }$m). These results (as well as Refs. [31,32]) suggested that an “effective emissivity” for snow/ice surfaces could be expressed conceptually as a linear combination of diffuse layer-scattering and quasi-specular surface fractions; that is,

$${ϵ}_{\nu }^{*}={\eta }_s{ϵ}_{\nu s}+(1-{\eta }_s){ϵ}_{\nu \rho },$$

(11)

where ${ϵ}_{\nu s}$ and ${ϵ}_{\nu \rho }$ are the emissivities for the snow and Fresnel reflecting ice-surface areas, respectively; ${\eta }_s$ is the fractional surface area that behaves as a multi-scattering snow layer (as in the WW80 model); and $1-{\eta }_s$ is the quasi-specular area arising from a surface made up of a quasi-random ensemble of ice crystal facet planes, oriented at an effective (average) oblique angle relative to the observer. For ${\eta }_s\to 1$, the snowpack surface reflects and emits as a scattering layer (as in the WW80 model), whereas ${\eta }_s\to 0$ implies a fused Fresnel ice surface.

In this vein, Hori et al. [53] proposed a “semi-empirical” model (hereafter, “H13”) that expresses the snow surface emissivity as a linear combination of an isotropic blackbody component, where ${ϵ}_{\nu s}\equiv 1$ and ${\eta }_s\equiv 1-{\eta }_{\rho }$ in Equation (11), along with a quasi-specular (ice facet) component, ${\eta }_{\rho }$, within the overall “bulk” surface, given by

$${ϵ}_{\nu \rho }(\theta ,r,N_{\nu })\equiv {\eta }_{\rho }\left(r\right)\left[1-{\rho }_{\nu }(\theta ,N_{\nu })\right]+\left[1-{\eta }_{\rho }\left(r\right)\right]\left[1-{\rho }_{\nu }\left(\overline{\theta },N_{\nu }\right)\right],$$

(12)

where $\overline{\theta }\equiv {45}^{\circ }$, and ${\rho }_{\nu }$ is the unpolarized Fresnel reflectance coefficient, taken to be the average of the polarized reflectances for intensities (i.e., the square of the absolute value of the amplitude coefficients). Using the field measurements from their earlier paper [52], Hori et al. [53] empirically determined the specular fractions for various snow samples, the results of which are summarized in

Table 2. Hori et al. [53] Snow Model Specular Fractions (${\eta }_{\rho }$) for Particle Sizes.

Particle Size, r ($\mathsf{\mu }$m)		${\mathit{\eta }}_{\mathit{\rho }}$	Snow Morphology
Median	Range
35	20–50	0.22	fine dendrite snow
300	150–550	0.29	medium granular snow
400	25–500	0.41	coarse-grained snow
550	400–750	0.53	sun crust
≳1000 (flat)		0.95	bare ice

.

Hori et al. [53] referred to their model as “semi-empirical” given that it relied on their earlier field measurements to derive their specular fractions. However, it should be noted that Equation (12) has a physical basis as an approximation for quasi-specular reflectance, which is characterized as having a finite reflection lobe with a significant peak centering around the specular angle [54]. Generally speaking, quasi-specular reflectance arises from large-scale surface roughness caused by surface elements with large size parameters (i.e., dimensions or curvature that are large relative to the wavelength of radiation, $r\gg \lambda$), although it has also been shown to arise from lattices of Mie-scattering spheres (size parameters $\chi =2$, $r\approx \lambda$) [55]. In the case of an idealized snowpack, the specular component can arise from randomly oriented snow facets with an ensemble effective orientation, $\overline{\theta }$, which may be approximated as the mean slope of the facets. Assuming spherical particles (as in the WW80 Mie-scattering model) and disregarding shadowing effects, the mean inclination happens to be $\overline{\theta }\equiv {45}^{\circ }$. Thus, while it may be “semi-empirical”, it should nevertheless be kept in mind that this is a physically reasonable approach in lieu of having an observed statistical description of snow/ice facet slopes, as is (fortuitously) the case in ocean emissivity models [28,56].

The H13 semi-empirical model is found to compare favorably for larger particle sizes, but unfortunately, this is not true for the small particle sizes ($r<50$ $\mathsf{\mu }$m) included in the ECOSTRESS data. However, it is precisely these smaller particle sizes where the WW80 albedo model shows good agreement. Because the WW80 and H13 models appear to capture the observed small and large particle size regimes, respectively (with a transitional region around 30–100 $\mathsf{\mu }$m), we adopted a modified “effective emissivity” approach based on Equations (5), (11) and (12). Rather than assuming a blackbody for ${ϵ}_{\nu s}$ in Equation (12), we instead assume that layer scattering dominates under these conditions [32], and thus, from Equations (5) and (11), we obtain

$${ϵ}_{\nu }^{*}({\theta }_o,r,N_{\nu })={\eta }_s\left(r\right)\left[1-{\alpha }_{\nu }({\theta }_o,r,N_{\nu })\right]+\left[1-{\eta }_s\left(r\right)\right]{ϵ}_{\nu \rho }({\theta }_o,r,N_{\nu }),$$

(13)

where ${\alpha }_{\nu }$ is the albedo predicted by the WW80 model given by Equation (7).

For larger particle sizes ($r\ge 400$ $\mathsf{\mu }$m), we use the “specular fractions”, ${\eta }_{\rho }\equiv 1-{\eta }_s$, proposed by Ref. [53], but for smaller particle sizes, we extrapolated these in log-r space to unity at $r=1$ $\mathsf{\mu }$m as a transition to the layer scattering regime (WW80 model) for these sizes, as illustrated in Figure 5. The physical interpretation of this hybrid physical model approach may be seen as a linear transition from a multiple scattering layer regime (modeled by small, Mie-scattering spherical snow grains), to a quasi-specular surface-reflectance regime consisting of large, fused ice crystals acting as randomly oriented facets (as in ocean reflectance models, e.g., [57]) with an effective (approximately average) inclination angle of 45${}^{\circ }$.

3. Results and Discussion

Both the hybrid physical model (v1.1), Equation (13), and the WW80 model (quasi-infinite optical depth limit), Equation (7), are simplified as 4-D lookup-tables (LUT) with dimensions $\nu$, ${\theta }_o$, r, and T; that is, ${ϵ}^{*}(\nu ,{\theta }_o,r,T)$ (see

Table 3. Snow/Ice Surface TIR Emissivity Model LUTs.

Model	${\mathit{\theta }}_{\mathit{o}}$	$\mathit{\nu }$ (cm${}^{-1}$)	Grain Size, r	T (K)
Original CRTM a priori	N/A	666–3333	“fresh” and “aged”	N/A
(CRTM release versions v1.0 to v2.3.0)
WW80 physical model	0–75${}^{\circ }$	600–3000	5–1000 $\mathsf{\mu }$m	230–270
(CRTM v3, snow emissivity v1.0)
Hybrid physical model	0–75${}^{\circ }$	50–3000	1–1000 $\mathsf{\mu }$m	230–270
(CRTM v3, snow/ice emissivity v1.1)

N/A = not applicable.

for LUT parameter ranges), for convenient application within fast-forward models (e.g., CRTM, RTTOV, PCRTM, SARTA, etc.), as well as within spectral libraries and atlases (e.g,. CAMEL). The results that follow are based upon these model output LUTs.

3.1. Preliminary OSE Using WW80 Model

Concurrent with researching the problem of larger particle sizes, a preliminary OSE was performed to test the impact of the initial CRTM snow emissivity model upgrade on global obs − calc based solely on the WW80 model (i.e., CRTM physical snow emissivity model v1). As with the control experiment briefly highlighted in Section 1 (cf. Figure 2), the OSE used the lowest resolution FV3GFS_V16 over the time period of 28 July to 30 September 2021, with obs obtained from the SNPP/NOAA-20 CrIS and the Metop-B/C IASI for a longwave TIR microwindow, $\nu \approx 962.5$ cm${}^{-1}$). All the satellite bias corrections were reset and a 5-week spin-up was conducted. The baseline (control) OSE was based on the existing CRTM v2.3.0 snow/ice emissivity a priori [4]. The test run was conducted using a stripped-down LUT from the v1 (WW80) snow/ice emissivity physical model that was hard-coded into the GSI for two zenith observing angles (${\theta }_o={10}^{\circ },{60}^{\circ }$) and a nominal particle size of $r=200$ $\mathsf{\mu }$m. The LUT-interpolated coarse-resolution model emissivity spectra were then adjusted based on a linear fit to the surface channel data.

Figure 6 shows the histograms from the test OSE presented in the same manner as Figure 2. A significant improvement can be seen in terms of both the spread and bias, with the standard deviations now closer to the 1 K range, which is more than a factor of 5 reduction. Note that these results have only used a subset of the initial snow emissivity model LUT (v1) based only on WW80, which is known to break down at larger particle sizes. It is, thus, believed that the improvement in global obs − calc is due primarily to the improved angular and spectral dependence afforded by the physical model (at least for this particular spectral channel) over the original CRTM snow/ice emissivity a priori [4]. Although significantly reduced, there remains a negative bias in these results, which may be the result of residual cloud/aerosol contamination [18] or some other interference not accounted for in the clear-sky RT, as well as the deficiency in modeling snowpacks with larger snow grain sizes, as is the case with aged snowpacks. Other factors not accounted for in the global OSE sample include non-homogeneous snow/ice surfaces (e.g., non-snow/ice surfaces within the sensor field-of-view); non-random, macroscale topographical features that change the mean inclination angle of the surface (e.g., sastrugi) [58]; non-spherical snow grain shapes [45]; and snowpack impurities such as aerosols [59]. Although the dependence of the complex refractive index $N_{\nu }$ on surface temperature, T [44], is included in our implementation of the three emissivity models (H13, WW80, and hybrid physical), this was not taken into consideration within the OSE. However, these are all most likely second order effects after the particle size and cloud contamination factors.

3.2. Comparison of Models against Published Laboratory and Field Measurements

We tested the output from the three snow emissivity models discussed in this paper (H13, WW80, and our hybrid physical model, Equation (13)) against published laboratory and field data. The results are summarized in multi-panel figures below.

Figure 7 shows a comparison of the snow emissivity model calculations (H13, WW80, hybrid physical model in the first three columns, respectively) against emissivity derived from laboratory measurements of snow albedo [51] from the ECOSTRESS library [29], shown in the rightmost column. These measurements were taken at a single near-nadir incidence angle (${\theta }_o={10}^{\circ }$), but they span fine, medium, and coarse snow grain sizes ($r\approx$ 30 $\mathsf{\mu }$m, 212.5 $\mathsf{\mu }$m, and 750 $\mathsf{\mu }$m; flat ice (effective $r\ge 1000$ $\mathsf{\mu }$m); and frost ($r\approx 3.25$ $\mathsf{\mu }$m). It can be seen that the H13 and WW80 models perform well for large and small particle sizes, respectively (left two columns, respectively), but break down in the opposite regimes. The hybrid physical model (third column from the left) captures both large and small particle size regimes as designed, including the prominent low-emissivity spectral features in the smaller particle size regime ($r⪅100$ $\mathsf{\mu }$m), known as reststrahlen bands (bottom plot), and the overall increase in spectral emissivity with particle size in this regime, as well the subsequent spectral “flattening” and decrease in emissivity (top plot) in the larger particle size regime ($r>100$ $\mathsf{\mu }$m).

As mentioned previously, the observer angle dependence (${\theta }_o$) in surface TIR-FIR emissivity is usually a first-order dependency for terrestrial surfaces, with emissivity generally decreasing with the observer angle as a result of increasing reflectance. To test the three models’ performance for ${\theta }_o>{10}^{\circ }$, we compared them against the Hori et al. [53] field measurements of snow cover emissivity (provided to us courtesy of M. Hori, University of Toyama), which span the ${\theta }_o$ range of 0–75${}^{\circ }$ and median particle sizes $r\ge 35$ $\mathsf{\mu }$m (i.e., where quasi-specular reflectance begins to dominate over layer multiple scattering effects); the results are summarized in Figure 8 and Figure 9, with the columns again arranged from left to right for the H13 model, WW80 model, hybrid physical model, and field measurements, respectively.

In Figure 8, the emissivities are plotted as a linear function of particle radii, r, for a selection of monochromatic longwave TIR channels, with the rows arranged top to bottom showing results for ${\theta }_o={30}^{\circ },{45}^{\circ },{60}^{\circ },{75}^{\circ }$, respectively. These plots clearly show the general decrease in emissivity with ${\theta }_o$ (top to bottom plots) for all the particle sizes considered $r\ge 35$ $\mathsf{\mu }$m, as well as the decrease in emissivity with r for these sizes. Here it is also evident that the WW80 model does not adequately capture the particle size dependence, remaining almost constant but otherwise reasonably capturing the angular dependency for the smallest particle sizes considered ($r\approx 35$ $\mathsf{\mu }$m). The H13 model (left column) shows the best overall agreement with the measurements (right column), but this is expected given that the H13 model was empirically tuned to agree with those measurements. The hybrid physical model yields very similar results to the H13 model, albeit exhibiting a somewhat greater decrease in emissivity with particle size at the largest observer angles, ${\theta }_o={75}^{\circ }$.

Finally, in Figure 9, the longwave TIR spectral emissivities are plotted for a selection of particle sizes in the same arrangement as Figure 8. These show the good agreements of H13 (left column) and the hybrid physical model (third column) with the Ref. [52] measurements. However, with the exception of the smallest particle size, $r\approx 35$ $\mathsf{\mu }$m, the WW80 model (second column) is clearly out-of-family. Note that all three models have the least dependence on observer angle in the spectral region around $\nu \approx 950$ cm${}^{-1}$, which is close to the channel considered in the OSE in Section 3.1 (962.5 cm${}^{-1}$). Assuming that a fraction of the geographical areas included in the OSE sample were fresh snow and/or frost with small particle sizes, these factors may explain the significant improvement in the obs − calc from only using the WW80 model over the original CRTM emissivity model.

4. Conclusions and Future Work

In this paper we have provided a summary of the research undertaken to develop a physical TIR snow/ice surface emissivity model for practical implementation within fast-forward models. This was specifically to address the need for an upgrade to the CRTM’s snow/ice emissivity a priori to reduce the observed biases between calculations (calc) and hyperspectral TIR observations (obs) within global NWP assimilation systems. The previously existing CRTM snow emissivity a priori dated back to the CRTM Version 1 [4] and was no longer satisfactory for today’s suite of hyperspectral TIR sounders. After an extensive literature review, the WW80 snow albedo model was chosen to be implemented as the first step toward this goal. The WW80 model is a physical snow albedo model based on Mie scattering and D-E approximation that was initially developed for solar spectrum albedo but adapted with some success by Dozier and Warren [35] for the TIR emissivity application, and today, it forms the basis of the SNICAR-ADv3 model [36]. We researched and implemented the WW80 model within our own research code and have subsequently provided a detailed theoretical basis and derivation, omitted from the original paper [31], in the Appendices.

A hybrid physical model (similar to the H13 model [53]) was subsequently developed to extend the WW80 physical model to larger particle sizes outside of its range of validity, $r⪆50$ $\mathsf{\mu }$m. The hybrid physical model assumes a linear transition between two snow particle size regimes, namely, a small particle size regime ($r⪅50$ $\mathsf{\mu }$m), where the surface behaves as a multiple scattering layer, and a larger particle size regime, where the surface behaves as a quasi-specular reflector resulting from randomly oriented snow crystal facets.

In parallel with the hybrid model development, the WW80 model was implemented as a v1 physical snow emissivity model within an offline test version of the CRTM (v2.3.0), and the preliminary results of an OSE of global obs − calc based on an abbreviated, hard-coded LUT were found to be encouraging, with over a factor of 5 improvement over the original CRTM snow emissivity a priori. This initial improvement in global obs − calc in the implementation of the WW80 model is believed to be due to the improved angular and spectral dependence afforded by the physical model. All three snow/ice emissivity models (H13, WW80, and the hybrid physical model) were compared against laboratory and field observations [51,52], where it was found that the H13 model agrees well with the larger particle sizes (e.g., aged snow), the WW80 for smaller particle sizes (e.g., newly fallen snow and frost), with the hybrid physical model showing good agreement in both regimes. The optical constants used in the hybrid physical model include temperature-dependence and span the TIR-FIR, thus, extending the model’s spectral range to the FIR region, which is of recent interest for polar remote sensing [14]. A caveat is warranted, however, in applying the model to the FIR for small particle sizes ($r\le 50$ $\mathsf{\mu }$m) given the breakdown of the far-field assumption employed by the WW80 albedo model, as discussed in Section 2.

Future work will include additional validation and/or development of the hybrid physical model against field and/or laboratory data obtained from well-calibrated, surface-based spectrometers [60], for example, the marine atmospheric emitted radiance interferometer (MAERI) [61] and the absolute radiance interferometer (ARI) [62]. These include ship-based polar field experiments, such as the Multidisciplinary drifting Observatory for the Study of Arctic Climate (MOSAiC) expedition [63], as well as the ARI measurements obtained from the field and a rooftop laboratory at the University of Wisconsin-Madison [64]. To account for non-uniform, mixed, or partially covered snow/ice surfaces, the hybrid physical model is planned to be merged with the CAMEL database [21] used by RTTOV and an offline version of NUCAPS. The hybrid physical model (v1.1) is also planned for implementation within a future version of LaRC’s PCRTM (v5.0) and is currently being implemented within the anticipated release version of CRTM (v3.0). Testing of the CRTM implementation and NWP impact within GSI global obs − calc OSEs will be the subject of future work.