Improving HJ-1B/IRS LST Retrieval of the Generalized Single-Channel Algorithm with Refined ERA5 Atmospheric Profile Database
Abstract
:1. Introduction
2. Experimental Data
2.1. Remote Sensing Data
2.1.1. HJ-1B IRS Data
2.1.2. ASTER GEDv3 Product
2.1.3. ASTER GDEM Product
2.1.4. MODIS Product
2.1.5. Multi-Source Data Synergized Quantitative (MUSYQ) Fractional Vegetation Cover (FVC) Product
2.2. Auxiliary Data
2.2.1. ERA5 Atmospheric Reanalysis Data
2.2.2. TIGR Atmospheric Profile Database
2.3. Ground Measurements
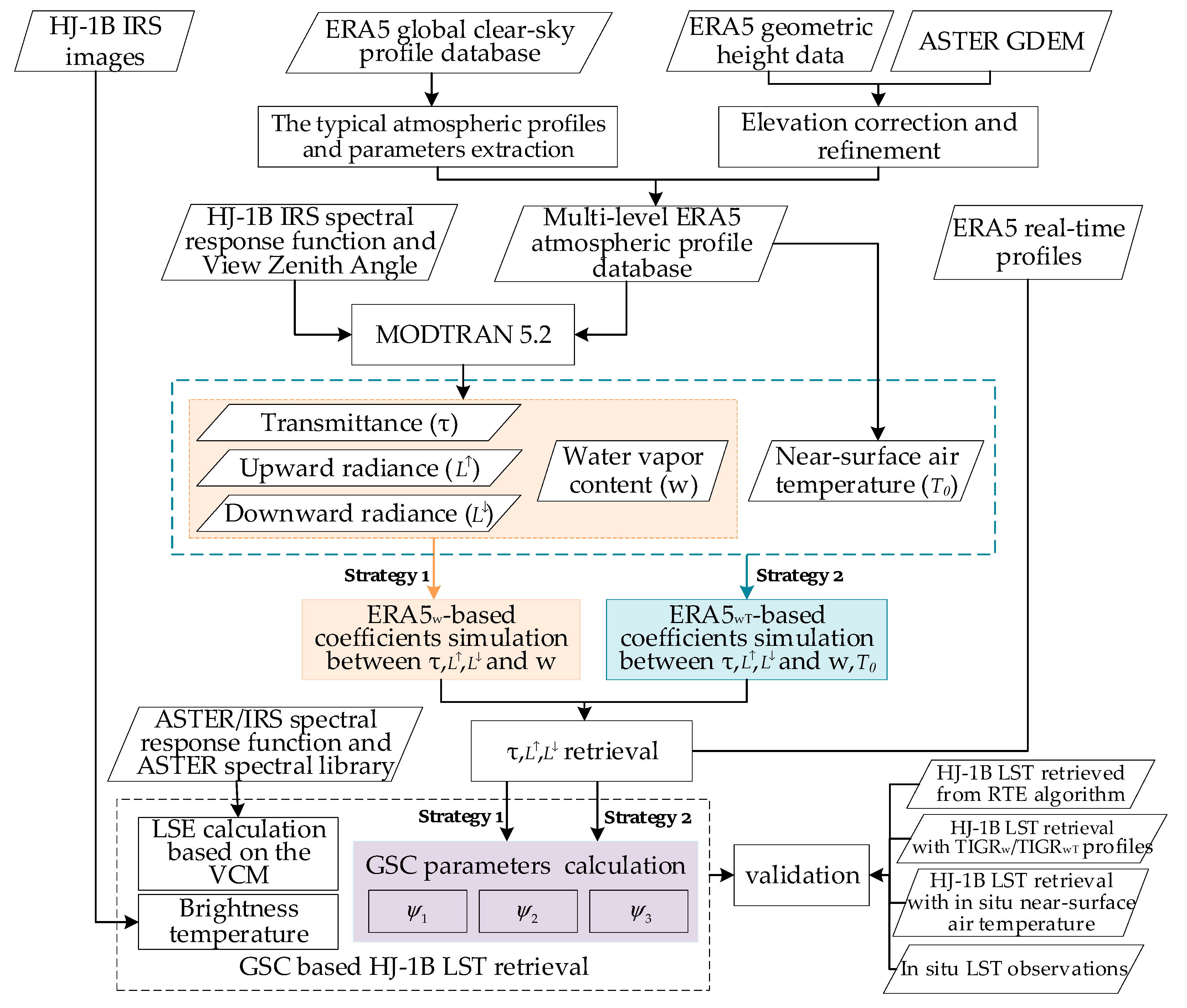
3. Methodology
3.1. LST Retrieval by the GSC Algorithms
3.1.1. Refined ERA5 Atmospheric Profile Database
3.1.2. Improved GSCw/GSCwT Algorithm
3.1.3. LSE Calculation
3.2. Validation Strategy
3.2.1. HJ-1B LST Retrieved from RTE Algorithm
3.2.2. HJ-1B LST Retrieval with TIGRw/TIGRwT Profiles
3.2.3. HJ-1B LST Retrieval with In Situ Near-Surface Air Temperature
4. Results
5. Discussion
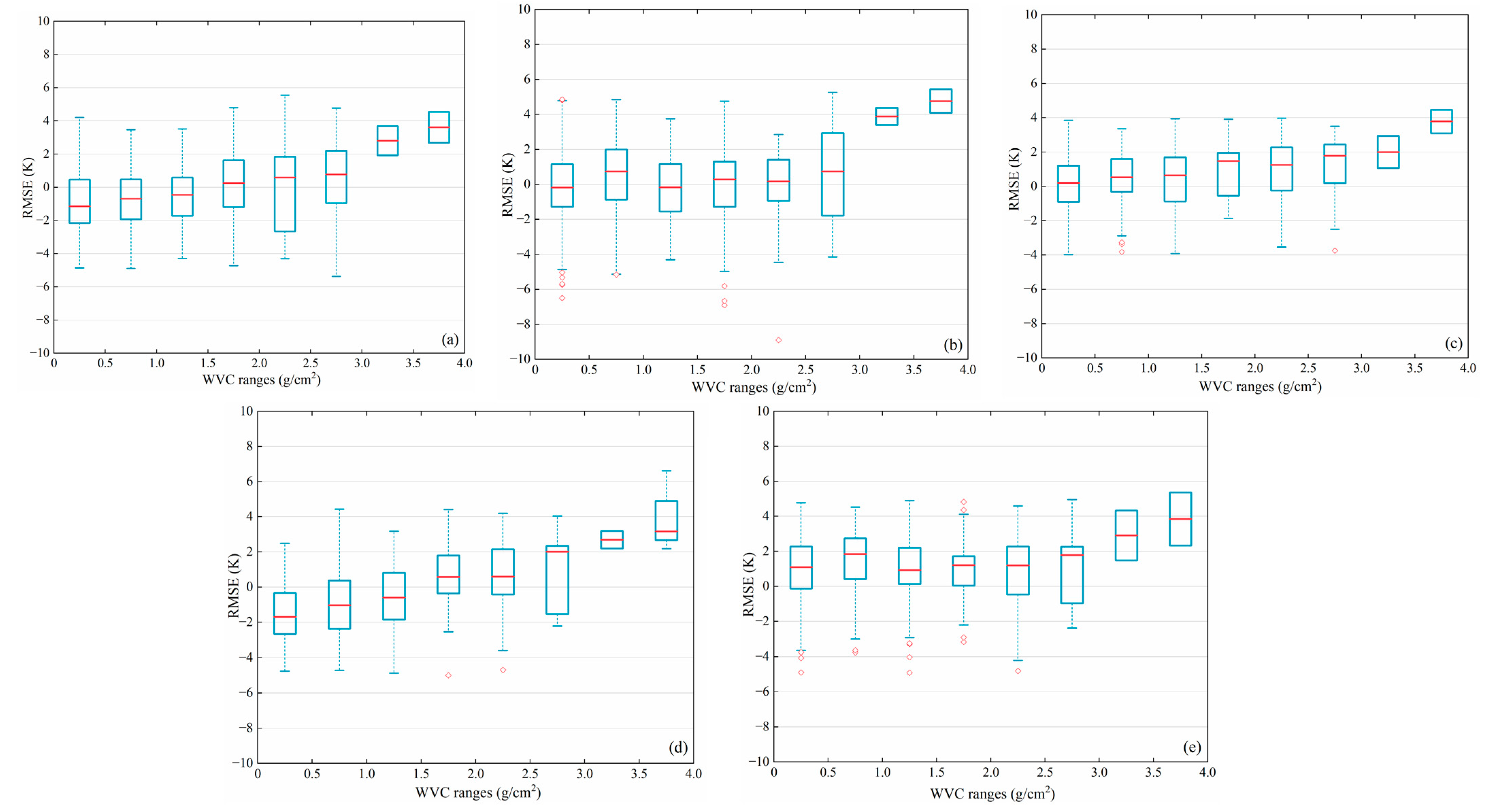
5.1. Effect of Site, Month, WVC, and VZA on LST Retrieval
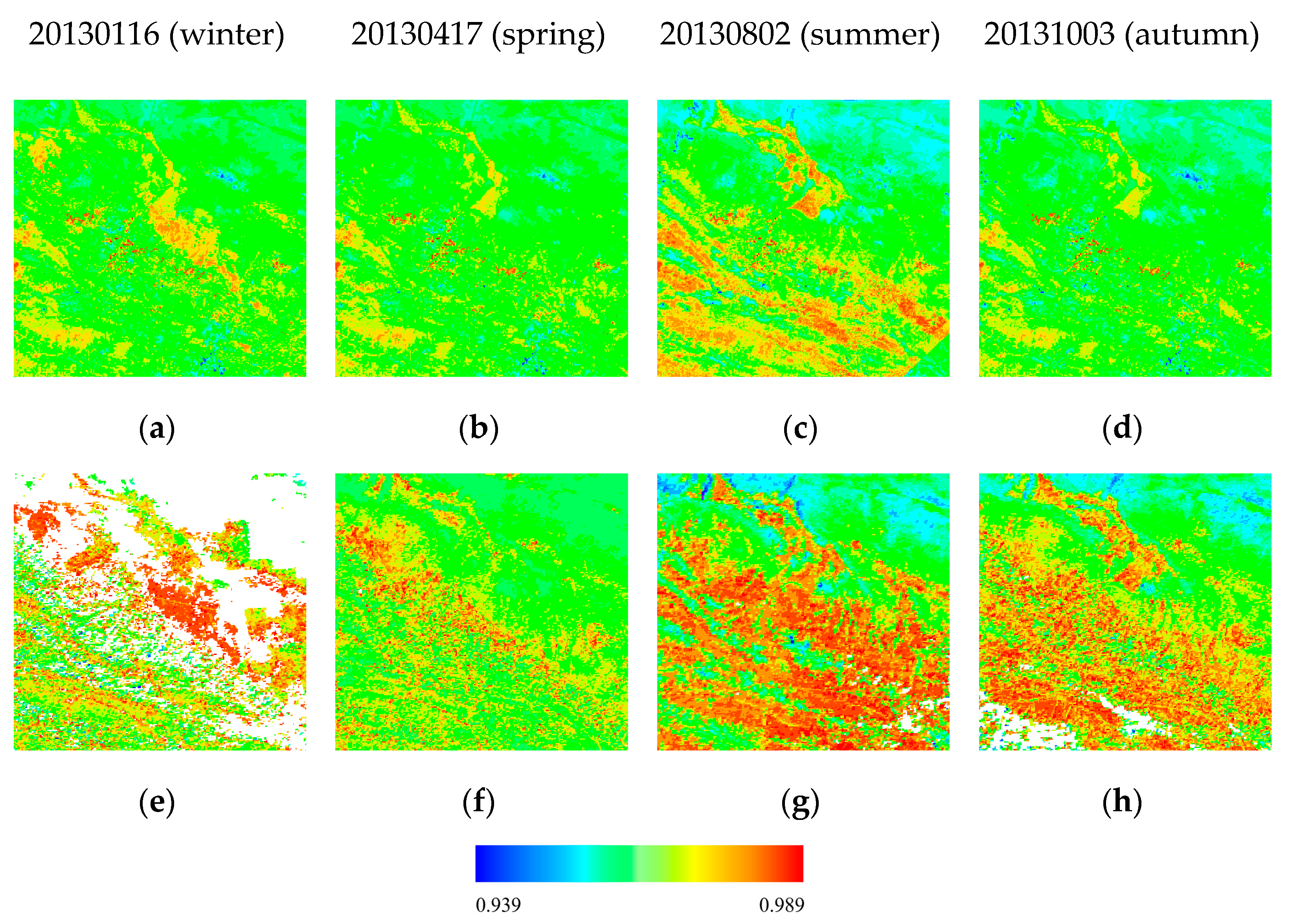
5.2. Effect of Different LSE Data on LSTs Retrieved by the GSC Algorithm
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, Z.-L.; Tang, B.-H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef]
- Lambin, E.F.; Ehrlich, D. Land-cover changes in sub-Saharan Africa (1982–1991): Application of a change index based on remotely sensed surface temperature and vegetation indices at a continental scale. Remote Sens. Environ. 1997, 61, 181–200. [Google Scholar] [CrossRef]
- Hansen, J.; Ruedy, R.; Sato, M.; Lo, K. Global Surface Temperature Change. Rev. Geophys. 2010, 48, RG4004. [Google Scholar] [CrossRef]
- Kogan, F.N. Operational space technology for global vegetation assessment. Bull. Am. Meteorol. Soc. 2001, 82, 1949–1964. [Google Scholar] [CrossRef]
- Hu, T.; van Dijk, A.I.J.M.; Renzullo, L.J.; Xu, Z.; He, J.; Tian, S.; Zhou, J.; Li, H. On agricultural drought monitoring in Australia using Himawari-8 geostationary thermal infrared observations. Int. J. Appl. Earth Obs. Geoinf. 2020, 91, 102153. [Google Scholar] [CrossRef]
- Wan, Z.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Trans. Geosci. Remote Sens. 1996, 34, 892–905. [Google Scholar]
- Li, H.; Sun, D.; Yu, Y.; Wang, H.; Liu, Y.; Liu, Q.; Du, Y.; Wang, H.; Cao, B. Evaluation of the VIIRS and MODIS LST products in an arid area of Northwest China. Remote Sens. Environ. 2014, 142, 111–121. [Google Scholar] [CrossRef]
- Coll, C.; Caselles, V.; Valor, E.; Niclòs, R.; Sánchez, J.M.; Galve, J.M.; Mira, M. Temperature and emissivity separation from ASTER data for low spectral contrast surfaces. Remote Sens. Environ. 2007, 110, 162–175. [Google Scholar] [CrossRef]
- Du, C.; Ren, H.; Qin, Q.; Meng, J.; Zhao, S. A Practical Split-Window Algorithm for Estimating Land Surface Temperature from Landsat 8 Data. Remote Sens. 2015, 7, 647–665. [Google Scholar] [CrossRef]
- Qin, Z.; Karnieli, A.; Berliner, P. A mono-window algorithm for retrieving land surface temperature from Landsat TM data and its application to the Israel-Egypt border region. Int. J. Remote Sens. 2001, 22, 3719–3746. [Google Scholar] [CrossRef]
- Li, R.; Li, H.; Hu, T.; Bian, Z.; Liu, F.; Cao, B.; Du, Y.; Sun, L.; Liu, Q. Land Surface Temperature Retrieval from Sentinel-3A SLSTR data: Comparison among Split-window, Dual-window, Three-channel and Dual-angle algorithms. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–14. [Google Scholar] [CrossRef]
- Gillespie, A.; Rokugawa, S.; Matsunaga, T.; Cothern, J.S.; Hook, S.; Kahle, A.B. A temperature and emissivity separation algorithm for Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) images. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1113–1126. [Google Scholar] [CrossRef]
- Li, H.; Liu, Q.; Du, Y.; Jiang, J.; Wang, H. Evaluation of the NCEP and MODIS Atmospheric Products for Single Channel Land Surface Temperature Retrieval With Ground Measurements: A Case Study of HJ-1B IRS Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 1399–1408. [Google Scholar] [CrossRef]
- Duan, S.-B.; Li, Z.-L.; Wang, C.; Zhang, S.; Tang, B.-H.; Leng, P.; Gao, M.-F. Land-surface temperature retrieval from Landsat 8 single-channel thermal infrared data in combination with NCEP reanalysis data and ASTER GED product. Int. J. Remote Sens. 2018, 40, 1763–1778. [Google Scholar] [CrossRef]
- Windahl, E.; Beurs, K.d. An intercomparison of Landsat land surface temperature retrieval methods under variable atmospheric conditions using in situ skin temperature. Int. J. Appl. Earth Obs. Geoinf. 2016, 51, 11–27. [Google Scholar] [CrossRef]
- Jiménez-Muñoz, J.C.; Sobrino, J.A. A generalized single-channel method for retrieving land surface temperature from remote sensing data. J. Geophys. Res. 2003, 109, 8112. [Google Scholar] [CrossRef]
- Jimenez-Munoz, J.C.; Cristobal, J.; Sobrino, J.A.; Soria, G.; Ninyerola, M.; Pons, X.; Pons, X. Revision of the Single-Channel Algorithm for Land Surface Temperature Retrieval From Landsat Thermal-Infrared Data. IEEE Trans. Geosci. Remote Sens. 2009, 47, 339–349. [Google Scholar] [CrossRef]
- Pandya, M.R.; Shah, D.B.; Trivedi, H.J.; Darji, N.P.; Ramakrishnan, R.; Panigrahy, S.; Parihar, J.S.; Kirankumar, A. Retrieval of land surface temperature from the Kalpana-1 VHRR data using a single-channel algorithm and its validation over western India. Isprs J. Photogramm. Remote Sens. 2014, 94, 160–168. [Google Scholar] [CrossRef]
- Wang, X.; Zhong, L.; Ma, Y. Estimation of 30 m land surface temperatures over the entire Tibetan Plateau based on Landsat-7 ETM+ data and machine learning methods. Int. J. Digit. Earth 2022, 15, 1038–1055. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Raissouni, N.; Li, Z.L. A Comparative Study of Land Surface Emissivity Retrieval from NOAA Data. Remote Sens. Environ. 2001, 75, 256–266. [Google Scholar] [CrossRef]
- Valor, E.; Caselles, V. Mapping land surface emissivity from NDVI: Application to European, African, and South American areas. Remote Sens. Environ. 1996, 57, 167–184. [Google Scholar] [CrossRef]
- Snyder, W.C.; Wan, Z.; Zhang, Y.; Feng, Y.Z. Classification-based emissivity for land surface temperature measurement from space. Int. J. Remote Sens. 1998, 19, 2753–2774. [Google Scholar] [CrossRef]
- Duan, S.-B.; Li, Z.-L.; Li, H.; Göttsche, F.-M.; Wu, H.; Zhao, W.; Leng, P.; Zhang, X.; Coll, C. Validation of Collection 6 MODIS land surface temperature product using in situ measurements. Remote Sens. Environ. 2019, 225, 16–29. [Google Scholar] [CrossRef]
- Hulley, G.C.; Hook, S.J.; Abbott, E.; Malakar, N.; Islam, T.; Abrams, M. The ASTER Global Emissivity Dataset (ASTER GED): Mapping Earth’s emissivity at 100 meter spatial scale. Geophys. Res. Lett. 2015, 42, 7966–7976. [Google Scholar] [CrossRef]
- Li, H.; Hu, T.; Meng, X.; Du, Y.; Cao, B.; Liu, Q. Improving HJ-1B IRS land surface temperature product using ASTER global emissivity dataset. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; 2016; pp. 2661–2664. [Google Scholar]
- Li, H.; Yang, Y.K.; Li, R.B.; Wang, H.S.; Cao, B.; Bian, Z.J.; Hu, T.; Du, Y.M.; Sun, L.; Liu, Q.H. Comparison of the MuSyQ and MODIS Collection 6 Land Surface Temperature Products Over Barren Surfaces in the Heihe River Basin, China. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8081–8094. [Google Scholar] [CrossRef]
- Zhang, S.; Duan, S.-B.; Li, Z.-L.; Huang, C.; Wu, H.; Han, X.-J.; Leng, P.; Gao, M. Improvement of Split-Window Algorithm for Land Surface Temperature Retrieval from Sentinel-3A SLSTR Data Over Barren Surfaces Using ASTER GED Product. Remote Sens. 2019, 11, 3025. [Google Scholar] [CrossRef]
- Wang, H.; Yu, Y.; Yu, P.; Liu, Y. Land Surface Emissivity Product for NOAA JPSS and GOES-R Missions: Methodology and Evaluation. IEEE Trans. Geosci. Remote Sens. 2020, 58, 307–318. [Google Scholar] [CrossRef]
- Li, R.; Li, H.; Sun, L.; Yang, Y.; Hu, T.; Bian, Z.; Cao, B.; Du, Y.; Liu, Q. An Operational Split-Window Algorithm for Retrieving Land Surface Temperature from Geostationary Satellite Data: A Case Study on Himawari-8 AHI Data. Remote Sens. 2020, 12, 2613. [Google Scholar] [CrossRef]
- Abrams, M.; Crippen, R.; Fujisada, H. ASTER Global Digital Elevation Model (GDEM) and ASTER Global Water Body Dataset (ASTWBD). Remote Sens. 2020, 12, 1156. [Google Scholar] [CrossRef]
- Zhao, J.; Li, J.; Liu, Q.; Xu, B.; Yu, W.; Lin, S.; Hu, Z. Estimating fractional vegetation cover from leaf area index and clumping index based on the gap probability theory. Int. J. Appl. Earth Obs. Geoinf. 2020, 90, 102112. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Cristóbal, J.; Jiménez-Muñoz, J.C.; Sobrino, J.A.; Ninyerola, M.; Pons, X. Improvements in land surface temperature retrieval from the Landsat series thermal band using water vapor and air temperature. J. Geophys. Res. Atmos. 2009, 114, D08103. [Google Scholar] [CrossRef]
- Li, X.; Cheng, G.; Liu, S.; Xiao, Q.; Ma, M.; Jin, R.; Che, T.; Liu, Q.; Wang, W.; Qi, Y.; et al. Heihe Watershed Allied Telemetry Experimental Research (HiWATER): Scientific Objectives and Experimental Design. Bull. Am. Meteorol. Soc. 2013, 94, 1145–1160. [Google Scholar] [CrossRef]
- Liu, S.; Li, X.; Xu, Z.; Che, T.; Xiao, Q.; Ma, M.; Liu, Q.; Jin, R.; Guo, J.; Wang, L.; et al. The Heihe Integrated Observatory Network: A Basin-Scale Land Surface Processes Observatory in China. Vadose Zone J. 2018, 17, 1–21. [Google Scholar] [CrossRef]
- Li, H.; Li, R.; Yang, Y.; Cao, B.; Liu, Q. Temperature-Based and Radiance-Based Validation of the Collection 6 MYD11 and MYD21 Land Surface Temperature Products Over Barren Surfaces in Northwestern China. IEEE Trans. Geosci. Remote Sens. 2021, 59, 1794–1807. [Google Scholar] [CrossRef]
- Li, H.; Li, R.; Tu, H.; Cao, B.; Liu, F.; Bian, Z.; Hu, T.; Du, Y.; Sun, L.; Liu, Q. An Operational Split-Window Algorithm for Generating Long-Term Land Surface Temperature Products from Chinese Fengyun-3 Series Satellite Data. IEEE Trans. Geosci. Remote Sens. 2023. [Google Scholar] [CrossRef]
- Ermida, S.L.; Trigo, I.F. A Comprehensive Clear-Sky Database for the Development of Land Surface Temperature Algorithms. Remote Sens. 2022, 14, 2329. [Google Scholar] [CrossRef]
- Peres, L.F.; DaCamara, C.C. Emissivity maps to retrieve land-surface temperature from MSG/SEVIRI. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1834–1844. [Google Scholar] [CrossRef]
- Baldridge, A.M.; Hook, S.J.; Grove, C.I.; Rivera, G. The ASTER spectral library version 2.0. Remote Sens. Environ. 2009, 113, 711–715. [Google Scholar] [CrossRef]
- Coll, C.; Caselles, V.; Galve, J.; Valor, E.; Niclos, R.; Sanchez, J.; Rivas, R. Ground measurements for the validation of land surface temperatures derived from AATSR and MODIS data. Remote Sens. Environ. 2005, 97, 288–300. [Google Scholar] [CrossRef]
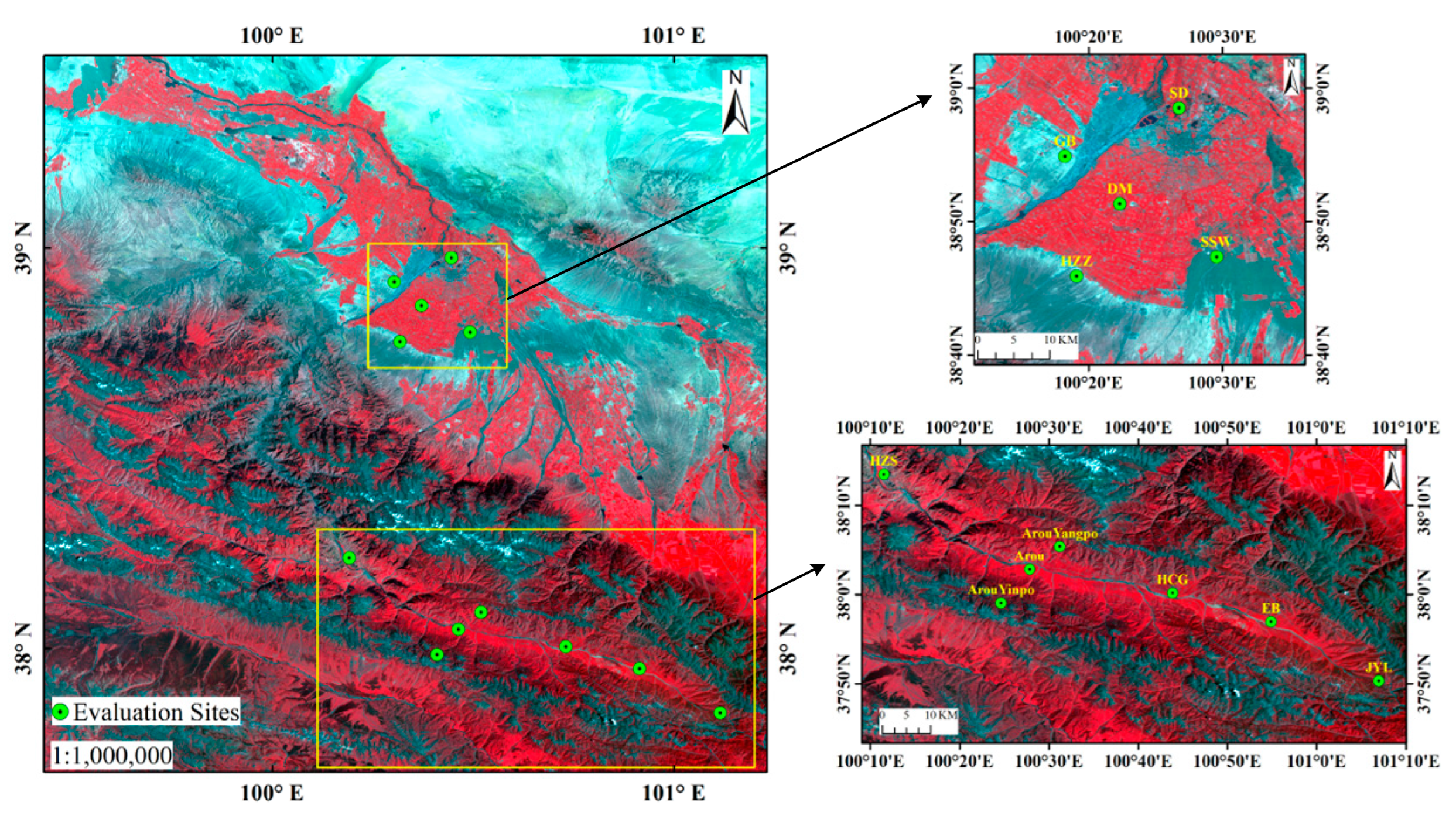




| Station Code | Location | Elevation (m) | Land Cover | Instrument | Measurement Height (m) | Period (Year/Month/Day) |
|---|---|---|---|---|---|---|
| GB | 100.3042°E 38.9150°N | 1567 | Gobi Desert | CNR1 | 6 | 2012/07/22–2014/06/30 |
| SSW | 100.4933°E 38.7892°N | 1555 | Sand dune | CNR1 | 6 | 2012/06/08–2014/06/30 |
| HZZ | 100.3186°E 38.7652°N | 1735 | Desert steppe | SI-111 | 2.65 | 2012/06/04–2014/06/30 |
| SD | 100.4464°E 38.9751°N | 1460 | Wetland | SI-111 | 6 | 2012/06/25–2014/06/30 |
| DM | 100.3722°E 38.8555°N | 1556 | Corn field | CNR1 | 12 | 2012/07/22–2014/06/30 |
| Arou | 100.4643°E 38.0473°N | 3033 | Alpine meadow | CNR1 | 5 | 2012/10/14–2014/06/30 |
| ArouYangpo | 100.5204°E 38.0898°N | 3529 | Alpine meadow | CNR1 | 6 | 2013/08/08–2014/06/30 |
| ArouYinpo | 100.4108°E 37.9841°N | 3536 | Alpine meadow | CNR1 | 6 | 2013/08/08–2014/06/30 |
| EB | 100.9151°E 37.9492°N | 3294 | Alpine meadow | CNR1 | 6 | 2013/06/11–2014/06/30 |
| HZS | 100.1918°E 38.2254°N | 3529 | Wheat field | CNR1 | 6 | 2013/06/10–2014/06/30 |
| HCG | 100.7312°E 38.0033°N | 3137 | Alpine meadow | CNR1 | 6 | 2013/06/07–2014/06/30 |
| JYL | 101.1160°E 37.8384°N | 3750 | Alpine meadow | CNR1 | 6 | 2013/08/15–2014/06/30 |
| RMSE(K) | ||||||||
|---|---|---|---|---|---|---|---|---|
| −0.1462 | 0.6874 | 1 | 0.1504 | −0.6975 | −2.5920 × 10−5 | 0.08 | 0.99994 | |
| −0.1778 | 0.6819 | 1 | 0.0284 | 0.0480 | −5.6100 × 10−6 | 0.07 | 0.99997 |
| RMSE(K) | ||||||
|---|---|---|---|---|---|---|
| 0.0043 | −0.0245 | −0.1034 | 0.9949 | 0.01 | 0.987934 | |
| −0.0500 | 0.3173 | 0.5079 | 0.0093 | 0.09 | 0.987204 | |
| −0.0790 | 0.4528 | 0.8269 | 0.0143 | 0.07 | 0.980075 |
| RMSE (K) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5.4666 | 4.5187 × 10−8 | −1.3998 × 10−1 | 4.0244 × 10−4 | −7.0588 × 10−9 | −6.2867 × 10−5 | 2.4552 × 10−6 | 2.7567 × 10−10 | 8.9606 × 10−1 | 0.01 | 0.985 | |
| 1.0163 | 5.4153 × 10−5 | 3.1412 | −2.2929 × 10−2 | 7.0086 × 10−5 | −2.9675 × 10−2 | −9.6015 × 10−3 | 2.2677 × 10−5 | 2.4271 | 0.04 | 0.981 | |
| 1.6853 | 1.1343 × 10−4 | 6.0363 | −4.9522 × 10−2 | 1.2667 × 10−4 | −5.5303 × 10−2 | −1.5440 × 10−2 | 3.5363 × 10−5 | 5.4054 | 0.08 | 0.982 |
| IGBP Class | Class Name | IRS 4 | F [40] |
|---|---|---|---|
| 1 | Evergreen Needleleaf Forest | 0.989 | 0.25 |
| 2 | Evergreen Broadleaf Forest | 0.973 | 0.25 |
| 3 | Deciduous Needleleaf Forest | 0.989 | 0.25 |
| 4 | Deciduous Broadleaf Forest | 0.973 | 0.25 |
| 5 | Mixed Forests | 0.981 | 0.25 |
| 6 | Closed Shrublands | 0.981 | 0.15 |
| 7 | Open Shrublands | 0.981 | 0.07 |
| 8 | Woody Savannas | 0.958 | 0.14 |
| 9 | Savannas | 0.953 | 0.11 |
| 10 | Grasslands | 0.986 | 0.03 |
| 12 | Croplands | 0.986 | - |
| 13 | Urban Areas | 0.984 | 0.13 |
| 14 | Cropland–Natural Vegetation Mosaic | 0.972 | - |
| 16 | Barren or Sparsely Vegetated | 0.953 | 0.03 |
| RMSE(K) | ||||||||
|---|---|---|---|---|---|---|---|---|
| −0.1660 | 0.6565 | 1 | −0.1564 | 0.6785 | 2.2310 × 10−5 | 0.16 | 0.99987 | |
| −0.1897 | 0.6675 | 1 | 0.0518 | 0.0904 | −3.6000 × 10−6 | 0.10 | 0.99991 |
| RMSE(K) | ||||||
|---|---|---|---|---|---|---|
| 0.0039 | −0.0300 | −0.0540 | 0.9730 | 0.02 | 0.977723 | |
| −0.0538 | 0.3865 | 0.1039 | 0.0823 | 0.02 | 0.977724 | |
| −0.0931 | 0.6155 | 0.1626 | 0.1348 | 0.07 | 0.979975 |
| RMSE(K) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 4.0544 × 10−3 | 2.5122 × 10−7 | 1.1235 × 10−1 | −8.8438 × 10−4 | 3.6262 × 10−8 | −1.2766 × 10−4 | −4.6067 × 10−6 | 1.3086 × 10−9 | 7.7834 × 10−1 | 0.01 | 0.983 | |
| 1.7100 × 10−2 | 8.4819 × 10−7 | −3.7269 × 10−2 | −2.6248 × 10−4 | −1.5567 × 10−6 | 4.8173 × 10−4 | −2.2103 × 10−4 | 7.1426 × 10−7 | 2.0307 × 10−2 | 0.13 | 0.960 | |
| 4.1393 × 10−4 | 3.5926 × 10−6 | −1.0993 × 10−3 | −1.0241 × 10−4 | −5.4112 × 10−6 | 1.5425 × 10−4 | −5.8084 × 10−5 | 2.0376 × 10−6 | 7.2981 × 10−4 | 0.18 | 0.957 |
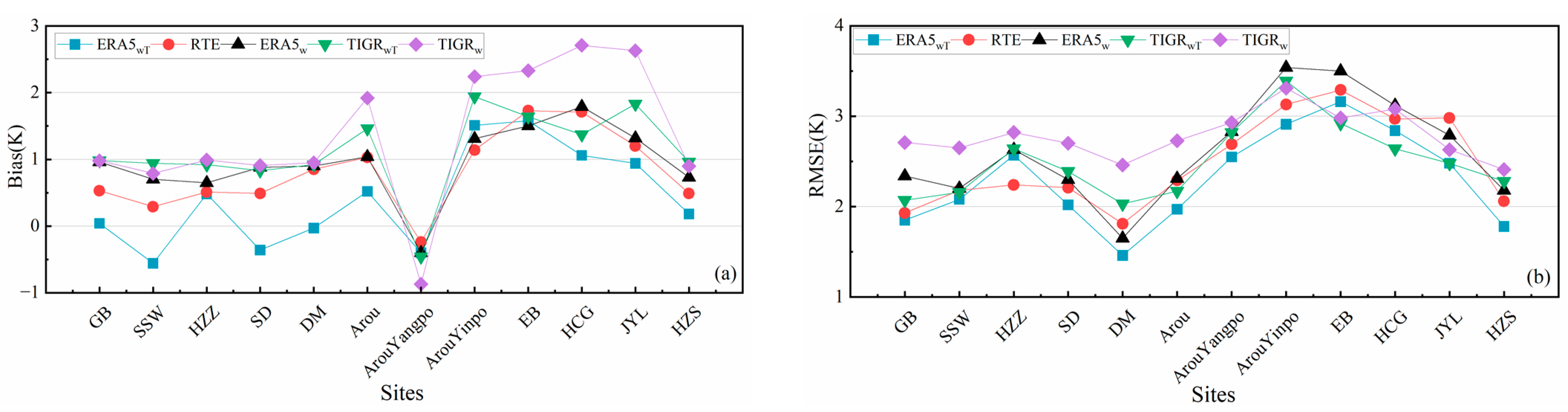
| Site | Land Types | ERA5wT (K) | RTE (K) | ERA5w (K) | TIGRwT (K) | TIGRw (K) | N | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bias | RMSE | Bias | RMSE | Bias | RMSE | Bias | RMSE | Bias | RMSE | |||
| GB | Gobi Desert | 0.04 | 1.85 | 0.53 | 1.93 | 0.96 | 2.34 | 0.98 | 2.07 | 0.98 | 2.71 | 107 |
| SSW | Sand dune | −0.56 | 2.08 | 0.29 | 2.18 | 0.70 | 2.20 | 0.94 | 2.16 | 0.79 | 2.65 | 110 |
| HZZ | Desert steppe | 0.48 | 2.57 | 0.51 | 2.24 | 0.65 | 2.63 | 0.92 | 2.64 | 0.99 | 2.82 | 102 |
| SD | Wetland | −0.36 | 2.02 | 0.49 | 2.21 | 0.88 | 2.30 | 0.83 | 2.39 | 0.91 | 2.70 | 112 |
| DM | Corn field | −0.03 | 1.46 | 0.85 | 1.81 | 0.90 | 1.65 | 0.92 | 2.03 | 0.95 | 2.46 | 110 |
| Arou | Alpine Meadows | 0.52 | 1.97 | 1.03 | 2.29 | 1.04 | 2.31 | 1.46 | 2.17 | 1.92 | 2.73 | 84 |
| Arou Yangpo | Alpine Meadows | −0.40 | 2.55 | −0.24 | 2.69 | −0.40 | 2.83 | −0.46 | 2.82 | −0.87 | 2.93 | 40 |
| Arou Yinpo | Alpine Meadows | 1.51 | 2.91 | 1.14 | 3.13 | 1.31 | 3.54 | 1.94 | 3.39 | 2.24 | 3.31 | 22 |
| EB | Alpine Meadows | 1.58 | 3.16 | 1.73 | 3.29 | 1.50 | 3.50 | 1.64 | 2.92 | 2.33 | 2.98 | 43 |
| HCG | Alpine Meadows | 1.06 | 2.84 | 1.71 | 2.97 | 1.79 | 3.12 | 1.37 | 2.64 | 2.71 | 3.08 | 44 |
| JYL | Alpine Meadows | 0.94 | 2.48 | 1.20 | 2.98 | 1.32 | 2.79 | 1.83 | 2.48 | 2.63 | 2.63 | 36 |
| HZS | Wheat field | 0.18 | 1.78 | 0.49 | 2.06 | 0.73 | 2.18 | 0.96 | 2.28 | 0.90 | 2.41 | 42 |
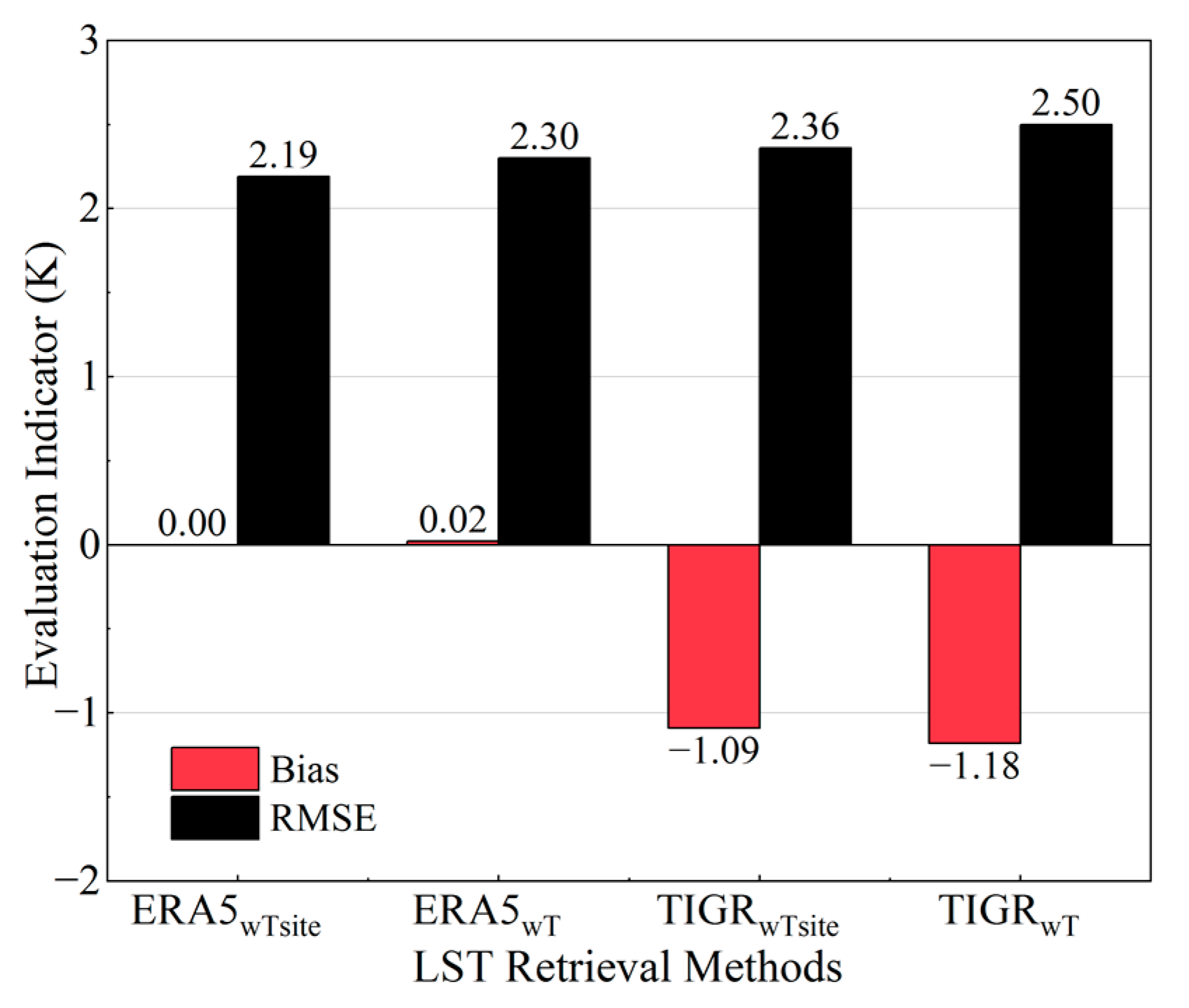
| All | 0.02 | 2.30 | 0.74 | 2.47 | 0.89 | 2.48 | −1.18 | 2.50 | 1.60 | 2.77 | 852 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; Li, D.; Li, H.; Xu, Z.; Hu, Z.; Zeng, J.; Yang, Y.; Jia, H. Improving HJ-1B/IRS LST Retrieval of the Generalized Single-Channel Algorithm with Refined ERA5 Atmospheric Profile Database. Remote Sens. 2023, 15, 5092. https://doi.org/10.3390/rs15215092
Zhang G, Li D, Li H, Xu Z, Hu Z, Zeng J, Yang Y, Jia H. Improving HJ-1B/IRS LST Retrieval of the Generalized Single-Channel Algorithm with Refined ERA5 Atmospheric Profile Database. Remote Sensing. 2023; 15(21):5092. https://doi.org/10.3390/rs15215092
Chicago/Turabian StyleZhang, Guoqin, Dacheng Li, Hua Li, Zhaopeng Xu, Zhiheng Hu, Jian Zeng, Yi Yang, and Hui Jia. 2023. "Improving HJ-1B/IRS LST Retrieval of the Generalized Single-Channel Algorithm with Refined ERA5 Atmospheric Profile Database" Remote Sensing 15, no. 21: 5092. https://doi.org/10.3390/rs15215092
APA StyleZhang, G., Li, D., Li, H., Xu, Z., Hu, Z., Zeng, J., Yang, Y., & Jia, H. (2023). Improving HJ-1B/IRS LST Retrieval of the Generalized Single-Channel Algorithm with Refined ERA5 Atmospheric Profile Database. Remote Sensing, 15(21), 5092. https://doi.org/10.3390/rs15215092






