GNSS-IR Soil Moisture Inversion Derived from Multi-GNSS and Multi-Frequency Data Accounting for Vegetation Effects
Abstract
:1. Introduction
2. Materials and Methods
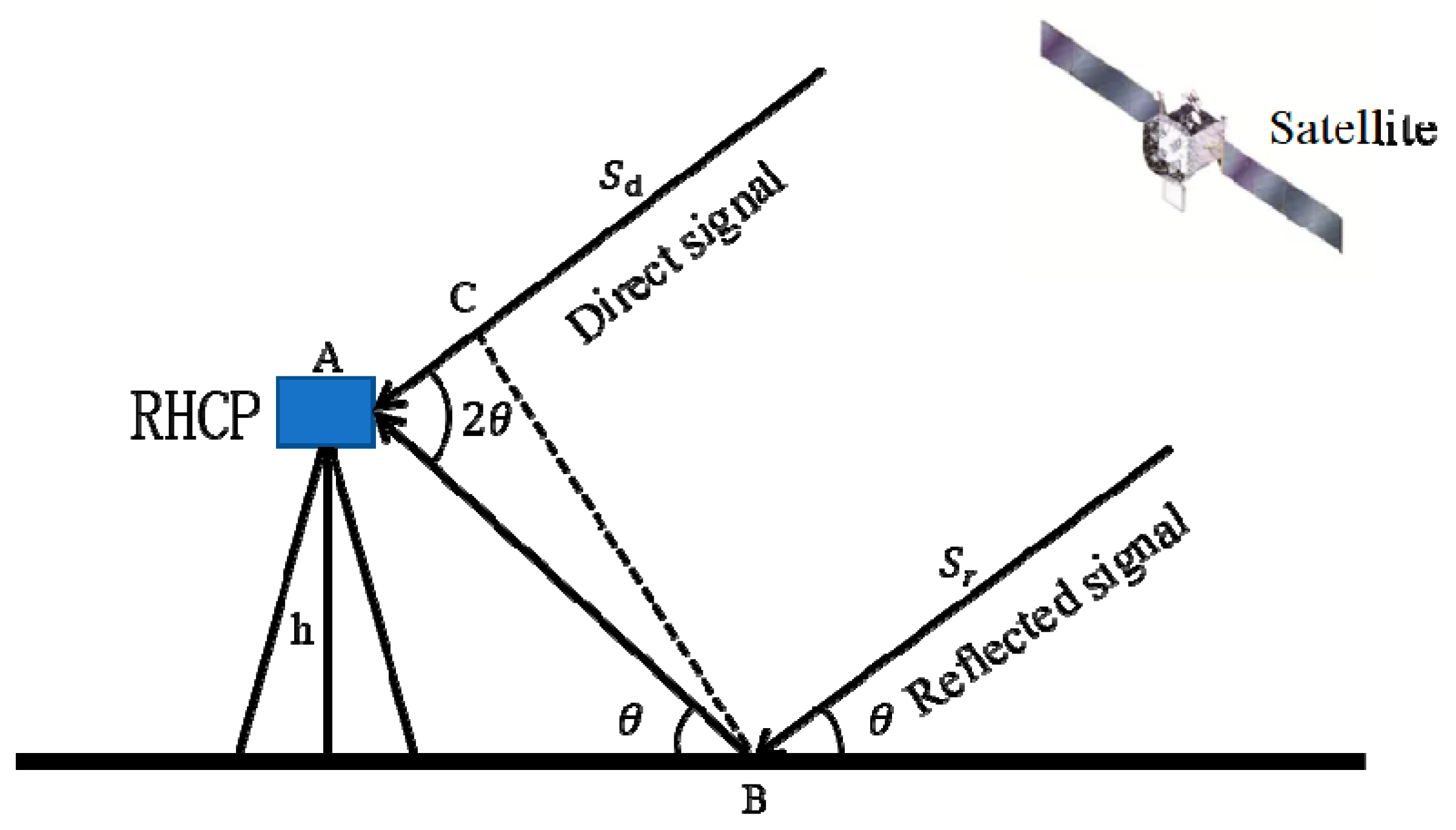
2.1. GNSS-IR SM Inversion Principle
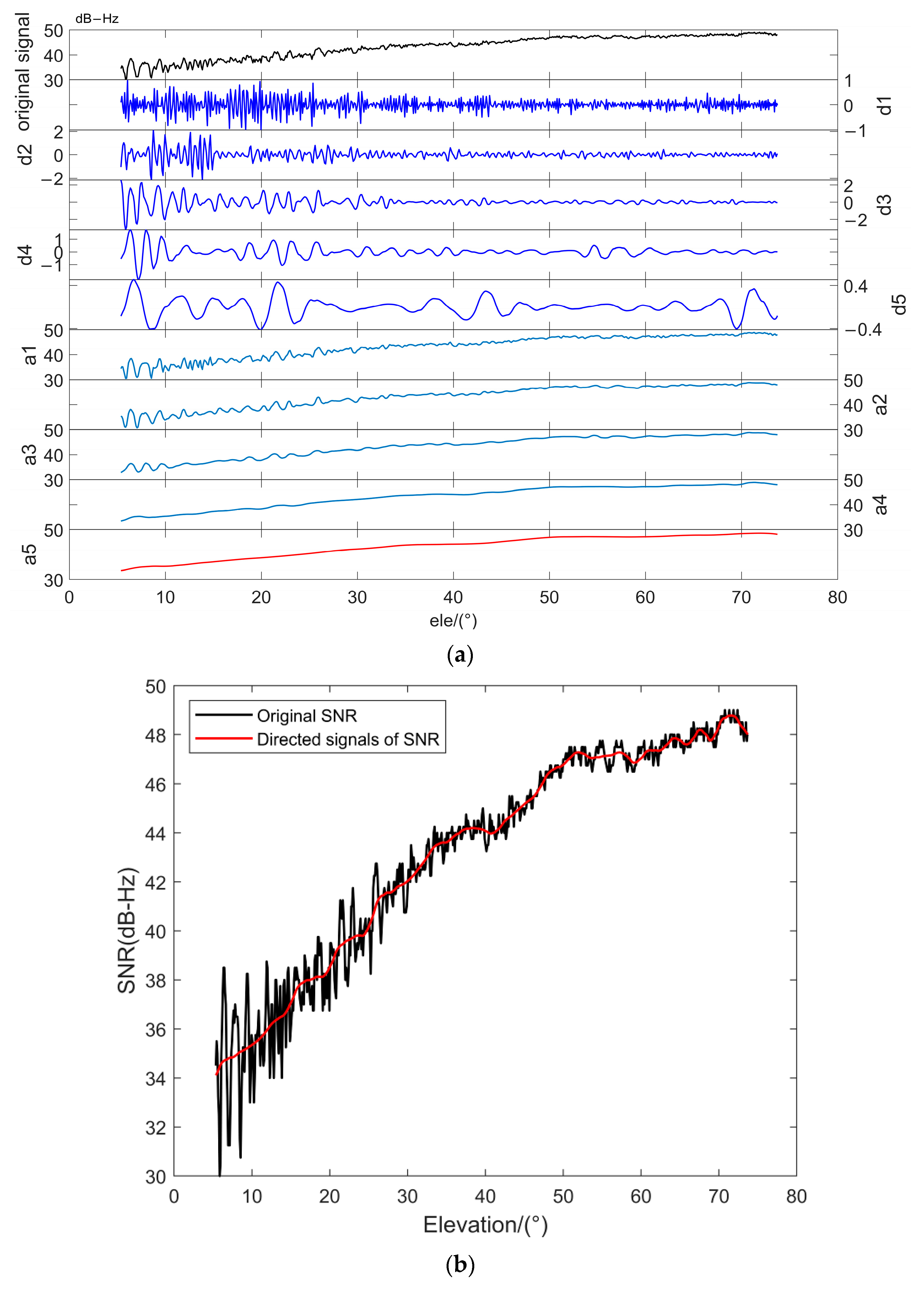
2.2. Wavelet Analysis Theory
2.3. Inversion of NDVI Based on Multi-Path Effects to Characterize Vegetation Effects
2.4. Random Forest Model
3. Data Sources
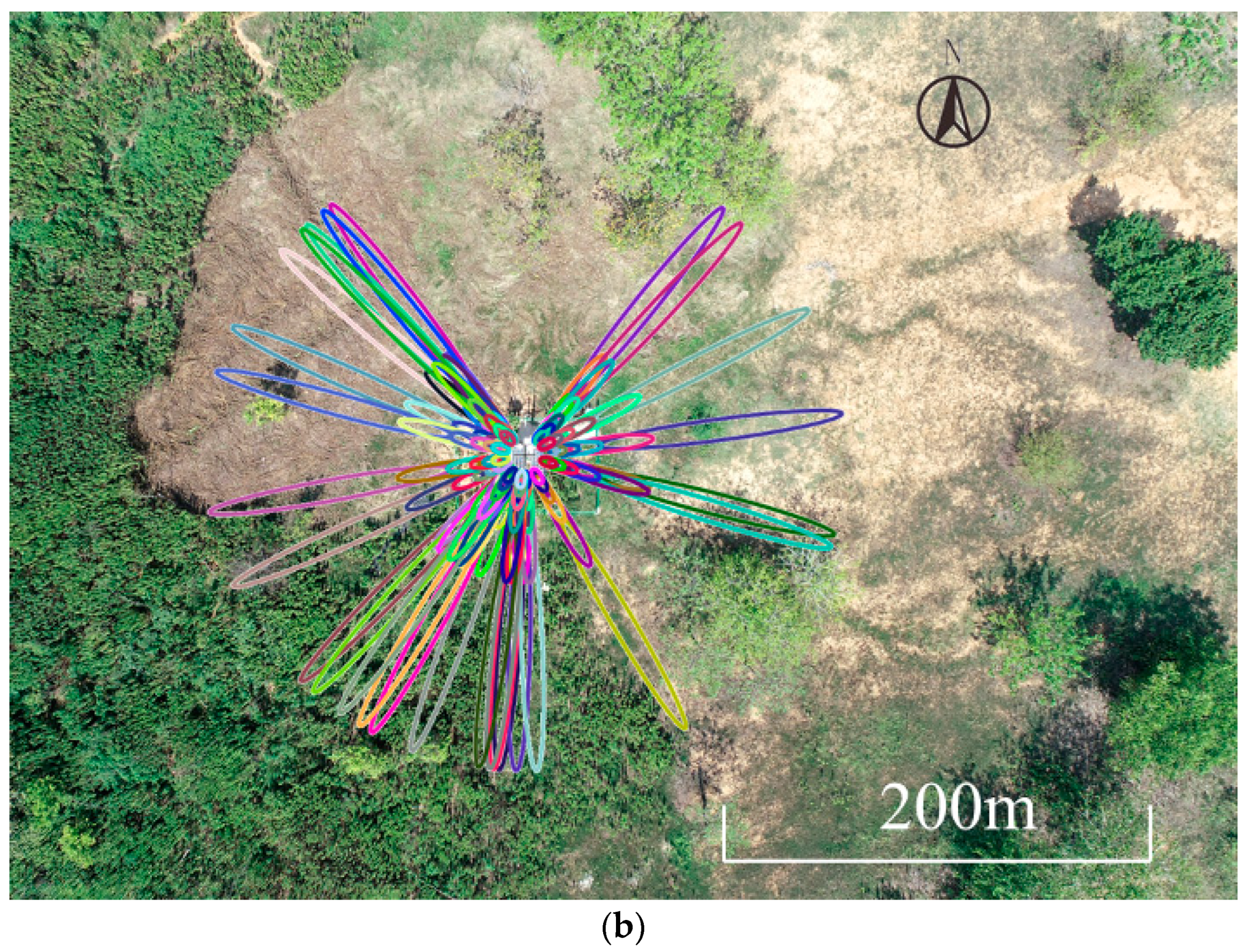
3.1. GNSS Observations
3.2. NDVI
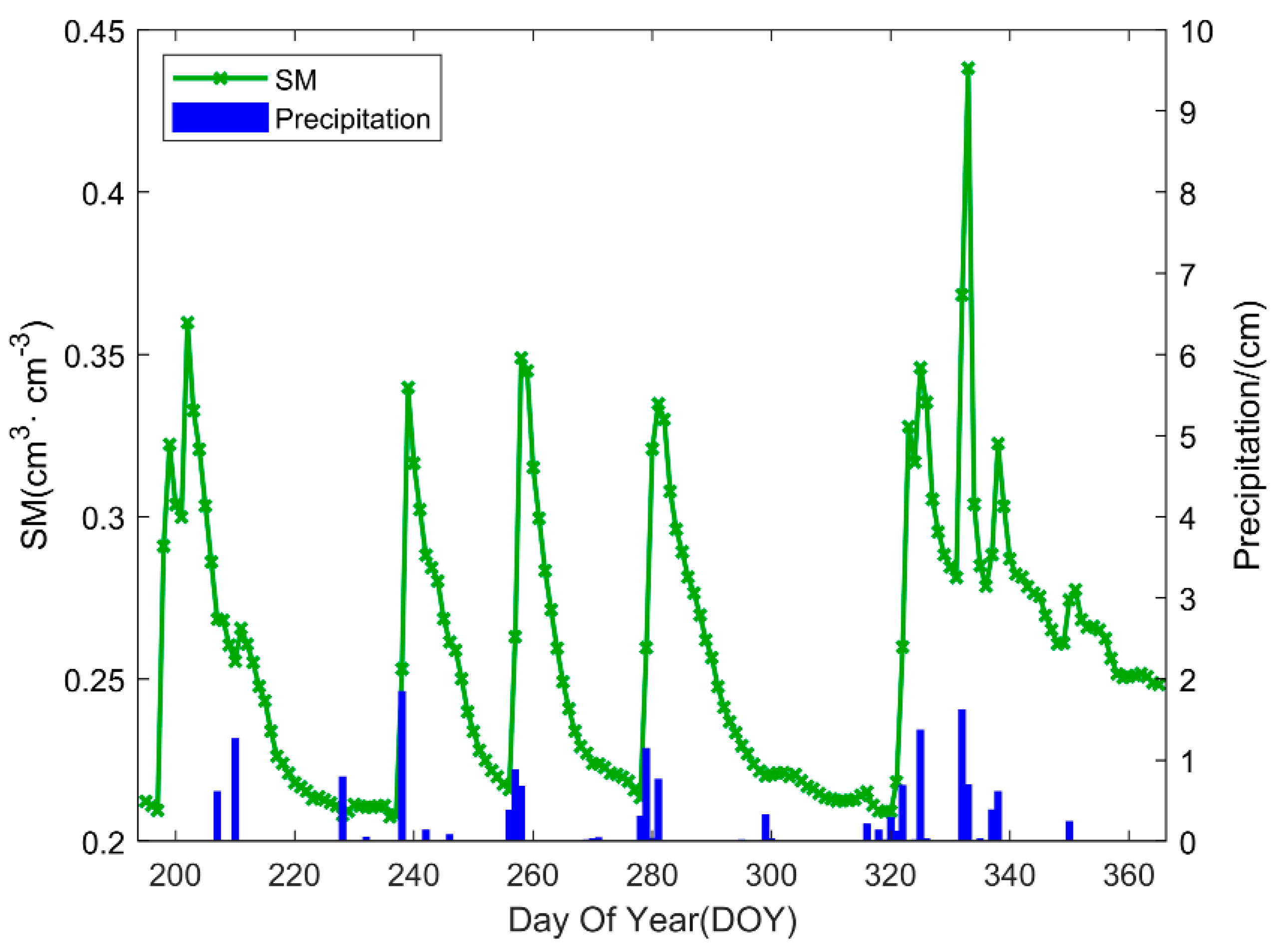
3.3. Auxiliary Data
4. Experiment and Results
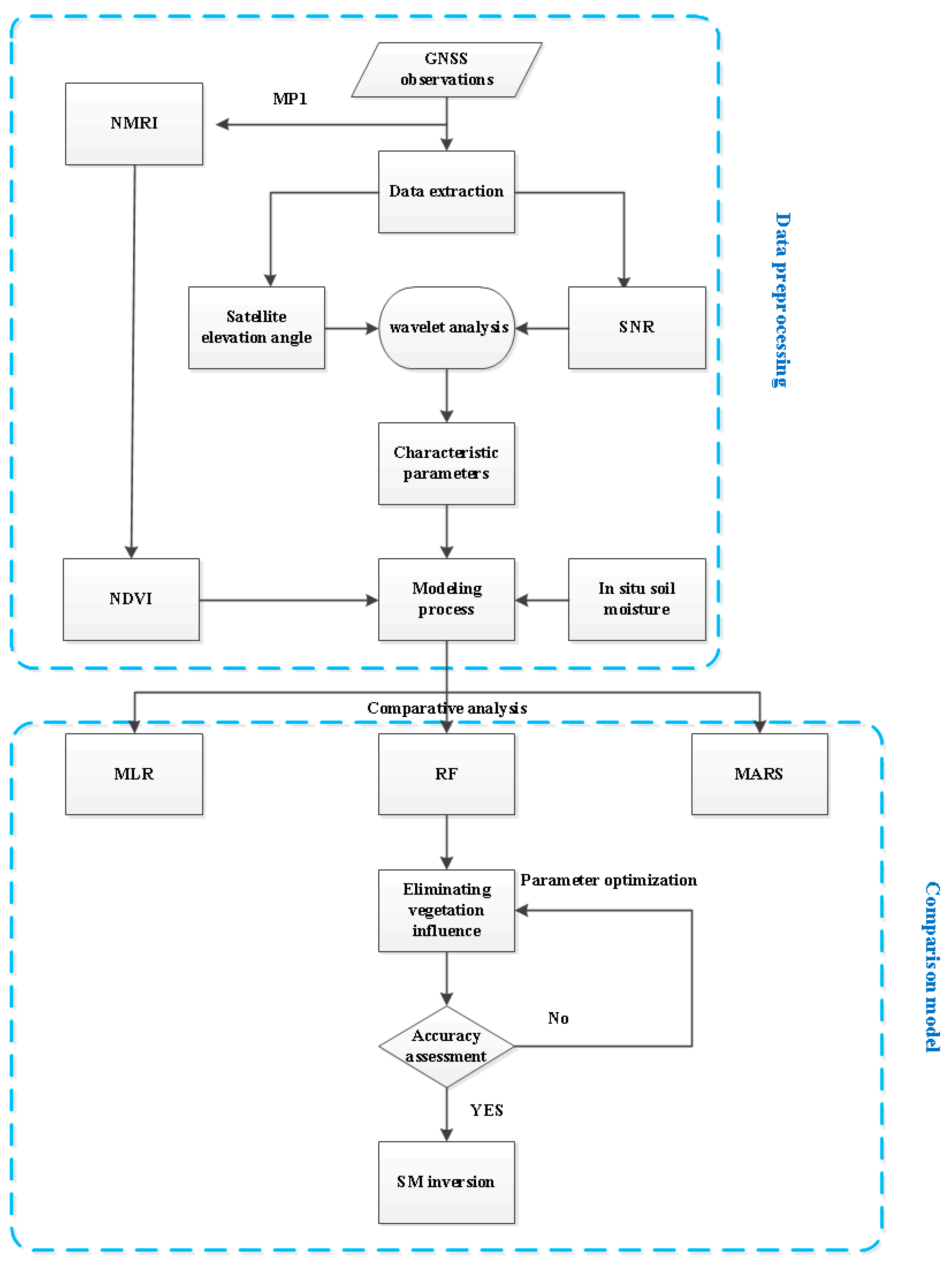
4.1. SM Retrieval Strategy
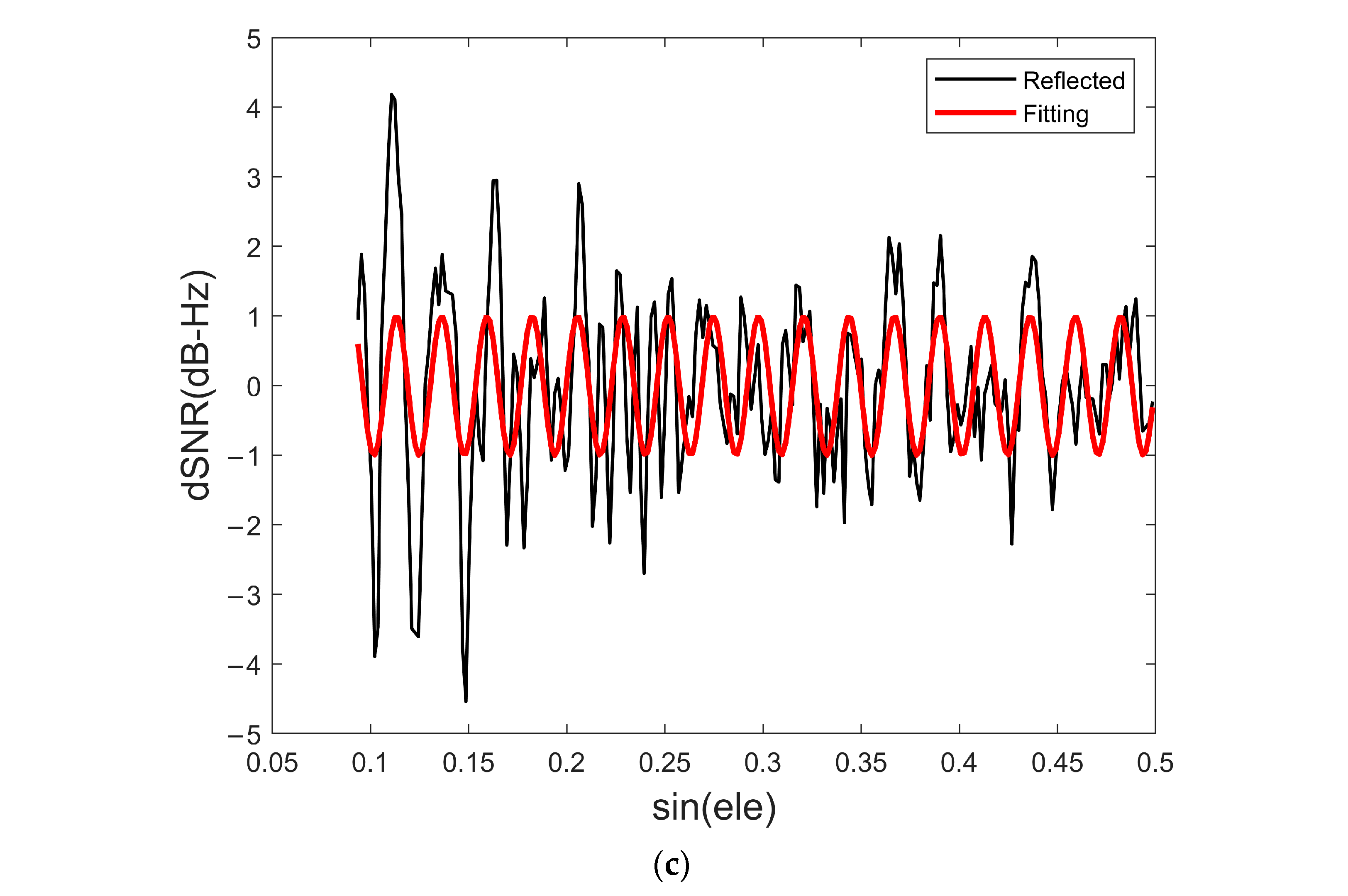
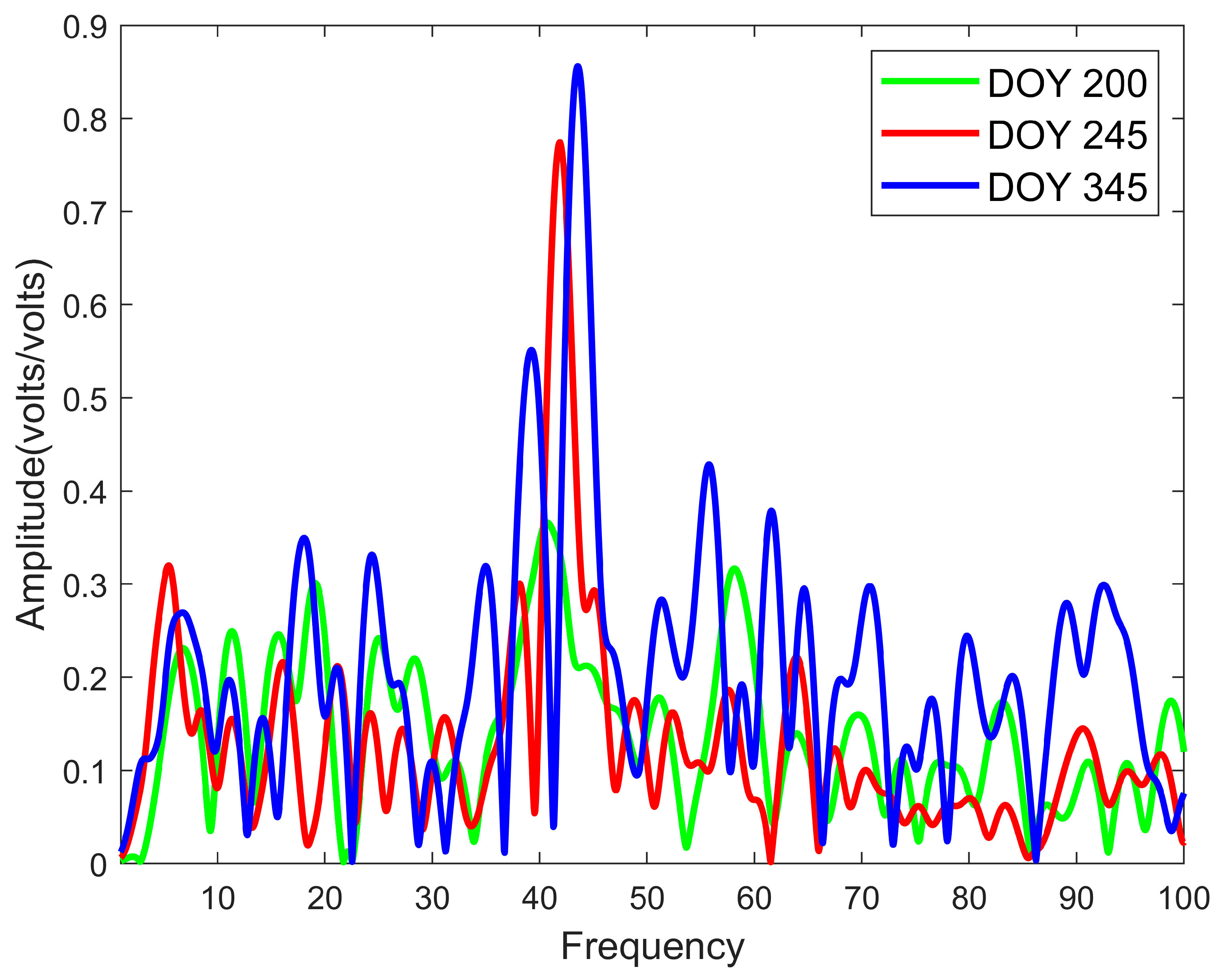
4.2. Reflected Signal Feature Parameter Extraction
4.3. Inversion of NDVI Representing Vegetation Effect
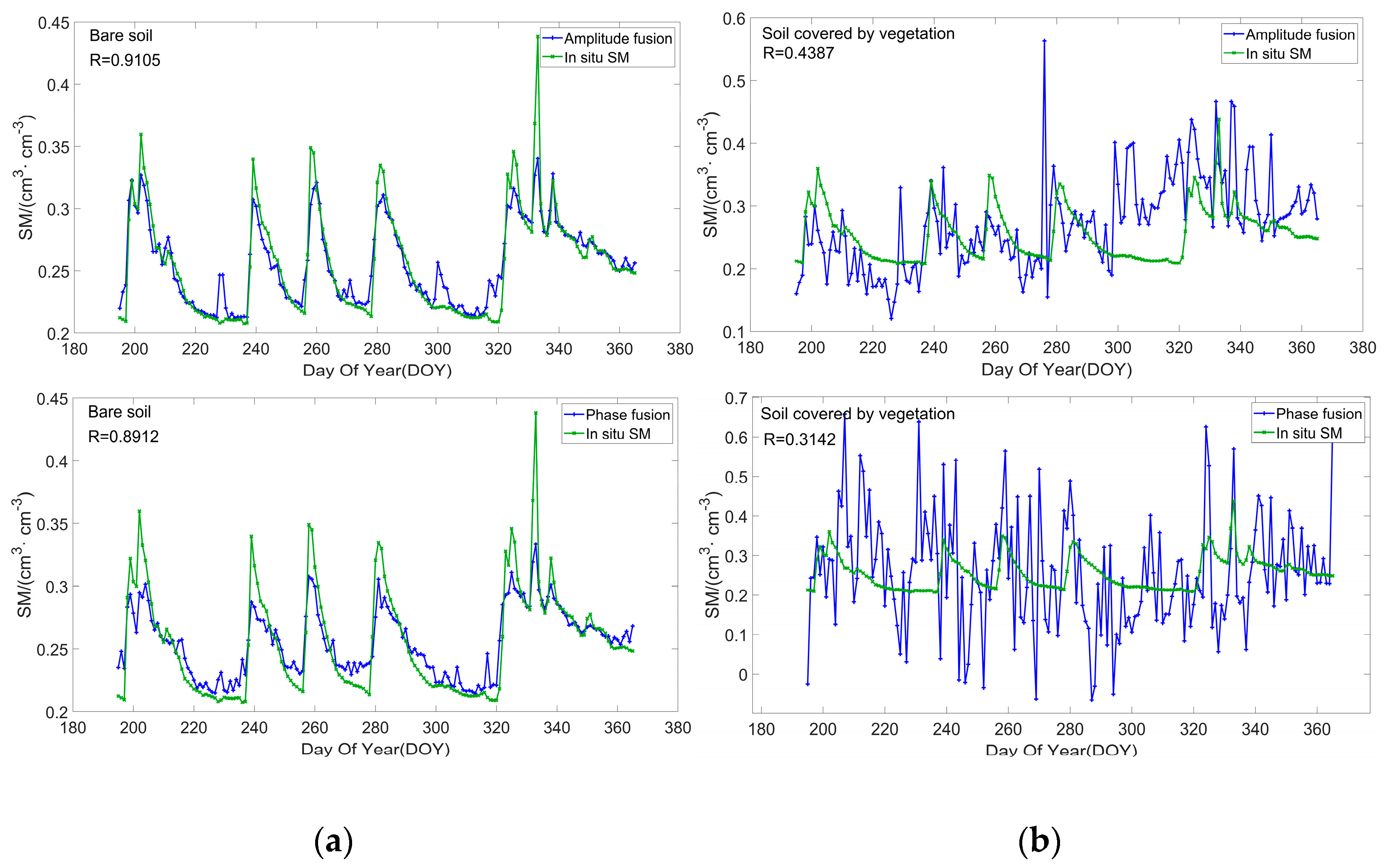
4.4. SM Retrieval Experiment and Results
5. Discussion
SM Inversion Correlation Analysis
6. Conclusions
- (1)
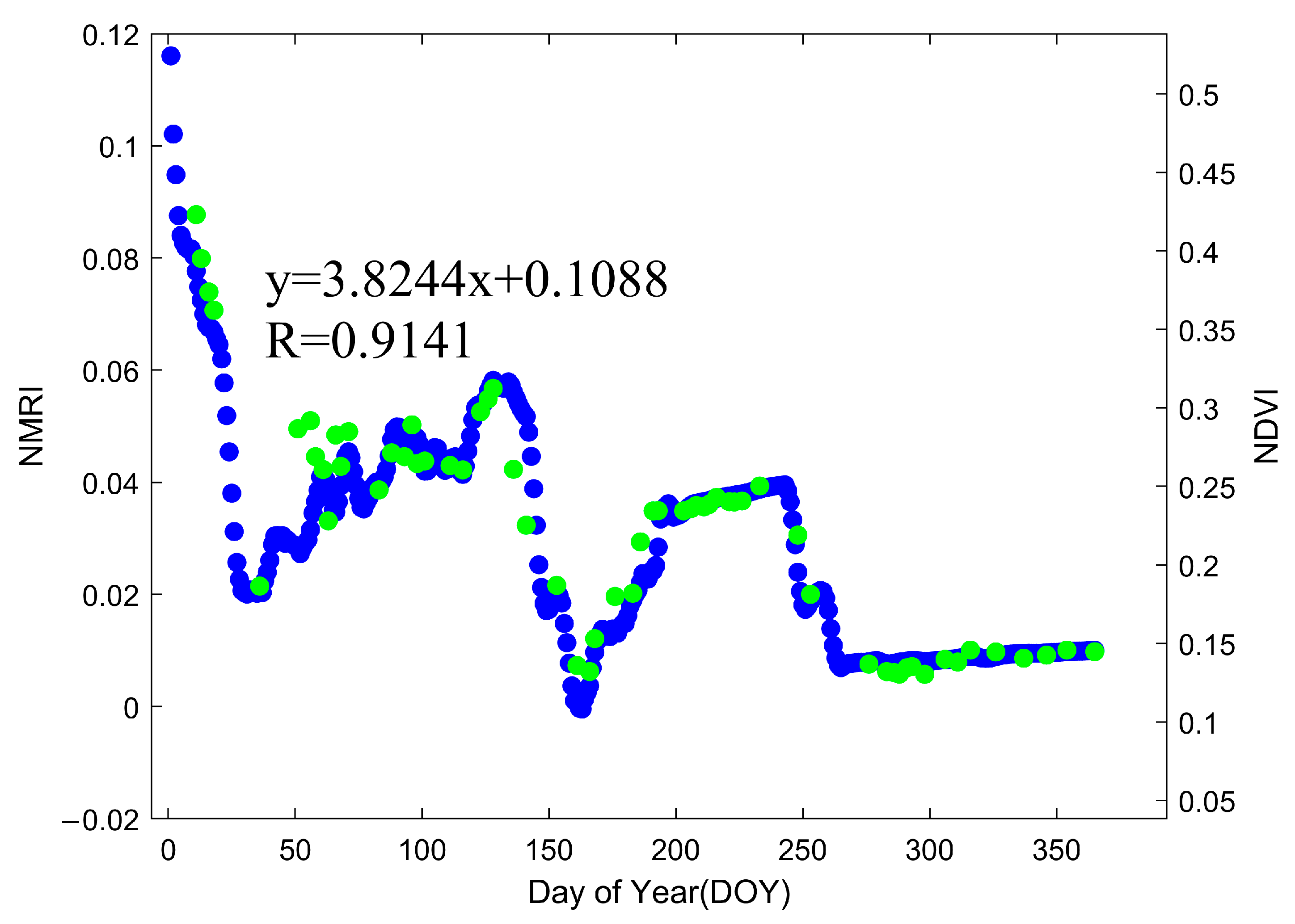
- The NMRI calculated from MP1 has a strong linear correlation with NDVI, which can fully correct the amplitude and phase offset of the reflected signal caused by the vegetation effects. Therefore, the NMRI calculated by GNSS multipath observations can be used to correct the vegetation error without measuring the VMC.
- (2)
- The RF algorithm gives full play to the advantages of multi-GNSS and multi-frequency data integration in SM inversion and effectively solves the problem that single-satellite data cannot fully reflect the actual situation of the surface. In addition, the addition of threshold and parameter adjustment in the RF model operation process helps to eliminate satellite data that seriously interfere with SM inversion and can determine the satellite combination with a good SM inversion accuracy while ensuring data utilization.
- (3)
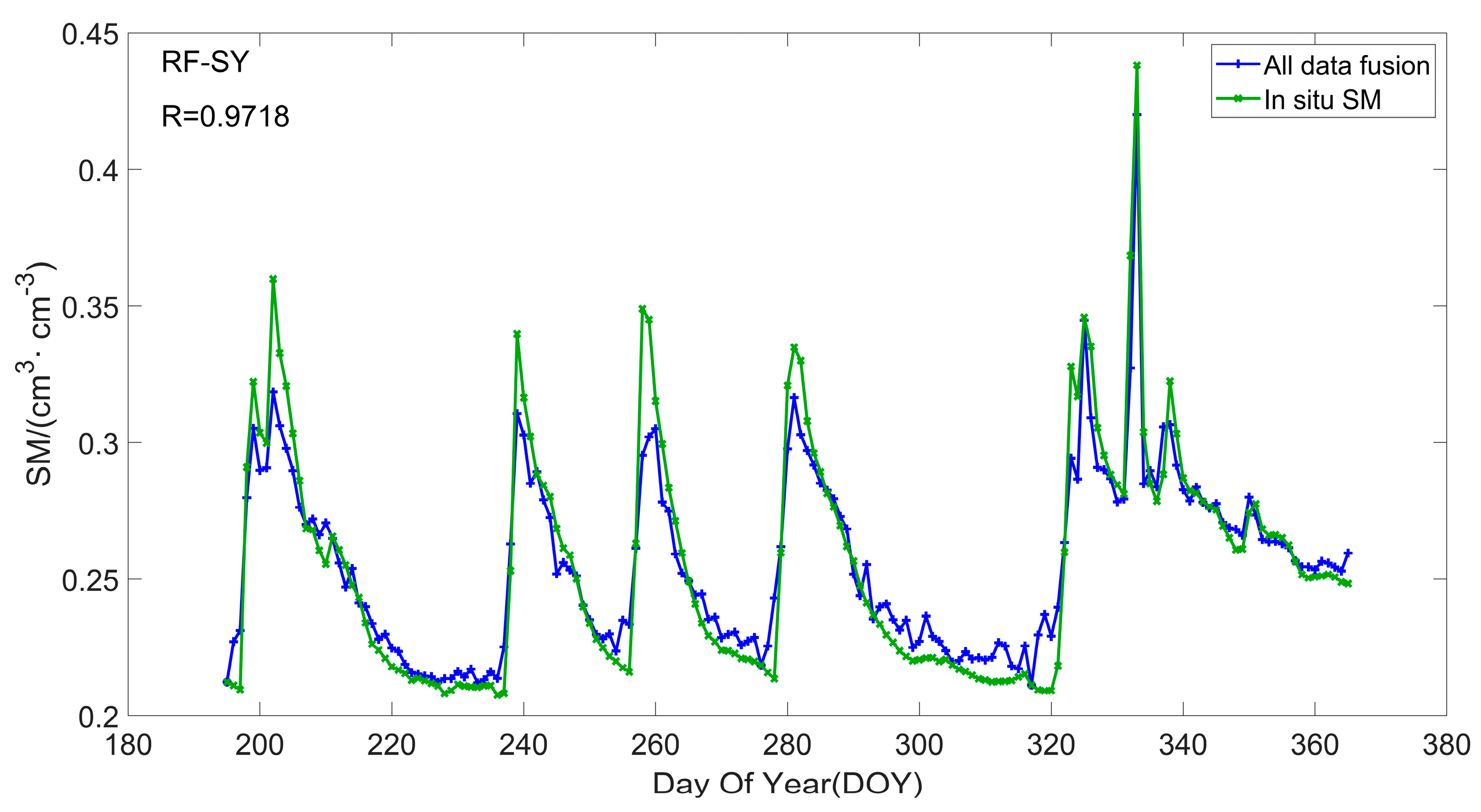
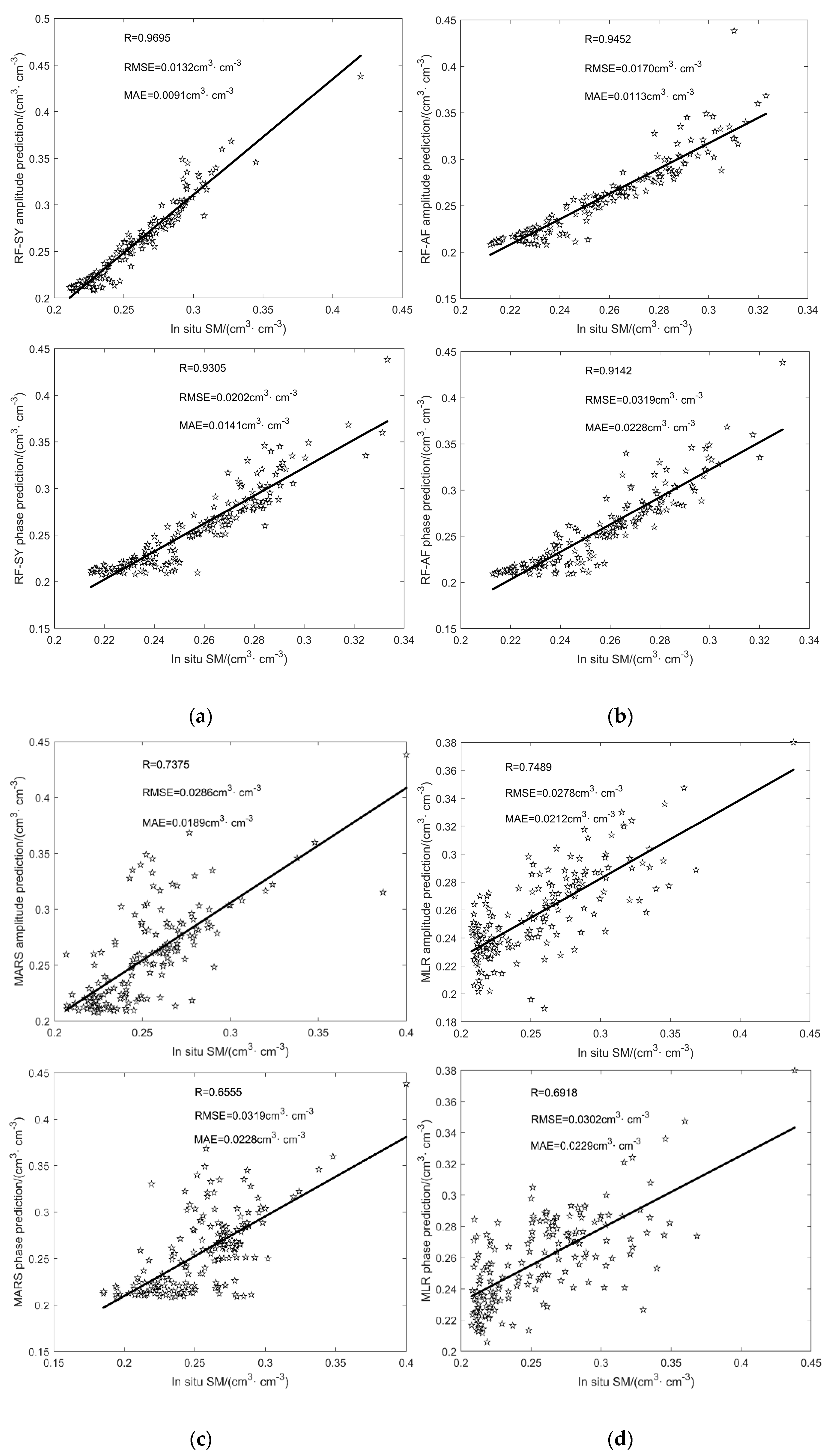
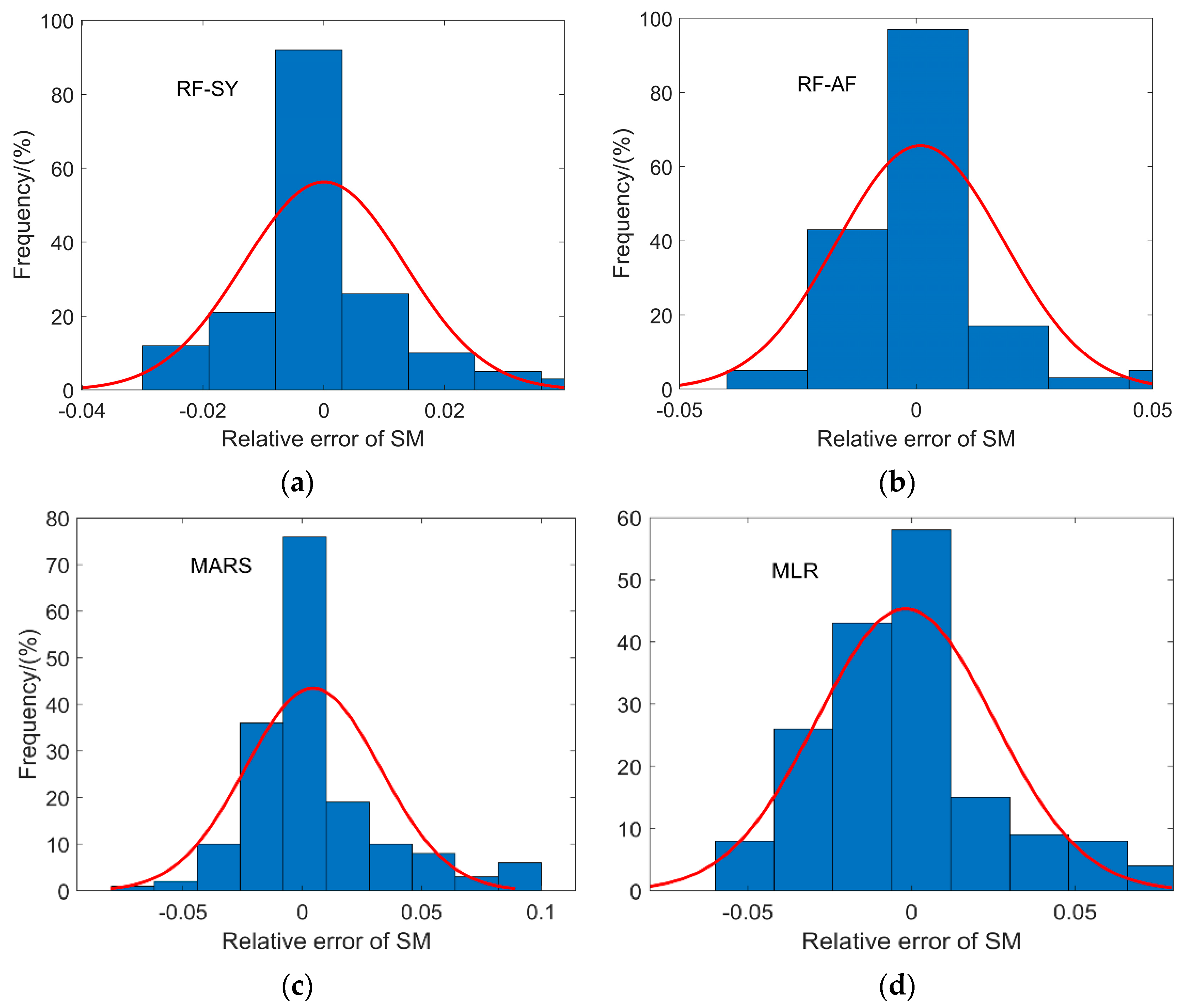
- Compared to the traditional MLR and MARS models, the RF model can obtain higher accuracy in the inversion of SM, which can obtain better satellite combinations by adjusting the threshold and parameters. Compared to the proposed RF-AF method, the proposed RF-SY strategy not only has higher accuracy but also reduces the steps of the RF-AF strategy to establish empirical models for each satellite to correct vegetation errors, thereby reducing gross errors and calculation time and increasing the accuracy and efficiency of GNSS-IR SM inversion.
- (4)
- Compared to the single feature parameter (amplitude or phase) fusion correction inversion method, the multi-feature parameter fusion correction inversion method that combines feature parameters extracted from GNSS signals with RF can improve the accuracy and reliability of SM inversion, which provides a new idea for GNSS-IR SM inversion.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Koster, R.D.; Dirmeyer, P.A.; Guo, Z.; Bonan, G.; Chan, E.; Cox, P.; Gordon, C.T.; Kanae, S.; Kowalczyk, E.; Lawrence, D. Regions of strong coupling between soil moisture and precipitation. Science 2004, 305, 1138–1140. [Google Scholar] [CrossRef] [PubMed]
- Jackson, T.J.; Schmugge, J.; Engman, E.T. Remote sensing applications to hydrology: Soil moisture. Hydrol. Sci. J. 1996, 41, 517–530. [Google Scholar] [CrossRef]
- Larson, K.M.; Small, E.E.; Gutmann, E.D.; Bilich, A.L.; Braun, J.J.; Zavorotny, V.U. Use of GPS receivers as a soil moisture network for water cycle studies. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Larson, K.M.; Gutmann, E.D.; Zavorotny, V.U.; Braun, J.J.; Williams, M.W.; Nievinski, F.G. Can we measure snow depth with GPS receivers? Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Larson, K.M.; Ray, R.D.; Nievinski, F.G.; Freymueller, J.T. The accidental tide gauge: A GPS reflection case study from Kachemak Bay, Alaska. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1200–1204. [Google Scholar] [CrossRef]
- Larson, K.M.; Löfgren, J.S.; Haas, R. Coastal sea level measurements using a single geodetic GPS receiver. Adv. Space Res. 2013, 51, 1301–1310. [Google Scholar] [CrossRef]
- Duan, J.J.; Schmude, J.M.; Larson, K.M. Effects of low temperature exposure on diapause, development, and reproductive fitness of the emerald ash borer (Coleoptera: Buprestidae): Implications for voltinism and laboratory rearing. J. Econ. Entomol. 2021, 114, 201–208. [Google Scholar] [CrossRef]
- Zavorotny, V.U.; Larson, K.M.; Braun, J.J.; Small, E.E.; Gutmann, E.D.; Bilich, A.L. A physical model for GPS multipath caused by land reflections: Toward bare soil moisture retrievals. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2009, 3, 100–110. [Google Scholar] [CrossRef]
- Chew, C.C.; Small, E.E.; Larson, K.M.; Zavorotny, V.U. Effects of near-surface soil moisture on GPS SNR data: Development of a retrieval algorithm for soil moisture. IEEE Trans. Geosci. Remote Sens. 2013, 52, 537–543. [Google Scholar] [CrossRef]
- Larson, K.M.; Small, E.E. Normalized microwave reflection index: A vegetation measurement derived from GPS networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1501–1511. [Google Scholar] [CrossRef]
- Roussel, N.; Darrozes, J.; Ha, C.; Boniface, K.; Frappart, F.; Ramillien, G.; Gavart, M.; Van de Vyvere, L.; Desenfans, O.; Baup, F. Multi-scale volumetric soil moisture detection from GNSS SNR data: Ground-based and airborne applications. In Proceedings of the 2016 IEEE Metrology for Aerospace (MetroAeroSpace), Florence, Italy, 21–23 June 2016; pp. 573–578. [Google Scholar]
- Larson, K.M.; Small, E.E.; Gutmann, E.; Bilich, A.; Axelrad, P.; Braun, J. Using GPS multipath to measure soil moisture fluctuations: Initial results. GPS Solut. 2008, 12, 173–177. [Google Scholar] [CrossRef]
- Larson, K.M.; Braun, J.J.; Small, E.E.; Zavorotny, V.U.; Gutmann, E.D.; Bilich, A.L. GPS multipath and its relation to near-surface soil moisture content. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2009, 3, 91–99. [Google Scholar] [CrossRef]
- Lv, J.; Zhang, R.; Tu, J.; Liao, M.; Pang, J.; Yu, B.; Li, K.; Xiang, W.; Fu, Y.; Liu, G. A GNSS-IR Method for Retrieving Soil Moisture Content from Integrated Multi-Satellite Data That Accounts for the Impact of Vegetation Moisture Content. Remote Sens. 2021, 13, 2442. [Google Scholar] [CrossRef]
- Zhan, J.; Zhang, R.; Xie, L.; Li, S.; Lv, J.; Tu, J. Vegetation Growth Monitoring Based on BDS Interferometry Reflectometry with Triple-Frequency SNR Data. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Chew, C.C.; Small, E.E.; Larson, K.M.; Zavorotny, V.U. Vegetation sensing using GPS-interferometric reflectometry: Theoretical effects of canopy parameters on signal-to-noise ratio data. IEEE Trans. Geosci. Remote Sens. 2014, 53, 2755–2764. [Google Scholar] [CrossRef]
- Chew, C.; Small, E.E.; Larson, K.M. An algorithm for soil moisture estimation using GPS-interferometric reflectometry for bare and vegetated soil. GPS Solut. 2016, 20, 525–537. [Google Scholar] [CrossRef]
- Small, E.E.; Larson, K.M.; Braun, J.J. Sensing vegetation growth with reflected GPS signals. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Small, E.E.; Larson, K.M.; Smith, W.K. Normalized microwave reflection index: Validation of vegetation water content estimates from Montana grasslands. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1512–1521. [Google Scholar] [CrossRef]
- Li, S.; Jing, H.; Yuan, Q.; Yue, L.; Li, T. Investigating the spatio-temporal variation of vegetation water content in the western United States by blending GNSS-IR, AMSR-E, and AMSR2 observables using machine learning methods. Sci. Remote Sens. 2022, 6, 100061. [Google Scholar] [CrossRef]
- Pan, Y.; Ren, C.; Liang, Y.; Zhang, Z.; Shi, Y. Inversion of surface vegetation water content based on GNSS-IR and MODIS data fusion. Satell. Navig. 2020, 1, 1–15. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, T.; Wang, L.; Zhang, J.; Peng, J.; Liu, Q. Evaluation of GNSS-IR for retrieving soil moisture and vegetation growth characteristics in wheat farmland. J. Surv. Eng. 2021, 147, 4021009. [Google Scholar] [CrossRef]
- Liang, Y.; Ren, C.; Wang, H.; Huang, Y.; Zheng, Z. Research on soil moisture inversion method based on GA-BP neural network model. Int. J. Remote Sens. 2019, 40, 2087–2103. [Google Scholar] [CrossRef]
- Larson, K.M.; Small, E.E. GPS ground networks for water cycle sensing. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 3822–3825. [Google Scholar]
- Larson, K.M. GPS interferometric reflectometry: Applications to surface soil moisture, snow depth, and vegetation water content in the western United States. Wiley Interdiscip. Rev. Water 2016, 3, 775–787. [Google Scholar] [CrossRef]
- Small, E.E.; Larson, K.M.; Chew, C.C.; Dong, J.; Ochsner, T.E. Validation of GPS-IR soil moisture retrievals: Comparison of different algorithms to remove vegetation effects. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4759–4770. [Google Scholar] [CrossRef]
- Yuan, Q.; Li, S.; Yue, L.; Li, T.; Shen, H.; Zhang, L. Monitoring the Variation of Vegetation Water Content with Machine Learning Methods: Point–Surface Fusion of MODIS Products and GNSS-IR Observations. Remote Sens. 2019, 11, 1440. [Google Scholar] [CrossRef]
- Zheng, N.; Chai, H.; Chen, L.; Ma, Y.; Tian, X. Snow depth retrieval by using robust estimation algorithm to perform multi-SNR and multi-system fusion in GNSS-IR. Adv. Space Res. 2023, 71, 1525–1542. [Google Scholar] [CrossRef]
- Liang, Y.; Lai, J.; Ren, C.; Lu, X.; Zhang, Y.; Ding, Q.; Hu, X. GNSS-IR multisatellite combination for soil moisture retrieval based on wavelet analysis considering detection and repair of abnormal phases. Measurement 2022, 203, 111881. [Google Scholar] [CrossRef]
- Ding, R.; Zheng, N.; Zhang, H.; Zhang, H.; Lang, F.; Ban, W. A Study of GNSS-IR Soil Moisture Inversion Algorithms Integrating Robust Estimation with Machine Learning. Sustainability 2023, 15, 6919. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Q.; Zhang, S. Water levels measured with SNR using wavelet decomposition and Lomb–Scargle periodogram. GPS Solut. 2017, 22, 22. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Q.; Zhang, S. Sea level estimation from SNR data of geodetic receivers using wavelet analysis. GPS Solut. 2018, 23, 6. [Google Scholar] [CrossRef]
- Wang, X.; He, X.; Xiao, R.; Song, M.; Jia, D. Millimeter to centimeter scale precision water-level monitoring using GNSS reflectometry: Application to the South-to-North Water Diversion Project, China. Remote Sens. Environ. 2021, 265, 112645. [Google Scholar] [CrossRef]
- Zhou, W.; Liu, Y.; Huang, L.; Ji, B.; Liu, L.; Bian, S. Multi-constellation GNSS interferometric reflectometry for the correction of long-term snow height retrieval on sloping topography. GPS Solut. 2022, 26, 140. [Google Scholar] [CrossRef]
- Camps, A.; Alonso-Arroyo, A.; Park, H.; Onrubia, R.; Pascual, D.; Querol, J. L-band vegetation optical depth estimation using transmitted GNSS signals: Application to GNSS-reflectometry and positioning. Remote Sens. 2020, 12, 2352. [Google Scholar] [CrossRef]
- Evans, S.G.; Small, E.E.; Larson, K.M. Comparison of vegetation phenology in the western USA determined from reflected GPS microwave signals and NDVI. Int. J. Remote Sens. 2014, 35, 2996–3017. [Google Scholar] [CrossRef]


| Project | Parameter |
|---|---|
| Type of receiver | M300_PLUS |
| Sampling interval | 15 s |
| Type of antenna | AT360 |
| Antenna height | 4.0 m |
| Signal Frequency Band | Satellite Number |
|---|---|
| S1C | G01, G02, G03, G05, G06, G09, G16, G17, G18, G29, G31, G32 |
| S2P | G02, G03, G14, G17, G19, G25 |
| S2X | G03, G12, G14, G17, G18, G25, G32 |
| S5I | G09, G32 |
| S2I | C12 |
| S6I | C06, C08 |
| S7I | C06 |
| Signal Frequency Band | Satellite Number |
|---|---|
| S1C | G01, G05, G05, G09 |
| S2P | G04, G10, G14, G16, G25 |
| S2X | G06, G29 |
| S5I | G04 |
| S2I | C06, C08 |
| S6I | C06, C11, C12 |
| Model Parameter | Parameter Meaning | Numerical Value |
|---|---|---|
| n_estimators | number of decision tree models in RF | 78 |
| max_depth | maximum depth of decision tree model | 10 |
| max_features | maximum number of features | 32 |
| min_samples_leaf | minimum number of samples for leaf nodes | 19 |
| in_samples_split | minimum number of samples | 10 |
| Amplitude Fusion | Phase Fusion | |||||||
|---|---|---|---|---|---|---|---|---|
| RF-SY | RF-AF | MARS | MLR | RF-SY | RF-AF | MARS | MLR | |
| R | 0.9695 | 0.9452 | 0.7375 | 0.7489 | 0.9305 | 0.9142 | 0.6555 | 0.6918 |
| RMSE (cm3·cm−3) | 0.0132 | 0.0170 | 0.0286 | 0.0278 | 0.0202 | 0.0211 | 0.0319 | 0.0302 |
| MAE (cm3·cm−3) | 0.0091 | 0.0113 | 0.0189 | 0.0212 | 0.0141 | 0.0148 | 0.0228 | 0.0229 |
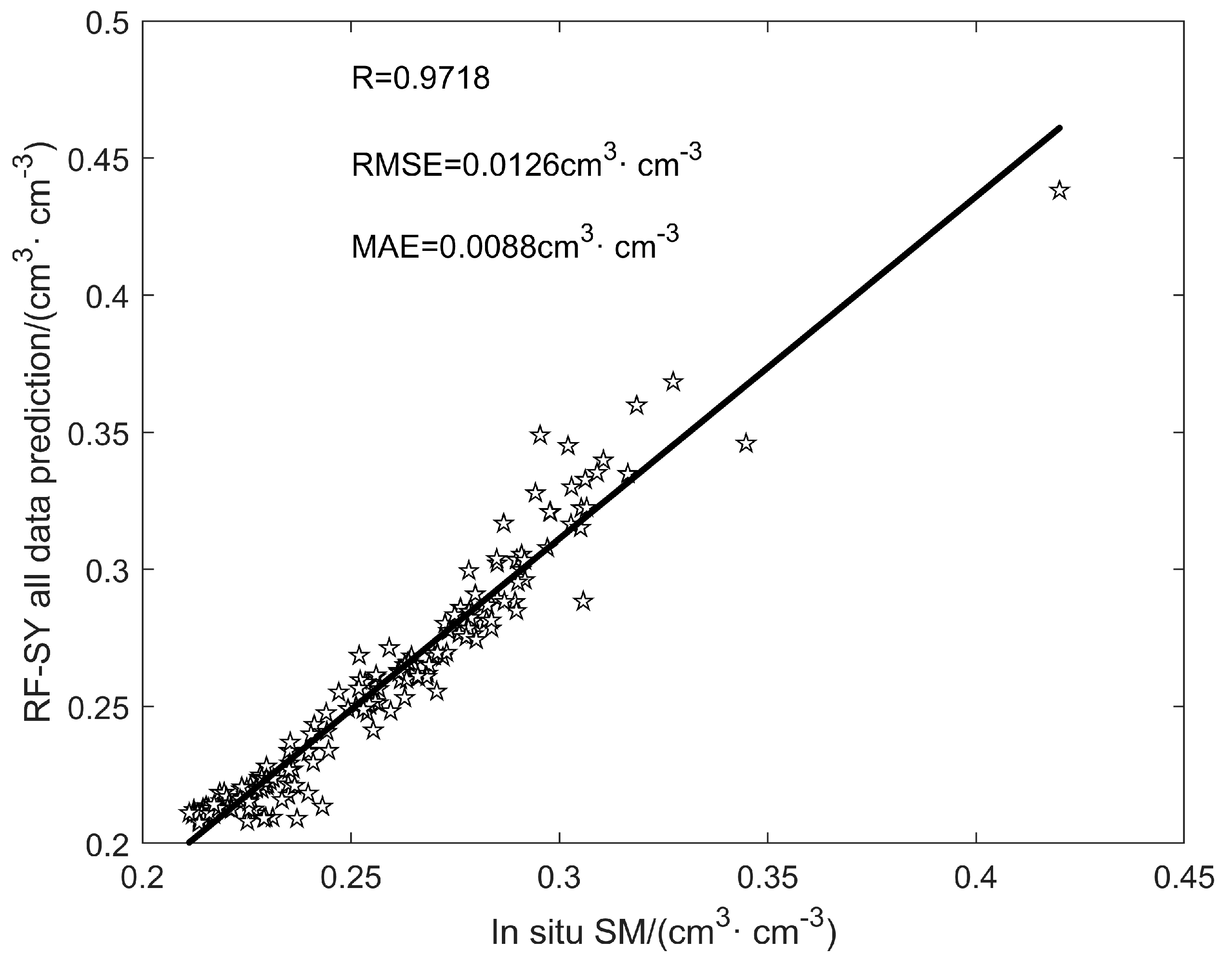
| Index of Precision | All Data Fusion | Amplitude Fusion | Phase Fusion |
|---|---|---|---|
| R | 0.9718 | 0.9695 | 0.9305 |
| RMSE (cm3·cm−3) | 0.0126 | 0.0132 | 0.0202 |
| MAE (cm3·cm−3) | 0.0088 | 0.0091 | 0.0141 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, H.; Yang, X.; Pan, Y.; Shen, F. GNSS-IR Soil Moisture Inversion Derived from Multi-GNSS and Multi-Frequency Data Accounting for Vegetation Effects. Remote Sens. 2023, 15, 5381. https://doi.org/10.3390/rs15225381
Wei H, Yang X, Pan Y, Shen F. GNSS-IR Soil Moisture Inversion Derived from Multi-GNSS and Multi-Frequency Data Accounting for Vegetation Effects. Remote Sensing. 2023; 15(22):5381. https://doi.org/10.3390/rs15225381
Chicago/Turabian StyleWei, Haohan, Xiaofeng Yang, Yuwei Pan, and Fei Shen. 2023. "GNSS-IR Soil Moisture Inversion Derived from Multi-GNSS and Multi-Frequency Data Accounting for Vegetation Effects" Remote Sensing 15, no. 22: 5381. https://doi.org/10.3390/rs15225381
APA StyleWei, H., Yang, X., Pan, Y., & Shen, F. (2023). GNSS-IR Soil Moisture Inversion Derived from Multi-GNSS and Multi-Frequency Data Accounting for Vegetation Effects. Remote Sensing, 15(22), 5381. https://doi.org/10.3390/rs15225381









