Characteristics Analysis of Influence of Multiple Parameters of Mixed Sea Waves on Delay–Doppler Map in Global Navigation Satellite System Reflectometry
Abstract
1. Introduction
- The results of various calculation methods of MSS on different kinds of sea surfaces have been analyzed, providing a solid foundation for the analysis of delay waveforms.
- For the impact of multiple parameters on delay waveforms, some evident parameters such as directionality variables, direction of wave spreading, and others have been investigated comprehensively. As for different types of wind waves, the comparison and analysis of short-crest wind waves, long-crest wind waves, and mixed wind waves in the application of sea surface generation have been performed.
- The impact of comprehensive parameters on the delay waveform on the basis of short-crest wind waves, long-crest wind waves, and mixed wind waves has been compared, predominantly illustrated to investigate the influence of short-crest wave components on the delay waveforms of a mixed sea surface.
2. Impact of Multiple Parameters on Typical Wind Waves
2.1. Theoretical Foundation of GNSS-R
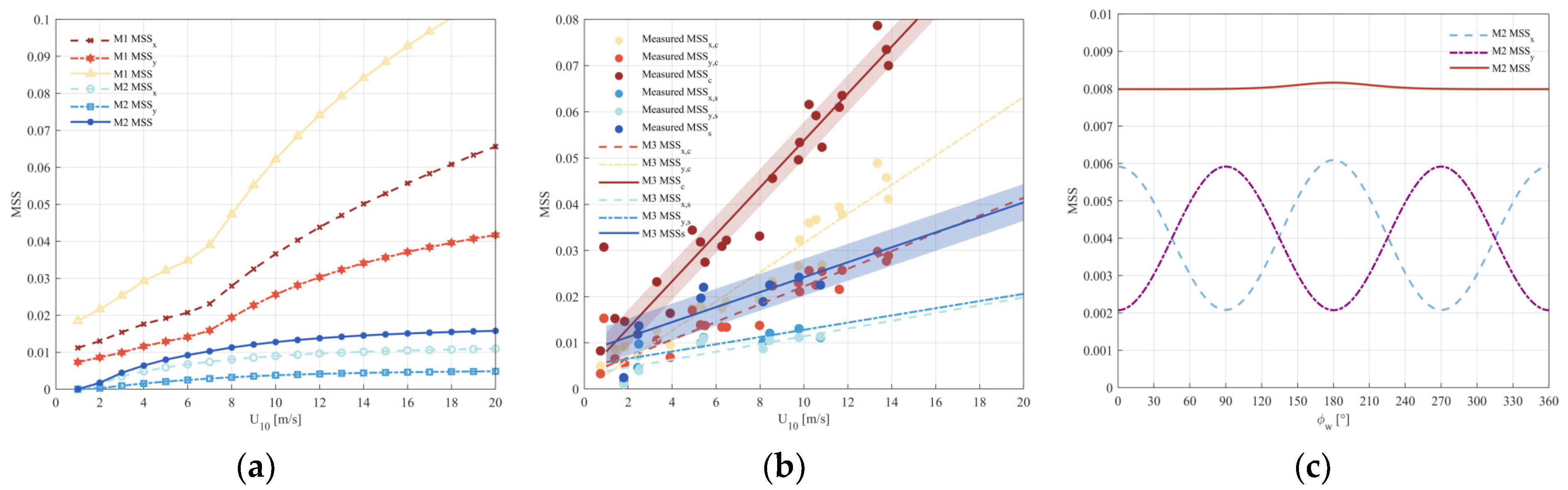
2.2. Impact of Wind Speed on Delay Waveform
3. Impact of Multiple Parameters on Long-Crest Wind Waves
3.1. Long-Crest Wind Sea Surface
3.2. Joint Influence of Parameters on Delay Waveforms of Wind Waves
3.3. 2-D Sinusoidal Wind Sea Surface
3.4. Joint Influence of Parameters on Delay Waveforms of 2-D Sinusoidal Wind Waves
4. Impact of Multiple Parameters on Mixed Sea Surface
4.1. Mixed Sea Surface
4.2. Joint Influence of Parameters on Delay Waveform of Mixed Sea Surface
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Jin, S.; Feng, G.; Gleason, S. Remote sensing using GNSS signals: Current status and future directions. Adv. Space Res. 2011, 47, 1645–1653. [Google Scholar] [CrossRef]
- Yu, K.; Rizos, C.; Burrage, D.; Dempster, A.G.; Zhang, K.; Markgraf, M. An overview of GNSS remote sensing. EURASIP J. Adv. Signal Process. 2014, 2014, 134. [Google Scholar] [CrossRef]
- Edokossi, K.; Calabia, A.; Jin, S.; Molina, I. GNSS-reflectometry and remote sensing of soil moisture: A review of measurement techniques, methods, and applications. Remote Sens. 2020, 12, 614. [Google Scholar] [CrossRef]
- Vaquero-Martínez, J.; Antón, M. Review on the role of GNSS meteorology in monitoring water vapor for atmospheric physics. Remote Sens. 2021, 13, 2287. [Google Scholar] [CrossRef]
- Yu, K. Theory and Practice of GNSS Reflectometry; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Jin, S.; Wang, Q.; Dardanelli, G. A review on multi-GNSS for earth observation and emerging applications. Remote Sens. 2022, 14, 3930. [Google Scholar] [CrossRef]
- Rodriguez-Alvarez, N.; Munoz-Martin, J.F.; Morris, M. Latest Advances in the Global Navigation Satellite System—Reflectometry (GNSS-R) Field. Remote Sens. 2023, 15, 2157. [Google Scholar] [CrossRef]
- Zavorotny, V.U.; Voronovich, A.G. Scattering of GPS signals from the ocean with wind remote sensing application. IEEE Trans. Geosci. Remote Sens. 2000, 38, 951–964. [Google Scholar] [CrossRef]
- Gleason, S.; Hodgart, S.; Sun, Y.; Gommenginger, C.; Mackin, S.; Adjrad, M.; Unwin, M. Detection and processing of bistatically reflected GPS signals from low earth orbit for the purpose of ocean remote sensing. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1229–1241. [Google Scholar] [CrossRef]
- Marchán-Hernández, J.F.; Camps, A.; Rodríguez-Álvarez, N.; Valencia, E.; Bosch-Lluis, X.; Ramos-Pérez, I. An efficient algorithm to the simulation of delay–Doppler maps of reflected global navigation satellite system signals. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2733–2740. [Google Scholar] [CrossRef]
- Clarizia, M.; Gommenginger, C.; Gleason, S.; Srokosz, M.; Galdi, C.; Di Bisceglie, M. Analysis of GNSS-R delay-Doppler maps from the UK-DMC satellite over the ocean. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Clarizia, M.P.; Gommenginger, C.; Di Bisceglie, M.; Galdi, C.; Srokosz, M.A. Simulation of L-band bistatic returns from the ocean surface: A facet approach with application to ocean GNSS reflectometry. IEEE Trans. Geosci. Remote Sens. 2011, 50, 960–971. [Google Scholar] [CrossRef]
- Guo, W.; Du, H.; Cheong, J.W.; Southwell, B.J.; Dempster, A.G. GNSS-R wind speed retrieval of sea surface based on particle swarm optimization algorithm. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–14. [Google Scholar] [CrossRef]
- Asgarimehr, M.; Arnold, C.; Weigel, T.; Ruf, C.; Wickert, J. GNSS reflectometry global ocean wind speed using deep learning: Development and assessment of CyGNSSnet. Remote Sens. Environ. 2022, 269, 112801. [Google Scholar] [CrossRef]
- Wang, X.; He, X.; Shi, J.; Chen, S.; Niu, Z. Estimating sea level, wind direction, significant wave height, and wave peak period using a geodetic GNSS receiver. Remote Sens. Environ. 2022, 279, 113135. [Google Scholar] [CrossRef]
- Xing, J.; Yu, B.; Yang, D.; Li, J.; Shi, Z.; Zhang, G.; Wang, F. A Real-Time GNSS-R System for Monitoring Sea Surface Wind Speed and Significant Wave Height. Sensors 2022, 22, 3795. [Google Scholar] [CrossRef] [PubMed]
- Ghavidel, A.; Camps, A. Impact of rain, swell, and surface currents on the electromagnetic bias in GNSS-reflectometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4643–4649. [Google Scholar] [CrossRef]
- Li, B.; Yang, L.; Zhang, B.; Yang, D.; Wu, D. Modeling and simulation of GNSS-R observables with effects of swell. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1833–1841. [Google Scholar] [CrossRef]
- Camps, A.; Park, H. Sensitivity of delay Doppler map in spaceborne GNSS-R to geophysical variables of the ocean. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 8624–8631. [Google Scholar] [CrossRef]
- Bu, J.; Yu, K.; Park, H.; Huang, W.; Han, S.; Yan, Q.; Qian, N.; Lin, Y. Estimation of Swell Height Using Spaceborne GNSS-R Data from Eight CYGNSS Satellites. Remote Sens. 2022, 14, 4634. [Google Scholar] [CrossRef]
- Munoz-Martin, J.F.; Onrubia, R.; Pascual, D.; Park, H.; Camps, A.; Rüdiger, C.; Walker, J.; Monerris, A. First Experimental Evidence of Wind and Swell Signatures in L5 GPS and E5A Galileo GNSS-R Waveforms. In Proceedings of the IGARSS 2020-2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; 2020; pp. 3369–3372. [Google Scholar]
- Munoz-Martin, J.F.; Onrubia, R.; Pascual, D.; Park, H.; Camps, A.; Rüdiger, C.; Walker, J.; Monerris, A. Experimental evidence of swell signatures in airborne L5/E5a GNSS-reflectometry. Remote Sens. 2020, 12, 1759. [Google Scholar] [CrossRef]
- Bu, J.; Yu, K.; Ni, J.; Huang, W. Combining ERA5 data and CYGNSS observations for the joint retrieval of global significant wave height of ocean swell and wind wave: A deep convolutional neural network approach. J. Geod. 2023, 97, 81. [Google Scholar] [CrossRef]
- Clarizia, M.P. Investigating the Effect of Ocean Waves on GNSS-R Microwave Remote Sensing Measurements. Ph.D. Thesis, University of Southampton, Southampton, UK, 2012. [Google Scholar]
- Zhang, G.; Yang, D.; Yu, Y.; Wang, F. Wind direction retrieval using spaceborne GNSS-R in nonspecular geometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 649–658. [Google Scholar] [CrossRef]
- Cardellach, E. Sea Surface Determination Using GNSS Reflected Signals. Ph.D. Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2001. [Google Scholar]
- Cox, C.; Munk, W. Slopes of the Sea Surface Deduced from Photographs of Sun Glitter; University of California Press: Berkeley, CA, USA; University of California Press: Los Angeles, CA, USA, 1956. [Google Scholar]
- Earthdata. Available online: https://podaac.jpl.nasa.gov/dataset/CYGNSS_L1_FULL_DDM_V3.0 (accessed on 11 April 2024).
- Jing, C.; Niu, X.; Duan, C.; Lu, F.; Di, G.; Yang, X. Sea surface wind speed retrieval from the first Chinese GNSS-R mission: Technique and preliminary results. Remote Sens. 2019, 11, 3013. [Google Scholar] [CrossRef]
- Brüning, C.; Alpers, W.; Hasselmann, K. Monte-Carlo simulation studies of the nonlinear imaging of a two dimensional surface wave field by a synthetic aperture radar. Int. J. Remote Sens. 1990, 11, 1695–1727. [Google Scholar] [CrossRef]
- Elfouhaily, T.; Chapron, B.; Katsaros, K.; Vandemark, D. A unified directional spectrum for long and short wind-driven waves. J. Geophys. Res. Ocean. 1997, 102, 15781–15796. [Google Scholar] [CrossRef]
- Cox, C.; Munk, W. Statistics of the sea surface derived from sun glitter. J. Mar. Res. 1954, 13, 198–227. [Google Scholar]
















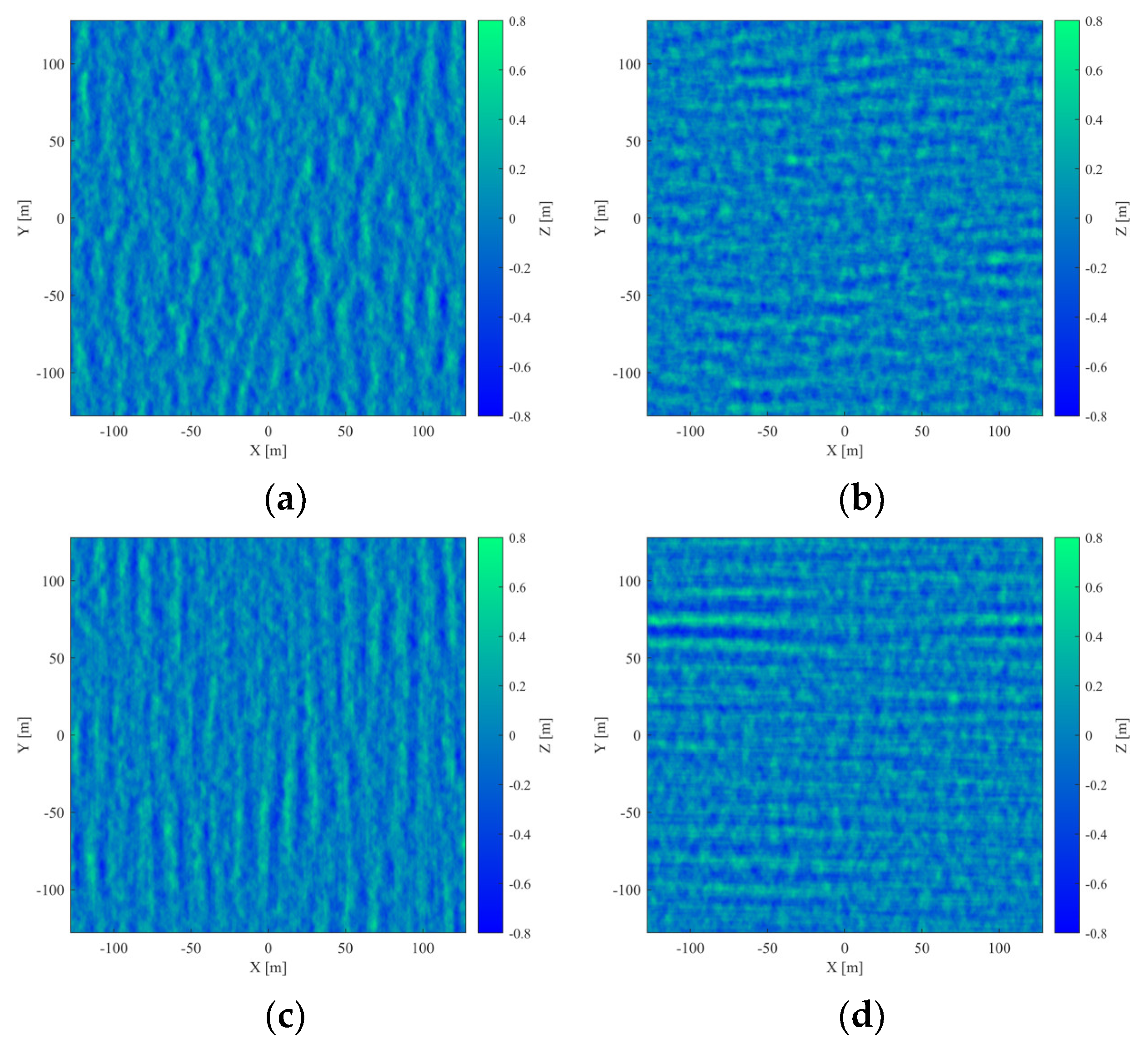
| Sea Surface Samples | U10 | ϕw | D | he |
|---|---|---|---|---|
| (a) | 5 m/s | 0° | 4 | 0.7721 m |
| (b) | 5 m/s | 0° | 40 | 0.7779 m |
| (c) | 5 m/s | 0° | 400 | 0.7961 m |
| (d) | 5 m/s | 90° | 400 | 0.7692 m |
| (e) | 10 m/s | 0° | 40 | 1.5774 m |
| (f) | 10 m/s | 90° | 400 | 1.5599 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, J.; Nie, D.; Zhang, K.; Zhang, M. Characteristics Analysis of Influence of Multiple Parameters of Mixed Sea Waves on Delay–Doppler Map in Global Navigation Satellite System Reflectometry. Remote Sens. 2024, 16, 1395. https://doi.org/10.3390/rs16081395
Yan J, Nie D, Zhang K, Zhang M. Characteristics Analysis of Influence of Multiple Parameters of Mixed Sea Waves on Delay–Doppler Map in Global Navigation Satellite System Reflectometry. Remote Sensing. 2024; 16(8):1395. https://doi.org/10.3390/rs16081395
Chicago/Turabian StyleYan, Jianan, Ding Nie, Kaicheng Zhang, and Min Zhang. 2024. "Characteristics Analysis of Influence of Multiple Parameters of Mixed Sea Waves on Delay–Doppler Map in Global Navigation Satellite System Reflectometry" Remote Sensing 16, no. 8: 1395. https://doi.org/10.3390/rs16081395
APA StyleYan, J., Nie, D., Zhang, K., & Zhang, M. (2024). Characteristics Analysis of Influence of Multiple Parameters of Mixed Sea Waves on Delay–Doppler Map in Global Navigation Satellite System Reflectometry. Remote Sensing, 16(8), 1395. https://doi.org/10.3390/rs16081395











