GF-1 WFV Surface Reflectance Quality Evaluation in Countries along “the Belt and Road”
Abstract
:1. Introduction
- This study validates the quality of GF-1 WFV surface reflectance data from Nepal, Azerbaijan, Kenya, and Sri Lanka. It provides quality information for the global application of GF-1 WFV and quality references for harmonization with Sentinel-2 MSI and Landsat-8 OLI.
- A nadir-view surface reflectance processing flow for WFV is proposed, including geometric corrections, atmospheric corrections, and BRDF corrections to reduce the wide field of view effect of the sensor.
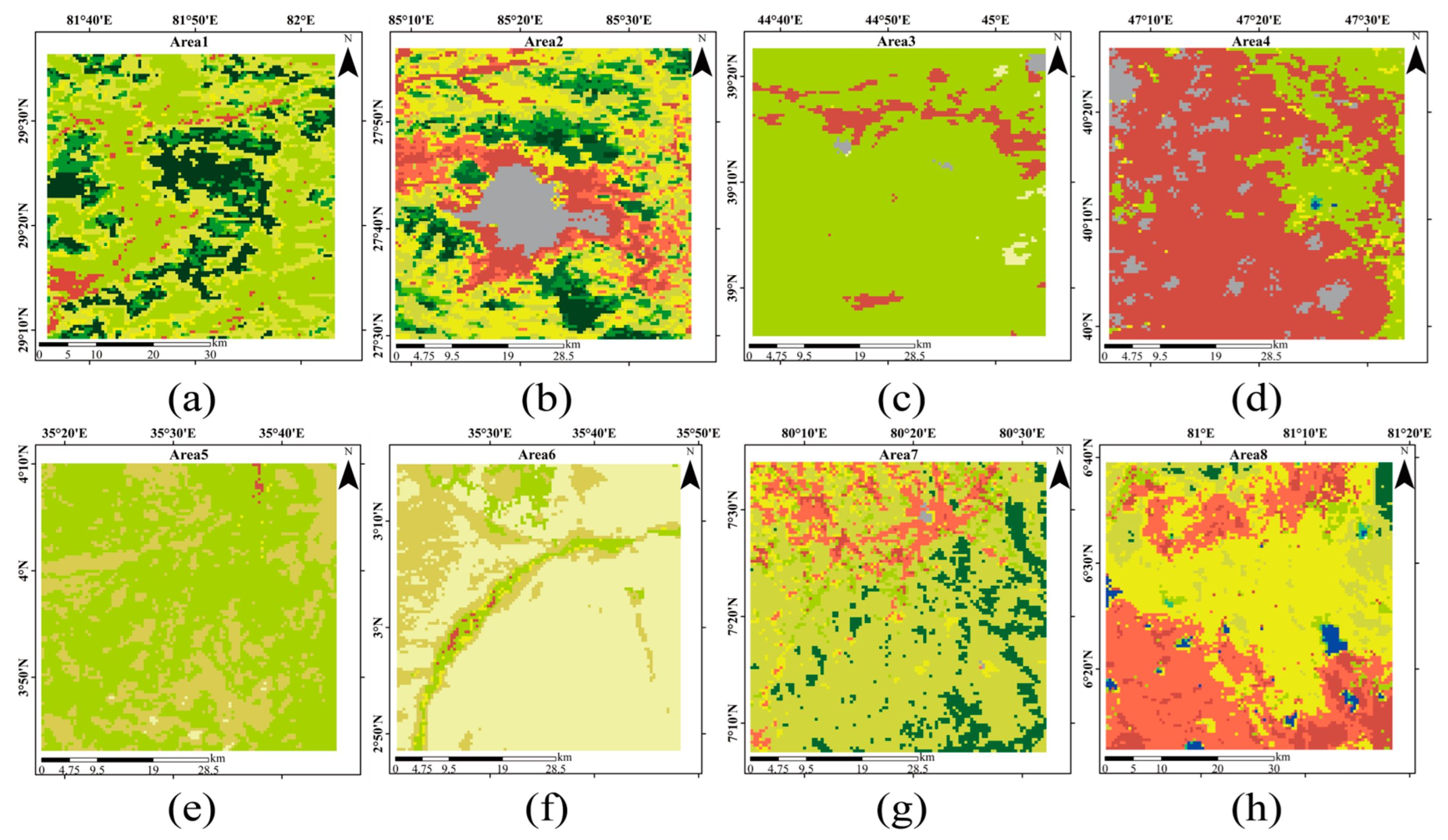
2. Study Area
3. Data and Methodology
3.1. GF-1 WFV Satellite Data and Auxiliary Data
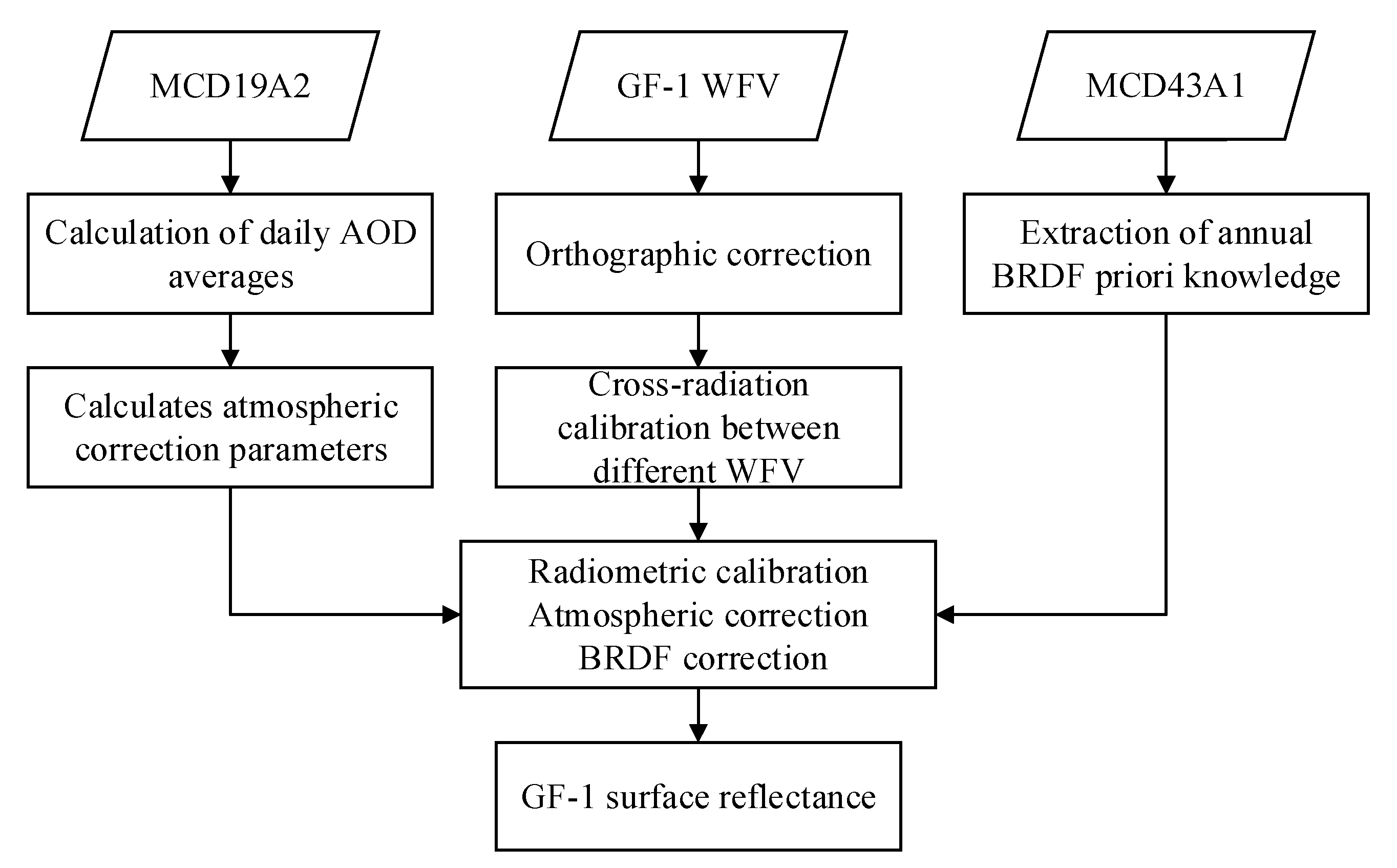
3.2. Inversion Method for GF-1 WFV Surface Reflectance
3.2.1. TOA Reflectance Calculations and Orthographic Correction
3.2.2. Cross-Radiation Calibrations and Atmospheric Correction
3.2.3. BRDF Calibration
3.3. Evaluation of GF-1 WFV Surface Reflectance
3.3.1. Selection Criteria for Sentinel-2 MSI, Landsat-8 OLI and MODIS Data
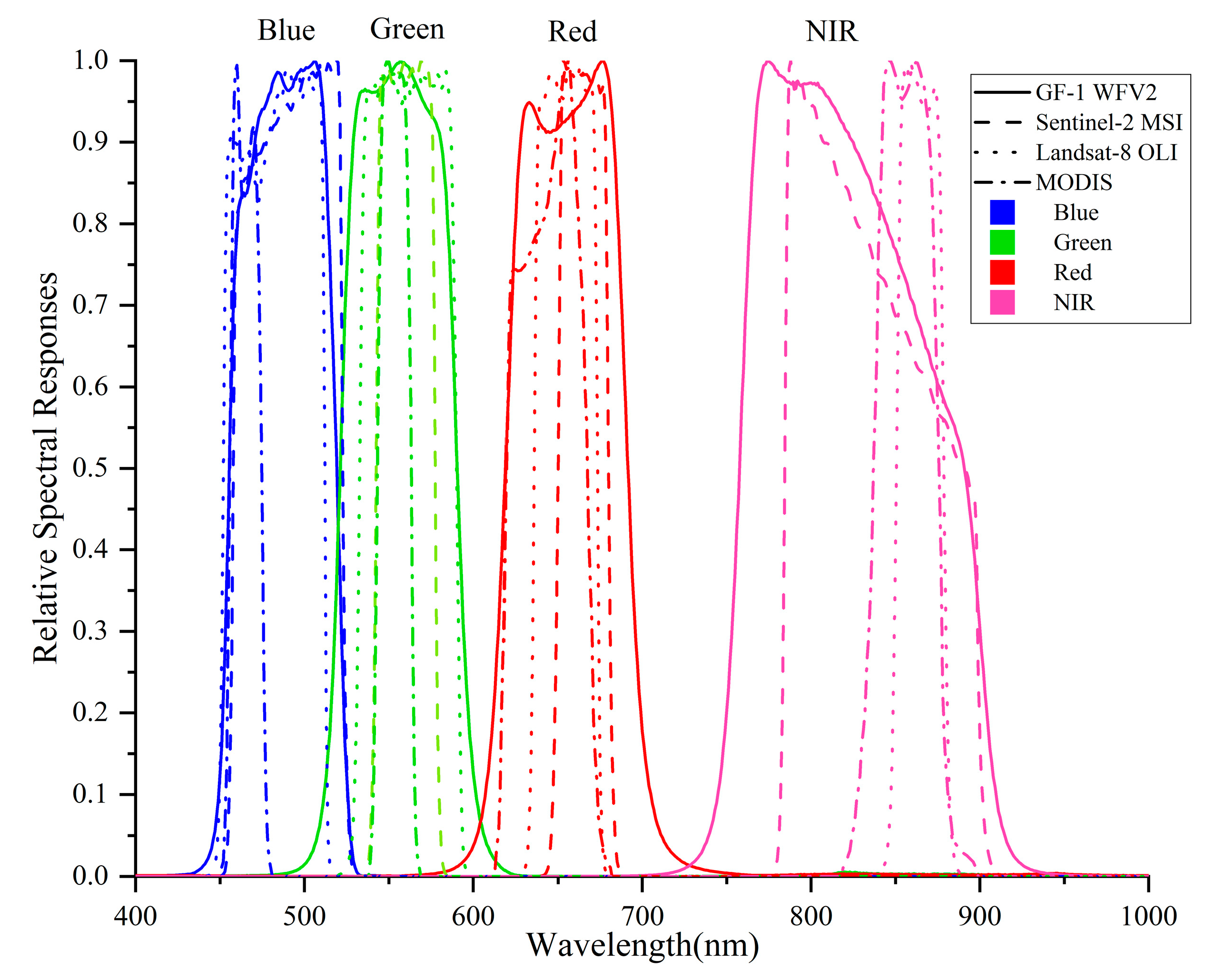
3.3.2. Spectral Adjustment
3.3.3. Comparison Metrics
4. Results
4.1. Satellite Image Selection Results
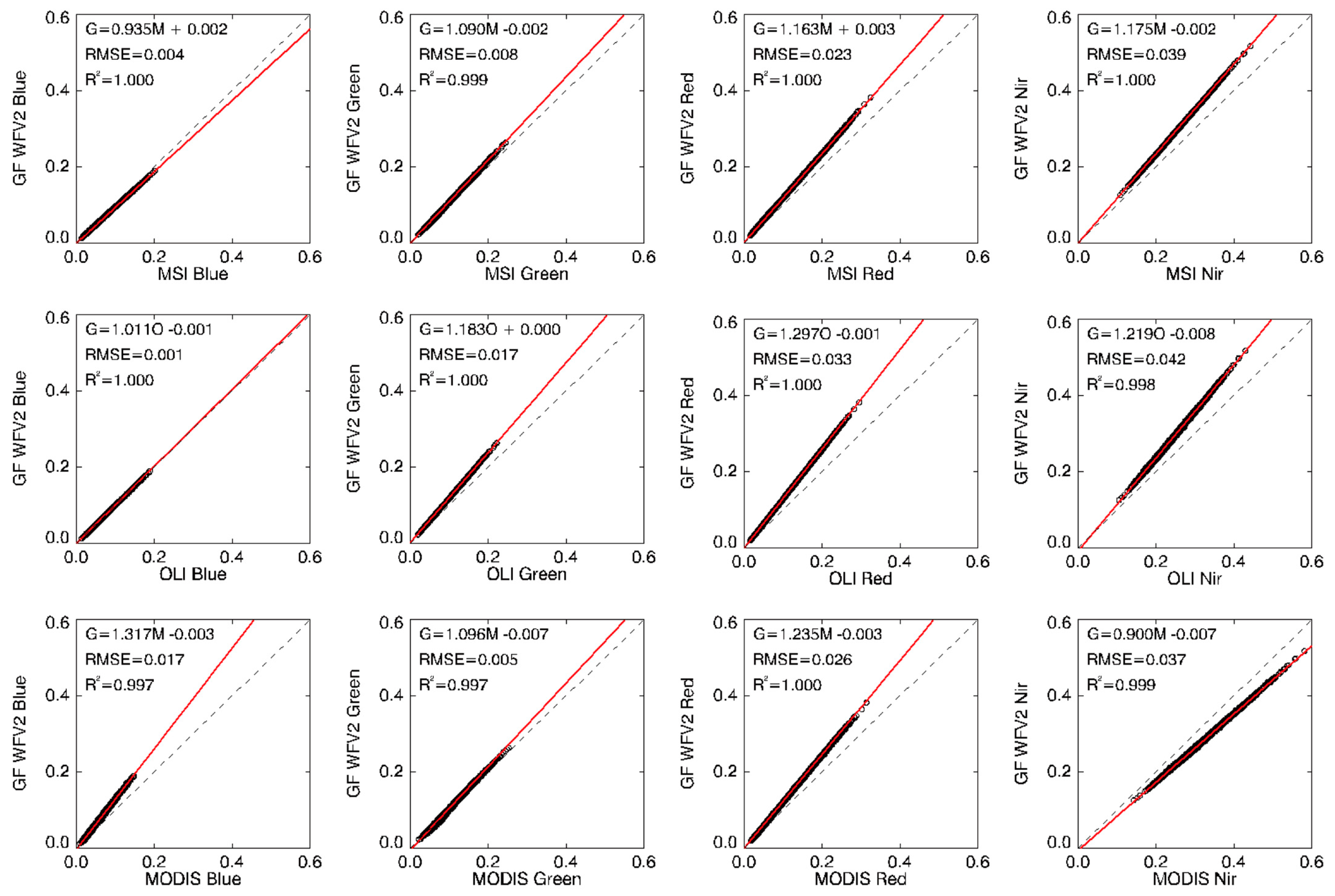
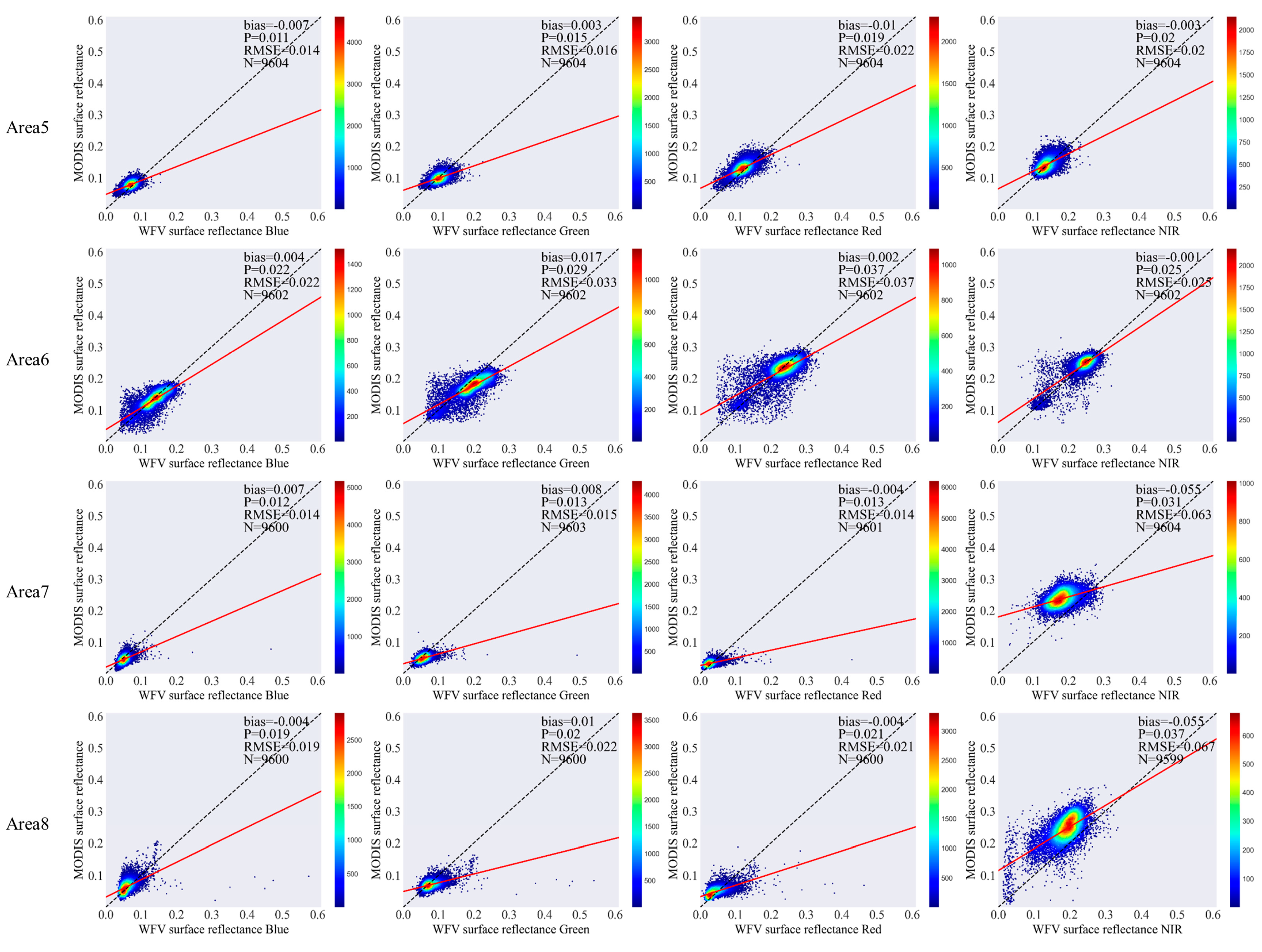
4.2. Evaluation Results of WFV and MSI Surface Reflectance
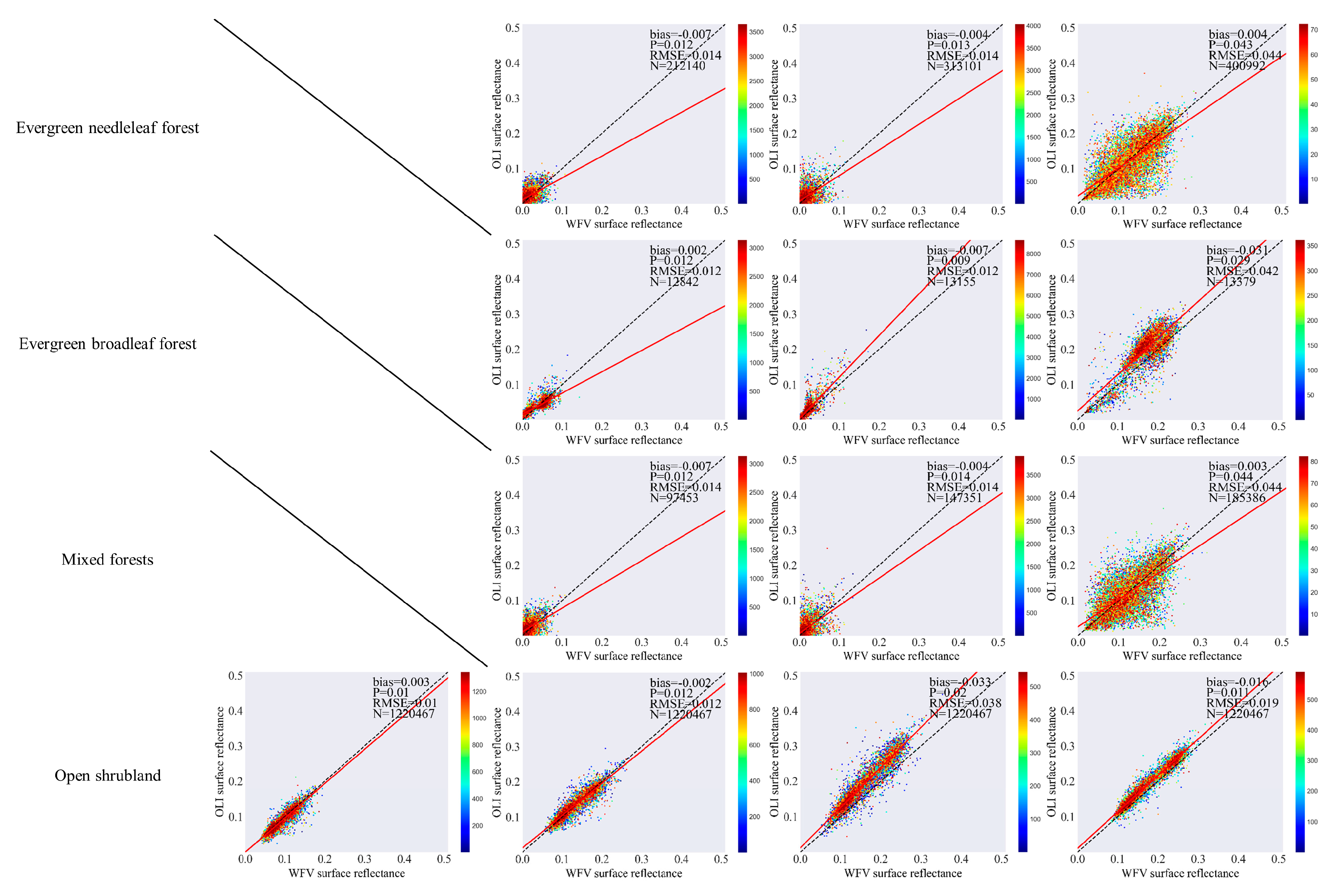
4.3. Evaluation Results of WFV and OLI Surface Reflectance
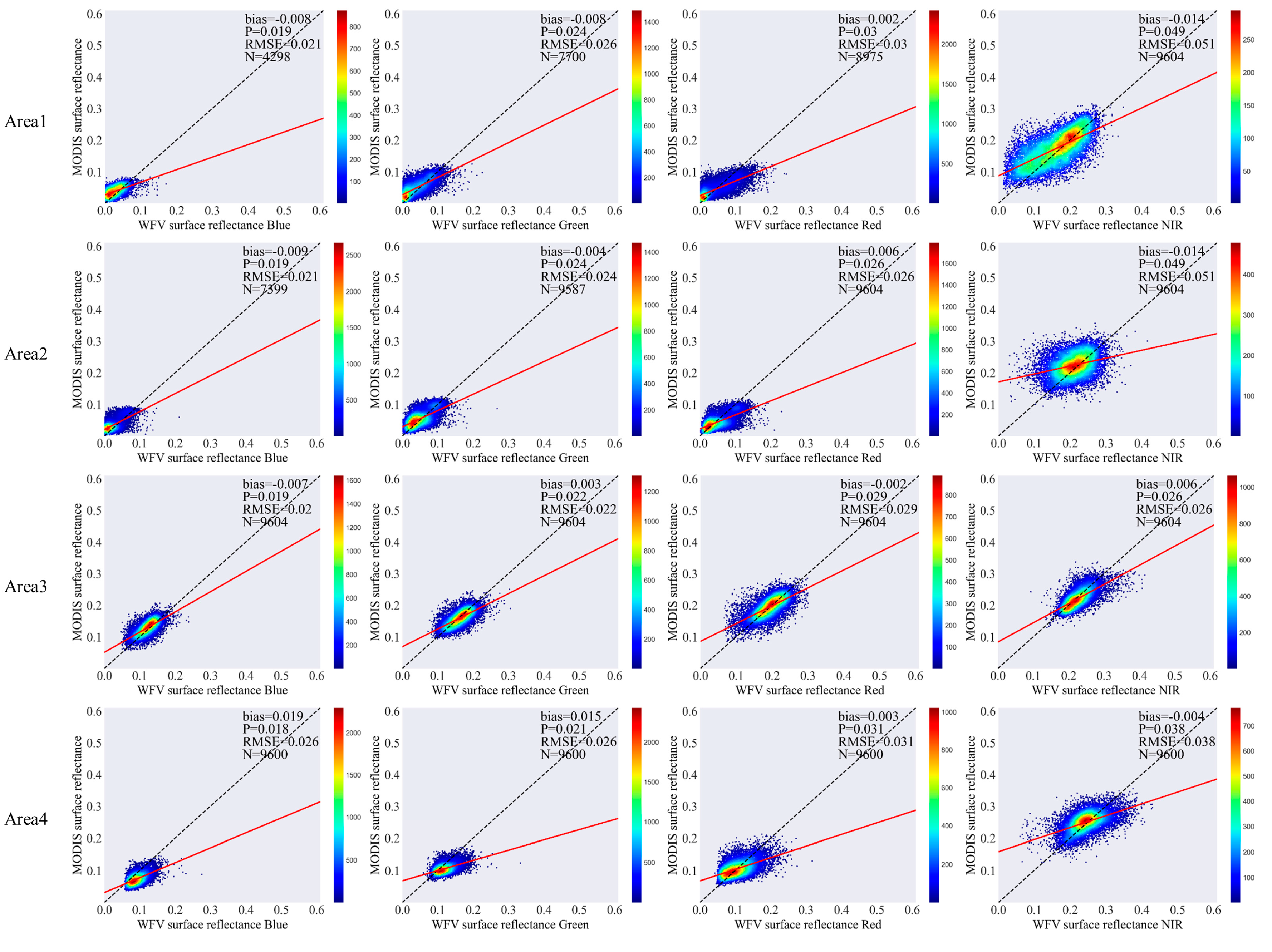
4.4. Evaluation Results of WFV and MODIS Surface Reflectance
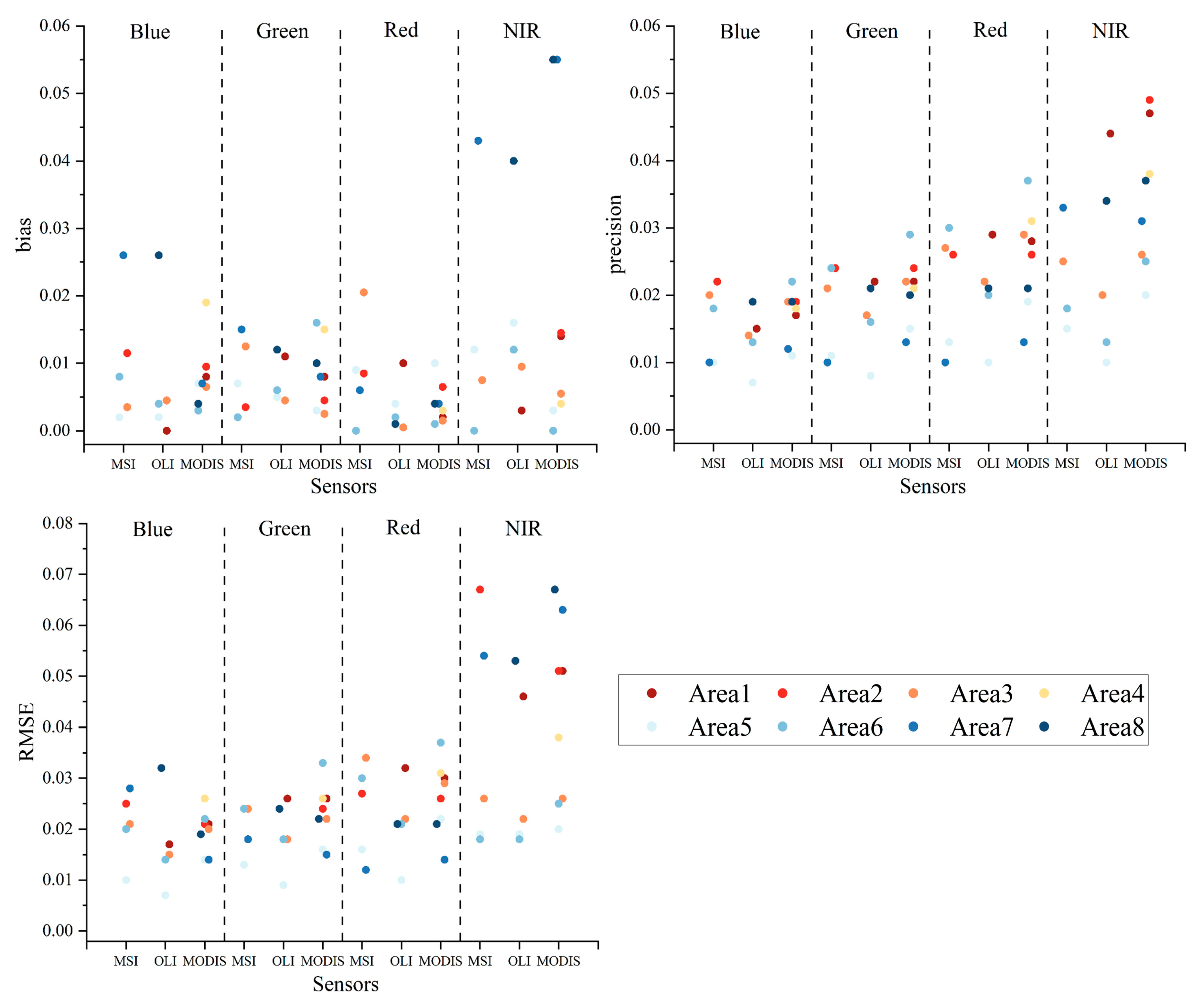
4.5. Comparison of Evaluation Results
5. Discussion
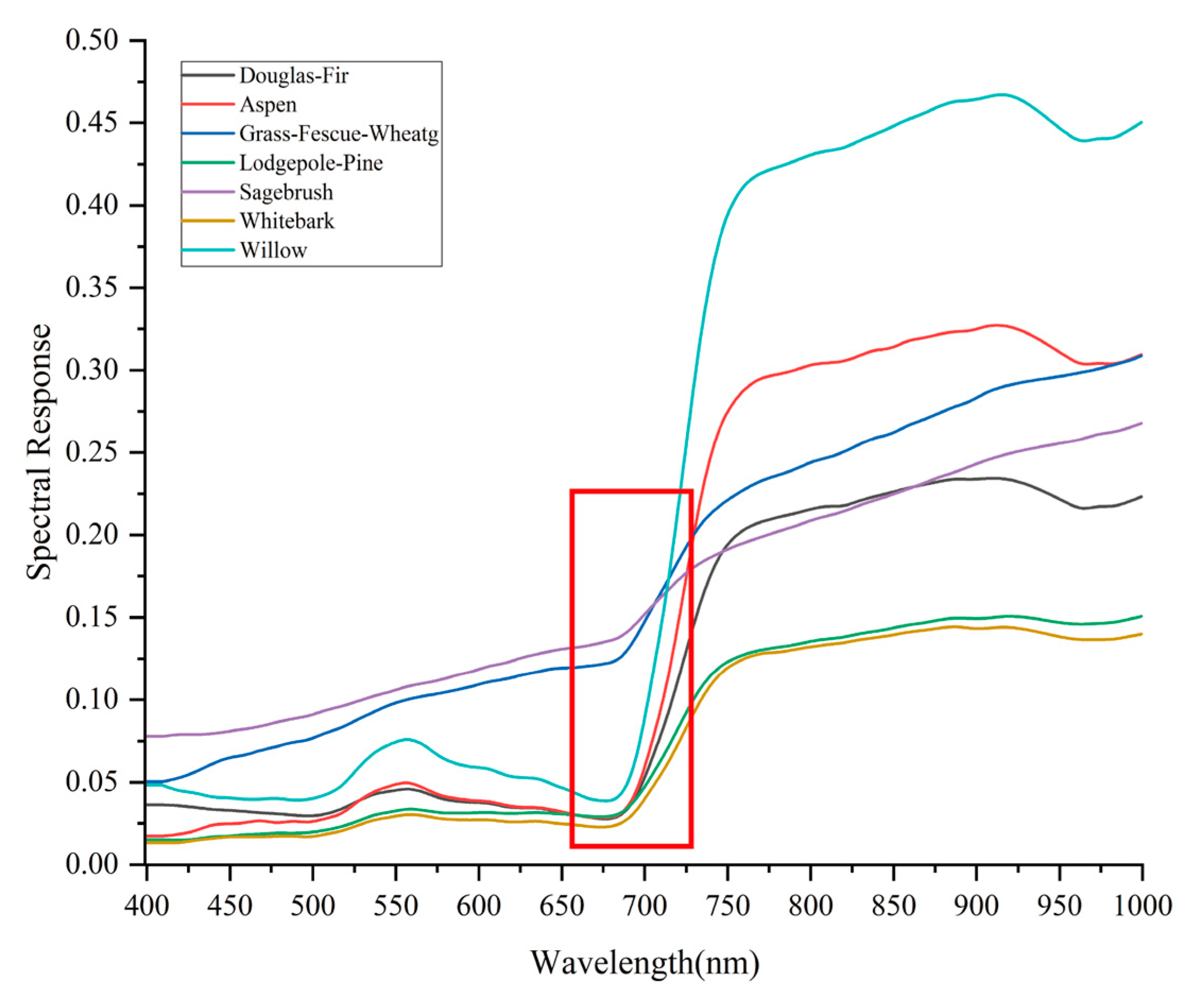
5.1. Effects of Landcover Type
5.2. Effects of Residual Clouds, Cloud Shadows, and Inconsistent Sensor Imaging Times
5.3. Effects of Geographic Alignment
5.4. Limitations and Future Prospects
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Feng, L.; Li, J.; Gong, W.S.; Zhao, X.; Chen, X.L.; Pang, X.P. Radiometric cross-calibration of Gaofen-1 WFV cameras using Landsat-8 OLI images: A solution for large view angle associated problems. Remote Sens. Environ. 2016, 174, 56–68. [Google Scholar] [CrossRef]
- Song, Q.; Hu, Q.; Zhou, Q.B.; Hovis, C.; Xiang, M.T.; Tang, H.J.; Wu, W.B. In-Season Crop Mapping with GF-1/WFV Data by Combining Object-Based Image Analysis and rRandom Forest. Remote Sens. 2017, 9, 1184. [Google Scholar] [CrossRef]
- Yang, N.; Liu, D.Y.; Feng, Q.L.; Xiong, Q.; Zhang, L.; Ren, T.W.; Zhao, Y.Y.; Zhu, D.H.; Huang, J.X. Large-Scale Crop Mapping Based on Machine Learning and Parallel Computation with Grids. Remote Sens. 2019, 11, 1500. [Google Scholar] [CrossRef]
- Lei, S.H.; Wu, D.; Li, Y.M.; Wang, Q.; Huang, C.C.; Liu, G.; Zheng, Z.B.; Du, C.G.; Mu, M.; Xu, J.; et al. Remote sensing monitoring of the suspended particle size in Hongze Lake based on GF-1 data. Int. J. Remote Sens. 2019, 40, 3179–3203. [Google Scholar] [CrossRef]
- Lu, X.M.; Situ, C.Y.; Wang, J.J.; Zhou, L.G.; Ma, W.C.; Li, L.N. Remote Estimation of the Chlorophyll-a Concentration in Lake Dianshan, China Using High-Spatial-Resolution Satellite Imagery. J. Indian Soc. Remote Sens. 2022, 50, 2465–2477. [Google Scholar] [CrossRef]
- Li, Z.; Yang, X.M. Fusion of High- and Medium-Resolution Optical Remote Sensing Imagery and GlobeLand30 Products for the Automated Detection of Intra-Urban Surface Water. Remote Sens. 2020, 12, 4037. [Google Scholar] [CrossRef]
- Li, H.; Chen, Z.X.; Jiang, Z.W.; Wu, W.B.; Ren, J.Q.; Liu, B.; Hasi, T. Comparative analysis of GF-1, HJ-1, and Landsat-8 data for estimating the leaf area index of winter wheat. J. Integr. Agric. 2017, 16, 266–285. [Google Scholar] [CrossRef]
- Li, W.; Niu, Z.; Wang, C.; Huang, W.J.; Chen, H.Y.; Gao, S.; Li, D.; Muhammad, S. Combined Use of Airborne LiDAR and Satellite GF-1 Data to Estimate Leaf Area Index, Height, and Aboveground Biomass of Maize During Peak Growing Season. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2015, 8, 4489–4501. [Google Scholar] [CrossRef]
- Jia, K.; Liang, S.L.; Gu, X.F.; Baret, F.; Wei, X.Q.; Wang, X.X.; Yao, Y.J.; Yang, L.Q.; Li, Y.W. Fractional vegetation cover estimation algorithm for Chinese GF-1 wide field view data. Remote Sens. Environ. 2016, 177, 184–191. [Google Scholar] [CrossRef]
- Zhu, Q.L.; Xu, X.G.; Sun, Z.D.; Liang, D.; An, X.F.; Chen, L.P.; Yang, G.J.; Huang, L.S.; Xu, S.Z.; Yang, M. Estimation of Winter Wheat Residue Coverage Based on GF-1 Imagery and Machine Learning Algorithm. Agronomy 2022, 12, 1051. [Google Scholar] [CrossRef]
- Tao, G.F.; Jia, K.; Zhao, X.; Wei, X.Q.; Xie, X.H.; Zhang, X.W.; Wang, B.; Yao, Y.J.; Zhang, X.T. Generating High Spatio-Temporal Resolution Fractional Vegetation Cover by Fusing GF-1 WFV and MODIS Data. Remote Sens. 2019, 11, 2324. [Google Scholar] [CrossRef]
- Sun, K.; Chen, X.L.; Zhu, Z.M.; Zhang, T.H. High Resolution Aerosol Optical Depth Retrieval Using Gaofen-1 WFV Camera Data. Remote Sens. 2017, 9, 89. [Google Scholar] [CrossRef]
- Zhang, Y.M.; Chen, H.; Wang, Z.T. Terrestrial aerosol retrieval over Beijing from Chinese GF-1 data based on the blue/red correlation. Remote Sens. Lett. 2021, 12, 216–225. [Google Scholar] [CrossRef]
- Sun, K.; Chen, X.L.; Wang, J.L.; Zhang, T.H.; Zhu, Z.M. Investigation of air quality over the largest city in central China using high resolution satellite derived aerosol optical depth data. Atmos. Pollut. Res. 2018, 9, 584–593. [Google Scholar] [CrossRef]
- Bao, F.W.; Gu, X.F.; Cheng, T.H.; Wang, Y.; Guo, H.; Chen, H.; Wei, X.; Xiang, K.S.; Li, Y.N. High-Spatial-Resolution Aerosol Optical Properties Retrieval Algorithm Using Chinese High-Resolution Earth Observation Satellite I. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5544–5552. [Google Scholar] [CrossRef]
- Zhong, B.; Yang, A.X.; Liu, Q.H.; Wu, S.L.; Shan, X.J.; Mu, X.H.; Hu, L.F.; Wu, J.J. Analysis Ready Data of the Chinese GaoFen Satellite Data. Remote Sens. 2021, 13, 1709. [Google Scholar] [CrossRef]
- Franch, B.; Vermote, E.F.; Sobrino, J.A.; Fedele, E. Analysis of directional effects on atmospheric correction. Remote Sens. Environ. 2013, 128, 276–288. [Google Scholar] [CrossRef]
- Barnsley, M.J.; Allison, D.; Lewis, P. On the information content of multiple view angle (MVA) images. Int. J. Remote Sens. 1997, 18, 1937–1960. [Google Scholar] [CrossRef]
- Schaaf, C.B.; Gao, F.; Strahler, A.H.; Lucht, W.; Li, X.W.; Tsang, T.; Strugnell, N.C.; Zhang, X.Y.; Jin, Y.F.; Muller, J.P.; et al. First operational BRDF, albedo nadir reflectance products from MODIS. Remote Sens. Environ. 2002, 83, 135–148. [Google Scholar] [CrossRef]
- Jin, Y.F.; Schaaf, C.B.; Woodcock, C.E.; Gao, F.; Li, X.W.; Strahler, A.H.; Lucht, W.; Liang, S.L. Consistency of MODIS surface bidirectional reflectance distribution function and albedo retrievals: 2. Validation. J. Geophys. Res.-Atmos. 2003, 108, D5. [Google Scholar] [CrossRef]
- Salomon, J.G.; Schaaf, C.B.; Strahler, A.H.; Gao, F.; Jin, Y.F. Validation of the MODIS Bidirectional Reflectance Distribution Function and Albedo retrievals using combined observations from the Aqua and Terra platforms. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1555–1565. [Google Scholar] [CrossRef]
- Fang, H.; Liang, S.; Chen, M.; Walthall, C.; Daughtry, C. Statistical comparison of MISR, ETM plus and MODIS land surface reflectance and albedo products of the BARC land validation core site, USA. Int. J. Remote Sens. 2004, 25, 409–422. [Google Scholar] [CrossRef]
- Li, J.; Chen, X.L.; Tian, L.Q.; Huang, J.; Feng, L. Improved capabilities of the Chinese high-resolution remote sensing satellite GF-1 for monitoring suspended particulate matter (SPM) in inland waters: Radiometric and spatial considerations. ISPRS-J. Photogramm. Remote Sens. 2015, 106, 145–156. [Google Scholar] [CrossRef]
- Dwyer, J.L.; Roy, D.P.; Sauer, B.; Jenkerson, C.B.; Zhang, H.K.K.; Lymburner, L. Analysis Ready Data: Enabling Analysis of the Landsat Archive. Remote Sens. 2018, 10, 1363. [Google Scholar] [CrossRef]
- Vermote, E.; Justice, C.; Claverie, M.; Franch, B. Preliminary analysis of the performance of the Landsat 8/OLI land surface reflectance product. Remote Sens. Environ. 2016, 185, 46–56. [Google Scholar] [CrossRef]
- Claverie, M.; Vermote, E.F.; Franch, B.; Masek, J.G. Evaluation of the Landsat-5 TM and Landsat-7 ETM + surface reflectance products. Remote Sens. Environ. 2015, 169, 390–403. [Google Scholar] [CrossRef]
- Masek, J.G.; Vermote, E.F.; Saleous, N.E.; Wolfe, R.; Hall, F.G.; Huemmrich, K.F.; Gao, F.; Kutler, J.; Lim, T.K. A Landsat surface reflectance dataset for North America, 1990–2000. IEEE Geosci. Remote Sens. Lett. 2006, 3, 68–72. [Google Scholar] [CrossRef]
- Roy, D.P.; Wulder, M.A.; Loveland, T.R.; Woodcock, C.E.; Allen, R.G.; Anderson, M.C.; Helder, D.; Irons, J.R.; Johnson, D.M.; Kennedy, R.; et al. Landsat-8: Science and product vision for terrestrial global change research. Remote Sens. Environ. 2014, 145, 154–172. [Google Scholar] [CrossRef]
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s Optical High-Resolution Mission for GMES Operational Services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Main-Knorn, M.; Pflug, B.; Louis, J.; Debaecker, V.; Muller-Wilm, U.; Gascon, F. Sen2Cor for Sentinel-2. In Proceedings of the Conference on Image and Signal Processing for Remote Sensing XXIII, Warsaw, Poland, 11–13 September 2017; Spie-Int Soc Optical Engineering: Warsaw, Poland, 2017. [Google Scholar]
- Louis, J.; Pflug, B.; Main-Knorn, M.; Debaecker, V.; Mueller-Wilm, U.; Iannone, R.Q.; Cadau, E.G.; Boccia, V.; Gascon, F. Sentinel-2 Global Surface Reflectance Level-2a Product Generated with Sen2cor. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Yokohama, Japan, 28 July–2 August 2019; IEEE: Yokohama, Japan, 2019; pp. 8522–8525. [Google Scholar]
- Paudel, B.; Zhang, Y.L.; Li, S.C.; Liu, L.S.; Wu, X.; Khanal, N.R. Review of studies on land use and land cover change in Nepal. J. Mt. Sci. 2016, 13, 643–660. [Google Scholar] [CrossRef]
- Mammadov, E.; Nowosad, J.; Glaesser, C. Estimation and mapping of surface soil properties in the Caucasus Mountains, Azerbaijan using high-resolution remote sensing data. Geoderma Reg. 2021, 26, 15. [Google Scholar] [CrossRef]
- Klisch, A.; Atzberger, C. Operational Drought Monitoring in Kenya Using MODIS NDVI Time Series. Remote Sens. 2016, 8, 267. [Google Scholar] [CrossRef]
- Giri, C.; Long, J.; Abbas, S.; Murali, R.M.; Qamer, F.M.; Pengra, B.; Thau, D. Distribution and dynamics of mangrove forests of South Asia. J. Environ. Manag. 2015, 148, 101–111. [Google Scholar] [CrossRef] [PubMed]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The shuttle radar topography mission. Rev. Geophys. 2007, 45, 2005RG000183. [Google Scholar] [CrossRef]
- Martins, V.S.; Lyapustin, A.; Wang, Y.J.; Giles, D.M.; Smirnov, A.; Slutsker, I.; Korkin, S. Global validation of columnar water vapor derived from EOS MODIS-MAIAC algorithm against the ground-based AERONET observations. Atmos. Res. 2019, 225, 181–192. [Google Scholar] [CrossRef]
- Long, D.; Gao, Y.C.; Singh, V.P. Estimation of daily average net radiation from MODIS data and DEM over the Baiyangdian watershed in North China for clear sky days. J. Hydrol. 2010, 388, 217–233. [Google Scholar] [CrossRef]
- Chander, G.; Markham, B.L.; Helder, D.L. Summary of current radiometric calibration coefficients for Landsat MSS, TM, ETM+, and EO-1 ALI sensors. Remote Sens. Environ. 2009, 113, 893–903. [Google Scholar] [CrossRef]
- Liu, L.; Gao, H.L.; Pan, Z.Q.; Qian, Y.G.; Han, Q.J.; Zhang, X.W.; Shi, T.T. Satellite-based time series calibration of GF-1 WFV sensors for large view zenith angle observations. Int. J. Remote Sens. 2018, 39, 8293–8316. [Google Scholar] [CrossRef]
- Fraser, C.S.; Dial, G.; Grodecki, J. Sensor orientation via RPCs. ISPRS-J. Photogramm. Remote Sens. 2006, 60, 182–194. [Google Scholar] [CrossRef]
- Fraser, C.S.; Hanley, H.B. Bias-compensated RPCs for sensor orientation of high-resolution satellite imagery. Photogramm. Eng. Remote Sens. 2005, 71, 909–915. [Google Scholar] [CrossRef]
- Yang, A.X.; Zhong, B.; Hu, L.F.; Wu, S.L.; Xu, Z.P.; Wu, H.B.; Wu, J.J.; Gong, X.S.; Wang, H.B.; Liu, Q.H. Radiometric Cross-Calibration of the Wide Field View Camera Onboard GaoFen-6 in Multispectral Bands. Remote Sens. 2020, 12, 1037. [Google Scholar] [CrossRef]
- Teillet, P.M.; Markham, B.L.; Irish, R.R. Landsat cross-calibration based on near simultaneous imaging of common ground targets. Remote Sens. Environ. 2006, 102, 264–270. [Google Scholar] [CrossRef]
- Liu, J.J.; Li, Z.; Qiao, Y.L.; Liu, Y.J.; Zhang, Y.X. A new method for cross-calibration of two satellite sensors. Int. J. Remote Sens. 2004, 25, 5267–5281. [Google Scholar] [CrossRef]
- Li, Z.W.; Shen, H.F.; Li, H.F.; Xia, G.S.; Gamba, P.; Zhang, L.P. Multi-feature combined cloud and cloud shadow detection in GaoFen-1 wide field of view imagery. Remote Sens. Environ. 2017, 191, 342–358. [Google Scholar] [CrossRef]
- Vermote, E.F.; Tanre, D.; Deuze, J.L.; Herman, M.; Morcrette, J.J. Second Simulation of the Satellite Signal in the Solar Spectrum, 6S: An overview. IEEE Trans. Geosci. Remote Sens. 1997, 35, 675–686. [Google Scholar] [CrossRef]
- Li, F.Q.; Jupp, D.L.B.; Reddy, S.; Lymburner, L.; Mueller, N.; Tan, P.; Islam, A. An Evaluation of the Use of Atmospheric and BRDF Correction to Standardize Landsat Data. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2010, 3, 257–270. [Google Scholar] [CrossRef]
- Wanner, W.; Li, X.; Strahler, A.H. On the derivation of kernels for kernel-driven models of bidirectional reflectance. J. Geophys. Res.-Atmos. 1995, 100, 21077–21089. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, M.Z.; Jiao, Z.T.; Lian, Y.; Chen, L.; Cui, L.; Zhang, X.N.; Liu, Y.; Dong, Y.D.; Qian, D.; et al. Reflectance Anisotropy from MODIS for Albedo Retrieval from a Single Directional Reflectance. Remote Sens. 2022, 14, 3627. [Google Scholar] [CrossRef]
- Chander, G.; Hewison, T.J.; Fox, N.; Wu, X.Q.; Xiong, X.X.; Blackwell, W.J. Overview of Intercalibration of Satellite Instruments. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1056–1080. [Google Scholar] [CrossRef]
- Chander, G.; Mishra, N.; Helder, D.L.; Aaron, D.B.; Angal, A.; Choi, T.; Xiong, X.X.; Doelling, D.R. Applications of Spectral Band Adjustment Factors (SBAF) for Cross-Calibration. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1267–1281. [Google Scholar] [CrossRef]
- Teillet, P.M.; Fedosejevs, G.; Gauthier, R.P.; O’Neill, N.T.; Thome, K.J.; Biggar, S.F.; Ripley, H.; Meygret, A. A generalized approach to the vicarious calibration of multiple Earth observation sensors using hyperspectral data. Remote Sens. Environ. 2001, 77, 304–327. [Google Scholar] [CrossRef]
- Zhao, J.; Li, J.; Mu, X.; Zhang, Z.; Dong, Y.; Wu, S.; Zhong, B.; Liu, Q. Validation and analysis the fractional vegetation cover product from GF-1 satellite data in China. J. Remote Sens. 2023, 27, 689–699. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, J.; Liu, Q.; Zhao, J.; Dong, Y.; Li, S.; Wen, Y.; Yu, W. Verification and analysis of high spatial-temporal resolution vegetation index product based on GF-1 satellite data. J. Remote Sens. 2023, 27, 665–676. [Google Scholar] [CrossRef]
- Zhang, H.; Li, J.; Liu, Q.; Zhang, Z.; Zhu, X.; Liu, C.; Zhao, J.; Dong, Y.; Xu, B.; Meng, J. GF-1 leaf area index product across China based on three-dimensional stochastic radiation transfer model. J. Remote Sens. 2023, 27, 677–688. [Google Scholar] [CrossRef]
- Zhang, F.; Li, J.; Wang, C.; Wang, S. Estimation of water quality parameters of GF-1 WFV in turbid water based on soft classification. J. Remote Sens. 2023, 27, 769–779. [Google Scholar] [CrossRef]
- Houborg, R.; McCabe, M.F. Impacts of dust aerosol and adjacency effects on the accuracy of Landsat 8 and RapidEye surface reflectances. Remote Sens. Environ. 2017, 194, 127–145. [Google Scholar] [CrossRef]
- Zhong, B.; Chen, W.H.; Wu, S.L.; Hu, L.F.; Luo, X.B.; Liu, Q.H. A Cloud Detection Method Based on Relationship Between Objects of Cloud and Cloud-Shadow for Chinese Moderate to High Resolution Satellite Imagery. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2017, 10, 4898–4908. [Google Scholar] [CrossRef]
- White, M.A.; de Beurs, K.M.; Didan, K.; Inouye, D.W.; Richardson, A.D.; Jensen, O.P.; O’Keefe, J.; Zhang, G.; Nemani, R.R.; van Leeuwen, W.J.D.; et al. Intercomparison, interpretation, and assessment of spring phenology in North America estimated from remote sensing for 1982–2006. Glob. Chang. Biol. 2009, 15, 2335–2359. [Google Scholar] [CrossRef]
- Zeng, L.L.; Wardlow, B.D.; Xiang, D.X.; Hu, S.; Li, D.R. A review of vegetation phenological metrics extraction using time-series, multispectral satellite data. Remote Sens. Environ. 2020, 237, 20. [Google Scholar] [CrossRef]
- Morgan, B.E.; Chipman, J.W.; Bolger, D.T.; Dietrich, J.T. Spatiotemporal Analysis of Vegetation Cover Change in a Large Ephemeral River: Multi-Sensor Fusion of Unmanned Aerial Vehicle (UAV) and Landsat Imagery. Remote Sens. 2021, 13, 51. [Google Scholar] [CrossRef]
- Yang, K.; Pan, A.N.; Yang, Y.; Zhang, S.; Ong, S.H.; Tang, H.L. Remote Sensing Image Registration Using Multiple Image Features. Remote Sens. 2017, 9, 581. [Google Scholar] [CrossRef]
- Zavorin, I.; Le Moigne, J. Use of multiresolution wavelet feature pyramids for automatic registration of multisensor imagery. IEEE Trans. Image Process. 2005, 14, 770–782. [Google Scholar] [CrossRef] [PubMed]





| Area ID | Country | Landcover Type | GF-1 WFV Imaging Date |
|---|---|---|---|
| 1 | Nepal | grassland with some mixed evergreen forest | 27 October 2020 |
| 2 | Nepal | impermeable surface in the central area and forested grassland at the edges | 30 October 2020 |
| 3 | Azerbaijan | grassland | 19 July 2020 |
| 4 | Azerbaijan | agricultural land | 19 July 2020 |
| 5 | Kenya | dominated by sparse shrubs with some grassland | 17 January 2020 |
| 6 | Kenya | bare ground with essentially no vegetation cover | 17 January 2020 |
| 7 | Sri Lanka | forested grassland | 11 December 2020 |
| 8 | Sri Lanka | mixed savanna and agricultural land | 11 December 2020 |
| Data | Purpose of the Data | Spatial Resolution (m) | Source of Data |
|---|---|---|---|
| GF-1 WFV | surface reflectance inversion | 16 | CRESDA |
| MCD19A2 | Provide atmospheric calibration parameter AOD | 500 | GEE |
| MCD43A1 | Provide BRDF calibration parameters | 500 | GEE |
| SRTM 1 | DEM | 30 | USGS |
| Sentinel-2 MSI | Surface reflectance quality evaluation reference data | 10 | GEE |
| Landsat-8 OLI | Surface reflectance quality evaluation reference data | 30 | GEE |
| MCD43A | Surface reflectance quality evaluation reference data | 500 | GEE |
| Sensors | WFV | MSI | OLI | MODIS | |
|---|---|---|---|---|---|
| Area ID | |||||
| 1 | 27 October 2020 | 25 October 2020 | 25 October 2020 | 27 October 2020 | |
| 2 | 30 October 2020 | 1 November 2020 | 20 October 2020 | 30 October 2020 | |
| 3 | 19 July 2020 | 20 July 2020 | 20 July 2020 | 19 July 2020 | |
| 4 | 19 July 2020 | 17 July 2020 | 13 July 2020 | 19 July 2020 | |
| 5 | 17 January 2020 | 17 January 2020 | 17 January 2020 | 17 January 2020 | |
| 6 | 17 January 2020 | 22 January 2020 | 17 January 2020 | 17 January 2020 | |
| 7 | 11 December 2020 | 11 December 2020 | 7 December 2020 | 11 December 2020 | |
| 8 | 11 December 2020 | 13 December 2020 | 7 December 2020 | 11 December 2020 | |
| Indicators | Bias | Precision | RMSE | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Area ID | ||||||||||||
| Sensors | MSI | OLI | MODIS | MSI | OLI | MODIS | MSI | OLI | MODIS | |||
| Band | ||||||||||||
| 1 | Blue | / | 0.0 | −0.008 | / | 0.017 | 0.019 | / | 0.017 | 0.021 | ||
| Green | / | −0.011 | −0.008 | 0.024 | 0.024 | / | 0.026 | 0.026 | ||||
| Red | / | −0.01 | 0.002 | 0.031 | 0.03 | / | 0.032 | 0.03 | ||||
| NIR | / | −0.003 | −0.014 | 0.046 | 0.049 | / | 0.046 | 0.051 | ||||
| 2 | Blue | 0.011 | / | −0.009 | 0.022 | / | 0.019 | 0.025 | / | 0.021 | ||
| Green | −0.003 | / | −0.004 | 0.024 | / | 0.024 | 0.024 | / | 0.024 | |||
| Red | 0.008 | / | 0.006 | 0.026 | / | 0.026 | 0.027 | / | 0.026 | |||
| NIR | 0.007 | / | −0.014 | 0.067 | / | 0.049 | 0.067 | / | 0.051 | |||
| 3 | Blue | −0.004 | 0.005 | −0.007 | 0.02 | 0.014 | 0.019 | 0.021 | 0.015 | 0.02 | ||
| Green | 0.013 | −0.005 | 0.003 | 0.021 | 0.017 | 0.022 | 0.024 | 0.018 | 0.022 | |||
| Red | 0.021 | −0.001 | −0.002 | 0.027 | 0.022 | 0.029 | 0.034 | 0.022 | 0.029 | |||
| NIR | 0.008 | −0.01 | 0.006 | 0.025 | 0.02 | 0.026 | 0.026 | 0.022 | 0.026 | |||
| 4 | Blue | / | / | 0.019 | / | / | 0.018 | / | / | 0.026 | ||
| Green | / | / | 0.015 | / | / | 0.021 | / | / | 0.026 | |||
| Red | / | / | 0.003 | / | / | 0.031 | / | / | 0.031 | |||
| NIR | / | / | −0.004 | / | / | 0.038 | / | / | 0.038 | |||
| 5 | Blue | 0.002 | 0.002 | −0.007 | 0.01 | 0.007 | 0.011 | 0.01 | 0.007 | 0.014 | ||
| Green | 0.007 | −0.005 | 0.003 | 0.011 | 0.008 | 0.015 | 0.013 | 0.009 | 0.016 | |||
| Red | 0.009 | 0.004 | −0.01 | 0.013 | 0.01 | 0.019 | 0.016 | 0.01 | 0.022 | |||
| NIR | −0.012 | −0.016 | −0.003 | 0.015 | 0.01 | 0.02 | 0.019 | 0.019 | 0.02 | |||
| 6 | Blue | 0.009 | 0.005 | 0.004 | 0.018 | 0.013 | 0.022 | 0.02 | 0.014 | 0.022 | ||
| Green | 0 | 0.007 | 0.017 | 0.024 | 0.016 | 0.029 | 0.024 | 0.018 | 0.033 | |||
| Red | −0.001 | 0.002 | 0.002 | 0.03 | 0.02 | 0.037 | 0.03 | 0.02 | 0.037 | |||
| NIR | −0.001 | −0.013 | −0.001 | 0.018 | 0.013 | 0.025 | 0.018 | 0.018 | 0.025 | |||
| 7 | Blue | 0.026 | / | 0.007 | 0.01 | / | 0.012 | 0.028 | / | 0.014 | ||
| Green | 0.015 | / | 0.008 | 0.01 | / | 0.013 | 0.018 | / | 0.015 | |||
| Red | 0.006 | / | −0.004 | 0.01 | / | 0.013 | 0.012 | / | 0.014 | |||
| NIR | −0.043 | / | −0.055 | 0.033 | / | 0.031 | 0.054 | / | 0.063 | |||
| 8 | Blue | / | 0.026 | −0.004 | / | 0.019 | 0.019 | / | 0.032 | 0.019 | ||
| Green | / | 0.012 | 0.01 | / | 0.021 | 0.02 | / | 0.024 | 0.022 | |||
| Red | / | −0.002 | −0.004 | / | 0.021 | 0.021 | / | 0.021 | 0.021 | |||
| NIR | / | −0.04 | −0.055 | / | 0.034 | 0.037 | / | 0.053 | 0.067 | |||
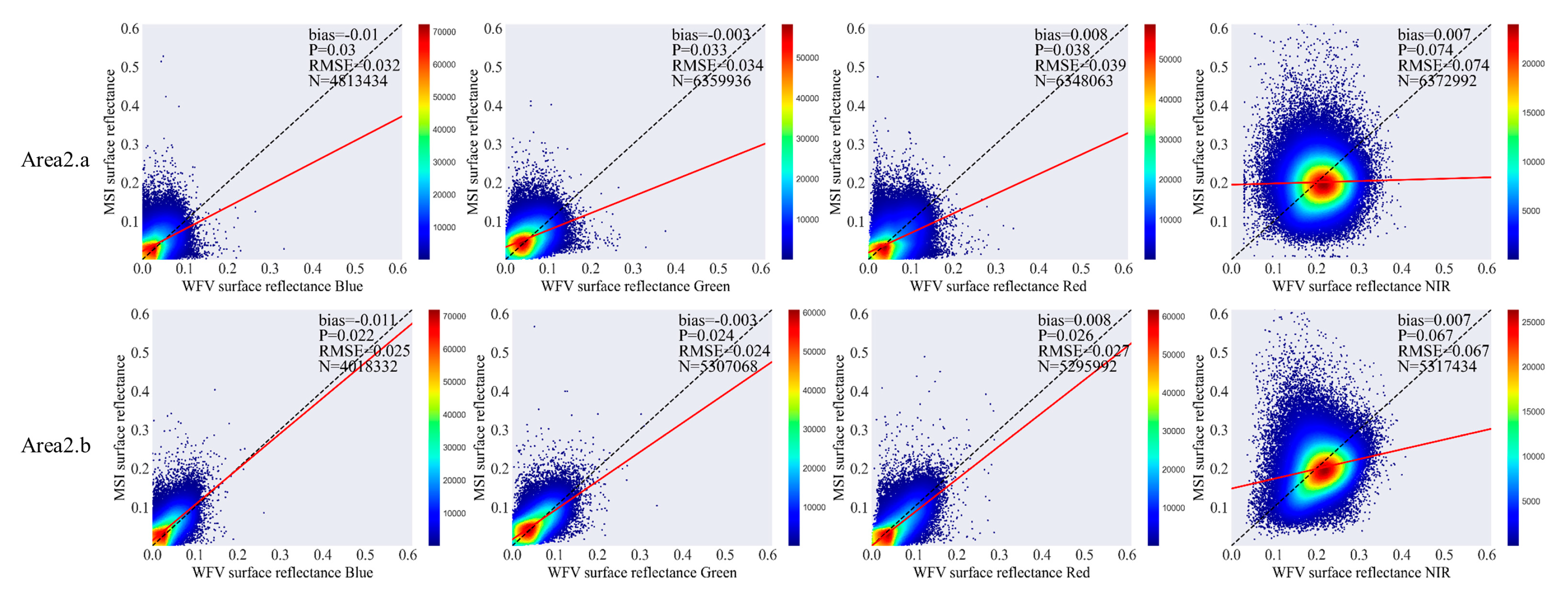
| Indicators | Band | Bias | Precision | RMSE | |
|---|---|---|---|---|---|
| Area ID | |||||
| Area 2.a | Blue | −0.01 | 0.03 | 0.032 | |
| Green | −0.003 | 0.033 | 0.034 | ||
| Red | 0.008 | 0.038 | 0.039 | ||
| NIR | 0.007 | 0.074 | 0.074 | ||
| Area 2.b | Blue | −0.011 | 0.022 | 0.025 | |
| Green | −0.003 | 0.024 | 0.024 | ||
| Red | 0.008 | 0.026 | 0.027 | ||
| NIR | 0.007 | 0.067 | 0.067 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, Y.; Gu, X.; Liu, Y.; Zhang, H.; Cheng, T.; Li, J.; Wei, X.; Gao, M.; Liang, M.; Zhang, Q. GF-1 WFV Surface Reflectance Quality Evaluation in Countries along “the Belt and Road”. Remote Sens. 2023, 15, 5382. https://doi.org/10.3390/rs15225382
Ding Y, Gu X, Liu Y, Zhang H, Cheng T, Li J, Wei X, Gao M, Liang M, Zhang Q. GF-1 WFV Surface Reflectance Quality Evaluation in Countries along “the Belt and Road”. Remote Sensing. 2023; 15(22):5382. https://doi.org/10.3390/rs15225382
Chicago/Turabian StyleDing, Yaozong, Xingfa Gu, Yan Liu, Hu Zhang, Tianhai Cheng, Juan Li, Xiangqin Wei, Min Gao, Man Liang, and Qian Zhang. 2023. "GF-1 WFV Surface Reflectance Quality Evaluation in Countries along “the Belt and Road”" Remote Sensing 15, no. 22: 5382. https://doi.org/10.3390/rs15225382
APA StyleDing, Y., Gu, X., Liu, Y., Zhang, H., Cheng, T., Li, J., Wei, X., Gao, M., Liang, M., & Zhang, Q. (2023). GF-1 WFV Surface Reflectance Quality Evaluation in Countries along “the Belt and Road”. Remote Sensing, 15(22), 5382. https://doi.org/10.3390/rs15225382









