Effects of Topside Ionosphere Modeling Parameters on Differential Code Bias (DCB) Estimation Using LEO Satellite Observations

Abstract

Given the potential of low-earth orbit (LEO) satellites in terms of navigation enhancement, accurately estimating the differential code bias (DCB) of GNSS satellites and LEO satellites is an important research topic. In this study, to obtain accurate DCB estimates, the effects of vertical total electron content (VTEC) modeling parameters of the topside ionosphere on DCB estimation were investigated using LEO observations for the first time. Different modeling parameters were set in the DCB estimations, encompassing modeling spacing in the dynamic temporal mode and degree and order (D&O) in spherical harmonic modeling. The DCB precisions were then evaluated, and the impacts were analyzed. Thus, a number of crucial and beneficial conclusions are drawn: (1) The maximum differences in the GPS DCB estimates after adopting different modeling spacings and different D&Os exhibit that the different modeling spacings or D&Os both affect the GPS DCB estimates and their root-mean square (RMS), and the effects of the two are at the same level. (2) The maximum differences in receiver DCBs using different modeling spacings indicate that the modeling spacing has a significant impact on the receiver DCBs, compared with GPS DCBs. Whereas, the maximum differences in receiver DCBs with different modeling D&Os are inferior to the differences in the GPS DCBs. That is, the modeling spacing has a greater impact on the LEO DCBs than those of the modeling D&O. (3) The experimental results indicate that the GPS DCB estimates using a modeling spacing of 12H have higher precisions than the others, whereas LEO receiver DCBs using a spacing of 4H or 6H obtain optimal STD. In terms of modeling D&O, adopting 8D&O in the LEO-based VTEC modeling can attain superior estimates and precisions for both GPS and LEO DCBs. The research conclusions can provide references for LEO-augmented DCB estimation.

1. Introduction

Differential code bias (DCB) is a critical error source in navigation positioning and ionosphere modeling [1,2,3,4,5,6,7,8]. Several DCB estimation methods based on ground station data are available: the first method, used by a few institutes such as the Center of Orbit Determination of Europe (CODE), uses observation data from global ground stations to estimate DCB and vertical total electron content (VTEC) simultaneously [1,4,9,10,11,12,13]; the second method proposed by the Chinese Academy of Science (CAS) applies single ground station observations to model the VTEC and estimate the DCB and VTEC parameters simultaneously [2,7,14,15]; the third method is similar to the one used by the German Aerospace Center (DLR) and estimates the DCB parameters of GNSS satellite and receiver after removing the ionosphere impact by introducing a more accurate prior ionosphere model [5,6]. The accuracy of DCB estimates depends critically on the amount of observation data and their distribution. Low-earth orbit (LEO) satellites can be used as space-based monitoring stations to estimate DCB parameters, compensating for the lack of ground stations. In addition, as LEO is above the F layer of the ionosphere and ionized electrons are derived from the topside ionosphere or plasmasphere, which is less variable in both spatial and temporal domains, the observations suffer from minor signal delays.

With the launch of tens of thousands of LEO satellites in the future, accurately estimating the DCB of GNSS and LEO satellites is an important research topic. In recent years, scholars have studied and used LEO onboard observation data to estimate DCB parameters. A few scholars estimated the DCBs of the GPS satellite and LEO receiver as unknown parameters simultaneously [16,17,18], and others [19,20,21,22,23,24,25] not only estimated the DCB parameters of GPS and LEO satellites but also estimated the corresponding VTEC parameters. Certain scholars introduced external GPS DCB products and estimated only the corresponding topside ionosphere VTEC and LEO receiver DCB parameters [26,27,28]. Presently, the aforementioned scholars have conducted research on DCB estimation employing LEO observation data by choosing different modeling parameters [20,24,25,28]. However, there is no research on the effects of topside ionosphere estimation strategies on DCB estimation, and superior modeling parameters must be determined to obtain accurate DCB estimates.

In this paper, the impacts of topside ionosphere VTEC modeling parameters on LEO-based DCB estimation are investigated and analyzed for the first time to obtain superior modeling parameters and accurate DCB estimates. The research conclusions can provide a reference for LEO-augmented DCB estimation. Section 2 presents the model and strategy for GPS and LEO DCB estimation using LEO observation data. Section 3 analyzes the results of experiments in which different modeling parameters are set in the DCB estimations, encompassing the modeling spacing in the dynamic temporal mode and the degree and order in spherical harmonic modeling, employing GRACE-FO [29] observation data. The differences in the GPS and LEO DCB estimates using different modeling parameters are shown, and the precision of the DCB estimates is evaluated. Then, the effects of the modeling parameters on DCB estimation are analyzed, and superior modeling parameters for DCB estimation are provided. Finally, the conclusions are summarized in Section 4.

2. Model and Strategy for DCB Estimation

The geometry-free (GF) combination observation estimation method involves a simpler calculation and does not require outlier information. Therefore, we employed GF combinations of pseudo-range observations to estimate the DCB parameters. The DCB values (P1-P2) for the GPS satellites and LEO receivers were estimated daily as constant values and simultaneously with the topside ionosphere VTEC parameters.

DCB estimation using LEO observations is not affected by the troposphere. Hence, dual-frequency code observations are commonly expressed as shown in Equation (1), and the GF combination of the pseudo-range observations is formed as expressed in Equation (2) [1,6,7].

$$\left\{\begin{array}{l}{P}_{r,1}^s={\rho }_r^s+c\cdot (d{t}_r-d{t}^s)+{\alpha }_1\cdot STEC+c\cdot (b^{s,1}+b_{r,1})+{\epsilon }_{r,1}^s , {\alpha }_1=\frac{40.28}{f_1^2}\\ P_{r,2}^s={\rho }_r^s+c\cdot (d{t}_r-d{t}^s)+{\alpha }_2\cdot STEC+c\cdot (b^{s,2}+b_{r,2})+{\epsilon }_{r,2}^s , {\alpha }_2=\frac{40.28}{f_2^2}\end{array}\right.$$

(1)

$$P_{r,GF}^s=P_{r,1}^s-P_{r,2}^s=\alpha \cdot STEC+DC{B}^s+DC{B}_r+{\epsilon }_{r,GF}^s, \alpha =40.28\cdot \left(\frac{1}{f_1^2}-\frac{1}{f_2^2}\right)$$

(2)

Here scripts s and r denote the GPS satellite and LEO receiver; 1 and 2 denote frequency numbers; $f_1 \mathrm{and} f_2$ denote the L1 and L2 frequencies of the GPS signal, respectively; ${\rho }_r^s$ represents the geometric distance; c is the light speed in vacuum; $d{t}_r \mathrm{and} t^s$ represent the LEO receiver and GPS satellite clock offsets, respectively; b^s,i and b_r,i (i = 1,2) refer to the instrument delays from GPS satellite s and LEO receiver r at two frequencies, respectively; STEC represents the slant total electron content of the LEO-based ionosphere; α₁, α₂, and α are the coefficients of the STEC related to the L1 and L2 frequencies of the GPS signal; DCB^s and DCB_r refer to the DCBs of the GPS satellite s and LEO receiver r; ${\epsilon }_{r,i}^s$ and ${\epsilon }_{r,GF}^s$ represent the noise from pseudo-range observations and the GF combination observations, respectively. $P_{r,1}^s$, $P_{r,2}^s$ denote the pseudo-range observations at the L1 and L2 frequencies of the GPS signals from GPS satellite s to LEO receiver r; and $P_{r,GF}^s$ represents the GF combination of pseudo-range observations.

In this study, we screen code observation data using residuals and LEO orbits derived from phase observations, and the preprocessing for pseudo-range also draws on the onboard data preprocessing method of LEO precise orbit determination. The pseudo-range is relatively clean in this way.

The F&K mapping function [30] was originally developed for slant-path atmospheric water vapor conversion and later applied to LEO-based total electron content (TEC) conversion [31]. It is more suitable than the single-layer mapping function (SLM) for LEO-based TEC conversion under certain conditions [32]. In this study, the F&K mapping function was applied to convert the LEO-based TEC from a vertical to a slant direction. The expected height of maximum electron density is called the ionospheric effective height (IEH) [32]. In the solar-geomagnetic reference frame, the LEO-based VTEC values were modeled using spherical harmonic expansion. The temporal modeling mode was set to dynamic status. The modeling spacing means the modeling interval, and it is the calculation period of the modeling parameters. A set of modeling coefficients can be estimated within each modeling spacing. The modeling spacing of the VTEC and the degree and order (D&O) of the spherical harmonic expansion are the main research objects. The sampling interval of the observation data was set at 30 s, and the cut-off elevation angle was set at 15° to reduce the effects of multipath. The LEO-based TEC model is expressed in Equation (3) [1,30,32,33].

$$\left\{\begin{array}{l}STEC=m{f}_{{}_{F\&K}}\cdot VTEC\\ m{f}_{F\&K}=\frac{1+(R_E+h_{IEH})/R_{LEO}}{\cos z+\sqrt{{(R_E+h_{IEH})}^2/R_{LEO}{}^2-{(\sin z)}^2}}\\ h_{IEH}=(0.0027F_{107}+1.79)h_{LEO}-5.52F_{107}+1350\\ modeled VTEC={\displaystyle \sum _{n=0}^{n_{\max }}{\displaystyle \sum _{m=0}^n{\tilde{P}}_{nm}(\sin \phi )}}\cdot ({\tilde{A}}_{nm}\cos (m\lambda )+{\tilde{B}}_{nm}\sin (m\lambda ))\end{array}\right.$$

(3)

where $m{f}_{F\&K}$ represents the F&K mapping function; $h_{IEH}$ denotes IEH; $R_E$ represents the earth radius; $h_{LEO}$ refers to the altitude of the LEO satellite above the surface of the Earth; $R_{LEO}=R_E+h_{LEO}$; $F_{107}$ denotes the solar radio flux at 10.7 cm; z represents the zenith angle of the slant ray path. STEC and VTEC denote the slant and vertical total electron content of the LEO-based topside ionosphere, respectively, $\phi$ and $\lambda$ represent the geomagnetic latitude and sun-fixed longitude in the equation of modeled VTEC, respectively; ${\tilde{P}}_{nm}$ denotes the normalized associated Legendre functions of degree n and order m; and ${\tilde{A}}_{nm}$ and ${\tilde{B}}_{nm}$ refer to the VTEC coefficients of the spherical harmonic function; $n_{\max }$ represents the maximum degree of the spherical harmonic expansion.

Introduced Equations (3) into (2), unknown estimation parameters contain DCBs of GNSS satellite and LEO receiver and LEO-based VTEC model coefficients. Equation (4) is obtained from Equations (2) and (3). The GPS and LEO DCBs can be estimated and determined together with the VTEC model coefficients. Assuming that the numbers of GPS and LEO DCB estimates are μ1 and μ2, then the number of estimated VTEC model coefficients is μ3. The parameter estimation equation can be written in matrix form as:

$$\left\{\begin{array}{l}\underset{n\times 1}{Z}=F\cdot \widehat{X}\\ \underset{n\times (\mu 1+\mu 2+\mu 3)}{F}=\left[\underset{n\times \mu 1}{A} \underset{n\times \mu 2}{B} \underset{n\times \mu 3}{C}\right]\\ \underset{(\mu 1+\mu 2+\mu 3)\times 1}{\widehat{X}}={\left[\underset{1\times \mu 1}{{\widehat{X}}_{\mathrm{s},dcb}{}^T} \underset{1\times \mu 2}{{\widehat{X}}_{r,dcb}{}^T} \underset{1\times \mu 3}{{\widehat{X}}_{vtec,coef}{}^T}\right]}^T\end{array}\right.$$

(4)

Here the vector Z with a total of n rows is related to DCB and VTEC modeling coefficients; F is the design matrix that consists of the matrix A, B, and C, related to GNSS DCB, LEO DCB, and VTEC modeling coefficients; and $\widehat{X}$ is the DCB estimate and VTEC modeling coefficient, which consists of the vectors of GNSS DCB (${\widehat{X}}_{\mathrm{s},dcb}$), LEO DCB (${\widehat{X}}_{r,dcb}$), and VTEC modeling coefficients (${\widehat{X}}_{vtec,coef}$). Assuming that the modeling spacing and D&O are s (in hours) and $n_{\max }$, respectively, the number of VTEC modeling parameters is ($n_{\max }$ + 1) × ($n_{\max }$ + 1) × (24/s + 1), the number of DCB parameters estimated daily as constant values for each GPS satellite and each LEO receiver is 32 + 1 = 33, and the number of total unknown parameters on one day is ($n_{\max }$ + 1) × ($n_{\max }$ + 1) × (24/s + 1) + 33.

Considering that the DCBs of the GPS satellite and LEO receiver are closely correlated, the DCB datum is defined by a zero-mean condition in the DCB estimation for de-correlation. Equation (5) represents the zero-mean condition [34]:

$${\displaystyle \sum _{s=1}^{S\max }DC{B}^s=0}$$

(5)

Here $S_{\max }$ denotes the total number of observed GPS satellites.

Daily DCB values were realigned by applying a shift from non-all satellite DCB values, which were calculated using a common set of satellites over the study period. After alignment [35], we evaluated the DCB estimates using their monthly stability to represent internal agreement as a standard deviation (STD) and compared them with CODE products to represent external agreement as mean differences and root-mean square (RMS). The monthly stability of the DCB values reflects the stability and reliability of the DCB estimates to a certain extent and can be expressed as follows:

$$ST{D}^s=\sqrt{\frac{{\displaystyle \sum _{d=1}^{\mathrm{D}}{(dc{b}_d^s-{\overline{dcb}}^s)}^2}}{D-1}}$$

(6)

Here scripts s and d denote one satellite and one day, respectively; D refers to the total days of a month; ${\overline{dcb}}^s$ represents the monthly mean of the DCB estimates of satellite s; $dc{b}_d^s$ denotes the DCB estimate of satellite s on day d in a month; and $ST{D}^s$ is the monthly stability of the DCB estimates of satellite s.

The RMS values for GPS DCB estimates with respect to external reference products after conducting the alignment procedures is calculated as follows:

$$RM{S}^s=\sqrt{\frac{{\displaystyle \sum _{d=1}^D{(dc{b}_d^s-edc{b}_d^s)}^2}}{D}}$$

(7)

Here $dc{b}_d^s$ represents the DCB estimate of satellite s on day d in a month; $edc{b}_d^s$ denotes the DCB values of satellite s from the external reference products on day d; D refers to the total number of days in one month; $RM{S}^s$ is the difference RMS of the DCB estimates of satellite s relative to the reference products.

3. Experiments and Results

To obtain suitable and superior topside ionospheric VTEC modeling parameters in LEO-based DCB estimation, we investigated the effects of the different modeling parameters on DCB estimates and precision, including modeling spacings in dynamic temporal mode and degrees and orders in spherical harmonic modeling. The precision of DCB estimates was then evaluated, and the effects of the parameters were analyzed. We used onboard GPS observation data from the twin GRACE-FO satellites (GRCC and GRCD) from 1–30 January 2019 to estimate the GPS and LEO satellite DCBs. We comprehensively evaluated the internal and external consistency precisions of GPS DCB estimation and compared the monthly stability of GPS and LEO DCB estimates as internal precision, which was presented STD. The comparisons between the GPS DCB estimates and CODE DCB products represent the external precision in the form of the mean and RMS of the difference between the estimates and CODE products. The LEO DCB can provide internal precision but not external precision owing to a lack of external reference products.

Additionally, this study requires the precise orbits of the twin GRACE-FO satellites owing to the needs of Equation (3). Before DCB estimation, we conducted precise orbit determination (POD) of the GRACE-FO satellites. The main data processing of LEO POD can be found in the references [36,37,38,39,40,41]. The LEO orbit determination is not necessary. If external reference orbits are available, they can also be used to carry out experiments.

3.1. Different Modeling Spacings

To investigate the effects of modeling spacings on DCB estimate and precision and to obtain superior parameter settings, we set different modeling spacings of 2H, 4H, 6H, and 12H in the LEO-based VTEC dynamic temporal modeling mode. The modeling degree and order were set to 8. Then, the effects of modeling spacing on DCB estimation were analyzed by evaluating the precision of the GPS and LEO DCB estimates.

3.1.1. GPS Satellite DCB Estimates

The mean DCB can exhibit the averaged ranges of DCBs in the form of specific and intuitive numbers; thereby,

Table 1. Mean GPS differential code bias (DCB) estimates based on different modeling spacings using GRCC (a) and GRCD (b) observations [ns].

(a) GRCC
GPS	2H	4H	6H	12H
G01	−7.4145	−7.4174	−7.4183	−7.4191
G02	9.1243	9.1298	9.1330	9.1375
G03	−5.0039	−5.0161	−5.0208	−5.0262
G05	2.9826	2.9782	2.9775	2.9772
G06	−6.6772	−6.6762	−6.6750	−6.6726
G07	3.3569	3.3536	3.3532	3.3534
G08	−7.5298	−7.5226	−7.5205	−7.5182
G09	−4.9578	−4.9469	−4.9431	−4.9388
G10	−5.0343	−5.0449	−5.0487	−5.0529
G11	3.7213	3.7332	3.7374	3.7420
G12	4.1600	4.1480	4.1436	4.1385
G13	3.4175	3.4277	3.4307	3.4336
G14	1.9124	1.9205	1.9223	1.9231
G15	2.6321	2.6467	2.6523	2.6588
G16	2.7966	2.7844	2.7801	2.7753
G17	2.9321	2.9406	2.9429	2.9452
G18	−0.2903	−0.2915	−0.2913	−0.2908
G19	5.6329	5.6405	5.6425	5.6440
G20	1.4707	1.4640	1.4621	1.4597
G21	2.2743	2.2791	2.2821	2.2857
G22	7.2749	7.2648	7.2612	7.2572
G23	9.1329	9.1434	9.1469	9.1511
G24	−5.5552	−5.5542	−5.5536	−5.5526
G25	−7.1077	−7.1219	−7.1273	−7.1336
G26	−8.5698	−8.5834	−8.5883	−8.5941
G27	−5.2432	−5.2366	−5.2348	−5.2330
G28	3.2078	3.1953	3.1910	3.1861
G29	2.2061	2.2135	2.2154	2.2167
G30	−6.0024	−6.0065	−6.0074	−6.0079
G31	4.9635	4.9588	4.9573	4.9560
G32	−4.3827	−4.3735	−4.3709	−4.3688
(b) GRCD
GPS	2H	4H	6H	12H
G01	−7.2909	−7.2886	−7.2910	−7.2904
G02	9.3020	9.3094	9.3125	9.3178
G03	−4.8126	−4.8174	−4.8270	−4.8316
G05	3.0288	3.0263	3.0288	3.0305
G06	−6.6031	−6.6008	−6.5987	−6.5960
G07	3.4199	3.4194	3.4154	3.4150
G08	−7.2286	−7.2240	−7.2212	−7.2195
G09	−4.7793	−4.7650	−4.7637	−4.7593
G10	−4.9828	−4.9938	−4.9933	−4.9963
G11	3.7889	3.8041	3.8055	3.8099
G12	4.2406	4.2284	4.2184	4.2111
G13	3.4716	3.4804	3.4854	3.4884
G14	2.0112	2.0114	2.0217	2.0232
G15	2.6436	2.6580	2.6637	2.6704
G16	2.9451	2.9338	2.9275	2.9224
G17	2.9843	2.9941	2.9956	2.9973
G18	−0.2142	−0.2115	−0.2117	−0.2098
G19	5.7302	5.7393	5.7411	5.7430
G20	1.5928	1.5863	1.5873	1.5864
G21	2.3455	2.3498	2.3554	2.3602
G22	7.5031	7.4949	7.4897	7.4856
G23	9.2814	9.2948	9.2958	9.3000
G24	−5.4638	−5.4579	−5.4583	−5.4559
G25	−7.1005	−7.1194	−7.1222	−7.1292
G26	−8.5873	−8.5992	−8.6059	−8.6114
G27	−5.1256	−5.1196	−5.1166	−5.1145
G28	3.2658	3.2526	3.2459	3.2399
G29	2.2501	2.2547	2.2610	2.2630
G30	−5.9075	−5.9087	−5.9144	−5.9158
G31	5.0344	5.0264	5.0264	5.0244
G32	−4.4046	−4.4053	−4.3915	−4.3886

presents the mean values of GPS satellite DCB estimates after adopting different modeling spacings of 2H, 4H, 6H, and 12H using the GRCC (a) and GRCD (b) observations. The GPS DCB values for G04 were not estimated owing to a lack of observations. The mean GPS DCB estimates range between −10 and 10 ns and are stable. There is no significant difference in mean GPS DCBs with different modeling spacings. 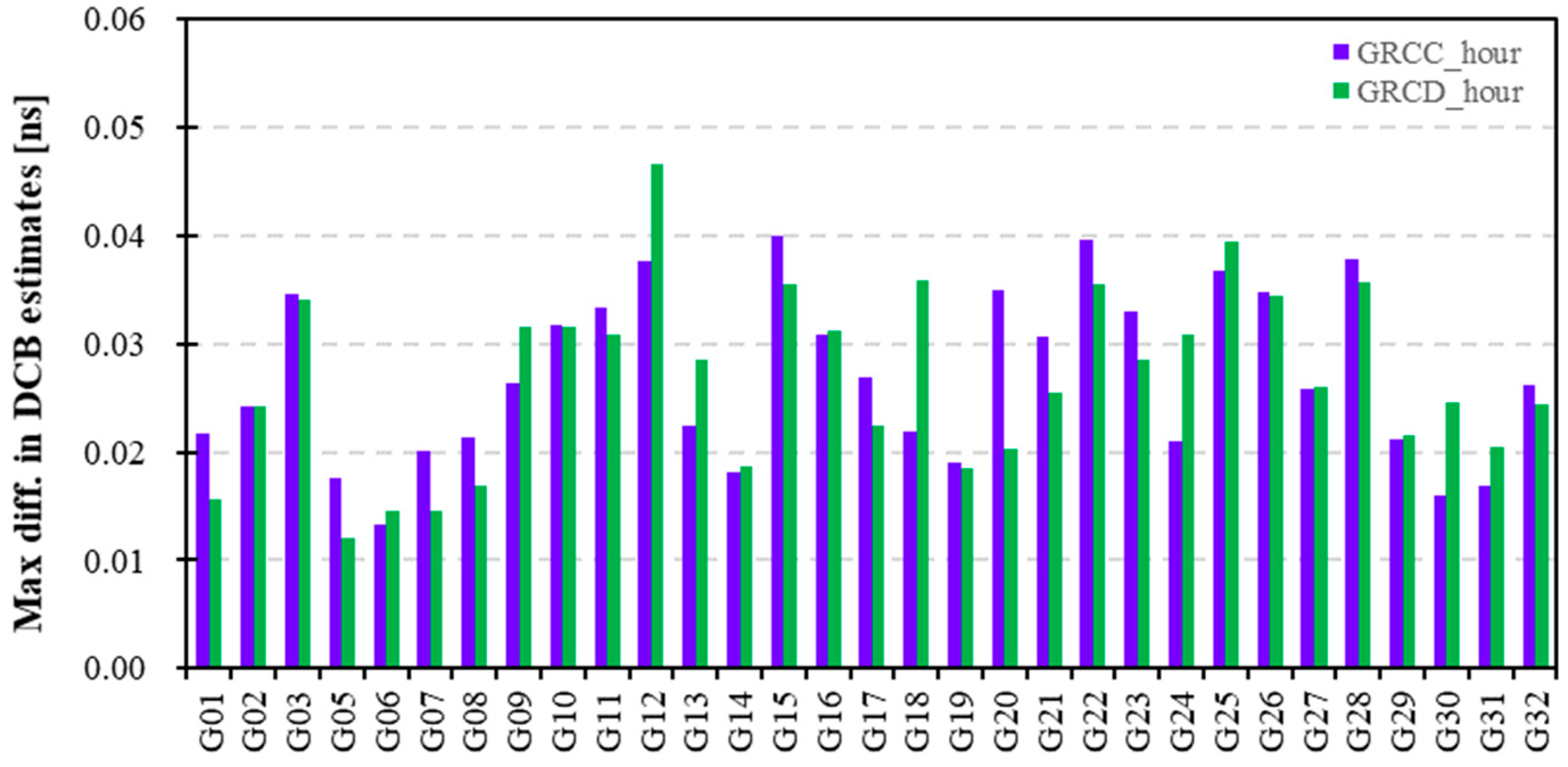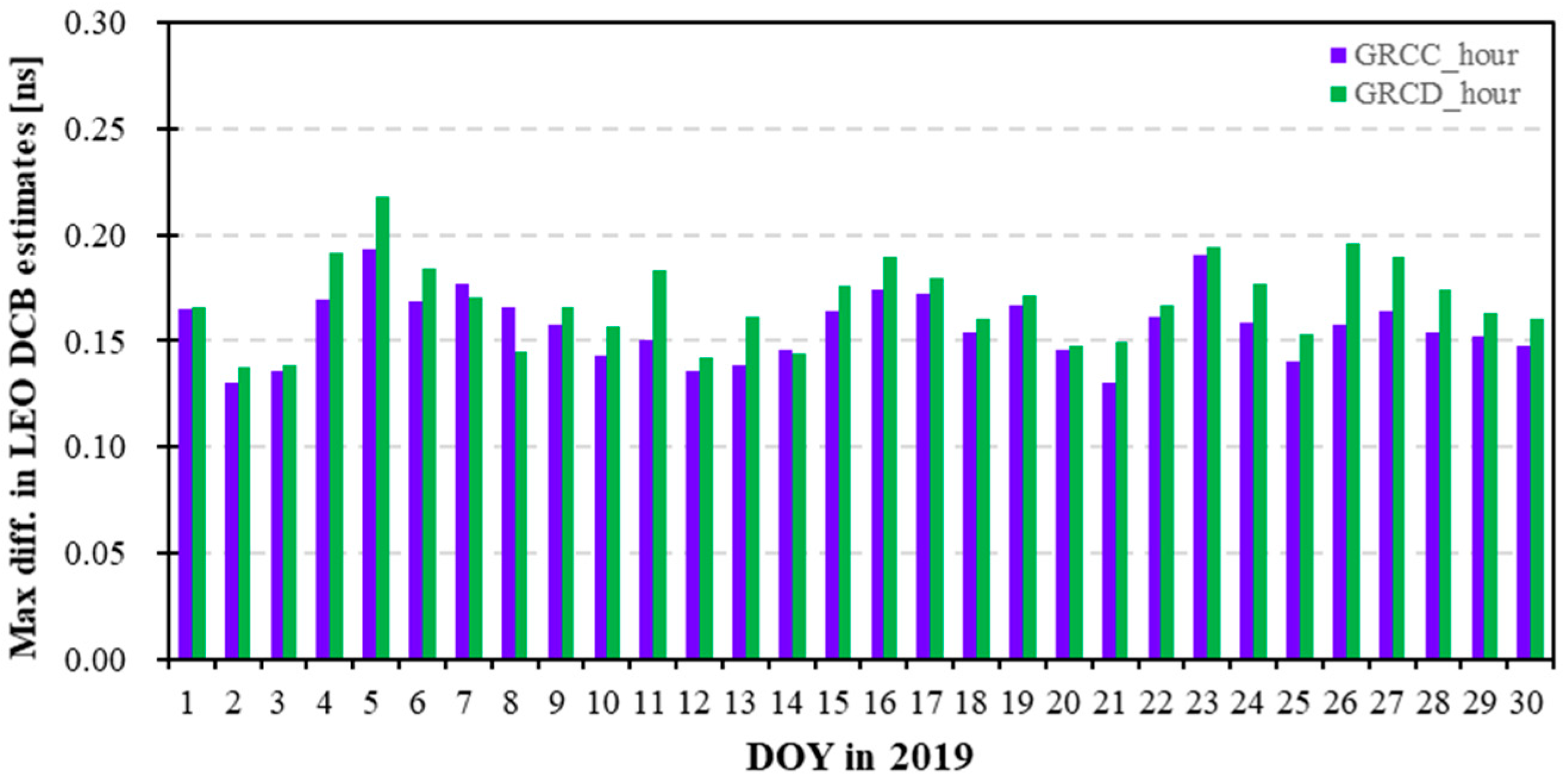Considering the limitation of mean statistics in Table 1 in terms of reflecting all DCB values, Figure 1 displays the maximum differences in the GPS satellite DCB estimates after adopting different modeling spacings using GRCC and GRCD observations during the experiment period. The differences in the GPS DCB estimates using different modeling spacings are in the range of 0.05 ns. Specifically, in Figure 1, the difference in G15 DCB estimates adopting different modeling spacings is the maximum value, 0.04 ns, when using GRCC data, whereas for GRCD data, the difference in G12 DCB is the largest, approximately 0.05 ns. Therefore, corresponding to Figure 1, the maximum, minimum, and differences in G15 and G12 DCB estimated based on different modeling spacings using GRCC and GRCD observations, respectively, are presented in

Table 2. Maximum, minimum, and differences in G15 and G12 DCB estimates based on different spacings using GRCC (a) and GRCD (b) observations [ns].

(a) GRCC-G15
DOY	Max	Min	Diff.
1	2.6576	2.6321	0.0255
2	2.6544	2.6300	0.0244
3	2.7129	2.6796	0.0333
4	2.6271	2.5960	0.0311
5	2.6815	2.6415	0.0400
6	2.6331	2.5947	0.0384
7	2.7436	2.7234	0.0202
8	2.6172	2.5813	0.0359
9	2.6517	2.6226	0.0291
10	2.6460	2.6130	0.0330
11	2.5914	2.5675	0.0239
12	2.7338	2.7149	0.0189
13	2.6573	2.6311	0.0262
14	2.6595	2.6303	0.0292
15	2.6239	2.5947	0.0292
16	2.7730	2.7469	0.0261
17	2.5507	2.5257	0.0250
18	2.7313	2.7119	0.0194
19	2.6108	2.5838	0.0270
20	2.5493	2.5269	0.0224
21	2.6050	2.5789	0.0261
22	2.5817	2.5608	0.0209
23	2.5638	2.5429	0.0209
24	2.6731	2.6508	0.0223
25	2.6441	2.6113	0.0328
26	2.7022	2.6726	0.0296
27	2.7357	2.7116	0.0241
28	2.7491	2.7288	0.0203
29	2.6788	2.6558	0.0230
30	2.7242	2.7011	0.0231
(b) GRCD-G12
DOY	Max	Min	Diff.
1	4.1929	4.1704	0.0225
2	4.3165	4.2822	0.0343
3	4.1862	4.1428	0.0434
4	4.3340	4.2874	0.0466
5	4.2277	4.1950	0.0327
6	4.2023	4.1731	0.0292
7	4.0969	4.0764	0.0205
8	4.1886	4.1454	0.0432
9	4.2370	4.1940	0.0430
10	4.2623	4.2294	0.0329
11	4.2704	4.2374	0.0330
12	4.2513	4.2283	0.0230
13	4.3040	4.2759	0.0281
14	4.1481	4.1161	0.0320
15	4.2978	4.2638	0.0340
16	4.3196	4.2997	0.0199
17	4.2499	4.2316	0.0183
18	4.2684	4.2436	0.0248
19	4.2586	4.2221	0.0365
20	4.2246	4.1879	0.0367
21	4.3187	4.2914	0.0273
22	4.2345	4.2127	0.0218
23	4.2593	4.2333	0.0260
24	4.2821	4.2526	0.0295
25	4.2135	4.1811	0.0324
26	4.2052	4.1790	0.0262
27	4.2133	4.1931	0.0202
28	4.2085	4.1896	0.0189
29	4.1718	4.1506	0.0212
30	4.2738	4.2484	0.0254

. In Table 2a using GRCC data, the difference in the G15 DCB estimates based on different modeling spacings on DOY 5 is the largest, and the maximum, minimum, and difference are 2.6815, 2.6415, and 0.0400 ns, respectively. In Table 2b using GRCD data, the difference in G12 DCB estimated on DOY 4 is the largest, and the maximum, minimum, and difference are 4.3340, 4.2874, and 0.0466 ns, respectively. Therefore, there is a difference in the GPS DCB estimated using different modeling spacings, within 0.05 ns. The different modeling spacings affect the GPS DCB estimates.

3.1.2. Precision Evaluation of GPS Satellite DCB Estimates

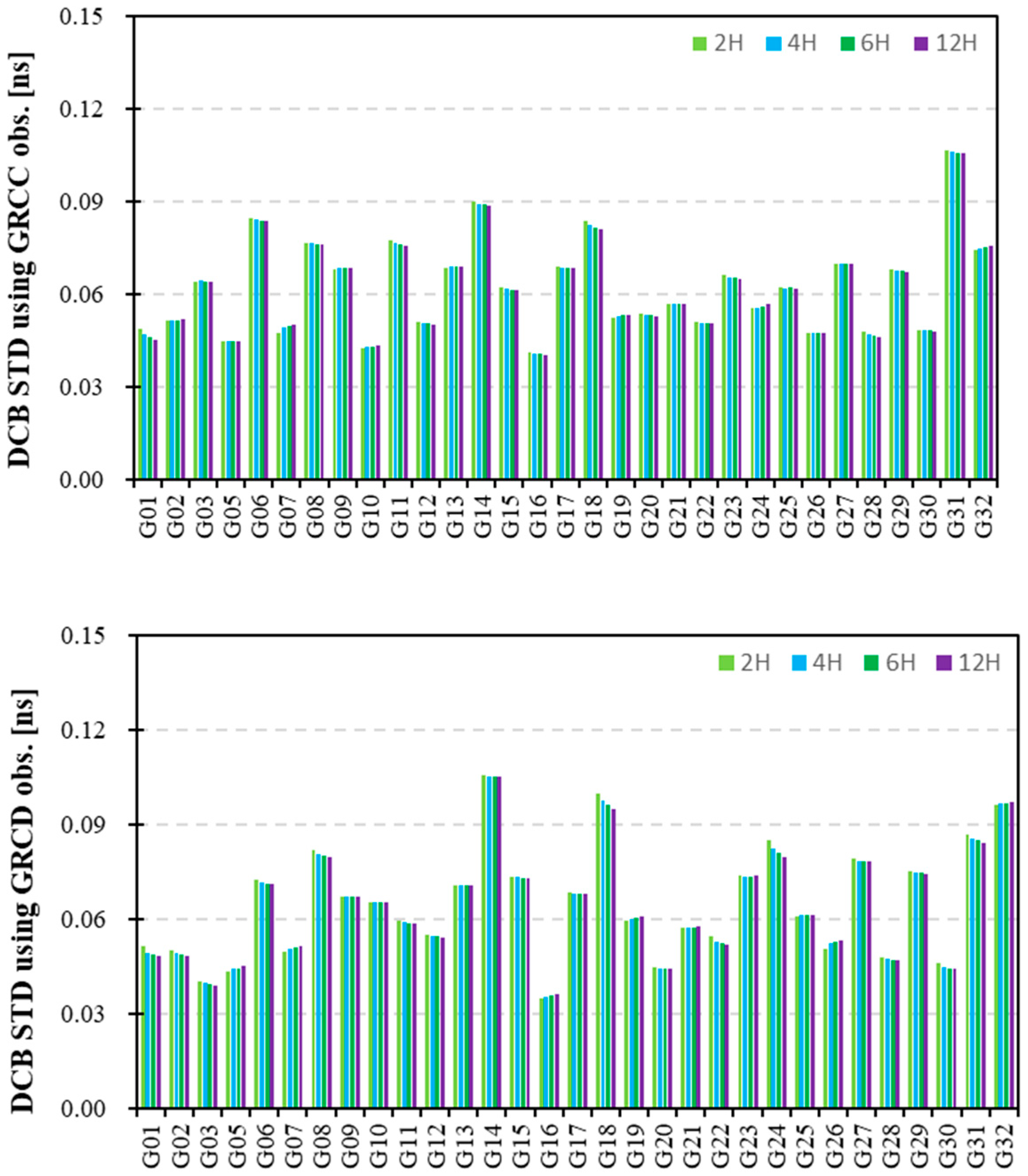
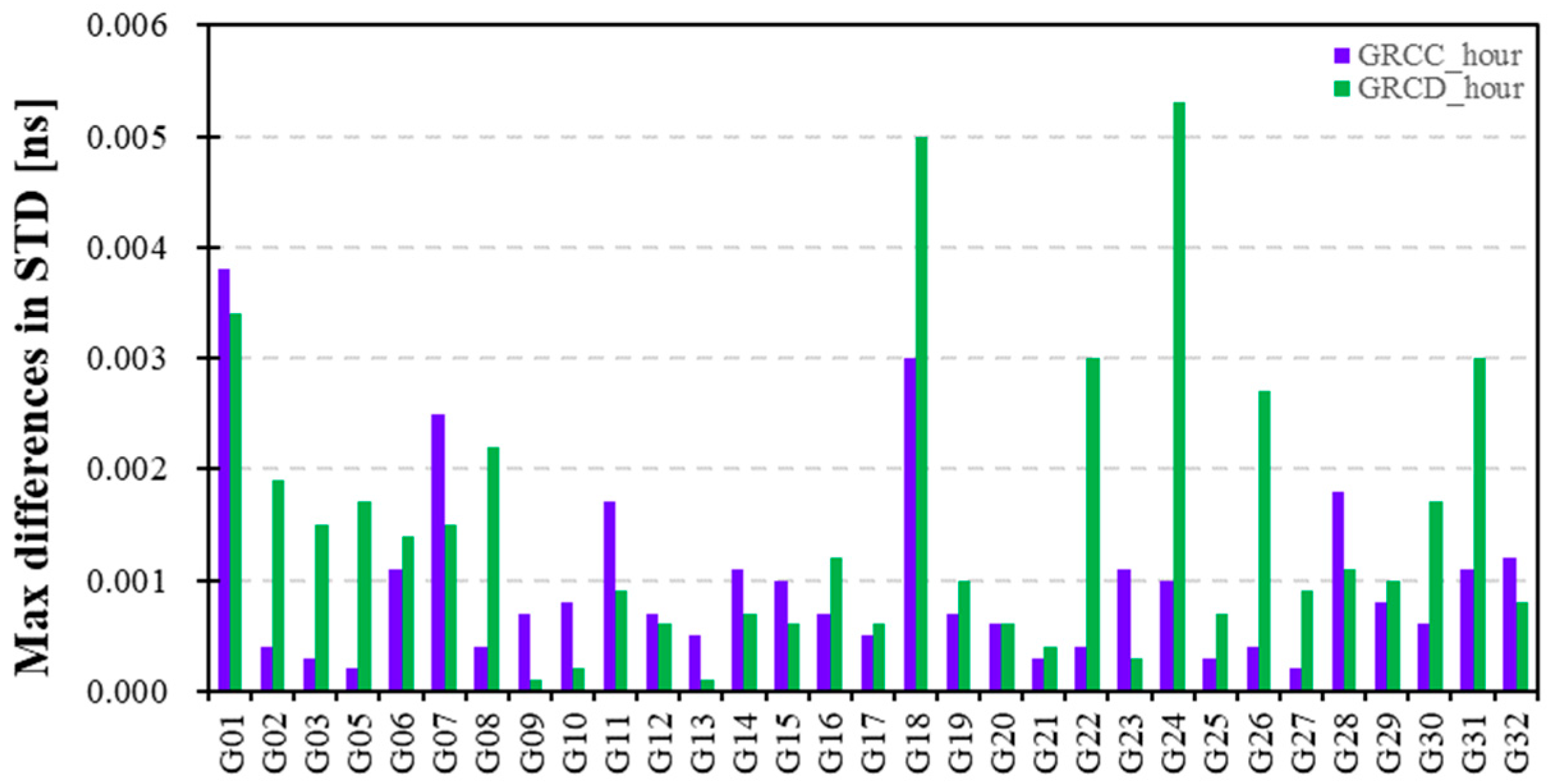
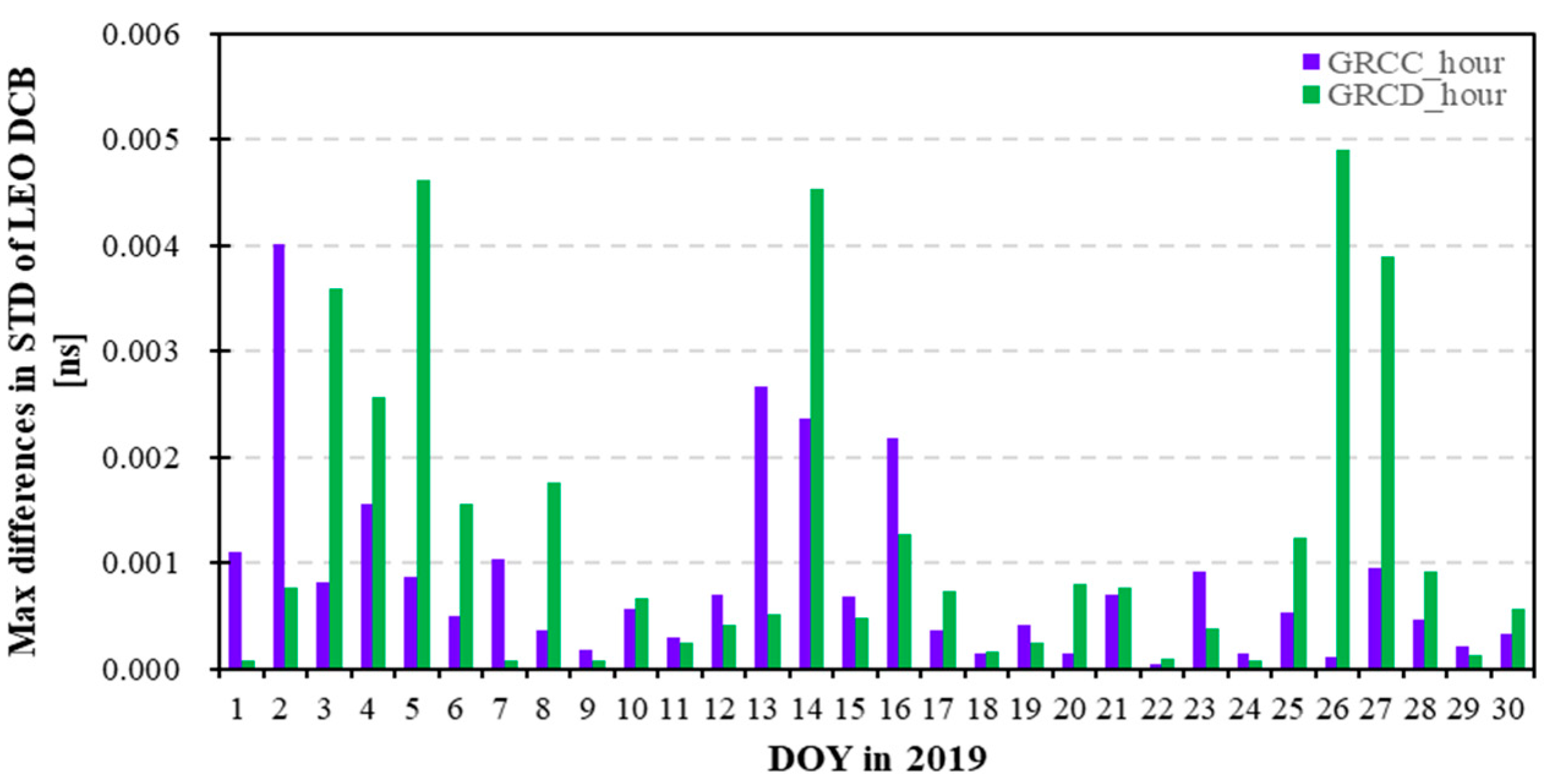
Figure 2 presents the monthly stabilities (STD) of the GPS satellite DCB estimates adopting different modeling spacings of 2H, 4H, 6H, and 12H using GRCC (top) and GRCD (bottom) observation data. The STDs of the GPS DCB estimates using GRCC and GRCD data are in the range of 0.11 ns with high stability. Meanwhile, the maximum differences in the STD of the GPS DCB estimates adopting different modeling spacings are shown in Figure 3. The maximum differences in the STD of the GPS DCB using different modeling spacings are within 0.006 ns. The STD values of the GPS DCB estimates adopting different modeling spacings exhibit no significant differences.

Table 3. Mean STD of GPS DCBs adopting different modeling spacings [ns].

LEO	Var.	STD	LEO	Var.	STD
GRCC	2H	0.0624	GRCD	2H	0.0648
	4H	0.0621		4H	0.0643
	6H	0.0620		6H	0.0641
	12H	0.0619		12H	0.0639

presents the mean STDs of the GPS DCB estimates adopting the different modeling spacings. Statistically, the mean STD values of GPS DCBs with modeling spacings of 2H, 4H, 6H, and 12H using GRCC and GRCD data are 0.0624, 0.0621, 0.0620, and 0.0619 ns and 0.0648, 0.0643, 0.0641, and 0.0639 ns, respectively. The GPS DCB estimates with modeling spacings of 12H have the optimal mean STD results. The GPS DCB estimates using twin LEO satellite data attain similar and high stability.

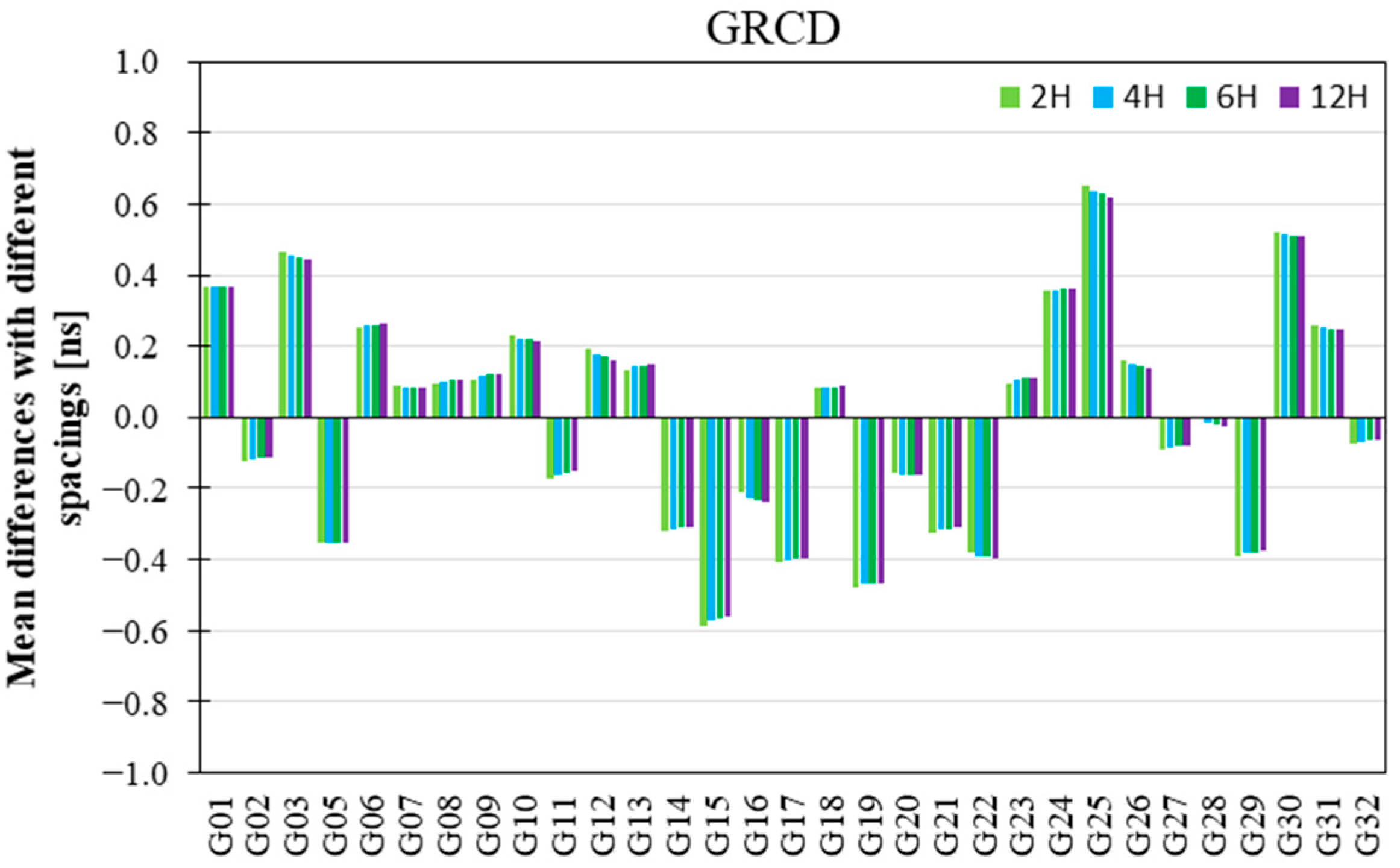
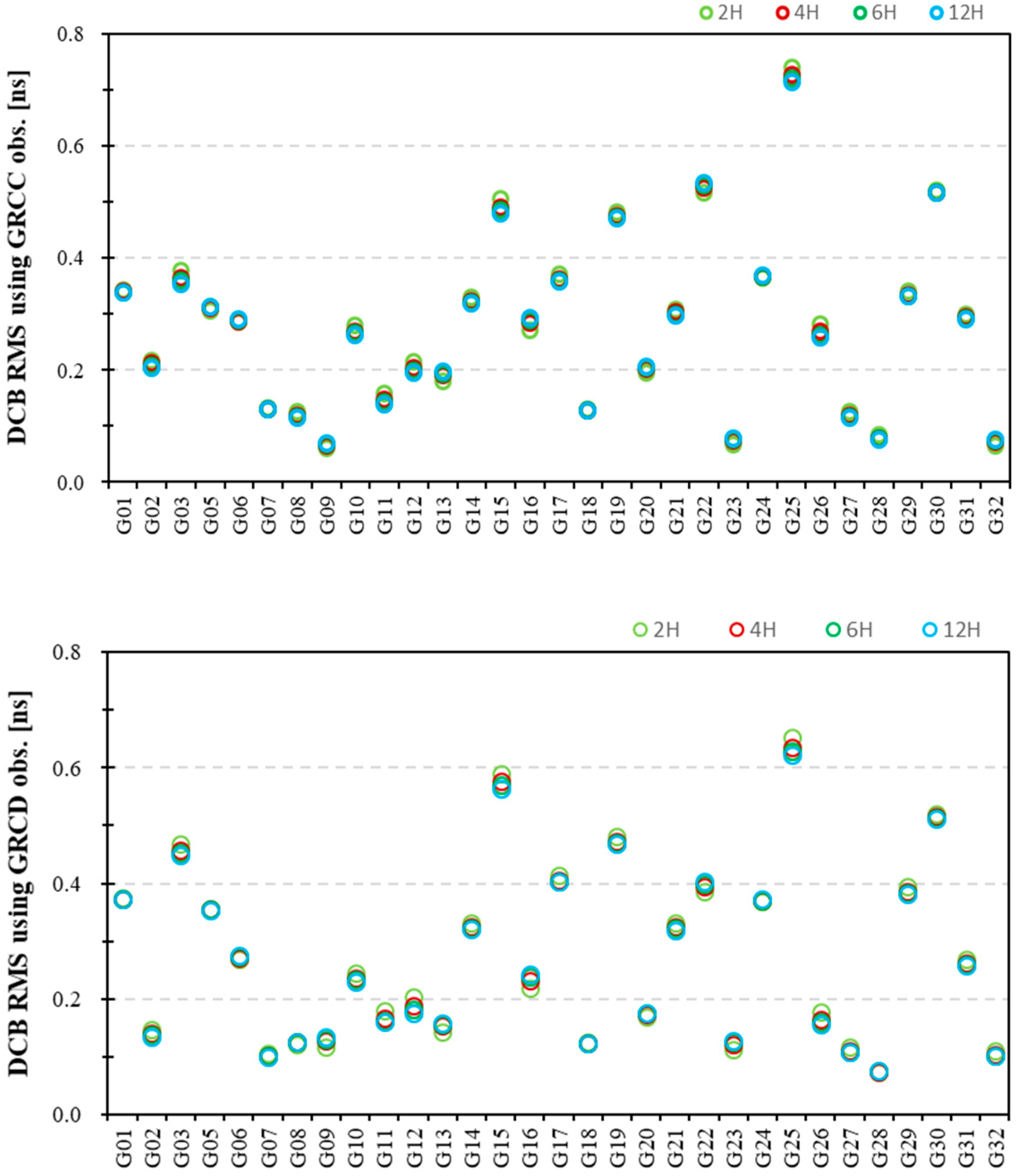
Figure 4 depicts the mean differences for GPS DCB estimates with different modeling spacings relative to CODE products. The mean differences in Figure 4 vary between −0.6 and 0.8 ns, which indicates that the GPS DCBs estimated by LEO satellite and ground station data have good consistency. Figure 5 showcases the RMS of the differences between the GPS DCB estimates adopting different modeling spacings (2H, 4H, 6H, and 12H) and the CODE DCB products. 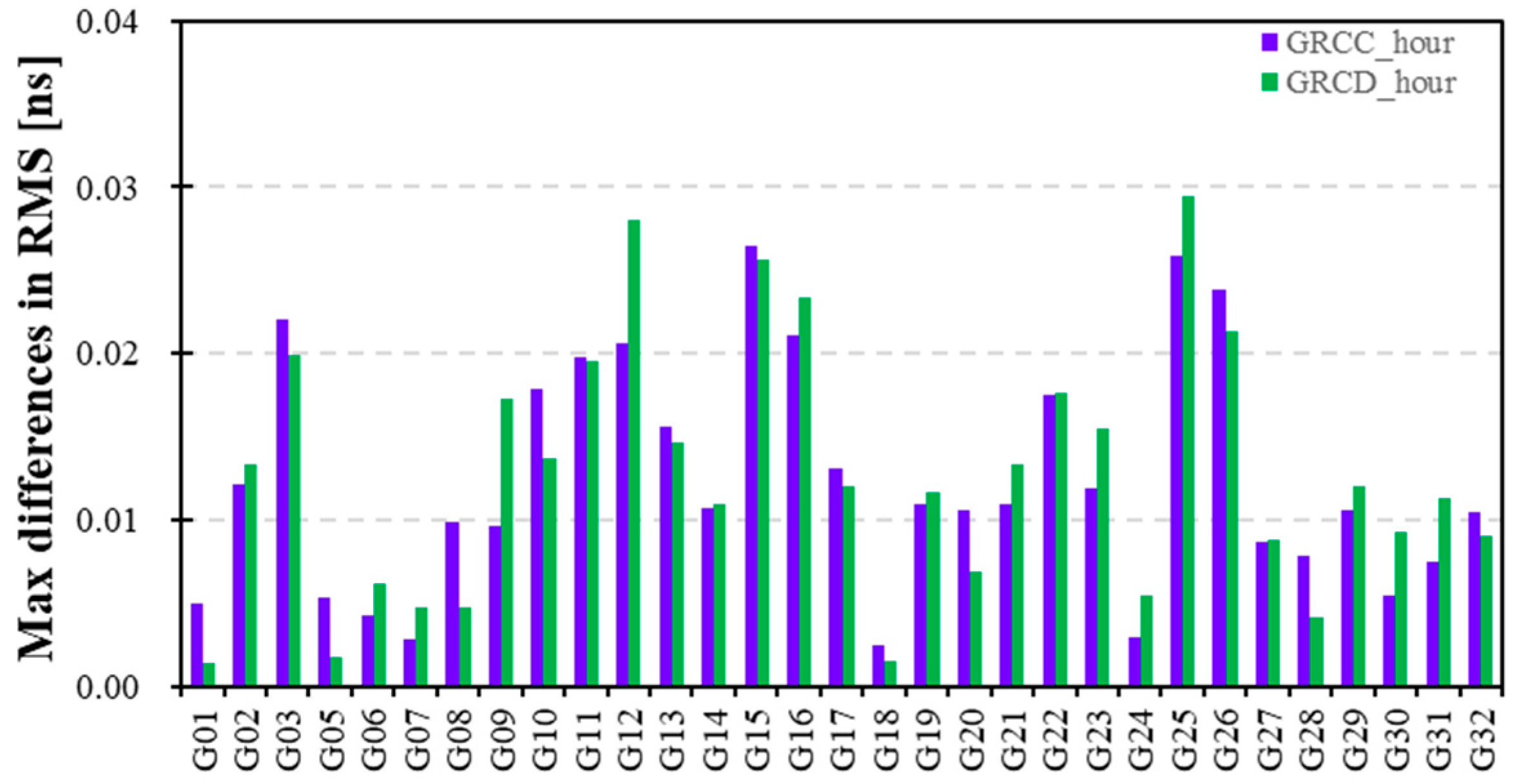To visually demonstrate the differences in RMS of GPS DCBs with different modeling spacings, Figure 6 displays the maximum differences in RMS of GPS DCB estimates using different modeling spacings. The maximum differences in RMS of GPS DCBs using different modeling spacings are in the range of 0.03 ns. The different modeling spacings affect the RMS of the GPS DCB estimates. The corresponding mean RMS values are listed in

Table 4. Mean RMS statistics for GPS DCBs using different modeling spacings [ns].

LEO	Var.	RMS	LEO	Var.	RMS
GRCC	2H	0.2801	GRCD	2H	0.2763
	4H	0.2769		4H	0.2732
	6H	0.2759		6H	0.2722
	12H	0.2748		12H	0.2711

. The RMS results of the GPS DCBs with different modeling spacings relative to the CODE products are in the range of 0.8 ns. The mean RMSs of the GPS DCBs are in the range of 0.3 ns, which indicates that the GPS DCBs estimated by LEO satellite and ground station data have good consistency. Statistically, the mean RMS results in Table 4 indicate that the GPS DCBs with a modeling spacing of 12H had slightly smaller RMS values than the others. Additionally, the GPS DCB estimates using twin satellite data have similar precisions, and the RMS results using GRCC observations are slightly poorer than those obtained using GRCD data.

3.1.3. LEO Receiver DCB Estimates and Stability Evaluation

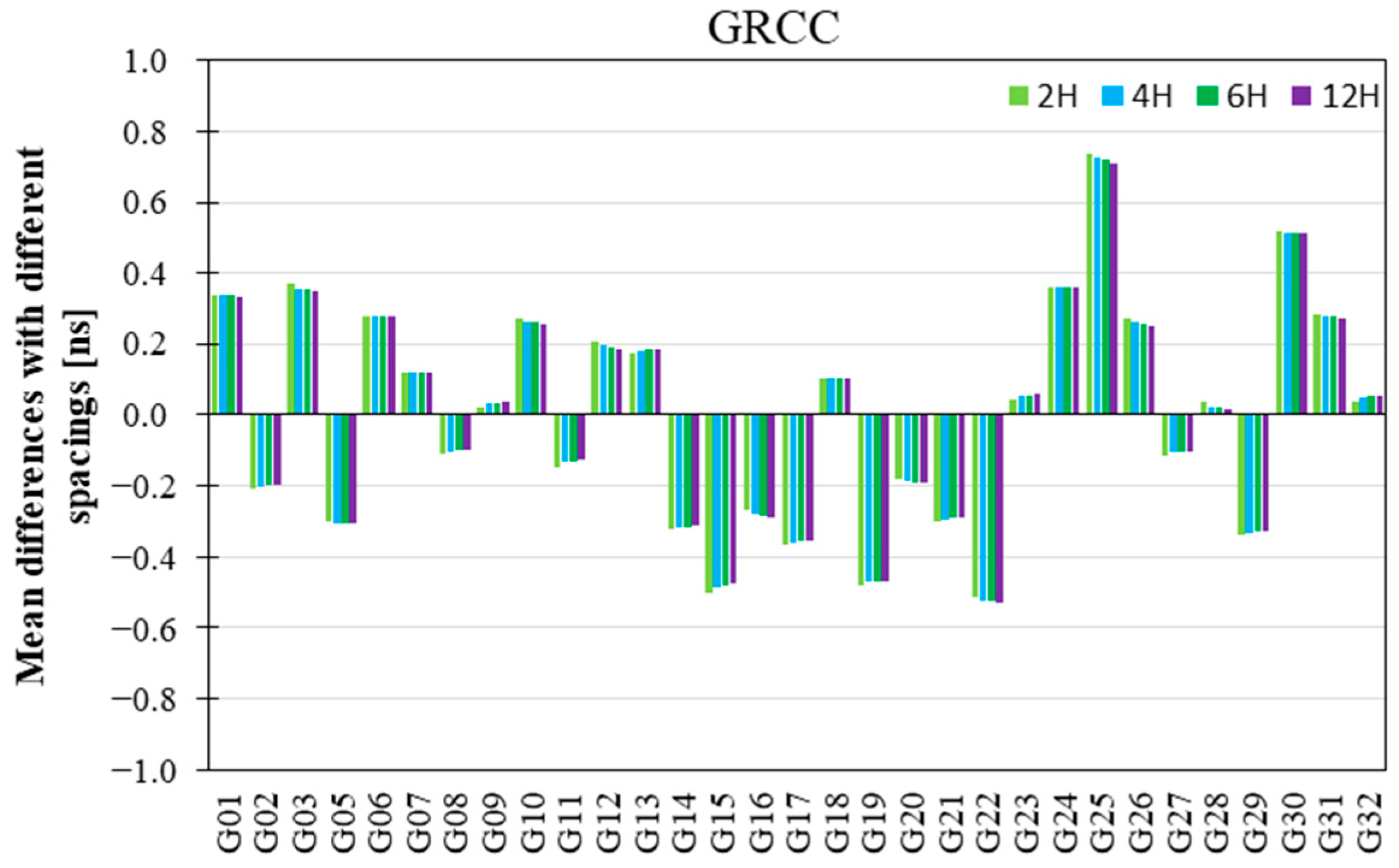
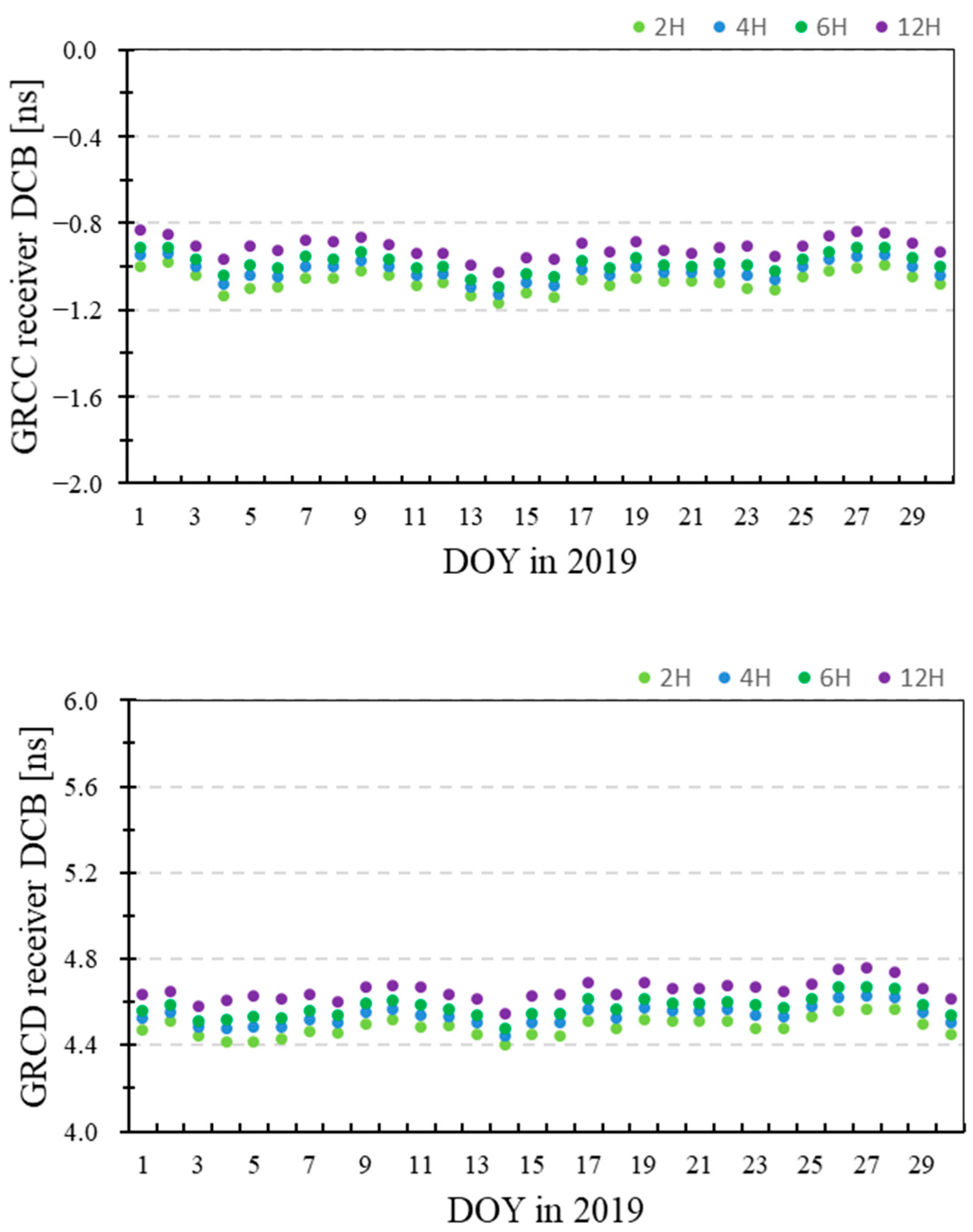
Figure 7 presents the time series of the receiver DCB estimates with modeling spacings of 2H, 4H, 6H, and 12H for the twin GRACE-FO satellites. The GRCC receiver DCB estimates are located at approximately −1.0 ns, whereas the GRCD DCB estimates fluctuate at approximately 4.6 ns, and their receiver DCB estimates are stable. In Figure 7, the GRCC and GRCD receiver DCB estimates are sorted in descending order as follows: receiver DCBs with modeling spacings of 12H, 6H, 4H, and 2H, where the receiver DCBs decrease as the modeling spacing decreases.

In order to visually demonstrate the differences in receiver DCBs with different modeling spacings, Figure 8 exhibits the maximum differences in the LEO receiver DCB estimates using different modeling spacings. Figure 9 shows the maximum differences in the STD of the receiver DCB using different modeling spacings. The maximum difference in receiver DCBs using different modeling spacings is 0.22 ns, whereas the maximum differences in STD of receiver DCBs are within 0.005 ns. This indicates that different modeling spacings have a significant impact on receiver DCB estimates.

The mean values and STD results for the LEO receiver DCB estimates with different modeling spacings are listed in

Table 5. Mean values and STD statistics for receiver DCBs with different modeling spacings [ns].

LEO	Var.	Mean	STD
GRCC	2H	−1.0684	0.0465
	4H	−1.0202	0.0459
	6H	−0.9833	0.0456
	12H	−0.9115	0.0458
GRCD	2H	4.4847	0.0439
	4H	4.5365	0.0434
	6H	4.5761	0.0450
	12H	4.6531	0.0468

. Statistically, the maximum receiver DCB values for both the GRCC and GRCD are the DCBs with modeling spacings of 12H, whereas the minimum receiver DCBs are those with modeling spacings of 2H. The differences in the mean receiver DCBs with different modeling spacings for the GRCC and GRCD are in the ranges of 0.1569 and 0.1684 ns, respectively. The GRCC and GRCD receiver DCBs achieve optimal STD results when modeling spacings of 6H and 4H are applied. The receiver DCBs of the twin GRACE-FO satellites are different; however, their DCB estimates have similar STD results.

In summary, the GPS DCB estimates using a modeling spacing of 12H have higher precision than the others, whereas LEO receiver DCBs applying the modeling spacings of 4H or 6H obtain optimal STD.

3.2. Different Modeling Degrees and Orders

This section investigates the impact of the D&O of spherical harmonic modeling on DCB estimates and precision, thereby obtaining suitable modeling D&O parameters. The 6, 8, and 10D&Os of spherical harmonic modeling were introduced into topside ionosphere modeling and DCB estimation. Subsequently, the GPS and LEO DCB estimates were analyzed and evaluated. The modeling spacing was fixed at 4H to improve the temporal resolution.

3.2.1. GPS Satellite DCB Estimates

The mean values of GPS DCB estimates adopting different modeling parameters of 6, 8, and 10D&Os using the GRCC (a) and GRCD (b) observations are listed in

Table 6. Mean GPS DCB estimates based on different modeling D&Os using GRCC (a) and GRCD (b) data [ns].

(a) GRCC
GPS	6D&O	8D&O	10D&O
G01	−7.4142	−7.4174	−7.4178
G02	9.1261	9.1298	9.1342
G03	−5.0144	−5.0161	−5.0181
G05	2.9686	2.9782	2.9862
G06	−6.6785	−6.6762	−6.6719
G07	3.3560	3.3536	3.3555
G08	−7.5223	−7.5226	−7.5236
G09	−4.9485	−4.9469	−4.9473
G10	−5.0425	−5.0449	−5.0479
G11	3.7338	3.7332	3.7316
G12	4.1486	4.1480	4.1491
G13	3.4254	3.4277	3.4261
G14	1.9223	1.9205	1.9152
G15	2.6427	2.6467	2.6493
G16	2.7812	2.7844	2.7874
G17	2.9411	2.9406	2.9395
G18	−0.2882	−0.2915	−0.2940
G19	5.6420	5.6405	5.6387
G20	1.4615	1.4640	1.4668
G21	2.2761	2.2791	2.2807
G22	7.2670	7.2648	7.2637
G23	9.1425	9.1434	9.1420
G24	−5.5488	−5.5542	−5.5550
G25	−7.1203	−7.1219	−7.1223
G26	−8.5842	−8.5834	−8.5830
G27	−5.2361	−5.2366	−5.2396
G28	3.1981	3.1953	3.1957
G29	2.2158	2.2135	2.2079
G30	−6.0024	−6.0065	−6.0056
G31	4.9613	4.9588	4.9594
G32	−4.3729	−4.3735	−4.3770
(b) GRCD
GPS	6D&O	8D&O	10D&O
G01	−7.2891	−7.2886	−7.2899
G02	9.3046	9.3094	9.3138
G03	−4.8226	−4.8174	−4.8238
G05	3.0169	3.0263	3.0372
G06	−6.6027	−6.6008	−6.5959
G07	3.4177	3.4194	3.4179
G08	−7.2217	−7.2240	−7.2245
G09	−4.7683	−4.7650	−4.7695
G10	−4.9894	−4.9938	−4.9927
G11	3.8018	3.8041	3.7994
G12	4.2273	4.2284	4.2246
G13	3.4802	3.4804	3.4802
G14	2.0213	2.0114	2.0155
G15	2.6549	2.6580	2.6601
G16	2.9295	2.9338	2.9345
G17	2.9945	2.9941	2.9910
G18	−0.2099	−0.2115	−0.2140
G19	5.7406	5.7393	5.7359
G20	1.5854	1.5863	1.5916
G21	2.3490	2.3498	2.3540
G22	7.4943	7.4949	7.4922
G23	9.2922	9.2948	9.2901
G24	−5.4554	−5.4579	−5.4609
G25	−7.1148	−7.1194	−7.1166
G26	−8.6021	−8.5992	−8.6001
G27	−5.1179	−5.1196	−5.1212
G28	3.2543	3.2526	3.2514
G29	2.2605	2.2547	2.2539
G30	−5.9095	−5.9087	−5.9124
G31	5.0311	5.0264	5.0287
G32	−4.3943	−4.4053	−4.3967

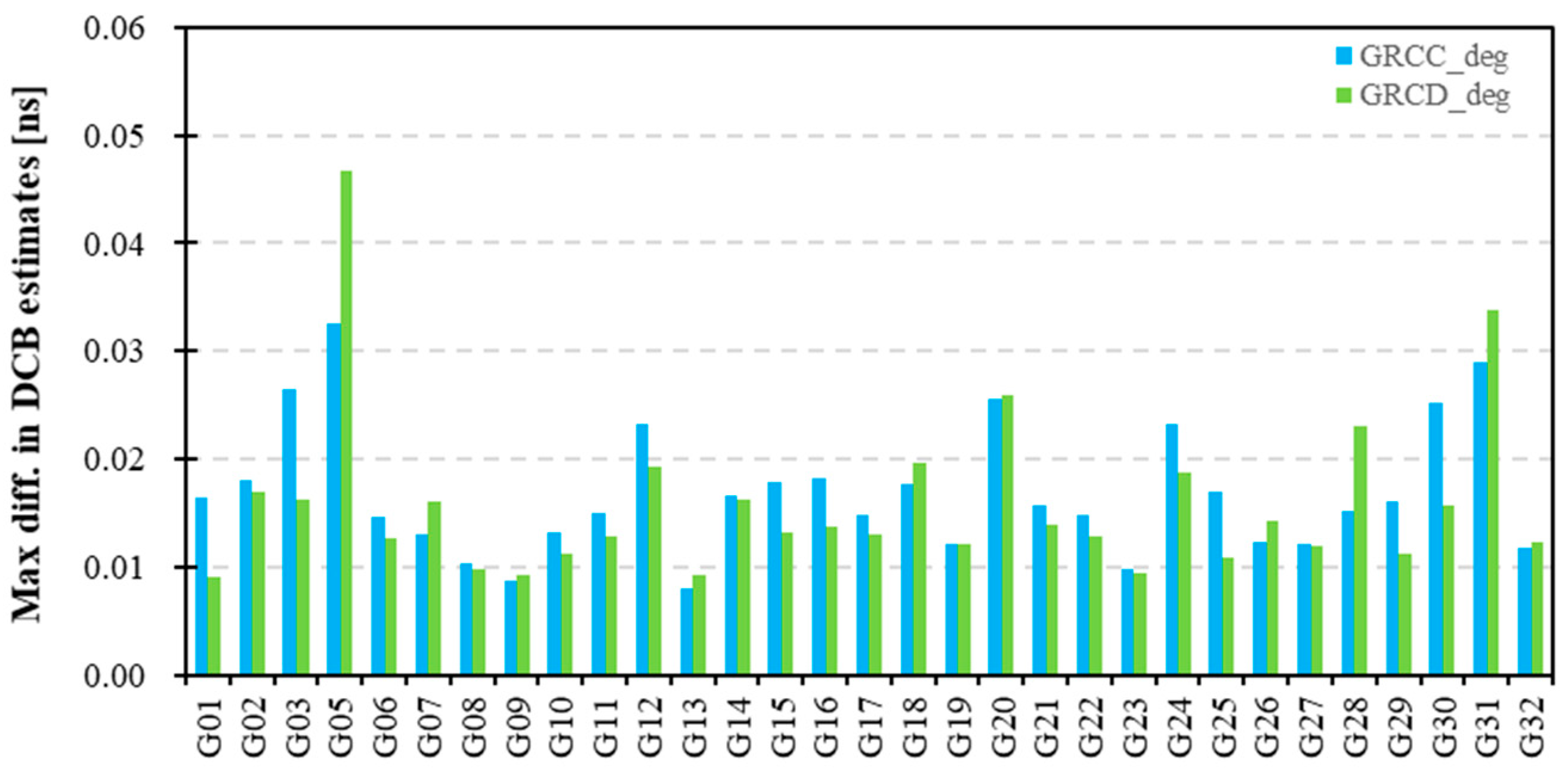
. The GPS DCB values for G04 were not estimated owing to a lack of observations. The mean GPS DCB estimates range between −10 and 10 ns and are stable. There is no significant difference in the GPS DCB estimates obtained using different modeling D&Os. Considering the limitation of mean statistics in Table 6, Figure 10 exhibits the maximum differences in GPS DCB estimates adopting different modeling D&Os using GRCC and GRCD data. The differences in the GPS DCB estimates using different modeling D&Os are in the range of 0.05 ns. It indicates that the effects of the modeling spacing and D&O on GPS DCB estimates are at the same level. Specifically, the differences in G05 DCB estimates adopting different modeling D&Os using GRCC and GRCD data are both the largest, within 0.04 and 0.05 ns, respectively. The maximum, minimum, and differences in G05 DCB estimated with different modeling D&Os using GRCC and GRCD observations are presented in

Table 7. Maximum, minimum, and differences in G05 DCB estimates with different D&Os using GRCC (a) and GRCD (b) data [ns].

(a) GRCC-G05
Day	Max	Min	Diff.
1	2.9753	2.9694	0.0059
2	2.9370	2.9083	0.0287
3	3.0535	3.0279	0.0256
4	3.0784	3.0584	0.0200
5	3.0444	3.0316	0.0128
6	3.0264	3.0202	0.0062
7	2.9724	2.9534	0.0190
8	2.9780	2.9507	0.0273
9	2.9906	2.9638	0.0268
10	2.9440	2.9432	0.0008
11	2.9463	2.9455	0.0008
12	3.0405	3.0269	0.0136
13	3.0099	2.9776	0.0323
14	3.0311	2.9985	0.0326
15	2.9426	2.9201	0.0225
16	3.0109	3.0031	0.0078
17	2.9305	2.9231	0.0074
18	2.9671	2.9454	0.0217
19	2.9606	2.9328	0.0278
20	2.9821	2.9593	0.0228
21	2.8937	2.8820	0.0117
22	3.0197	3.0148	0.0049
23	2.9796	2.9683	0.0113
24	3.0198	2.9933	0.0265
25	2.9709	2.9403	0.0306
26	3.0022	2.9846	0.0176
27	2.9335	2.9278	0.0057
28	2.9700	2.9640	0.0060
29	2.9186	2.8980	0.0206
30	3.0551	3.0252	0.0299
(b) GRCD-G05
Day	Max	Min	Diff.
1	2.9849	2.9719	0.0130
2	2.9826	2.9522	0.0304
3	3.0770	3.0400	0.0370
4	3.0551	3.0259	0.0292
5	3.0523	3.0351	0.0172
6	3.0177	3.0086	0.0091
7	3.0611	3.0390	0.0221
8	3.0289	3.0009	0.0280
9	3.0317	2.9964	0.0353
10	2.9661	2.9488	0.0173
11	3.0090	3.0080	0.0010
12	3.1287	3.1131	0.0156
13	3.0902	3.0569	0.0333
14	3.0515	3.0048	0.0467
15	2.9874	2.9643	0.0231
16	3.0414	3.0352	0.0062
17	2.9714	2.9672	0.0042
18	3.0320	3.0124	0.0196
19	3.0503	3.0195	0.0308
20	3.0253	3.0044	0.0209
21	2.9572	2.9451	0.0121
22	3.0951	3.0901	0.0050
23	3.0627	3.0507	0.0120
24	3.1039	3.0770	0.0269
25	3.0341	3.0054	0.0287
26	3.0661	3.0466	0.0195
27	2.9857	2.9789	0.0068
28	3.0339	3.0263	0.0076
29	3.0092	2.9864	0.0228
30	3.1241	3.0964	0.0277

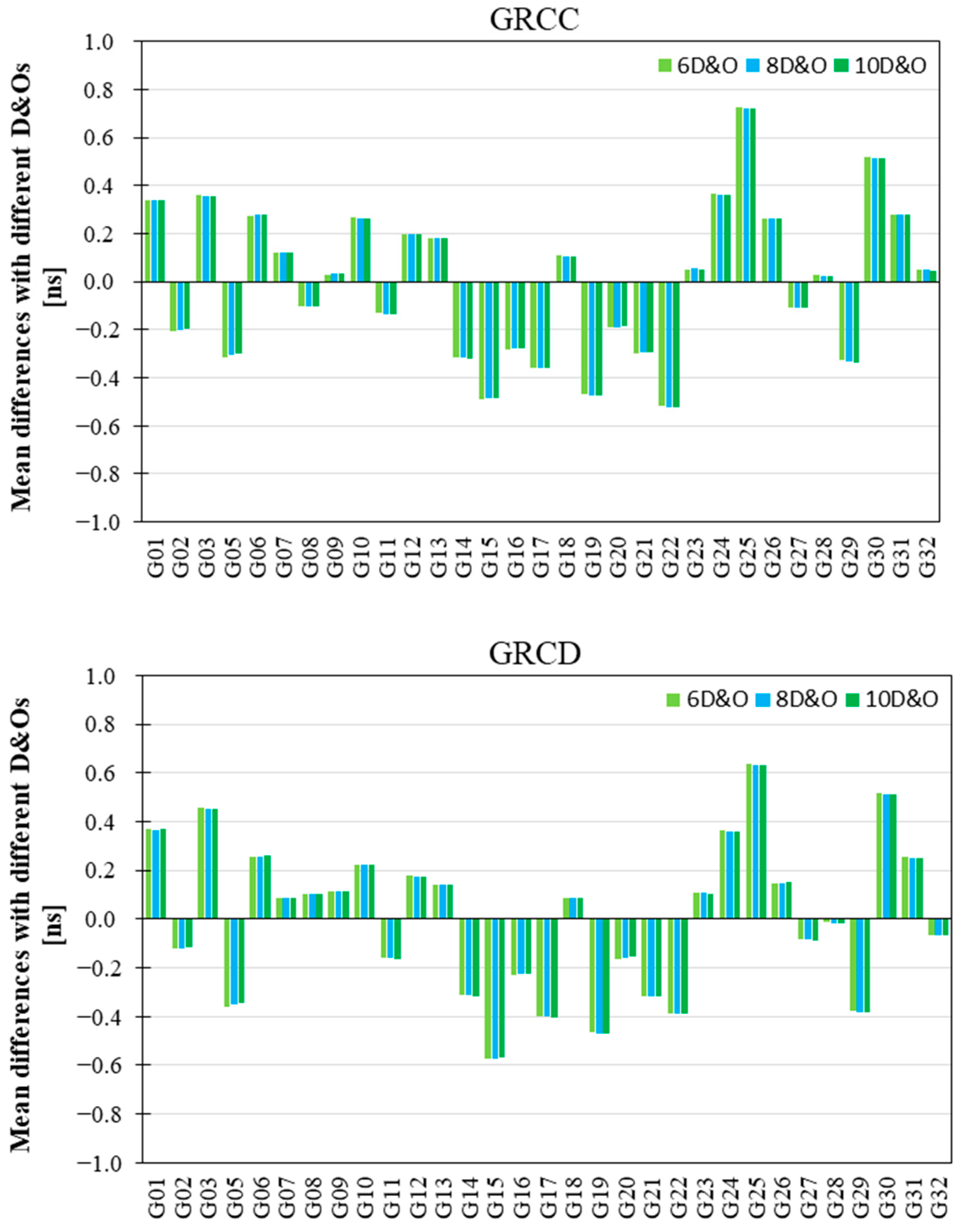
. In Table 7a, using GRCC data, the difference in G05 DCB estimates between different modeling D&Os on DOY 13 is the largest, and the maximum, minimum, and difference are 3.0099, 2.9776, and 0.0323 ns, respectively. In Table 7b, using GRCD data, the difference in G12 DCB estimated on DOY 4 is the largest, and the maximum, minimum, and difference are 3.0515, 3.0048, and 0.0467 ns, respectively. Therefore, there is a certain difference in the GPS DCB estimates using different modeling D&Os, all within 0.05 ns. The different modeling D&Os have certain effects on the GPS DCB estimates.

3.2.2. Precision Evaluation of GPS DCB Estimates

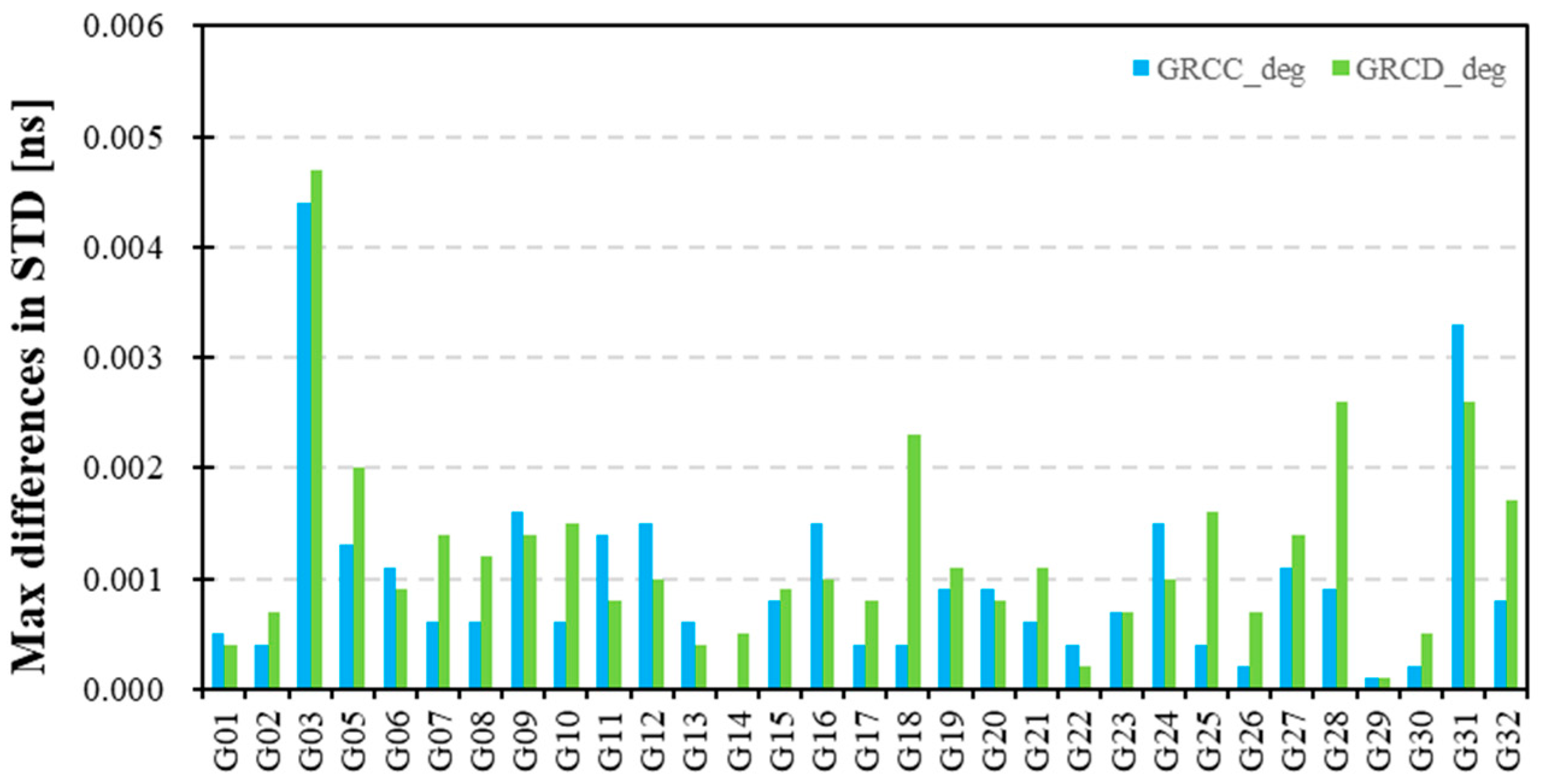
Figure 11 showcases the STD of GPS DCB estimates adopting different modeling D&Os of 6, 8, and 10 using GRCC and GRCD data. The STDs of GPS DCB estimates based on GRCC and GRCD data are within 0.11 ns. Additionally, Figure 12 displays the maximum differences in the STD of the GPS DCB estimates by applying different modeling D&Os. The maximum differences are within 0.005 ns. The STDs of the GPS DCB estimates adopting different modeling D&Os show no marked differences.

Table 8. Mean STD of GPS DCBs using different modeling D&Os [ns].

LEO	Var.	STD	LEO	Var.	STD
GRCC	6D&O	0.0620	GRCD	6D&O	0.0643
	8D&O	0.0621		8D&O	0.0643
	10D&O	0.0623		10D&O	0.0644

presents the mean STDs of GPS satellite DCB estimates by applying different modeling D&Os. Statistically, the mean STD values of GPS DCBs with modeling D&Os of 6, 8, and 10 using GRCC and GRCD data are 0.0620, 0.0621, and 0.0623 ns and 0.0643, 0.0643, and 0.0644 ns, respectively. The GPS DCB estimates, with modeling D&Os of 6 and 8, attain the optimal STD results.

Figure 13 exhibits the mean differences for GPS DCB estimates with different D&Os relative to CODE products. The mean differences in Figure 13 vary between −0.6 and 0.7 ns, which indicates that the GPS DCBs estimated by LEO satellite and ground station data have good consistency. Figure 14 presents the RMS of the differences between the GPS DCB estimates adopting different modeling D&Os of 6, 8, and 10 and the CODE DCB products. To visually exhibit the differences in the RMS, Figure 15 displays the maximum differences in the RMS of the GPS DCB estimates using different modeling D&Os. The maximum differences reach 0.02 ns. The different modeling D&Os have certain effects on the RMS of the GPS DCB estimates. The corresponding mean RMS values are listed in

Table 9. Mean RMS statistics for GPS DCBs using different modeling D&Os [ns].

LEO	Var.	RMS	LEO	Var.	RMS
GRCC	6D&O	0.2780	GRCD	6D&O	0.2742
	8D&O	0.2769		8D&O	0.2732
	10D&O	0.2768		10D&O	0.2732

. These RMS results are in the range of 0.8 ns. The mean RMS values are in the range of 0.3 ns, which indicates that the GPS DCBs estimated by LEO satellite and ground station data have good consistency. Statistically, Table 9 shows that the GPS DCBs with modeling D&Os of 8 and 10 have slightly higher RMS than the others. The RMS results using the GRCD observations are slightly higher than those obtained using the GRCC data. Considering the STD and RMS results of the GPS DCBs, the GPS DCB estimates with modeling D&Os of 8 attain superior precision.

3.2.3. LEO Receiver DCB Estimates and Stability Evaluation

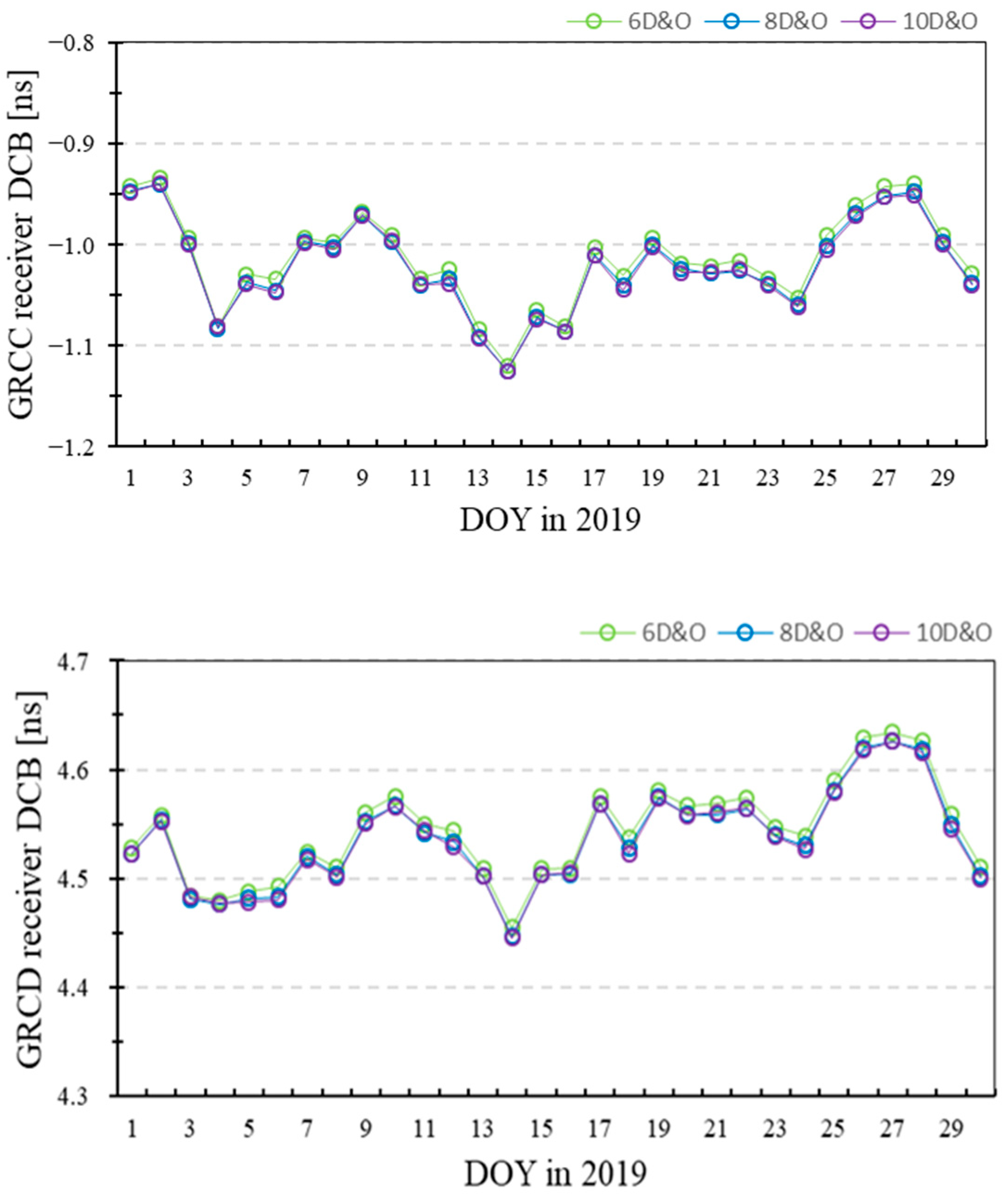
Figure 16 exhibits the time series of the receiver DCB estimates with different modeling D&Os of 6, 8, and 10 for twin GRACE-FO satellites. The GRCC receiver DCB estimates are located at approximately −1.0 ns, whereas the GRCD DCB estimates fluctuate at approximately 4.55 ns. The GRCC and GRCD receiver DCBs with the 6 D&O in spherical harmonic modeling are greater than the others. In order to visually present the differences in receiver DCBs with different modeling D&Os, Figure 17 shows the maximum differences in LEO DCB estimates using different modeling D&Os. 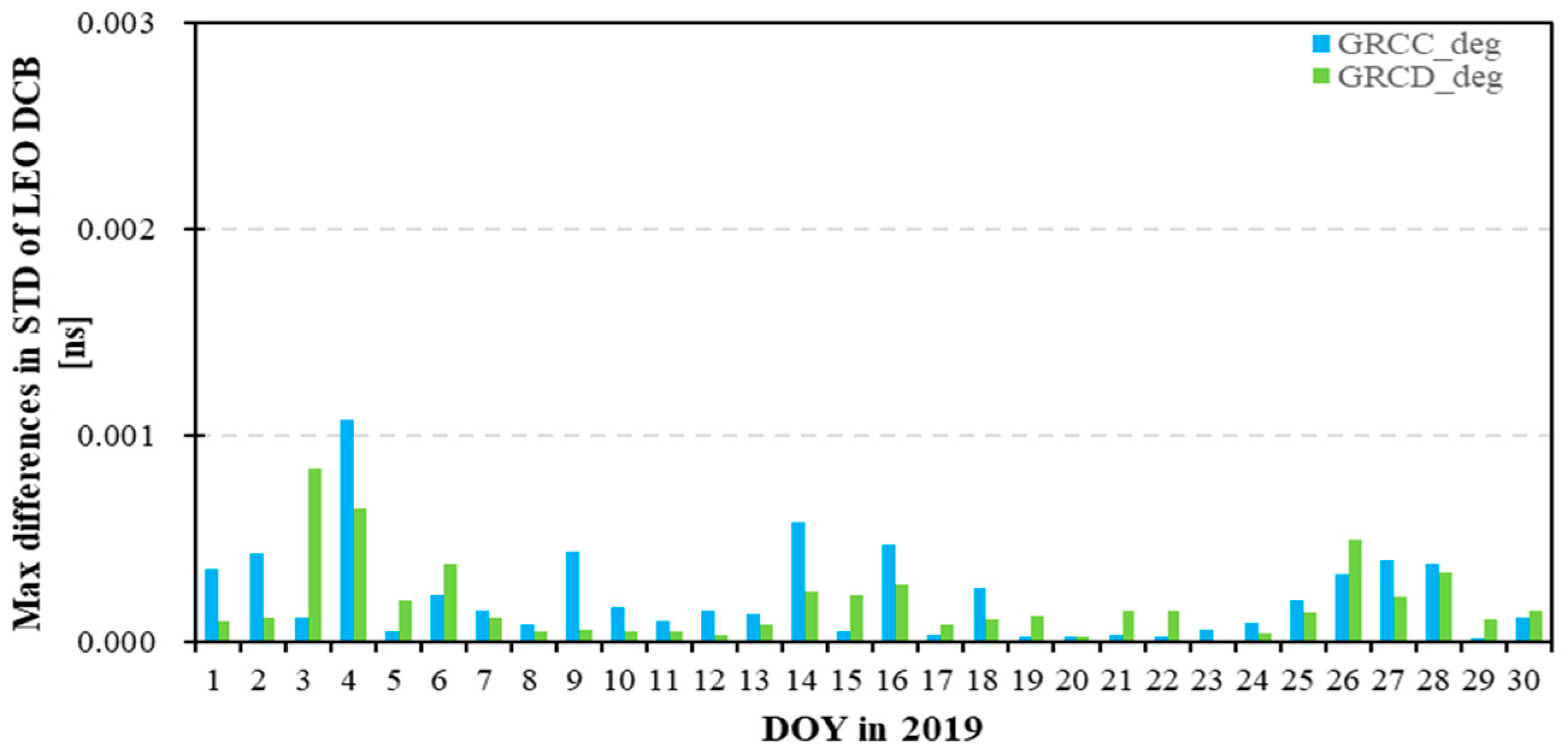Meanwhile, Figure 18 displays the maximum differences in the STD of the receiver DCB using different modeling D&Os. The maximum differences are within 0.02 ns, inferior to the differences in the GPS DCBs, while the maximum differences in STDs are within 0.002 ns.

The mean values and STD results for the receiver DCB estimates with different modeling D&Os are listed in

Table 10. Mean values and STD statistics for receiver DCBs with different modeling D&Os [ns].

LEO	Var.	Mean	STD
GRCC	6D&O	−1.0132	0.0460
	8D&O	−1.0202	0.0459
	10D&O	−1.0215	0.0457
GRCD	6D&O	4.5439	0.0449
	8D&O	4.5365	0.0434
	10D&O	4.5353	0.0441

. Statistically, the mean receiver DCBs for GRCC and GRCD are both sorted in descending order as follows: receiver DCBs with 6, 8, and 10D&Os modeling, where the receiver DCBs decrease as the modeling D&Os increase. The GRCC receiver DCBs with 10D&O modeling gain the minimum STD result, whereas the GRCD DCBs applying 8 and 10D&Os have a better STD than the others. The receiver DCBs of the GRCC and GRCD differ; however, their DCB estimates have similar STD results.

In summary, adopting 8D&O in the LEO-based VTEC modeling exhibits superior estimates and precisions for both GPS and LEO DCBs. Additionally, compared to the results in Section 3.1, this demonstrates that the impact of modeling spacing on DCB estimates is greater than that of modeling D&O.

4. Conclusions

The effects of topside ionosphere VTEC modeling parameters on LEO-based DCB estimates and precision were investigated using GRACE-FO observation data to obtain superior modeling parameters. Different modeling parameters were set into the DCB estimations, encompassing the modeling spacing in the dynamic temporal mode and D&O in LEO-based VTEC modeling. The differences in GPS and LEO DCB estimates with the different modeling parameters were showcased, the precision of the DCB estimates was evaluated, and the effects of these parameters on DCB estimation were analyzed. The beneficial conclusions are drawn as follows:

(1) The mean GPS DCB estimates range between −10 and 10 ns. Although there is no significant difference in the mean GPS DCB estimates obtained using different modeling spacings, the mean DCB may have a limitation in reflecting all real DCBs. The maximum differences in the GPS DCB estimates after adopting different modeling spacings reach 0.05 ns. The different modeling spacings affect the GPS DCB estimates. The maximum differences in the RMS with different modeling spacings are in the range of 0.03 ns. The different modeling spacings have certain effects on the RMS of the GPS DCBs. The GPS DCB estimates with a modeling spacing of 12H have slightly higher precisions than the others.

The maximum difference in receiver DCBs adopting different modeling spacings is 0.22 ns, which indicates that modeling spacing has a significant impact on the receiver DCBs compared with GPS DCBs. The GRCC and GRCD receiver DCBs gain more optimal STD than the others when applying modeling spacings of 6H and 4H, respectively.

In summary, the GPS DCB estimates using a modeling spacing of 12H have higher precisions than the others, whereas LEO DCBs applying the modeling spacings of 4H or 6H obtain optimal STD results.

(2) The differences in the GPS DCB estimates using different modeling D&Os of 6, 8, and 10 are also in the range of 0.05 ns. The different modeling D&Os affect the GPS DCB estimates. The maximum difference in the RMS with different modeling spacings is 0.02 ns. The GPS DCB estimates, with a modeling D&O of 8, attain superior STD and RMS values.

In terms of receiver DCBs, the maximum differences in receiver DCBs using different modeling D&Os are within 0.02 ns, inferior to the differences in the GPS DCBs. The GRCC and GRCD DCBs achieve the optimal STD when adopting modeling D&Os of 10 and 8, respectively.

In summary, adopting 8D&O in the LEO-based VTEC modeling can obtain superior estimates and precisions for both GPS and LEO DCBs.

(3) The modeling spacing has a greater effect on the LEO receiver DCBs than on the GPS DCBs. The effects of the different modeling spacings and D&Os on the GPS DCB estimates and their RMS are at the same level. The modeling spacing has a greater impact on the LEO receiver DCBs than those of the modeling D&O. The research conclusions in this study can provide references for estimating the GNSS and LEO satellite DCBs using LEO onboard observation data.