The Seasonal Variations Analysis of Permanent GNSS Station Time Series in the Central-East of Europe
Abstract
1. Introduction
2. Materials and Methods
3. Results
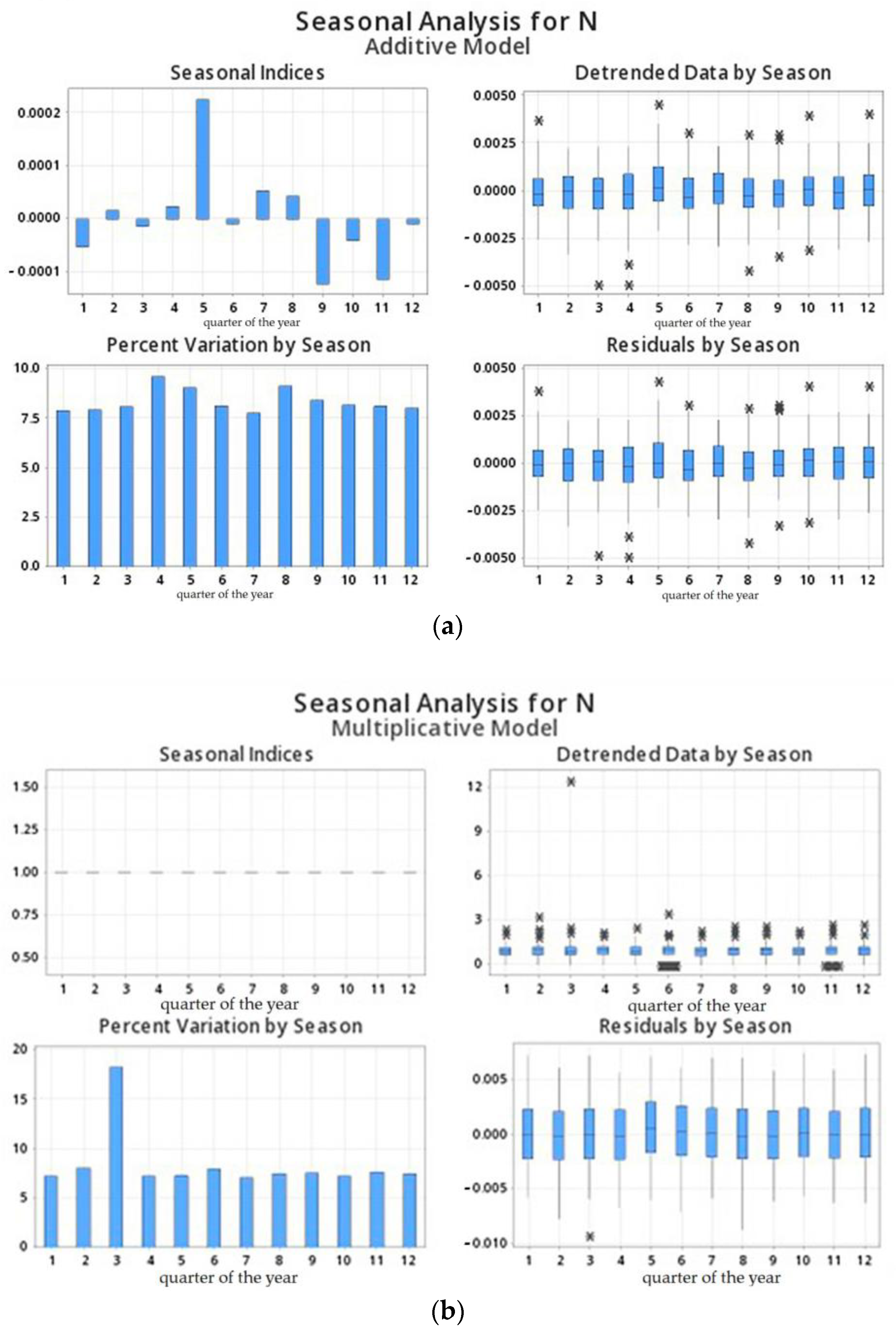
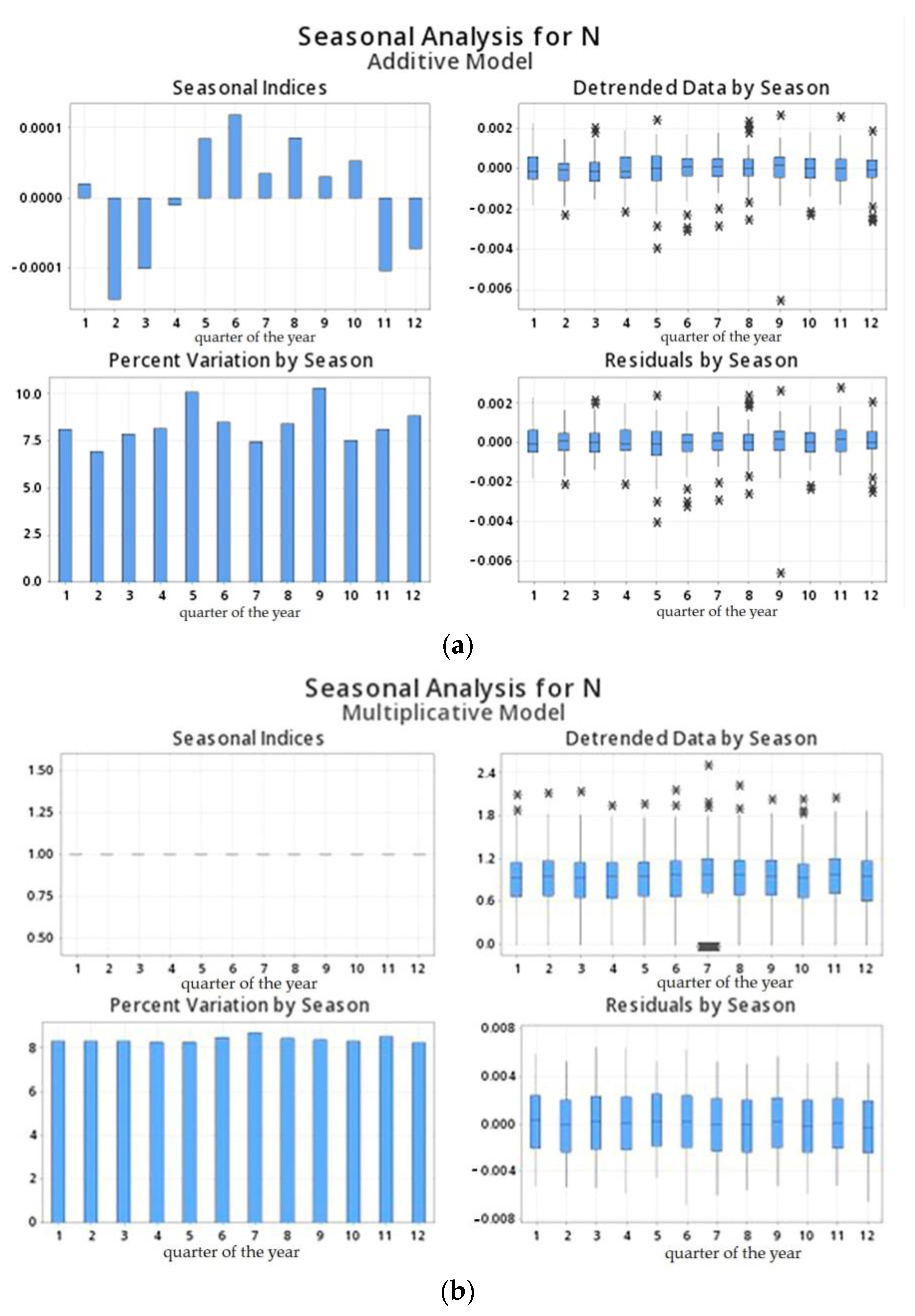
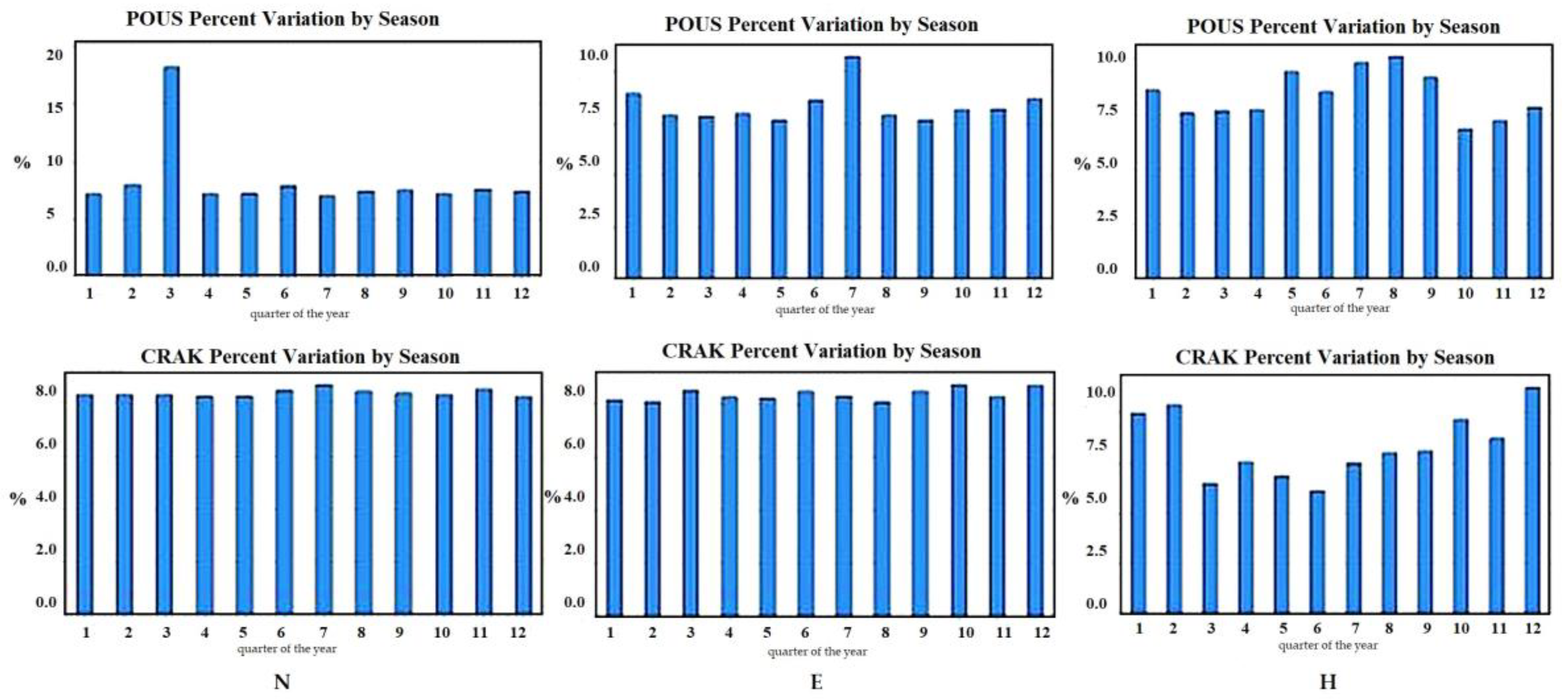
3.1. Modeling the Seasonal Signal with Constant Amplitude in Long GNSS Time Series
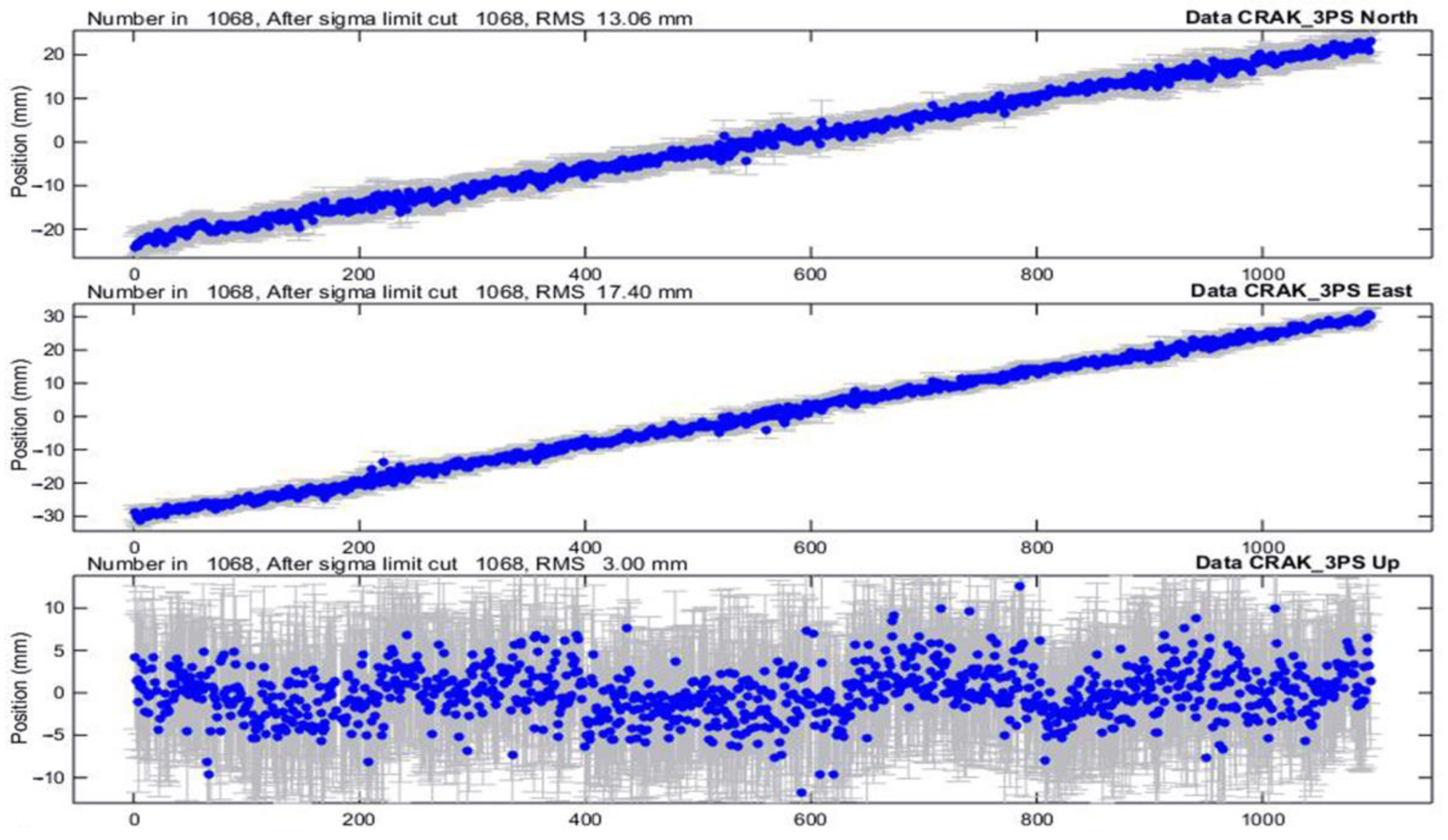
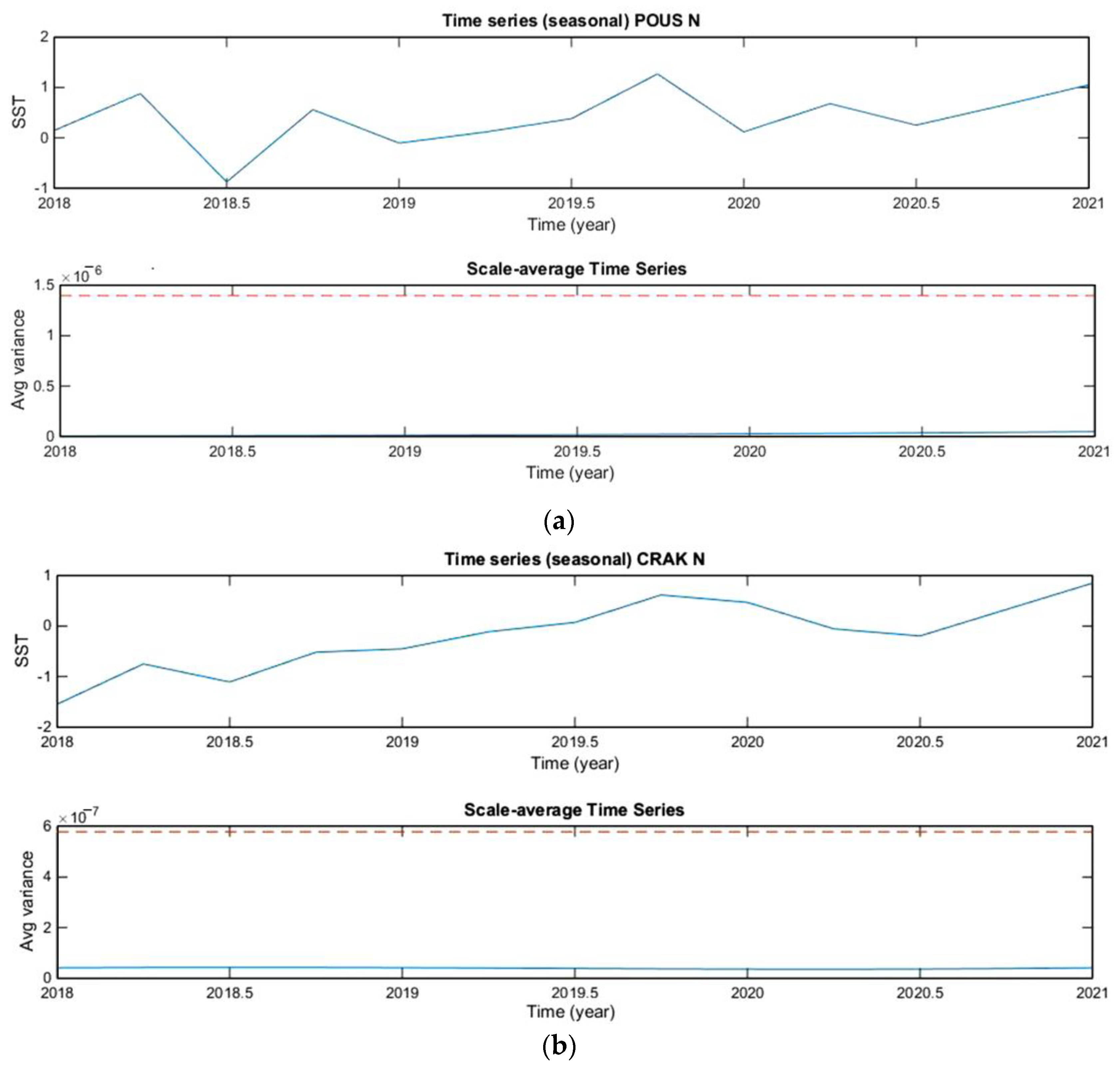
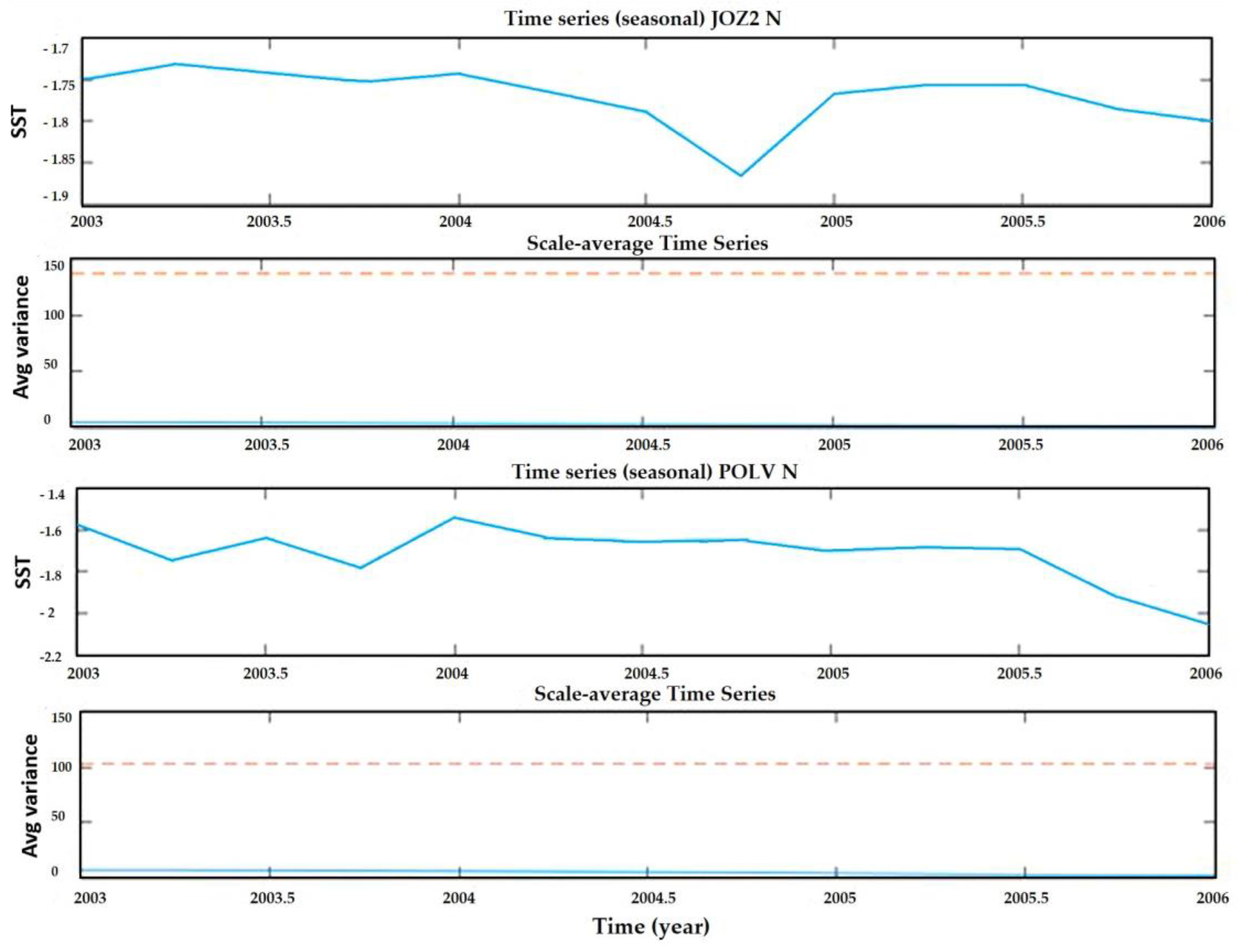
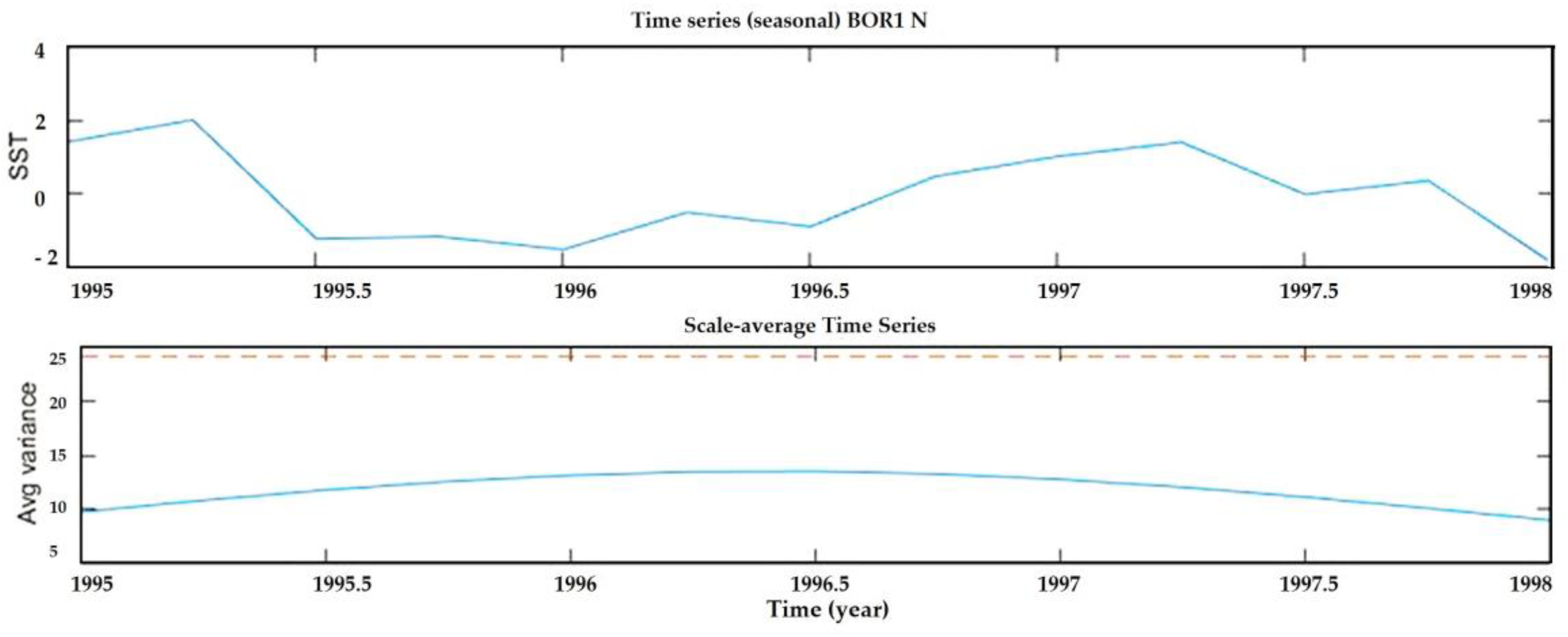
3.2. Decomposition of GNSS Time Series
4. Discussions and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bos, M.S.; Bastos, L.; Fernandes, R.M.S. The influence of seasonal signals on the estimation of the tectonic motion in short continuous GPS time-series. J. Geodyn. 2010, 49, 205–209. [Google Scholar] [CrossRef]
- He, X.; Montillet, J.-P.; Fernandes, R.; Bos, M.; Yu, K.; Hua, X.; Jiang, W. Review of current GPS methodologies for producing accurate time series and their error sources. J. Geodyn. 2017, 106, 12–29. [Google Scholar] [CrossRef]
- Bock, Y.; Melgar, D. Physical applications of GPS geodesy: A review. Rep. Prog. Phys. 2016, 79, 106801. [Google Scholar] [CrossRef] [PubMed]
- Montillet, J.P.; Bos, M. Geodetic Time Series Analysis in Earth Sciences; Springer Geophysics; Springer: Berlin/Heidelberg, Germany, 2020; 422p. [Google Scholar] [CrossRef]
- Savchyn, I.; Brusak, I.; Tretyak, K. Analysis of recent Antarctic plate kinematics based on GNSS data. Geodesy Geodyn. 2023, 14, 99–110. [Google Scholar] [CrossRef]
- Savchyn, I. Establishing the correlation between changes of absolute rotation poles of major tectonic plates based on continuous GNSS stations data. Acta Geodyn. Geomater. 2022, 19, 167–176. [Google Scholar] [CrossRef]
- Haritonova, D. The Impact of the Baltic Sea Non-tidal Loading on GNSS Station Coordinate Time Series: The Case of Latvia. Balt. J. Mod. Comput. 2019, 7, 541–549. [Google Scholar] [CrossRef]
- Wang, H.; Ren, Y.; Hou, Y.; Wang, J.; Zhang, Y.; Cheng, Y.; Xue, S.; Fang, S. The refinement of reprocessed GNSS three-decade displacement trajectory model with spectral analysis and hypothesis test. Adv. Space Res. 2022, 70, 1810–1829. [Google Scholar] [CrossRef]
- Dvulit, P.; Savchuk, S.; Sosonka, I. Accuracy estimation of site coordinates derived from GNSS-observations by non-classical error theory of measurements. Geodesy Geodyn. 2021, 12, 347–355. [Google Scholar] [CrossRef]
- Blewitt, G.; Lavallée, D. Effect of annual signals on geodetic velocity. J. Geophys. Res. Solid Earth 2002, 107, ETG 9-1–ETG 9-16. [Google Scholar] [CrossRef]
- Bogusz, J.; Klos, A. On the significance of periodic signals in noise analysis of GPS station coordinates time series. GPS Solut. 2015, 20, 655–664. [Google Scholar] [CrossRef]
- Dong, D.; Fang, P.; Bock, Y.; Cheng, M.K.; Miyazaki, S. Anatomy of apparent seasonal variations from GPS-derived site position time series. J. Geophys. Res. Solid Earth 2002, 107, ETG 9-1–ETG 9-16. [Google Scholar] [CrossRef]
- Maciuk, K. The Study of Seasonal Changes of Permanent Stations Coordinates based on Weekly EPN Solutions. Artif. Satell. 2016, 51, 1–18. [Google Scholar] [CrossRef]
- Larochelle, S.; Gualandi, A.; Chanard, K.; Avouac, J. Identification and Extraction of Seasonal Geodetic Signals Due to Surface Load Variations. J. Geophys. Res. Solid Earth 2018, 123, 11031–11047. [Google Scholar] [CrossRef]
- Petit, G.; Luzum, B. IERS Conventions (2010); (No. IERS-TN-36); Bureau International des Poids et Mesures Sevres: Frankfurt am Main, Germany, 2010. [Google Scholar] [CrossRef]
- Herring, T.A.; King, R.W.; Floyd, M.A.; McClusky, S.C. Introduction to GAMIT/GLOBK, Release 10.7. 2018, pp. 1–54. Available online: http://geoweb.mit.edu/gg/docs/Intro_GG.pdf (accessed on 27 July 2023).
- Santamaría-Gómez, A. SARI: Interactive GNSS position time series analysis software. GPS Solut. 2019, 23, 52. [Google Scholar] [CrossRef]
- Global Geophysical Fluid Center (GGFC). Available online: http://geophy.uni.lu (accessed on 27 July 2023).
- Klos, A.; Bos, M.S.; Bogusz, J. Detecting time-varying seasonal signal in GPS position time series with different noise levels. GPS Solut. 2017, 22, 21. [Google Scholar] [CrossRef]
- Langbein, J. Methods for Rapidly Estimating Velocity Precision from GNSS Time Series in the Presence of Temporal Correlation: A New Method and Comparison of Existing Methods. J. Geophys. Res. Solid Earth 2020, 125, e2019JB019132. [Google Scholar] [CrossRef]
- Santamaría-Gómez, A.; Bouin, M.-N.; Collilieux, X.; Wöppelmann, G. Correlated errors in GPS position time series: Implications for velocity estimates. J. Geophys. Res. Atmos. 2011, 116, e2010jb007701. [Google Scholar] [CrossRef]
- Kudrys, J. Spectral analysis of multi-year GNSS code multipath time-series. Bud. i Arch. 2020, 18, 15–22. [Google Scholar] [CrossRef]
- Ren, Y.; Wang, H.; Lian, L.; Wang, J.; Cheng, Y.; Zhang, Y.; Zhu, W.; Zhang, S. A method based on MTLS and ILSP for GNSS coordinate time series analysis with missing data. Adv. Space Res. 2021, 68, 3546–3561. [Google Scholar] [CrossRef]
- Amiri-Simkooei, A.R. Non-negative least-squares variance component estimation with application to GPS time series. J. Geod. 2016, 90, 451–466. [Google Scholar] [CrossRef]
- Tian, Y.; Shen, Z.-K. Extracting the regional common-mode component of GPS station position time series from dense continuous network. J. Geophys. Res. Solid Earth 2016, 121, 1080–1096. [Google Scholar] [CrossRef]
- Agnieszka, W.; Kudas, D. Modeling seasonal oscillations in GNSS time series with Complementary Ensemble Empirical Mode Decomposition. GPS Solut. 2022, 26, 101. [Google Scholar] [CrossRef]
- Chen, Q.; van Dam, T.; Sneeuw, N.; Collilieux, X.; Weigelt, M.; Rebischung, P. Singular spectrum analysis for modeling seasonal signals from GPS time series. J. Geodyn. 2013, 72, 25–35. [Google Scholar] [CrossRef]
- Gruszczynska, M.; Rosat, S.; Klos, A.; Gruszczynski, M.; Bogusz, J. Multichannel Singular Spectrum Analysis in the Estimates of Common Environmental Effects Affecting GPS Observations. Pure Appl. Geophys. 2018, 175, 1805–1822. [Google Scholar] [CrossRef]
- Chen, B.; Bian, J.; Ding, K.; Wu, H.; Li, H. Extracting Seasonal Signals in GNSS Coordinate Time Series via Weighted Nuclear Norm Minimization. Remote Sens. 2020, 12, 2027. [Google Scholar] [CrossRef]
- Jiang, W.; Ma, J.; Li, Z.; Zhou, X.; Zhou, B. Effect of removing the common mode errors on linear regression analysis of noise amplitudes in position time series of a regional GPS network & a case study of GPS stations in Southern California. Adv. Space Res. 2018, 61, 2521–2530. [Google Scholar] [CrossRef]
- Stallone, A.; Cicone, A.; Materassi, M. New insights and best practices for the successful use of Empirical Mode Decomposition, Iterative Filtering and derived algorithms. Sci. Rep. 2020, 10, 15161. [Google Scholar] [CrossRef]
- Chen, G.; Zhao, Q.; Wei, N.; Liu, J. Impacts on Noise Analyses of GNSS Position Time Series Caused by Seasonal Signal, Weight Matrix, Offset, and Helmert Transformation Parameters. Remote Sens. 2018, 10, 1584. [Google Scholar] [CrossRef]
- Böhm, J.; Moeller, G.; Schindelegger, M.; Pain, G.; Weber, R. Development of an improved empirical model for slant delays in the troposphere (GPT2w). GPS Solut. 2015, 19, 433–441. [Google Scholar] [CrossRef]
- EPN Solutions. Available online: https://epncb.oma.be/ (accessed on 27 July 2023).
- U.S. Census Bureau. X-13ARIMA-SEATS Seasonal Adjustment Program. 2022. Available online: https://www.census.gov/data/software/x13as.Win_X-13.html#list-tab-635278563 (accessed on 27 July 2023).
- Minitab. Statistical Software. 2022. Available online: https://www.minitab.com/en-us/products/minitab/ (accessed on 27 July 2023).
- MATLAB Wavelet Toolbox. Available online: https://www.mathworks.com/products/wavelet.html (accessed on 27 July 2023).





| Satellite Orbit | IGS Tabulated Ephemeris |
|---|---|
| The motion of the Earth in inertial space | Analytical models for precession and nutation (tabulated); IERS observed values for pole position (wobble) and axial rotation (UT1) Solid Earth tide analytical model (IERS2010) Ocean and atmospheric tidal loading model (FES2004) Solar radiation pressure parameters model (Berne) |
| Propagation of the signal | Zenith hydrostatic (dry) delay (ZHD) from the ECMWF meteorological model through the VMF3 grids Zenith wet delay (ZWD) and ZHD mapped to line-of-sight with mapping functions (VMF3 grid) Variations in the phase centers of the ground and satellite antennas (ANTEX file) |
| N | E | H | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mm | c | d | e | f | c | D | e | f | c | d | e | f |
| CRAO | 0.1 | −0.2 | 0.1 | 0.1 | −1.1 | 2.0 | 0.6 | 0.3 | 2.4 | 1.7 | −0.4 | −0.2 |
| GANP | −0.3 | −0.5 | 0.5 | 0.0 | −0.3 | −0.3 | 0.3 | 0.3 | 7.0 | 2.8 | 3.2 | 1.7 |
| GLSV | −2.2 | −0.1 | 0.4 | 0.2 | −0.3 | 0.6 | 0.3 | 0.4 | −1.2 | −2.5 | −0.3 | −1.0 |
| JOZ2 | −0.2 | 0.3 | 0.0 | 0.4 | −0.6 | 0.1 | 0.2 | 0.6 | 0.2 | 0.0 | 0.0 | −0.4 |
| KHAR | −2.7 | −0.9 | 1.5 | 0.5 | 1.2 | −0.2 | 0.3 | 0.6 | −1.4 | −2.7 | 0.5 | −1.3 |
| LAMA | 0.0 | −0.1 | 0.1 | 0.1 | −0.2 | 0.0 | 0.0 | 0.1 | −0.2 | 0.1 | 0.1 | 0.2 |
| MIKL | 0.0 | 0.1 | 0.0 | 0.1 | −0.7 | 0.1 | 0.1 | 0.4 | −0.1 | 0.0 | 0.0 | 0.0 |
| POLV | −0.5 | 0.1 | 0.2 | 0.2 | 0.3 | 0.3 | 0.0 | 0.7 | −0.6 | −2.5 | 0.1 | −1.5 |
| SULP | −1.1 | −0.7 | −0.1 | −0.2 | −0.3 | −0.4 | −0.2 | −0.1 | −1.6 | −3.3 | −1.1 | −2.7 |
| UZHL | 0.2 | 0.0 | 0.2 | 0.1 | −0.4 | −1.1 | 1.0 | 0.4 | 1.0 | −0.8 | 0.6 | 0.3 |
| Min | −2.7 | −0.9 | −0.1 | −0.2 | −1.1 | −1.1 | −0.2 | −0.1 | −1.6 | −3.3 | −1.1 | −2.7 |
| Max | 0.2 | 0.3 | 1.5 | 0.5 | 1.2 | 2.0 | 1.0 | 0.7 | 7.0 | 2.8 | 3.2 | 1.7 |
| mean | −0.7 | −0.2 | 0.3 | 0.2 | −0.2 | 0.1 | 0.3 | 0.4 | 0.5 | −0.7 | 0.3 | −0.5 |
| N | E | H | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| mm | c | d | e | f | c | d | e | f | c | d | e | f |
| sub-network C0−C1 | ||||||||||||
| min | −1.2 | −1.5 | −0.6 | −0.7 | −1.7 | −1.5 | −0.4 | −2.6 | −2.6 | −3.5 | −2.8 | −4.1 |
| max | 2.1 | 1.5 | 1.1 | 1.0 | 2.6 | 1.3 | 0.8 | 0.6 | 6.7 | 2.4 | 2.0 | 1.8 |
| mean | −0.2 | 0.1 | 0.0 | 0.1 | −0.1 | 0.0 | 0.0 | 0.0 | 0.4 | −0.6 | 0.0 | −0.1 |
| sub-network C6 | ||||||||||||
| min | −3.4 | −3.6 | −2.4 | −3.0 | −2.6 | −14.4 | −1.8 | −2.7 | −8.1 | −3.8 | −2.6 | −2.5 |
| max | 4.4 | 8.3 | 0.6 | 0.7 | 5.2 | 1.0 | 2.8 | 3.5 | 6.7 | 3.8 | 8.1 | 4.0 |
| mean | 0.1 | 3.7 | −0.5 | −0.3 | 0.4 | −5.2 | 0.5 | 0.5 | 0.6 | −2.9 | 3.7 | 1.8 |
| Station | N | E | H | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| mm | ∆c | ∆d | ∆e | ∆f | ∆c | ∆d | ∆e | ∆f | ∆c | ∆d | ∆e | ∆f |
| BRUX | 0.1 | −0.2 | 0.1 | −0.4 | 0.3 | 5.0 | 0.1 | 2.4 | −0.2 | 0.3 | −0.5 | −0.1 |
| CRAK | −0.3 | −0.1 | −0.1 | −0.1 | 0.1 | 0.5 | −0.1 | −0.3 | −0.1 | −0.3 | −0.4 | −0.2 |
| POUS | −0.3 | −0.1 | 0.0 | −0.3 | 0.2 | 1.1 | −0.3 | 0.1 | 1.8 | 0.0 | −0.2 | −0.8 |
| WARE | −0.1 | 0.1 | 0.1 | −0.2 | 0.9 | 0.5 | −0.1 | −0.2 | 0.0 | 0.1 | −0.3 | −0.1 |
| min | −0.3 | −0.2 | −0.1 | −0.4 | 0.1 | 0.5 | −0.3 | −0.3 | −0.2 | −0.3 | −0.5 | −0.8 |
| max | 0.1 | 0.1 | 0.1 | −0.1 | 0.9 | 5.0 | 0.1 | 2.4 | 1.8 | 0.3 | −0.2 | −0.1 |
| mean | −0.2 | −0.1 | 0.0 | −0.2 | 0.4 | 1.8 | −0.1 | 0.5 | 0.4 | 0.0 | −0.3 | −0.3 |
| Station | Seasonality | Seasonal Values |
|---|---|---|
| POUS | 0 | 1 |
| CRAK | 0 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Savchuk, S.; Doskich, S.; Gołda, P.; Rurak, A. The Seasonal Variations Analysis of Permanent GNSS Station Time Series in the Central-East of Europe. Remote Sens. 2023, 15, 3858. https://doi.org/10.3390/rs15153858
Savchuk S, Doskich S, Gołda P, Rurak A. The Seasonal Variations Analysis of Permanent GNSS Station Time Series in the Central-East of Europe. Remote Sensing. 2023; 15(15):3858. https://doi.org/10.3390/rs15153858
Chicago/Turabian StyleSavchuk, Stepan, Sofiia Doskich, Paweł Gołda, and Adam Rurak. 2023. "The Seasonal Variations Analysis of Permanent GNSS Station Time Series in the Central-East of Europe" Remote Sensing 15, no. 15: 3858. https://doi.org/10.3390/rs15153858
APA StyleSavchuk, S., Doskich, S., Gołda, P., & Rurak, A. (2023). The Seasonal Variations Analysis of Permanent GNSS Station Time Series in the Central-East of Europe. Remote Sensing, 15(15), 3858. https://doi.org/10.3390/rs15153858








