Author Contributions
Conceptualization, J.W.; methodology, J.W.; validation, J.W. and X.L.; formal analysis, J.W. and X.L.; investigation, J.W. and X.L.; resources, X.L.; data curation, X.L., Z.S. and K.J.; writing—original draft preparation, J.W. and X.L.; writing—review and editing, Z.S., X.L., K.J. and X.Z.; visualization, X.L.; supervision, K.J.; project administration, X.Z.; funding acquisition, X.L. All authors have read and agreed to the published version of the manuscript.
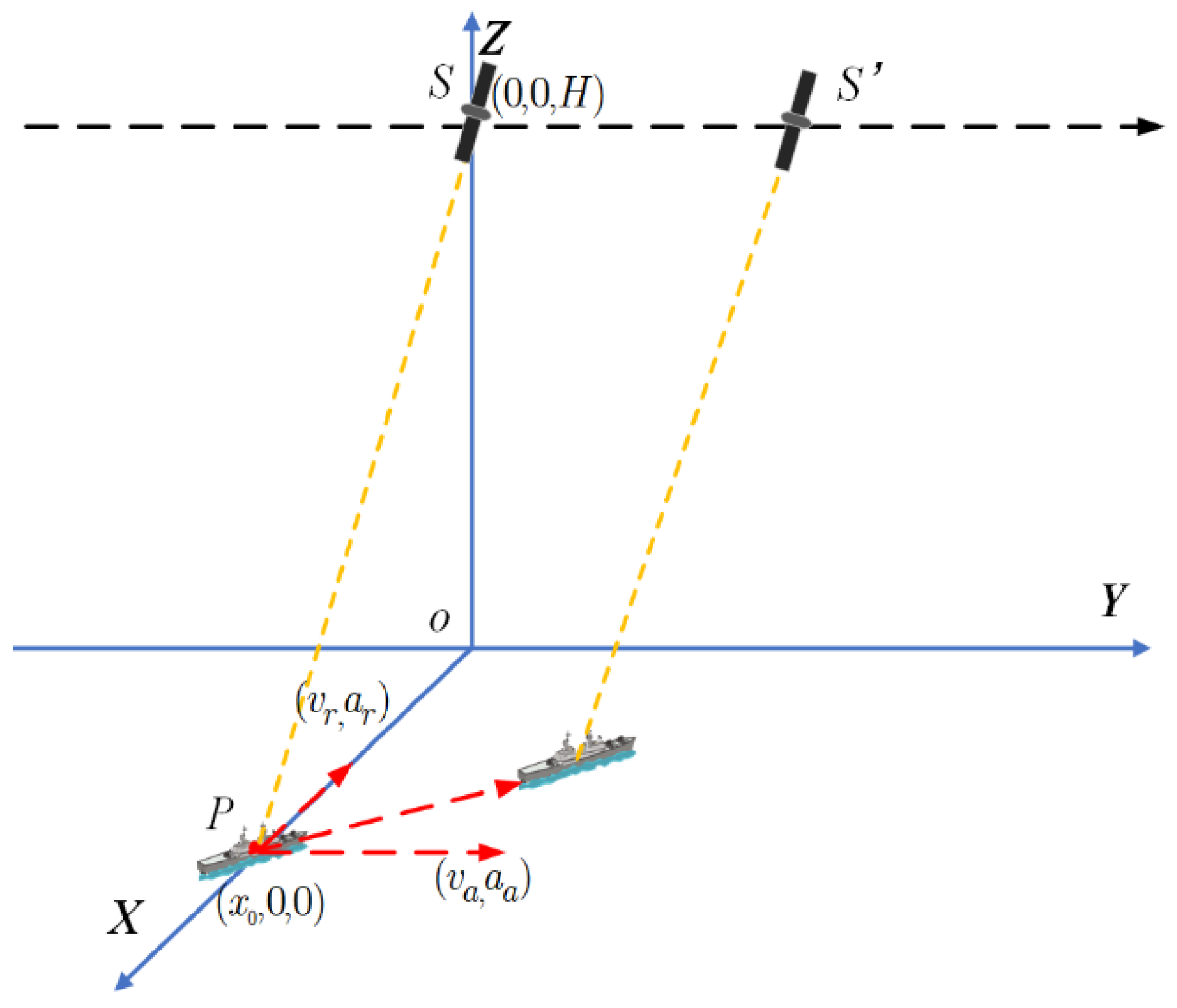
Figure 1.
Geometric relationship diagram between the linear moving ship and SAR platform.
Figure 1.
Geometric relationship diagram between the linear moving ship and SAR platform.
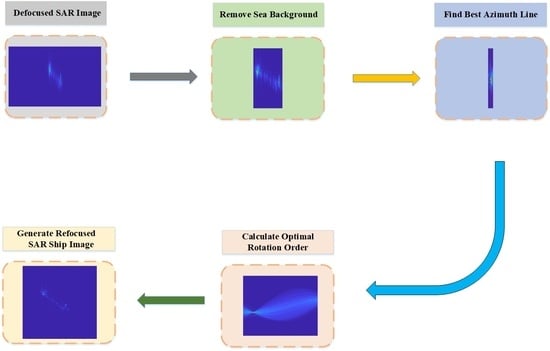
Figure 2.
The flowchart of the proposed scheme.
Figure 2.
The flowchart of the proposed scheme.
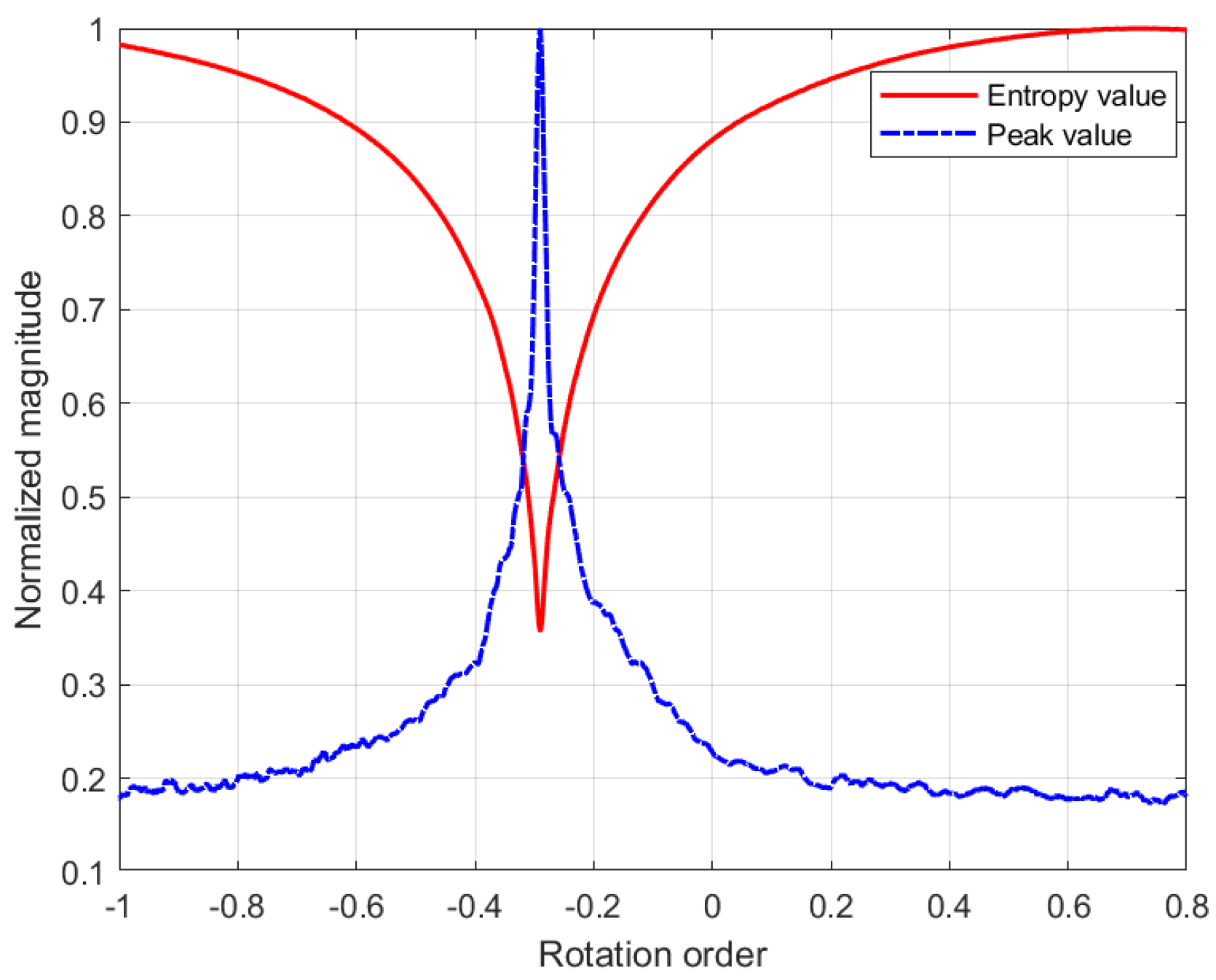
Figure 3.
The normalized peak and entropy of one azimuth line after FrFT.
Figure 3.
The normalized peak and entropy of one azimuth line after FrFT.
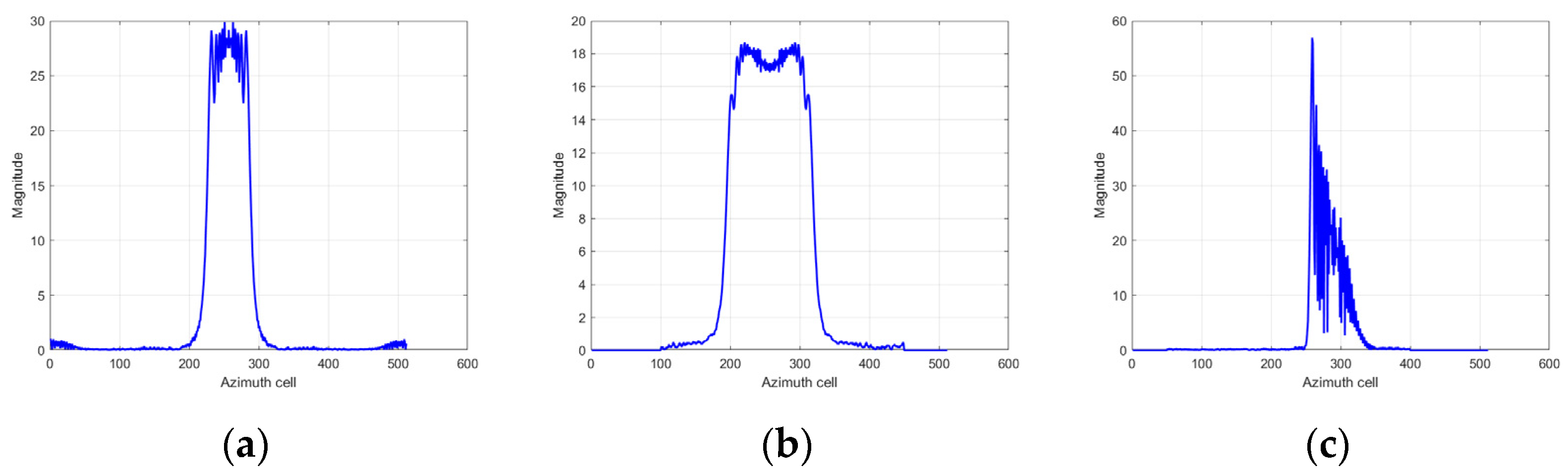
Figure 4.
Azimuth profiles of SAR imaging results for different moving states of a point target. (a) Azimuth velocity of 20 m/s. (b) Range acceleration of 10 m/s2. (c) Azimuth acceleration of 15 m/s2.
Figure 4.
Azimuth profiles of SAR imaging results for different moving states of a point target. (a) Azimuth velocity of 20 m/s. (b) Range acceleration of 10 m/s2. (c) Azimuth acceleration of 15 m/s2.
Figure 5.
Time–frequency distribution of signals in different motion states. (a) Azimuth velocity of 20 m/s. (b) Range acceleration of 10 m/s2. (c) Azimuth acceleration of 15 m/s2.
Figure 5.
Time–frequency distribution of signals in different motion states. (a) Azimuth velocity of 20 m/s. (b) Range acceleration of 10 m/s2. (c) Azimuth acceleration of 15 m/s2.
Figure 6.
Distribution of signals with different motion states in the FrFT domain. (a) Azimuth velocity of 20 m/s. (b) Range acceleration of 10 m/s2. (c) Azimuth acceleration of 15 m/s2.
Figure 6.
Distribution of signals with different motion states in the FrFT domain. (a) Azimuth velocity of 20 m/s. (b) Range acceleration of 10 m/s2. (c) Azimuth acceleration of 15 m/s2.
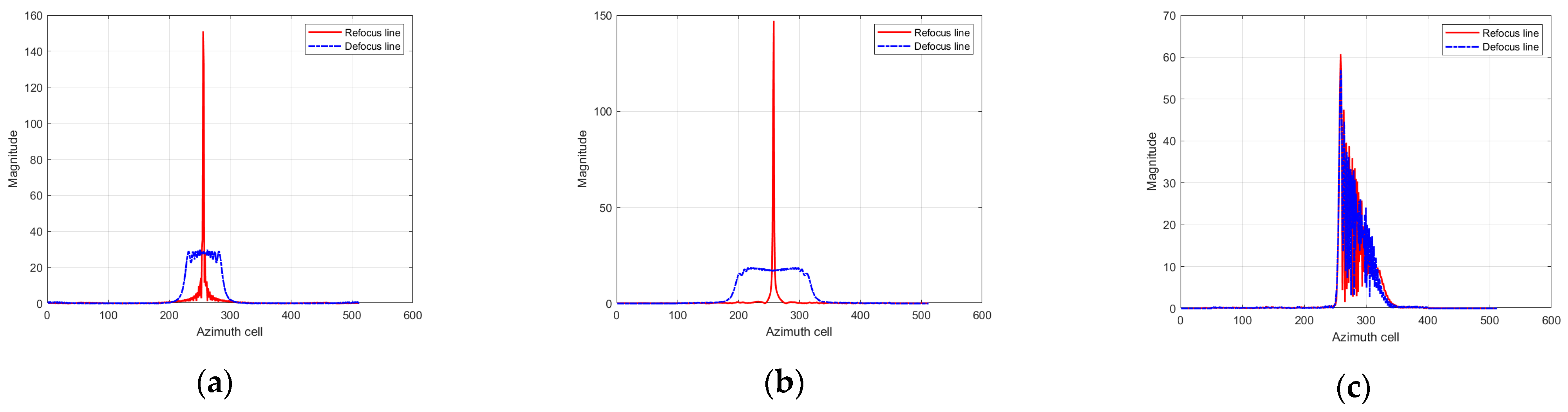
Figure 7.
The results of the defocused signals with different motion states after FrFT at optimal rotation order. (a) Azimuth velocity of 20 m/s. (b) Range acceleration of 10 m/s2. (c) Azimuth acceleration of 15 m/s2.
Figure 7.
The results of the defocused signals with different motion states after FrFT at optimal rotation order. (a) Azimuth velocity of 20 m/s. (b) Range acceleration of 10 m/s2. (c) Azimuth acceleration of 15 m/s2.
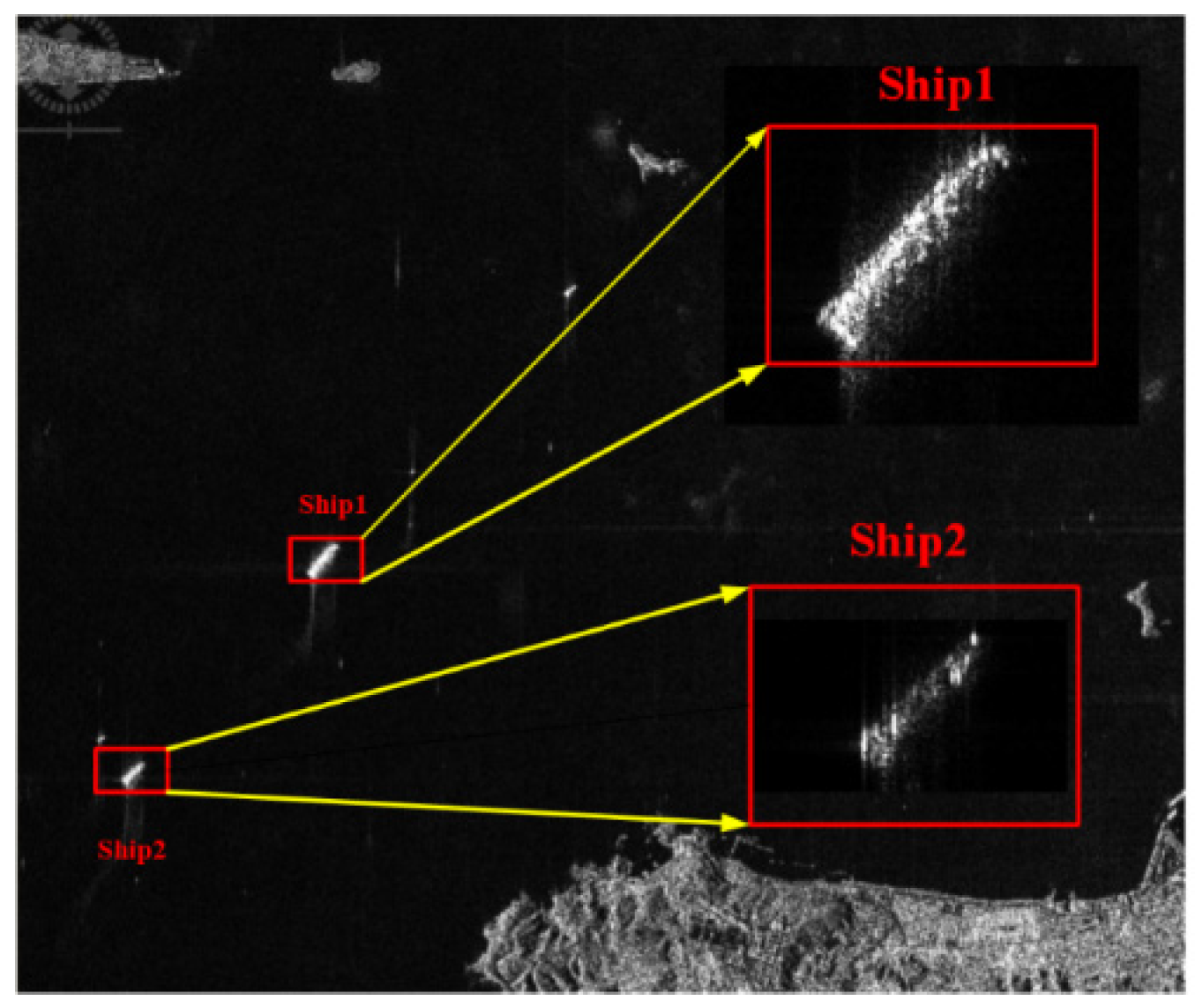
Figure 8.
The SAR image in Gaofen-3 UFS mode.
Figure 8.
The SAR image in Gaofen-3 UFS mode.
Figure 9.
Time–frequency distribution of the ship’s best azimuth line. (a) ship1 (b) ship2.
Figure 9.
Time–frequency distribution of the ship’s best azimuth line. (a) ship1 (b) ship2.
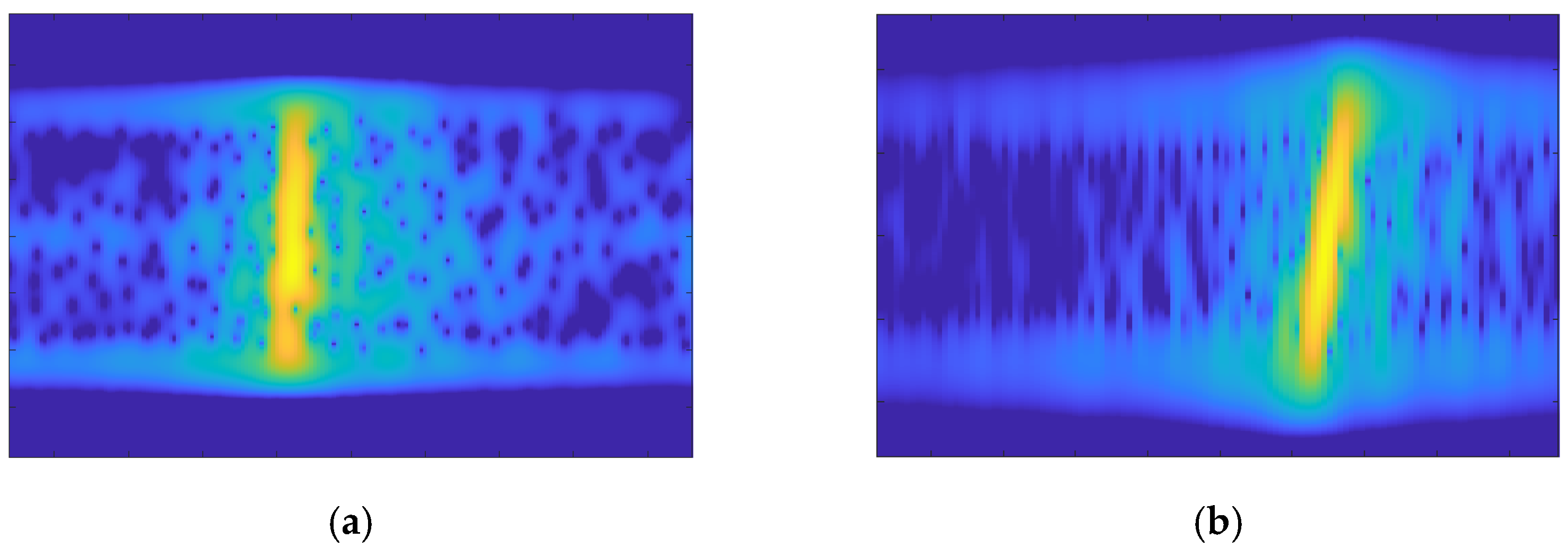
Figure 10.
Distribution of the best azimuth line in the FrFT domain. (a) Ship1 (b) Ship2.
Figure 10.
Distribution of the best azimuth line in the FrFT domain. (a) Ship1 (b) Ship2.
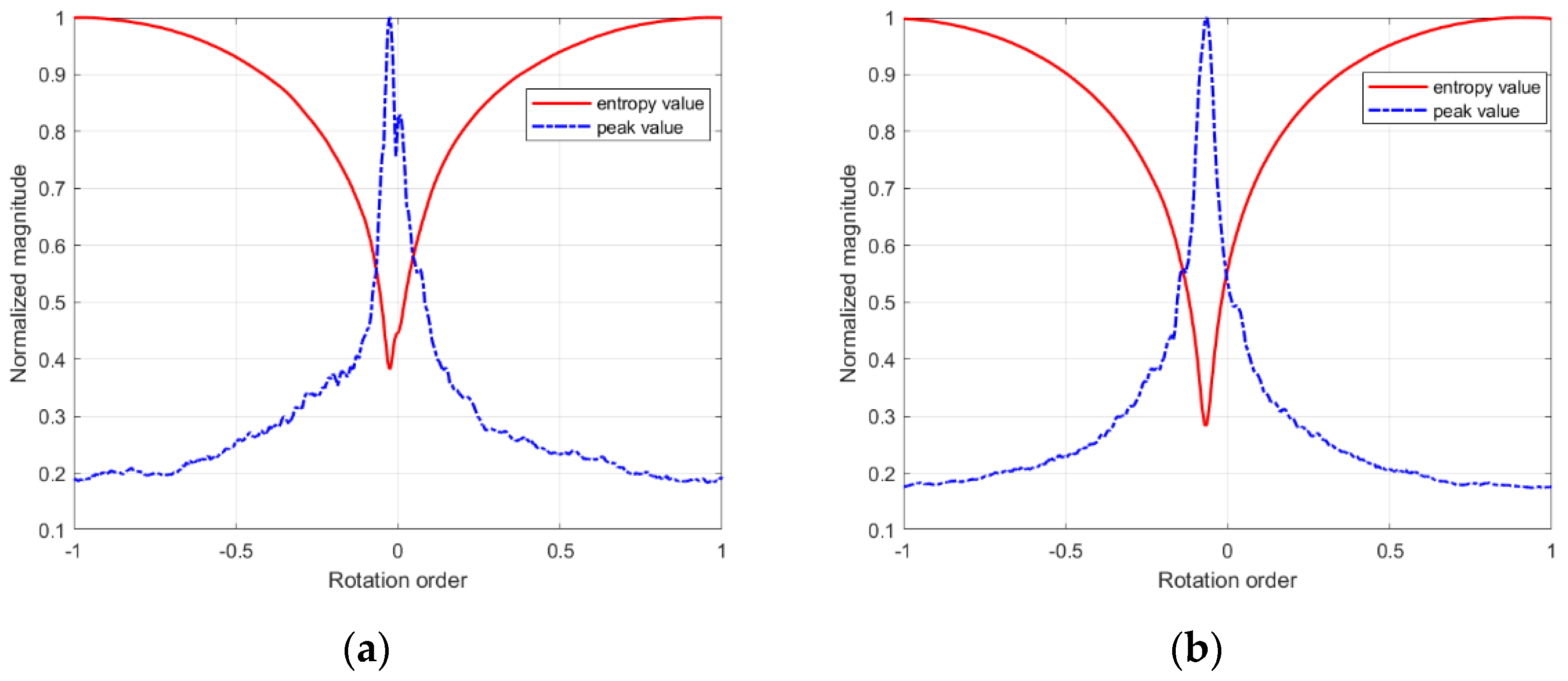
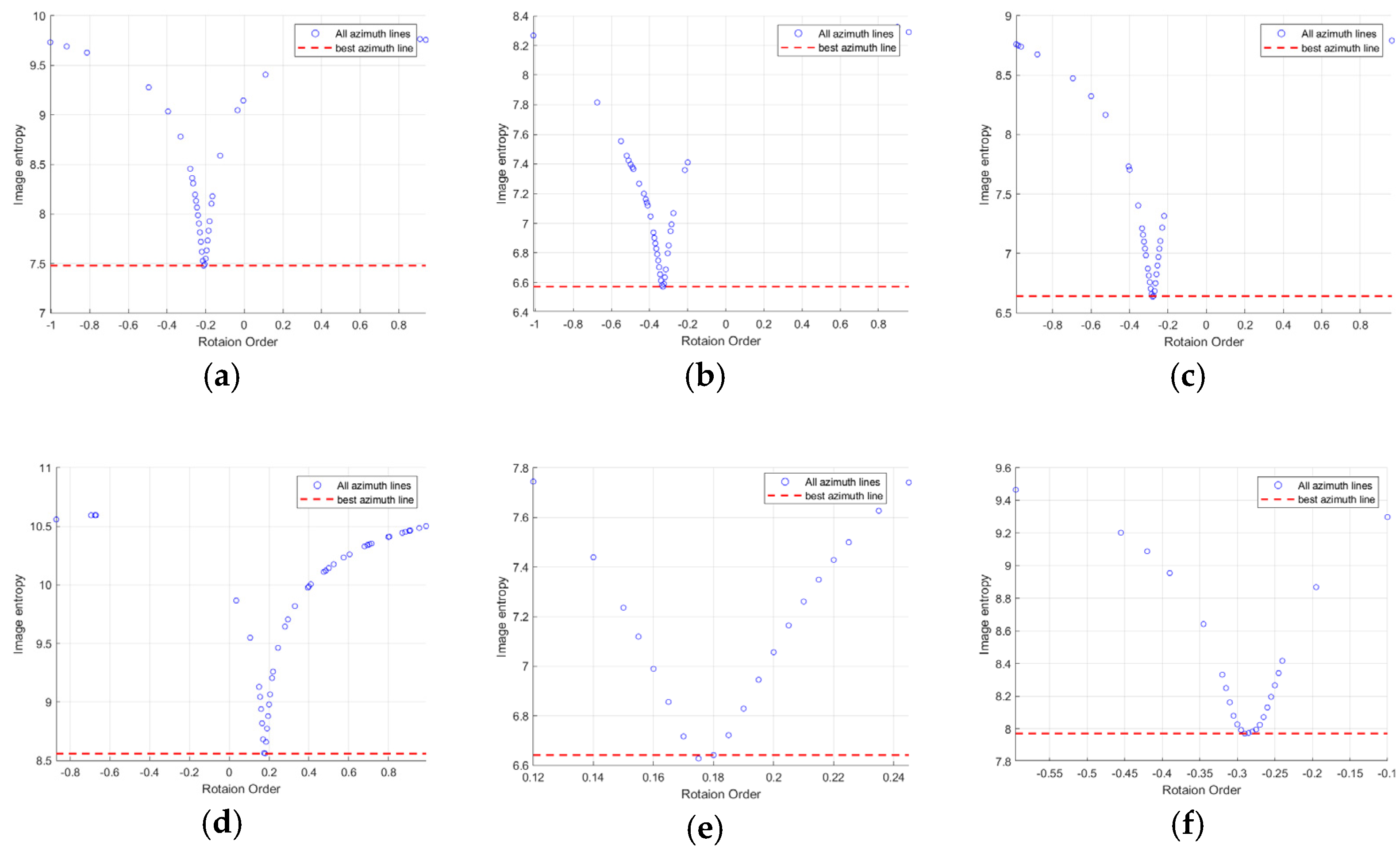
Figure 11.
Variation of entropy values and peak values with rotation order. (a) Ship1 (b) Ship2.
Figure 11.
Variation of entropy values and peak values with rotation order. (a) Ship1 (b) Ship2.
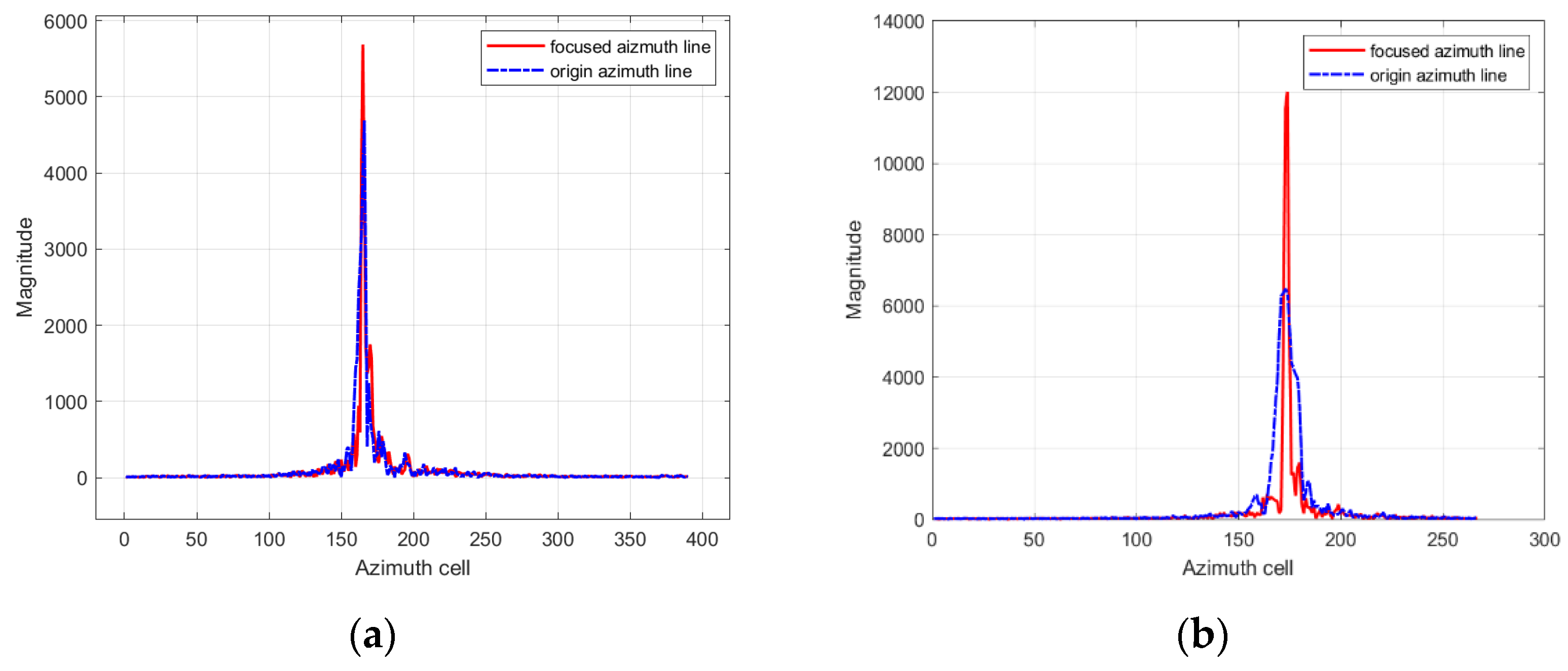
Figure 12.
The result of signal after FrFT at the optimal rotation order. (a) Ship1 (b) Ship2.
Figure 12.
The result of signal after FrFT at the optimal rotation order. (a) Ship1 (b) Ship2.
Figure 13.
Distribution of optimal rotation order for ship’s each azimuth line. (a) Ship1 (b) Ship2.
Figure 13.
Distribution of optimal rotation order for ship’s each azimuth line. (a) Ship1 (b) Ship2.
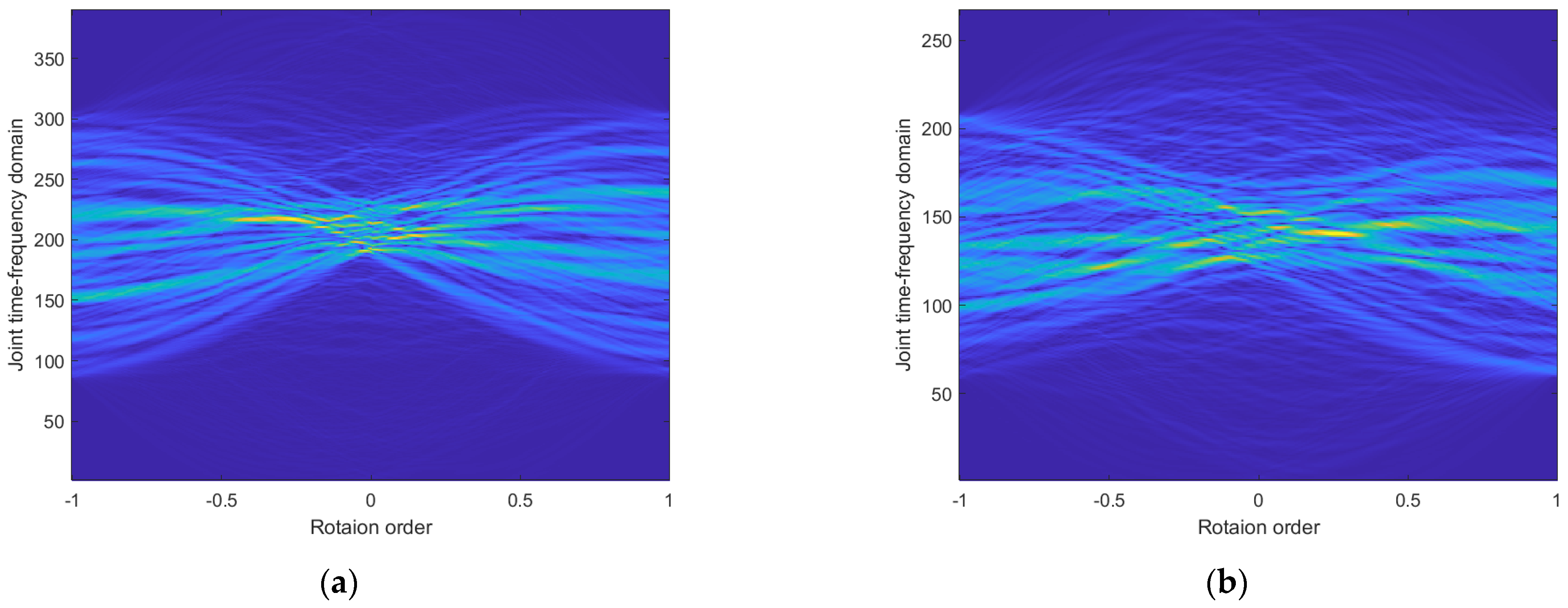
Figure 14.
Distribution in FrFT domain of non-dominant scattering point range cells. (a) Ship1 (b) Ship2.
Figure 14.
Distribution in FrFT domain of non-dominant scattering point range cells. (a) Ship1 (b) Ship2.
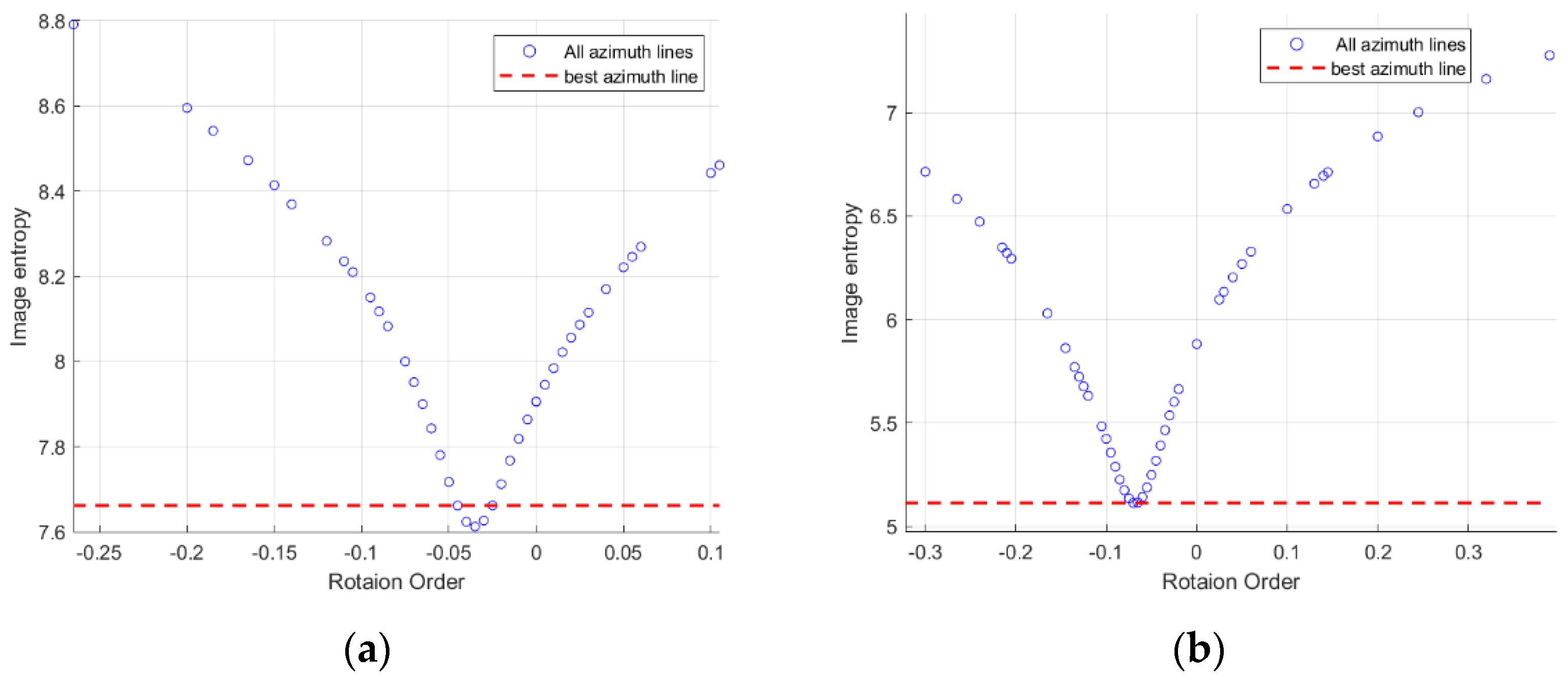
Figure 15.
Image entropy at different range cell’s optimal rotation order. (a) Ship1 (b) Ship2.
Figure 15.
Image entropy at different range cell’s optimal rotation order. (a) Ship1 (b) Ship2.
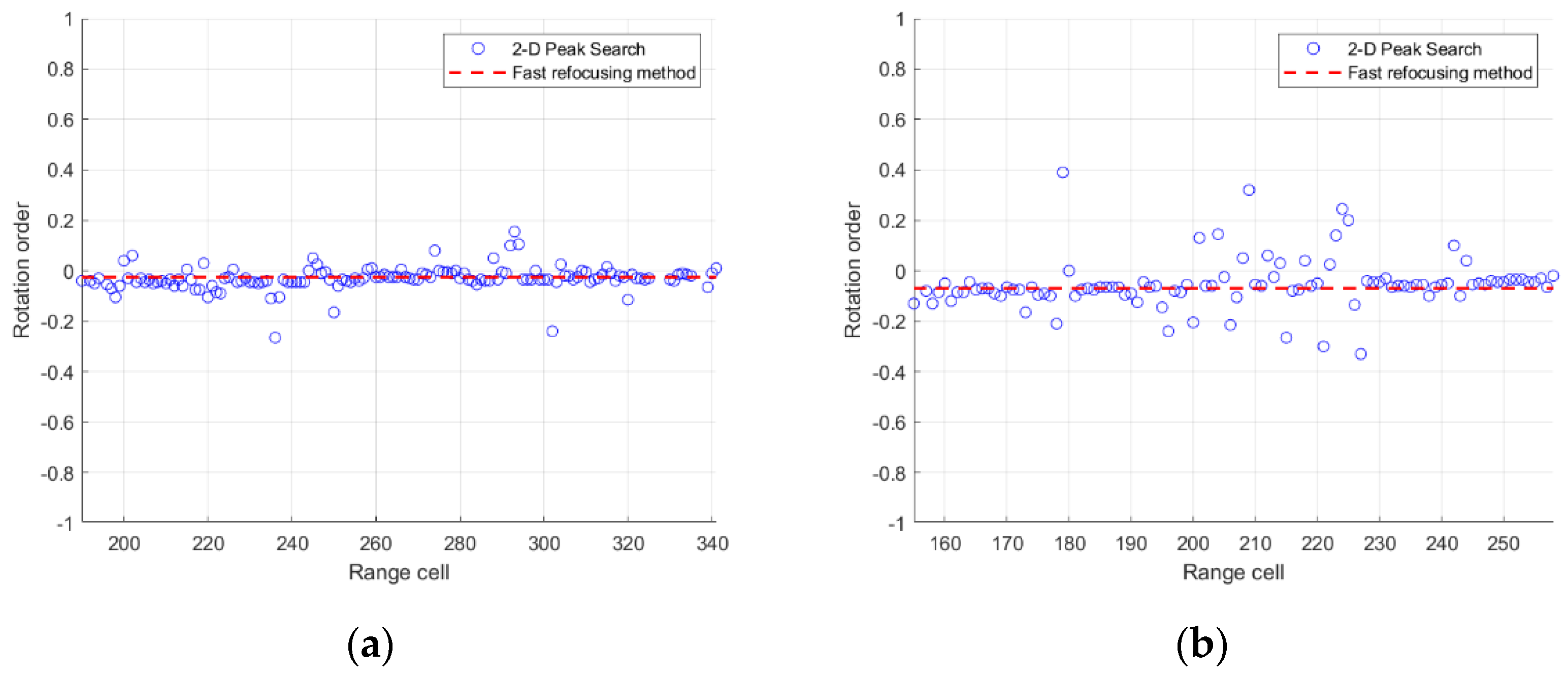
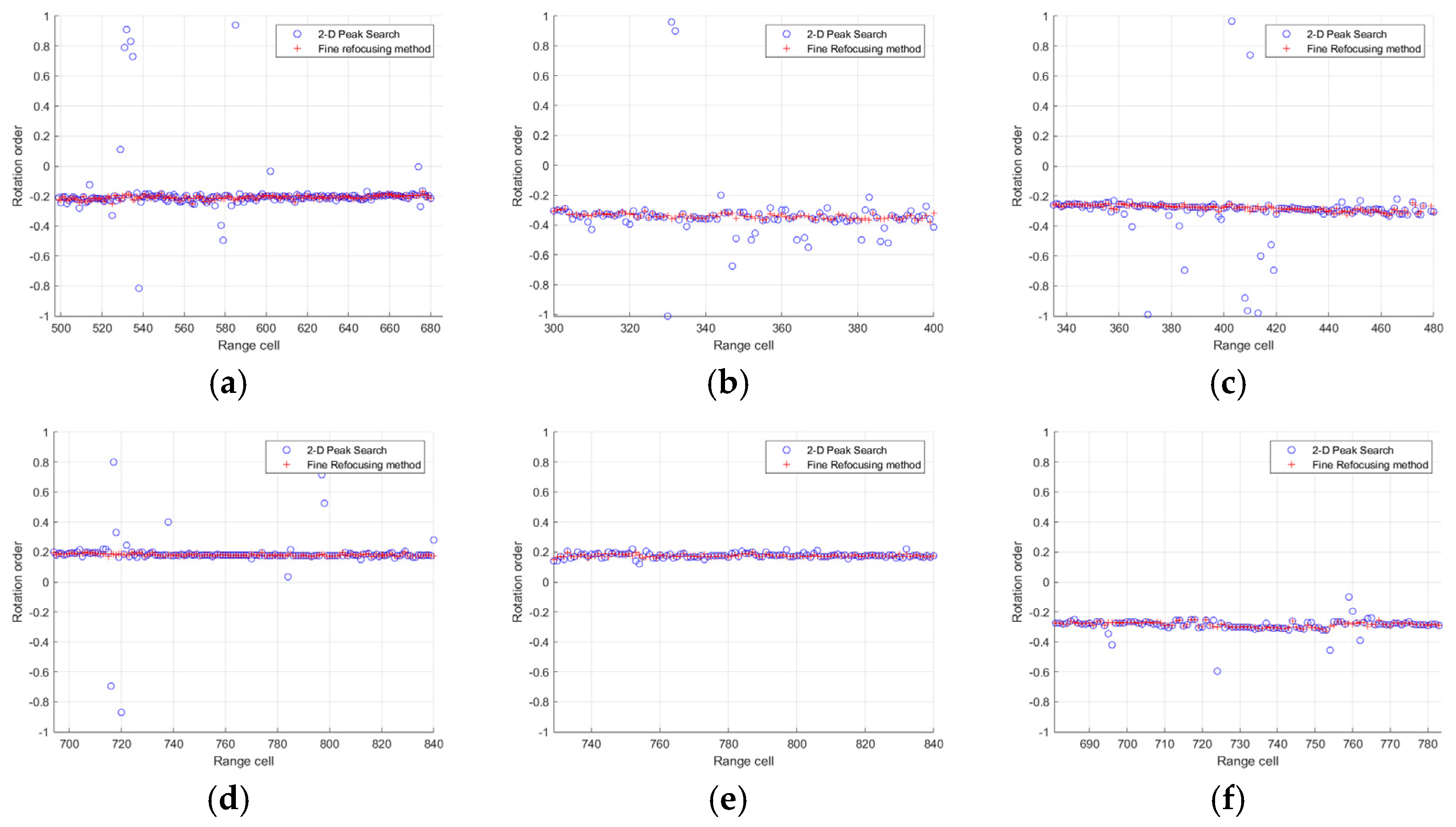
Figure 16.
The optimal rotation order of each range cell on the ship obtained by different methods. (a) Ship1. (b) Ship2.
Figure 16.
The optimal rotation order of each range cell on the ship obtained by different methods. (a) Ship1. (b) Ship2.
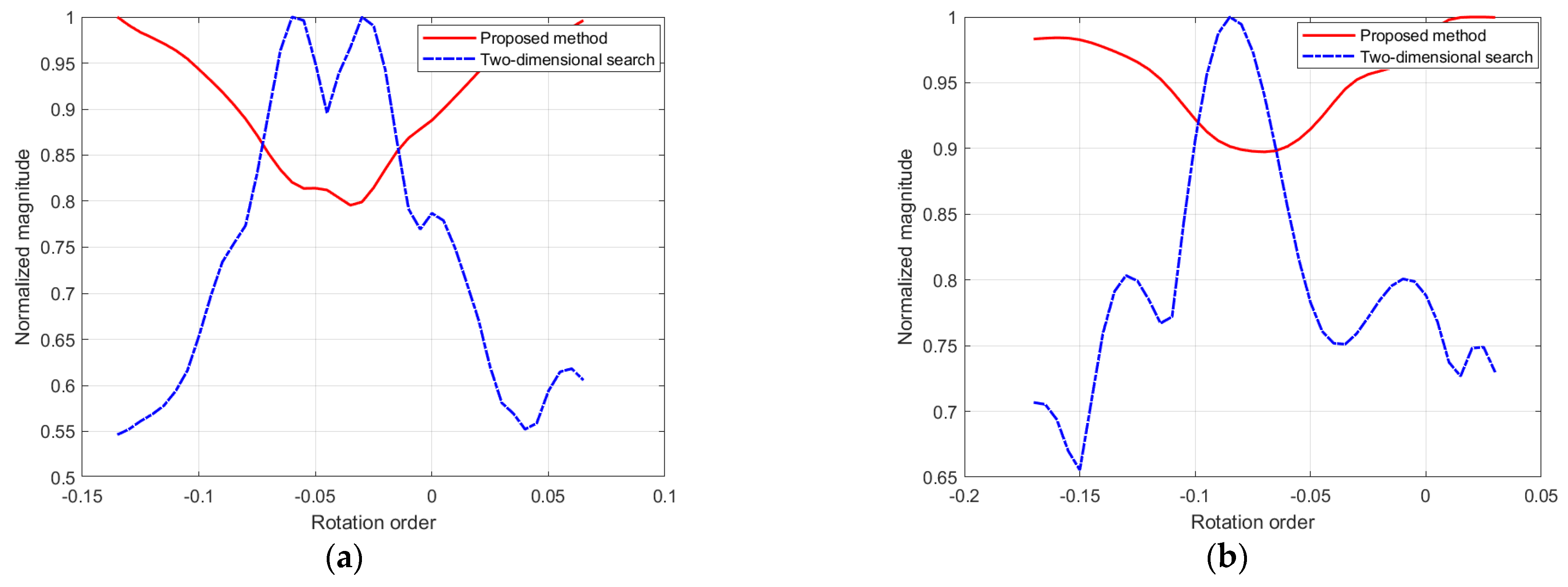
Figure 17.
The relationship between the peak and entropy of the signal after FrFT and the rotation order. (a) Ship1. (b) Ship2.
Figure 17.
The relationship between the peak and entropy of the signal after FrFT and the rotation order. (a) Ship1. (b) Ship2.
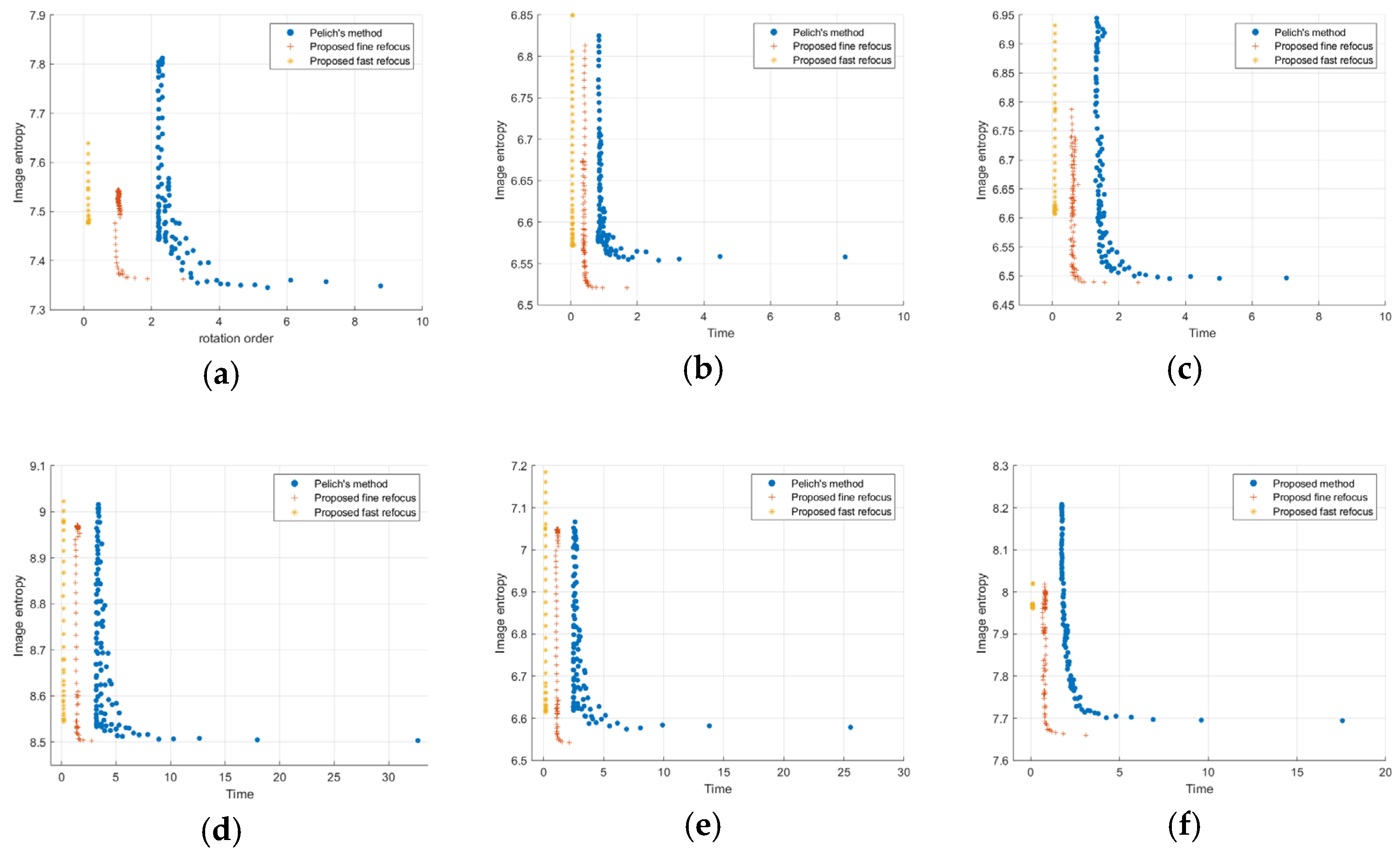
Figure 18.
Relationship between the image entropy and the processing time. (a) Ship1. (b) Ship2.
Figure 18.
Relationship between the image entropy and the processing time. (a) Ship1. (b) Ship2.
Figure 19.
The refocused image of ship1 by different methods. (a) Origin image. (b) PGA. (c) FMEPC. (d) Pelich’s method. (e) Proposed fast refocusing approach. (f) Proposed fine refocusing approach.
Figure 19.
The refocused image of ship1 by different methods. (a) Origin image. (b) PGA. (c) FMEPC. (d) Pelich’s method. (e) Proposed fast refocusing approach. (f) Proposed fine refocusing approach.
Figure 20.
The refocused image of ship2 by different methods. (a) Origin image. (b) PGA. (c) FMEPC. (d) Pelich’s method. (e) Proposed fast refocusing approach. (f) Proposed fine refocusing approach.
Figure 20.
The refocused image of ship2 by different methods. (a) Origin image. (b) PGA. (c) FMEPC. (d) Pelich’s method. (e) Proposed fast refocusing approach. (f) Proposed fine refocusing approach.
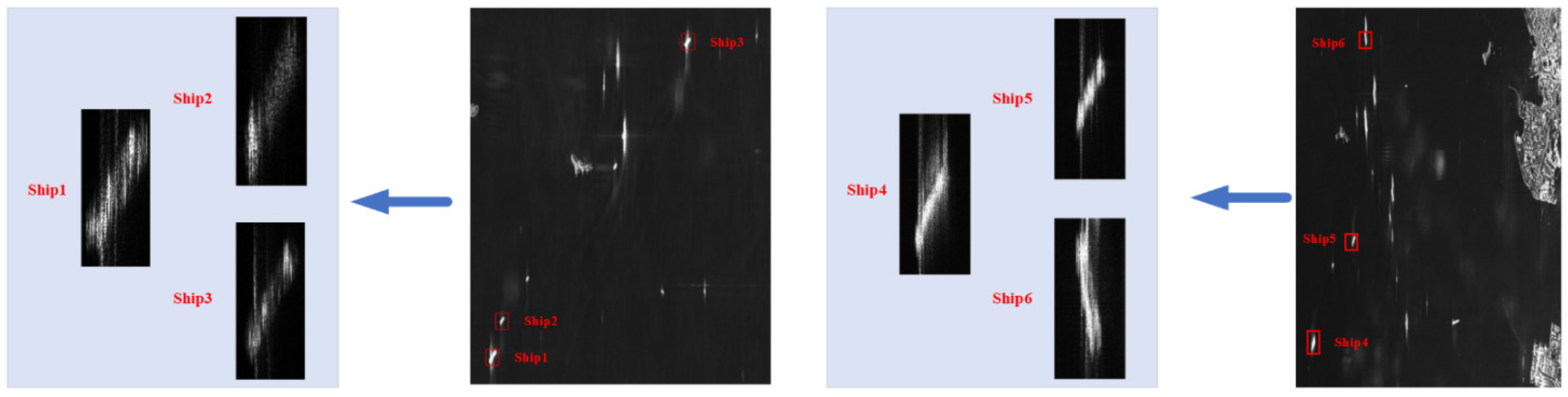
Figure 21.
Six moving ships in Gaofen-3 SL mode.
Figure 21.
Six moving ships in Gaofen-3 SL mode.
Figure 22.
Time–frequency distribution of each ship’s best azimuth line after STFT. (a) Ship1. (b) Ship2. (c) Ship3. (d) Ship4. (e) Ship5. (f) Ship6.
Figure 22.
Time–frequency distribution of each ship’s best azimuth line after STFT. (a) Ship1. (b) Ship2. (c) Ship3. (d) Ship4. (e) Ship5. (f) Ship6.
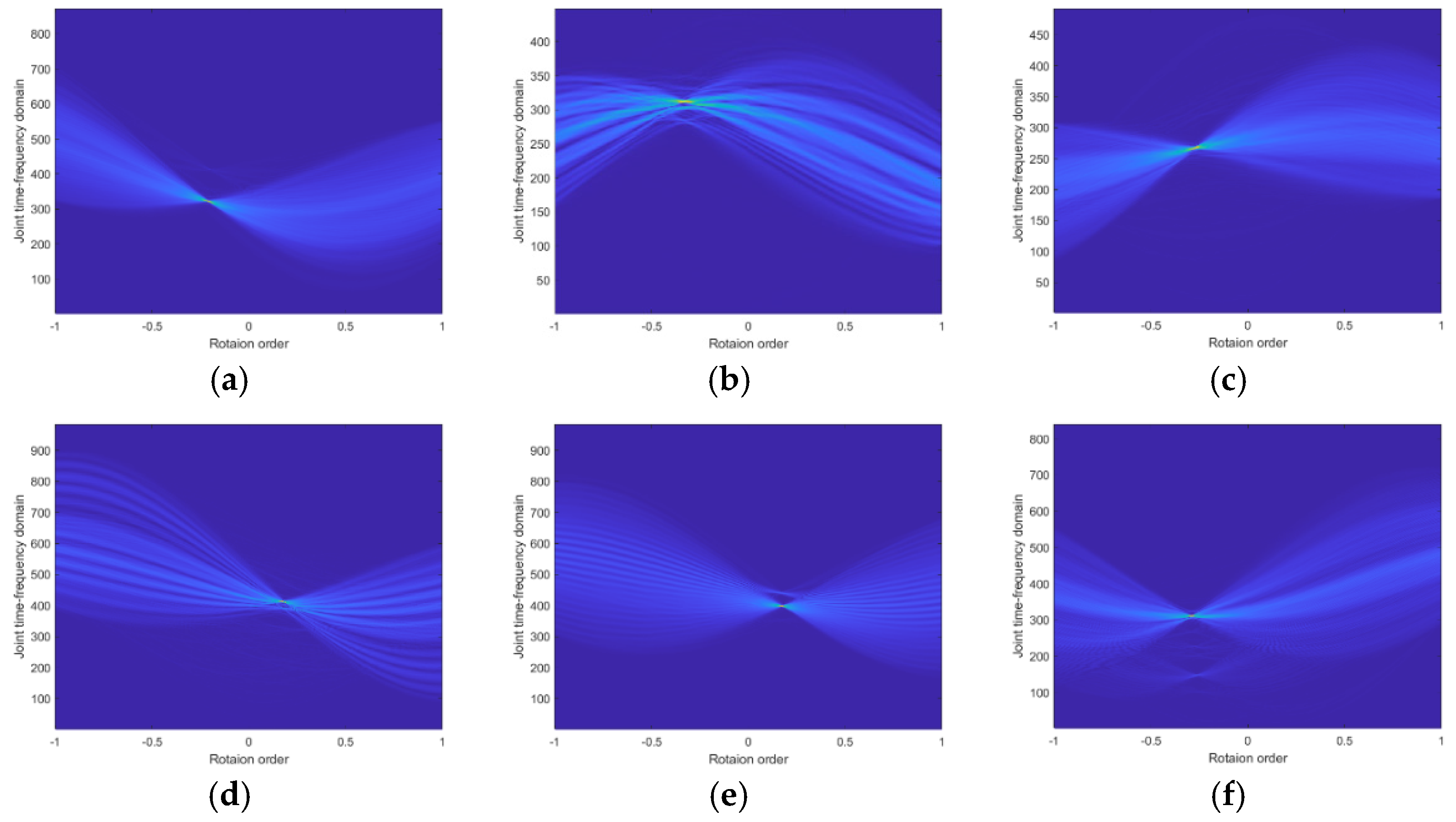
Figure 23.
Distribution of each ship’s best azimuth line in the FrFT domain. (a) Ship1. (b) Ship2. (c) Ship3. (d) Ship4. (e) Ship5. (f) Ship6.
Figure 23.
Distribution of each ship’s best azimuth line in the FrFT domain. (a) Ship1. (b) Ship2. (c) Ship3. (d) Ship4. (e) Ship5. (f) Ship6.
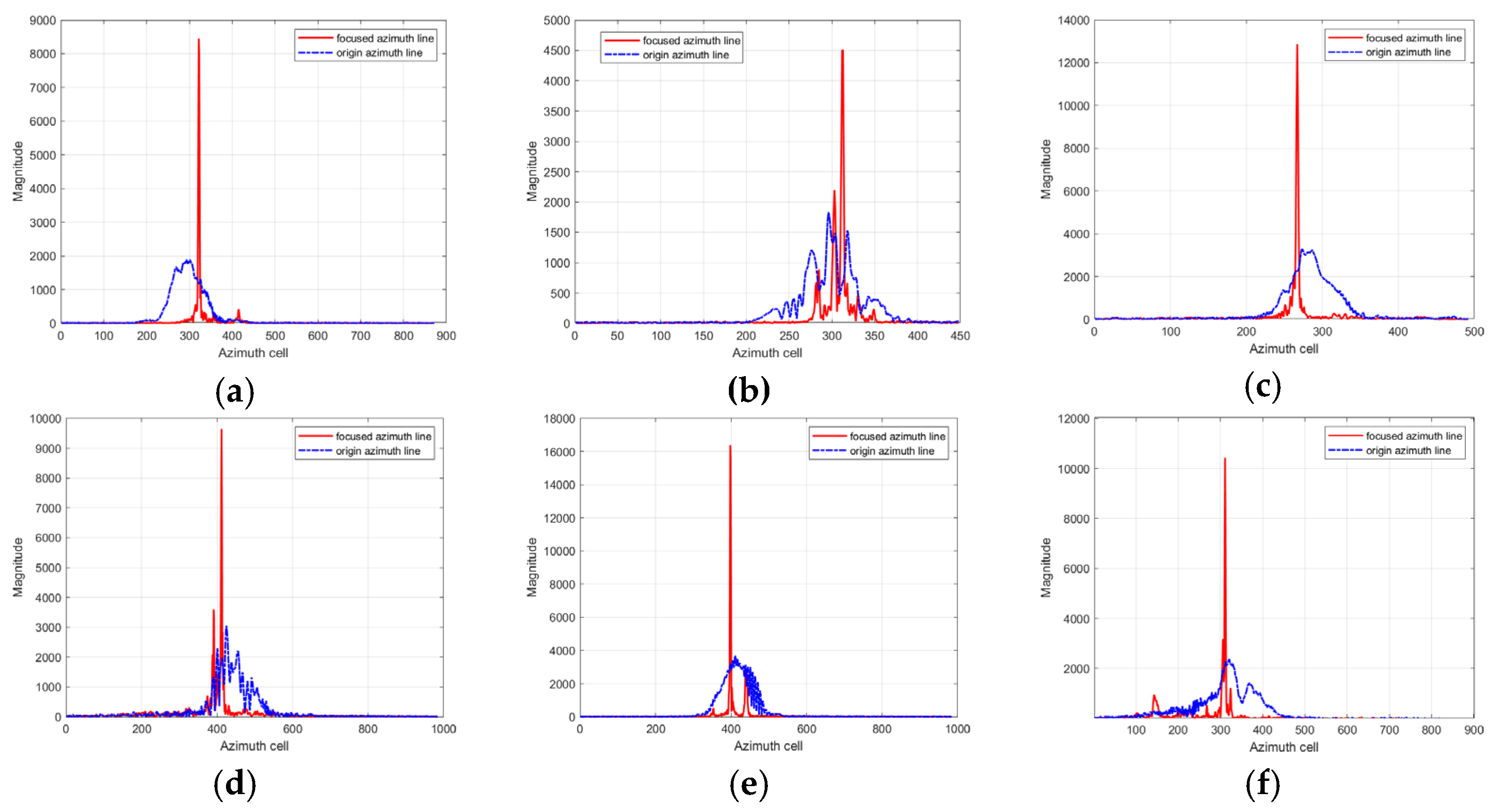
Figure 24.
The result of each best azimuth line after FrFT at the optimal rotation order. (a) Ship1. (b) Ship2. (c) Ship3. (d) Ship4. (e) Ship5. (f) Ship6.
Figure 24.
The result of each best azimuth line after FrFT at the optimal rotation order. (a) Ship1. (b) Ship2. (c) Ship3. (d) Ship4. (e) Ship5. (f) Ship6.
Figure 25.
Distribution of the optimal rotation order for each range cell. (a) Ship1. (b) Ship2. (c) Ship3. (d) Ship4. (e) Ship5. (f) Ship6.
Figure 25.
Distribution of the optimal rotation order for each range cell. (a) Ship1. (b) Ship2. (c) Ship3. (d) Ship4. (e) Ship5. (f) Ship6.
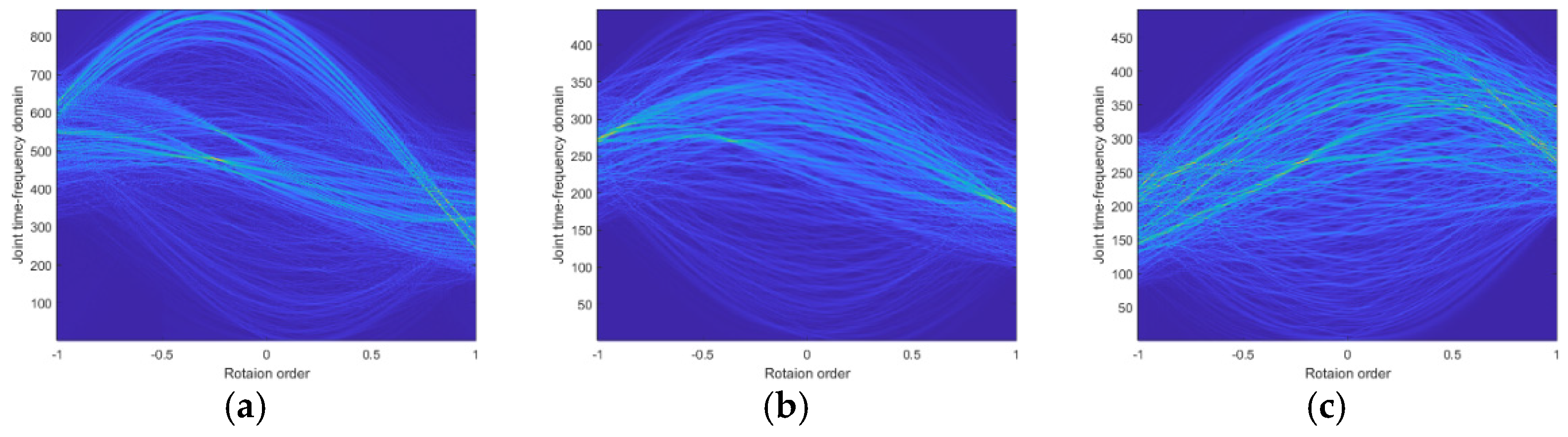
Figure 26.
Distributions of non-dominant scattering point range cells in FrFT domain. (a) Ship1. (b) Ship2. (c) Ship3.
Figure 26.
Distributions of non-dominant scattering point range cells in FrFT domain. (a) Ship1. (b) Ship2. (c) Ship3.
Figure 27.
Image entropy at different range cell’s optimal rotation order. (a) Ship1. (b) Ship2. (c) Ship3. (d) Ship4. (e) Ship5. (f) Ship6.
Figure 27.
Image entropy at different range cell’s optimal rotation order. (a) Ship1. (b) Ship2. (c) Ship3. (d) Ship4. (e) Ship5. (f) Ship6.
Figure 28.
The optimal rotation order of each range cell on the ship obtained by different methods. (a) Ship1. (b) Ship2. (c) Ship3. (d) Ship4. (e) Ship5. (f) Ship6.
Figure 28.
The optimal rotation order of each range cell on the ship obtained by different methods. (a) Ship1. (b) Ship2. (c) Ship3. (d) Ship4. (e) Ship5. (f) Ship6.
Figure 29.
Relationship between the entropy and the processing time. (a) Ship1. (b) Ship2. (c) Ship3. (d) Ship4. (e) Ship5. (f) Ship6.
Figure 29.
Relationship between the entropy and the processing time. (a) Ship1. (b) Ship2. (c) Ship3. (d) Ship4. (e) Ship5. (f) Ship6.
Figure 30.
The refocused image of Ship1–Ship6 obtained by different methods which are shown from the first row to the sixth row, respectively. (a) Origin image. (b) Refocused by PGA. (c) Refocused by FMEPC. (d) Refocused by Pelich’s method using FrFT. (e) Refocused by the proposed fast refocusing approach. (f) Refocused by the proposed fine refocusing approach.
Figure 30.
The refocused image of Ship1–Ship6 obtained by different methods which are shown from the first row to the sixth row, respectively. (a) Origin image. (b) Refocused by PGA. (c) Refocused by FMEPC. (d) Refocused by Pelich’s method using FrFT. (e) Refocused by the proposed fast refocusing approach. (f) Refocused by the proposed fine refocusing approach.
Table 1.
The SAR system parameters of the simulation experiment.
Table 1.
The SAR system parameters of the simulation experiment.
| Parameter | Value |
|---|
| Carrier Frequency | 3 GHZ |
| Pulse Repetition Frequency | 188 HZ |
| Band Width | 150 MHZ |
| Platform Height | 3000 m |
| Antenna Length | 2 m |
| Platform Velocity | 150 m/s |
| Pulse Width | 1.5 μs |
Table 2.
The numbers of FrFT required for different algorithms.
Table 2.
The numbers of FrFT required for different algorithms.
| | Proposed Algorithm | 2D Peak Search Method |
|---|
| Uniform motion in azimuth | 12 | 60 |
| Acceleration in range | 15 | 60 |
Table 3.
The SAR system parameters of the Gaofen-3 UFS mode.
Table 3.
The SAR system parameters of the Gaofen-3 UFS mode.
| Parameter | Value |
|---|
| Carrier frequency (GHZ) | 5.4 |
| Platform velocity (m/s) | 7568 |
| Band width (MHZ) | 80 |
| Pulse Width (μs) | 55 |
| Pulse repetition frequency (Hz) | 2179 |
Table 4.
The image entropy obtained by different methods.
Table 4.
The image entropy obtained by different methods.
| | Original | PGA | FMEPC | Pelich’s Method | Fast Refocusing | Fine Refocusing |
|---|
| Ship1 | 7.91 | 7.61 | 7.61 | 7.6 | 7.66 | 7.54 |
| Ship2 | 5.88 | 5.09 | 5.08 | 5.05 | 5.1 | 5 |
Table 5.
The processing time of different methods.
Table 5.
The processing time of different methods.
| | PGA | FMEPC | Pelich’s Method | Fast Refocusing | Fine Refocusing |
|---|
| Ship1 | 0.53 s | 3.14 s | 4.06 s | 0.085 s | 0.43 s |
| Ship2 | 0.48 s | 1.16 s | 1.2 s | 0.03 s | 0.15 s |
Table 6.
The SAR system parameters of Gaofen-3 SL mode.
Table 6.
The SAR system parameters of Gaofen-3 SL mode.
| Parameter | Value |
|---|
| Carrier frequency (GHZ) | 5.4 |
| Platform velocity (m/s) | 7567 |
| Band width (MHZ) | 240 |
| Pulse Width (μs) | 45 |
| Pulse repetition frequency (Hz) | 3738 |
Table 7.
The image entropy of different algorithms.
Table 7.
The image entropy of different algorithms.
| Sub-Image | Ship1 | Ship2 | Ship3 | Ship4 | Ship5 | Ship6 | Mean |
|---|
| Original Image | 9.16 | 7.92 | 8.35 | 9.98 | 8.54 | 9.55 | 8.92 |
| PGA | 7.51 | 6.72 | 6.7 | 8.58 | 7.15 | 8.1 | 7.46 |
| FMEPC | 7.5 | 6.64 | 6.66 | 8.57 | 7.12 | 8.07 | 7.43 |
| Pelich’s method using FrFT | 7.34 | 6.56 | 6.5 | 8.51 | 6.58 | 7.71 | 7.20 |
| Proposed fast refocusing approach | 7.46 | 6.56 | 6.62 | 8.56 | 6.62 | 7.96 | 7.30 |
| Proposedfine refocusing approach | 7.35 | 6.51 | 6.49 | 8.52 | 6.57 | 7.67 | 7.18 |
Table 8.
The processing time of different algorithms (in seconds).
Table 8.
The processing time of different algorithms (in seconds).
| Sub-Image | Ship1 | Ship2 | Ship3 | Ship4 | Ship5 | Ship6 | Mean |
|---|
| PGA | 2.05 | 0.75 | 0.67 | 1.62 | 3.01 | 2.25 | 1.73 |
| FMEPC | 4.46 | 1.23 | 1.49 | 16 | 10.18 | 11.65 | 7.50 |
| Pelich’s method using FrFT | 8.7 | 2.6 | 3.78 | 9.08 | 7.05 | 4.85 | 6.01 |
| Proposed fast refocusing approach | 0.17 | 0.06 | 0.11 | 0.2 | 0.15 | 0.1 | 0.13 |
| Proposedfine refocusing approach | 0.9 | 0.39 | 0.48 | 0.85 | 0.63 | 0.57 | 0.64 |