1. Introduction
The rising levels of
in the atmosphere and its effects on the environment have drawn public attention and have been addressed as a worldwide problem in recent decades. Forest areas play a significant role in measuring the global carbon cycle and climate change in this case [
1]. Forests are the most structurally complex and functionally rich terrestrial ecosystems and among the regions with the richest natural resources around the world [
2]. Sustainable forest management depends extensively on the quantitative monitoring of stand parameters, such as growing stem volume (GSV), BA, AGB, S, forest height, etc. [
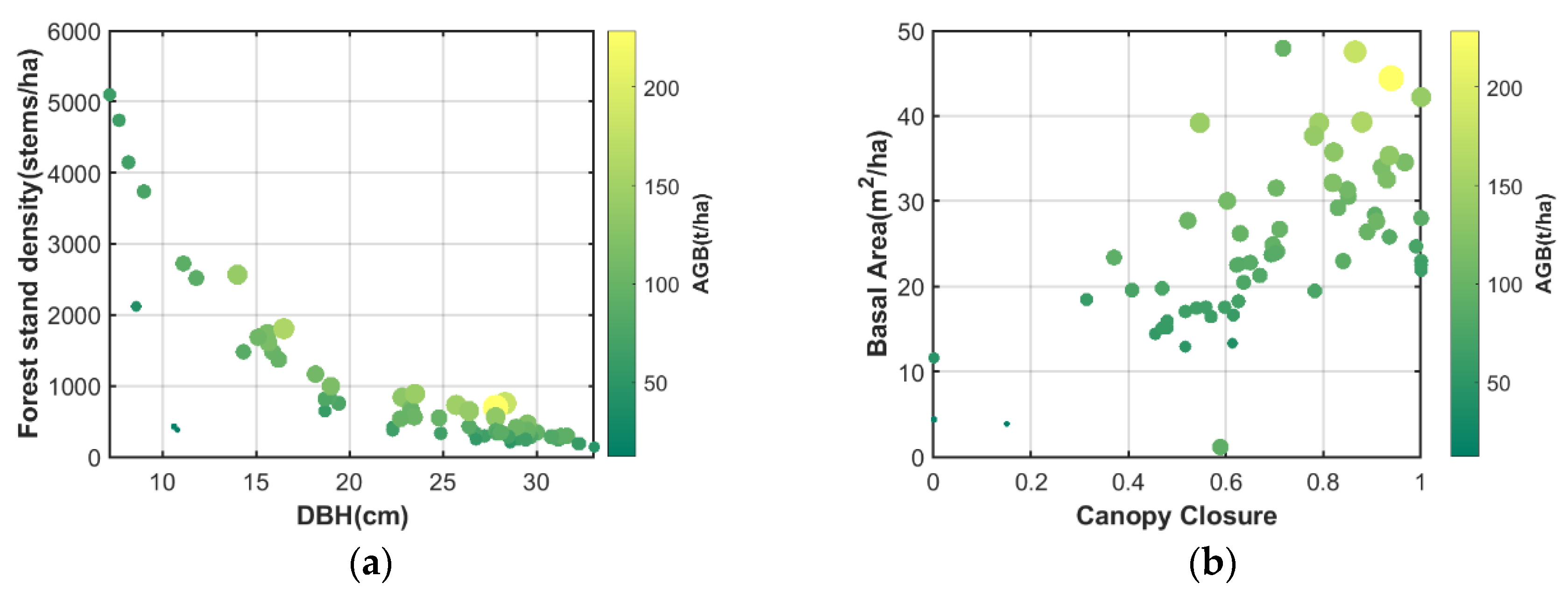
3]. Canopy closure refers to the ratio of the total projected area (crown width) of the tree crowns in the forest under direct sunlight to the total area of the forest (stand), visually reflecting the denseness of the forest canopy and the planting density of single trees, and laterally reflecting the efficiency of photosynthesis and measuring the growth of the forest [
4,
5]. Forest stand density is the main factor affecting the structure and function of the forest ecosystem and is an important indicator in forest resources surveys, with a very important impact on the growth and development of forest trees [
6]. The increase in the basal area implies an increase in forest stand density and an increase in the number of elements (branches and leaves) that scatter and absorb electromagnetic radiation [
7]. Aboveground biomass is the mass of organic matter growing above the ground per unit area and is one of the key parameters for assessing aboveground carbon stocks and carbon emissions [
8,
9]. The accurate estimation of forest structure parameters on a global scale contributes to a better understanding of ecosystems and carbon cycling processes [
10]. Boreal coniferous forests are the largest biomes in the world, with abundant carbon accumulation capacity, and so the estimation of their forest parameters is particularly noteworthy [
8].
Remote sensing has the advantages of long time series, active and passive sensors, repeated earth observations, acceptable accuracy, and relatively low cost. It has a wide range of applications for obtaining information on biophysical variables and forest structure parameters over large areas [
11]. In terms of data archiving, availability, spatial coverage, resolution, and data processing load, optical images with high spatial and temporal resolution are the best option for the extensive dynamic monitoring of forest parameters [
12]. Over the years, optical sensors have evolved into a major source of information to support forest decision support tools that utilize the natural radiation of the sun to capture canopy information and associated canopy shading, providing a two-dimensional view of forest and other surface features. Aggregated spectral features (reflectance or vegetation indices) have the advantages of global coverage, repeatability, and cost-effectiveness and contain vegetation information that characterizes the distribution of forest structure [
13,
14,
15,
16]. As far as optical sensors are concerned, Landsat is one of the most widely used datasets because it provides freely acquired images with high temporal coverage and medium spatial resolution [
17]. Landsat has continuously covered the land surface for more than 50 years since the first satellite was launched in 1972 and has been used effectively for the regular monitoring of forest and vegetation dynamics [
18]. The AGB and Landsat 8 spectral variables were found to be linearly correlated in the Gizachew study, which came to the conclusion that this approach is appropriate for the baseline monitoring as well as reporting of biomass in low-biomass, low-density stands in REDD+ programs [
19]. The Sentinel-2 series of satellites launched through the EU Copernicus program offer new opportunities for the large-scale enhancement of forest monitoring in tropical countries. Compared to Landsat, Sentinel-2 data provide four additional spectral bands that are highly sensitive to chlorophyll changes and can be effectively used to estimate forest parameters strategically located in red edge regions [
20]. Therefore, Sentinel-2 data can offer the potential for the more cost-effective mapping of forest parameters accurately. Sentinel-2 can obtain more precise information representing vegetation since it has a greater spatial resolution than Landsat. Its six 20 m resolution bands and four 10 m resolution bands can more accurately reflect forest changes [
21]. Sentinel-2 and Landsat data are now the primary sensors used to calculate forest characteristics [
22].
The optical sensor data mainly respond to the physicochemical properties of vegetation, and the vegetation spectral reflectance contains information on the vegetation chlorophyll absorption bands in the visible region (especially in the blue and red regions) and the sustained high reflectance in the near-infrared (NIR) region. Since the visible and NIR spectra only react with green leaves, theoretically only information on the leaves of trees can be obtained, which cannot reflect information on the trunk, and the use of spectral information to estimate forest parameters actually uses the relative growth relationship between trees and leaves for the purpose of indirect estimation [
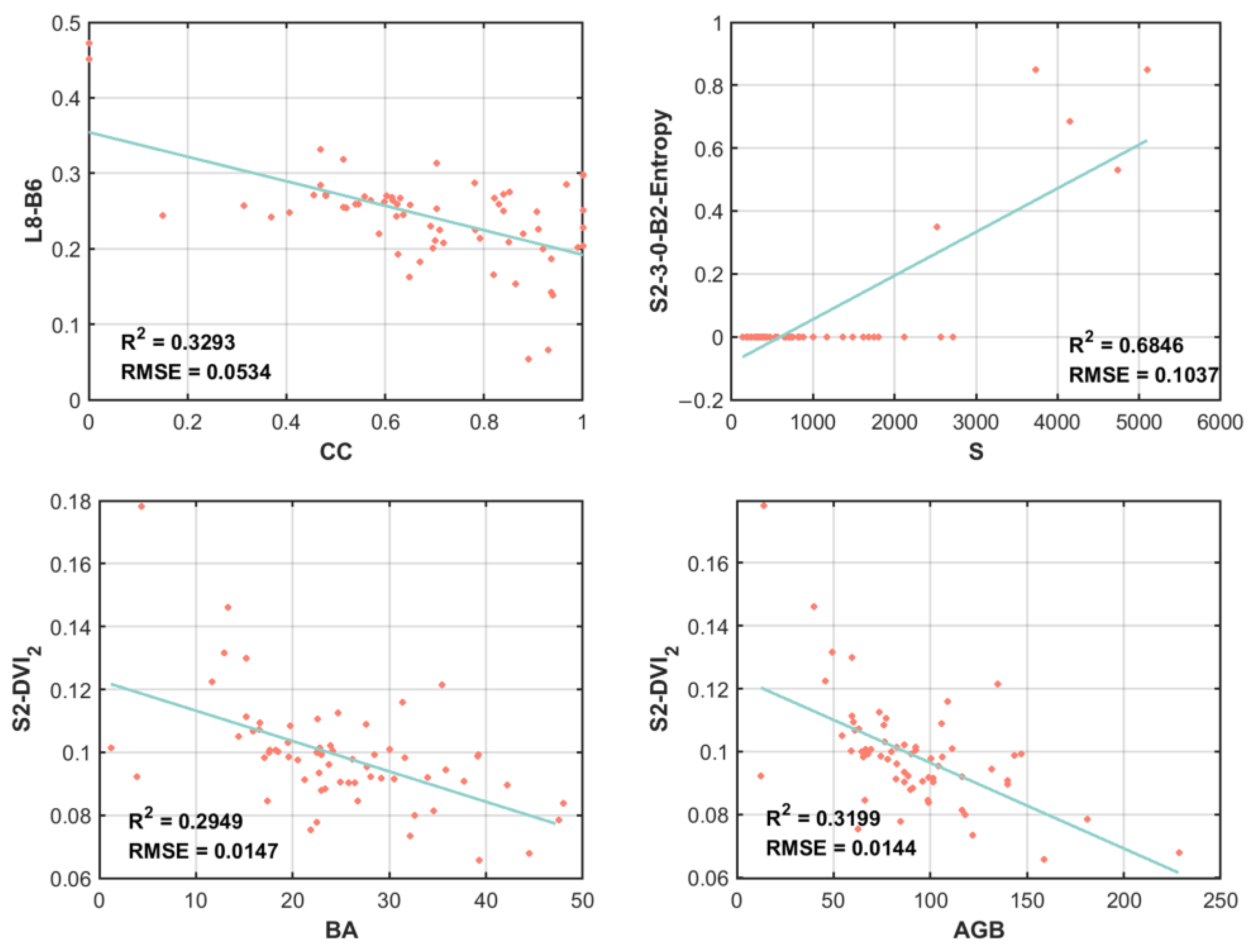
13]. The better accuracy obtained by Jiarui Li for CC estimation using the NIR band can explain 57% of CC [
23]. Chen used Sentinel-2 images to research AGB in bamboo forests in Zhejiang Province, China and reported that the red edge band and NIR band in Sentinel-2 improved the identification of AGB [
24].
Most of the popular vegetation indices are based on the interrelationship between the red and NIR bands, enhancing the spectral contribution of green vegetation while minimizing the contribution of other factors, such as atmospheric effects, solar and sensor perspectives, and soil factors [
25]. The vegetation index technique, which has the advantage of maintaining detailed spectral information and image clarity, is a more accurate element of vegetation cover detection, obtained by means of arithmetic operations on the spectral information of the radiation reflected by vegetation at different wavelengths. These indicators are employed to assess the biophysical characteristics of the canopy, including its leaf area index, biomass, etc. [
26]. Delpasand found that the infrared percent vegetation index (IPVI) was the best predictor of forest stand density [
27]. Gunlu found that the enhanced vegetation index (EVI) could explain 60% of the biomass and the vegetation index could better estimate AGB compared to individual band reflectance [
28]. Adel Nouri used Landsat 8 to extract NDVI linear estimates of canopy cover, S, and BA, with the
reaching 0.83, 0.86, and 0.82, respectively, proving that linear regression is a feasible solution for estimating forest stand parameters [
29]. Lu Dengsheng compared different vegetation indices in the Brazilian region and found that vegetation indices that incorporated NIR improved the correlation with AGB in a relatively simple stand structure [
30]. Other studies have demonstrated that the addition of the red edge band improves correlation and can be used to determine biophysical parameters and other forest attributes such as canopy cover, volume, and BA [
31,
32,
33]. Modified soil adjusted vegetation index (MSAVI) was shown to have a strong correlation with biomass, with an
of 0.69 [
34]. However, previous studies have shown saturation in the vegetation index results in areas with moderate or high levels of canopy closure [
35]. Gitelson adjusted the relative contribution of NIR and red reflectance to the vegetation index by adding a weighting factor to the NIR reflectance in the NDVI index to mitigate saturation [
36]. Several studies have shown that, for some vegetation features, available spectral indices do not always obtain the most accurate results, neglecting important information contained in other bands and leading to the embellishment of mainstream spectral indices [
37]. Dimitris Stratoulias used the spectral ratio of band 8 and band 2 of Sentinel-2 to obtain an
of 0.70, while the best performing popular spectral index, EVI, achieved an
of 0.65. The study found that a full wave combination survey of small-scale studies, which can make use of current satellite systems to obtain amplified information and avoid assumptions about environmental, structural, and ecosystem characteristics for the selection of the vegetation index, can provide stronger correlations and more accurate results than the blind application of popular spectral indices [
38].
In order to characterize complex forest structures and improve the biophysical qualities of fine vegetation, it is possible to use the relationship between image texture metrics and forest property measures. This relationship enables the retrieval of data on forest parameters based on the distribution of reflectance along neighboring pixels. Texture may help to derive variables that do not reach saturation and allow the identification of different aspects of forest structure, including forest stand density, age, and leaf area index [
35]. The study of Fugen Jiang showed that the textural features of Sentinel-2 red edge bands can significantly improve the accuracy of GSV estimation [
21]. Ibrahim Ozdemir performed the linear estimation of BA and volume using entropy in the blue band, with the
reaching 0.54 and 0.42, which is the best predictor and explains a significant proportion of BA variation [
39]. Kayitakire used texture features to predict S and BA with
of 0.82 and 0.35, respectively, proving that texture features, window size, and offsets are the most important parameters [
40]. However, studies have shown that raw textures cannot eliminate the effect of terrain on reflected radiation and the errors associated with sensor angle and sunlight radiation. Latifur Rahman Sarker demonstrated that using texture parameters with high resolution optical data can significantly improve biomass estimation performance, while using the ratio of texture parameters can further improve biomass estimation performance as it combines the advantages of texture and ratio [
41]. Sizwe Thamsanqa Hlatshwayo illustrated that the combination of two textures (
= 0.85) provided better AGB detection results compared to a single texture (
= 0.64). Therefore, opening new avenues for forest parameter estimation by introducing texture combinations using multi-band texture ratio has been shown to be closely related to biomass, delaying the saturation point to a large extent [
42]. The use of texture band combinations has been highly successful in estimating forest AGB, especially when compared with original texture bands and vegetation indices [
35]. However, existing studies do not consider the information contained in different texture features and the response relationships between them, ignore their relative contributions to the texture indices, and do not make better use of the performance of texture and ratio techniques.
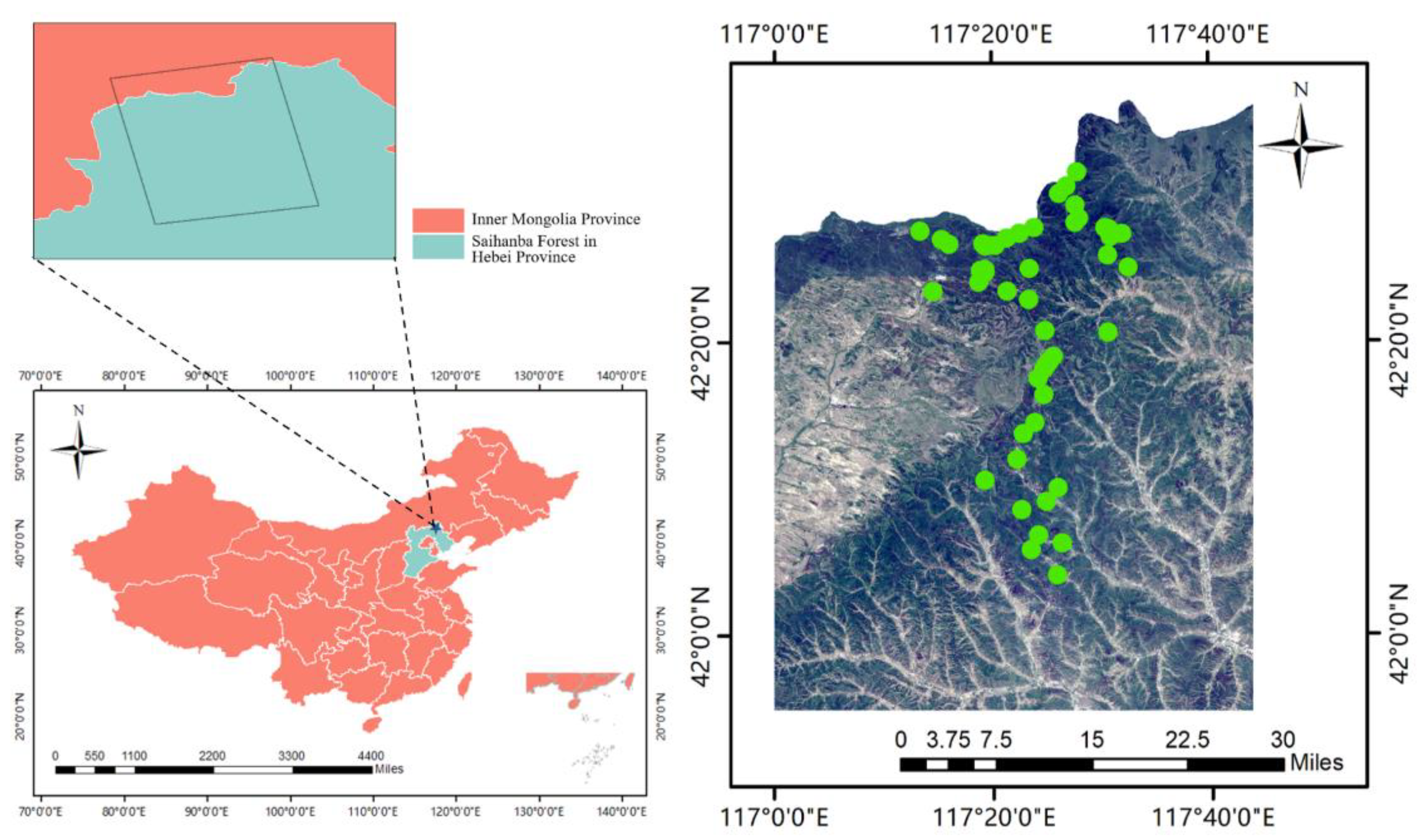
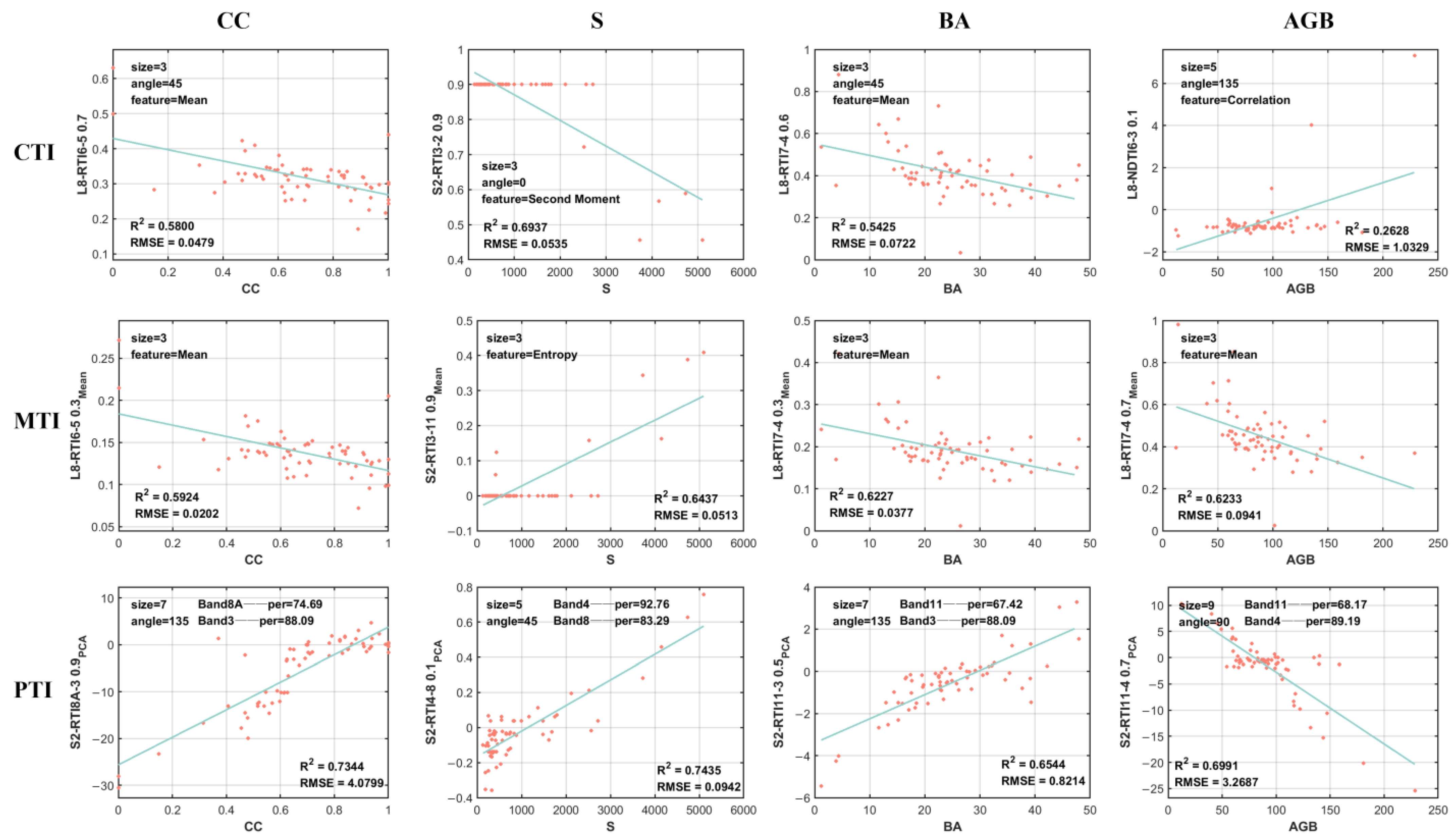
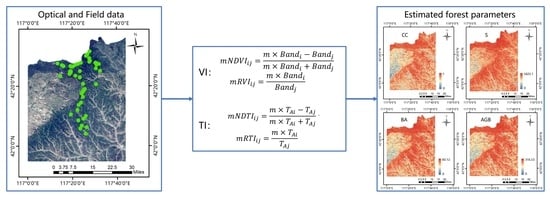
In this context, Landsat 8 and Sentinel-2A images were used to estimate the CC, S, BA, and AGB of the Saihanba forest farm in Hebei Province. This study extends the linear relationship between forest parameters and vegetation index and texture features, fully exploits the advantage of using the response between different bands and texture features and alleviates the saturation limitation of existing studies. The main research activities of this paper are as follows:
- (1)
We analyze the correlation and response relationship of each sensor’s raw bands, popular vegetation indices, raw band textures, the average value of texture features in each direction, and textures extracted by means of principal component analysis of the raw bands with forest parameters.
- (2)
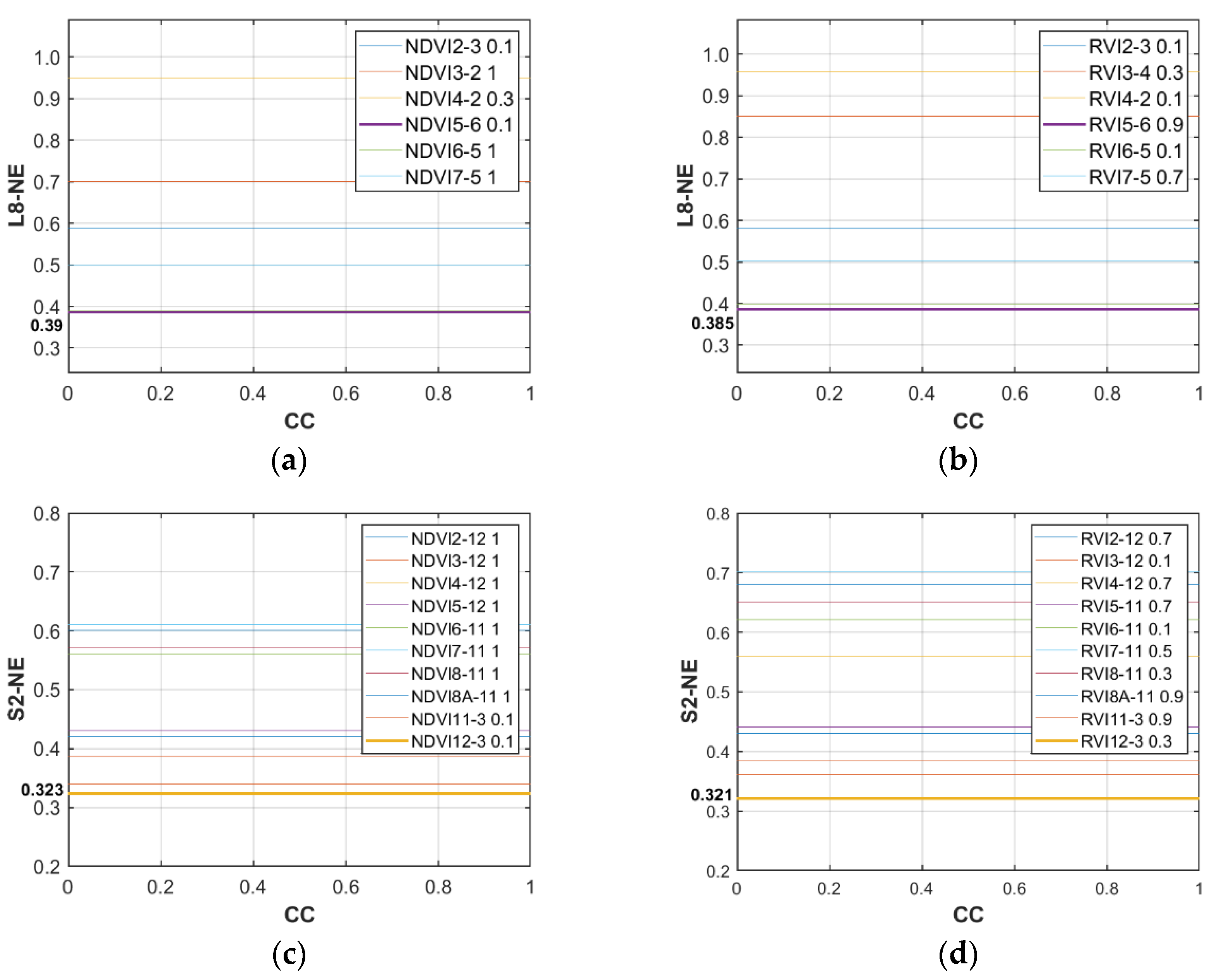
In order to more accurately characterize the biophysical characteristics of vegetation, an extensive band combination normalization and ratio vegetation indices are established, and the sensitivity of vegetation index band weight to variations in vegetation parameters was analyzed by relative sensitivity and noise equivalent.
- (3)
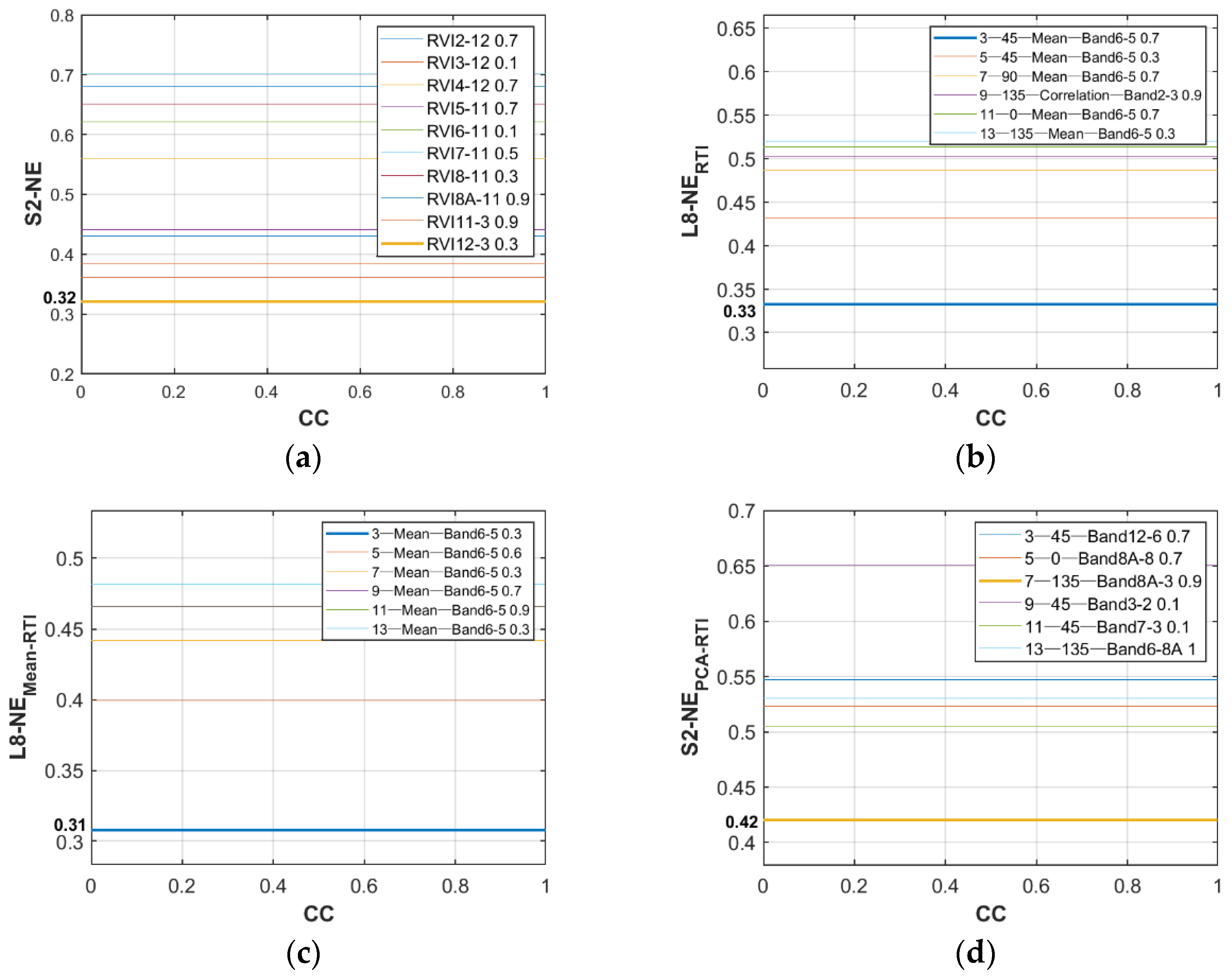
The normalized and ratio texture indices containing weight are established by using the original texture features, the average value of features in each direction, and the features after principal component analysis, respectively, analyzing the response characteristics between windows, directions, and different texture features, taking advantage of the information of different vegetation parameters contained in different textures, and analyzing the influence of texture features with different windows and different directions on vegetation parameters by combining the noise equivalent to establish the optimal texture indices.
This paper is organized as follows:
Section 2 presents some basic information about the sample points and the measured data, the processing of the optical data, and the extraction of variables. The theory of the proposed method is explained in
Section 3.
Section 4 describes the results and
Section 5 explores the effects of noise equivalent and band saturation on forest parameters and provides a detailed interpretation and analysis of the results.
Section 6 is the conclusion.
6. Conclusions
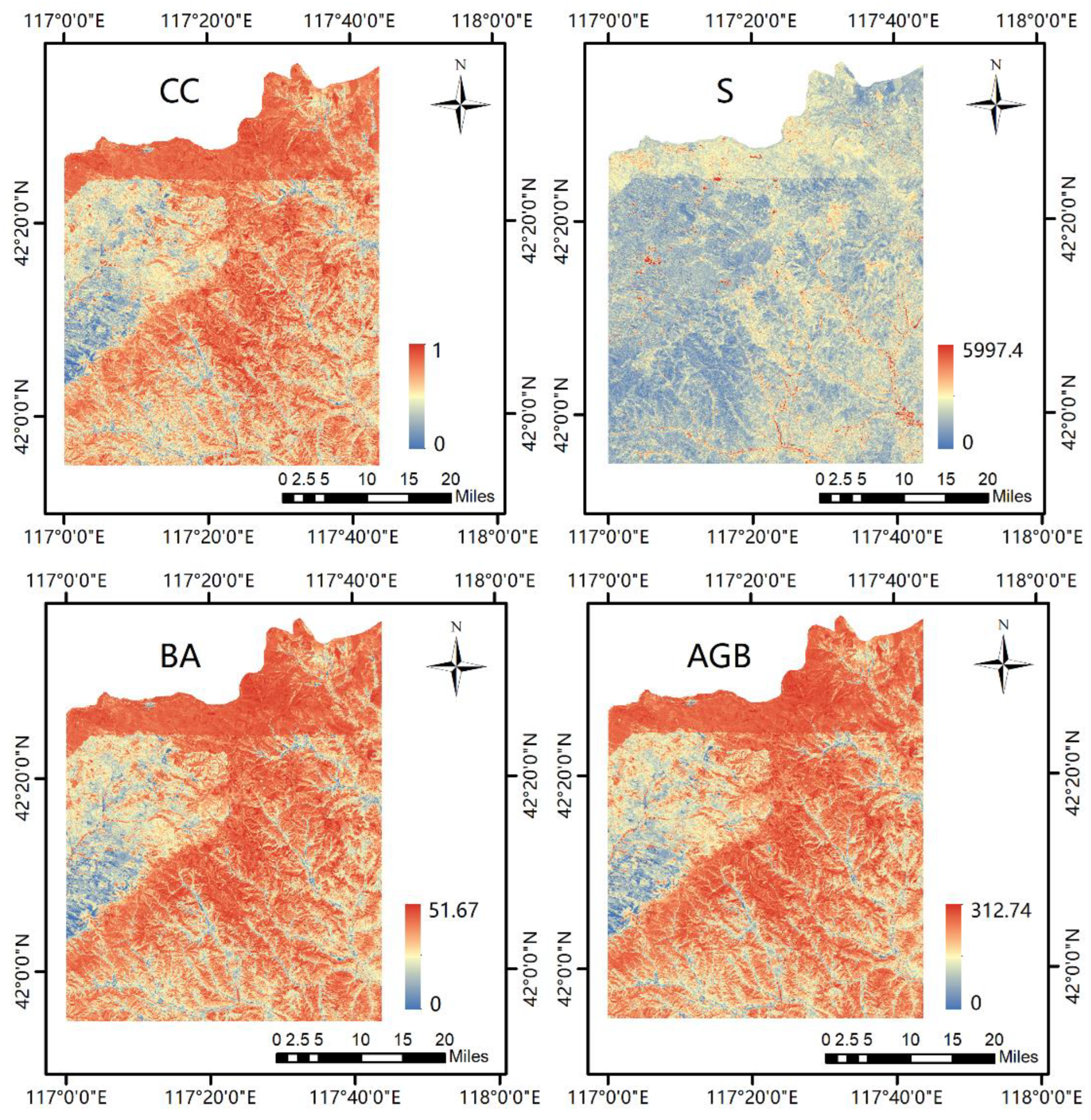
In this study, the response characteristics between different bands and textures are used and combined with normalization and ratio techniques to effectively extend the linear relationship between variables and forest parameters, avoiding to some extent the saturation problem arising between optical sensors and forest parameters. The newly developed indices and forest parameters produced better results when compared to spectral bands, popular vegetation indices, and textures. The results show that the form of the vegetation index has no effect on the response information between spectral bands and vegetation characteristics, but that it does have an impact on the weight. The vegetation ratio index and texture ratio index developed using S2A produced the best results. The ratio technique better eliminated sensor and terrain effects, and adding weight to the ratio index based on band and texture sensitivity can effectively improve the response differences in the bands and textures, enhancing the sensitivity of the index. However, different bands and texture features contain different information, which will affect the magnitude of the weight. In this paper, by combining the principal component analysis with the texture ratio technique and adding appropriate weight according to the sensitivity between different texture features, more valid information can be retained while reducing the dimensionality of the data. The results show that variables containing more information amount of texture features have better estimation performance, and using a single texture feature does not reflect the variation of each forest parameter well. In addition, the selection of different windows and texture features can affect the selection direction differently. The results demonstrate that CC, BA, and AGB are less affected by direction, and removing the differences in direction can improve the estimation performance of forest parameters, but S is more affected by direction and has the strongest response to the texture features in the direction. S is also associated with the orderliness based texture features, and CC, BA, and AGB are associated with statistically based texture features.
The study area comprises artificial coniferous forests, and the main tree species are Larix principis-rupprechtii Mayr and Pinus sylvestris var. mongholica Litv, so most of the areas have similar spectral characteristics. Because optical canopy reflectance depends on a complex interaction of internal and external factors and most stand features are spatially and temporally dependent, and because the remote sensing data and sample site data in this study are not perfectly matched in time, which may vary significantly in time and space. Therefore, empirical relationships will vary by location, time, and species type and are not directly applicable to large-scale operational use. In addition, this study uses only optical data, which can only obtain surface features of forest structure, and it is expected that combining SAR or LiDAR data to combine vertical structure information can obtain better results.